CS专业课学习笔记
与えられた条件の下で何らかの関数を最小または最大にする問題
変数, 条件(等式, 不等式で記述される))が有限個数学的に記述された最適化問題
m i n f ( x ) 条件 g i ( x ) = 0 ( i = 1 , . . . , m ) h j ( x ) ≤ 0 ( i = 1 , . . . , l ) \begin{matrix}
min&\ f(\mathbf{x})
\\
\text{条件}&g_i(\mathbf{x}) &=& 0 (i = 1,...,m)
\\
&h_j(\mathbf{x}) &\leq& 0 (i = 1,...,l)
\end{matrix}
m i n 条件 f ( x ) g i ( x ) h j ( x ) = ≤ 0 ( i = 1 , . . . , m ) 0 ( i = 1 , . . . , l )
f: R n \mathbb{R}^{n} R n R \mathbb{R} R g i : R n g_i: \mathbb{R}^{n} g i : R n R ( i = 1 , . . . , m ) \mathbb{R} (i = 1,...,m) R ( i = 1 , . . . , m ) h j : R n h_j: \mathbb{R}^{n} h j : R n R ( j = 1 , . . . , l ) \mathbb{R} (j = 1,...,l) R ( j = 1 , . . . , l )
例
m i n x 1 2 + 4 x 2 2 − 3 x 1 x 2 条件 x 1 + x 2 − 5 = 0 ( x 1 − 1 ) 2 + ( x 2 − 2 ) 2 − 5 ≤ 0 − x 1 ≤ 0 \begin{matrix}
min&\ x_1^2 + 4x_2^2 - 3x_1x_2
\\
\text{条件}& x_1 + x_2 - 5 &=& 0
\\
& (x_1 - 1)^2 + (x_2 - 2)^2 - 5 &\leq& 0
\\
& -x_1 &\leq& 0
\end{matrix}
m i n 条件 x 1 2 + 4 x 2 2 − 3 x 1 x 2 x 1 + x 2 − 5 ( x 1 − 1 ) 2 + ( x 2 − 2 ) 2 − 5 − x 1 = ≤ ≤ 0 0 0
(n = 2, m = 1, l = 2)
g = [ g 1 ( x ) ⋮ g m ( x ) ] h = [ h 1 ( x ) ⋮ h l ( x ) ] m i n f ( x ) 条件 g i ( x ) = 0 h j ( x ) ≤ 0 \mathbf{g}=\begin{bmatrix}
g_1(\mathbf{x})
\\
\vdots
\\
g_m(\mathbf{x})
\end{bmatrix}
\qquad
\mathbf{h}=\begin{bmatrix}
h_1(\mathbf{x})
\\
\vdots
\\
h_l(\mathbf{x})
\end{bmatrix}
\qquad
\begin{matrix}
min&\ f(\mathbf{x})
\\
\text{条件}&g_i(\mathbf{x}) = 0
\\
&h_j(\mathbf{x}) \leq 0
\end{matrix}
g = ⎣ ⎢ ⎢ ⎡ g 1 ( x ) ⋮ g m ( x ) ⎦ ⎥ ⎥ ⎤ h = ⎣ ⎢ ⎢ ⎡ h 1 ( x ) ⋮ h l ( x ) ⎦ ⎥ ⎥ ⎤ m i n 条件 f ( x ) g i ( x ) = 0 h j ( x ) ≤ 0
f ( x ) : 線形関数 g i ( x ) , h j ( x ) : 1 次関数 f(\mathbf{x}): \text{線形関数}
\qquad
g_i(\mathbf{x}), h_j(\mathbf{x}): 1\text{次関数}
f ( x ) : 線形関数 g i ( x ) , h j ( x ) : 1 次関数
例
m i n x 1 − 3 x 2 条件 x 1 + x 2 = 5 ↔ g 1 ( x ) = x 1 + x 2 − 5 x 1 − x 2 ≥ − 1 ↔ h 1 ( x ) = − x 1 + x 2 − 1 x 1 , x 2 ≥ 0 ↔ h 2 ( x ) = − x 1 , h 3 ( x ) = − x 2 \begin{matrix}
min & \ x_1 - 3x_2
\\
\text{条件} & x_1 + x_2 = 5 \leftrightarrow g_1(x) &=& x_1 + x_2 - 5
\\
& x_1 - x_2 \geq -1 \leftrightarrow h_1(x) &=& -x_1 + x_2 -1 \\
& x_1, x_2 \geq 0 \leftrightarrow h_2(x) &=& -x_1, h_3(x) = -x_2
\end{matrix}
m i n 条件 x 1 − 3 x 2 x 1 + x 2 = 5 ↔ g 1 ( x ) x 1 − x 2 ≥ − 1 ↔ h 1 ( x ) x 1 , x 2 ≥ 0 ↔ h 2 ( x ) = = = x 1 + x 2 − 5 − x 1 + x 2 − 1 − x 1 , h 3 ( x ) = − x 2
例の場合
C = ( 1 − 3 ) x = ( x 1 x 2 ) \mathbf{C} =
\begin{pmatrix}
1
\\
-3
\end{pmatrix}
\qquad
\mathbf{x} =
\begin{pmatrix}
x_1
\\
x_2
\end{pmatrix}
C = ( 1 − 3 ) x = ( x 1 x 2 )
m i n C T x 条件 A x = a B x ≤ b \begin{matrix}
min&\ \mathbf{C}^T\mathbf{x}
\\
\text{条件}&A\mathbf{x} = \mathbf{a}
\\
&B\mathbf{x} \leq \mathbf{b}
\end{matrix}
m i n 条件 C T x A x = a B x ≤ b
f ( x ) = { 1 2 ∑ i = 1 n ∑ j = 1 n q i j x i x j + ∑ i = 1 n c i x i ( q i j = q j i ) 1 2 x T Q x + c T x ( Q T = Q ) f(x) = \begin{cases}
\frac{1}{2}\sum^n_{i=1}\sum^n_{j=1}q_{ij}x_ix_j+\sum^n_{i=1}c_ix_i \quad (q_{ij} = q_{ji})
\\
\frac{1}{2}\mathbf{x}^TQ\mathbf{x} + \mathbf{c}^T\mathbf{x} \quad (Q^T = Q)
\end{cases}
f ( x ) = { 2 1 ∑ i = 1 n ∑ j = 1 n q i j x i x j + ∑ i = 1 n c i x i ( q i j = q j i ) 2 1 x T Q x + c T x ( Q T = Q )
例
f ( x 1 , x 2 ) = x 1 2 + 4 x 2 2 − 3 x 1 x 2 + 5 x 1 − 3 x 2 = 1 2 ( 2 x 1 2 + 8 x 2 2 − 3 x 1 x 2 − 3 x 1 x 2 ) + 5 x 1 − 3 x 2 = 1 2 ( x 1 , x 2 ) ( 2 − 3 − 3 8 ) ( x 1 x 2 ) + ( 5 − 3 ) ( x 1 x 2 ) = 1 2 x T Q x + c T x ( Q T = Q ) \begin{aligned}
f(x_1,x_2) &= x_1^2 + 4x_2^2 - 3x_1x_2 + 5x_1 - 3x_2
\\
&= \frac{1}{2} (2x_1^2 + 8x_2^2 - 3x_1x_2 - 3x_1x_2) + 5x_1 - 3x_2
\\
&= \frac{1}{2} (x_1,x_2)
\begin{pmatrix}
2 & -3
\\
-3 & 8
\end{pmatrix}
\begin{pmatrix}
x_1
\\
x_2
\end{pmatrix}
+
\begin{pmatrix}
5 & -3
\end{pmatrix}
\begin{pmatrix}
x_1
\\
x_2
\end{pmatrix}
\\
&= \frac{1}{2}\mathbf{x}^TQ\mathbf{x} + \mathbf{c}^T\mathbf{x} \quad (Q^T = Q)
\end{aligned}
f ( x 1 , x 2 ) = x 1 2 + 4 x 2 2 − 3 x 1 x 2 + 5 x 1 − 3 x 2 = 2 1 ( 2 x 1 2 + 8 x 2 2 − 3 x 1 x 2 − 3 x 1 x 2 ) + 5 x 1 − 3 x 2 = 2 1 ( x 1 , x 2 ) ( 2 − 3 − 3 8 ) ( x 1 x 2 ) + ( 5 − 3 ) ( x 1 x 2 ) = 2 1 x T Q x + c T x ( Q T = Q )
m i n f ( x ) = 1 2 x t Q x + c T x 条件 A x = a B x ≤ b \begin{matrix}
min&\ f(\mathbf{x}) = \frac{1}{2}\mathbf{x}^tQ\mathbf{x} + \mathbf{c}^T\mathbf{x}
\\
\text{条件}&A\mathbf{x} = \mathbf{a}
\\
&B\mathbf{x} \leq \mathbf{b}
\end{matrix}
m i n 条件 f ( x ) = 2 1 x t Q x + c T x A x = a B x ≤ b
Q : n × m A : m × n a : m 次元 c : n 次元 B : l × n b : l 次元 \begin{matrix}
Q\text{:}n\times m & A\text{:}m\times n & \mathbf{a}\text{:}m\text{次元}
\\
\mathbf{c}\text{:}n\text{次元} & B\text{:}l\times n & \mathbf{b}\text{:}l\text{次元}
\end{matrix}
Q : n × m c : n 次元 A : m × n B : l × n a : m 次元 b : l 次元
m i n f ( x ) min \ f(\mathbf{x}) m i n f ( x ) x ∈ R n \mathbf{x} \in \mathbb{R}^n x ∈ R n ( f : R n → R ) (f: \mathbb{R}^{n} \rightarrow \mathbb{R}) ( f : R n → R )
整数計画問題:「変数は整数」条件 など…
生産計画問題
物体の運動 ( 時刻 , 位置 ) のデータ ( t 1 , b 1 ) ⋮ ( t p , b p ) \begin{aligned}
\text{物体の運動}
&\begin{pmatrix}
\text{時刻},& \text{位置}
\end{pmatrix}&
\text{のデータ}
\\
&\begin{pmatrix}
t_1,& b_1
\end{pmatrix}&
\\
&\qquad\vdots&
\\
&\begin{pmatrix}
t_p, & b_p
\end{pmatrix}&
\end{aligned}
物体の運動 ( 時刻 , 位置 ) ( t 1 , b 1 ) ⋮ ( t p , b p ) のデータ
モデル式: b i = x 0 + x 1 t i + e i ( 誤差 ) ( i = 1 , . . . , p ) b_i = x_0 + x_1t_i + e_i(\text{誤差}) (i = 1,...,p) b i = x 0 + x 1 t i + e i ( 誤差 ) ( i = 1 , . . . , p )
∑ e i 2 → m i n x 0 , x 1 を推定 \begin{aligned}
\sum e_i^2 \rightarrow min
\\
x_0, x_1\text{を推定}
\end{aligned}
∑ e i 2 → m i n x 0 , x 1 を推定
Support Vector Hachineに関する問題
f : R n → R f: \mathbb{R}^n \rightarrow \mathbb{R} f : R n → R f f f
∇ f ( x ) = ( ∂ f ∂ x 1 ∂ f ∂ x n ) ∈ R n \nabla f(x) = \begin{pmatrix}
\frac{\partial f}{\partial x_1}
\\
\frac{\partial f}{\partial x_n}
\end{pmatrix}
\in \mathbb{R}^n
∇ f ( x ) = ( ∂ x 1 ∂ f ∂ x n ∂ f ) ∈ R n
勾配ベクトルは目的関数が最も増加する方向
f f f
∇ 2 f ( x ) = [ ( i , j ) 成分 = ∂ 2 f ∂ x i x j である n × n 行列 ] \nabla^2f(\mathbf{x}) = [(i, j)\text{成分} = \frac{\partial^2 f}{\partial x_i x_j}\text{である}n\times n\text{行列}]
∇ 2 f ( x ) = [ ( i , j ) 成分 = ∂ x i x j ∂ 2 f である n × n 行列 ]
例
f ( x 1 , x 2 ) = 1 2 ( 2 x 1 2 + 8 x 2 2 − 6 x 1 x 2 ) + 5 x 1 − 3 x 2 ∇ f ( x ) = ( 2 x 1 − 3 x 2 + 5 8 x 2 − 3 x 1 − 3 ) = ( 2 − 3 − 3 8 ) ( x 1 x 2 ) + ( 5 − 3 ) ∇ 2 f ( x ) = ( 2 − 3 − 3 8 ) \begin{aligned}
f(x_1,x_2) &= \frac{1}{2} (2x_1^2 + 8x_2^2 -6x_1x_2) + 5x_1 - 3x_2
\\
\nabla f(\mathbf{x}) &=
\begin{pmatrix}
2x_1 - 3x_2 + 5
\\
8x_2 - 3x_1 - 3
\end{pmatrix}=
\begin{pmatrix}
2 & -3
\\
-3 & 8
\end{pmatrix}
\begin{pmatrix}
x_1
\\
x_2
\end{pmatrix}
+\begin{pmatrix}
5
\\
-3
\end{pmatrix}
\\
\nabla^2 f(\mathbf{x}) &= \begin{pmatrix}
2 & -3
\\
-3 & 8
\end{pmatrix}
\end{aligned}
f ( x 1 , x 2 ) ∇ f ( x ) ∇ 2 f ( x ) = 2 1 ( 2 x 1 2 + 8 x 2 2 − 6 x 1 x 2 ) + 5 x 1 − 3 x 2 = ( 2 x 1 − 3 x 2 + 5 8 x 2 − 3 x 1 − 3 ) = ( 2 − 3 − 3 8 ) ( x 1 x 2 ) + ( 5 − 3 ) = ( 2 − 3 − 3 8 )
g g g ヤコビ行列
∇ g ( x ) = [ ∇ g 1 ( x ) , ⋯ , ∇ g p ( x ) ] = ( ∂ g 1 ∂ x 1 . . . ∂ g p ∂ x 1 ⋮ ⋱ ⋮ ∂ g 1 ∂ x n ⋯ ∂ g p ∂ x n ) ∈ R n × p \begin{aligned}
\nabla g(\mathbf{x}) = [\nabla g_1(\mathbf{x}),\cdots,\nabla g_p(\mathbf{x})] =
\begin{pmatrix}
\frac{\partial g_1}{\partial x_1} & ... & \frac{\partial g_p}{\partial x_1}
\\
\vdots & \ddots & \vdots
\\
\frac{\partial g_1}{\partial x_n} & \cdots & \frac{\partial g_p}{\partial x_n}
\end{pmatrix}
\in \mathbb{R}^{n \times p}
\end{aligned}
∇ g ( x ) = [ ∇ g 1 ( x ) , ⋯ , ∇ g p ( x ) ] = ⎝ ⎜ ⎜ ⎜ ⎛ ∂ x 1 ∂ g 1 ⋮ ∂ x n ∂ g 1 . . . ⋱ ⋯ ∂ x 1 ∂ g p ⋮ ∂ x n ∂ g p ⎠ ⎟ ⎟ ⎟ ⎞ ∈ R n × p
で定義し,その転置行列∇ g ( x ) T \nabla g(\mathbf{x})^T ∇ g ( x ) T
1 次: f ( x ∗ + d ) = f ( x ∗ ) + ∇ f ( x ∗ ) T d + 残差 2 次: f ( x ∗ + d ) = f ( x ∗ ) + ∇ f ( x ∗ ) T d + 1 2 d T ∇ 2 f ( x ∗ ) d + 残差 1 変数: f ( x + d ) = f ( x ) + f ′ ( x ) d + 1 2 f ′ ′ ( x ) T d 2 + 残差 \begin{aligned}
&1\text{次:}f(\mathbf{x}^* + \mathbf{d}) = f(\mathbf{x}^*) + \nabla f(\mathbf{x}^*)^T\mathbf{d} + \text{残差}
\\
&2\text{次:}f(\mathbf{x}^* + \mathbf{d}) = f(\mathbf{x}^*) + \nabla f(\mathbf{x}^*)^T\mathbf{d} + \frac{1}{2}\mathbf{d}^T\nabla^2f(\mathbf{x}^*)\mathbf{d}+\text{残差}
\\
&1\text{変数:}f(x + d) = f(x) + f'(x)d + \frac{1}{2}f''(x)^Td^2 + \text{残差}
\end{aligned}
1 次: f ( x ∗ + d ) = f ( x ∗ ) + ∇ f ( x ∗ ) T d + 残差 2 次: f ( x ∗ + d ) = f ( x ∗ ) + ∇ f ( x ∗ ) T d + 2 1 d T ∇ 2 f ( x ∗ ) d + 残差 1 変数: f ( x + d ) = f ( x ) + f ′ ( x ) d + 2 1 f ′ ′ ( x ) T d 2 + 残差
设c ∈ R , Q ∈ R n × n \mathbf{c} \in \mathbb{R}, \mathbb{Q} \in \mathbb{R}^{n \times n} c ∈ R , Q ∈ R n × n
∇ ( c T x ) = c \nabla(\mathbf{c}^T\mathbf{x}) = \mathbf{c} ∇ ( c T x ) = c ∇ ( x Q T x ) = Q + Q T x = 2 Q x ( Q T = Q ) \nabla(\mathbf{x}Q^T\mathbf{x})=Q+Q^T\mathbf{x}=2Q\mathbf{x}(Q^T = Q) ∇ ( x Q T x ) = Q + Q T x = 2 Q x ( Q T = Q ) ∇ 2 ( x T Q x ) = Q + Q T = 2 Q ( Q T = Q ) \nabla^2(\mathbf{x}^TQ\mathbf{x})=Q+Q^T=2Q(Q^T = Q) ∇ 2 ( x T Q x ) = Q + Q T = 2 Q ( Q T = Q )
例
f ( x ) = 1 2 x T Q x + c T x ( Q T = Q ) ∇ f ( x ) = Q x + c ∇ 2 f ( x ) = Q \begin{aligned}
f(\mathbf{x}) &= \frac{1}{2} \mathbf{x}^TQ\mathbf{x} + \mathbf{c}^T\mathbf{x} \qquad (Q^T = Q)
\\
\nabla f(\mathbf{x}) &= Q\mathbf{x}+\mathbf{c}
\\
\ \nabla^2f(\mathbf{x}) &= Q
\end{aligned}
f ( x ) ∇ f ( x ) ∇ 2 f ( x ) = 2 1 x T Q x + c T x ( Q T = Q ) = Q x + c = Q
イメージ ヘコミのない集合
S ∈ R n , u , v ∈ S , ∀ λ ∈ [ 0 , 1 ] \mathbf{S} \in \mathbb{R}^n, \mathbf{u},\mathbf{v} \in \mathbf{S}\text{,}^\forall\lambda \in [0, 1] S ∈ R n , u , v ∈ S , ∀ λ ∈ [ 0 , 1 ]
λ u + ( 1 − λ ) v ∈ S \begin{aligned}
\lambda \mathbf{u} +(1 - \lambda)\mathbf{v} \in \mathbf{S}
\end{aligned}
λ u + ( 1 − λ ) v ∈ S
u , v ∈ S ⇒ u と v \mathbf{u},\mathbf{v} \in S \Rightarrow \mathbf{u}\text{と}\mathbf{v} u , v ∈ S ⇒ u と v 凸集合 という.(空集合∅ \varnothing ∅
例: 以下を証明せよ
A ∈ R m × n , b ∈ R m , S = { x ∈ R n ∣ A x = b , x ≥ 0 } \begin{aligned}
A \in \mathbb{R}^{m \times n}, b \in \mathbb{R}^m,
\mathbf{S} = \{x \in \mathbb{R}^n | A\mathbf{x} = \mathbf{b}, \mathbf{x} \geq \mathbf{0}\}
\end{aligned}
A ∈ R m × n , b ∈ R m , S = { x ∈ R n ∣ A x = b , x ≥ 0 }
は凸集合である.
示すべきこと:
{ u , v ∈ S λ ∈ [ 0 , 1 ] ⇔ ( A u = b , u ≥ 0 A v = b , v ≥ 0 ) ⇓ w = λ u + ( 1 − λ ) v ∈ S ⇔ ( A w = b , w ≥ 0 ) A w = A ( λ u + ( 1 − λ ) v ) = λ A u + ( 1 − λ ) A v = λ b + ( 1 − λ ) b = b \begin{aligned}
\begin{cases}
\mathbf{u}, \mathbf{v} \in \mathbf{S}
\\
\lambda \in [0, 1]
\end{cases}
&\Leftrightarrow
\begin{pmatrix}
A\mathbf{u}=\mathbf{b}, \mathbf{u}\geq \mathbf{0}
\\
A\mathbf{v}=\mathbf{b}, \mathbf{v}\geq \mathbf{0}
\end{pmatrix}
\\
&\Downarrow
\\
\mathbf{w} = \lambda \mathbf{u} + (1 - \lambda)\mathbf{v} \in \mathbf{S} &\Leftrightarrow (A\mathbf{w} = \mathbf{b}, \mathbf{w} \geq \mathbf{0})
\\
A\mathbf{w} &= A(\lambda \mathbf{u} + (1 - \lambda) \mathbf{v})
\\
&= \lambda A \mathbf{u} + (1 - \lambda)A\mathbf{v}
\\
&= \lambda\mathbf{b} + (1 - \lambda)\mathbf{b} = \mathbf{b}
\end{aligned}
{ u , v ∈ S λ ∈ [ 0 , 1 ] w = λ u + ( 1 − λ ) v ∈ S A w ⇔ ( A u = b , u ≥ 0 A v = b , v ≥ 0 ) ⇓ ⇔ ( A w = b , w ≥ 0 ) = A ( λ u + ( 1 − λ ) v ) = λ A u + ( 1 − λ ) A v = λ b + ( 1 − λ ) b = b
また, λ ≤ 0 , 1 − λ ≤ 0 \lambda \leq 0, 1 - \lambda \leq 0 λ ≤ 0 , 1 − λ ≤ 0 λ u ≥ 0 , ( 1 − λ ) v ≥ 0 \lambda\mathbf{u} \geq \mathbf{0}, (1 - \lambda)\mathbf{v} \geq \mathbf{0} λ u ≥ 0 , ( 1 − λ ) v ≥ 0 w = λ u + ( 1 − λ ) v ≥ 0 \mathbf{w} = \lambda \mathbf{u} + (1 - \lambda)\mathbf{v} \geq \mathbf{0} w = λ u + ( 1 − λ ) v ≥ 0
次の二次関数
f ( x ) = f ( x 1 , x 2 , x 3 ) = 3 x 1 2 + x 2 2 + 2 x 3 2 + 2 x 1 x 2 + 3 x 1 x 3 − 4 x 2 x 3 + x 1 − 4 x 2 + 6 x 3 \begin{aligned}
f(x) = f(x_1,x_2,x_3) = 3x_1^2 + x_2^2 + 2x_3^2 + 2x_1x_2 + 3x_1x_3 - 4x_2x_3 + x_1 - 4x_2 + 6x_3
\end{aligned}
f ( x ) = f ( x 1 , x 2 , x 3 ) = 3 x 1 2 + x 2 2 + 2 x 3 2 + 2 x 1 x 2 + 3 x 1 x 3 − 4 x 2 x 3 + x 1 − 4 x 2 + 6 x 3
をf ( x ) = 1 2 x T Q x + c T x f(x) = \frac{1}{2} x^TQx + c^Tx f ( x ) = 2 1 x T Q x + c T x
f ( x ) = 1 2 ( x 1 , x 2 , x 3 ) ( 6 2 3 2 2 − 4 3 − 4 4 ) ( x 1 x 2 x 3 ) + ( 1 , − 4 , 6 ) ( x 1 x 2 x 3 ) \begin{aligned}
f(x) = \frac{1}{2} (x_1,x_2,x_3)
\begin{pmatrix}
6 & 2 & 3
\\
2 & 2 & -4
\\
3 & -4 & 4
\end{pmatrix}
\begin{pmatrix}
x_1
\\
x_2
\\
x_3
\end{pmatrix}+
(1,-4,6)
\begin{pmatrix}
x_1
\\
x_2
\\
x_3
\end{pmatrix}
\end{aligned}
f ( x ) = 2 1 ( x 1 , x 2 , x 3 ) ⎝ ⎛ 6 2 3 2 2 − 4 3 − 4 4 ⎠ ⎞ ⎝ ⎛ x 1 x 2 x 3 ⎠ ⎞ + ( 1 , − 4 , 6 ) ⎝ ⎛ x 1 x 2 x 3 ⎠ ⎞
次のそれぞれの関数の勾配ベクトルとヘッセ行列を求めよ.
∇ f ( x ) = ( 6 x 1 + 2 x 2 + 3 x 3 + 1 2 x 2 + 2 x 1 − 4 x 3 − 4 4 x 3 + 3 x 1 − 4 x 2 + 6 ) = ( 6 2 3 2 2 − 4 4 3 − 4 ) ( x 1 x 2 x 3 ) + ( 1 − 4 6 ) ∇ 2 f ( x ) = ( 6 2 3 2 2 − 4 4 3 − 4 ) \begin{aligned}
\nabla f(\mathbf{x}) &=
\begin{pmatrix}
6x_1 + 2x_2 + 3x_3 + 1
\\
2x_2 + 2x_1 - 4x_3 - 4
\\
4x_3 + 3x_1 - 4x_2 + 6
\end{pmatrix}=
\begin{pmatrix}
6 & 2 & 3
\\
2 & 2 & -4
\\
4 & 3 & -4
\end{pmatrix}
\begin{pmatrix}
x_1
\\
x_2
\\
x_3
\end{pmatrix}+
\begin{pmatrix}
1
\\
-4
\\
6
\end{pmatrix}
\\
\nabla^2 f(\mathbf{x}) &=
\begin{pmatrix}
6 & 2 & 3
\\
2 & 2 & -4
\\
4 & 3 & -4
\end{pmatrix}
\end{aligned}
∇ f ( x ) ∇ 2 f ( x ) = ⎝ ⎛ 6 x 1 + 2 x 2 + 3 x 3 + 1 2 x 2 + 2 x 1 − 4 x 3 − 4 4 x 3 + 3 x 1 − 4 x 2 + 6 ⎠ ⎞ = ⎝ ⎛ 6 2 4 2 2 3 3 − 4 − 4 ⎠ ⎞ ⎝ ⎛ x 1 x 2 x 3 ⎠ ⎞ + ⎝ ⎛ 1 − 4 6 ⎠ ⎞ = ⎝ ⎛ 6 2 4 2 2 3 3 − 4 − 4 ⎠ ⎞
f ( x ) = e x 1 x 2 + x 1 2 x 2 3 − 3 x 1 + 5 x 2 f(x) = e^{x_1x_2} + x_1^2x_2^3 - 3x_1 + 5x_2 f ( x ) = e x 1 x 2 + x 1 2 x 2 3 − 3 x 1 + 5 x 2
∇ f ( x ) = ( x 2 e x 1 x 2 + 2 x 2 3 x 1 − 3 x 1 e x 1 x 2 + 3 x 1 2 x 2 2 + 5 ) ∇ 2 f ( x ) = ( x 2 2 e x 1 x 2 + 2 x 2 3 ( 1 + x 1 x 2 ) e x 1 x 2 + 6 x 1 x 2 2 ( 1 + x 2 x 1 ) e x 1 x 2 + 6 x 2 2 x 1 x 1 2 e x 1 x 2 + 6 x 1 2 x 2 ) \begin{aligned}
\nabla f(\mathbf{x}) &=
\begin{pmatrix}
x_2e^{x_1x_2} + 2x_2^3x_1 -3
\\
x_1e^{x_1x_2} + 3x_1^2x_2^2 + 5
\end{pmatrix}
\\
\nabla^2 f(\mathbf{x}) &=
\begin{pmatrix}
x_2^2e^{x_1x_2} + 2x_2^3 & (1 + x_1x_2)e^{x_1x_2} + 6x_1x_2^2
\\
(1 + x_2x_1)e^{x_1x_2} + 6x_2^2x_1 & x_1^2e^{x_1x_2} + 6x_1^2x_2
\end{pmatrix}
\end{aligned}
∇ f ( x ) ∇ 2 f ( x ) = ( x 2 e x 1 x 2 + 2 x 2 3 x 1 − 3 x 1 e x 1 x 2 + 3 x 1 2 x 2 2 + 5 ) = ( x 2 2 e x 1 x 2 + 2 x 2 3 ( 1 + x 2 x 1 ) e x 1 x 2 + 6 x 2 2 x 1 ( 1 + x 1 x 2 ) e x 1 x 2 + 6 x 1 x 2 2 x 1 2 e x 1 x 2 + 6 x 1 2 x 2 )
次の集合が凸集合であることを示せ.
S = { x ∈ R n ∣ A x = a , B x ≤ b } \begin{aligned}
S = \{\mathbf{x} \in \mathbb{R}^n | A\mathbf{x} = \mathbf{a}, B\mathbf{x} \leq \mathbf{b}\}
\end{aligned}
S = { x ∈ R n ∣ A x = a , B x ≤ b }
ただし,A ∈ R m × n , a ∈ R m , B ∈ R l × n , b ∈ R l A \in \mathbb{R}^{m \times n}, \mathbf{a} \in \mathbb{R}^m, B \in \mathbb{R}^{l \times n}, \mathbf{b} \in \mathbb{R}^l A ∈ R m × n , a ∈ R m , B ∈ R l × n , b ∈ R l
{ u , v ∈ S λ ∈ [ 0 , 1 ] ⇔ ( A u = a , B u ≤ 0 A v = a , B v ≤ 0 ) ⇓ w = λ u + ( 1 − λ ) v ∈ S ⇔ ( A w = a , B w ≤ b ) A w = A ( λ u + ( 1 − λ ) v ) = λ A u + ( 1 − λ ) A v = λ a + ( 1 − λ ) a = a \begin{aligned}
\begin{cases}
\mathbf{u}, \mathbf{v} \in \mathbf{S}
\\
\lambda \in [0, 1]
\end{cases}
&\Leftrightarrow
\begin{pmatrix}
A\mathbf{u}=\mathbf{a}, B\mathbf{u}\leq \mathbf{0}
\\
A\mathbf{v}=\mathbf{a}, B\mathbf{v}\leq \mathbf{0}
\end{pmatrix}
\\
&\Downarrow
\\
\mathbf{w} = \lambda \mathbf{u} + (1 - \lambda)\mathbf{v} \in \mathbf{S} &\Leftrightarrow (A\mathbf{w} = \mathbf{a}, B\mathbf{w} \leq \mathbf{b})
\\
A\mathbf{w} &= A(\lambda\mathbf{u} + (1 - \lambda)\mathbf{v})
\\
&= \lambda A \mathbf{u} + (1 - \lambda)A\mathbf{v}
\\
&= \lambda\mathbf{a} + (1 - \lambda)\mathbf{a} = \mathbf{a}
\end{aligned}
{ u , v ∈ S λ ∈ [ 0 , 1 ] w = λ u + ( 1 − λ ) v ∈ S A w ⇔ ( A u = a , B u ≤ 0 A v = a , B v ≤ 0 ) ⇓ ⇔ ( A w = a , B w ≤ b ) = A ( λ u + ( 1 − λ ) v ) = λ A u + ( 1 − λ ) A v = λ a + ( 1 − λ ) a = a
また,λ ≥ 0 , ( 1 − λ ) ≥ 0 , B u ≤ b , B v ≤ b \lambda \geq 0, (1 - \lambda) \geq 0, B\mathbf{u} \leq \mathbf{b}, B\mathbf{v} \leq \mathbf{b} λ ≥ 0 , ( 1 − λ ) ≥ 0 , B u ≤ b , B v ≤ b B w = B ( λ u + ( 1 − λ ) v ) ≤ b B\mathbf{w} = B(\lambda\mathbf{u} + (1 - \lambda)\mathbf{v}) \leq \mathbf{b} B w = B ( λ u + ( 1 − λ ) v ) ≤ b
R n \mathbb{R}^n R n a \mathbf{a} a α \alpha α
H = { x ∈ R n ∣ a T x = α } \begin{aligned}
H = \lbrace \mathbf{x} \in \mathbb{R}^n \ |\ \mathbf{a}^T \mathbf{x} = \alpha \rbrace
\end{aligned}
H = { x ∈ R n ∣ a T x = α }
をa \mathbf{a} a α \alpha α H \mathbb{H} H
H + = { x ∈ R n ∣ a T x ≥ α } , H − = { x ∈ R n ∣ a T x ≤ α } \begin{aligned}
H^+ = \lbrace \mathbf{x} \in \mathbb{R}^n \ |\ \mathbf{a}^T \mathbf{x} \geq \alpha \rbrace, \quad H^- = \lbrace \mathbf{x} \in \mathbb{R}^n \ |\ \mathbf{a}^T \mathbf{x} \leq \alpha \rbrace
\end{aligned}
H + = { x ∈ R n ∣ a T x ≥ α } , H − = { x ∈ R n ∣ a T x ≤ α }
をそれぞれ超平面Hを境界にもつ正の閉半空間, 負の閉半空間という.
有限個の閉半空間の共通部分として表される空でない集合を凸多面集合(polyhedral convex set)という.具体的には,零でないベクトルa 1 , ⋯ , a m ∈ R n \mathbf{a}_1, \cdots, \mathbf{a}_m \in \mathbb{R}^n a 1 , ⋯ , a m ∈ R n b 1 , ⋯ , b m b_1, \cdots, b_m b 1 , ⋯ , b m
X = { x ∈ R n ∣ a i T x ≤ b i , i = 1 , ⋯ , m } \begin{aligned}
X = \lbrace \mathbf{x} \in \mathbb{R}^n \ |\ \mathbf{a}_i^T \mathbf{x} \leq b_i, i = 1, \cdots, m \rbrace
\end{aligned}
X = { x ∈ R n ∣ a i T x ≤ b i , i = 1 , ⋯ , m }
は凸多面集合になる.あるいは,a i T \mathbf{a}_i^T a i T A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n b i b_i b i b ∈ R m b \in \mathbb{R}^m b ∈ R m
X = { x ∈ R n ∣ A x ≤ b } \begin{aligned}
X = \lbrace \mathbf{x} \in \mathbb{R}^n \ |\ A\mathbf{x} \leq \mathbf{b} \rbrace
\end{aligned}
X = { x ∈ R n ∣ A x ≤ b }
は凸多面集合になる.また,等式a i T x = b i \mathbf{a}_i^T \mathbf{x} = b_i a i T x = b i
{ x ∈ R n ∣ a i T x ≤ b i } , { x ∈ R n ∣ a i T x ≥ b i } \begin{aligned}
\lbrace \mathbf{x} \in \mathbb{R}^n \ |\ \mathbf{a}_i^T \mathbf{x} \leq b_i \rbrace, \quad \lbrace \mathbf{x} \in \mathbb{R}^n \ |\ \mathbf{a}_i^T \mathbf{x} \geq b_i \rbrace
\end{aligned}
{ x ∈ R n ∣ a i T x ≤ b i } , { x ∈ R n ∣ a i T x ≥ b i }
の共通部分として表せるのでX = { x ∈ R n ∣ A x = b } X = \lbrace \mathbf{x} \in \mathbb{R}^n \ |\ A\mathbf{x} = \mathbf{b} \rbrace X = { x ∈ R n ∣ A x = b }
R n \mathbb{R}^n R n x \mathbf{x} x u , v \mathbf{u},\mathbf{v} u , v u ≠ v \mathbf{u} \ne \mathbf{v} u = v
x = ( 1 − λ ) u + λ v ( 0 < λ < 1 ) \begin{aligned}
\mathbf{x} = (1-\lambda)\mathbf{u} + \lambda\mathbf{v} (0 < \lambda < 1)
\end{aligned}
x = ( 1 − λ ) u + λ v ( 0 < λ < 1 )
と表すことができないとき,x \mathbf{x} x
また集合Sに属する互いに異なる2点u , v \mathbf{u}, \mathbf{v} u , v u , v \mathbf{u}, \mathbf{v} u , v
R n \mathbb{R}^n R n x ∈ C \mathbf{x} \in C x ∈ C λ ≥ 0 \lambda \geq 0 λ ≥ 0 λ x ∈ C \lambda \mathbf{x} \in C λ x ∈ C
R n \mathbb{R}^n R n x \mathbf{x} x
{ λ x ∣ λ > 0 , λ ∈ R } \begin{aligned}
\lbrace \lambda \mathbf{x} \ |\ \lambda > 0, \lambda \in \mathbb{R} \rbrace
\end{aligned}
{ λ x ∣ λ > 0 , λ ∈ R }
をx \mathbf{x} x R n \mathbb{R}^n R n
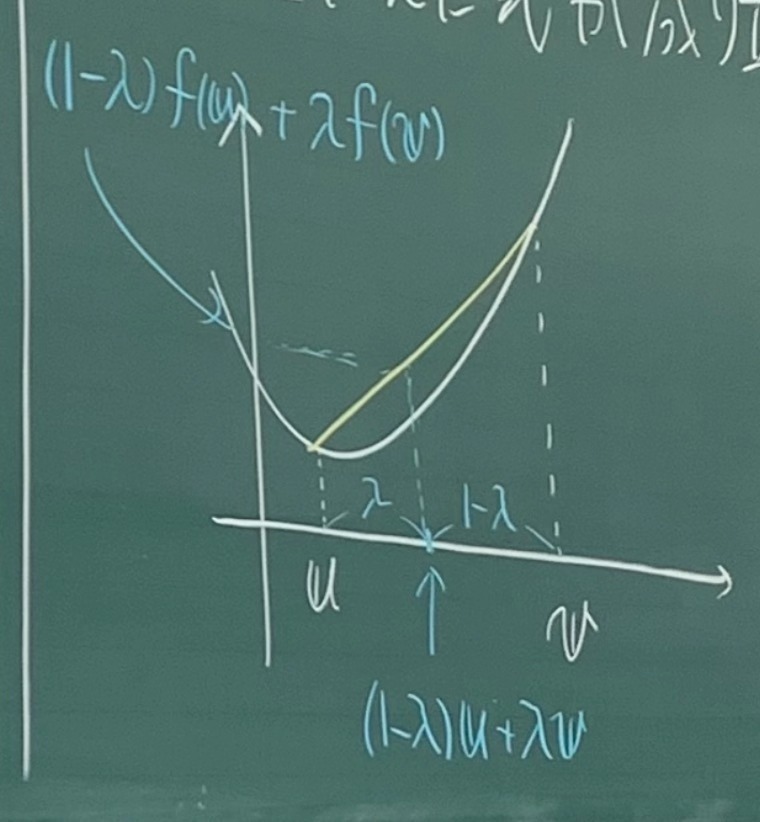
f : R n → R , f が凸関数 ∀ u , v ∈ R , ∀ λ ∈ ( 0 , 1 ) f: \mathbb{R}^n \rightarrow \mathbb{R},f\text{が凸関数}^\forall \mathbf{u,v} \in \mathbb{R}, ^\forall \lambda \in (0,1) f : R n → R , f が凸関数 ∀ u , v ∈ R , ∀ λ ∈ ( 0 , 1 )
( 1 − λ ) f ( u ) + λ f ( v ) ≥ f ( ( 1 − λ ) u + λ v ) \begin{aligned}
(1 - \lambda)f(\mathbf{u}) + \lambda f(\mathbf{v}) \geq f((1 - \lambda)\mathbf{u} + \lambda \mathbf{v})
\end{aligned}
( 1 − λ ) f ( u ) + λ f ( v ) ≥ f ( ( 1 − λ ) u + λ v )
f: 狭義凸関数(strictly convex function)
( 1 − λ ) f ( u ) + λ f ( v ) > f ( ( 1 − λ ) u + λ v ) \begin{aligned}
(1 - \lambda)f(\mathbf{u}) + \lambda f(\mathbf{v}) > f((1 - \lambda)\mathbf{u} + \lambda \mathbf{v})
\end{aligned}
( 1 − λ ) f ( u ) + λ f ( v ) > f ( ( 1 − λ ) u + λ v )
凸関数: グラフ上2点を線分で結ぶと,その線分がグラフの上にある(下にならない)ような関数
f : R n → R f:\mathbb{R}^n \rightarrow \mathbb{R} f : R n → R ( − f ) (-f) ( − f )
例
(1)f ( x ) = c T x = c 1 x 1 + c 2 x 2 + . . . + c n x n f(\mathbf{x}) = \mathbf{c}^T\mathbf{x} = c_1x_1 + c_2x_2 + ... + c_nx_n f ( x ) = c T x = c 1 x 1 + c 2 x 2 + . . . + c n x n h i : R n → R h_i:\mathbb{R}^n \rightarrow \mathbb{R} h i : R n → R i = 1 , ⋯ , l i = 1,\cdots,l i = 1 , ⋯ , l ⇒ S = { x ∈ R n ∣ h i ( x ) ≤ 0 ( i = 1 , ⋯ , l ) } \Rightarrow S = \lbrace \mathbf{x} \in \mathbb{R}^n \ |\ h_i(\mathbf{x}) \leq 0 (i=1,\cdots,l) \rbrace ⇒ S = { x ∈ R n ∣ h i ( x ) ≤ 0 ( i = 1 , ⋯ , l ) }
(1)の証明f ( ( 1 − λ ) u + λ v ) = ( 1 − λ ) f ( u ) + λ f ( v ) f((1 - \lambda) \mathbf{u} + \lambda \mathbf{v}) = (1 - \lambda)f(\mathbf{u})+\lambda f(\mathbf{v}) f ( ( 1 − λ ) u + λ v ) = ( 1 − λ ) f ( u ) + λ f ( v )
補足
f , g : R n → R f,g:\mathbb{R}^n \rightarrow \mathbb{R} f , g : R n → R λ > 0 \lambda > 0 λ > 0
f + g
λ f \lambda f λ f m a x ( f , g ) max(f,g) m a x ( f , g )
f : R n → R f:\mathbb{R}^n \rightarrow \mathbb{R} f : R n → R 連続的微分可能 = C 1 C^1 C 1 ∇ f ( x ) \nabla f(\mathbf{x}) ∇ f ( x ) 2回連続的微分可能 = C 2 C^2 C 2 ∇ f ( x ) , ∇ 2 f ( x ) \nabla f(\mathbf{x}), \nabla^2 f(\mathbf{x}) ∇ f ( x ) , ∇ 2 f ( x )
f , g : R n → R f,g:\mathbb{R}^n \rightarrow \mathbb{R} f , g : R n → R C 1 C^1 C 1
f : f: f : ⇔ ( 1 ) , ( 2 ) \Leftrightarrow (1),(2) ⇔ ( 1 ) , ( 2 )
(1) ∀ x , y ∈ R n ^\forall x,y \in \mathbb{R}^n ∀ x , y ∈ R n f ( y ) ≥ f ( x ) + ∇ f ( x ) T ( y − x ) f(\mathbf{y}) \geq f(\mathbf{x}) + \nabla f(\mathbf{x})^T(\mathbf{y} - \mathbf{x}) f ( y ) ≥ f ( x ) + ∇ f ( x ) T ( y − x ) 接線はグラフの下になる )
(2) ∀ x , y ∈ R n ^\forall x,y \in \mathbb{R}^n ∀ x , y ∈ R n ( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) ≥ 0 (\nabla f(\mathbf{x}) - \nabla f(\mathbf{y}))^T(\mathbf{x} - \mathbf{y}) \geq 0 ( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) ≥ 0 ∇ f \nabla f ∇ f 単調性 という)
f ( x ) = 1 2 x T Q x + c T x ( Q ∈ R n × n , 対称 , c ∈ R n ) \begin{aligned}
f(\mathbf{x}) = \frac{1}{2} \mathbf{x}^TQ\mathbf{x} + \mathbf{c}^T\mathbf{x} \qquad (Q \in \mathbb{R}^{n \times n},\text{対称},\mathbf{c} \in \mathbb{R}^n)
\end{aligned}
f ( x ) = 2 1 x T Q x + c T x ( Q ∈ R n × n , 対称 , c ∈ R n )
(1)f : 凸関数 ⇔ Q : 半正定値 ⇔ d T Q d ≥ 0 ( ∀ d ∈ R n ) ⇔ 対称 n × n 行列 Q の固有値がすべて非負 f:\text{凸関数} \Leftrightarrow Q:\text{半正定値} \Leftrightarrow \mathbf{d}^TQ\mathbf{d} \geq 0(^\forall d \in \mathbb{R}^n) \Leftrightarrow \text{対称}n \times n\text{行列}Q\text{の固有値がすべて非負} f : 凸関数 ⇔ Q : 半正定値 ⇔ d T Q d ≥ 0 ( ∀ d ∈ R n ) ⇔ 対称 n × n 行列 Q の固有値がすべて非負 f : 狭義凸関数 ⇔ Q : 正定値 ⇔ d T Q d > 0 ( ∀ d ∈ R n , d ≠ 0 ) ⇔ 対称 n × n 行列 Q の固有値がすべて正 f:\text{狭義凸関数} \Leftrightarrow Q:\text{正定値} \Leftrightarrow \mathbf{d}^TQ\mathbf{d} > 0(^\forall d \in \mathbb{R}^n, d \ne 0) \Leftrightarrow \text{対称}n \times n\text{行列}Q\text{の固有値がすべて正} f : 狭義凸関数 ⇔ Q : 正定値 ⇔ d T Q d > 0 ( ∀ d ∈ R n , d = 0 ) ⇔ 対称 n × n 行列 Q の固有値がすべて正
(1)の証明∇ f ( x ) = Q x + c \nabla f(\mathbf{x}) = Q\mathbf{x} + \mathbf{c} ∇ f ( x ) = Q x + c x , y ∈ R n x,y \in \mathbb{R}^n x , y ∈ R n
( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) = ( x − y ) T Q ( x − y ) \begin{aligned}
(\nabla f(\mathbf{x}) - \nabla f(\mathbf{y}))^T (\mathbf{x} - \mathbf{y}) = (\mathbf{x} - \mathbf{y})^TQ(\mathbf{x} - \mathbf{y})
\end{aligned}
( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) = ( x − y ) T Q ( x − y )
が成り立つ.( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) ≥ 0 (\nabla f(\mathbf{x}) - \nabla f(\mathbf{y}))^T(\mathbf{x} - \mathbf{y}) \geq 0 ( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) ≥ 0 f f f
(2)の証明x ≠ y \mathbf{x} \ne \mathbf{y} x = y f f f Q Q Q
f : R n → R f:\mathbb{R}^n \rightarrow \mathbb{R} f : R n → R C 2 C^2 C 2 f : 凸関数 ⇔ ヘッセ行列 ∇ 2 f ( x ) f:\text{凸関数} \Leftrightarrow \text{ヘッセ行列}\nabla^2 f(\mathbf{x}) f : 凸関数 ⇔ ヘッセ行列 ∇ 2 f ( x ) ( ∀ x ∈ R ) (^\forall x \in \mathbb{R}) ( ∀ x ∈ R ) ∇ 2 f ( x ) \nabla^2 f(\mathbf{x}) ∇ 2 f ( x ) ( ∀ x ∈ R ) ⇒ f : (^\forall x \in \mathbb{R}) \Rightarrow f: ( ∀ x ∈ R ) ⇒ f :
(2)の必要性の反例f ( x ) = x 4 f(x) = x^4 f ( x ) = x 4 f ′ ( x ) = 12 x 2 ≥ 0 f'(x) = 12x^2 \geq 0 f ′ ( x ) = 1 2 x 2 ≥ 0 f ′ ′ ( 0 ) = 0 f''(0) = 0 f ′ ′ ( 0 ) = 0
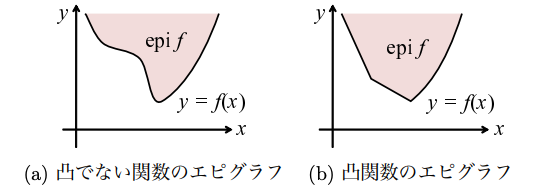
エピグラフ(epigraph) : 実数値関数f f f f f f
e p i f = { ( x , y ) ∈ R n × R : y ≥ f ( x ) } \begin{aligned}
epif = \{(\mathbf{x},y) \in \mathbb{R}^n \times \mathbb{R}: y \geq f(\mathbf{x})\}
\end{aligned}
e p i f = { ( x , y ) ∈ R n × R : y ≥ f ( x ) }
実数値関数f f f f f f
ハイポグラフ (hypograph) : 実数値関数f f f f f f
h y p f = { ( x , y ) ∈ R n × R : y ≤ f ( x ) } \begin{aligned}
hypf = \{(\mathbf{x},y) \in \mathbb{R}^n \times \mathbb{R}: y \leq f(\mathbf{x})\}
\end{aligned}
h y p f = { ( x , y ) ∈ R n × R : y ≤ f ( x ) }
実数値関数f f f f f f
例題:
最大値 5 x 1 + 4 x 2 制約条件 5 x 1 + 2 x 2 ≤ 30 x 1 + 2 x 2 ≤ 14 x 1 ≥ 0 \begin{aligned}
\text{最大値} \qquad &5x_1 + 4x_2
\\
\text{制約条件} \qquad &5x_1 + 2x_2 \leq 30
\\
&x_1 + 2x_2 \leq 14
\\
&x_1 \geq 0
\end{aligned}
最大値 制約条件 5 x 1 + 4 x 2 5 x 1 + 2 x 2 ≤ 3 0 x 1 + 2 x 2 ≤ 1 4 x 1 ≥ 0
スラック変数x 3 , x 4 x_3,x_4 x 3 , x 4
5 x 1 + 2 x 2 + x 3 = 30 x 1 + 2 x 2 + x 4 = 14 x 3 , x 4 ≥ 0 \begin{aligned}
5x_1 + 2x_2 + x_3 &= 30
\\
x_1 + 2x_2 + x_4 &= 14
\\
x_3,x_4 &\geq 0
\end{aligned}
5 x 1 + 2 x 2 + x 3 x 1 + 2 x 2 + x 4 x 3 , x 4 = 3 0 = 1 4 ≥ 0
自由変数x 2 を x 2 + , x 2 − x_2\text{を}x_2^+, x_2^- x 2 を x 2 + , x 2 −
x 2 = x 2 + − x 2 − , x 2 + , x 2 − ≥ 0 x_2 = x_2^+ - x_2^-, \qquad x_2^+, x_2^- \geq 0
x 2 = x 2 + − x 2 − , x 2 + , x 2 − ≥ 0
最小値 − 5 x 1 − 4 x 2 + + 4 x 2 − + 0 x 3 + 0 x 4 制約条件 5 x 1 + 2 x 2 + − 2 x 2 − + x 3 = 30 x 1 + 2 x 2 + − 2 x 2 − + x 4 = 14 x 1 , x 2 + , x 2 − , x 3 , x 4 ≥ 0 \begin{aligned}
\text{最小値} \qquad &-5x_1 - 4x_2^+ + 4x_2^- + 0x_3 + 0x_4
\\
\text{制約条件} \qquad &5x_1 + 2x_2^+ - 2x_2^- + x_3 = 30
\\
&x_1 + 2x_2^+ - 2x_2^- + x_4 = 14
\\
&x_1, x_2^+, x_2^-, x_3, x_4 \geq 0
\end{aligned}
最小値 制約条件 − 5 x 1 − 4 x 2 + + 4 x 2 − + 0 x 3 + 0 x 4 5 x 1 + 2 x 2 + − 2 x 2 − + x 3 = 3 0 x 1 + 2 x 2 + − 2 x 2 − + x 4 = 1 4 x 1 , x 2 + , x 2 − , x 3 , x 4 ≥ 0
線形計画問題A ∈ R m × n , b ∈ R m , C ∈ R n A \in \mathbb{R}^{m \times n}, \mathbf{b} \in \mathbb{R}^m, \mathbb{C} \in \mathbb{R}^n A ∈ R m × n , b ∈ R m , C ∈ R n
m i n C T x s . t A x = b , x ≥ 0 \begin{aligned}
min \qquad &\mathbb{C}^T \mathbf{x}
\\
s.t \qquad &A\mathbf{x} = \mathbf{b}, \quad \mathbf{x} \geq \mathbf{0}
\end{aligned}
m i n s . t C T x A x = b , x ≥ 0
r a n k A = m ( m < n ) rank A = m \quad (m < n) r a n k A = m ( m < n )
制約条件を満足する点を実行可能解(feasible solution)と呼び,さらに,そのような点の集合を実行可能領域(feasible region)という.標準形の場合には
S = { x ∈ R n ∣ A x = b , x ≥ 0 } S = \lbrace \mathbf{x} \in \mathbb{R}^n \ |\ A\mathbf{x} = \mathbf{b}, \quad \mathbf{x} \geq 0 \rbrace
S = { x ∈ R n ∣ A x = b , x ≥ 0 }
が実行可能領域になる.
Aから線形独立なベクトルをm本とって作られる正方行列をB ∈ R m × m B \in \mathbb{R}^{m \times m} B ∈ R m × m x B \mathbf{x}_B x B x N \mathbf{x}_N x N
A = ( B N ) , x = ( x B x N ) A = (B \quad N), \mathbf{x} = \begin{pmatrix}\mathbf{x}_B \\ \mathbf{x}_N \end{pmatrix}
A = ( B N ) , x = ( x B x N )
と分割されて,このとき等式制約A x = b は B x B + N x N = b A\mathbf{x} = \mathbf{b}\text{は}B\mathbf{x}_B + N\mathbf{x}_N = \mathbf{b} A x = b は B x B + N x N = b x B = B − 1 b \mathbf{x}_B = B^{-1}\mathbf{b} x B = B − 1 b
こうして定まる変数
x = ( x B x N ) = ( B − 1 b 0 ) \begin{aligned}
\mathbf{x} = \begin{pmatrix} \mathbf{x}_B \\ \mathbf{x}_N \end{pmatrix} = \begin{pmatrix} B^{-1}\mathbf{b} \\ \mathbf{0} \end{pmatrix}
\end{aligned}
x = ( x B x N ) = ( B − 1 b 0 )
を基底解(basic solution)と呼ぶ.
基底解の全ての変数が非負のとき(x B = B − 1 b ≥ 0 , x N = 0 \mathbf{x}_B = B^{-1}\mathbf{b} \geq \mathbf{0}, \mathbf{x}_N = \mathbf{0} x B = B − 1 b ≥ 0 , x N = 0
実行可能基底解でちょうどm個の基底変数の値が正であるとき非退化(nondegenerate)であるといい,それを非退化実行可能基底解(nondegenerate basic feasible solution)と呼ぶ(x B > 0 , x N = 0 \mathbf{x}_B > 0, \mathbf{x}_N = \mathbf{0} x B > 0 , x N = 0
基底行列Bに対応して目的関数の係数もc = ( c B , c N ) T \mathbf{c} = (\mathbf{c}_B, \mathbf{c}_N)^T c = ( c B , c N ) T ( B − 1 ) T c B (B^{-1})^T \mathbf{c}_B ( B − 1 ) T c B
目的関数を最小に実行可能解を最適解(optimal solution)という.
例題
A = ( 5 2 4 7 1 1 2 4 3 − 3 ) b = ( 14 5 ) \begin{aligned}
A = \begin{pmatrix}
5 & 2 & 4 & 7 & 1
\\
1 & 2 & 4 & 3 & -3
\end{pmatrix} \qquad \mathbf{b} = \begin{pmatrix}
14
\\
5
\end{pmatrix}
\end{aligned}
A = ( 5 1 2 2 4 4 7 3 1 − 3 ) b = ( 1 4 5 )
(1) (x 1 , x 2 x_1, x_2 x 1 , x 2
x B = B − 1 b = ( 2 2 ) \begin{aligned}
\mathbf{x}_B = B^{-1}\mathbf{b} = \binom{2}{2}
\end{aligned}
x B = B − 1 b = ( 2 2 )
基底解はx = ( 2 , 2 , 0 , 0 , 0 ) T \mathbf{x} = (2,2,0,0,0)^T x = ( 2 , 2 , 0 , 0 , 0 ) T
(2) (x 1 , x 4 x_1, x_4 x 1 , x 4
x B = B − 1 b = ( 0 2 ) \begin{aligned}
\mathbf{x}_B = B^{-1}\mathbf{b} = \binom{0}{2}
\end{aligned}
x B = B − 1 b = ( 2 0 )
基底解はx = ( 0 , 0 , 0 , 2 , 0 ) T \mathbf{x} = (0,0,0,2,0)^T x = ( 0 , 0 , 0 , 2 , 0 ) T
(3) (x 1 , x 5 x_1, x_5 x 1 , x 5
x B = B − 1 b = ( 3 − 1 ) \begin{aligned}
\mathbf{x}_B = B^{-1}\mathbf{b} = \binom{3}{-1}
\end{aligned}
x B = B − 1 b = ( − 1 3 )
基底解はx = ( 3 , 0 , 0 , 0 , − 1 ) T \mathbf{x} = (3,0,0,0,-1)^T x = ( 3 , 0 , 0 , 0 , − 1 ) T
(4) (x 2 , x 3 x_2, x_3 x 2 , x 3
B = ( 2 4 2 4 ) \begin{aligned}
B = \begin{pmatrix}
2 & 4
\\
2 & 4
\end{pmatrix}
\end{aligned}
B = ( 2 2 4 4 )
基底解が作れない.
次の線形計画問題を標準形に書き換えよ.
最大化 − 3 x 1 + 4 x 2 − x 3 制約条件 x 1 + x 2 ≥ 5 4 x 1 + x 2 + 2 x 3 ≤ 1 3 x 1 + 4 x 2 + 2 x 3 = 8 x 1 , x 2 ≥ 0 \begin{aligned}
\text{最大化} \qquad &-3x_1 + 4x_2 - x_3
\\
\text{制約条件} \qquad &x_1 + x_2 \geq 5
\\
&4x_1 + x_2 + 2x_3 \leq 1
\\
&3x_1 + 4x_2 + 2x_3 = 8
\\
&x_1, x_2 \geq 0
\end{aligned}
最大化 制約条件 − 3 x 1 + 4 x 2 − x 3 x 1 + x 2 ≥ 5 4 x 1 + x 2 + 2 x 3 ≤ 1 3 x 1 + 4 x 2 + 2 x 3 = 8 x 1 , x 2 ≥ 0
最小化 3 x 1 − 4 x 2 + x 3 + − x 3 − + 0 x 4 + 0 x 5 制約条件 x 1 + x 2 − x 4 = 5 4 x 1 + x 2 + 2 x 3 + − 2 x 3 − + x 5 = 1 3 x 1 + 4 x 2 + 2 x 3 + − 2 x 3 − = 8 x 1 , x 2 , x 3 + , x 3 − , x 4 , x 5 ≥ 0 \begin{aligned}
\text{最小化} \qquad &3x_1 - 4x_2 + x_3^+ - x_3^- + 0x_4 + 0x_5
\\
\text{制約条件} \qquad &x_1 + x_2 - x_4 = 5
\\
&4x_1 + x_2 + 2x_3^+ - 2x_3^- + x_5 = 1
\\
&3x_1 + 4x_2 + 2x_3^+ - 2x_3^- = 8
\\
&x_1, x_2, x_3^+, x_3^-, x_4, x_5 \geq 0
\end{aligned}
最小化 制約条件 3 x 1 − 4 x 2 + x 3 + − x 3 − + 0 x 4 + 0 x 5 x 1 + x 2 − x 4 = 5 4 x 1 + x 2 + 2 x 3 + − 2 x 3 − + x 5 = 1 3 x 1 + 4 x 2 + 2 x 3 + − 2 x 3 − = 8 x 1 , x 2 , x 3 + , x 3 − , x 4 , x 5 ≥ 0
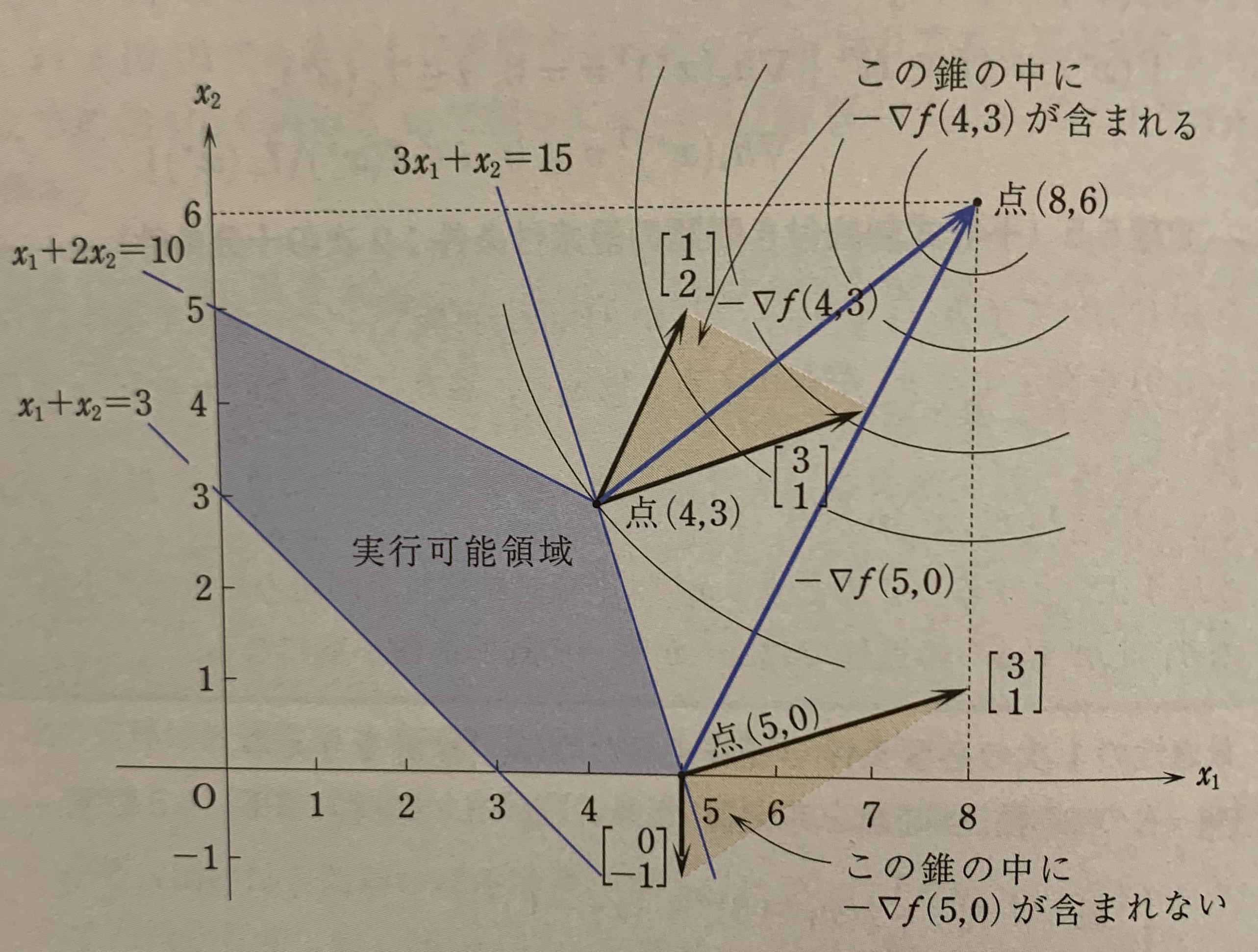
次の線形計画問題それぞれに対し,実行可能領域と目的関数の等高線を図示せよ.さらに,最適解を持つならばそれを求めよ.
まず,標準形に書き換える.ただし,標準形は割愛する.
(1)
最小化 3 x 1 − x 2 制約条件 x 1 − x 2 ≤ 1 − x 1 + x 2 ≤ 2 x 1 , x 2 ≥ 0 \begin{aligned}
\text{最小化} \qquad &3x_1 - x_2
\\
\text{制約条件} \qquad &x_1 - x_2 \leq 1
\\
&-x_1 + x_2 \leq 2
\\
&x_1, x_2 \geq 0
\end{aligned}
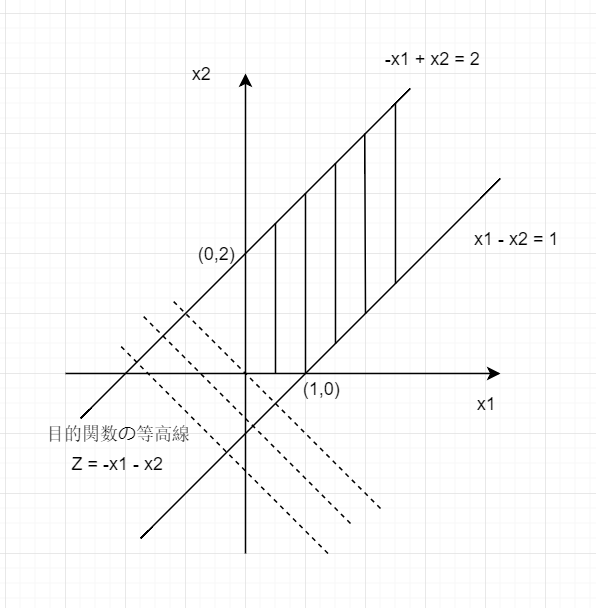
最小化 制約条件 3 x 1 − x 2 x 1 − x 2 ≤ 1 − x 1 + x 2 ≤ 2 x 1 , x 2 ≥ 0
最適解を持つ,最適解はx = ( 0 , 2 ) T \mathbf{x} = (0, 2)^T x = ( 0 , 2 ) T Z m i n = − 2 Z_{min} = -2 Z m i n = − 2
(2)
最小化 − x 1 − x 2 制約条件 x 1 − x 2 ≤ 1 − x 1 + x 2 ≤ 2 x 1 , x 2 ≥ 0 \begin{aligned}
\text{最小化} \qquad &-x_1 - x_2
\\
\text{制約条件} \qquad &x_1 - x_2 \leq 1
\\
&-x_1 + x_2 \leq 2
\\
&x_1, x_2 \geq 0
\end{aligned}
最小化 制約条件 − x 1 − x 2 x 1 − x 2 ≤ 1 − x 1 + x 2 ≤ 2 x 1 , x 2 ≥ 0
最適解が存在しない.
(3)
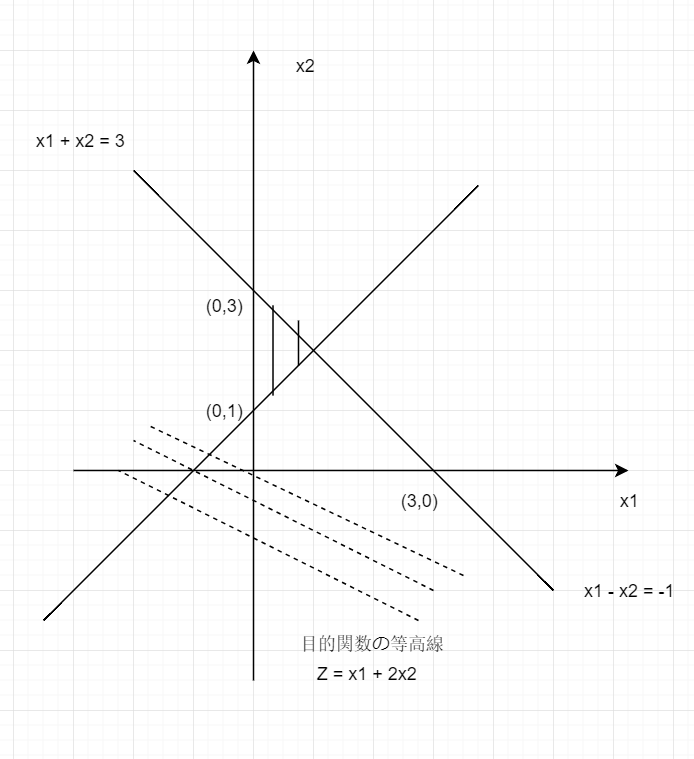
最小化 x 1 + 2 x 2 制約条件 x 1 + x 2 ≤ 3 x 1 − x 2 ≤ − 1 x 1 , x 2 ≥ 0 \begin{aligned}
\text{最小化} \qquad &x_1 + 2x_2
\\
\text{制約条件} \qquad &x_1 + x_2 \leq 3
\\
&x_1 - x_2 \leq -1
\\
&x_1, x_2 \geq 0
\end{aligned}
最小化 制約条件 x 1 + 2 x 2 x 1 + x 2 ≤ 3 x 1 − x 2 ≤ − 1 x 1 , x 2 ≥ 0
最適解を持つ,最適解はx = ( 0 , 1 ) T \mathbf{x} = (0, 1)^T x = ( 0 , 1 ) T Z m i n = 2 Z_{min} = 2 Z m i n = 2
(4)
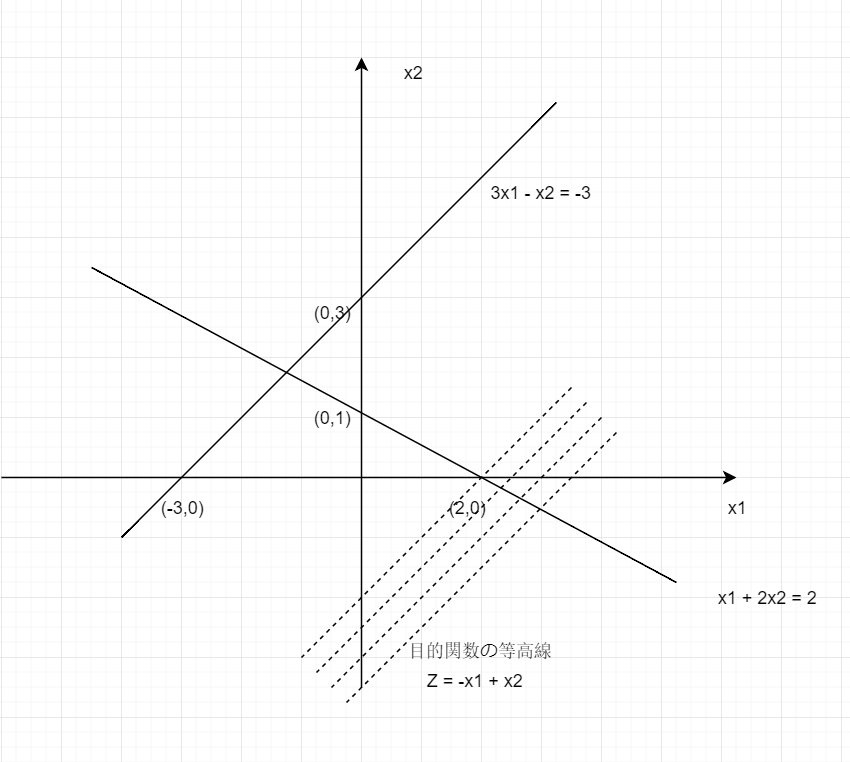
最小化 − x 1 + 2 x 2 制約条件 x 1 + 2 x 2 ≤ 2 3 x 1 − x 2 ≤ − 3 x 1 , x 2 ≥ 0 \begin{aligned}
\text{最小化} \qquad &-x_1 + 2x_2
\\
\text{制約条件} \qquad &x_1 + 2x_2 \leq 2
\\
&3x_1 - x_2 \leq -3
\\
&x_1, x_2 \geq 0
\end{aligned}
最小化 制約条件 − x 1 + 2 x 2 x 1 + 2 x 2 ≤ 2 3 x 1 − x 2 ≤ − 3 x 1 , x 2 ≥ 0
最適解が存在しない.
次の制約条件で定義される実行可能領域において,実行可能基底解を全て求めよ.
A x = b , x ≥ 0 A\mathbf{x} = \mathbf{b}, \qquad \mathbf{x} \geq 0
A x = b , x ≥ 0
A = ( 1 2 2 4 1 3 1 6 ) , x = ( x 1 x 2 x 3 x 4 ) , b = ( 4 5 ) \begin{aligned}
A = \begin{pmatrix}
1 & 2 & 2 & 4
\\
1 & 3 & 1 & 6
\end{pmatrix},
\mathbf{x} = \begin{pmatrix}
x_1
\\
x_2
\\
x_3
\\
x_4
\end{pmatrix},
\mathbf{b} = \begin{pmatrix}
4
\\
5
\end{pmatrix}
\end{aligned}
A = ( 1 1 2 3 2 1 4 6 ) , x = ⎝ ⎜ ⎜ ⎜ ⎛ x 1 x 2 x 3 x 4 ⎠ ⎟ ⎟ ⎟ ⎞ , b = ( 4 5 )
明らかにr a n k A = 2 rank A = 2 r a n k A = 2
(1) (x 1 , x 2 x_1, x_2 x 1 , x 2
x B = B − 1 b = ( 2 1 ) \begin{aligned}
\mathbf{x}_B = B^{-1}\mathbf{b} = \binom{2}{1}
\end{aligned}
x B = B − 1 b = ( 1 2 )
基底解はx = ( 2 , 1 , 0 , 0 ) T \mathbf{x} = (2,1,0,0)^T x = ( 2 , 1 , 0 , 0 ) T
(2) (x 1 , x 3 x_1,x_3 x 1 , x 3
x B = B − 1 b = ( 6 − 1 ) \begin{aligned}
\mathbf{x}_B = B^{-1}\mathbf{b} = \binom{6}{-1}
\end{aligned}
x B = B − 1 b = ( − 1 6 )
基底解はx = ( 6 , 0 , − 1 , 0 ) T \mathbf{x} = (6,0,-1,0)^T x = ( 6 , 0 , − 1 , 0 ) T
(3) (x 1 , x 4 x_1,x_4 x 1 , x 4
x B = B − 1 b = ( 2 1 2 ) \begin{aligned}
\mathbf{x}_B = B^{-1}\mathbf{b} = \binom{2}{\frac{1}{2}}
\end{aligned}
x B = B − 1 b = ( 2 1 2 )
基底解はx = ( 2 , 0 , 0 , 1 2 ) T \mathbf{x} = (2,0,0,\frac{1}{2})^T x = ( 2 , 0 , 0 , 2 1 ) T
(4) (x 2 , x 3 x_2,x_3 x 2 , x 3
x B = B − 1 b = ( 3 2 1 2 ) \begin{aligned}
\mathbf{x}_B = B^{-1}\mathbf{b} = \binom{\frac{3}{2}}{\frac{1}{2}}
\end{aligned}
x B = B − 1 b = ( 2 1 2 3 )
基底解はx = ( 0 , 3 2 , 1 2 , 0 ) T \mathbf{x} = (0,\frac{3}{2},\frac{1}{2},0)^T x = ( 0 , 2 3 , 2 1 , 0 ) T
(5) (x 2 , x 4 x_2,x_4 x 2 , x 4
行列Aの2列目と3列目は線型従属なので,(x 2 , x 4 x_2,x_4 x 2 , x 4
(6) (x 3 , x 4 x_3,x_4 x 3 , x 4
x B = B − 1 b = ( 1 2 3 4 ) \begin{aligned}
\mathbf{x}_B = B^{-1}\mathbf{b} = \binom{\frac{1}{2}}{\frac{3}{4}}
\end{aligned}
x B = B − 1 b = ( 4 3 2 1 )
基底解はx = ( 0 , 0 , 1 2 , 3 4 ) T \mathbf{x} = (0,0,\frac{1}{2},\frac{3}{4})^T x = ( 0 , 0 , 2 1 , 4 3 ) T
定理: 線型計画問題の標準形が与られたとき,以下のことが成り立つ.
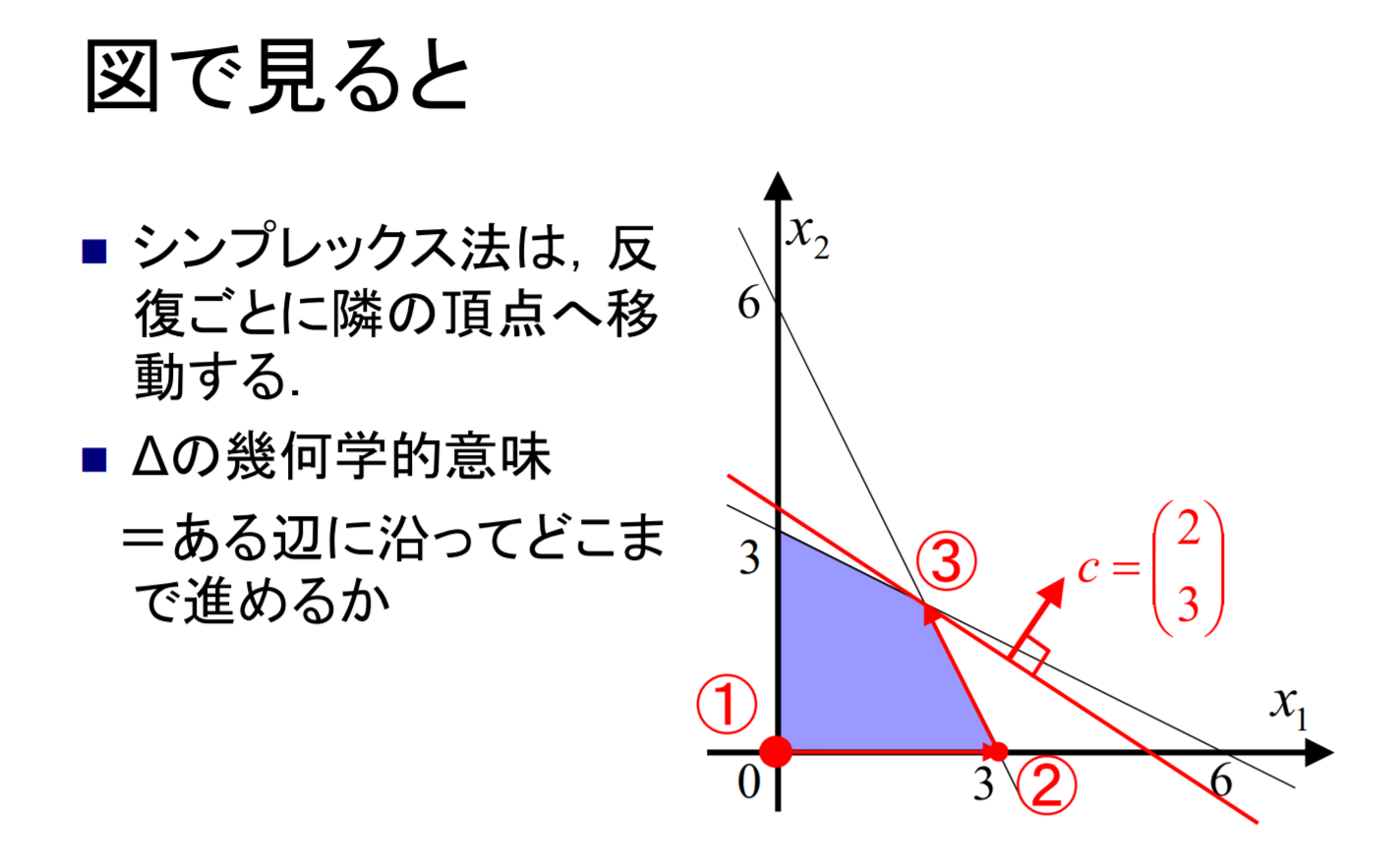
この定理から分かること:基底解のみを考えれば十分
この節では,線型計画問題の標準形を解くための単体法(シンプレックス法,simplex method)を紹介する.単体法基本的な原理は,1組の実行可能基底解が与られた時,目的関数値がより低くなるような新しい実行可能基底解を効率よく求め,そうした実行可能基底形式を順々に求めていくことによって,最終的に最適解に到達するものである.
標準形A x = b , x ≥ 0 A : R m × n ( m < n , r a n k A = m ) A\mathbf{x} = \mathbf{b}, x \geq 0 \quad A:\mathbb{R}^{m \times n} (m < n, rank A = m) A x = b , x ≥ 0 A : R m × n ( m < n , r a n k A = m )
A = ( B , N ) , x = ( x B x N ) ⇒ B x B + N x N = b c = ( c B c N ) ⇒ c T x = c B T x B + c N T x N = c B T B − 1 b + ( c N T − c B T B − 1 N ) x N \begin{aligned}
A &= (B, N), \mathbf{x} = \binom{x_B}{x_N} \Rightarrow B\mathbf{x}_B + N\mathbf{x}_N = \mathbf{b}
\\
\mathbf{c} &= \binom{c_B}{c_N} \Rightarrow \mathbf{c}^T\mathbf{x} = \mathbf{c}_B^T \mathbf{x}_B + \mathbf{c}_N^T \mathbf{x}_N = \mathbf{c}_B^T B^{-1} \mathbf{b} + (\mathbf{c}_N^T - \mathbf{c}_B^T B^{-1}N) \mathbf{x}_N
\end{aligned}
A c = ( B , N ) , x = ( x N x B ) ⇒ B x B + N x N = b = ( c N c B ) ⇒ c T x = c B T x B + c N T x N = c B T B − 1 b + ( c N T − c B T B − 1 N ) x N
ここで,B B B x = ( B − 1 b 0 ) \mathbf{x} = \binom{B^{-1}\mathbf{b}}{0} x = ( 0 B − 1 b )
B − 1 b ≥ 0 かつ c N T − c B T B − 1 N ≥ 0 ⇒ 最適解 B^{-1}\mathbf{b} \geq 0 \text{かつ} \mathbf{c}_N^T - \mathbf{c}_B^T B^{-1}N \geq 0 \Rightarrow \text{最適解}
B − 1 b ≥ 0 かつ c N T − c B T B − 1 N ≥ 0 ⇒ 最適解
c N T − c B T B − 1 N ≥ 0 \mathbf{c}_N^T - \mathbf{c}_B^T B^{-1}N \geq 0 c N T − c B T B − 1 N ≥ 0 ( c N T − c B T B − 1 N ) k < 0 (\mathbf{c}_N^T - \mathbf{c}_B^T B^{-1}N)_k < 0 ( c N T − c B T B − 1 N ) k < 0 x k : 0 → Δ x_k:0 \rightarrow \Delta x k : 0 → Δ
よって,目的関数値が減少,現在の基底解は最適解ではない.なら,x k x_k x k
x k : 0 → Δ > 0 x_k:0 \rightarrow \Delta > 0 x k : 0 → Δ > 0
目的関数c B T B − 1 b + ( c N T − c B T B − 1 N ) k Δ \mathbf{c}_B^T B^{-1} \mathbf{b} + (\mathbf{c}_N^T - \mathbf{c}_B^T B^{-1}N)_k \Delta c B T B − 1 b + ( c N T − c B T B − 1 N ) k Δ
基底変数x B = B − 1 b → x B ‾ = B − 1 b − Δ B − 1 A k ( A k は行列 A の第 k 列 ) \mathbf{x}_B = B^{-1}\mathbf{b} \rightarrow \overline{\mathbf{x}_B} = B^{-1} \mathbf{b} - \Delta B^{-1} A_k (A_k\text{は行\text{列}}A\text{の第}k\text{列}) x B = B − 1 b → x B = B − 1 b − Δ B − 1 A k ( A k は行 列 A の第 k 列 )
x k ‾ ≥ 0 \overline{\mathbf{x}_k} \geq 0 x k ≥ 0 b ‾ = B − 1 b , y = B − 1 A k \overline{\mathbf{b}} = B^{-1}\mathbf{b}, y = B^{-1}A_k b = B − 1 b , y = B − 1 A k
Δ = min { b i ‾ / y i ∣ y i > 0 ( i = i , K , m ) } \Delta = \min \lbrace \overline{\mathbf{b}_i} / y_i \ |\ y_i > 0(i = i,K,m) \rbrace
Δ = min { b i / y i ∣ y i > 0 ( i = i , K , m ) }
まで大きくできる.
そして,x k : 0 → Δ > 0 x_k:0 \rightarrow \Delta > 0 x k : 0 → Δ > 0
Δ = b i ‾ / y i \Delta = \overline{\mathbf{b}_i} / y_i Δ = b i / y i x i → 0 x_i \rightarrow 0 x i → 0
x i → 非基底変数 \mathbf{x}_i \rightarrow \text{非基底変数} x i → 非基底変数 x k → 基底変数 \mathbf{x}_k \rightarrow \text{基底変数} x k → 基底変数
というピボット操作(基底変数の入れ替え)を行う.
x B ‾ = x B − Δ y ≥ 0 \overline{\mathbf{x}_B} = \mathbf{x}_B - \Delta y \geq 0 x B = x B − Δ y ≥ 0 y i > 0 y_i > 0 y i > 0
Δ : \Delta: Δ : 目的関数をいくらでも小さくできる,つまり,有界でない.
step0:初期実行可能基底解(x B , x N x_B,x_N x B , x N B − 1 b , 0 B^{-1}b,0 B − 1 b , 0 b ‾ = B − 1 b \overline{b} = B^{-1}b b = B − 1 b
step1:c N T − c B T B − 1 N ≥ 0 c_N^T - c_B^T B^{-1}N \geq 0 c N T − c B T B − 1 N ≥ 0 x B x_B x B ( c N T − c B T B − 1 N ) k < 0 (c_N^T - c_B^T B^{-1}N)_k < 0 ( c N T − c B T B − 1 N ) k < 0 x k x_k x k
step2:y = B − 1 A k y = B^{-1}A_k y = B − 1 A k
step3:y ≤ 0 y \leq 0 y ≤ 0 Δ \Delta Δ Δ = b i ‾ / y i \Delta = \overline{b_i} / y_i Δ = b i / y i Δ = min { b i ‾ / y i ∣ y i > 0 ( i = 1 , K , m ) } \Delta = \min \lbrace \overline{b_i} / y_i \ |\ y_i > 0(i = 1,K,m) \rbrace Δ = min { b i / y i ∣ y i > 0 ( i = 1 , K , m ) }
step4:非基底変数x k ← Δ x_k \leftarrow \Delta x k ← Δ x B ← b ‾ − Δ y x_B \leftarrow \overline{b} - \Delta y x B ← b − Δ y
簡単な言葉で言い換えると
step0:実行可能基底解を得る
step1:入る変数を選ぶ.wの係数 < 0の非基底変数.もし,そのような変数がない場合は⇒ \Rightarrow ⇒
step2:出る変数を選ぶ.入る変数を0から増やす時,最終に0になる変数(基底変数).入る変数の列を見て,正のところの比をとって,比の最小値を選ぶ.
step3:もし,全ての入る変数の列が全て0以下ならば,LPは非有界と判定して,終了.そうでなければ,step1へ.
例題:以下の標準形をシンプレックス法で求める
最小化 − 2 x 1 + 3 x 2 制約条件 2 x 1 + x 2 + x 3 = 6 x 1 + 2 x 2 + x 4 = 6 x 1 , x 2 , x 3 , x 4 ≥ 0 \begin{aligned}
\text{最小化} \qquad &-2x_1 + 3x_2
\\
\text{制約条件} \qquad &2x_1 + x_2 + x_3 = 6
\\
&x_1 + 2x_2 + x_4 = 6
\\
&x_1, x_2, x_3, x_4 \geq 0
\end{aligned}
最小化 制約条件 − 2 x 1 + 3 x 2 2 x 1 + x 2 + x 3 = 6 x 1 + 2 x 2 + x 4 = 6 x 1 , x 2 , x 3 , x 4 ≥ 0
注意すること: 常に基底変数x B x_B x B x N x_N x N
次は単体表で求める.
例題1:次の最小化問題を考える.
最小化 w = − 5 x 1 − 4 x 2 制約条件 5 x 1 + 2 x 2 ≤ 30 x 1 + 2 x 2 ≤ 14 x 1 ≥ 0 , x 2 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = -5x_1 - 4x_2
\\
\text{制約条件} \qquad &5x_1 + 2x_2 \leq 30
\\
&x_1 + 2x_2 \leq 14
\\
&x_1 \geq 0, \quad x_2 \geq 0
\end{aligned}
最小化 制約条件 w = − 5 x 1 − 4 x 2 5 x 1 + 2 x 2 ≤ 3 0 x 1 + 2 x 2 ≤ 1 4 x 1 ≥ 0 , x 2 ≥ 0
標準形の形にする.
最小化 w = − 5 x 1 − 4 x 2 制約条件 5 x 1 + 2 x 2 + x 3 = 30 x 1 + 2 x 2 + x 4 = 14 x 1 , x 2 , x 3 , x 4 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = -5x_1 - 4x_2
\\
\text{制約条件} \qquad &5x_1 + 2x_2 + x_3 = 30
\\
&x_1 + 2x_2 + x_4 = 14
\\
&x_1, x_2, x_3, x_4 \geq 0
\end{aligned}
最小化 制約条件 w = − 5 x 1 − 4 x 2 5 x 1 + 2 x 2 + x 3 = 3 0 x 1 + 2 x 2 + x 4 = 1 4 x 1 , x 2 , x 3 , x 4 ≥ 0
実行可能基底解がある
目的関数wにおいて基底変数の係数は全て0
非基底変数のいずれかの値を0から増やす
選ぶ基準:wの値が改善するもの → \rightarrow →
入る変数:最大係数規則 → \rightarrow →
ピポット演算:表の書き換え
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 定数
比
5
2
1
0
30
30 5 \frac{30}{5} 5 3 0
1
2
0
1
14
14 1 \frac{14}{1} 1 1 4
− w -w − w -5
-4
0
0
0
-
基底変数 x 3 , x 4 x_3,x_4 x 3 , x 4 基底変数の値 30,14単位行列 目的関数において基底変数の係数は全て0
ここで,非基底変数x 1 , x 2 x_1,x_2 x 1 , x 2 x 1 = − 5 , x 2 = − 4 x_1 = -5, x_2 = -4 x 1 = − 5 , x 2 = − 4 x 1 x_1 x 1
どこまでx 1 x_1 x 1 x 3 , x 4 ≥ 0 x_3,x_4 \geq 0 x 3 , x 4 ≥ 0
ここで,x 2 x_2 x 2
5 x 1 + x 3 = 30 → x 3 = 30 − 5 x 1 ≥ 0 → x 1 ≤ 30 5 5x_1 + x_3 = 30 \rightarrow x_3 = 30 - 5x_1 \geq 0 \rightarrow x_1 \leq \frac{30}{5} 5 x 1 + x 3 = 3 0 → x 3 = 3 0 − 5 x 1 ≥ 0 → x 1 ≤ 5 3 0 x 1 + x 4 = 14 → x 4 = 14 − x 1 ≥ 0 → x 1 ≤ 14 1 x_1 + x_4 = 14 \rightarrow x_4 = 14 - x_1 \geq 0 \rightarrow x_1 \leq \frac{14}{1} x 1 + x 4 = 1 4 → x 4 = 1 4 − x 1 ≥ 0 → x 1 ≤ 1 1 4
つまり,x 1 x_1 x 1 x 3 x_3 x 3 x 1 = 6 の時 , x 3 = 0 x 1 と x 3 の役割が交換 x_1 = 6\text{の時},x_3 = 0 x_1\text{と}x_3\text{の役割が交換} x 1 = 6 の時 , x 3 = 0 x 1 と x 3 の役割が交換
x 1 : 非基底変数 → 基底変数 x_1:\text{非基底変数} \rightarrow \text{基底変数} x 1 : 非基底変数 → 基底変数 x 3 : 基底変数 → 非基底変数 x_3:\text{基底変数} \rightarrow \text{非基底変数} x 3 : 基底変数 → 非基底変数 出る変数:x 3 x_3 x 3
次に入る変数の列を掃き出す:
基底変数の列を集めると単位行列になる
wの係数は0
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 定数
比
1
2 5 \frac{2}{5} 5 2 1 5 \frac{1}{5} 5 1 0
6
30 2 \frac{30}{2} 2 3 0
0
8 5 \frac{8}{5} 5 8 − 1 5 -\frac{1}{5} − 5 1 1
8
40 8 \frac{40}{8} 8 4 0
− w -w − w 0
-2
1
0
30
-
ここで,非基底変数x 2 , x 3 x_2,x_3 x 2 , x 3 x 2 x_2 x 2 x 2 x_2 x 2
第2反復では,入る変数はx 2 x_2 x 2
x 1 = 6 − 2 5 x 2 ≥ 0 → x 2 ≤ 30 2 x_1 = 6 - \frac{2}{5}x_2 \geq 0 \rightarrow x_2 \leq \frac{30}{2} x 1 = 6 − 5 2 x 2 ≥ 0 → x 2 ≤ 2 3 0 x 4 = 8 − 8 5 x 2 ≥ 0 → x 2 ≤ 40 8 x_4 = 8 - \frac{8}{5}x_2 \geq 0 \rightarrow x_2 \leq \frac{40}{8} x 4 = 8 − 5 8 x 2 ≥ 0 → x 2 ≤ 8 4 0
比はx 4 x_4 x 4 x 4 x_4 x 4
次に入る変数x 2 x_2 x 2 x 2 と x 4 x_2\text{と}x_4 x 2 と x 4
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 定数
1
0
1 4 \frac{1}{4} 4 1 − 1 4 -\frac{1}{4} − 4 1 4
0
1
− 1 8 -\frac{1}{8} − 8 1 5 8 \frac{5}{8} 8 5 5
− w -w − w 0
0
3 4 \frac{3}{4} 4 3 5 4 \frac{5}{4} 4 5 40
第3反復で,目的関数の非基底変数の関数≥ 0 \geq 0 ≥ 0
最適値と最適解は
x 1 ∗ = 4 , x 2 ∗ = 5 , ( x 3 ∗ = 0 , x 4 ∗ = 0 ) w ∗ = − 40 x_1^* = 4, x_2^* = 5, (x_3^* = 0, x_4^* = 0) \quad w^* = -40
x 1 ∗ = 4 , x 2 ∗ = 5 , ( x 3 ∗ = 0 , x 4 ∗ = 0 ) w ∗ = − 4 0
となる.
例題2:次の最小化問題を考える.
最小化 w = − 5 x 1 − 4 x 2 − 3 x 3 制約条件 2 x 1 + 3 x 2 + x 3 ≤ 5 4 x 1 + x 2 + x 3 ≤ 11 3 x 1 + 4 x 2 + 2 x 3 ≤ 8 x 1 ≥ 0 , x 2 ≥ 0 , x 3 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = -5x_1 - 4x_2 - 3x_3
\\
\text{制約条件} \qquad &2x_1 + 3x_2 + x_3 \leq 5
\\
&4x_1 + x_2 + x_3 \leq 11
\\
&3x_1 + 4x_2 + 2x_3 \leq 8
\\
&x_1 \geq 0, \quad x_2 \geq 0, \quad x_3 \geq 0
\end{aligned}
最小化 制約条件 w = − 5 x 1 − 4 x 2 − 3 x 3 2 x 1 + 3 x 2 + x 3 ≤ 5 4 x 1 + x 2 + x 3 ≤ 1 1 3 x 1 + 4 x 2 + 2 x 3 ≤ 8 x 1 ≥ 0 , x 2 ≥ 0 , x 3 ≥ 0
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
比
2
3
1
1
0
0
5
5 2 \frac{5}{2} 2 5
4
1
1
0
1
0
11
11 4 \frac{11}{4} 4 1 1
3
4
2
0
0
1
8
3 8 \frac{3}{8} 8 3
− w -w − w -5
-4
-3
0
0
0
0
-
まず,非基底変数x 1 , x 2 , x 3 x_1,x_2,x_3 x 1 , x 2 , x 3 x 1 = − 5 , x 2 = − 4 , x 3 = − 3 x_1 = -5, x_2 = -4, x_3 = -3 x 1 = − 5 , x 2 = − 4 , x 3 = − 3 x 1 x_1 x 1
次に出る変数を選ぶ.比を計算すると,値が一番小さいのは5 2 \frac{5}{2} 2 5 x 4 x_4 x 4
よって,ピボット演算をやる.
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
比
1
3 2 \frac{3}{2} 2 3 1 2 \frac{1}{2} 2 1 1 2 \frac{1}{2} 2 1 0
0
5 1 \frac{5}{1} 1 5
0
-5
-1
-2
1
0
1
-
0
− 1 2 -\frac{1}{2} − 2 1 1 2 \frac{1}{2} 2 1 − 3 2 -\frac{3}{2} − 2 3 0
1
1 1 \frac{1}{1} 1 1
− w -w − w 0
7 2 \frac{7}{2} 2 7 − 1 2 -\frac{1}{2} − 2 1 5 2 \frac{5}{2} 2 5 0
0
25 2 \frac{25}{2} 2 2 5 -
次にx 3 x_3 x 3 x 5 = 1 + x 3 → x 3 に制限なし ( x 3 ≥ − 1 ) x_5 = 1 + x_3 \rightarrow x_3\text{に制限なし}(x_3 \geq -1) x 5 = 1 + x 3 → x 3 に制限なし ( x 3 ≥ − 1 )
x 6 x_6 x 6 x 6 x_6 x 6
次はピボットをする.
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
比
1
2
0
2
0
-1
2
5 1 \frac{5}{1} 1 5
0
-6
0
-5
1
2
2
-
0
-1
1
-3
0
2
1
1 1 \frac{1}{1} 1 1
− w -w − w 0
3
0
1
0
1
13
-
非基底変数x 2 , x 4 , x 6 x_2,x_4,x_6 x 2 , x 4 , x 6
出る変数を選ぶ時に,列を縦で見て,係数がマイナスとゼロものがいたら,それは比には参加しない.
例題3:次の最小化問題を考える.
最小化 w = − 5 x 1 − 4 x 2 制約条件 4 x 1 − 5 x 2 ≤ 12 − 4 x 1 + 5 x 2 ≤ 15 x 1 ≥ 0 , x 2 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = -5x_1 - 4x_2
\\
\text{制約条件} \qquad &4x_1 - 5x_2 \leq 12
\\
&-4x_1 + 5x_2 \leq 15
\\
&x_1 \geq 0, \quad x_2 \geq 0
\end{aligned}
最小化 制約条件 w = − 5 x 1 − 4 x 2 4 x 1 − 5 x 2 ≤ 1 2 − 4 x 1 + 5 x 2 ≤ 1 5 x 1 ≥ 0 , x 2 ≥ 0
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 定数
4
0
1
0
-4
1
0
1
-
− w -w − w -5
0
0
0
0
まず,非基底変数x 1 x_1 x 1 x 1 x_1 x 1
次に比を計算すると一番小さいx 3 x_3 x 3
ピボットをやると(ピボットの点を1になる)
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 定数
1
− 5 4 -\frac{5}{4} − 4 5 1 4 \frac{1}{4} 4 1 0
3
0
0
1
1
27
− w -w − w 0
− 41 4 -\frac{41}{4} − 4 4 1 5 4 \frac{5}{4} 4 5 0
15
今度入る変数を選ぶと,x 2 x_2 x 2
⇒ x 2 \Rightarrow x_2 ⇒ x 2 ⇒ x 2 \Rightarrow x_2 ⇒ x 2 ⇒ \Rightarrow ⇒
入る変数を選んだ後,出る変数が選べなかったら,それは入る変数は好きなだけ大きくしていいよっていうことだから.元のLPが非有界で安定されて終了になる.
次の線型計画問題それぞれに対して単体法を適用せよ
(1)
最小化 w = − x 1 − 3 x 2 − 2 x 3 制約条件 − x 1 + 2 x 2 − x 3 ≤ 4 − x 1 + 2 x 2 + 2 x 3 ≤ 2 x 1 − x 2 + x 3 ≤ 2 x 1 , x 2 , x 3 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = -x_1 - 3x_2 - 2x_3
\\
\text{制約条件} \qquad &-x_1 + 2x_2 - x_3 \leq 4
\\
&-x_1 + 2x_2 + 2x_3 \leq 2
\\
&x_1 - x_2 + x_3 \leq 2
\\
&x_1, x_2, x_3 \geq 0
\end{aligned}
最小化 制約条件 w = − x 1 − 3 x 2 − 2 x 3 − x 1 + 2 x 2 − x 3 ≤ 4 − x 1 + 2 x 2 + 2 x 3 ≤ 2 x 1 − x 2 + x 3 ≤ 2 x 1 , x 2 , x 3 ≥ 0
入る変数x 2 x_2 x 2 x 5 x_5 x 5
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
比
-1
2
-1
1
0
0
4
4 2 \frac{4}{2} 2 4
-1
2
2
0
1
0
2
2 2 \frac{2}{2} 2 2
1
-1
1
0
0
1
2
-
− w -w − w -1
-3
-2
0
0
0
0
-
入る変数x 1 x_1 x 1 x 6 x_6 x 6
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
比
0
0
-3
1
-1
0
2
-
1
1
0
1 2 \frac{1}{2} 2 1 0
1
-
1 2 \frac{1}{2} 2 1 0
2
0
1 2 \frac{1}{2} 2 1 1
3
3 1 2 \frac{3}{\frac{1}{2}} 2 1 3
− w -w − w − 5 2 -\frac{5}{2} − 2 5 0
1
0
3 2 \frac{3}{2} 2 3 0
3
-
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
0
0
-3
1
-1
0
2
0
1
3
0
1
1
4
1
0
4
0
1
2
6
− w -w − w 0
0
11
0
4
5
18
目的関数の非基底変数の関数 ≥ 0 \geq 0 ≥ 0 x 1 = 6 , x 2 = 4 , x 3 = 0 x_1 = 6, x_2 = 4, x_3 = 0 x 1 = 6 , x 2 = 4 , x 3 = 0
(2)
最小化 w = − x 1 − 2 x 2 制約条件 x 1 − 2 x 2 ≤ 1 − x 1 + x 2 ≤ 2 x 1 , x 2 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = -x_1 - 2x_2
\\
\text{制約条件} \qquad &x_1 - 2x_2 \leq 1
\\
&-x_1 + x_2 \leq 2
\\
&x_1, x_2 \geq 0
\end{aligned}
最小化 制約条件 w = − x 1 − 2 x 2 x 1 − 2 x 2 ≤ 1 − x 1 + x 2 ≤ 2 x 1 , x 2 ≥ 0
入る変数x 2 x_2 x 2 x 4 x_4 x 4
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 定数
比
1
-2
1
0
1
-
-1
1
0
1
2
2 1 \frac{2}{1} 1 2
− w -w − w -1
-2
0
0
0
-
掃き出しをすると
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 定数
-1
0
1
2
5
-1
1
0
1
2
− w -w − w -3
0
0
2
4
第1列の値が全部0以下で,出る変数が選べなかったので,元のLPは非有界である.
今までの例から類推できることをまとめると次の通りである.
初期実行可能基底が容易に分からない時(そもそも実行可能かも分からない時)に適用する方法.
第1段階は補助変数(人為変数)を加えた補助問題を作り,解く.この補助問題の特徴は元のLPが実行可能⇔ \Leftrightarrow ⇔
第2段階は補助問題最適解=0の時:最終的な単体表から元のLPの実行可能基底が作れる.この基底解を初期段階として単体表を適用する.
例題1:
最小化 w = 2 x 1 + 3 x 2 制約条件 4 x 1 + x 2 ≥ 13 3 x 1 + 2 x 2 ≥ 16 x 1 + 2 x 2 ≥ 8 x 1 , x 2 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = 2x_1 + 3x_2
\\
\text{制約条件} \qquad &4x_1 + x_2 \geq 13
\\
&3x_1 + 2x_2 \geq 16
\\
&x_1 + 2x_2 \geq 8
\\
&x_1, x_2 \geq 0
\end{aligned}
最小化 制約条件 w = 2 x 1 + 3 x 2 4 x 1 + x 2 ≥ 1 3 3 x 1 + 2 x 2 ≥ 1 6 x 1 + 2 x 2 ≥ 8 x 1 , x 2 ≥ 0
明らかに実行可能ではないため,スラック変数を入れる.
最小化 w = 2 x 1 + 3 x 2 制約条件 4 x 1 + x 2 − x 3 = 13 3 x 1 + 2 x 2 − x 4 = 16 x 1 + 2 x 2 − x 5 = 8 x 1 , x 2 , x 3 , x 4 , x 5 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = 2x_1 + 3x_2
\\
\text{制約条件} \qquad &4x_1 + x_2 - x_3 = 13
\\
&3x_1 + 2x_2 - x_4 = 16
\\
&x_1 + 2x_2 - x_5 = 8
\\
&x_1, x_2, x_3, x_4, x_5 \geq 0
\end{aligned}
最小化 制約条件 w = 2 x 1 + 3 x 2 4 x 1 + x 2 − x 3 = 1 3 3 x 1 + 2 x 2 − x 4 = 1 6 x 1 + 2 x 2 − x 5 = 8 x 1 , x 2 , x 3 , x 4 , x 5 ≥ 0
各式に補助変数v i v_i v i
最小化 w = 2 x 1 + 3 x 2 制約条件 4 x 1 + x 2 − x 3 + v 1 = 13 3 x 1 + 2 x 2 − x 4 + v 2 = 16 x 1 + 2 x 2 − x 5 + v 3 = 8 x 1 , x 2 , x 3 , x 4 , x 5 ≥ 0 , v 1 , v 2 , v 3 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = 2x_1 + 3x_2
\\
\text{制約条件} \qquad &4x_1 + x_2 - x_3 + v_1 = 13
\\
&3x_1 + 2x_2 - x_4 + v_2 = 16
\\
&x_1 + 2x_2 - x_5 + v_3 = 8
\\
&x_1, x_2, x_3, x_4, x_5 \geq 0, v_1, v_2, v_3 \geq 0
\end{aligned}
最小化 制約条件 w = 2 x 1 + 3 x 2 4 x 1 + x 2 − x 3 + v 1 = 1 3 3 x 1 + 2 x 2 − x 4 + v 2 = 1 6 x 1 + 2 x 2 − x 5 + v 3 = 8 x 1 , x 2 , x 3 , x 4 , x 5 ≥ 0 , v 1 , v 2 , v 3 ≥ 0
こういう形にすると,強制的に入れたv 1 , v 2 , v 3 v_1,v_2,v_3 v 1 , v 2 , v 3
目的関数はu = v 1 + v 2 + v 3 u = v_1 + v_2 + v_3 u = v 1 + v 2 + v 3 ⇔ u ∗ = 0 \Leftrightarrow u^* = 0 ⇔ u ∗ = 0
最小化 v 1 + v 2 + v 3 制約条件 4 x 1 + x 2 − x 3 + v 1 = 13 3 x 1 + 2 x 2 − x 4 + v 2 = 16 x 1 + 2 x 2 − x 5 + v 3 = 8 x 1 , x 2 , x 3 , x 4 , x 5 ≥ 0 , v 1 , v 2 , v 3 ≥ 0 \begin{aligned}
\text{最小化} \qquad &v_1 + v_2 + v_3
\\
\text{制約条件} \qquad &4x_1 + x_2 - x_3 + v_1 = 13
\\
&3x_1 + 2x_2 - x_4 + v_2 = 16
\\
&x_1 + 2x_2 - x_5 + v_3 = 8
\\
&x_1, x_2, x_3, x_4, x_5 \geq 0, v_1, v_2, v_3 \geq 0
\end{aligned}
最小化 制約条件 v 1 + v 2 + v 3 4 x 1 + x 2 − x 3 + v 1 = 1 3 3 x 1 + 2 x 2 − x 4 + v 2 = 1 6 x 1 + 2 x 2 − x 5 + v 3 = 8 x 1 , x 2 , x 3 , x 4 , x 5 ≥ 0 , v 1 , v 2 , v 3 ≥ 0
こんなLPになるが,問題は目的関数が非基底変数であり,目的関数uをx 1 , ⋯ , x 5 x_1, \cdots, x_5 x 1 , ⋯ , x 5
v 1 = 13 − 4 x 1 − x 2 + x 3 v 2 = 16 − 3 x 1 − 2 x 2 + x 4 v 3 = 8 − x 1 − 2 x 2 + x 5 v 1 + v 2 + v 3 = 37 − 8 x 1 − 5 x 2 + x 3 + x 4 + x 5 \begin{aligned}
v_1 &= 13 - 4x_1 - x_2 + x_3
\\
v_2 &= 16 - 3x_1 - 2x_2 + x_4
\\
v_3 &= 8 - x_1 - 2x_2 + x_5
\\
v_1 + v_2 + v_3 &= 37 - 8x_1 - 5x_2 + x_3 + x_4 + x_5
\end{aligned}
v 1 v 2 v 3 v 1 + v 2 + v 3 = 1 3 − 4 x 1 − x 2 + x 3 = 1 6 − 3 x 1 − 2 x 2 + x 4 = 8 − x 1 − 2 x 2 + x 5 = 3 7 − 8 x 1 − 5 x 2 + x 3 + x 4 + x 5
という準備が必要である.この準備をしとけば,単体法の要件であった目的関数は基底変数の係数が全部0というものを満たすことができる.
次に単体表を作る:
反復1
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 v 1 v_1 v 1 v 2 v_2 v 2 v 3 v_3 v 3 定数
比
v 1 v_1 v 1 4
1
-1
0
0
1
0
0
13
13 4 \frac{13}{4} 4 1 3
v 2 v_2 v 2 3
2
0
-1
0
0
1
0
16
16 3 \frac{16}{3} 3 1 6
v 3 v_3 v 3 1
2
0
0
-1
0
0
1
8
8 1 \frac{8}{1} 1 8
-u
-8
-5
1
1
1
0
0
0
-37
-
-w
2
3
0
0
0
0
0
0
0
-
表の色の部分に注目すると,基底変数v 1 , v 2 , v 3 v_1,v_2,v_3 v 1 , v 2 , v 3
では,ピボット演算をする.まず,入る変数を選ぶ.入る変数は目的関数uの係数がマイナスものかつ絶対値が大きい方x 1 x_1 x 1
次は,x 1 x_1 x 1 v 1 v_1 v 1 v 1 v_1 v 1
反復2
v 1 v_1 v 1 x 1 x_1 x 1 x 1 x_1 x 1
掃き出しをしたら,入る変数としてx 2 x_2 x 2
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 v 1 v_1 v 1 v 2 v_2 v 2 v 3 v_3 v 3 定数
比
x 1 x_1 x 1 1
1 4 \frac{1}{4} 4 1 − 1 4 -\frac{1}{4} − 4 1 0
0
1 4 \frac{1}{4} 4 1 0
0
13 4 \frac{13}{4} 4 1 3 13
v 2 v_2 v 2 0
5 4 \frac{5}{4} 4 5 3 4 \frac{3}{4} 4 3 -1
0
− 3 4 -\frac{3}{4} − 4 3 1
0
25 4 \frac{25}{4} 4 2 5 5
v 3 v_3 v 3 0
7 4 \frac{7}{4} 4 7 1 4 \frac{1}{4} 4 1 0
-1
− 1 4 -\frac{1}{4} − 4 1 0
1
19 4 \frac{19}{4} 4 1 9 19 7 \frac{19}{7} 7 1 9
-u
0
-3
-2
1
1
2
0
0
-11
-
-w
0
5 2 \frac{5}{2} 2 5 1 2 \frac{1}{2} 2 1 0
0
− 1 2 -\frac{1}{2} − 2 1 0
0
− 13 2 -\frac{13}{2} − 2 1 3 -
v 3 v_3 v 3
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 v 1 v_1 v 1 v 2 v_2 v 2 v 3 v_3 v 3 定数
比
x 1 x_1 x 1 1
0
− 2 7 -\frac{2}{7} − 7 2 0
1 7 \frac{1}{7} 7 1 2 7 \frac{2}{7} 7 2 0
− 1 7 -\frac{1}{7} − 7 1 18 7 \frac{18}{7} 7 1 8 18
v 2 v_2 v 2 0
0
4 7 \frac{4}{7} 7 4 -1
5 7 \frac{5}{7} 7 5 − 4 7 -\frac{4}{7} − 7 4 1
− 5 7 -\frac{5}{7} − 7 5 20 7 \frac{20}{7} 7 2 0 4
x 2 x_2 x 2 0
1
1 7 \frac{1}{7} 7 1 0
− 1 7 -\frac{1}{7} − 7 1 0
4 7 \frac{4}{7} 7 4 19 7 \frac{19}{7} 7 1 9 -
-u
0
0
− 4 7 -\frac{4}{7} − 7 4 1
− 5 7 -\frac{5}{7} − 7 5 11 7 \frac{11}{7} 7 1 1 0
12 7 \frac{12}{7} 7 1 2 − 20 7 -\frac{20}{7} − 7 2 0 -
-w
0
0
1 7 \frac{1}{7} 7 1 0
10 7 \frac{10}{7} 7 1 0 15 14 \frac{15}{14} 1 4 1 5 0
12 7 \frac{12}{7} 7 1 2 − 93 7 -\frac{93}{7} − 7 9 3 -
x 5 x_5 x 5 v 2 v_2 v 2
また,x 3 と v 1 x_3\text{と}v_1 x 3 と v 1 v 1 , v 2 , v 3 v_1,v_2,v_3 v 1 , v 2 , v 3 x 1 , x 2 , x 3 , x 4 , x 5 x_1,x_2,x_3,x_4,x_5 x 1 , x 2 , x 3 , x 4 , x 5
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 定数
x 1 x_1 x 1 1
0
− 2 5 -\frac{2}{5} − 5 2 1 5 \frac{1}{5} 5 1 0
2
x 5 x_5 x 5 0
0
4 5 \frac{4}{5} 5 4 − 7 5 -\frac{7}{5} − 5 7 1
4
x 2 x_2 x 2 0
1
3 5 \frac{3}{5} 5 3 − 4 5 -\frac{4}{5} − 5 4 0
5
-u
0
0
0
0
0
0
-w
0
0
-1
2
0
-19
-uの定数のところは0になるので,元のLPは実行可能と分かった.
第1段階において,wを単体表に含めた意味:第1段階終了した時点で{ x 1 , x 2 , x 5 } \lbrace x_1,x_2,x_5 \rbrace { x 1 , x 2 , x 5 } x 1 , x 2 , x 5 x_1,x_2,x_5 x 1 , x 2 , x 5 x 1 , x 2 x_1,x_2 x 1 , x 2
単体表から
x 1 = 2 + 2 5 x 3 − 1 5 x 4 x 2 = 5 − 3 5 x 3 + 4 5 x 4 w = 2 x 1 + 3 x 2 = 19 − x 3 + 2 x 4 \begin{aligned}
x_1 &= 2 + \frac{2}{5}x_3 - \frac{1}{5}x_4
\\
x_2 &= 5 - \frac{3}{5}x_3 + \frac{4}{5}x_4
\\
w &= 2x_1 + 3x_2 = 19 - x_3 + 2x_4
\end{aligned}
x 1 x 2 w = 2 + 5 2 x 3 − 5 1 x 4 = 5 − 5 3 x 3 + 5 4 x 4 = 2 x 1 + 3 x 2 = 1 9 − x 3 + 2 x 4
今から第2段階を入る.また入る変数を選ぶ.目的関数の行を見ると,マイナスものが一つしかないので,x 3 x_3 x 3 x 5 x_5 x 5
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 定数
比
x 1 x_1 x 1 1
0
1 5 \frac{1}{5} 5 1 0
2
-
x 5 x_5 x 5 0
0
4 5 \frac{4}{5} 5 4 − 7 5 -\frac{7}{5} − 5 7 1
4
5
x 2 x_2 x 2 0
1
3 5 \frac{3}{5} 5 3 − 4 5 -\frac{4}{5} − 5 4 0
5
25 3 \frac{25}{3} 3 2 5
-u
0
0
0
0
0
0
-
-w
0
0
-1
2
0
-19
-
掃き出しをすると
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 定数
x 1 x_1 x 1 1
0
0
− 1 2 -\frac{1}{2} − 2 1 1 2 \frac{1}{2} 2 1 4
x 3 x_3 x 3 0
0
1
− 7 4 -\frac{7}{4} − 4 7 5 4 \frac{5}{4} 4 5 5
x 2 x_2 x 2 0
1
0
1 4 \frac{1}{4} 4 1 − 3 4 -\frac{3}{4} − 4 3 2
-w
0
0
0
1 4 \frac{1}{4} 4 1 5 4 \frac{5}{4} 4 5 -14
この時に目的関数の行を見ると,係数が全部0以上なので,終了.
例題2:実行可能解が存在しない問題
最小化 w = 2 x 1 + 3 x 2 制約条件 4 x 1 + x 2 ≥ 13 3 x 1 + 2 x 2 ≥ 16 x 1 + 2 x 2 ≥ 8 x 1 + x 2 ≤ 3 x 1 ≥ 0 , x 2 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = 2x_1 + 3x_2
\\
\text{制約条件} \qquad &4x_1 + x_2 \geq 13
\\
&3x_1 + 2x_2 \geq 16
\\
&x_1 + 2x_2 \geq 8
\\
&x_1 + x_2 \leq 3
\\
&x_1 \geq 0, x_2 \geq 0
\end{aligned}
最小化 制約条件 w = 2 x 1 + 3 x 2 4 x 1 + x 2 ≥ 1 3 3 x 1 + 2 x 2 ≥ 1 6 x 1 + 2 x 2 ≥ 8 x 1 + x 2 ≤ 3 x 1 ≥ 0 , x 2 ≥ 0
スラック変数と人工変数を導入する
最小化 w = 2 x 1 + 3 x 2 制約条件 4 x 1 + x 2 − x 3 + v 1 = 13 3 x 1 + 2 x 2 − x 4 + v 2 = 16 x 1 + 2 x 2 − x 5 + v 3 = 8 x 1 + x 2 + x 6 = 3 x 1 , x 2 , x 3 , x 4 , x 5 , x 6 ≥ 0 , v 1 , v 2 , v 3 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = 2x_1 + 3x_2
\\
\text{制約条件} \qquad &4x_1 + x_2 - x_3 + v_1 = 13
\\
&3x_1 + 2x_2 - x_4 + v_2 = 16
\\
&x_1 + 2x_2 - x_5 + v_3 = 8
\\
&x_1 + x_2 + x_6 = 3
\\
&x_1, x_2, x_3, x_4, x_5, x_6 \geq 0, v_1, v_2, v_3 \geq 0
\end{aligned}
最小化 制約条件 w = 2 x 1 + 3 x 2 4 x 1 + x 2 − x 3 + v 1 = 1 3 3 x 1 + 2 x 2 − x 4 + v 2 = 1 6 x 1 + 2 x 2 − x 5 + v 3 = 8 x 1 + x 2 + x 6 = 3 x 1 , x 2 , x 3 , x 4 , x 5 , x 6 ≥ 0 , v 1 , v 2 , v 3 ≥ 0
x 6 x_6 x 6 v 4 v_4 v 4 v 4 v_4 v 4 x 6 x_6 x 6 x 6 x_6 x 6 v 4 v_4 v 4
単体表を作る:v 1 , v 2 , v 3 v_1,v_2,v_3 v 1 , v 2 , v 3
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
比
v 1 v_1 v 1 4
1
-1
0
0
0
13
13 4 \frac{13}{4} 4 1 3
v 2 v_2 v 2 3
2
0
-1
0
0
16
16 3 \frac{16}{3} 3 1 6
v 3 v_3 v 3 1
2
0
0
-1
0
8
8
x 6 x_6 x 6 1
1
0
0
0
1
3
3
-u
-8
-5
1
1
1
0
-37
-
-w
2
3
0
0
0
0
0
-
入る変数x 1 x_1 x 1 x 6 x_6 x 6
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
v 1 v_1 v 1 0
-3
-1
0
0
-4
1
v 2 v_2 v 2 0
-1
0
-1
0
-3
7
v 3 v_3 v 3 0
1
0
0
-1
0
5
x 1 x_1 x 1 1
1
0
0
0
1
3
-u
0
3
1
1
1
0
-13
-w
0
1
0
0
0
-2
-6
-uの行を見ると,目的関数の係数が全部0以上のため,非基底変数のどれかを選んで増やしても,これ以上目的関数はよくなれない.u = 13 > 0 u = 13 > 0 u = 1 3 > 0 v 1 = 1 , v 2 = 7 , v 3 = 5 v_1 = 1, v_2 = 7, v_3 = 5 v 1 = 1 , v 2 = 7 , v 3 = 5
次の線形計画問題に対して2段階法を適用せよ.
最小化 w = − x 1 + x 2 − x 3 制約条件 2 x 1 − x 2 + 2 x 3 ≤ 4 − 2 x 1 + 3 x 2 − x 3 ≥ 5 x 1 − x 2 + 2 x 3 ≥ 1 x 1 ≥ 0 , x 2 ≥ 0 , x 3 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = -x_1 + x_2 - x_3
\\
\text{制約条件} \qquad &2x_1 - x_2 + 2x_3 \leq 4
\\
&-2x_1 + 3x_2 - x_3 \geq 5
\\
&x_1 - x_2 + 2x_3 \geq 1
\\
&x_1 \geq 0, x_2 \geq 0, x_3 \geq 0
\end{aligned}
最小化 制約条件 w = − x 1 + x 2 − x 3 2 x 1 − x 2 + 2 x 3 ≤ 4 − 2 x 1 + 3 x 2 − x 3 ≥ 5 x 1 − x 2 + 2 x 3 ≥ 1 x 1 ≥ 0 , x 2 ≥ 0 , x 3 ≥ 0
スラック変数x 4 , x 5 , x 6 ≥ 0 x_4,x_5,x_6 \geq 0 x 4 , x 5 , x 6 ≥ 0 v 1 , v 2 v_1,v_2 v 1 , v 2
最小化 w = − x 1 + x 2 − x 3 制約条件 2 x 1 − x 2 + 2 x 3 + x 4 = 4 − 2 x 1 + 3 x 2 − x 3 − x 5 + v 1 = 5 x 1 − x 2 + 2 x 3 − x 6 + v 2 = 1 x 1 , x 2 , x 3 , x 4 , x 5 , x 6 ≥ 0 , v 1 , v 2 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = -x_1 + x_2 - x_3
\\
\text{制約条件} \qquad &2x_1 - x_2 + 2x_3 + x_4 = 4
\\
&-2x_1 + 3x_2 - x_3 - x_5 + v_1 = 5
\\
&x_1 - x_2 + 2x_3 - x_6 + v_2 = 1
\\
&x_1, x_2, x_3, x_4, x_5, x_6 \geq 0, v_1, v_2 \geq 0
\end{aligned}
最小化 制約条件 w = − x 1 + x 2 − x 3 2 x 1 − x 2 + 2 x 3 + x 4 = 4 − 2 x 1 + 3 x 2 − x 3 − x 5 + v 1 = 5 x 1 − x 2 + 2 x 3 − x 6 + v 2 = 1 x 1 , x 2 , x 3 , x 4 , x 5 , x 6 ≥ 0 , v 1 , v 2 ≥ 0
u = v 1 + v 2 = 6 + x 1 − 2 x 2 − x 3 + x 5 + x 6 u = v_1 + v_2 = 6 + x_1 - 2x_2 - x_3 + x_5 + x_6 u = v 1 + v 2 = 6 + x 1 − 2 x 2 − x 3 + x 5 + x 6
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
比
x 4 x_4 x 4 2
2
1
0
0
4
-
v 1 v_1 v 1 -2
3
-1
0
-1
0
5
5 3 \frac{5}{3} 3 5
v 2 v_2 v 2 1
2
0
0
-1
1
-
-u
1
-2
-1
0
1
1
-6
-
-w
-1
1
-1
0
0
0
0
-
入る変数x 2 x_2 x 2 v 1 v_1 v 1
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
比
x 4 x_4 x 4 4 3 \frac{4}{3} 3 4 0
5 3 \frac{5}{3} 3 5 1
− 1 3 -\frac{1}{3} − 3 1 0
17 3 \frac{17}{3} 3 1 7 17 5 \frac{17}{5} 5 1 7
x 2 x_2 x 2 − 2 3 -\frac{2}{3} − 3 2 1
0
− 1 3 -\frac{1}{3} − 3 1 0
5 3 \frac{5}{3} 3 5 -
v 2 v_2 v 2 1 3 \frac{1}{3} 3 1 0
5 3 \frac{5}{3} 3 5 0
− 1 3 -\frac{1}{3} − 3 1 -1
8 3 \frac{8}{3} 3 8 8 5 \frac{8}{5} 5 8
-u
− 1 3 -\frac{1}{3} − 3 1 0
− 5 3 -\frac{5}{3} − 3 5 0
1 3 \frac{1}{3} 3 1 1
− 8 3 -\frac{8}{3} − 3 8 -
-w
− 1 3 -\frac{1}{3} − 3 1 0
− 2 3 -\frac{2}{3} − 3 2 0
1 3 \frac{1}{3} 3 1 0
− 5 3 -\frac{5}{3} − 3 5 -
入る変数x 3 x_3 x 3 v 2 v_2 v 2
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
x 4 x_4 x 4 1
0
0
1
0
1
3
x 2 x_2 x 2 − 3 5 -\frac{3}{5} − 5 3 1
0
0
− 2 5 -\frac{2}{5} − 5 2 − 1 5 -\frac{1}{5} − 5 1 11 5 \frac{11}{5} 5 1 1
x 3 x_3 x 3 1 5 \frac{1}{5} 5 1 0
1
0
− 1 5 -\frac{1}{5} − 5 1 − 3 5 -\frac{3}{5} − 5 3 8 5 \frac{8}{5} 5 8
-u
0
0
0
0
0
0
0
-w
− 1 5 -\frac{1}{5} − 5 1 0
0
0
1 5 \frac{1}{5} 5 1 − 2 5 -\frac{2}{5} − 5 2 − 3 5 -\frac{3}{5} − 5 3
-uの定数のところは0になるので,元のLPは実行可能と分かった.
第1段階において,wを単体表に含めた意味:第1段階終了した時点で{ x 2 , x 3 , x 4 } \lbrace x_2,x_3,x_4 \rbrace { x 2 , x 3 , x 4 } x 2 , x 3 , x 4 x_2,x_3,x_4 x 2 , x 3 , x 4 x 2 , x 3 x_2,x_3 x 2 , x 3
x 1 = 3 − x 4 − x 6 x 2 = 11 5 + 3 5 x 1 + 2 5 x 5 + 1 5 x 6 x 3 = 8 5 − 1 5 x 1 + 1 5 x 5 + 3 5 x 6 w = − x 1 + x 2 − x 3 = 3 5 − 1 5 x 1 + 1 5 x 5 − 2 5 x 6 \begin{aligned}
x_1 &= 3 - x_4 - x_6
\\
x_2 &= \frac{11}{5} + \frac{3}{5}x_1 + \frac{2}{5}x_5 + \frac{1}{5}x_6
\\
x_3 &= \frac{8}{5} - \frac{1}{5}x_1 + \frac{1}{5}x_5 + \frac{3}{5}x_6
\\
w &= -x_1 + x_2 - x_3 = \frac{3}{5} - \frac{1}{5}x_1 + \frac{1}{5}x_5 - \frac{2}{5}x_6
\end{aligned}
x 1 x 2 x 3 w = 3 − x 4 − x 6 = 5 1 1 + 5 3 x 1 + 5 2 x 5 + 5 1 x 6 = 5 8 − 5 1 x 1 + 5 1 x 5 + 5 3 x 6 = − x 1 + x 2 − x 3 = 5 3 − 5 1 x 1 + 5 1 x 5 − 5 2 x 6
第2段階では,入る変数x 6 x_6 x 6 x 4 x_4 x 4
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
x 6 x_6 x 6 1
0
0
1
0
1
3
x 2 x_2 x 2 − 2 5 -\frac{2}{5} − 5 2 1
0
1 5 \frac{1}{5} 5 1 − 2 5 -\frac{2}{5} − 5 2 0
14 5 \frac{14}{5} 5 1 4
x 3 x_3 x 3 4 5 \frac{4}{5} 5 4 0
1
3 5 \frac{3}{5} 5 3 − 1 5 -\frac{1}{5} − 5 1 0
17 5 \frac{17}{5} 5 1 7
-w
1 5 \frac{1}{5} 5 1 0
0
2 5 \frac{2}{5} 5 2 1 5 \frac{1}{5} 5 1 0
3 5 \frac{3}{5} 5 3
この時,目的関数の行を見ると,係数が全て0以上なので,終了.( x 1 , x 2 , x 3 ) = ( 0 , 14 5 , 17 5 ) (x_1, x_2, x_3) = (0, \frac{14}{5}, \frac{17}{5}) ( x 1 , x 2 , x 3 ) = ( 0 , 5 1 4 , 5 1 7 ) − 3 5 -\frac{3}{5} − 5 3
アルゴリズムとして機能するためには有限回で停止必要あり(無限ループに陥ってはダメ).
m i n c T x s . t A x = b , x ≥ 0 高々 ( n m ) = C n m 個 ( n 変数 , m 制約 ) \begin{aligned}
min \qquad &\mathbf{c}^T \mathbf{x}
\\
s.t \qquad &A\mathbf{x} = \mathbf{b} ,\quad \mathbf{x} \geq 0
\\
&\text{高々}\binom{n}{m} = C_n^m \text{個}(n\text{変数},m\text{制約})
\end{aligned}
m i n s . t c T x A x = b , x ≥ 0 高々 ( m n ) = C n m 個 ( n 変数 , m 制約 )
全ての基底解が非退化の時
x 1 x_1 x 1 ⋯ \cdots ⋯ x n x_n x n 定数
全て正
全て正
全て正
-w
-
入る変数は正の値として基底に入る
(1) wの値は厳密に減少⇒ \Rightarrow ⇒
退化した基底解があると稀に終了しないことあり,この現象を巡回(cycling)という.
例題:巡回現象が起こる例
最小化 w = − 2 x 1 − 3 x 2 + x 3 + 12 x 4 制約条件 − 2 x 1 − 9 x 2 + x 3 + 9 x 4 ≤ 0 1 3 x 1 + x 2 − 1 3 x 3 − 2 x 4 ≤ 0 2 x 1 + 3 x 2 − x 3 − 12 x 4 ≤ 2 x 1 ≥ 0 , x 2 ≥ 0 , x 3 ≥ 0 , x 4 ≥ 0 \begin{aligned}
\text{最小化} \qquad &w = -2x_1 - 3x_2 + x_3 + 12x_4
\\
\text{制約条件} \qquad &-2x_1 - 9x_2 + x_3 + 9x_4 \leq 0
\\
&\frac{1}{3}x_1 + x_2 - \frac{1}{3}x_3 - 2x_4 \leq 0
\\
&2x_1 + 3x_2 - x_3 - 12x_4 \leq 2
\\
&x_1 \geq 0, x_2 \geq 0, x_3 \geq 0, x_4 \geq 0
\end{aligned}
最小化 制約条件 w = − 2 x 1 − 3 x 2 + x 3 + 1 2 x 4 − 2 x 1 − 9 x 2 + x 3 + 9 x 4 ≤ 0 3 1 x 1 + x 2 − 3 1 x 3 − 2 x 4 ≤ 0 2 x 1 + 3 x 2 − x 3 − 1 2 x 4 ≤ 2 x 1 ≥ 0 , x 2 ≥ 0 , x 3 ≥ 0 , x 4 ≥ 0
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 x 7 x_7 x 7 定数
比
x 5 x_5 x 5 -2
-9
1
9
1
0
0
0
-
x 6 x_6 x 6 1 3 \frac{1}{3} 3 1 1
− 1 3 -\frac{1}{3} − 3 1 -2
0
1
0
0
0 1 \frac{0}{1} 1 0
x 7 x_7 x 7 2
3
-1
-12
0
0
1
2
2 3 \frac{2}{3} 3 2
-w
-2
-3
1
12
0
0
0
0
-
退化している.入る変数x 2 x_2 x 2 x 6 x_6 x 6
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 x 7 x_7 x 7 定数
比
x 5 x_5 x 5 1
0
-2
-9
1
9
0
0
0 1 \frac{0}{1} 1 0
x 2 x_2 x 2 1 3 \frac{1}{3} 3 1 1
− 1 3 -\frac{1}{3} − 3 1 -1
0
1
0
0
0 1 3 \frac{0}{\frac{1}{3}} 3 1 0
x 7 x_7 x 7 1
0
0
-6
0
-3
1
2
2 1 \frac{2}{1} 1 2
-w
-1
0
0
6
0
3
0
0
-
解自体は変化せず,入る変数x 1 x_1 x 1 x 5 x_5 x 5
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 x 7 x_7 x 7 定数
比
x 1 x_1 x 1 1
0
-2
-9
1
9
0
0
-
x 2 x_2 x 2 0
1
− 1 3 -\frac{1}{3} − 3 1 1
− 1 3 -\frac{1}{3} − 3 1 -2
0
0
0 1 \frac{0}{1} 1 0
x 7 x_7 x 7 0
0
2
3
-1
-12
1
2
2 3 \frac{2}{3} 3 2
-w
0
0
-2
-3
1
12
0
0
-
解自体は変化せず,入る変数x 4 x_4 x 4 x 2 x_2 x 2
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 x 7 x_7 x 7 定数
比
x 1 x_1 x 1 1
9
1
0
-2
-9
0
0
0 1 \frac{0}{1} 1 0
x 4 x_4 x 4 0
1
1 3 \frac{1}{3} 3 1 1
− 1 3 -\frac{1}{3} − 3 1 -2
0
0
0 1 3 \frac{0}{\frac{1}{3}} 3 1 0
x 7 x_7 x 7 0
-3
1
0
0
-6
1
2
2 1 \frac{2}{1} 1 2
-w
0
3
-1
0
0
6
0
0
-
解は変化せず.
基底変数 x 5 , x 6 , x 7 → x 5 , x 2 , x 7 → x 1 , x 2 , x 7 → x 1 , x 4 , x 7 → x 3 , x 4 , x 7 → x 3 , x 6 , x 7 → x 5 , x 6 , x 7 \begin{aligned}
&\text{基底変数}
\\
&x_5,x_6,x_7
\\
&\rightarrow x_5,x_2,x_7
\\
&\rightarrow x_1,x_2,x_7
\\
&\rightarrow x_1,x_4,x_7
\\
&\rightarrow x_3,x_4,x_7
\\
&\rightarrow x_3,x_6,x_7
\\
&\rightarrow x_5,x_6,x_7
\end{aligned}
基底変数 x 5 , x 6 , x 7 → x 5 , x 2 , x 7 → x 1 , x 2 , x 7 → x 1 , x 4 , x 7 → x 3 , x 4 , x 7 → x 3 , x 6 , x 7 → x 5 , x 6 , x 7
続けてやると,反復6が反復0に一致しているので,巡回現象が起きている.
巡回が起きた時の対策
摂動法:基底変数の0,ϵ \epsilon ϵ ϵ \epsilon ϵ 0 < ϵ ≤ 1 0 < \epsilon \leq 1 0 < ϵ ≤ 1
Blandのピボット規則(最小添字規則)
最小添字規則:
入る変数:wの係数 < 0の非基底変数で添字が最小のもの
出る変数:入る変数の値を増やした時,最初に0になる基底変数複数ある時は最小の添字を持つもの
続いて,巡回対策を用いた場合の単体表を作る.
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 x 7 x_7 x 7 定数
比
x 5 x_5 x 5 -2
-9
1
9
1
0
0
0
-
x 6 x_6 x 6 1 3 \frac{1}{3} 3 1 1
− 1 3 -\frac{1}{3} − 3 1 -2
0
1
0
0
0 1 \frac{0}{1} 1 0
x 7 x_7 x 7 2
3
-1
-12
0
0
1
2
2 3 \frac{2}{3} 3 2
-w
-2
-3
1
12
0
0
0
0
-
入る変数今度x 1 x_1 x 1 x 6 x_6 x 6
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 x 7 x_7 x 7 定数
比
x 5 x_5 x 5 1
-3
-1
3
1
6
0
0
-
x 1 x_1 x 1 0
3
-1
-6
0
3
0
0
-
x 7 x_7 x 7 0
-3
1
0
0
-6
1
2
2 1 \frac{2}{1} 1 2
-w
0
3
-1
6
0
6
0
0
-
入る変数x 3 x_3 x 3 x 7 x_7 x 7
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 x 7 x_7 x 7 定数
x 5 x_5 x 5 1
-6
0
-3
1
0
0
2
x 1 x_1 x 1 0
0
0
-6
0
-3
0
2
x 3 x_3 x 3 0
-3
1
0
0
-6
1
2
-w
0
0
0
0
0
0
0
2
定理:Blandの巡回対策を用いた単体法の収束性
他のピボット規則として,最大改善規則がある.
最大改善規則:
例題:
最小値 − 5 x 1 − 4 x 2 制約条件 5 x 1 + 2 x 2 ≤ 30 x 1 + 2 x 2 ≤ 14 x 1 ≥ 0 , x 2 ≥ 0 \begin{aligned}
\text{最小値} \qquad &-5x_1 - 4x_2
\\
\text{制約条件} \qquad &5x_1 + 2x_2 \leq 30
\\
&x_1 + 2x_2 \leq 14
\\
&x_1 \geq 0, x_2 \geq 0
\end{aligned}
最小値 制約条件 − 5 x 1 − 4 x 2 5 x 1 + 2 x 2 ≤ 3 0 x 1 + 2 x 2 ≤ 1 4 x 1 ≥ 0 , x 2 ≥ 0
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 定数
x 3 x_3 x 3 5
2
1
0
30
x 4 x_4 x 4 1
2
0
1
14
-w
-5
-4
0
0
0
入る変数候補:x 1 , x 2 x_1,x_2 x 1 , x 2
x 1 x_1 x 1
x 1 x_1 x 1 定数
比
x 3 x_3 x 3 5
30
6
x 4 x_4 x 4 1
14
14
-w
-5
-
-
wの改善値 = − 5 × 6 = − 30 -5 \times 6 = -30 − 5 × 6 = − 3 0
x 2 x_2 x 2
x 2 x_2 x 2 定数
比
x 3 x_3 x 3 2
30
15
x 4 x_4 x 4 2
14
7
-w
-4
-
-
wの改善値 = − 4 × 7 = − 28 -4 \times 7 = -28 − 4 × 7 = − 2 8
∣ − 30 ∣ > ∣ − 28 ∣ ⇒ x 1 |-30| > |-28| \Rightarrow x_1 ∣ − 3 0 ∣ > ∣ − 2 8 ∣ ⇒ x 1
単体法が要するピボット回数
一般には
最大改善 < 最大係数 < 最小添字
多くの場合は制約式に比例する.ピボット数で終了.
ただし,どのピボット規則に対してもn,mの指数回のピボットを要する例が作れる.(Klee-Minty)
⇒ \Rightarrow ⇒
次の線形計画問題に対して最小添え字規則に基づく単体法を適用せよ.
最小値 − x 1 − 3 x 2 − 2 x 3 制約条件 − x 1 + 2 x 2 − x 3 ≤ 4 − x 1 + 2 x 2 + 2 x 3 ≤ 2 x 1 − x 2 + x 3 ≤ 2 x 1 ≥ 0 , x 2 ≥ 0 , x 3 ≥ 0 \begin{aligned}
\text{最小値} \qquad &-x_1 - 3x_2 - 2x_3
\\
\text{制約条件} \qquad &-x_1 + 2x_2 - x_3 \leq 4
\\
&-x_1 + 2x_2 + 2x_3 \leq 2
\\
&x_1 - x_2 + x_3 \leq 2
\\
&x_1 \geq 0, x_2 \geq 0, x_3 \geq 0
\end{aligned}
最小値 制約条件 − x 1 − 3 x 2 − 2 x 3 − x 1 + 2 x 2 − x 3 ≤ 4 − x 1 + 2 x 2 + 2 x 3 ≤ 2 x 1 − x 2 + x 3 ≤ 2 x 1 ≥ 0 , x 2 ≥ 0 , x 3 ≥ 0
標準形は以下となる.
最小値 − x 1 − 3 x 2 − 2 x 3 制約条件 − x 1 + 2 x 2 − x 3 + x 4 = 4 − x 1 + 2 x 2 + 2 x 3 + x 5 = 2 x 1 − x 2 + x 3 + x 6 = 2 x 1 , ⋯ , x 6 ≥ 0 \begin{aligned}
\text{最小値} \qquad &-x_1 - 3x_2 - 2x_3
\\
\text{制約条件} \qquad &-x_1 + 2x_2 - x_3 + x_4 = 4
\\
&-x_1 + 2x_2 + 2x_3 + x_5 = 2
\\
&x_1 - x_2 + x_3 + x_6 = 2
\\
&x_1, \cdots, x_6 \geq 0
\end{aligned}
最小値 制約条件 − x 1 − 3 x 2 − 2 x 3 − x 1 + 2 x 2 − x 3 + x 4 = 4 − x 1 + 2 x 2 + 2 x 3 + x 5 = 2 x 1 − x 2 + x 3 + x 6 = 2 x 1 , ⋯ , x 6 ≥ 0
次の単体表を作る.
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
比
x 4 x_4 x 4 -1
2
-1
1
0
0
4
-
x 5 x_5 x 5 -1
2
2
0
1
0
2
-
x 6 x_6 x 6 1
-1
1
0
0
1
2
2
-w
-1
-3
-2
0
0
0
0
-
最小添字規則に基づいて,x 1 x_1 x 1 x 6 x_6 x 6
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
比
x 4 x_4 x 4 0
1
0
1
0
1
6
-
x 5 x_5 x 5 0
1
3
0
1
1
4
4 3 \frac{4}{3} 3 4
x 1 x_1 x 1 1
-1
1
0
0
1
2
2
-w
0
-4
-1
0
0
1
2
-
最小添字規則に基づいて,x 3 x_3 x 3 x 5 x_5 x 5
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
比
x 4 x_4 x 4 0
1
0
1
0
1
6
6
x 3 x_3 x 3 0
1 3 \frac{1}{3} 3 1 1
0
1 3 \frac{1}{3} 3 1 1 3 \frac{1}{3} 3 1 4 3 \frac{4}{3} 3 4 4
x 1 x_1 x 1 1
0
0
− 1 3 -\frac{1}{3} − 3 1 2 3 \frac{2}{3} 3 2 2 3 \frac{2}{3} 3 2 -
-w
0
− 11 3 -\frac{11}{3} − 3 1 1 0
0
1 3 \frac{1}{3} 3 1 4 3 \frac{4}{3} 3 4 10 3 \frac{10}{3} 3 1 0 -
目的関数の係数マイナスのもの一つしかないので,x 2 x_2 x 2 x 3 x_3 x 3
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 定数
x 4 x_4 x 4 0
0
-3
1
-1
0
2
x 2 x_2 x 2 0
1
3
0
1
1
4
x 1 x_1 x 1 1
0
4
0
1
2
6
-w
0
0
11
0
4
3
18
目的関数の係数は全て0以上のため,終了.目的関数は( x 1 , x 2 , x 3 ) = ( 6 , 4 , 0 ) (x_1,x_2,x_3) = (6, 4, 0) ( x 1 , x 2 , x 3 ) = ( 6 , 4 , 0 ) w = − 18 w = -18 w = − 1 8
線形計画問題の標準形
主問題 { 最小化 f p = c T x ( x ∈ R n ) 制約条件 A x = b ( x ≥ 0 ) \begin{aligned}
\text{主問題}
\begin{cases}
\text{最小化} \quad & f_p = \mathbf{c}^T \mathbf{x} (\mathbf{x} \in \mathbb{R}^n)
\\
\text{制約条件} \quad & A\mathbf{x} = \mathbf{b} (\mathbf{x} \geq 0)
\end{cases}
\end{aligned}
主問題 { 最小化 制約条件 f p = c T x ( x ∈ R n ) A x = b ( x ≥ 0 )
に対して,次の線形計画問題を双対問題(dual problem)という.
双対問題 { 最大化 f d = b T y ( y ∈ R m ) 制約条件 A T y ≤ c \begin{aligned}
\text{双対問題}
\begin{cases}
\text{最大化} \quad & f_d = \mathbf{b}^T \mathbf{y} (\mathbf{y} \in \mathbb{R}^m)
\\
\text{制約条件} \quad & A^T\mathbf{y} \leq \mathbf{c}
\end{cases}
\end{aligned}
双対問題 { 最大化 制約条件 f d = b T y ( y ∈ R m ) A T y ≤ c
あるいはスラック変数z ∈ R n \mathbf{z} \in \mathbb{R}^n z ∈ R n
最大化 f d = b T y ( y , z について ) 制約条件 A T y + z = c ( z ≥ 0 ) \begin{aligned}
\text{最大化} \quad & f_d = \mathbf{b}^T \mathbf{y} (\mathbf{y}, \mathbf{z} \text{について})
\\
\text{制約条件} \quad & A^T\mathbf{y} + \mathbf{z} = \mathbf{c} (\mathbf{z} \geq 0)
\end{aligned}
最大化 制約条件 f d = b T y ( y , z について ) A T y + z = c ( z ≥ 0 )
となる.双対問題に対して元の最小化問題を主問題(primal problem)という.そして変数xは主変数(primal variable),変数y と z \mathbf{y} \text{と} \mathbf{z} y と z
主問題と双対問題には非常に重要な関係があり,その関係を双対性(duality)という.
例題
m i n w = − 5 x 1 − 4 x 2 + 0 x 3 + 0 x 4 s . t 5 x 1 + 2 x 2 + x 3 = 30 ⋯ y 1 x 1 + 2 x 2 + x 4 = 14 ⋯ y 2 x 1 , ⋯ , x 4 ≥ 0 \begin{aligned}
min \qquad & w = -5x_1 - 4x_2 + 0x_3 + 0x_4
\\
s.t \qquad & 5x_1 + 2x_2 + x_3 = 30 \cdots y_1
\\
& x_1 + 2x_2 + x_4 = 14 \cdots y_2
\\
& x_1, \cdots, x_4 \geq 0
\end{aligned}
m i n s . t w = − 5 x 1 − 4 x 2 + 0 x 3 + 0 x 4 5 x 1 + 2 x 2 + x 3 = 3 0 ⋯ y 1 x 1 + 2 x 2 + x 4 = 1 4 ⋯ y 2 x 1 , ⋯ , x 4 ≥ 0
最適値w ∗ w^* w ∗ w ∗ w^* w ∗
1式× ( − 2 ) \times (-2) × ( − 2 )
− 10 x 1 − 4 x 2 − 2 x 3 + 0 x 4 = − 60 − 5 x 1 − 4 x 2 + 0 x 3 + 0 x 4 = w \begin{aligned}
-10x_1 - 4x_2 - 2x_3 + 0x_4 &= -60
\\
-5x_1 - 4x_2 + 0x_3 + 0x_4 &= w
\end{aligned}
− 1 0 x 1 − 4 x 2 − 2 x 3 + 0 x 4 − 5 x 1 − 4 x 2 + 0 x 3 + 0 x 4 = − 6 0 = w
x 1 x_1 x 1 − 10 ≤ − 5 -10 \leq -5 − 1 0 ≤ − 5
x 1 ≥ 0 x_1 \geq 0 x 1 ≥ 0 − 10 x 1 ≤ − 5 x 1 -10x_1 \leq -5x_1 − 1 0 x 1 ≤ − 5 x 1
x 2 x_2 x 2 − 4 ≤ − 4 -4 \leq -4 − 4 ≤ − 4
x 2 ≥ 0 x_2 \geq 0 x 2 ≥ 0 − 4 x 2 ≤ − 4 x 2 -4x_2 \leq -4x_2 − 4 x 2 ≤ − 4 x 2
x 3 , x 4 x_3,x_4 x 3 , x 4
− 2 x 3 ≥ 0 x 3 , 0 x 4 ≥ 0 x 4 -2x_3 \geq 0x_3, 0x_4 \geq 0x_4 − 2 x 3 ≥ 0 x 3 , 0 x 4 ≥ 0 x 4
これらから,( x 1 ⋯ x 4 ) T (x_1 \cdots x_4)^T ( x 1 ⋯ x 4 ) T
− 60 = − 10 x 1 − 4 x 2 − 2 x 3 + 0 x 4 ≤ − 5 x 1 − 4 x 2 + 0 x 3 + 0 x 4 = w \begin{aligned}
-60 &= -10x_1 - 4x_2 - 2x_3 + 0x_4
\\
&\leq -5x_1 - 4x_2 + 0x_3 + 0x_4 = w
\end{aligned}
− 6 0 = − 1 0 x 1 − 4 x 2 − 2 x 3 + 0 x 4 ≤ − 5 x 1 − 4 x 2 + 0 x 3 + 0 x 4 = w
よって,w ∗ ≥ − 60 w^* \geq -60 w ∗ ≥ − 6 0
1式× ( − 1 ) + \times (-1) + × ( − 1 ) + × ( − 1 ) \times (-1) × ( − 1 )
− 6 x 1 − 4 x 2 − x 3 − x 4 = − 44 − 5 x 1 − 4 x 2 + 0 x 3 + 0 x 4 = w \begin{aligned}
&-6x_1 - 4x_2 - x_3 - x_4 = -44
\\
&-5x_1 - 4x_2 + 0x_3 + 0x_4 = w
\end{aligned}
− 6 x 1 − 4 x 2 − x 3 − x 4 = − 4 4 − 5 x 1 − 4 x 2 + 0 x 3 + 0 x 4 = w
同様の議論により,w ∗ ≥ − 44 w^* \geq -44 w ∗ ≥ − 4 4
系統的に行う. 1式× y 1 + \times y_1 + × y 1 + × y 2 \times y_2 × y 2
( 5 y 1 + y 2 ) x 1 + ( 2 y 1 + 2 y 2 ) x 2 + y 1 x 3 + y 2 x 4 = 30 y 1 + 14 y 2 \begin{aligned}
(5y_1 + y_2)x_1 + (2y_1 + 2y_2)x_2 + y_1x_3 + y_2x_4 = 30y_1 + 14y_2
\end{aligned}
( 5 y 1 + y 2 ) x 1 + ( 2 y 1 + 2 y 2 ) x 2 + y 1 x 3 + y 2 x 4 = 3 0 y 1 + 1 4 y 2
この式からw ∗ w^* w ∗
y 1 , y 2 y_1,y_2 y 1 , y 2
x 1 の係数 5 y 1 + y 2 ≤ − 5 x 2 の係数 2 y 1 + 2 y 2 ≤ − 4 x 3 の係数 y 1 ≤ 0 x 4 の係数 y 2 ≤ 0 \begin{aligned}
&x_1 \text{の係数} 5y_1 + y_2 \leq -5
\\
&x_2 \text{の係数} 2y_1 + 2y_2 \leq -4
\\
&x_3 \text{の係数} y_1 \leq 0
\\
&x_4 \text{の係数} y_2 \leq 0
\end{aligned}
x 1 の係数 5 y 1 + y 2 ≤ − 5 x 2 の係数 2 y 1 + 2 y 2 ≤ − 4 x 3 の係数 y 1 ≤ 0 x 4 の係数 y 2 ≤ 0
この時30 y 1 + 14 y 2 ‾ ≤ w ∗ \underline{30y_1 + 14y_2} \leq w^* 3 0 y 1 + 1 4 y 2 ≤ w ∗
双対問題
m a x 30 y 1 + 14 y 2 s . t 5 y 1 + y 2 ≤ − 5 2 y 1 + 2 y 2 ≤ − 4 y 1 ≤ 0 y 2 ≤ 0 \begin{aligned}
max \qquad & 30y_1 + 14y_2
\\
s.t \qquad & 5y_1 + y_2 \leq -5
\\
& 2y_1 + 2y_2 \leq -4
\\
& y_1 \leq 0
\\
& y_2 \leq 0
\end{aligned}
m a x s . t 3 0 y 1 + 1 4 y 2 5 y 1 + y 2 ≤ − 5 2 y 1 + 2 y 2 ≤ − 4 y 1 ≤ 0 y 2 ≤ 0
m a x ( 30 , 14 ) ( y 1 y 2 ) s . t ( 5 1 2 2 1 0 0 1 ) ( y 1 y 2 ) ≤ ( − 5 − 4 0 0 ) \begin{aligned}
max \qquad & (30,14)\binom{y_1}{y_2}
\\
s.t \qquad & \begin{pmatrix}
5 & 1
\\
2 & 2
\\
1 & 0
\\
0 & 1
\end{pmatrix}
\begin{pmatrix}
y_1
\\
y_2
\end{pmatrix}
\leq \begin{pmatrix}
-5
\\
-4
\\
0
\\
0
\end{pmatrix}
\end{aligned}
m a x s . t ( 3 0 , 1 4 ) ( y 2 y 1 ) ⎝ ⎜ ⎜ ⎜ ⎛ 5 2 1 0 1 2 0 1 ⎠ ⎟ ⎟ ⎟ ⎞ ( y 1 y 2 ) ≤ ⎝ ⎜ ⎜ ⎜ ⎛ − 5 − 4 0 0 ⎠ ⎟ ⎟ ⎟ ⎞
例題
主問題
m i n f p = 3 x 1 + 2 x 2 + 5 x 3 + x 4 s . t 2 x 1 + x 2 − 3 x 3 + 5 x 4 = 10 3 x 1 − 7 x 2 + 4 x 3 + x 4 = 15 x 1 , ⋯ , x 4 ≥ 0 \begin{aligned}
min \qquad & f_p = 3x_1 + 2x_2 + 5x_3 + x_4
\\
s.t \qquad & 2x_1 + x_2 - 3x_3 + 5x_4 = 10
\\
& 3x_1 - 7x_2 + 4x_3 + x_4 = 15
\\
& x_1, \cdots, x_4 \geq 0
\end{aligned}
m i n s . t f p = 3 x 1 + 2 x 2 + 5 x 3 + x 4 2 x 1 + x 2 − 3 x 3 + 5 x 4 = 1 0 3 x 1 − 7 x 2 + 4 x 3 + x 4 = 1 5 x 1 , ⋯ , x 4 ≥ 0
が与えられた時,双対問題は次のように表される.
m a x f d = 10 y 1 + 15 y 2 s . t 2 y 1 + 3 y 2 ≤ 3 y 1 − 7 y 2 ≤ 2 − 3 y 1 + 4 y 2 ≤ 5 5 y 1 + y 2 ≤ 1 \begin{aligned}
max \qquad & f_d = 10y_1 + 15y_2
\\
s.t \qquad & 2y_1 + 3y_2 \leq 3
\\
& y_1 - 7y_2 \leq 2
\\
& -3y_1 + 4y_2 \leq 5
\\
& 5y_1 + y_2 \leq 1
\end{aligned}
m a x s . t f d = 1 0 y 1 + 1 5 y 2 2 y 1 + 3 y 2 ≤ 3 y 1 − 7 y 2 ≤ 2 − 3 y 1 + 4 y 2 ≤ 5 5 y 1 + y 2 ≤ 1
(y 1 , y 2 y_1,y_2 y 1 , y 2
標準形に書き換える
m i n − 10 ( y 1 + − y 1 − ) − 15 ( y 2 + − y 2 − ) s . t 2 ( y 1 + − y 1 − ) + 3 ( y 2 + − y 2 − ) + z 1 = 3 ← x 1 ( y 1 + − y 1 − ) − 7 ( y 2 + − y 2 − ) + z 2 = 2 ← x 2 − 3 ( y 1 + − y 1 − ) + 4 ( y 2 + − y 2 − ) + z 3 = 5 ← x 3 5 ( y 1 + − y 1 − ) + ( y 2 + − y 2 − ) + z 4 = 1 ← x 4 y 1 + , y 1 − , y 2 + , y 2 − , z 1 , ⋯ , z 4 ≥ 0 \begin{aligned}
min \qquad & -10(y_1^+ - y_1^-) - 15(y_2^+ - y_2^-)
\\
s.t \qquad & 2(y_1^+ - y_1^-) + 3(y_2^+ - y_2^-) + z_1 = 3 \leftarrow x_1
\\
&(y_1^+ - y_1^-) - 7(y_2^+ - y_2^-) + z_2 = 2 \leftarrow x_2
\\
&-3(y_1^+ - y_1^-) + 4(y_2^+ - y_2^-) + z_3 = 5 \leftarrow x_3
\\
&5(y_1^+ - y_1^-) + (y_2^+ - y_2^-) + z_4 = 1 \leftarrow x_4
\\
&y_1^+, y_1^-, y_2^+, y_2^-, z_1, \cdots, z_4 \geq 0
\end{aligned}
m i n s . t − 1 0 ( y 1 + − y 1 − ) − 1 5 ( y 2 + − y 2 − ) 2 ( y 1 + − y 1 − ) + 3 ( y 2 + − y 2 − ) + z 1 = 3 ← x 1 ( y 1 + − y 1 − ) − 7 ( y 2 + − y 2 − ) + z 2 = 2 ← x 2 − 3 ( y 1 + − y 1 − ) + 4 ( y 2 + − y 2 − ) + z 3 = 5 ← x 3 5 ( y 1 + − y 1 − ) + ( y 2 + − y 2 − ) + z 4 = 1 ← x 4 y 1 + , y 1 − , y 2 + , y 2 − , z 1 , ⋯ , z 4 ≥ 0
m a x 3 x 1 + 2 x 2 + 5 x 3 + x 4 s . t 2 x 1 + x 2 − 3 x 3 + 5 x 4 ≤ − 10 3 x 1 − 7 x 2 + 4 x 3 + x 4 ≤ − 15 x 1 , ⋯ , x 4 ≤ 0 \begin{aligned}
max \qquad & 3x_1 + 2x_2 + 5x_3 + x_4
\\
s.t \qquad & 2x_1 + x_2 - 3x_3 + 5x_4 \leq -10
\\
& 3x_1 - 7x_2 + 4x_3 + x_4 \leq -15
\\
& x_1, \cdots, x_4 \leq 0
\end{aligned}
m a x s . t 3 x 1 + 2 x 2 + 5 x 3 + x 4 2 x 1 + x 2 − 3 x 3 + 5 x 4 ≤ − 1 0 3 x 1 − 7 x 2 + 4 x 3 + x 4 ≤ − 1 5 x 1 , ⋯ , x 4 ≤ 0
− x 1 → x 1 − x 2 → x 2 − x 3 → x 3 − x 4 → x 4 \begin{aligned}
-x_1 \rightarrow x_1
\\
-x_2 \rightarrow x_2
\\
-x_3 \rightarrow x_3
\\
-x_4 \rightarrow x_4
\end{aligned}
− x 1 → x 1 − x 2 → x 2 − x 3 → x 3 − x 4 → x 4
とおいて書き直すと主問題が得られる
対応
双対変数 ↔ \leftrightarrow ↔
双対制約 ↔ \leftrightarrow ↔
弱双対定理(weak duality theorem):x ^ \mathbf{\hat{x}} x ^ y ^ \mathbf{\hat{y}} y ^ ⇒ c T x ^ ≥ b T y ^ \Rightarrow \mathbf{c}^T\mathbf{\hat{x}} \geq \mathbf{b}^T \mathbf{\hat{y}} ⇒ c T x ^ ≥ b T y ^
この定理より,主問題の実行可能解x \mathbf{x} x y , z \mathbf{y},\mathbf{z} y , z c T x − b T y \mathbf{c}^T \mathbf{x} - \mathbf{b}^T \mathbf{y} c T x − b T y
弱双対定理から次の結果が容易に得られる
(1) x ^ , y ^ \mathbf{\hat{x}}, \mathbf{\hat{y}} x ^ , y ^ c T x ^ = b T y ^ \mathbf{c}^T\mathbf{\hat{x}} = \mathbf{b}^T \mathbf{\hat{y}} c T x ^ = b T y ^ ⇒ x ^ , y ^ \Rightarrow \mathbf{\hat{x}}, \mathbf{\hat{y}} ⇒ x ^ , y ^
(2) 主問題が非有界(min f p = − ∞ \min f_p = -\infty min f p = − ∞ ⇒ \Rightarrow ⇒
注意:(2)の逆は成立しない⇏ \nRightarrow ⇏
(1) 主問題が最適解を持つならば,それに対応する単体乗数が双対問題の最適解になる.さらに,それぞれの最適値は等しい(min f p = max f d \min f_p = \max f_d min f p = max f d
主問題と双対問題
実行可能
実行可能でない
実行可能
min f p = max f d \min f_p = \max f_d min f p = max f d min f p = − ∞ \min f_p = -\infty min f p = − ∞
実行可能でない
max f d = + ∞ \max f_d = +\infty max f d = + ∞ -
単体乗数(( B T ) − 1 c B (B^T)^{-1} \mathbf{c}_B ( B T ) − 1 c B
m i n c T x s . t A x = b , x ≥ 0 \begin{aligned}
min \qquad & \mathbf{c}^T \mathbf{x}
\\
s.t \qquad & A\mathbf{x} = \mathbf{b}, \mathbf{x} \geq 0
\end{aligned}
m i n s . t c T x A x = b , x ≥ 0
B:基底行列c B \mathbf{c}_B c B c \mathbf{c} c
例題
主問題
m i n ( − 5 , − 4 , 0 , 0 ) ( x 1 x 2 x 3 x 4 ) s . t ( 5 2 1 0 1 2 0 1 ) ( x 1 x 2 x 3 x 4 ) = ( 30 14 ) \begin{aligned}
&min \qquad (-5,-4,0,0)\begin{pmatrix}
x_1
\\
x_2
\\
x_3
\\
x_4
\end{pmatrix}
\\
&s.t \qquad \begin{pmatrix}
5 & 2 & 1 & 0
\\
1 & 2 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x_1
\\
x_2
\\
x_3
\\
x_4
\end{pmatrix}
= \binom{30}{14}
\end{aligned}
m i n ( − 5 , − 4 , 0 , 0 ) ⎝ ⎜ ⎜ ⎜ ⎛ x 1 x 2 x 3 x 4 ⎠ ⎟ ⎟ ⎟ ⎞ s . t ( 5 1 2 2 1 0 0 1 ) ⎝ ⎜ ⎜ ⎜ ⎛ x 1 x 2 x 3 x 4 ⎠ ⎟ ⎟ ⎟ ⎞ = ( 1 4 3 0 )
その双対問題は
m a x ( 30 , 14 ) ( y 1 y 2 ) s . t ( 5 1 2 2 1 0 0 1 ) ( y 1 y 2 ) ≤ ( − 5 − 4 0 0 ) \begin{aligned}
&max \qquad (30,14) \binom{y_1}{y_2}
\\
&s.t \qquad \begin{pmatrix}
5 & 1
\\
2 & 2
\\
1 & 0
\\
0 & 1
\end{pmatrix}
\binom{y_1}{y_2} \leq \begin{pmatrix}
-5
\\
-4
\\
0
\\
0
\end{pmatrix}
\end{aligned}
m a x ( 3 0 , 1 4 ) ( y 2 y 1 ) s . t ⎝ ⎜ ⎜ ⎜ ⎛ 5 2 1 0 1 2 0 1 ⎠ ⎟ ⎟ ⎟ ⎞ ( y 2 y 1 ) ≤ ⎝ ⎜ ⎜ ⎜ ⎛ − 5 − 4 0 0 ⎠ ⎟ ⎟ ⎟ ⎞
最後の単体表
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 定数
x 1 x_1 x 1 1
0
1 4 \frac{1}{4} 4 1 − 1 4 -\frac{1}{4} − 4 1 4
x 2 x_2 x 2 0
1
− 1 8 -\frac{1}{8} − 8 1 5 8 \frac{5}{8} 8 5 5
-w
0
0
40
基底行列は
B ∗ = ( x 1 , x 2 ) = ( 5 2 1 2 ) \begin{aligned}
B_* = (x_1, x_2) =\begin{pmatrix}
5 & 2
\\
1 & 2
\end{pmatrix}
\end{aligned}
B ∗ = ( x 1 , x 2 ) = ( 5 1 2 2 )
となり,基底変数に対するc \mathbf{c} c c B = ( − 5 − 4 ) \mathbf{c}_B = \binom{-5}{-4} c B = ( − 4 − 5 )
従って,y ∗ y^* y ∗ y ∗ = ( B ∗ T ) − 1 c B y^* = (B_*^T)^{-1} \mathbf{c}_B y ∗ = ( B ∗ T ) − 1 c B
y ∗ = ( B ∗ T ) − 1 c B = 1 8 ( 2 − 1 − 2 5 ) ( − 5 − 4 ) = ( − 3 4 − 5 4 ) \begin{aligned}
y^* = (B_*^T)^{-1} \mathbf{c}_B = \frac{1}{8}\begin{pmatrix}
2 & -1
\\
-2 & 5
\end{pmatrix}
\binom{-5}{-4} = \binom{-\frac{3}{4}}{-\frac{5}{4}}
\end{aligned}
y ∗ = ( B ∗ T ) − 1 c B = 8 1 ( 2 − 2 − 1 5 ) ( − 4 − 5 ) = ( − 4 5 − 4 3 )
y 1 ∗ = − 3 4 , y 2 ∗ = − 5 4 , f d = 30 y 1 ∗ + 14 y 2 ∗ = − 40 y_1^* = -\frac{3}{4}, y_2^* = -\frac{5}{4}, f_d = 30y_1^* + 14y_2^* = -40 y 1 ∗ = − 4 3 , y 2 ∗ = − 4 5 , f d = 3 0 y 1 ∗ + 1 4 y 2 ∗ = − 4 0
5 y 1 ∗ + y 2 ∗ = − 5 ≤ − 5 2 y 1 ∗ + 2 y 2 ∗ = − 4 ≤ − 4 \begin{aligned}
5y_1^* + y_2^* = -5 \leq -5
\\
2y_1^* + 2y_2^* = -4 \leq -4
\end{aligned}
5 y 1 ∗ + y 2 ∗ = − 5 ≤ − 5 2 y 1 ∗ + 2 y 2 ∗ = − 4 ≤ − 4
が成り立つので,y ∗ y^* y ∗ f p = c T x = b T y = f d f_p = \mathbf{c}^T \mathbf{x} = \mathbf{b}^T \mathbf{y} = f_d f p = c T x = b T y = f d y ∗ = ( y 1 ∗ y 2 ∗ ) y^* = \binom{y_1^*}{y_2^*} y ∗ = ( y 2 ∗ y 1 ∗ )
例題
m i n ( − 5 , − 4 , − 3 , 0 , 0 , 0 ) ( x 1 x 2 x 3 x 4 x 5 x 6 ) s . t ( 2 3 1 1 0 0 4 1 1 0 1 0 3 4 2 0 0 1 ) ( x 1 x 2 x 3 x 4 x 5 x 6 ) = ( 5 11 8 ) x 1 , ⋯ , x 6 ≥ 0 \begin{aligned}
&min \qquad (-5,-4,-3,0,0,0)\begin{pmatrix}
x_1
\\
x_2
\\
x_3
\\
x_4
\\
x_5
\\
x_6
\end{pmatrix}
\\
&s.t \qquad \begin{pmatrix}
2 & 3 & 1 & 1 & 0 & 0
\\
4 & 1 & 1 & 0 & 1 & 0
\\
3 & 4 & 2 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x_1
\\
x_2
\\
x_3
\\
x_4
\\
x_5
\\
x_6
\end{pmatrix}
= \begin{pmatrix}
5
\\
11
\\
8
\end{pmatrix}
\\
&x_1, \cdots, x_6 \geq 0
\end{aligned}
m i n ( − 5 , − 4 , − 3 , 0 , 0 , 0 ) ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ x 1 x 2 x 3 x 4 x 5 x 6 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ s . t ⎝ ⎛ 2 4 3 3 1 4 1 1 2 1 0 0 0 1 0 0 0 1 ⎠ ⎞ ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ x 1 x 2 x 3 x 4 x 5 x 6 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = ⎝ ⎛ 5 1 1 8 ⎠ ⎞ x 1 , ⋯ , x 6 ≥ 0
その双対問題は
m a x ( 5 , 11 , 8 ) ( y 1 y 2 y 3 ) s . t ( 2 4 3 3 1 4 1 1 2 1 0 0 0 1 0 0 0 1 ) ( y 1 y 2 y 3 ) ≤ ( − 5 − 4 − 3 0 0 0 ) \begin{aligned}
&max \qquad (5,11,8) \begin{pmatrix}
y_1
\\
y_2
\\
y_3
\end{pmatrix}
\\
&s.t \qquad \begin{pmatrix}
2 & 4 & 3
\\
3 & 1 & 4
\\
1 & 1 & 2
\\
1 & 0 & 0
\\
0 & 1 & 0
\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
y_1
\\
y_2
\\
y_3
\end{pmatrix} \leq \begin{pmatrix}
-5
\\
-4
\\
-3
\\
0
\\
0
\\
0
\end{pmatrix}
\end{aligned}
m a x ( 5 , 1 1 , 8 ) ⎝ ⎛ y 1 y 2 y 3 ⎠ ⎞ s . t ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 2 3 1 1 0 0 4 1 1 0 1 0 3 4 2 0 0 1 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ ⎝ ⎛ y 1 y 2 y 3 ⎠ ⎞ ≤ ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ − 5 − 4 − 3 0 0 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞
最後の単体表
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 5 x_5 x 5 定数
x 1 x_1 x 1 1
2
0
2
0
-1
2
0
-6
0
-5
1
2
2
x 3 x_3 x 3 0
-1
1
-3
0
2
1
-w
0
3
0
1
0
1
13
基底行列は
B ∗ = ( x 1 , x 5 , x 3 ) = ( 2 0 1 4 1 1 3 0 2 ) \begin{aligned}
B_* = (x_1,x_5,x_3) = \begin{pmatrix}
2 & 0 & 1
\\
4 & 1 & 1
\\
3 & 0 & 2
\end{pmatrix}
\end{aligned}
B ∗ = ( x 1 , x 5 , x 3 ) = ⎝ ⎛ 2 4 3 0 1 0 1 1 2 ⎠ ⎞
となり,基底変数に対するc \mathbf{c} c c B = ( − 5 , 0 , − 3 ) T \mathbf{c}_B = (-5, 0, -3)^T c B = ( − 5 , 0 , − 3 ) T
従って,y ∗ y^* y ∗ y ∗ = ( B ∗ T ) − 1 c B y^* = (B_*^T)^{-1} \mathbf{c}_B y ∗ = ( B ∗ T ) − 1 c B
y ∗ = ( B ∗ T ) − 1 c B = ( 2 − 5 − 3 0 1 0 − 1 2 2 ) ( − 5 0 − 3 ) = ( − 1 0 − 1 ) \begin{aligned}
y^* = (B_*^T)^{-1} \mathbf{c}_B = \begin{pmatrix}
2 & -5 & -3
\\
0 & 1 & 0
\\
-1 & 2 & 2
\end{pmatrix}
\begin{pmatrix}
-5
\\
0
\\
-3
\end{pmatrix} = \begin{pmatrix}
-1
\\
0
\\
-1
\end{pmatrix}
\end{aligned}
y ∗ = ( B ∗ T ) − 1 c B = ⎝ ⎛ 2 0 − 1 − 5 1 2 − 3 0 2 ⎠ ⎞ ⎝ ⎛ − 5 0 − 3 ⎠ ⎞ = ⎝ ⎛ − 1 0 − 1 ⎠ ⎞
f d = 5 y 1 ∗ + 11 y 2 ∗ + 8 y 3 ∗ = − 13 f_d = 5y_1^* + 11y_2^* + 8y_3^* = -13 f d = 5 y 1 ∗ + 1 1 y 2 ∗ + 8 y 3 ∗ = − 1 3
2 y 1 ∗ + 4 y 2 ∗ + 3 y 3 ∗ = − 5 = − 5 ↔ x 1 ∗ > 0 3 y 1 ∗ + y 2 ∗ + 4 y 3 ∗ = − 7 ≤ − 4 ↔ x 2 ∗ = 0 y 1 ∗ + y 2 ∗ + 2 y 3 ∗ = − 3 = − 3 ↔ x 3 ∗ > 0 \begin{aligned}
2y_1^* + 4y_2^* + 3y_3^* = -5 = -5 \leftrightarrow x_1^* > 0
\\
3y_1^* + y_2^* + 4y_3^* = -7 \leq -4 \leftrightarrow x_2^* = 0
\\
y_1^* + y_2^* + 2y_3^* = -3 = -3 \leftrightarrow x_3^* > 0
\end{aligned}
2 y 1 ∗ + 4 y 2 ∗ + 3 y 3 ∗ = − 5 = − 5 ↔ x 1 ∗ > 0 3 y 1 ∗ + y 2 ∗ + 4 y 3 ∗ = − 7 ≤ − 4 ↔ x 2 ∗ = 0 y 1 ∗ + y 2 ∗ + 2 y 3 ∗ = − 3 = − 3 ↔ x 3 ∗ > 0
が成り立つので,y ∗ y^* y ∗ f p = c T x = b T y = f d f_p = \mathbf{c}^T \mathbf{x} = \mathbf{b}^T \mathbf{y} = f_d f p = c T x = b T y = f d y ∗ = ( y 1 ∗ , y 2 ∗ , y 3 ∗ ) T y^* = (y_1^*, y_2^*, y_3^*)^T y ∗ = ( y 1 ∗ , y 2 ∗ , y 3 ∗ ) T
y ∗ = ( − 1 , 0 , − 1 ) T y^* = (-1, 0, -1)^T y ∗ = ( − 1 , 0 , − 1 ) T y 1 ∗ y_1^* y 1 ∗ x 4 x_4 x 4 x 5 x_5 x 5 x 6 x_6 x 6 y 1 ∗ , x 4 ; y 2 ∗ , x 6 y_1^*, x_4; y_2^*, x_6 y 1 ∗ , x 4 ; y 2 ∗ , x 6 x 5 x_5 x 5
また,上の式等号のところを見ると
双対問題1番目の制約式は主変数x 1 ∗ x_1^* x 1 ∗ x 2 ∗ x_2^* x 2 ∗ x 3 ∗ x_3^* x 3 ∗ x 1 , x 3 x_1,x_3 x 1 , x 3 x 2 x_2 x 2
双対最適解
主問題min c T x \min \quad \mathbf{c}^T \mathbf{x} min c T x s . t A x = b , x ≥ 0 s.t \quad A\mathbf{x} = \mathbf{b}, \mathbf{x} \geq 0 s . t A x = b , x ≥ 0 y i ∗ y_i^* y i ∗ x n + i ∗ x_{n+i}^* x n + i ∗ × ( − 1 ) \times (-1) × ( − 1 )
x , y \mathbf{x}, \mathbf{y} x , y
(OPT1) A x = b , x ≥ 0 A\mathbf{x} = \mathbf{b}, \mathbf{x} \geq 0 A x = b , x ≥ 0 A T y ≤ c A^T \mathbf{y} \leq \mathbf{c} A T y ≤ c x i ( c − A T y ) x_i(\mathbf{c} - A^T \mathbf{y}) x i ( c − A T y )
x i > 0 ⇒ x_i > 0 \Rightarrow x i > 0 ⇒
条件(OPT1),(OPT2),(OPT3)は第5章で述べるKarush-Kuhn-Tucker条件(KKT条件)に相当する.
相補性定理条件を使って解の最適性がチェック可能
x ( A x = b , x ≥ 0 \mathbf{x} (A\mathbf{x} = \mathbf{b}, \mathbf{x} \geq 0 x ( A x = b , x ≥ 0
(OPT2),(OPT3)を満たすy \mathbf{y} y
次の線形計画問題について考える.
最小値 − x 1 − 3 x 2 − 2 x 3 制約条件 − x 1 + 2 x 2 − x 3 ≤ 4 − x 1 + 2 x 2 + 2 x 3 ≤ 2 x 1 − x 2 + x 3 ≤ 2 x 1 ≥ 0 , x 2 ≥ 0 , x 3 ≥ 0 \begin{aligned}
\text{最小値} \qquad &-x_1 - 3x_2 - 2x_3
\\
\text{制約条件} \qquad &-x_1 + 2x_2 - x_3 \leq 4
\\
&-x_1 + 2x_2 + 2x_3 \leq 2
\\
&x_1 - x_2 + x_3 \leq 2
\\
&x_1 \geq 0, x_2 \geq 0, x_3 \geq 0
\end{aligned}
最小値 制約条件 − x 1 − 3 x 2 − 2 x 3 − x 1 + 2 x 2 − x 3 ≤ 4 − x 1 + 2 x 2 + 2 x 3 ≤ 2 x 1 − x 2 + x 3 ≤ 2 x 1 ≥ 0 , x 2 ≥ 0 , x 3 ≥ 0
(1) スラック変数を追加して(等式)標準形に書き換えたうえで,双対問題を作れ.
主問題
m i n ( − 1 , − 3 , − 2 , 0 , 0 , 0 ) ( x 1 x 2 x 3 x 4 x 5 x 6 ) s . t ( − 1 2 − 1 1 0 0 − 1 2 2 0 1 0 1 − 1 1 0 0 1 ) ( x 1 x 2 x 3 x 4 x 5 x 6 ) = ( 4 2 2 ) x 1 , ⋯ , x 6 ≥ 0 \begin{aligned}
&min \qquad (-1,-3,-2,0,0,0)\begin{pmatrix}
x_1
\\
x_2
\\
x_3
\\
x_4
\\
x_5
\\
x_6
\end{pmatrix}
\\
&s.t \qquad \begin{pmatrix}
-1 & 2 & -1 & 1 & 0 & 0
\\
-1 & 2 & 2 & 0 & 1 & 0
\\
1 & -1 & 1 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x_1
\\
x_2
\\
x_3
\\
x_4
\\
x_5
\\
x_6
\end{pmatrix}
= \begin{pmatrix}
4
\\
2
\\
2
\end{pmatrix}
\\
& x_1, \cdots, x_6 \geq 0
\end{aligned}
m i n ( − 1 , − 3 , − 2 , 0 , 0 , 0 ) ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ x 1 x 2 x 3 x 4 x 5 x 6 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ s . t ⎝ ⎛ − 1 − 1 1 2 2 − 1 − 1 2 1 1 0 0 0 1 0 0 0 1 ⎠ ⎞ ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ x 1 x 2 x 3 x 4 x 5 x 6 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = ⎝ ⎛ 4 2 2 ⎠ ⎞ x 1 , ⋯ , x 6 ≥ 0
その双対問題は
m a x ( 4 , 2 , 2 ) ( y 1 y 2 y 3 ) s . t ( − 1 − 1 1 2 2 − 1 − 1 2 1 1 0 0 0 1 0 0 0 1 ) ( y 1 y 2 y 3 ) ≤ ( − 1 − 3 − 2 0 0 0 ) \begin{aligned}
&max \qquad (4,2,2) \begin{pmatrix}
y_1
\\
y_2
\\
y_3
\end{pmatrix}
\\
&s.t \qquad \begin{pmatrix}
-1 & -1 & 1
\\
2 & 2 & -1
\\
-1 & 2 & 1
\\
1 & 0 & 0
\\
0 & 1 & 0
\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
y_1
\\
y_2
\\
y_3
\end{pmatrix} \leq \begin{pmatrix}
-1
\\
-3
\\
-2
\\
0
\\
0
\\
0
\end{pmatrix}
\end{aligned}
m a x ( 4 , 2 , 2 ) ⎝ ⎛ y 1 y 2 y 3 ⎠ ⎞ s . t ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ − 1 2 − 1 1 0 0 − 1 2 2 0 1 0 1 − 1 1 0 0 1 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ ⎝ ⎛ y 1 y 2 y 3 ⎠ ⎞ ≤ ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ − 1 − 3 − 2 0 0 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞
最後の単体表は
x 1 x_1 x 1 x 2 x_2 x 2 x 3 x_3 x 3 x 4 x_4 x 4 定数
0
0
-3
1
-1
0
2
x 2 x_2 x 2 0
1
3
0
1
1
4
x 1 x_1 x 1 1
0
4
0
1
2
6
− w -w − w 0
0
11
0
4
5
18
基底行列は
B ∗ = ( x 4 , x 2 , x 1 ) = ( 1 2 − 1 0 2 − 1 0 − 1 1 ) \begin{aligned}
B_* = (x_4,x_2,x_1) = \begin{pmatrix}
1 & 2 & -1
\\
0 & 2 & -1
\\
0 & -1 & 1
\end{pmatrix}
\end{aligned}
B ∗ = ( x 4 , x 2 , x 1 ) = ⎝ ⎛ 1 0 0 2 2 − 1 − 1 − 1 1 ⎠ ⎞
となり,基底変数に対するc \mathbf{c} c c B = ( 0 , − 3 , − 1 ) T \mathbf{c}_B = (0, -3, -1)^T c B = ( 0 , − 3 , − 1 ) T
従って,y ∗ y^* y ∗ y ∗ = ( B ∗ T ) − 1 c B y^* = (B_*^T)^{-1} \mathbf{c}_B y ∗ = ( B ∗ T ) − 1 c B
y ∗ = ( B ∗ T ) − 1 c B = ( 1 0 0 − 1 1 1 0 1 2 ) ( 0 − 3 − 1 ) = ( 0 − 4 − 5 ) \begin{aligned}
y^* = (B_*^T)^{-1} \mathbf{c}_B = \begin{pmatrix}
1 & 0 & 0
\\
-1 & 1 & 1
\\
0 & 1 & 2
\end{pmatrix}
\begin{pmatrix}
0
\\
-3
\\
-1
\end{pmatrix} = \begin{pmatrix}
0
\\
-4
\\
-5
\end{pmatrix}
\end{aligned}
y ∗ = ( B ∗ T ) − 1 c B = ⎝ ⎛ 1 − 1 0 0 1 1 0 1 2 ⎠ ⎞ ⎝ ⎛ 0 − 3 − 1 ⎠ ⎞ = ⎝ ⎛ 0 − 4 − 5 ⎠ ⎞
f d = 4 y 1 ∗ + 2 y 2 ∗ + 2 y 3 ∗ = − 18 f_d = 4y_1^* + 2y_2^* + 2y_3^* = -18 f d = 4 y 1 ∗ + 2 y 2 ∗ + 2 y 3 ∗ = − 1 8
− y 1 ∗ − y 2 ∗ + y 3 ∗ = − 1 = − 1 ↔ x 1 ∗ > 0 2 y 1 ∗ + 2 y 2 ∗ − y 3 ∗ = − 3 = − 3 ↔ x 2 ∗ > 0 − y 1 ∗ + 2 y 2 ∗ + y 3 ∗ = − 13 ≤ − 2 ↔ x 3 ∗ = 0 \begin{aligned}
-y_1^* - y_2^* + y_3^* = -1 = -1 \leftrightarrow x_1^* > 0
\\
2y_1^* + 2y_2^* - y_3^* = -3 = -3 \leftrightarrow x_2^* > 0
\\
-y_1^* + 2y_2^* + y_3^* = -13 \leq -2 \leftrightarrow x_3^* = 0
\end{aligned}
− y 1 ∗ − y 2 ∗ + y 3 ∗ = − 1 = − 1 ↔ x 1 ∗ > 0 2 y 1 ∗ + 2 y 2 ∗ − y 3 ∗ = − 3 = − 3 ↔ x 2 ∗ > 0 − y 1 ∗ + 2 y 2 ∗ + y 3 ∗ = − 1 3 ≤ − 2 ↔ x 3 ∗ = 0
が成り立つので,y ∗ y^* y ∗ f p = c T x = b T y = f d f_p = \mathbf{c}^T \mathbf{x} = \mathbf{b}^T \mathbf{y} = f_d f p = c T x = b T y = f d y ∗ = ( y 1 ∗ , y 2 ∗ , y 3 ∗ ) T = ( 0 , − 4 , − 5 ) T y^* = (y_1^*, y_2^*, y_3^*)^T = (0, -4, -5)^T y ∗ = ( y 1 ∗ , y 2 ∗ , y 3 ∗ ) T = ( 0 , − 4 , − 5 ) T
次の線形計画問題について考える
最小化 x 1 − x 2 + 2 x 3 − 2 x 4 + 3 x 5 − 3 x 6 制約 x 1 + 2 x 2 + 3 x 3 + x 4 − x 5 + x 6 = 3 3 x 1 + 4 x 2 + x 3 + 2 x 4 − 2 x 6 = 9 x 1 , x 2 , x 3 , x 4 , x 5 , x 6 ≥ 0 \begin{aligned}
\text{最小化} \qquad & x_1 - x_2 + 2x_3 - 2x_4 + 3x_5 - 3x_6
\\
\text{制約} \qquad & x_1 + 2x_2 + 3x_3 + x_4 - x_5 + x_6 = 3
\\
& 3x_1 + 4x_2 + x_3 + 2x_4 - 2x_6 = 9
\\
& x_1,x_2,x_3,x_4,x_5,x_6 \geq 0
\end{aligned}
最小化 制約 x 1 − x 2 + 2 x 3 − 2 x 4 + 3 x 5 − 3 x 6 x 1 + 2 x 2 + 3 x 3 + x 4 − x 5 + x 6 = 3 3 x 1 + 4 x 2 + x 3 + 2 x 4 − 2 x 6 = 9 x 1 , x 2 , x 3 , x 4 , x 5 , x 6 ≥ 0
この問題に対して
x 1 ∗ = 0 , x 2 ∗ = 9 4 , x 3 ∗ = 0 , x 4 ∗ = 0 , x 5 ∗ = 3 2 , x 6 ∗ = 0 x_1^* = 0, x_2^* = \frac{9}{4}, x_3^* = 0, x_4^* = 0, x_5^* = \frac{3}{2}, x_6^* = 0
x 1 ∗ = 0 , x 2 ∗ = 4 9 , x 3 ∗ = 0 , x 4 ∗ = 0 , x 5 ∗ = 2 3 , x 6 ∗ = 0
が最適解であるかを判定せよ.(相補性条件を用いる)
主問題
m i n ( 1 , − 1 , 2 , − 2 , 3 , − 3 ) ( x 1 x 2 x 3 x 4 x 5 x 6 ) s . t ( 1 2 3 1 − 1 2 3 4 1 2 0 − 2 ) ( x 1 x 2 x 3 x 4 x 5 x 6 ) = ( 3 9 ) x 1 , ⋯ , x 6 ≥ 0 \begin{aligned}
&min \qquad (1,-1,2,-2,3,-3)\begin{pmatrix}
x_1
\\
x_2
\\
x_3
\\
x_4
\\
x_5
\\
x_6
\end{pmatrix}
\\
&s.t \qquad \begin{pmatrix}
1 & 2 & 3 & 1 & -1 & 2
\\
3 & 4 & 1 & 2 & 0 & -2
\end{pmatrix}
\begin{pmatrix}
x_1
\\
x_2
\\
x_3
\\
x_4
\\
x_5
\\
x_6
\end{pmatrix}
= \begin{pmatrix}
3
\\
9
\end{pmatrix}
\\
& x_1, \cdots, x_6 \geq 0
\end{aligned}
m i n ( 1 , − 1 , 2 , − 2 , 3 , − 3 ) ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ x 1 x 2 x 3 x 4 x 5 x 6 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ s . t ( 1 3 2 4 3 1 1 2 − 1 0 2 − 2 ) ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ x 1 x 2 x 3 x 4 x 5 x 6 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = ( 3 9 ) x 1 , ⋯ , x 6 ≥ 0
その双対問題は
m a x ( 3 , 9 ) ( y 1 y 2 ) s . t ( 1 3 2 4 3 1 1 2 − 1 0 2 − 2 ) ( y 1 y 2 ) + ( z 1 z 2 z 3 z 4 z 5 z 6 ) = ( 3 9 0 0 0 0 0 0 ) z 1 ≥ 0 , z 2 ≥ 0 , z 3 ≥ 0 , z 4 ≥ 0 , z 5 ≥ 0 , z 6 ≥ 0 \begin{aligned}
&max \qquad (3,9) \begin{pmatrix}
y_1
\\
y_2
\end{pmatrix}
\\
&s.t \qquad \begin{pmatrix}
1 & 3
\\
2 & 4
\\
3 & 1
\\
1 & 2
\\
-1 & 0
\\
2 & -2
\end{pmatrix}
\begin{pmatrix}
y_1
\\
y_2
\end{pmatrix} +
\begin{pmatrix}
z_1
\\
z_2
\\
z_3
\\
z_4
\\
z_5
\\
z_6
\end{pmatrix} = \begin{pmatrix}
3
\\
9
\\
0
\\
0
\\
0
\\
0
\\
0
\\
0
\end{pmatrix}
\\
& z_1 \geq 0, z_2 \geq 0, z_3 \geq 0, z_4 \geq 0, z_5 \geq 0, z_6 \geq 0
\end{aligned}
m a x ( 3 , 9 ) ( y 1 y 2 ) s . t ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 1 2 3 1 − 1 2 3 4 1 2 0 − 2 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ ( y 1 y 2 ) + ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ z 1 z 2 z 3 z 4 z 5 z 6 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 3 9 0 0 0 0 0 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ z 1 ≥ 0 , z 2 ≥ 0 , z 3 ≥ 0 , z 4 ≥ 0 , z 5 ≥ 0 , z 6 ≥ 0
となる.従って,( x 1 , x 2 , x 3 , x 4 , x 5 , x 6 ) (x_1,x_2,x_3,x_4,x_5,x_6) ( x 1 , x 2 , x 3 , x 4 , x 5 , x 6 ) ( y 1 , y 2 , z 1 , z 2 , z 3 , z 4 , z 5 , z 6 ) (y_1,y_2,z_1,z_2,z_3,z_4,z_5,z_6) ( y 1 , y 2 , z 1 , z 2 , z 3 , z 4 , z 5 , z 6 )
{ x 1 + 2 x 2 + 3 x 3 + x 4 − x 5 + x 6 = 3 3 x 1 + 4 x 2 + x 3 + 2 x 4 − 2 x 6 = 9 y 1 + 3 y 2 + z 1 = 3 2 y 1 + 4 y 2 + z 2 = 9 3 y 1 + y 2 + z 3 = 0 y 1 + 2 y 2 + z 4 = 0 − y 1 + z 5 = 0 − 2 y 1 − 2 y 2 + z 6 = 0 x 1 z 1 + x 2 z 2 + ⋯ + x 6 z 6 = 0 x 1 , ⋯ , x 6 ≥ 0 , z 1 , ⋯ , z 6 ≥ 0 \begin{aligned}
\begin{cases}
& x_1 + 2x_2 + 3x_3 + x_4 - x_5 + x_6 = 3
\\
& 3x_1 + 4x_2 + x_3 + 2x_4 - 2x_6 = 9
\\
& y_1 + 3y_2 + z_1 = 3
\\
& 2y_1 + 4y_2 + z_2 = 9
\\
& 3y_1 + y_2 + z_3 = 0
\\
& y_1 + 2y_2 + z_4 = 0
\\
& -y_1 + z_5 = 0
\\
& -2y_1 - 2y_2 + z_6 = 0
\\
& x_1z_1 + x_2z_2 + \cdots + x_6z_6 = 0
\\
& x_1, \cdots, x_6 \geq 0, z_1, \cdots, z_6 \geq 0
\end{cases}
\end{aligned}
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ x 1 + 2 x 2 + 3 x 3 + x 4 − x 5 + x 6 = 3 3 x 1 + 4 x 2 + x 3 + 2 x 4 − 2 x 6 = 9 y 1 + 3 y 2 + z 1 = 3 2 y 1 + 4 y 2 + z 2 = 9 3 y 1 + y 2 + z 3 = 0 y 1 + 2 y 2 + z 4 = 0 − y 1 + z 5 = 0 − 2 y 1 − 2 y 2 + z 6 = 0 x 1 z 1 + x 2 z 2 + ⋯ + x 6 z 6 = 0 x 1 , ⋯ , x 6 ≥ 0 , z 1 , ⋯ , z 6 ≥ 0
条件x 1 z 1 + x 2 z 2 + ⋯ + x 6 z 6 = 0 x_1z_1 + x_2z_2 + \cdots + x_6z_6 = 0 x 1 z 1 + x 2 z 2 + ⋯ + x 6 z 6 = 0
x 1 z 1 = 0 , x 2 z 2 = 0 , x 3 z 3 = 0 , x 4 z 4 = 0 , x 5 z 5 = 0 , x 6 z 6 = 0 x_1z_1 = 0, x_2z_2 = 0, x_3z_3 = 0, x_4z_4 = 0, x_5z_5 = 0, x_6z_6 = 0 x 1 z 1 = 0 , x 2 z 2 = 0 , x 3 z 3 = 0 , x 4 z 4 = 0 , x 5 z 5 = 0 , x 6 z 6 = 0
と同値である.
x 1 ∗ = 0 , x 2 ∗ = 9 4 , x 3 ∗ = 0 , x 4 ∗ = 0 , x 5 ∗ = 3 2 , x 6 ∗ = 0 x_1^* = 0, x_2^* = \frac{9}{4}, x_3^* = 0, x_4^* = 0, x_5^* = \frac{3}{2}, x_6^* = 0 x 1 ∗ = 0 , x 2 ∗ = 4 9 , x 3 ∗ = 0 , x 4 ∗ = 0 , x 5 ∗ = 2 3 , x 6 ∗ = 0 z 2 = 0 , z 5 = 0 z_2 = 0, z_5 = 0 z 2 = 0 , z 5 = 0 y 1 = 0 , y 2 = 4 9 , z 1 = − 4 15 , z 2 = 0 , z 3 = − 4 9 , z 4 = − 2 9 , z 5 = 0 , z 6 = 2 9 y_1 = 0, y_2 = \frac{4}{9}, z_1 = -\frac{4}{15}, z_2 = 0, z_3 = -\frac{4}{9}, z_4 = -\frac{2}{9}, z_5 = 0, z_6 = \frac{2}{9} y 1 = 0 , y 2 = 9 4 , z 1 = − 1 5 4 , z 2 = 0 , z 3 = − 9 4 , z 4 = − 9 2 , z 5 = 0 , z 6 = 9 2
この時,条件z 1 , z 3 , z 4 ≥ 0 z_1,z_3,z_4 \geq 0 z 1 , z 3 , z 4 ≥ 0
f : R n → R f:\mathbb{R}^n \rightarrow \mathbb{R} f : R n → R x ∗ : \mathbf{x}^*: x ∗ : f ( x ) ∗ ≤ f ( x ) , ∀ x ∈ R n f(\mathbf{x})^* \leq f(\mathbf{x}),^\forall x \in \mathbb{R}^n f ( x ) ∗ ≤ f ( x ) , ∀ x ∈ R n x ∗ : \mathbf{x}^*: x ∗ : ∃ ε > 0 , f ( x ) ∗ ≤ f ( x ) , ∀ x , ∣ ∣ x ∗ − x ∣ ∣ < ε ^\exists \varepsilon > 0, f(\mathbf{x})^* \leq f(\mathbf{x}) ,^\forall \mathbf{x},||\mathbf{x}^* - \mathbf{x}|| < \varepsilon ∃ ε > 0 , f ( x ) ∗ ≤ f ( x ) , ∀ x , ∣ ∣ x ∗ − x ∣ ∣ < ε
(1)x ∗ \mathbf{x}^* x ∗ 局所的最小解 で,f : R n → R f:\mathbb{R}^n \rightarrow \mathbb{R} f : R n → R x ∗ \mathbf{x}^* x ∗ 連続的微分可能 であるならば,
∇ f ( x ∗ ) = 0 \begin{aligned}
\nabla f(\mathbf{x}^*) = \mathbf{0}
\end{aligned}
∇ f ( x ∗ ) = 0
が成り立つ(1次の必要条件 ).f f f x ∗ \mathbf{x}^* x ∗ 2回連続微分可能 ならば,
∇ 2 f ( x ∗ ) は半正定値行列 \begin{aligned}
\nabla^2 f(\mathbf{x}^*)\text{は半正定値行列}
\end{aligned}
∇ 2 f ( x ∗ ) は半正定値行列
になる(2次必要条件 ).
(2)f : R n → R f:\mathbb{R}^n \rightarrow \mathbb{R} f : R n → R x ∗ \mathbf{x}^* x ∗ 2回連続的微分可能 である時,x ∗ \mathbf{x}^* x ∗
∇ f ( x ∗ ) = 0 かつ ∇ 2 f ( x ∗ ) 正定値行列 \begin{aligned}
\nabla f(\mathbf{x}^*) = \mathbf{0} \text{かつ} \nabla^2 f(\mathbf{x}^*) \text{正定値行列}
\end{aligned}
∇ f ( x ∗ ) = 0 かつ ∇ 2 f ( x ∗ ) 正定値行列
ならば,x ∗ \mathbf{x}^* x ∗ 局所的最小解 になる(2次の十分条件).
x ∗ : f \mathbf{x}^*:f x ∗ : f 停留点(stationary point) .∇ f ( x ∗ ) = 0 \nabla f(\mathbf{x}^*) = \mathbf{0} ∇ f ( x ∗ ) = 0
極小点 → ∇ 2 f ( x ) \rightarrow \nabla^2 f(\mathbf{x}) → ∇ 2 f ( x )
極大点 → − ∇ 2 f ( x ) : \rightarrow - \nabla^2 f(\mathbf{x}): → − ∇ 2 f ( x ) :
鞍点(saddle point) → \rightarrow →
まとめ:【極大値,極小値,鞍点の判定】
二変数の場合,ヘッセ行列の行列式(H < 0 H < 0 H < 0 H > 0 H > 0 H > 0 f f f x x x y y y f x x f_{xx} f x x f y y f_{yy} f y y
ヘッセ行列の行列式が0のときは,極大値なのか極小値なのか鞍点なのか全く違うものか一切の判断がつかない.
多変数で一般化した場合,ヘッセ行列が正定値行列なら極小値,負定値行列なら極大値,固有値に正も負も(0ではない)含まれるとき鞍点,それ以外は何もでもない.
例
最小化 f ( x ) = 1 2 x T Q x + c T x \begin{aligned}
\text{最小化} f(\mathbf{x}) = \frac{1}{2} \mathbf{x}^TQ\mathbf{x} + \mathbf{c}^T\mathbf{x}
\end{aligned}
最小化 f ( x ) = 2 1 x T Q x + c T x
∇ f ( x ) = Q x + c \nabla f(\mathbf{x}) = Q\mathbf{x} + \mathbf{c} ∇ f ( x ) = Q x + c
Q x + c = 0 \begin{aligned}
Q\mathbf{x} + \mathbf{c} = \mathbf{0}
\end{aligned}
Q x + c = 0
となる.Q Q Q g l o b a l m i n global \ min g l o b a l m i n
関数f , g : R n → R f,g:\mathbf{R}^n \rightarrow \mathbf{R} f , g : R n → R h : h: h :
h ( x ) = m a x ( f ( x ) , g ( x ) ) ( x ∈ R n ) \begin{aligned}
h(x) = max(f(x),g(x)) \qquad (x \in \mathbb{R}^n)
\end{aligned}
h ( x ) = m a x ( f ( x ) , g ( x ) ) ( x ∈ R n )
も凸関数になることを示せ.∀ u , ∀ v ∈ R n , λ ∈ ( 0 , 1 ) ^\forall \mathbf{u},^\forall \mathbf{v} \in \mathbb{R}^n,\lambda \in (0,1) ∀ u , ∀ v ∈ R n , λ ∈ ( 0 , 1 )
f ( λ u + ( 1 − λ ) v ) ≤ λ f ( u ) + ( 1 − λ ) f ( v ) g ( λ u + ( 1 − λ ) v ) ≤ λ g ( u ) + ( 1 − λ ) g ( v ) m a x ( f ( λ u + ( 1 − λ ) v ) , g ( λ u + ( 1 − λ ) v ) ) ≤ m a x ( λ f ( u ) + ( 1 − λ ) f ( v ) , g ( λ u + ( 1 − λ ) v ) , λ g ( u ) + ( 1 − λ ) g ( v ) ) ≤ λ m a x ( f ( u ) , g ( u ) ) + ( 1 − λ ) m a x ( f ( v ) , g ( v ) ) \begin{aligned}
f(\lambda \mathbf{u} + (1 - \lambda)\mathbf{v}) &\leq \lambda f(\mathbf{u}) + (1 - \lambda)f(\mathbf{v})
\\
g(\lambda \mathbf{u} + (1 - \lambda)\mathbf{v}) &\leq \lambda g(\mathbf{u}) + (1 - \lambda)g(\mathbf{v})
\\
max(f(\lambda \mathbf{u} + (1 - \lambda)\mathbf{v}), g(\lambda \mathbf{u} + (1 - \lambda)\mathbf{v})) &\leq max(\lambda f(\mathbf{u}) + (1 - \lambda)f(\mathbf{v}), g(\lambda \mathbf{u} + (1 - \lambda)\mathbf{v}), \lambda g(\mathbf{u}) + (1 - \lambda)g(\mathbf{v}))
\\
&\leq \lambda max(f(\mathbf{u}), g(\mathbf{u})) + (1 - \lambda)max(f(\mathbf{v}), g(\mathbf{v}))
\end{aligned}
f ( λ u + ( 1 − λ ) v ) g ( λ u + ( 1 − λ ) v ) m a x ( f ( λ u + ( 1 − λ ) v ) , g ( λ u + ( 1 − λ ) v ) ) ≤ λ f ( u ) + ( 1 − λ ) f ( v ) ≤ λ g ( u ) + ( 1 − λ ) g ( v ) ≤ m a x ( λ f ( u ) + ( 1 − λ ) f ( v ) , g ( λ u + ( 1 − λ ) v ) , λ g ( u ) + ( 1 − λ ) g ( v ) ) ≤ λ m a x ( f ( u ) , g ( u ) ) + ( 1 − λ ) m a x ( f ( v ) , g ( v ) )
従って,h ( x ) = m a x ( f ( x ) , g ( x ) ) h(x) = max(f(x), g(x)) h ( x ) = m a x ( f ( x ) , g ( x ) )
以下の2次関数f ( x ) f(x) f ( x )
(1)
f ( x 1 , x 2 ) = 1 2 ( x 1 , x 2 ) ( 2 2 2 3 ) ( x 1 x 2 ) + ( 2 2 , − 1 ) ( x 1 x 2 ) \begin{aligned}
f(x_1,x_2) = \frac{1}{2}(x_1,x_2)
\begin{pmatrix}
2 & \sqrt{2}
\\
\sqrt{2} & 3
\end{pmatrix}
\begin{pmatrix}
x_1
\\
x_2
\end{pmatrix}+
(2\sqrt{2},-1)
\begin{pmatrix}
x_1
\\
x_2
\end{pmatrix}
\end{aligned}
f ( x 1 , x 2 ) = 2 1 ( x 1 , x 2 ) ( 2 2 2 3 ) ( x 1 x 2 ) + ( 2 2 , − 1 ) ( x 1 x 2 )
固有値はλ \lambda λ d e t ( λ I − Q ) = 0 det(\lambda I - Q) = 0 d e t ( λ I − Q ) = 0 λ = 1 , λ = 4 \lambda = 1, \lambda = 4 λ = 1 , λ = 4
(2)
f ( x 1 , x 2 ) = 1 2 ( x 1 , x 2 ) ( 1 − 2 2 − 2 2 3 ) ( x 1 x 2 ) + ( 5 , 0 ) ( x 1 x 2 ) \begin{aligned}
f(x_1,x_2) = \frac{1}{2}(x_1,x_2)
\begin{pmatrix}
1 & -2\sqrt{2}
\\
-2\sqrt{2} & 3
\end{pmatrix}
\begin{pmatrix}
x_1
\\
x_2
\end{pmatrix}+
(5,0)
\begin{pmatrix}
x_1
\\
x_2
\end{pmatrix}
\end{aligned}
f ( x 1 , x 2 ) = 2 1 ( x 1 , x 2 ) ( 1 − 2 2 − 2 2 3 ) ( x 1 x 2 ) + ( 5 , 0 ) ( x 1 x 2 )
固有値はλ \lambda λ d e t ( λ I − Q ) = 0 det(\lambda I - Q) = 0 d e t ( λ I − Q ) = 0 λ = − 1 , λ = 5 \lambda = -1, \lambda = 5 λ = − 1 , λ = 5
次の関数f ( x ) : f(x): f ( x ) :
f ( x 1 , x 2 ) = x 1 2 − 2 x 1 x 2 + 1 4 x 2 4 − 1 3 x 2 3 \begin{aligned}
f(x_1,x_2) = x_1^2 -2x_1x_2 + \frac{1}{4}x_2^4 - \frac{1}{3}x_2^3
\end{aligned}
f ( x 1 , x 2 ) = x 1 2 − 2 x 1 x 2 + 4 1 x 2 4 − 3 1 x 2 3
の停留点をすべて求め, それぞれの停留点が局所的最小(極小点),極大点,鞍点のいずれであるか判定せよ.
∇ f ( x ) = 0 ⇔ { f x 1 ( x 1 , x 2 ) = 2 x 1 − 2 x 2 = 0 f x 2 ( x 1 , x 2 ) = − 2 x 1 + x 2 3 − x 2 2 = 0 \begin{aligned}
&\nabla f(\mathbf{x}) = \mathbf{0}
\\
\Leftrightarrow &\begin{cases}
f_{x_1}(x_1,x_2) = 2x_1 - 2x_2 = 0
\\
f_{x_2}(x_1,x_2) = -2x_1 + x_2^3 - x_2^2 = 0
\end{cases}
\end{aligned}
⇔ ∇ f ( x ) = 0 { f x 1 ( x 1 , x 2 ) = 2 x 1 − 2 x 2 = 0 f x 2 ( x 1 , x 2 ) = − 2 x 1 + x 2 3 − x 2 2 = 0
よって,停留点は
( x 1 x 2 ) = ( − 1 − 1 ) , ( 0 0 ) , ( 2 2 ) \begin{aligned}
\begin{pmatrix}
x_1
\\
x_2
\end{pmatrix}=
\begin{pmatrix}
-1
\\
-1
\end{pmatrix},
\begin{pmatrix}
0
\\
0
\end{pmatrix},
\begin{pmatrix}
2
\\
2
\end{pmatrix}
\end{aligned}
( x 1 x 2 ) = ( − 1 − 1 ) , ( 0 0 ) , ( 2 2 )
( x 1 x 2 ) = ( − 1 − 1 ) \binom{x_1}{x_2} = \binom{-1}{-1} ( x 2 x 1 ) = ( − 1 − 1 )
∇ 2 f ( x ) = ∇ 2 f ( − 1 , − 1 ) ) = ( 2 − 2 − 2 5 ) \begin{aligned}
\nabla^2 f(\mathbf{x}) = \nabla^2 f(-1,-1)) =
\begin{pmatrix}
2 & -2
\\
-2 & 5
\end{pmatrix}
\end{aligned}
∇ 2 f ( x ) = ∇ 2 f ( − 1 , − 1 ) ) = ( 2 − 2 − 2 5 )
この時,∇ 2 f ( − 1 , − 1 ) \nabla^2 f(-1,-1) ∇ 2 f ( − 1 , − 1 ) λ \lambda λ
d e t ( λ I − ∇ 2 f ( − 1 , − 1 ) ) = 0 → λ 2 − 7 λ + 6 = 0 \begin{aligned}
det(\lambda I - \nabla^2 f(-1,-1)) = 0
\\
\rightarrow \lambda^2 - 7\lambda + 6 = 0
\end{aligned}
d e t ( λ I − ∇ 2 f ( − 1 , − 1 ) ) = 0 → λ 2 − 7 λ + 6 = 0
λ = 7 ± 25 2 > 0 \lambda = \frac{7 \pm \sqrt{25}}{2} > 0 λ = 2 7 ± 2 5 > 0 ∇ 2 f ( − 1 , − 1 ) \nabla^2 f(-1,-1) ∇ 2 f ( − 1 , − 1 ) ( − 1 − 1 ) \binom{-1}{-1} ( − 1 − 1 )
( x 1 x 2 ) = ( 0 0 ) \binom{x_1}{x_2} = \binom{0}{0} ( x 2 x 1 ) = ( 0 0 )
∇ 2 f ( x ) = ∇ 2 f ( 0 , 0 ) ) = ( 2 − 2 − 2 0 ) \begin{aligned}
\nabla^2 f(\mathbf{x}) = \nabla^2 f(0,0)) =
\begin{pmatrix}
2 & -2
\\
-2 & 0
\end{pmatrix}
\end{aligned}
∇ 2 f ( x ) = ∇ 2 f ( 0 , 0 ) ) = ( 2 − 2 − 2 0 )
固有値λ \lambda λ d e t ( λ I − ∇ 2 f ( 0 , 0 ) ) = 0 det(\lambda I - \nabla^2 f(0,0)) = 0 d e t ( λ I − ∇ 2 f ( 0 , 0 ) ) = 0 λ 2 − 2 λ − 4 = 0 \lambda^2 -2\lambda -4 = 0 λ 2 − 2 λ − 4 = 0 λ = 2 ± 20 2 \lambda = \frac{2 \pm \sqrt{20}}{2} λ = 2 2 ± 2 0 2 − 20 2 < 0 < 2 + 20 2 \frac{2 - \sqrt{20}}{2} < 0 < \frac{2 + \sqrt{20}}{2} 2 2 − 2 0 < 0 < 2 2 + 2 0 ∇ 2 f ( 0 , 0 ) \nabla^2 f(0,0) ∇ 2 f ( 0 , 0 ) ( 0 0 ) \binom{0}{0} ( 0 0 )
( x 1 x 2 ) = ( 2 2 ) \binom{x_1}{x_2} = \binom{2}{2} ( x 2 x 1 ) = ( 2 2 )
∇ 2 f ( x ) = ∇ 2 f ( − 1 , − 1 ) ) = ( 2 − 2 − 2 8 ) \begin{aligned}
\nabla^2 f(\mathbf{x}) = \nabla^2 f(-1,-1)) =
\begin{pmatrix}
2 & -2
\\
-2 & 8
\end{pmatrix}
\end{aligned}
∇ 2 f ( x ) = ∇ 2 f ( − 1 , − 1 ) ) = ( 2 − 2 − 2 8 )
同様に固有値λ \lambda λ d e t ( λ I − ∇ 2 f ( 2 , 2 ) ) = 0 det(\lambda I - \nabla^2 f(2,2)) = 0 d e t ( λ I − ∇ 2 f ( 2 , 2 ) ) = 0 λ 2 − 10 λ + 12 = 0 \lambda^2 -10\lambda + 12 = 0 λ 2 − 1 0 λ + 1 2 = 0 λ = 10 ± 52 2 > 0 \lambda = \frac{10 \pm \sqrt{52}}{2} > 0 λ = 2 1 0 ± 5 2 > 0 ∇ 2 f ( 2 , 2 ) \nabla^2 f(2,2) ∇ 2 f ( 2 , 2 ) ( 2 2 ) \binom{2}{2} ( 2 2 )
従って,( − 1 − 1 ) , ( 2 2 ) \binom{-1}{-1}, \binom{2}{2} ( − 1 − 1 ) , ( 2 2 ) ( 0 0 ) \binom{0}{0} ( 0 0 )
A ∈ R m × n , b ∈ R m ( m ≥ n ) A \in \mathbb{R}^{m \times n}, \mathbf{b} \in \mathbb{R}^m (m \geq n) A ∈ R m × n , b ∈ R m ( m ≥ n )
f ( x ) = 1 2 ∥ A x − b ∥ 2 → m i n f ( x ) = 1 2 ( A x − b ) T ( A x − b ) = 1 2 ( x T A T − b T ) ( A x − b ) = 1 2 { x ( A T A ) x − x T A T b − b T A x + b T b } = 1 2 x T ( A T A ) x − ( A T b ) T x + 1 2 b T b \begin{aligned}
f(\mathbf{x}) &= \frac{1}{2} \parallel A\mathbf{x} - \mathbf{b} \parallel^2 \rightarrow min
\\
f(\mathbf{x}) &= \frac{1}{2}(A\mathbf{x} - \mathbf{b})^T(A\mathbf{x} - \mathbf{b})
\\
&= \frac{1}{2}(\mathbf{x}^TA^T - \mathbf{b}^T)(A\mathbf{x} - \mathbf{b})
\\
&= \frac{1}{2} \{\mathbf{x} (A^TA)\mathbf{x} - \mathbf{x}^T A^T \mathbf{b} - \mathbf{b}^T A\mathbf{x} + \mathbf{b}^T\mathbf{b}\}
\\
&= \frac{1}{2}\mathbf{x}^T (A^TA) \mathbf{x} - (A^T \mathbf{b})^T \mathbf{x} + \frac{1}{2} \mathbf{b}^T \mathbf{b}
\end{aligned}
f ( x ) f ( x ) = 2 1 ∥ A x − b ∥ 2 → m i n = 2 1 ( A x − b ) T ( A x − b ) = 2 1 ( x T A T − b T ) ( A x − b ) = 2 1 { x ( A T A ) x − x T A T b − b T A x + b T b } = 2 1 x T ( A T A ) x − ( A T b ) T x + 2 1 b T b
最小化問題において,Q = A T A , c = − A T b Q = A^TA, \mathbf{c} = -A^T\mathbf{b} Q = A T A , c = − A T b 1 2 b T b \frac{1}{2}\mathbf{b}^T\mathbf{b} 2 1 b T b r a n k A = n rank A = n r a n k A = n A T A A^TA A T A
A T A x = A T b \begin{aligned}
A^TA\mathbf{x} = A^T\mathbf{b}
\end{aligned}
A T A x = A T b
を解くことは同値になる.これを正規方程式(normal equation)と呼ぶ.
数値解法は直接法(direct method)と反復法(iterative method)とに大別される.直接法は有限回の手順で真の解を得るような数値解法の総称であり,線形計画問題に対する単体法や連立一次方程式を解くためのガウスの消去法などは直接法に分類される.
反復法は,適切な初期点x 0 \mathbf{x}_0 x 0 x k + 1 = x k + d k \mathbf{x}_{k+1} = \mathbf{x}_k + \mathbf{d}_k x k + 1 = x k + d k { x k } \lbrace \mathbf{x}_k \rbrace { x k } x ∗ \mathbf{x}^* x ∗ x k \mathbf{x}_k x k k k k x ∗ \mathbf{x}^* x ∗
探索方向(search direction)d k \mathbf{d}_k d k x k \mathbf{x}_k x k f ( x ) f(\mathbf{x}) f ( x ) x k \mathbf{x}_k x k f ( x ) f(\mathbf{x}) f ( x ) d k \mathbf{d}_k d k f ( x ) f(\mathbf{x}) f ( x )
lim t → + 0 f ( x k + t d k ) − f ( x k ) t = ∇ f ( x k ) T d k < 0 \begin{aligned}
\lim_{t \rightarrow +0} \frac{f(\mathbf{x}_k + t\mathbf{d}_k) - f(\mathbf{x}_k)}{t} = \nabla f(\mathbf{x}_k)^T\mathbf{d}_k < 0
\end{aligned}
t → + 0 lim t f ( x k + t d k ) − f ( x k ) = ∇ f ( x k ) T d k < 0
と書ける.探索方向d k \mathbf{d}_k d k f ( x ) f(\mathbf{x}) f ( x ) α k > 0 \alpha_k > 0 α k > 0
x k + 1 = x k + α k d k \begin{aligned}
\mathbf{x}_{k+1} = \mathbf{x}_{k} + \alpha_{k}\mathbf{d}_{k}
\end{aligned}
x k + 1 = x k + α k d k
として生成していく.こうしたステップ幅の調整を直線探索(line search)という,
∇ f ( x ) : x \nabla f(\mathbf{x}): \mathbf{x} ∇ f ( x ) : x f ( x ) f(\mathbf{x}) f ( x ) 方向微分係数の意味:x \mathbf{x} x v \mathbf{v} v f ( x ) f(\mathbf{x}) f ( x )
step0 初期設定をする(初期点x 0 \mathbf{x_0} x 0 k = 0 k = 0 k = 0
step1 停止条件が満たされていれば,x k \mathbf{x_k} x k
step2 探索方向d k \mathbf{d}_k d k
step3 d k \mathbf{d}_k d k α k \alpha_k α k
step4 x k + 1 = x k + α k d k \mathbf{x}_{k+1} = \mathbf{x}_k + \alpha_k \mathbf{d}_k x k + 1 = x k + α k d k
step5 k : = k + 1 k := k + 1 k : = k + 1
step1においてよく用いられる停止条件は,勾配ベクトルの大きさ∥ ∇ f ( x k ) ∥ \parallel \nabla f(\mathbf{x}_k) \parallel ∥ ∇ f ( x k ) ∥ { x k } \lbrace \mathbf{x}_k \rbrace { x k } ∥ x k − x k − 1 ∥ \parallel \mathbf{x}_k - \mathbf{x}_{k-1} \parallel ∥ x k − x k − 1 ∥
反復法は点列{ x } \lbrace \mathbf{x} \rbrace { x }
{ x } \lbrace \mathbf{x} \rbrace { x } 収束するなら,どのぐらいのスピードか
アルゴリズムの収束性は大域的収束性と局所的収束性の2つに分けられる.
大域的収束性(global convergence)とは,任意の初期点から出発した時,有限の反復回数でx ∗ \mathbf{x}^* x ∗ x ∗ \mathbf{x}^* x ∗ x ∗ \mathbf{x}^* x ∗ { x k } \lbrace \mathbf{x}_k \rbrace { x k } x ∗ \mathbf{x}^* x ∗ ∥ ∇ f ( x k ) ∥ → 0 \parallel \nabla f(\mathbf{x}_k) \parallel \rightarrow 0 ∥ ∇ f ( x k ) ∥ → 0
局所的収束性(local convergence)とは初期点をx ∗ \mathbf{x}^* x ∗ x ∗ \mathbf{x}^* x ∗
この場合には収束率(rate of convergence)が重要になる.x \mathbf{x} x { x k } \lbrace \mathbf{x}_k \rbrace { x k } k 0 k_0 k 0 k > k 0 k > k_0 k > k 0 r k ∈ ( 0 , 1 ) r_k \in (0, 1) r k ∈ ( 0 , 1 )
∥ x k + 1 − x ∥ < r k ∥ x k + 1 − x ∥ p \begin{aligned}
\parallel \mathbf{x_{k+1}} - \mathbf{x} \parallel < r_k \parallel \mathbf{x_{k+1}} - \mathbf{x} \parallel^p
\end{aligned}
∥ x k + 1 − x ∥ < r k ∥ x k + 1 − x ∥ p
が成り立つ時,p p p { r k } k ∈ N \lbrace r_k \rbrace_{k \in \mathbb{N}} { r k } k ∈ N 0 0 0
直線探索法(line search method)は解法の大域的収束性を実現するための手段の1つである.
d k \mathbf{d}_k d k
f ( x k + α k d k ) = min a { f ( x k + α d k ) ∣ α > 0 } \begin{aligned}
f(\mathbf{x}_k + \alpha_k\mathbf{d}_k) = \min_a \lbrace f(\mathbf{x}_k + \alpha \mathbf{d}_k)\ |\ \alpha > 0 \rbrace
\end{aligned}
f ( x k + α k d k ) = a min { f ( x k + α d k ) ∣ α > 0 }
となるα k \alpha_k α k α k \alpha_k α k
α k = min { α ∣ ∇ f ( x k + α d k ) T d k = 0 , α > 0 } \begin{aligned}
\alpha_k = \min \lbrace \alpha \ |\ \nabla f(\mathbf{x}_k + \alpha \mathbf{d}_k)^T \mathbf{d}_k = 0, \alpha > 0 \rbrace
\end{aligned}
α k = min { α ∣ ∇ f ( x k + α d k ) T d k = 0 , α > 0 }
となるα k \alpha_k α k
f ( x ) = 1 2 x T A x + b T x \begin{aligned}
f(\mathbf{x}) = \frac{1}{2} \mathbf{x}^T A\mathbf{x} + \mathbf{b}^T \mathbf{x}
\end{aligned}
f ( x ) = 2 1 x T A x + b T x
を考える.近似解x k \mathbf{x}_k x k d k \mathbf{d}_k d k α k \alpha_k α k
α k = − d k T ∇ f ( x k ) d k T A d k \alpha_k = -\frac{\mathbf{d}_k^T \nabla f(\mathbf{x}_k)}{\mathbf{d}_k^T A\mathbf{d}_k}
α k = − d k T A d k d k T ∇ f ( x k )
(1)Armijo(アルミホ)条件
0 < ξ < 1 0 < \xi < 1 0 < ξ < 1 ξ \xi ξ
f ( x k + α d k ) ≤ f ( x k ) + ξ α ∇ f ( x k ) T d k \begin{aligned}
f(\mathbf{x}_k + \alpha \mathbf{d}_k) \leq f(\mathbf{x}_k) + \xi \alpha \nabla f(\mathbf{x}_k)^T \mathbf{d}_k
\end{aligned}
f ( x k + α d k ) ≤ f ( x k ) + ξ α ∇ f ( x k ) T d k
を満たすα > 0 \alpha > 0 α > 0
(2)Wolfe(ウルフ)条件
0 < ξ 1 < ξ 2 < 1 0 < \xi_1 < \xi_2 < 1 0 < ξ 1 < ξ 2 < 1 ξ 1 , ξ 2 \xi_1, \xi_2 ξ 1 , ξ 2
f ( x k + α d k ) ≤ f ( x k ) + ξ 1 α ∇ f ( x k ) T d k ξ 2 ∇ f ( x k ) T d k ≤ ∇ f ( x k + α d k ) T d k \begin{aligned}
f(\mathbf{x}_k + \alpha \mathbf{d}_k) \leq f(\mathbf{x}_k) + \xi_1 \alpha \nabla f(\mathbf{x}_k)^T \mathbf{d}_k
\\
\xi_2 \nabla f(\mathbf{x}_k)^T \mathbf{d}_k \leq \nabla f(\mathbf{x}_k + \alpha \mathbf{d}_k)^T \mathbf{d}_k
\end{aligned}
f ( x k + α d k ) ≤ f ( x k ) + ξ 1 α ∇ f ( x k ) T d k ξ 2 ∇ f ( x k ) T d k ≤ ∇ f ( x k + α d k ) T d k
を満たすα > 0 \alpha > 0 α > 0
step0 現在の近似解x k \mathbf{x}_k x k 0 < ξ < 1 , 0 < τ < 1 0 < \xi < 1, 0 < \tau < 1 0 < ξ < 1 , 0 < τ < 1
step1 探索方向d k \mathbf{d}_k d k α k \alpha_k α k
step1.0 β k , 0 = 1 , i = 0 \beta_{k,0} = 1, i = 0 β k , 0 = 1 , i = 0
step1.1 Armijo条件f ( x k + β k , i d k ) ≤ f ( x k ) + ξ β k , i ∇ f ( x k ) T d k f(\mathbf{x}_k + \beta_{k,i} \mathbf{d}_k) \leq f(\mathbf{x}_k) + \xi \beta_{k,i} \nabla f(\mathbf{x}_k)^T \mathbf{d}_k f ( x k + β k , i d k ) ≤ f ( x k ) + ξ β k , i ∇ f ( x k ) T d k step2へいく.さもなければstep1.2へいく.
step1.2 β k , i + 1 = τ β k , i , i : = i + 1 \beta_{k,i+1} = \tau \beta_{k,i}, i := i+1 β k , i + 1 = τ β k , i , i : = i + 1 step1.1へいく.
step2 α k = β k , i \alpha_k = \beta_{k,i} α k = β k , i
函数f : R n → R f:\mathbb{R}^n \rightarrow \mathbb{R} f : R n → R
x ∗ ∈ R n が局所最小解 ⇒ x ∗ が大域的最小解 \begin{aligned}
\mathbf{x}^* \in \mathbb{R}^n \text{が局所最小解} \Rightarrow \mathbf{x}^*\text{が大域的最小解}
\end{aligned}
x ∗ ∈ R n が局所最小解 ⇒ x ∗ が大域的最小解
であることを示せ.なお,函数f f f
[証明の方法1]x ∗ ∈ S \mathbf{x}^* \in S x ∗ ∈ S { min f ( x ) ∣ x ∈ S } \lbrace \min f(\mathbf{x}) \ |\ \mathbf{x} \in S \rbrace { min f ( x ) ∣ x ∈ S } x ∗ \mathbf{x}^* x ∗
f ( x ∗ ) > f ( y ∗ ) \begin{aligned}
f(\mathbf{x}^*) > f(\mathbf{y}^*)
\end{aligned}
f ( x ∗ ) > f ( y ∗ )
を満たす大域的最適解y ∗ ∈ S \mathbf{y}^* \in S y ∗ ∈ S f ( x ) f(\mathbf{x}) f ( x ) 0 ≤ α ≤ 1 0 \leq \alpha \leq 1 0 ≤ α ≤ 1 ∀ α ^\forall \alpha ∀ α
x ( α ) = α x ∗ + ( 1 − α ) y ∗ \begin{aligned}
\mathbf{x}(\alpha) = \alpha \mathbf{x}^* + (1 - \alpha) \mathbf{y}^*
\end{aligned}
x ( α ) = α x ∗ + ( 1 − α ) y ∗
とおくと
f ( x ( α ) ≤ α f ( x ∗ ) + ( 1 − α ) f ( y ∗ ) < f ( x ∗ ) \begin{aligned}
f(\mathbf{x}(\alpha) \leq \alpha f(\mathbf{x}^*) + (1 - \alpha)f(\mathbf{y}^*) < f(\mathbf{x}^*)
\end{aligned}
f ( x ( α ) ≤ α f ( x ∗ ) + ( 1 − α ) f ( y ∗ ) < f ( x ∗ )
仮説と矛盾になり,従って,局所的最適解は大域的最適解であること証明された.
[証明の方法2]∇ f ( x ∗ ) = 0 \nabla f(\mathbf{x}^*) = 0 ∇ f ( x ∗ ) = 0 ⇒ ∇ f ( x ∗ ) = 0 \Rightarrow \nabla f(\mathbf{x}^*) = 0 ⇒ ∇ f ( x ∗ ) = 0
f f f
∀ x , y に対して f ( x ) − f ( y ) ≥ ∇ f ( y ) T ( x − y ) \begin{aligned}
^\forall \mathbf{x}, \mathbf{y}\text{に対して}f(\mathbf{x}) - f(\mathbf{y}) \geq \nabla f(\mathbf{y})^T (\mathbf{x} - \mathbf{y})
\end{aligned}
∀ x , y に対して f ( x ) − f ( y ) ≥ ∇ f ( y ) T ( x − y )
y = x ∗ \mathbf{y} = \mathbf{x}^* y = x ∗
f ( x ) − f ( x ∗ ) ≥ 0 \begin{aligned}
f(\mathbf{x}) - f(\mathbf{x}^*) \geq 0
\end{aligned}
f ( x ) − f ( x ∗ ) ≥ 0
従って,x ∗ \mathbf{x}^* x ∗
以下の点列{ x k } \lbrace \mathbf{x}_k \rbrace { x k } ∥ x k − x ∗ ∥ < 1 0 − 8 \parallel \mathbf{x}_k - \mathbf{x}^* \parallel < 10^{-8} ∥ x k − x ∗ ∥ < 1 0 − 8 ∥ x k − x ∗ ∥ < 1 0 − 15 \parallel \mathbf{x}_k - \mathbf{x}^* \parallel < 10^{-15} ∥ x k − x ∗ ∥ < 1 0 − 1 5 k k k
(1)点列{ x k } \lbrace \mathbf{x}_k \rbrace { x k }
∥ x 1 − x ∗ ∥ = 0.01 , ∥ x k + 1 − x ∗ ∥ = 0.99 ∥ x k − x ∗ ∥ ( k = 1 , 2 , ⋯ ) \begin{aligned}
\parallel \mathbf{x}_1 - \mathbf{x}^* \parallel = 0.01, \parallel \mathbf{x}_{k + 1} - \mathbf{x}^* \parallel = 0.99 \parallel \mathbf{x}_k - \mathbf{x}^* \parallel (k = 1,2,\cdots)
\end{aligned}
∥ x 1 − x ∗ ∥ = 0 . 0 1 , ∥ x k + 1 − x ∗ ∥ = 0 . 9 9 ∥ x k − x ∗ ∥ ( k = 1 , 2 , ⋯ )
r k = ∥ x k − x ∗ ∥ r_k = \parallel x_k - x^* \parallel r k = ∥ x k − x ∗ ∥
r 1 = ∥ x 1 − x ∗ ∥ r 2 = 0.99 r 1 r 3 = 0.99 r 2 = 0.9 9 2 r 1 ⋮ r k = 0.9 9 k − 1 r 1 = 0.9 9 k − 1 × 0.01 \begin{aligned}
r_1 &= \parallel x_1 - x^* \parallel
\\
r_2 &= 0.99r_1
\\
r_3 &= 0.99r_2 = 0.99^2r_1
\\
&\vdots
\\
r_k &= 0.99^{k-1} r_1 = 0.99^{k-1} \times 0.01
\end{aligned}
r 1 r 2 r 3 r k = ∥ x 1 − x ∗ ∥ = 0 . 9 9 r 1 = 0 . 9 9 r 2 = 0 . 9 9 2 r 1 ⋮ = 0 . 9 9 k − 1 r 1 = 0 . 9 9 k − 1 × 0 . 0 1
0.9 9 k − 1 < 1 0 − 6 0.9 9 k − 1 < 1 0 − 13 \begin{aligned}
0.99^{k-1} < 10^{-6} \quad 0.99^{k-1} < 10^{-13}
\end{aligned}
0 . 9 9 k − 1 < 1 0 − 6 0 . 9 9 k − 1 < 1 0 − 1 3
をそれぞれ解くと,
1 2 3 4 5 6 >>> import math >>> math.log(10**-6, 0.99) 1374.6317296601653 >>> >>> math.log(10**-13, 0.99) 2978.368747597025
よって,条件を満たす最小のk k k k = 1375 , k = 2979 k = 1375, k = 2979 k = 1 3 7 5 , k = 2 9 7 9
(2)点列{ x k } \lbrace \mathbf{x}_k \rbrace { x k }
∥ x 1 − x ∗ ∥ = 0.25 , ∥ x k + 1 − x ∗ ∥ = 2.0 ∥ x k − x ∗ ∥ 2 ( k = 1 , 2 , ⋯ ) \begin{aligned}
\parallel \mathbf{x}_1 - \mathbf{x}^* \parallel = 0.25, \parallel \mathbf{x}_{k + 1} - \mathbf{x}^* \parallel = 2.0 \parallel \mathbf{x}_k - \mathbf{x}^* \parallel^2 (k = 1,2,\cdots)
\end{aligned}
∥ x 1 − x ∗ ∥ = 0 . 2 5 , ∥ x k + 1 − x ∗ ∥ = 2 . 0 ∥ x k − x ∗ ∥ 2 ( k = 1 , 2 , ⋯ )
r k = ∥ x k − x ∗ ∥ r_k = \parallel x_k - x^* \parallel r k = ∥ x k − x ∗ ∥
r 1 = ∥ x 1 − x ∗ ∥ r 2 = 2 r 1 2 r 3 = 2 r 2 2 = 2 3 r 1 4 r 4 = 2 r 3 2 = 2 7 r 1 8 ⋮ r k = 2 2 k − 1 − 1 r 1 2 k − 1 \begin{aligned}
r_1 &= \parallel x_1 - x^* \parallel
\\
r_2 &= 2r_1^2
\\
r_3 &= 2r_2^2 = 2^3r_1^4
\\
r_4 &= 2r_3^2 = 2^7r_1^8
\\
&\vdots
\\
r_k &= 2^{2^{k-1}-1}r_1^{2^{k-1}}
\end{aligned}
r 1 r 2 r 3 r 4 r k = ∥ x 1 − x ∗ ∥ = 2 r 1 2 = 2 r 2 2 = 2 3 r 1 4 = 2 r 3 2 = 2 7 r 1 8 ⋮ = 2 2 k − 1 − 1 r 1 2 k − 1
r k < 1 0 − 8 r_k < 10^{-8} r k < 1 0 − 8
2 2 k − 1 − 1 r 1 2 k − 1 < 1 0 − 8 1 2 2 k − 1 < 2 × 1 0 − 8 \begin{aligned}
2^{2^{k-1}-1}r_1^{2^{k-1}} &< 10^{-8}
\\
\frac{1}{2}^{2^{k-1}} &< 2 \times 10^{-8}
\end{aligned}
2 2 k − 1 − 1 r 1 2 k − 1 2 1 2 k − 1 < 1 0 − 8 < 2 × 1 0 − 8
これと2回log \log log
1 2 3 4 >>> math.log(2*10**-8, 0.5) 25.5754247590989 >>> math.log(25.5754247590989, 2) 4.676686295474069
k − 1 < 4.676686295474069 k-1 < 4.676686295474069 k − 1 < 4 . 6 7 6 6 8 6 2 9 5 4 7 4 0 6 9 k k k k = 5 k = 5 k = 5
同様に,r k < 1 0 − 15 r_k < 10^{-15} r k < 1 0 − 1 5
2 2 k − 1 − 1 r 1 2 k − 1 < 1 0 − 15 1 2 2 k − 1 < 2 × 1 0 − 15 \begin{aligned}
2^{2^{k-1}-1}r_1^{2^{k-1}} &< 10^{-15}
\\
\frac{1}{2}^{2^{k-1}} &< 2 \times 10^{-15}
\end{aligned}
2 2 k − 1 − 1 r 1 2 k − 1 2 1 2 k − 1 < 1 0 − 1 5 < 2 × 1 0 − 1 5
2回log \log log
1 2 3 4 >>> math.log(2*10**-15, 0.5) 48.82892142331043 >>> math.log(48.82892142331043, 2) 5.609664005682176
k − 1 < 5.609664005682176 k-1 < 5.609664005682176 k − 1 < 5 . 6 0 9 6 6 4 0 0 5 6 8 2 1 7 6 k k k k = 6 k = 6 k = 6
次の函数
f ( x 1 , x 2 ) = 10 ( x 1 − x 2 2 ) 2 + ( x 2 − 1 ) 2 \begin{aligned}
f(x_1,x_2) = 10(x_1 - x_2^2)^2 + (x_2 - 1)^2
\end{aligned}
f ( x 1 , x 2 ) = 1 0 ( x 1 − x 2 2 ) 2 + ( x 2 − 1 ) 2
は( x 1 ∗ , x 2 ∗ ) = ( 1 , 1 ) (x_1^*, x_2^*) = (1,1) ( x 1 ∗ , x 2 ∗ ) = ( 1 , 1 ) ( x 1 ∗ , x 2 ∗ ) = ( 1 , 1 ) (x_1^*, x_2^*) = (1,1) ( x 1 ∗ , x 2 ∗ ) = ( 1 , 1 ) f ( x 1 , x 2 ) f(x_1,x_2) f ( x 1 , x 2 ) ∇ 2 f ( 1 , 1 ) \nabla^2 f(1,1) ∇ 2 f ( 1 , 1 )
q ( x 1 , x 2 ) = 1 2 ( x 1 , x 2 ) ∇ 2 f ( 1 , 1 ) ( x 1 x 2 ) + ∇ f ( 1 , 1 ) T ( x 1 x 2 ) \begin{aligned}
q(x_1,x_2) = \frac{1}{2}(x_1,x_2) \nabla^2 f(1,1) \binom{x_1}{x_2} + \nabla f(1,1)^T \binom{x_1}{x_2}
\end{aligned}
q ( x 1 , x 2 ) = 2 1 ( x 1 , x 2 ) ∇ 2 f ( 1 , 1 ) ( x 2 x 1 ) + ∇ f ( 1 , 1 ) T ( x 2 x 1 )
の等高線の概形を示せ.
f ( x 1 , x 2 ) = 10 x 1 2 − 20 x 1 x 2 2 + 10 x 2 4 + x 2 2 − 2 x 2 + 1 \begin{aligned}
f(x_1,x_2) = 10x_1^2 - 20x_1x_2^2 + 10x_2^4 + x_2^2 - 2x_2 + 1
\end{aligned}
f ( x 1 , x 2 ) = 1 0 x 1 2 − 2 0 x 1 x 2 2 + 1 0 x 2 4 + x 2 2 − 2 x 2 + 1
偏微分をすると,
f x 1 x 1 ( x 1 , x 2 ) = 20 f x 2 x 2 ( x 1 , x 2 ) = − 40 x 1 + 120 x 2 2 + 2 f x 1 x 2 ( x 1 , x 2 ) = f x 2 x 1 ( x 1 , x 2 ) = − 40 x 2 \begin{aligned}
f_{x_1x_1}(x_1,x_2) &= 20
\\
f_{x_2x_2}(x_1,x_2) &= -40x_1 + 120x_2^2 + 2
\\
f_{x_1x_2}(x_1,x_2) &= f_{x_2x_1}(x_1,x_2) = -40x_2
\end{aligned}
f x 1 x 1 ( x 1 , x 2 ) f x 2 x 2 ( x 1 , x 2 ) f x 1 x 2 ( x 1 , x 2 ) = 2 0 = − 4 0 x 1 + 1 2 0 x 2 2 + 2 = f x 2 x 1 ( x 1 , x 2 ) = − 4 0 x 2
となる.よって,点( x 1 ∗ , x 2 ∗ ) = ( 1 , 1 ) (x_1^*, x_2^*) = (1, 1) ( x 1 ∗ , x 2 ∗ ) = ( 1 , 1 ) f ( x 1 , x 2 ) f(x_1, x_2) f ( x 1 , x 2 )
∇ 2 f ( 1 , 1 ) = [ 20 − 40 − 40 82 ] \begin{aligned}
\nabla^2 f(1, 1) =\begin{bmatrix}
20 & -40
\\
-40 & 82
\end{bmatrix}
\end{aligned}
∇ 2 f ( 1 , 1 ) = [ 2 0 − 4 0 − 4 0 8 2 ]
d e t ( λ I − ∇ 2 f ( 1 , 1 ) ) = 0 → λ 2 − 102 λ + 40 = 0 \begin{aligned}
det(\lambda I - \nabla^2 f(1,1)) = 0
\\
\rightarrow \lambda^2 - 102\lambda + 40 = 0
\end{aligned}
d e t ( λ I − ∇ 2 f ( 1 , 1 ) ) = 0 → λ 2 − 1 0 2 λ + 4 0 = 0
よって,固有値は
λ = 51 ± 2561 \begin{aligned}
\lambda = 51 \pm \sqrt{2561}
\end{aligned}
λ = 5 1 ± 2 5 6 1
従って,2次近似は
q ( x 1 , x 2 ) = 1 2 ( x 1 , x 2 ) ∇ 2 [ 20 − 40 − 40 82 ] ( x 1 x 2 ) + ∇ f ( 1 , 1 ) T ( x 1 x 2 ) \begin{aligned}
q(x_1,x_2) = \frac{1}{2}(x_1,x_2) \nabla^2 \begin{bmatrix}
20 & -40
\\
-40 & 82
\end{bmatrix} \binom{x_1}{x_2} + \nabla f(1,1)^T \binom{x_1}{x_2}
\end{aligned}
q ( x 1 , x 2 ) = 2 1 ( x 1 , x 2 ) ∇ 2 [ 2 0 − 4 0 − 4 0 8 2 ] ( x 2 x 1 ) + ∇ f ( 1 , 1 ) T ( x 2 x 1 )
となる.Pythonで等高線のグラフを作ると,
本節では, 降下方向と直線探索を組合わせた反復法の大域的収束性に関する定理を証明する.
探査方向d k \mathbf{d}_k d k ∇ f ( x k ) T d k < 0 \nabla f(\mathbf{x}_k)^T \mathbf{d}_k < 0 ∇ f ( x k ) T d k < 0 α k \alpha_k α k f ( x ) f(x) f ( x ) min f ( x ) > − ∞ \min f(x) > -\infty min f ( x ) > − ∞ x 0 \mathbf{x}_0 x 0 { x ∈ R n ∣ f ( x ) ≤ f ( x 0 ) } \lbrace \mathbf{x} \in \mathbb{R}^n \ |\ f(\mathbf{x}) \leq f(\mathbf{x}_0) \rbrace { x ∈ R n ∣ f ( x ) ≤ f ( x 0 ) } N \mathbb{N} N ∇ f ( x ) \nabla f(\mathbf{x}) ∇ f ( x ) N \mathbb{N} N
∥ ∇ f ( x ) − ∇ f ( y ) ∥ ≤ L ∥ x − y ∥ \begin{aligned}
\parallel \nabla f(\mathbf{x}) - \nabla f(\mathbf{y}) \parallel \leq L \parallel \mathbf{x} - \mathbf{y} \parallel
\end{aligned}
∥ ∇ f ( x ) − ∇ f ( y ) ∥ ≤ L ∥ x − y ∥
を満たす定数L > 0 L > 0 L > 0 x k + 1 = x k + α k d k \mathbf{x}_{k+1} = \mathbf{x}_k + \alpha_k \mathbf{d}_k x k + 1 = x k + α k d k { x k } \lbrace \mathbf{x}_k \rbrace { x k }
∑ k = 0 ∞ ( ∇ f ( x k ) T d k ∥ d k ∥ ) 2 < ∞ \begin{aligned}
\sum_{k=0}^\infty (\frac{\nabla f(\mathbf{x}_k)^T \mathbf{d}_k}{\parallel \mathbf{d}_k \parallel})^2 < \infty
\end{aligned}
k = 0 ∑ ∞ ( ∥ d k ∥ ∇ f ( x k ) T d k ) 2 < ∞
が成り立つ.あるいは同値な式として
∑ k = 0 ∞ ( ∥ ∇ f ( x k ) ∥ cos θ k ) 2 < ∞ \begin{aligned}
\sum_{k=0}^\infty (\parallel \nabla f(\mathbf{x}_k)\parallel \cos\theta_k)^2 < \infty
\end{aligned}
k = 0 ∑ ∞ ( ∥ ∇ f ( x k ) ∥ cos θ k ) 2 < ∞
が成り立つ.ただし,θ k \theta_k θ k − ∇ f ( x k ) -\nabla f(\mathbf{x}_k) − ∇ f ( x k ) d k \mathbf{d}_k d k
cos θ k = ( − ∇ f ( x k ) ) T d k ∥ ∇ f ( x k ) ∥ ∥ d k ∥ \begin{aligned}
\cos\theta_k = \frac{(-\nabla f(\mathbf{x}_k))^T \mathbf{d}_k}{\parallel \nabla f(\mathbf{x}_k) \parallel \parallel \mathbf{d}_k \parallel}
\end{aligned}
cos θ k = ∥ ∇ f ( x k ) ∥ ∥ d k ∥ ( − ∇ f ( x k ) ) T d k
と定義される.
上の2つの式をZoutendijk(ズーテンダイク)条件という.また,無限級数が収束するための必要条件より
lim k → ∞ ∇ f ( x k ) T d k ∥ d k ∥ = 0 \begin{aligned}
\lim_{k \rightarrow \infty} \frac{\nabla f(\mathbf{x}_k)^T \mathbf{d}_k}{\parallel \mathbf{d}_k \parallel} = 0
\end{aligned}
k → ∞ lim ∥ d k ∥ ∇ f ( x k ) T d k = 0
あるいは
lim k → ∞ ∥ ∇ f ( x k ) ∥ cos θ k = 0 \lim_{k \rightarrow \infty} \parallel \nabla f(\mathbf{x}_k) \parallel \cos\theta_k = 0
k → ∞ lim ∥ ∇ f ( x k ) ∥ cos θ k = 0
が成り立つ.最急降下法を用いることを考え,θ k \theta_k θ k cos θ k ≥ δ > 0 ( ∀ k ) \cos\theta_k \geq \delta > 0(\forall k) cos θ k ≥ δ > 0 ( ∀ k ) δ > 0 \delta > 0 δ > 0
lim k → ∞ ∥ ∇ f ( x k ) ∥ = 0 \begin{aligned}
\lim_{k \rightarrow \infty} \parallel \nabla f(\mathbf{x}_k) \parallel = 0
\end{aligned}
k → ∞ lim ∥ ∇ f ( x k ) ∥ = 0
これは,直線探索付き最急降下法の大域的収束性を表している.
補充: 特にd k = − ∇ f ( x k ) \mathbf{d}_k = -\nabla f(\mathbf{x}_k) d k = − ∇ f ( x k ) d k \mathbf{d}_k d k ∇ f ( x k ) ⋅ d k = − ∥ f ( x k ) ∥ 2 < 0 \nabla f(\mathbf{x}_k) \cdot \mathbf{d}_k = -\parallel f(\mathbf{x}_k) \parallel^2 < 0 ∇ f ( x k ) ⋅ d k = − ∥ f ( x k ) ∥ 2 < 0
Cauchy-Schwarzの不等式における等号成立条件から,∥ d k ∥ \parallel \mathbf{d}_k \parallel ∥ d k ∥ d k \mathbf{d}_k d k ∇ f ( x k ) ⋅ d k \nabla f(\mathbf{x}_k) \cdot \mathbf{d}_k ∇ f ( x k ) ⋅ d k d k = − ∇ f ( x k ) \mathbf{d}_k = -\nabla f(\mathbf{x}_k) d k = − ∇ f ( x k )
考えるべきこと:d k \mathbf{d}_k d k
f ( x k + d ) ≃ l ( d ) = f ( x k ) + ∇ f ( x k ) T d \begin{aligned}
f(\mathbf{x}_k + \mathbf{d}) \simeq l(\mathbf{d}) = f(\mathbf{x}_k) + \nabla f(\mathbf{x}_k)^T \mathbf{d}
\end{aligned}
f ( x k + d ) ≃ l ( d ) = f ( x k ) + ∇ f ( x k ) T d
二次モデルに基づく方法: 共役勾配法,ニュートン法,準ニュートン法
f ( x k + d ) ≃ q ( d ) = f ( x k ) + ∇ f ( x k ) T d + 1 2 d T ∇ 2 f ( x k ) d \begin{aligned}
f(\mathbf{x}_k + \mathbf{d}) \simeq q(\mathbf{d}) = f(\mathbf{x}_k) + \nabla f(\mathbf{x}_k)^T \mathbf{d} + \frac{1}{2}\mathbf{d}^T \nabla^2 f(\mathbf{x}_k) \mathbf{d}
\end{aligned}
f ( x k + d ) ≃ q ( d ) = f ( x k ) + ∇ f ( x k ) T d + 2 1 d T ∇ 2 f ( x k ) d
最急降下法(steepest descent method)では,k k k ∇ f ( x k ) T d \nabla f(\mathbf{x}_k)^T \mathbf{d} ∇ f ( x k ) T d
d k = − ∇ f ( x k ) \begin{aligned}
\mathbf{d}_k = -\nabla f(\mathbf{x}_k)
\end{aligned}
d k = − ∇ f ( x k )
これを最急降下方向という.
最急降下法は,必ず停留点(∇ f ( x ) = 0 \nabla f(\mathbf{x}) = 0 ∇ f ( x ) = 0
出発点の選ぶ方次第では,局所的最適解に収束
凸関数の場合,必ず大域的最適解に収束
ある種の凸関数(狭義凸2次関数)に対しては,一次収束をする
一次収束:毎回の反復で,現在の点と極限との距離が,一定の割合で減少すること.ある定数0 < β < 1 0 < \beta < 1 0 < β < 1 k 0 k_0 k 0 k > k 0 k > k_0 k > k 0 ∥ x k + 1 − x ∗ ∥ ≤ β ∥ x k − x ∗ ∥ \parallel x^{k+1} - x^* \parallel \leq \beta \parallel x^k - x^* \parallel ∥ x k + 1 − x ∗ ∥ ≤ β ∥ x k − x ∗ ∥ x ∗ x^* x ∗
一次収束する場合でも,収束スピードは遅いこともある
step0 初期点x 0 \mathbf{x}_0 x 0 k = 0 k = 0 k = 0 x k \mathbf{x}_k x k step2へいく.d k = − ∇ f ( x k ) \mathbf{d}_k = - \nabla f(\mathbf{x}_k) d k = − ∇ f ( x k ) f k \mathbf{f}_k f k α k \alpha_k α k x k + 1 = x k + α k d k \mathbf{x}_{k+1} = \mathbf{x}_k + \alpha_k \mathbf{d}_k x k + 1 = x k + α k d k k : = k + 1 k := k+1 k : = k + 1 step1へいく.
探査方向d k \mathbf{d}_k d k ∇ f ( x k ) T d k < 0 \nabla f(\mathbf{x}_k)^T \mathbf{d}_k < 0 ∇ f ( x k ) T d k < 0 α k \alpha_k α k f ( x ) f(x) f ( x ) min f ( x ) > − ∞ \min f(x) > -\infty min f ( x ) > − ∞ x 0 \mathbf{x}_0 x 0 { x ∈ R n ∣ f ( x ) ≤ f ( x 0 ) } \lbrace \mathbf{x} \in \mathbb{R}^n \ |\ f(\mathbf{x}) \leq f(\mathbf{x}_0) \rbrace { x ∈ R n ∣ f ( x ) ≤ f ( x 0 ) } N \mathbb{N} N ∇ f ( x ) \nabla f(\mathbf{x}) ∇ f ( x ) N \mathbb{N} N { x k } \lbrace \mathbf{x}_k \rbrace { x k }
lim k → ∞ ∥ ∇ f ( x k ) ∥ = 0 \begin{aligned}
\lim_{k \rightarrow \infty} \parallel \nabla f(\mathbf{x}_k) \parallel = 0
\end{aligned}
k → ∞ lim ∥ ∇ f ( x k ) ∥ = 0
この定理は,解から離れた初期点を選んでも勾配ベクトルの点列{ ∇ f ( x k ) } \lbrace \nabla f(\mathbf{x}_k) \rbrace { ∇ f ( x k ) }
行列A ∈ R n × n A \in \mathbb{R}^{n \times n} A ∈ R n × n b ∈ R n \mathbf{b} \in \mathbb{R}^n b ∈ R n
f ( x ) = 1 2 x T A x + b T x \begin{aligned}
f(\mathbf{x}) = \frac{1}{2} \mathbf{x}^T A\mathbf{x} + \mathbf{b}^T \mathbf{x}
\end{aligned}
f ( x ) = 2 1 x T A x + b T x
を考える.この時,正確な直線探索を用いた最急降下法で生成された点列{ x k } \lbrace \mathbf{x}_k \rbrace { x k }
∥ x k + 1 − x ∗ ∥ ≤ ∣ λ 1 − λ n λ 1 + λ n ∣ ∥ x k − x ∗ ∥ A \begin{aligned}
\parallel \mathbf{x}_{k+1} - \mathbf{x}^* \parallel \leq \left\lvert \frac{\lambda_1 - \lambda_n}{\lambda_1 + \lambda_n} \right\rvert \parallel \mathbf{x}_k - \mathbf{x}^* \parallel_A
\end{aligned}
∥ x k + 1 − x ∗ ∥ ≤ ∣ ∣ ∣ ∣ ∣ λ 1 + λ n λ 1 − λ n ∣ ∣ ∣ ∣ ∣ ∥ x k − x ∗ ∥ A
を満たす.ただし,0 < λ 1 ≤ λ n 0 < \lambda_1 \leq \lambda_n 0 < λ 1 ≤ λ n A A A x ∗ \mathbf{x}^* x ∗ ∥ v ∥ A = v T A v \parallel \mathbf{v} \parallel_A = \sqrt{\mathbf{v}^T A\mathbf{v}} ∥ v ∥ A = v T A v
この定理により,最小固有値に比べて最大固有値が非常に大きい場合(すなわち行列Aの条件数が非常に大きい場合)には係数が1に近い値になるので,収束が遅いことがわかる.
勾配ベクトルのみを用いる方法である.
What’s Newton’s method is trying to do is It’s trying to find x-intercepts of functions.Suppose I take some random point and I plug that in and well it’s not the x-intercept, but what you do is you find an equation of a tangent line and then you use the equation of the tangent line to find a new point we’ll call that x 2 x_2 x 2 x 3 x_3 x 3
ニュートン法は2次モデルの最小化に基づいた解法である.q ( d ) q(\mathbf{d}) q ( d ) ∇ q ( d ) = 0 \nabla q(\mathbf{d}) = \mathbf{0} ∇ q ( d ) = 0 d \mathbf{d} d q ( d ) q(\mathbf{d}) q ( d ) d \mathbf{d} d
∇ q ( d ) = ∇ f ( x k ) + ∇ 2 f ( x k ) d \begin{aligned}
\nabla q(\mathbf{d}) = \nabla f(\mathbf{x}_k) + \nabla^2 f(\mathbf{x}_k)\mathbf{d}
\end{aligned}
∇ q ( d ) = ∇ f ( x k ) + ∇ 2 f ( x k ) d
となるので,探索方向を求めるためには連立1次方程式
∇ 2 f ( x k ) d = − ∇ f ( x k ) \begin{aligned}
\nabla^2 f(\mathbf{x}_k) \mathbf{d} = -\nabla f(\mathbf{x}_k)
\end{aligned}
∇ 2 f ( x k ) d = − ∇ f ( x k )
を解けば良い.この方程式をニュートン方程式(Newton equation),その解d k \mathbf{d}_k d k
もし∇ 2 f ( x k ) \nabla^2 f(\mathbf{x}_k) ∇ 2 f ( x k )
∇ f ( x k ) T d k = − ∇ f ( x k ) T ∇ 2 f ( x k ) − 1 ∇ f ( x k ) < 0 \begin{aligned}
\nabla f(\mathbf{x}_k)^T \mathbf{d}_k = -\nabla f(\mathbf{x}_k)^T \nabla^2 f(\mathbf{x}_k)^{-1} \nabla f(\mathbf{x}_k) < 0
\end{aligned}
∇ f ( x k ) T d k = − ∇ f ( x k ) T ∇ 2 f ( x k ) − 1 ∇ f ( x k ) < 0
となるので,ニュートン方向は目的関数の降下方向になる.幾何学的に解釈すれば,点x k \mathbf{x}_k x k x k \mathbf{x}_k x k d k \mathbf{d}_k d k
step0 初期点x 0 \mathbf{x}_0 x 0 k = 0 k = 0 k = 0
step1 停止条件が満たされていれば,x k \mathbf{x}_k x k step2へいく
step2 ニュートン方程式を解いて,探索方向d k \mathbf{d}_k d k
step3 x k + 1 = x k + d k \mathbf{x}_{k+1} = \mathbf{x}_k + \mathbf{d}_k x k + 1 = x k + d k
step4 k : = k + 1 k := k + 1 k : = k + 1 step1へいく
ステップ幅α k = 1 \alpha_k = 1 α k = 1 x k + 1 = x k + d k \mathbf{x}_{k+1} = \mathbf{x}_k + \mathbf{d}_k x k + 1 = x k + d k d k \mathbf{d}_k d k
目的関数f ( x ) f(\mathbf{x}) f ( x ) x ∗ \mathbf{x}^* x ∗ D D D ∇ 2 f ( x ∗ ) \nabla^2 f(\mathbf{x}^*) ∇ 2 f ( x ∗ ) ∇ 2 f ( x ) \nabla^2 f(\mathbf{x}) ∇ 2 f ( x ) D D D x , y ∈ D \mathbf{x}, \mathbf{y} \in D x , y ∈ D ∥ ∇ 2 f ( x ) − ∇ 2 f ( y ) ∥ ≤ γ ∥ x − y ∥ \parallel \nabla^2 f(\mathbf{x}) - \nabla^2 f(\mathbf{y}) \parallel \leq \gamma \parallel \mathbf{x} - \mathbf{y} \parallel ∥ ∇ 2 f ( x ) − ∇ 2 f ( y ) ∥ ≤ γ ∥ x − y ∥ γ \gamma γ x 0 \mathbf{x}_0 x 0 x ∗ \mathbf{x}^* x ∗ { x k } \lbrace \mathbf{x}_k \rbrace { x k } x ∗ \mathbf{x}^* x ∗
∥ x k + 1 − x ∗ ∥ ≤ ν ∥ x k − x ∗ ∥ 2 \begin{aligned}
\parallel \mathbf{x}_{k+1} - \mathbf{x}^* \parallel \leq \nu \parallel \mathbf{x}_k - \mathbf{x}^* \parallel^2
\end{aligned}
∥ x k + 1 − x ∗ ∥ ≤ ν ∥ x k − x ∗ ∥ 2
が成り立つ.ただし,ν \nu ν
x 0 \mathbf{x}_0 x 0 { x k } \lbrace \mathbf{x}_k \rbrace { x k }
関数f : R n → R m f:\mathbb{R}^n \rightarrow \mathbb{R}^m f : R n → R m f f f
証明:f f f ϵ > 0 \epsilon > 0 ϵ > 0 δ = ϵ L \delta = \frac{\epsilon}{L} δ = L ϵ
∣ x 1 − x 2 ∣ < δ ⇒ ∣ f ( x 1 ) − f ( x 2 ) ∣ ≤ L ∣ x 1 − x 2 ∣ < L ⋅ δ = L ⋅ ϵ L = ϵ \begin{aligned}
\lvert \mathbf{x_1} - \mathbf{x_2} \rvert < \delta \Rightarrow \lvert f(\mathbf{x}_1) - f(\mathbf{x}_2) \rvert \leq L \lvert \mathbf{x_1} - \mathbf{x_2} \rvert < L \cdot \delta = L \cdot \frac{\epsilon}{L} = \epsilon
\end{aligned}
∣ x 1 − x 2 ∣ < δ ⇒ ∣ f ( x 1 ) − f ( x 2 ) ∣ ≤ L ∣ x 1 − x 2 ∣ < L ⋅ δ = L ⋅ L ϵ = ϵ
となる.従って,f f f
行列A = ( 3 − 1 − 1 1 ) A = \begin{pmatrix} 3 & -1 \\\\ -1 & 1 \end{pmatrix} A = ⎝ ⎛ 3 − 1 − 1 1 ⎠ ⎞ b = ( − 4 2 ) \mathbf{b} = \binom{-4}{2} b = ( 2 − 4 ) f ( x ) f(\mathbf{x}) f ( x )
f ( x ) = 1 2 x T A x + b T x \begin{aligned}
f(\mathbf{x}) = \frac{1}{2} \mathbf{x}^T A\mathbf{x} + \mathbf{b}^T \mathbf{x}
\end{aligned}
f ( x ) = 2 1 x T A x + b T x
(1)行列A A A
d e t ( λ I − A ) = 0 → λ 2 − 4 λ + 2 = 0 \begin{aligned}
det(\lambda I - A) &= 0
\\
\rightarrow \lambda^2 - 4\lambda + 2 &= 0
\end{aligned}
d e t ( λ I − A ) → λ 2 − 4 λ + 2 = 0 = 0
λ = 4 ± 2 2 2 > 0 \lambda = \frac{4 \pm 2\sqrt{2}}{2} > 0 λ = 2 4 ± 2 2 > 0 2 ± 2 2 \pm \sqrt{2} 2 ± 2
(2)関数f ( x ) f(\mathbf{x}) f ( x ) x 0 = ( 2 3 ) \mathbf{x}_0 = \binom{2}{3} x 0 = ( 3 2 ) x 1 x_1 x 1
f ( x , y ) = 3 2 x 2 + 1 2 y 2 − x y − 4 x + 2 y f(x,y) = \frac{3}{2} x^2 + \frac{1}{2} y^2 - xy - 4x + 2y f ( x , y ) = 2 3 x 2 + 2 1 y 2 − x y − 4 x + 2 y x , y x,y x , y
f x ( x , y ) = 3 x − y − 4 f y ( x , y ) = − x + y + 2 \begin{aligned}
f_x(x,y) &= 3x - y - 4
\\
f_y(x,y) &= -x + y + 2
\end{aligned}
f x ( x , y ) f y ( x , y ) = 3 x − y − 4 = − x + y + 2
よって,(( x 0 y 0 ) \binom{x_0}{y_0} ( y 0 x 0 ) ( 2 3 ) \binom{2}{3} ( 3 2 ) ( − 1 3 ) \binom{-1}{3} ( 3 − 1 ) d k = ( 1 − 3 ) \mathbf{d}_k = \binom{1}{-3} d k = ( − 3 1 )
ステップ幅をα k \alpha_k α k
x 1 = x 0 + α k ( 1 − 3 ) \begin{aligned}
\mathbf{x}_1 = \mathbf{x}_0 + \alpha_k \binom{1}{-3}
\end{aligned}
x 1 = x 0 + α k ( − 3 1 )
f ( x 1 ) = 9 α 2 − 10 α − 2 \begin{aligned}
f(\mathbf{x_1}) = 9\alpha^2 - 10\alpha - 2
\end{aligned}
f ( x 1 ) = 9 α 2 − 1 0 α − 2
f ( x 1 ) f(\mathbf{x}_1) f ( x 1 ) α \alpha α α = 5 9 \alpha = \frac{5}{9} α = 9 5
よって, x 1 = ( 23 9 4 3 ) \mathbf{x}_1 = \binom{\frac{23}{9}}{\frac{4}{3}} x 1 = ( 3 4 9 2 3 )
正定値対称行列A ∈ R n × n A \in \mathbb{R}^{n \times n} A ∈ R n × n b ∈ R n \mathbf{b} \in \mathbb{R}^n b ∈ R n f ( x ) f(\mathbf{x}) f ( x )
f ( x ) = 1 2 x T A x + b T x \begin{aligned}
f(\mathbf{x}) = \frac{1}{2} \mathbf{x}^T A\mathbf{x} + \mathbf{b}^T \mathbf{x}
\end{aligned}
f ( x ) = 2 1 x T A x + b T x
に対して,正確な直線探索を用いた最急降下法を適用した時,点x k + 1 \mathbf{x}_{k+1} x k + 1 A , b A,b A , b x k \mathbf{x}_k x k
最適解x ∗ \mathbf{x}^* x ∗ f f f x \mathbf{x} x
A x ∗ − b = 0 \begin{aligned}
A\mathbf{x}^* - \mathbf{b} = 0
\end{aligned}
A x ∗ − b = 0
より,x ∗ = A − 1 b \mathbf{x}^* = A^{-1} \mathbf{b} x ∗ = A − 1 b
x k + 1 = x − α k ∇ f ( x k ) \begin{aligned}
\mathbf{x}_{k+1} = \mathbf{x} - \alpha_k \nabla f(\mathbf{x}_k)
\end{aligned}
x k + 1 = x − α k ∇ f ( x k )
に従って更新する.∇ f ( x k ) = A x k − b \nabla f(\mathbf{x}_k) = A\mathbf{x}_k - \mathbf{b} ∇ f ( x k ) = A x k − b α k \alpha_k α k
f ( x k − α ∇ f ( x k ) ) − 1 2 ( x k − α ∇ f ( x k ) ) T A ( x k − α ∇ f ( x k ) ) − b T ( x k − α ∇ f ( x k ) ) \begin{aligned}
f(\mathbf{x}_k - \alpha \nabla f(\mathbf{x}_k)) - \frac{1}{2} (\mathbf{x}_k - \alpha \nabla f(\mathbf{x}_k))^T A (\mathbf{x}_k - \alpha \nabla f(\mathbf{x}_k)) - \mathbf{b}^T (\mathbf{x}_k - \alpha \nabla f(\mathbf{x}_k))
\end{aligned}
f ( x k − α ∇ f ( x k ) ) − 2 1 ( x k − α ∇ f ( x k ) ) T A ( x k − α ∇ f ( x k ) ) − b T ( x k − α ∇ f ( x k ) )
の最小解をα k \alpha_k α k
α k = ∇ f ( x k ) T ∇ f ( x k ) ∇ f ( x k ) T A ∇ f ( x k ) \begin{aligned}
\alpha_k = \frac{\nabla f(\mathbf{x}_k)^T \nabla f(\mathbf{x}_k)}{\nabla f(\mathbf{x}_k)^T A \nabla f(\mathbf{x}_k)}
\end{aligned}
α k = ∇ f ( x k ) T A ∇ f ( x k ) ∇ f ( x k ) T ∇ f ( x k )
が得られる.従って,最急降下法を適用した場合,x k + 1 \mathbf{x}_{k+1} x k + 1
x k + 1 = x k − ( A x k − b ) T ( A x k − b ) ( A x k − b ) T A ( A x k − b ) ( A x k − b ) \begin{aligned}
\mathbf{x}_{k+1} = \mathbf{x}_k - \frac{(A\mathbf{x}_k - \mathbf{b})^T (A\mathbf{x}_k - \mathbf{b})}{(A\mathbf{x}_k - \mathbf{b})^T A (A\mathbf{x}_k - \mathbf{b})} (A\mathbf{x}_k - \mathbf{b})
\end{aligned}
x k + 1 = x k − ( A x k − b ) T A ( A x k − b ) ( A x k − b ) T ( A x k − b ) ( A x k − b )
ニュートン方程式
∇ 2 f ( x k ) d = − ∇ f ( x k ) \begin{aligned}
\nabla^2 f(\mathbf{x}_k) \mathbf{d} = -\nabla f(\mathbf{x}_k)
\end{aligned}
∇ 2 f ( x k ) d = − ∇ f ( x k )
いつもヘッセ行列∇ 2 f ( x k ) \nabla^2 f(\mathbf{x}_k) ∇ 2 f ( x k ) f ( x k ) f(\mathbf{x}_k) f ( x k )
そこで,ヘッセ行列を適当な正定値対称行列B k B_k B k
Q ( d ) = f ( x k ) + ∇ f ( x k ) T d + 1 2 d T B k d \begin{aligned}
Q(\mathbf{d}) = f(\mathbf{x}_k) + \nabla f(\mathbf{x}_k)^T \mathbf{d} + \frac{1}{2} \mathbf{d}^T B_k \mathbf{d}
\end{aligned}
Q ( d ) = f ( x k ) + ∇ f ( x k ) T d + 2 1 d T B k d
を考えて,連立1次方程式B k d = − ∇ f ( x k ) B_k \mathbf{d} = -\nabla f(\mathbf{x}_k) B k d = − ∇ f ( x k ) d k \mathbf{d}_k d k
B k : 正定値 ⇒ d k は降下方向 B k : 正定値 ⇔ B k − 1 が正定値 \begin{aligned}
&B_k: \text{正定値} \Rightarrow \mathbf{d}_k\text{は降下方向}
\\
&B_k: \text{正定値} \Leftrightarrow B_k^{-1}\text{が正定値}
\end{aligned}
B k : 正定値 ⇒ d k は降下方向 B k : 正定値 ⇔ B k − 1 が正定値
d k = − B k − 1 ∇ f ( x k ) \mathbf{d}_k = -B_k^{-1} \nabla f(\mathbf{x}_k) d k = − B k − 1 ∇ f ( x k )
∇ f ( x k ) T d k = − ∇ f ( x k ) T B k − 1 ∇ f ( x k ) < 0 \begin{aligned}
\nabla f(\mathbf{x}_k)^T \mathbf{d}_k = -\nabla f(\mathbf{x}_k)^T B_k^{-1} \nabla f(\mathbf{x}_k) < 0
\end{aligned}
∇ f ( x k ) T d k = − ∇ f ( x k ) T B k − 1 ∇ f ( x k ) < 0
となるので,探索方向d k \mathbf{d}_k d k
この方向はB k B_k B k ∇ 2 f ( x k ) \nabla^2 f(\mathbf{x}_k) ∇ 2 f ( x k ) ∇ f ( x ) \nabla f(\mathbf{x}) ∇ f ( x )
∇ f ( x k ) − ∇ f ( x k + 1 ) ≃ ∇ 2 f ( x k ) ( x k − x k + 1 ) \begin{aligned}
\nabla f(\mathbf{x}_k) - \nabla f(\mathbf{x}_{k+1}) \simeq \nabla^2 f(\mathbf{x}_k)(\mathbf{x}_k - \mathbf{x}_{k+1})
\end{aligned}
∇ f ( x k ) − ∇ f ( x k + 1 ) ≃ ∇ 2 f ( x k ) ( x k − x k + 1 )
となるので,B k B_k B k
s k = x k + 1 − x y k = ∇ f ( x k + 1 ) − ∇ f ( x ) \begin{aligned}
\mathbf{s}_k &= \mathbf{x}_{k+1} - \mathbf{x}
\\
\mathbf{y}_k &= \nabla f(\mathbf{x}_{k+1}) - \nabla f(\mathbf{x})
\end{aligned}
s k y k = x k + 1 − x = ∇ f ( x k + 1 ) − ∇ f ( x )
とした時,
y k = B k + 1 s k \begin{aligned}
\mathbf{y}_k = B_{k+1} \mathbf{s}_k
\end{aligned}
y k = B k + 1 s k
となるようにする.この条件をセカント条件と呼ぶ.セカント条件を満足するようにB k B_k B k B k + 1 B_{k+1} B k + 1
step0 初期設定をする(初期点x 0 \mathbf{x}_0 x 0 B 0 B_0 B 0 k = 0 k = 0 k = 0
step1 停止条件が満たされていれば,x k \mathbf{x}_k x k step2へいく.
step2 連立1次方程式B k d = − ∇ f ( x k ) B_k \mathbf{d} = -\nabla f(\mathbf{x}_k) B k d = − ∇ f ( x k ) d k \mathbf{d}_k d k
step3 d k \mathbf{d}_k d k α k \alpha_k α k
step4 x k + 1 = x k + α k d k \mathbf{x}_{k+1} = \mathbf{x}_k + \alpha_k \mathbf{d}_k x k + 1 = x k + α k d k
step5 B k B_k B k B k + 1 B_{k+1} B k + 1 k : = k + 1 k := k + 1 k : = k + 1 step1へいく.
セカント条件を満足するB k + 1 B_{k+1} B k + 1
D F P ( D a v i d o n − F l e t c h e r − P o w e l l ) DFP(Davidon-Fletcher-Powell) D F P ( D a v i d o n − F l e t c h e r − P o w e l l ) y = y k , s = s k , B = B k \mathbf{y} = \mathbf{y}_k, \mathbf{s} = \mathbf{s}_k, B = B_k y = y k , s = s k , B = B k
B k + 1 = B − B s y T + y T ( B s ) T s T y + ( 1 + s T B s s T y ) y y T s T y \begin{aligned}
\color{red}{B_{k+1} = B - \frac{B\mathbf{s}\mathbf{y}^T + \mathbf{y}^T (B\mathbf{s})^T}{\mathbf{s}^T \mathbf{y}} + (1 + \frac{\mathbf{s}^T B\mathbf{s}}{\mathbf{s}^T \mathbf{y}}) \frac{\mathbf{y}\mathbf{y}^T}{\mathbf{s}^T \mathbf{y}}}
\end{aligned}
B k + 1 = B − s T y B s y T + y T ( B s ) T + ( 1 + s T y s T B s ) s T y y y T
B F G S ( B r o y d e n − F l e t c h e r − G o l d f a r b − S h a n n o ) BFGS(Broyden-Fletcher-Goldfarb-Shanno) B F G S ( B r o y d e n − F l e t c h e r − G o l d f a r b − S h a n n o ) B k + 1 = B − ( B s ) ( B s ) T s T B s + y y T s T y \begin{aligned}
\color{red}{B_{k+1} = B - \frac{(B\mathbf{s})(B\mathbf{s})^T}{\mathbf{s}^T B\mathbf{s}} + \frac{\mathbf{y}\mathbf{y}^T}{\mathbf{s}^T \mathbf{y}}}
\end{aligned}
B k + 1 = B − s T B s ( B s ) ( B s ) T + s T y y y T
B F G S BFGS B F G S
step0 初期点x 0 \mathbf{x}_0 x 0 B 0 B_0 B 0 k = 0 k = 0 k = 0
step1 連立1次方程式B k d = − ∇ f ( x k ) B_k \mathbf{d} = -\nabla f(\mathbf{x}_k) B k d = − ∇ f ( x k ) d k \mathbf{d}_k d k
step2 Armijo(またはWolfe)条件を用いた直線探索によって,d k \mathbf{d}_k d k α k \alpha_k α k
step3 x k + 1 = x k + α k d k \mathbf{x}_{k+1} = \mathbf{x}_k + \alpha_k \mathbf{d}_k x k + 1 = x k + α k d k
step4 停止条件が満たされていれば,x k + 1 \mathbf{x}_{k+1} x k + 1 step5へいく
step5 s k \mathbf{s}_k s k y k \mathbf{y}_k y k s k = x k + 1 − x k , y = ∇ f ( x k + 1 ) − ∇ f ( x k ) \mathbf{s}_k = \mathbf{x}_{k+1} - \mathbf{x}_k, \mathbf{y} = \nabla f(\mathbf{x}_{k+1}) - \nabla f(\mathbf{x}_k) s k = x k + 1 − x k , y = ∇ f ( x k + 1 ) − ∇ f ( x k )
step6 B F G S BFGS B F G S
step7 k : = k + 1 k := k + 1 k : = k + 1 step1へいく.
B F G S BFGS B F G S B F G S BFGS B F G S { x k } \lbrace \mathbf{x}_k \rbrace { x k } { B k } \lbrace B_k \rbrace { B k } x ∗ \mathbf{x}^* x ∗ ∇ f ( x ∗ ) = 0 \nabla f(\mathbf{x}^*) = \mathbf{0} ∇ f ( x ∗ ) = 0
行列{ B k } \lbrace B_k \rbrace { B k }
B k B_k B k B k + 1 B_{k+1} B k + 1 B k B_k B k s k \mathbf{s}_k s k y k \mathbf{y}_k y k s k T y k > 0 \mathbf{s}_k^T \mathbf{y}_k > 0 s k T y k > 0 B k + 1 B_{k+1} B k + 1 D D D x ∗ \mathbf{x}^* x ∗ x ∗ \mathbf{x}^* x ∗ ∇ 2 f ( x ∗ ) \nabla^2 f(\mathbf{x}^*) ∇ 2 f ( x ∗ ) ∇ 2 f ( x ) \nabla^2 f(\mathbf{x}) ∇ 2 f ( x ) D D D x k + 1 = x k − B k − 1 ∇ f ( x k ) \mathbf{x}_{k+1} = \mathbf{x}_k - B_k^{-1} \nabla f(\mathbf{x}_k) x k + 1 = x k − B k − 1 ∇ f ( x k ) { x k } \lbrace \mathbf{x}_k \rbrace { x k } x ∗ \mathbf{x}^* x ∗ B 0 B_0 B 0 ∇ 2 f ( x ∗ ) \nabla^2 f(\mathbf{x}^*) ∇ 2 f ( x ∗ ) ∇ 2 f ( x ∗ ) \nabla^2 f(\mathbf{x}^*) ∇ 2 f ( x ∗ ) f ( x ) f(\mathbf{x}) f ( x ) B 0 B_0 B 0 d k d_k d k lim inf k → ∞ ∥ ∇ f ( x k ) ∥ = 0 \liminf_{k \rightarrow \infty} \parallel \nabla f(\mathbf{x}_k) \parallel = 0 l i m i n f k → ∞ ∥ ∇ f ( x k ) ∥ = 0 ∇ 2 f ( x ) \nabla^2 f(\mathbf{x}) ∇ 2 f ( x ) lim k → ∞ x k = x ∗ \lim_{k \rightarrow \infty} \mathbf{x}_k = \mathbf{x}^* lim k → ∞ x k = x ∗ 狭義凸2次関数f ( x ) = 1 2 x T A x − b T x ( x , b ∈ R n , A ∈ R n × n ) は正定値対称 f(\mathbf{x}) = \frac{1}{2} \mathbf{x}^T A\mathbf{x} - \mathbf{b}^T \mathbf{x} \quad (\mathbf{x}, \mathbf{b} \in \mathbb{R}^n, A \in \mathbb{R}^{n \times n})\text{は正定値対称} f ( x ) = 2 1 x T A x − b T x ( x , b ∈ R n , A ∈ R n × n ) は正定値対称 B 0 = I B_0 = I B 0 = I A A A n n n x ∗ = A − 1 b \mathbf{x}^* = A^{-1}\mathbf{b} x ∗ = A − 1 b B n = A B_{n} = A B n = A
ヘッセ行列∇ 2 f ( x k ) − 1 \nabla^2 f(\mathbf{x}_k)^{-1} ∇ 2 f ( x k ) − 1 H k H_k H k H k = B k − 1 H_k = B_k^{-1} H k = B k − 1
d k = − H k ∇ f ( x k ) \begin{aligned}
\mathbf{d}_k = -H_k \nabla f(\mathbf{x}_k)
\end{aligned}
d k = − H k ∇ f ( x k )
として求まる.セカント条件はs k = H k + 1 y k \mathbf{s}_k = H_{k+1}\mathbf{y}_k s k = H k + 1 y k
H H H B F G S BFGS B F G S H k + 1 = H k − H k y k s k T + s k ( H k y k ) T s k T y k + ( 1 + y k T H k y k s k T y k ) s k s k T s k T y k \begin{aligned}
H_{k+1} = H_k - \frac{H_k \mathbf{y}_k \mathbf{s}_k^T + \mathbf{s}_k (H_k \mathbf{y}_k)^T}{\mathbf{s}_k^T \mathbf{y}_k} + (1 + \frac{\mathbf{y}_k^T H_k \mathbf{y}_k}{\mathbf{s}_k^T \mathbf{y}_k}) \frac{\mathbf{s}_k \mathbf{s}_k^T}{\mathbf{s}_k^T \mathbf{y}_k}
\end{aligned}
H k + 1 = H k − s k T y k H k y k s k T + s k ( H k y k ) T + ( 1 + s k T y k y k T H k y k ) s k T y k s k s k T
H H H B F G S BFGS B F G S
step0 初期点x 0 \mathbf{x}_0 x 0 H 0 H_0 H 0 k = 0 k = 0 k = 0
step1 探査方向d k = − H k ∇ f ( x k ) \mathbf{d}_k = -H_k \nabla f(\mathbf{x}_k) d k = − H k ∇ f ( x k )
step2 Armijo(またはWolfe)条件を用いた直線探索によって,d k \mathbf{d}_k d k α k \alpha_k α k
step3 x k + 1 = x k + α k d k \mathbf{x}_{k+1} = \mathbf{x}_k + \alpha_k \mathbf{d}_k x k + 1 = x k + α k d k
step4 停止条件が満たされていれば,x k + 1 \mathbf{x}_{k+1} x k + 1 step5へいく
step5 s k \mathbf{s}_k s k y k \mathbf{y}_k y k s k = x k + 1 − x k , y = ∇ f ( x k + 1 ) − ∇ f ( x k ) \mathbf{s}_k = \mathbf{x}_{k+1} - \mathbf{x}_k, \mathbf{y} = \nabla f(\mathbf{x}_{k+1}) - \nabla f(\mathbf{x}_k) s k = x k + 1 − x k , y = ∇ f ( x k + 1 ) − ∇ f ( x k )
step6 H H H B F G S BFGS B F G S
step7 k : = k + 1 k := k + 1 k : = k + 1 step1へいく.
B B B D F P DFP D F P B k , s k , y k B_k,\mathbf{s}_k,\mathbf{y}_k B k , s k , y k H k , y k , s k H_k,\mathbf{y}_k,\mathbf{s}_k H k , y k , s k H H H B F G S BFGS B F G S B B B B F G S BFGS B F G S H H H D F P DFP D F P B k + 1 H k + 1 = I B_{k+1}H_{k+1} = I B k + 1 H k + 1 = I
H k + 1 : = H k + ( s k − H k y k ) ( s k − H k y k ) T y k T ( s k − H k y k ) \begin{aligned}
\color{red}{H_{k+1} := H_k + \frac{(\mathbf{s}_k - H_k \mathbf{y}_k)(\mathbf{s}_k - H_k \mathbf{y}_k)^T}{\mathbf{y}_k^T (\mathbf{s}_k - H_k \mathbf{y}_k)}}
\end{aligned}
H k + 1 : = H k + y k T ( s k − H k y k ) ( s k − H k y k ) ( s k − H k y k ) T
行列A = ( 3 1 1 1 ) A = \begin{pmatrix} 3 & 1 \\\\ 1 & 1 \end{pmatrix} A = ⎝ ⎛ 3 1 1 1 ⎠ ⎞ b = ( − 3 1 ) \mathbf{b} = \binom{-3}{1} b = ( 1 − 3 ) f ( x ) f(\mathbf{x}) f ( x )
f ( x ) = 1 2 x T A x + b T x \begin{aligned}
f(\mathbf{x}) = \frac{1}{2} \mathbf{x}^T A \mathbf{x} + \mathbf{b}^T \mathbf{x}
\end{aligned}
f ( x ) = 2 1 x T A x + b T x
この問題に対して,以下のような準ニュートン法を実行して得られる点列を求めよ(2回の反復で終了する).x 0 = ( 1 − 2 ) \mathbf{x}_0 = \binom{1}{-2} x 0 = ( − 2 1 ) B 0 = I B_0 = I B 0 = I B k B_k B k B F G S BFGS B F G S
f ( x ) = 3 2 x 1 2 + x 1 x 2 + 1 2 x 2 2 − 3 x 1 + x 2 \begin{aligned}
f(x) &= \frac{3}{2} x_1^2 + x_1x_2 + \frac{1}{2} x_2^2 - 3x_1 + x_2
\end{aligned}
f ( x ) = 2 3 x 1 2 + x 1 x 2 + 2 1 x 2 2 − 3 x 1 + x 2
∇ f ( x ) = ( 3 x 1 + x 2 − 3 x 1 + x 2 + 1 ) \begin{aligned}
\nabla f(\mathbf{x}) &= \binom{3x_1 + x_2 - 3}{x_1 + x_2 + 1}
\end{aligned}
∇ f ( x ) = ( x 1 + x 2 + 1 3 x 1 + x 2 − 3 )
(1) k = 0 k = 0 k = 0
ここで,x 0 \mathbf{x}_0 x 0
∇ f ( x 0 ) = ( − 2 0 ) \nabla f(\mathbf{x}_0) = \binom{-2}{0}
∇ f ( x 0 ) = ( 0 − 2 )
となる.
d 0 = − B 0 − 1 ∇ f ( x 0 ) = ( 2 0 ) \mathbf{d}_0 = -B_0^{-1} \nabla f(\mathbf{x}_0) = \binom{2}{0} d 0 = − B 0 − 1 ∇ f ( x 0 ) = ( 0 2 ) α k \alpha_k α k α k \alpha_k α k
α k = − d k T ∇ f ( x k ) d k T A d k \begin{aligned}
\alpha_k = -\frac{d_k^T \nabla f(\mathbf{x}_k)}{\mathbf{d}_k^T A \mathbf{d}_k}
\end{aligned}
α k = − d k T A d k d k T ∇ f ( x k )
であるから,α 0 = 1 3 \alpha_0 = \frac{1}{3} α 0 = 3 1
x 1 = x 0 + α 0 d 0 = ( 5 3 − 2 ) \mathbf{x}_1 = \mathbf{x}_0 + \alpha_0 \mathbf{d}_0 = \binom{\frac{5}{3}}{-2} x 1 = x 0 + α 0 d 0 = ( − 2 3 5 ) ∇ f ( x 1 ) = ( 0 2 3 ) \nabla f(\mathbf{x}_1) = \binom{0}{\frac{2}{3}} ∇ f ( x 1 ) = ( 3 2 0 )
s 0 = x 1 − x 0 = ( 2 3 0 ) y 0 = ∇ f ( x 1 ) − ∇ f ( x ) = ( 2 2 3 ) \begin{aligned}
\mathbf{s}_0 &= \mathbf{x}_1 - \mathbf{x}_0 = \binom{\frac{2}{3}}{0}
\\
\mathbf{y}_0 &= \nabla f(\mathbf{x}_1) - \nabla f(\mathbf{x}) = \binom{2}{\frac{2}{3}}
\end{aligned}
s 0 y 0 = x 1 − x 0 = ( 0 3 2 ) = ∇ f ( x 1 ) − ∇ f ( x ) = ( 3 2 2 )
B 0 s 0 = ( 2 3 0 ) , s 0 T y 0 = 4 3 , s 0 T B 0 s 0 = 4 9 B_0 \mathbf{s}_0 = \binom{\frac{2}{3}}{0}, \quad \mathbf{s}_0^T \mathbf{y}_0 = \frac{4}{3}, \quad \mathbf{s}_0^T B_0 \mathbf{s}_0 = \frac{4}{9} B 0 s 0 = ( 0 3 2 ) , s 0 T y 0 = 3 4 , s 0 T B 0 s 0 = 9 4
B F G S BFGS B F G S
B 1 = ( 3 1 1 4 3 ) \begin{aligned}
B_1 = \begin{pmatrix}
3 & 1
\\
1 & \frac{4}{3}
\end{pmatrix}
\end{aligned}
B 1 = ( 3 1 1 3 4 )
となる.
(2) k = 1 k = 1 k = 1
∇ f ( x 1 ) = ( 0 2 3 ) , d 1 = ( 2 9 3 2 ) , α = ( 3 2 ) \nabla f(\mathbf{x}_1) = \binom{0}{\frac{2}{3}}, \quad \mathbf{d}_1 = \binom{\frac{2}{9}}{\frac{3}{2}}, \alpha = \binom{3}{2} ∇ f ( x 1 ) = ( 3 2 0 ) , d 1 = ( 2 3 9 2 ) , α = ( 2 3 )
x 2 = x 1 + α 1 d 1 = ( 2 − 3 ) \mathbf{x}_2 = \mathbf{x}_1 + \alpha_1 \mathbf{d}_1 = \binom{2}{-3}
x 2 = x 1 + α 1 d 1 = ( − 3 2 )
この時,∇ f ( x 2 ) = ( 0 0 ) \nabla f(\mathbf{x}_2) = \binom{0}{0} ∇ f ( x 2 ) = ( 0 0 )
例題(4.8.1)において,H H H B F G S BFGS B F G S H 1 H_1 H 1 d 1 = − H 1 ∇ f ( x 1 ) \mathbf{d}_1 = -H_1 \nabla f(\mathbf{x}_1) d 1 = − H 1 ∇ f ( x 1 ) x 0 = ( 1 − 2 ) , H 0 = I \mathbf{x}_0 = \binom{1}{-2}, H_0 = I x 0 = ( − 2 1 ) , H 0 = I
(1) k = 0 k = 0 k = 0
∇ f ( x 0 ) = ( − 2 0 ) \nabla f(\mathbf{x}_0) = \binom{-2}{0} ∇ f ( x 0 ) = ( 0 − 2 ) d 0 = − H 0 ∇ f ( x 0 ) = ( 2 0 ) \mathbf{d}_0 = -H_0 \nabla f(\mathbf{x}_0) = \binom{2}{0} d 0 = − H 0 ∇ f ( x 0 ) = ( 0 2 )
ここで,d 0 T ∇ f ( x 0 ) = − 4 , d 0 T A d 0 = 12 \mathbf{d}_0^T \nabla f(\mathbf{x}_0) = -4, \quad \mathbf{d}_0^T A \mathbf{d}_0 = 12 d 0 T ∇ f ( x 0 ) = − 4 , d 0 T A d 0 = 1 2 α 0 = 1 3 \alpha_0 = \frac{1}{3} α 0 = 3 1
x 1 = x 0 + α 0 d 0 = ( 5 3 − 2 ) \mathbf{x}_1 = \mathbf{x}_0 + \alpha_0 \mathbf{d}_0 = \binom{\frac{5}{3}}{-2}
x 1 = x 0 + α 0 d 0 = ( − 2 3 5 )
この時,∇ f ( x 1 ) = ( 0 2 3 ) \nabla f(\mathbf{x}_1) = \binom{0}{\frac{2}{3}} ∇ f ( x 1 ) = ( 3 2 0 )
次にベクトル
s 0 = x 1 − x 0 = ( 2 3 0 ) , y 0 = ∇ f ( x 1 ) − ∇ f ( x 0 ) = ( 2 2 3 ) \mathbf{s}_0 = \mathbf{x}_1 - \mathbf{x}_0 = \binom{\frac{2}{3}}{0}, \quad \mathbf{y}_0 = \nabla f(\mathbf{x}_1) - \nabla f(\mathbf{x}_0) = \binom{2}{\frac{2}{3}}
s 0 = x 1 − x 0 = ( 0 3 2 ) , y 0 = ∇ f ( x 1 ) − ∇ f ( x 0 ) = ( 3 2 2 )
を計算すれば,s 0 y 0 = 4 3 , y 0 T H 0 y 0 = 40 9 \mathbf{s}_0 \mathbf{y}_0 = \frac{4}{3}, \quad \mathbf{y}_0^T H_0 \mathbf{y}_0 = \frac{40}{9} s 0 y 0 = 3 4 , y 0 T H 0 y 0 = 9 4 0
H 0 y 0 s 0 T + s 0 y 0 T H 0 s 0 T y 0 = ( 2 1 3 1 3 0 ) \begin{aligned}
\frac{H_0 \mathbf{y}_0 \mathbf{s}_0^T + \mathbf{s}_0 \mathbf{y}_0^T H_0}{\mathbf{s}_0^T \mathbf{y}_0} = \begin{pmatrix}
2 & \frac{1}{3}
\\
\frac{1}{3} & 0
\end{pmatrix}
\end{aligned}
s 0 T y 0 H 0 y 0 s 0 T + s 0 y 0 T H 0 = ( 2 3 1 3 1 0 )
( 1 + y 0 H 0 y 0 s 0 y 0 ) s 0 s 0 T s 0 T y 0 = ( 13 9 0 0 0 ) \begin{aligned}
(1 + \frac{\mathbf{y}_0 H_0 \mathbf{y}_0}{\mathbf{s}_0 \mathbf{y}_0}) \frac{\mathbf{s}_0 \mathbf{s}_0^T}{\mathbf{s}_0^T \mathbf{y}_0} = \begin{pmatrix}
\frac{13}{9} & 0
\\
0 & 0
\end{pmatrix}
\end{aligned}
( 1 + s 0 y 0 y 0 H 0 y 0 ) s 0 T y 0 s 0 s 0 T = ( 9 1 3 0 0 0 )
なので,B F G S BFGS B F G S
H 1 = ( 4 9 − 1 3 − 1 3 1 ) \begin{aligned}
H_1 = \begin{pmatrix}
\frac{4}{9} & -\frac{1}{3}
\\
-\frac{1}{3} & 1
\end{pmatrix}
\end{aligned}
H 1 = ( 9 4 − 3 1 − 3 1 1 )
(2) k = 1 k = 1 k = 1
d 1 = − H 1 ∇ f ( x 1 ) = ( 2 9 − 2 3 ) \begin{aligned}
\mathbf{d}_1 = -H_1 \nabla f(\mathbf{x}_1) = \binom{\frac{2}{9}}{-\frac{2}{3}}
\end{aligned}
d 1 = − H 1 ∇ f ( x 1 ) = ( − 3 2 9 2 )
正規行列M ∈ R n × n M \in \mathbb{R}^{n \times n} M ∈ R n × n u T v ≠ − 1 , v T M − 1 u ≠ − 1 \mathbf{u}^T\mathbf{v} \neq -1, \mathbf{v}^T M^{-1} \mathbf{u} \neq -1 u T v = − 1 , v T M − 1 u = − 1 u , v ∈ R n \mathbf{u}, \mathbf{v} \in \mathbb{R}^n u , v ∈ R n
( M + u v T ) − 1 = M − 1 − M − 1 u v T M − 1 1 + v T M − 1 u \begin{aligned}
(M + \mathbf{u} \mathbf{v}^T)^{-1} = M^{-1} - \frac{M^{-1} \mathbf{u}\mathbf{v}^T M^{-1}}{1 + \mathbf{v}^T M^{-1} \mathbf{u}}
\end{aligned}
( M + u v T ) − 1 = M − 1 − 1 + v T M − 1 u M − 1 u v T M − 1
が成り立つことを,M = ( 2 1 2 3 ) M = \begin{pmatrix} 2 & 1 \\\\ 2 & 3 \end{pmatrix} M = ⎝ ⎛ 2 2 1 3 ⎠ ⎞ u = ( 1 0 ) \mathbf{u} = \binom{1}{0} u = ( 0 1 ) v = ( 2 1 ) \mathbf{v} = \binom{2}{1} v = ( 1 2 )
数値を代入すると,左辺は
( M + u v T ) − 1 = ( ( 2 1 2 3 ) + ( 1 0 ) ( 2 1 ) ) − 1 = 1 8 ( 3 − 2 − 2 4 ) \begin{aligned}
(M + \mathbf{u} \mathbf{v}^T)^{-1} = (\begin{pmatrix}
2 & 1
\\
2 & 3
\end{pmatrix} + \binom{1}{0}(2\quad1))^{-1} = \frac{1}{8} \begin{pmatrix}
3 & -2
\\
-2 & 4
\end{pmatrix}
\end{aligned}
( M + u v T ) − 1 = ( ( 2 2 1 3 ) + ( 0 1 ) ( 2 1 ) ) − 1 = 8 1 ( 3 − 2 − 2 4 )
となる.右辺は
M − 1 − M − 1 u v T M − 1 1 + v T M − 1 u = 1 8 ( 3 − 2 − 2 4 ) \begin{aligned}
M^{-1} - \frac{M^{-1} \mathbf{u}\mathbf{v}^T M^{-1}}{1 + \mathbf{v}^T M^{-1} \mathbf{u}} = \frac{1}{8} \begin{pmatrix}
3 & -2
\\
-2 & 4
\end{pmatrix}
\end{aligned}
M − 1 − 1 + v T M − 1 u M − 1 u v T M − 1 = 8 1 ( 3 − 2 − 2 4 )
となるから,Sherman-Morrisonの公式が確認された.
手法
収束性
メモリ
ニュートン法
◎
× \times ×
準ニュートン法
○
△ \triangle △
共役勾配法
△ \triangle △ ○
最急降下法
× \times × ◎
本章では等式制約あるいは不等式制約のついた最小化問題を考える.
まずはじめに,最適解であるための条件として,Fritz-Johnの定理とKuhn-Tuckerの定理を紹介する
続いて,非線形計画法の双対定理について学習する
さらに,線形計画問題の拡張として,2次計画問題,線形相補性問題,2次錐計画問題,半正定値計画問題についても触れる
最後に,非線形計画問題の代表的な数値解法としてペナルティ関数法,乗数法,逐次2次計画法,主双対内点法を紹介する
本章では,制約付きのついた非線形最小化問題を扱う.
f : R n → R , g i : R n → R ( i = 1 , ⋯ , m ( m < n ) ) , h j : R n → R ( j = 1 , ⋯ , l ) f:\mathbb{R}^n \rightarrow \mathbb{R}, g_i:\mathbb{R}^n \rightarrow \mathbb{R}(i = 1,\cdots,m(m < n)), h_j:\mathbb{R}^n \rightarrow \mathbb{R}(j = 1,\cdots,l) f : R n → R , g i : R n → R ( i = 1 , ⋯ , m ( m < n ) ) , h j : R n → R ( j = 1 , ⋯ , l )
{ 最小化 f ( x ) 制約条件 g i ( x ) = 0 ( i = 1 , ⋯ , m ) : 等式制約 h j ( x ) ≤ 0 ( j = 1 , ⋯ , l ) : 不等式制約 \begin{aligned}
\begin{cases}
\text{最小化} \qquad &f(\mathbf{x})
\\
\text{制約条件} \qquad &g_i(\mathbf{x}) = 0 (i = 1,\cdots,m):\text{等式制約}
\\
&h_j(\mathbf{x}) \leq 0 (j = 1,\cdots,l):\text{不等式制約}
\end{cases}
\end{aligned}
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 最小化 制約条件 f ( x ) g i ( x ) = 0 ( i = 1 , ⋯ , m ) : 等式制約 h j ( x ) ≤ 0 ( j = 1 , ⋯ , l ) : 不等式制約
定義5.1(実行可能解と最小解)
制約付き問題において,制約条件を満たす点を実行可能解(feasible solution)または許容解といい,そうした点の集合
F = { x ∈ R n ∣ g i ( x ) = 0 ( i = 1 , ⋯ , m ) , h j ( x ) ≤ 0 ( j = 1 , ⋯ , l ) } \mathcal{F} = \lbrace \mathbf{x} \in \mathbb{R}^n \ |\ g_i(\mathbf{x}) = 0 (i = 1,\cdots,m), h_j(\mathbf{x}) \leq 0 (j = 1,\cdots,l) \rbrace
F = { x ∈ R n ∣ g i ( x ) = 0 ( i = 1 , ⋯ , m ) , h j ( x ) ≤ 0 ( j = 1 , ⋯ , l ) }
を実行可能領域(feasible region)または許容領域という.
実行可能解x ∗ ∈ F x^* \in \mathcal{F} x ∗ ∈ F x ∈ F \mathbf{x} \in \mathcal{F} x ∈ F f ( x ∗ ) ≤ f ( x ) f(\mathbf{x}^*) \leq f(\mathbf{x}) f ( x ∗ ) ≤ f ( x )
実行可能解x ∗ ∈ F x^* \in \mathcal{F} x ∗ ∈ F x ∗ x^* x ∗ N ( x , ϵ ) = { x ∈ R n ∣ ∥ x − x ∗ ∥ < ϵ } \mathcal{N}(\mathbf{x},\epsilon) = \lbrace \mathbf{x} \in \mathbb{R}^n \ |\ \parallel \mathbf{x} - \mathbf{x}^* \parallel < \epsilon \rbrace N ( x , ϵ ) = { x ∈ R n ∣ ∥ x − x ∗ ∥ < ϵ } x ∈ F ∩ N ( x ∗ , ϵ ) \mathbf{x} \in \mathcal{F} \cap \mathcal{N}(\mathbf{x}^*,\epsilon) x ∈ F ∩ N ( x ∗ , ϵ ) f ( x ∗ ) ≤ f ( x ) f(\mathbf{x}^*) \leq f(\mathbf{x}) f ( x ∗ ) ≤ f ( x )
以下では,
g ( x ) = [ g 1 ( x ) , ⋯ , g m ( x ) ] T ∈ R m h ( x ) = [ h 1 ( x ) , ⋯ , h l ( x ) ] T ∈ R l ∇ g ( x ) = [ ∇ g 1 ( x ) , ⋯ , ∇ g m ( x ) ] T ∈ R n × m ∇ h ( x ) = [ ∇ h 1 ( x ) , ⋯ , ∇ h l ( x ) ] T ∈ R n × l \begin{aligned}
\mathbf{g}(\mathbf{x}) &= [g_1(\mathbf{x}), \cdots, g_m(\mathbf{x})]^T \in \mathbb{R}^m
\\
\mathbf{h}(\mathbf{x}) &= [h_1(\mathbf{x}), \cdots, h_l(\mathbf{x})]^T \in \mathbb{R}^l
\\
\nabla \mathbf{g}(\mathbf{x}) &= [\nabla g_1(\mathbf{x}), \cdots, \nabla g_m(\mathbf{x})]^T \in \mathbb{R}^{n \times m}
\\
\nabla \mathbf{h}(\mathbf{x}) &= [\nabla h_1(\mathbf{x}), \cdots, \nabla h_l(\mathbf{x})]^T \in \mathbb{R}^{n \times l}
\end{aligned}
g ( x ) h ( x ) ∇ g ( x ) ∇ h ( x ) = [ g 1 ( x ) , ⋯ , g m ( x ) ] T ∈ R m = [ h 1 ( x ) , ⋯ , h l ( x ) ] T ∈ R l = [ ∇ g 1 ( x ) , ⋯ , ∇ g m ( x ) ] T ∈ R n × m = [ ∇ h 1 ( x ) , ⋯ , ∇ h l ( x ) ] T ∈ R n × l
と定義する.
まず等式制約がついた問題を考える
最小化 f ( x ) 制約条件 g i ( x ) = 0 ( i = 1 , ⋯ , m ) \begin{aligned}
\text{最小化} \qquad & f(\mathbf{x})
\\
\text{制約条件} \qquad & g_i(\mathbf{x}) = 0 (i = 1, \cdots, m)
\end{aligned}
最小化 制約条件 f ( x ) g i ( x ) = 0 ( i = 1 , ⋯ , m )
この問題について,次の関数を定義する
L ( x , y ) = f ( x ) + y T g ( x ) ( = f ( x ) + ∑ i = 1 m y i g i ( x ) ) L(\mathbf{x, y}) = f(\mathbf{x}) + \mathbf{y}^T \mathbf{g}(\mathbf{x}) (= f(\mathbf{x}) + \sum_{i=1}^m y_ig_i(\mathbf{x}))
L ( x , y ) = f ( x ) + y T g ( x ) ( = f ( x ) + i = 1 ∑ m y i g i ( x ) )
これをラグランジュ関数(Lagrangian function)と呼ぶ.ただし,
y = ( y 1 , ⋯ , y m ) T \mathbf{y} = (y_1,\cdots,y_m)^T
y = ( y 1 , ⋯ , y m ) T
とし,y 1 y_1 y 1 g i ( x ) = 0 g_i(\mathbf{x}) = 0 g i ( x ) = 0 y \mathbf{y} y
ラグランジュ関数の停留点,すなわち,ラグランジュ関数の勾配ベクトルを零にする点は等式制約付き問題の最適解と密接な関係がある.
定理5.1(等式制約付き問題の最適性条件:1次の必要条件)
f , g i ( i = 1 , ⋯ , m ) f,g_i(i = 1,\cdots,m) f , g i ( i = 1 , ⋯ , m ) x ∗ x^* x ∗
この時,∇ g 1 ( x ∗ ) , ⋯ , ∇ g m ( x ∗ ) \nabla g_1(x^*), \cdots, \nabla g_m(x^*) ∇ g 1 ( x ∗ ) , ⋯ , ∇ g m ( x ∗ ) y ∗ = [ y 1 ∗ , ⋯ , y m ∗ ] T \mathbf{y}^* = [y_1^*, \cdots, y_m^*]^T y ∗ = [ y 1 ∗ , ⋯ , y m ∗ ] T
∇ x L ( x ∗ , y ∗ ) = ∇ f ( x ∗ ) + ∑ i = 1 m y i ∗ ∇ g i ( x ∗ ) = 0 ∇ y L ( x ∗ , y ∗ ) = g ( x ∗ ) = 0 \begin{aligned}
\nabla_\mathbf{x} L(\mathbf{x}^*,\mathbf{y}^*) &= \nabla f(\mathbf{x}^*) + \sum_{i=1}^m y_i^* \nabla g_i(\mathbf{x}^*) = \mathbf{0}
\\
\nabla_\mathbf{y} L(\mathbf{x}^*,\mathbf{y}^*) &= \mathbf{g}(\mathbf{x}^*) = \mathbf{0}
\end{aligned}
∇ x L ( x ∗ , y ∗ ) ∇ y L ( x ∗ , y ∗ ) = ∇ f ( x ∗ ) + i = 1 ∑ m y i ∗ ∇ g i ( x ∗ ) = 0 = g ( x ∗ ) = 0
が成り立つ.ただし,∇ x L , ∇ y L \nabla_\mathbf{x} L, \nabla_\mathbf{y} L ∇ x L , ∇ y L x , y \mathbf{x,y} x , y
簡単な問題なら定理から局所的最適解が計算できる⇒ \Rightarrow ⇒
例題1
m i n 2 x 1 2 + 3 x 2 2 s . t x 1 + x 2 − 1 = 0 \begin{aligned}
min \quad &2x_1^2 + 3x_2^2
\\
s.t \quad &x_1 + x_2 - 1 = 0
\end{aligned}
m i n s . t 2 x 1 2 + 3 x 2 2 x 1 + x 2 − 1 = 0
ラグランジュ関数は
L ( x 1 , x 2 , y ) = 2 x 1 2 + 3 x 2 2 + y ( x 1 + x 2 − 1 ) L(x_1,x_2,y) = 2x_1^2 + 3x_2^2 + y(x_1 + x_2 - 1)
L ( x 1 , x 2 , y ) = 2 x 1 2 + 3 x 2 2 + y ( x 1 + x 2 − 1 )
となるので
∇ x L ( x , y ) = ( 4 x 1 + y 6 x 2 + y ) = ( 0 0 ) ∇ y L ( x , y ) = x 1 + x 2 − 1 = 0 ⇒ ( x 1 , x 2 , y ) = ( 3 5 , 2 5 , − 12 5 ) \begin{aligned}
&\nabla_\mathbf{x} L(\mathbf{x}, \mathbf{y}) = \begin{pmatrix}
4x_1 + y
\\
6x_2 + y
\end{pmatrix} = \begin{pmatrix}
0
\\
0
\end{pmatrix}
\\
&\nabla_\mathbf{y} L(\mathbf{x},\mathbf{y}) = x_1 + x_2 - 1 = 0
\\
&\Rightarrow (x_1, x_2, y) = (\frac{3}{5}, \frac{2}{5}, -\frac{12}{5})
\end{aligned}
∇ x L ( x , y ) = ( 4 x 1 + y 6 x 2 + y ) = ( 0 0 ) ∇ y L ( x , y ) = x 1 + x 2 − 1 = 0 ⇒ ( x 1 , x 2 , y ) = ( 5 3 , 5 2 , − 5 1 2 )
ここでは次のような不等式制約付き最小化問題を考える
最小化 f ( x ) 制約条件 h i ( x ) ≤ 0 ( i = 1 , ⋯ , l ) \begin{aligned}
\text{最小化} \qquad & f(\mathbf{x})
\\
\text{制約条件} \qquad & h_i(\mathbf{x}) \leq 0 (i = 1, \cdots, l)
\end{aligned}
最小化 制約条件 f ( x ) h i ( x ) ≤ 0 ( i = 1 , ⋯ , l )
実行可能解x 0 \mathbf{x}^0 x 0 h i ( x 0 ) = 0 h_i(\mathbf{x}^0) = 0 h i ( x 0 ) = 0 x 0 \mathbf{x}^0 x 0 x 0 \mathbf{x}^0 x 0 h i ( x 0 ) < 0 h_i(\mathbf{x}^0) < 0 h i ( x 0 ) < 0 x 0 \mathbf{x}^0 x 0
x ∗ \mathbf{x}^* x ∗ I ( x ∗ ) = { i ∣ h i ( x ∗ ) = 0 , i = 1 , ⋯ , l } I(\mathbf{x}^*) = \lbrace i \ |\ h_i(\mathbf{x}^*) = 0, i = 1,\cdots,l \rbrace I ( x ∗ ) = { i ∣ h i ( x ∗ ) = 0 , i = 1 , ⋯ , l }
定理5.2: Fritz-Johnの定理
不等式制約付き問題の局所的最小解x ∗ x^* x ∗ f , h i ( i = 1 , ⋯ , l ) f, h_i(i = 1, \cdots, l) f , h i ( i = 1 , ⋯ , l ) ( z 0 ∗ , z ∗ ) ≠ ( 0 , 0 ) (z_0^*, \mathbf{z}^*) \neq (0, \mathbf{0}) ( z 0 ∗ , z ∗ ) = ( 0 , 0 ) z 0 ∗ z_0^* z 0 ∗ z ∗ = [ z 1 ∗ , ⋯ , z l ∗ ] T \mathbf{z}^* = [z_1^*, \cdots, z_l^*]^T z ∗ = [ z 1 ∗ , ⋯ , z l ∗ ] T
z 0 ∗ ∇ f ( x ∗ ) + ∑ i = 1 l z i ∗ ∇ h i ( x ∗ ) = 0 h ( x ∗ ) ≤ 0 , z i ∗ ≥ 0 ( i = 0 , 1 , ⋯ , l ) , z i ∗ h i ( x ∗ ) = 0 ( i = 1 , ⋯ , l ) \begin{aligned}
& z_0^* \nabla f(\mathbf{x}^*) + \sum_{i=1}^l z_i^* \nabla h_i(\mathbf{x}^*) = \mathbf{0}
\\
& \mathbf{h}(\mathbf{x}^*) \leq \mathbf{0}, z_i^* \geq 0 (i = 0,1,\cdots,l),\quad z_i^* h_i(\mathbf{x}^*) = 0 (i = 1, \cdots, l)
\end{aligned}
z 0 ∗ ∇ f ( x ∗ ) + i = 1 ∑ l z i ∗ ∇ h i ( x ∗ ) = 0 h ( x ∗ ) ≤ 0 , z i ∗ ≥ 0 ( i = 0 , 1 , ⋯ , l ) , z i ∗ h i ( x ∗ ) = 0 ( i = 1 , ⋯ , l )
ラグランジュ乗数:z i ∗ ( i = 0 , ⋯ , l ) z_i^*(i=0,\cdots,l) z i ∗ ( i = 0 , ⋯ , l )
相補性条件:z i ∗ h i ( x ∗ ) = 0 ( i = 1 , ⋯ , l ) z_i^* h_i(\mathbf{x}^*) = 0 (i = 1, \cdots, l) z i ∗ h i ( x ∗ ) = 0 ( i = 1 , ⋯ , l )
狭義相補性条件:h i ( x ∗ ) = 0 , z i ∗ = 0 h_i(\mathbf{x}^*) = 0, z_i^* = 0 h i ( x ∗ ) = 0 , z i ∗ = 0
Fritz-Johnの定理において, z 0 ∗ = 0 z_0^* = 0 z 0 ∗ = 0 z 0 ∗ > 0 z_0^* > 0 z 0 ∗ > 0
L ( x , z ) = f ( x ) + z T h ( x ) ( = f ( x ) + ∑ i = 1 l z i h i ( x ) ) z = ( z 1 , ⋯ , z l ) T \begin{aligned}
L(\mathbf{x},\mathbf{z}) &= f(\mathbf{x}) + \mathbf{z}^T \mathbf{h}(\mathbf{x}) \quad (= f(\mathbf{x}) + \sum_{i=1}^l z_i h_i(\mathbf{x}))
\\
\mathbf{z} &= (z_1,\cdots,z_l)^T
\end{aligned}
L ( x , z ) z = f ( x ) + z T h ( x ) ( = f ( x ) + i = 1 ∑ l z i h i ( x ) ) = ( z 1 , ⋯ , z l ) T
と定義する.
定理5.3: Kuhn-Tuckerの定理:最適性の1次の必要条件
不等式制約付き問題の局所的最小解x ∗ \mathbf{x}^* x ∗ f , h i ( i = 1 , ⋯ , l ) f,h_i(i = 1,\cdots,l) f , h i ( i = 1 , ⋯ , l ) i ∈ I ( x ∗ ) i \in I(\mathbf{x}^*) i ∈ I ( x ∗ ) ∇ h i ( x ∗ ) \nabla h_i(\mathbf{x}^*) ∇ h i ( x ∗ ) z ∗ = ( z 1 ∗ , ⋯ , z l ∗ ) T \mathbf{z}^* = (z_1^*, \cdots, z_l^*)^T z ∗ = ( z 1 ∗ , ⋯ , z l ∗ ) T ( x ∗ , z ∗ ) (\mathbf{x}^*,\mathbf{z}^*) ( x ∗ , z ∗ )
∇ x L ( x ∗ , z ∗ ) = ∇ f ( x ∗ ) + ∑ i = 1 l z i ∗ ∇ h i ( x ∗ ) = 0 ∇ z L ( x ∗ , z ∗ ) = h ( x ∗ ) ≤ 0 z i ∗ ≥ 0 ( i = 1 , ⋯ , l ) z i ∗ h i ( x ∗ ) = 0 ( i = 1 , ⋯ , l ) ( 相補性 ) \begin{aligned}
\nabla_\mathbf{x} L(\mathbf{x}^*, \mathbf{z}^*) &= \nabla f(\mathbf{x}^*) + \sum_{i=1}^l z_i^* \nabla h_i(\mathbf{x}^*) = \mathbf{0}
\\
\nabla_\mathbf{z} L(\mathbf{x}^*, \mathbf{z}^*) &= \mathbf{h}(\mathbf{x}^*) \leq \mathbf{0}
\\
z_i^* &\geq 0 \quad (i = 1,\cdots,l)
\\
z_i^* h_i(\mathbf{x}^*) &= 0 \quad (i = 1,\cdots,l) (\text{相補性})
\end{aligned}
∇ x L ( x ∗ , z ∗ ) ∇ z L ( x ∗ , z ∗ ) z i ∗ z i ∗ h i ( x ∗ ) = ∇ f ( x ∗ ) + i = 1 ∑ l z i ∗ ∇ h i ( x ∗ ) = 0 = h ( x ∗ ) ≤ 0 ≥ 0 ( i = 1 , ⋯ , l ) = 0 ( i = 1 , ⋯ , l ) ( 相補性 )
以上の四つ条件合わせて,Karush-Kuhn-Tucker条件といい,略してKKT条件という.
例題:次の2次計画問題を考える
m i n 1 2 { ( x 1 − 8 ) 2 + ( x 2 − 6 ) 2 } s . t 3 x 1 + x 2 ≤ 15 x 1 + 2 x 2 ≤ 10 x 1 + x 2 ≥ 3 x 1 ≥ 0 , x 2 ≥ 0 \begin{aligned}
min \qquad & \frac{1}{2} \lbrace (x_1 - 8)^2 + (x_2 - 6)^2 \rbrace
\\
s.t \qquad & 3x_1 + x_2 \leq 15
\\
& x_1 + 2x_2 \leq 10
\\
& x_1 + x_2 \geq 3
\\
& x_1 \geq 0, x_2 \geq 0
\end{aligned}
m i n s . t 2 1 { ( x 1 − 8 ) 2 + ( x 2 − 6 ) 2 } 3 x 1 + x 2 ≤ 1 5 x 1 + 2 x 2 ≤ 1 0 x 1 + x 2 ≥ 3 x 1 ≥ 0 , x 2 ≥ 0
この問題のラグランジュ関数は
L ( x 1 , x 2 , z 1 , z 2 , z 3 , z 4 , z 5 ) = 1 2 ( x 1 − 8 ) 2 + ( x 2 − 6 ) 2 + z 1 ( 3 x 1 + x 2 − 15 ) + z 2 ( x 1 + 2 x 2 − 10 ) + z 3 ( 3 − x 1 − x 2 ) − z 4 x 1 − z 5 x 2 \begin{aligned}
L(x_1,x_2,z_1,z_2,z_3,z_4,z_5) = &\frac{1}{2}{(x_1 - 8)^2 + (x_2 - 6)^2}
\\
& + z_1(3x_1 + x_2 -15) + z_2(x_1 + 2x_2 - 10)
\\
& + z_3(3 - x_1 - x_2) - z_4x_1 - z_5x_2
\end{aligned}
L ( x 1 , x 2 , z 1 , z 2 , z 3 , z 4 , z 5 ) = 2 1 ( x 1 − 8 ) 2 + ( x 2 − 6 ) 2 + z 1 ( 3 x 1 + x 2 − 1 5 ) + z 2 ( x 1 + 2 x 2 − 1 0 ) + z 3 ( 3 − x 1 − x 2 ) − z 4 x 1 − z 5 x 2
となるので,KKT条件は次式で表される.
∇ x L ( x , z ) = ( x 1 − 8 x 2 − 6 ) + z 1 ( 3 1 ) + z 2 ( 1 2 ) + z 3 ( − 1 − 1 ) + z 4 ( − 1 0 ) + z 5 ( 0 − 1 ) = ( 0 0 ) ∇ z L ( x , z ) = ( 3 x 1 + x 2 − 15 x 1 + x 2 − 10 − x 1 − x 2 + 3 − x 1 − x 2 ) ≤ ( 0 0 0 0 0 ) z 1 , ⋯ , z 5 ≥ 0 , z 1 ( 3 x 1 + x 2 − 15 ) = 0 , z 2 ( x 1 + x 2 − 10 ) = 0 , z 3 ( − x 1 − x 2 + 3 ) = 0 , z 4 x 1 = 0 , z 5 x 2 = 0 \begin{aligned}
&\begin{aligned}
\nabla_\mathbf{x} L(\mathbf{x,z}) = &\binom{x_1 - 8}{x_2 - 6} + z_1\binom{3}{1} + z_2\binom{1}{2}
\\
& + z_3\binom{-1}{-1} + z_4\binom{-1}{0} + z_5\binom{0}{-1} = \binom{0}{0}
\end{aligned}
\\
&\begin{aligned}
\nabla_\mathbf{z} L(\mathbf{x,z}) &= \begin{pmatrix}
3x_1 + x_2 - 15
\\
x_1 + x_2 - 10
\\
-x_1 - x_2 + 3
\\
-x_1
\\
-x_2
\end{pmatrix} \leq \begin{pmatrix}
0
\\
0
\\
0
\\
0
\\
0
\end{pmatrix}
\end{aligned}
\\
&\begin{aligned}
&z_1,\cdots,z_5 \geq 0,
\\
&z_1(3x_1 + x_2 - 15) = 0, z_2(x_1 + x_2 - 10) = 0,z_3(-x_1 - x_2 + 3) = 0, z_4x_1 = 0, z_5x_2 = 0
\end{aligned}
\end{aligned}
∇ x L ( x , z ) = ( x 2 − 6 x 1 − 8 ) + z 1 ( 1 3 ) + z 2 ( 2 1 ) + z 3 ( − 1 − 1 ) + z 4 ( 0 − 1 ) + z 5 ( − 1 0 ) = ( 0 0 ) ∇ z L ( x , z ) = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 3 x 1 + x 2 − 1 5 x 1 + x 2 − 1 0 − x 1 − x 2 + 3 − x 1 − x 2 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ ≤ ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 0 0 0 0 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ z 1 , ⋯ , z 5 ≥ 0 , z 1 ( 3 x 1 + x 2 − 1 5 ) = 0 , z 2 ( x 1 + x 2 − 1 0 ) = 0 , z 3 ( − x 1 − x 2 + 3 ) = 0 , z 4 x 1 = 0 , z 5 x 2 = 0
図により明らかに点(4,3)が最適解になる.
2つの実行可能解(4,3),(5,0)においてKKT条件が成り立つかどうかを吟味する
(1) 最適解(4,3)において:相補性条件より
0 ⋅ z 1 = 0 , 0 ⋅ z 2 = 0 , − 4 z 3 = 0 , 4 z 4 = 0 , 3 z 5 = 0 , 0 \cdot z_1 = 0, 0 \cdot z_2 = 0, -4z_3 = 0, 4z_4 = 0, 3z_5 = 0,
0 ⋅ z 1 = 0 , 0 ⋅ z 2 = 0 , − 4 z 3 = 0 , 4 z 4 = 0 , 3 z 5 = 0 ,
なので,z 3 = z 4 = z 5 = 0 z_3 = z_4 = z_5 = 0 z 3 = z 4 = z 5 = 0 ∇ x L ( x , z ) = 0 \nabla_\mathbf{x} L(\mathbf{x},\mathbf{z}) = \mathbf{0} ∇ x L ( x , z ) = 0
z 1 ( 3 1 ) + z 2 ( 1 2 ) = − ∇ f ( 4 , 3 ) = ( 4 3 ) z_1\binom{3}{1} + z_2\binom{1}{2} = -\nabla f(4,3) = \binom{4}{3}
z 1 ( 1 3 ) + z 2 ( 2 1 ) = − ∇ f ( 4 , 3 ) = ( 3 4 )
なので,z 1 = 1 > 0 , z 2 = 1 > 0 z_1 = 1 > 0, z_2 = 1 > 0 z 1 = 1 > 0 , z 2 = 1 > 0
(2) 点(5,0)において:相補性条件より
z 2 = z 3 = z 4 = 0 z_2 = z_3 = z_4 = 0
z 2 = z 3 = z 4 = 0
なので,KKT条件の∇ x L ( x , z ) = 0 \nabla_\mathbf{x} L(\mathbf{x},\mathbf{z}) = \mathbf{0} ∇ x L ( x , z ) = 0
z 1 ( 3 1 ) + z 5 ( 0 − 1 ) = − ∇ f ( 5 , 0 ) = ( 3 6 ) z_1\binom{3}{1} + z_5\binom{0}{-1} = -\nabla f(5,0) = \binom{3}{6}
z 1 ( 1 3 ) + z 5 ( − 1 0 ) = − ∇ f ( 5 , 0 ) = ( 6 3 )
となる(線形独立制約想定は成り立っている).これにより,z 1 = 1 > 0 , z 5 = − 5 < 0 z_1 = 1 > 0, z_5 = -5 < 0 z 1 = 1 > 0 , z 5 = − 5 < 0
∇ f ( x ∗ ) ≠ 0 ⇒ − ∇ f ( x ∗ ) \nabla f(\mathbf{x}^*) \neq \mathbf{0} \Rightarrow -\nabla f(\mathbf{x}^*) ∇ f ( x ∗ ) = 0 ⇒ − ∇ f ( x ∗ ) ∑ z i ∗ ∇ h i ( x ∗ ) = − ∇ f ( x ∗ ) \sum z_i^* \nabla h_i(\mathbf{x}^*) = -\nabla f(\mathbf{x}^*) ∑ z i ∗ ∇ h i ( x ∗ ) = − ∇ f ( x ∗ )
KKT条件は制約想定を仮定しなければ,そのままでは最適解であるための必要条件になるとは限らないことを注意すること.次の例題を見てみよう.
例題:次の最小化問題を考える
min − x 1 s . t x 2 ≤ ( 1 − x 1 ) 3 x 2 ≥ 0 \begin{aligned}
\min \quad &-x_1
\\
s.t \quad &x_2 \leq (1 - x_1)^3
\\
&x_2 \geq 0
\end{aligned}
min s . t − x 1 x 2 ≤ ( 1 − x 1 ) 3 x 2 ≥ 0
f ( x 1 , x 2 ) = − x 1 , h 1 ( x 1 , x 2 ) = x 2 − ( 1 − x 1 ) 3 , h 2 ( x 1 , x 2 ) = − x 2 f(x_1,x_2) = -x_1, h_1(x_1,x_2) = x_2 - (1 - x_1)^3, h_2(x_1,x_2) = -x_2 f ( x 1 , x 2 ) = − x 1 , h 1 ( x 1 , x 2 ) = x 2 − ( 1 − x 1 ) 3 , h 2 ( x 1 , x 2 ) = − x 2
∇ f ( x 1 , x 2 ) = ( − 1 0 ) , ∇ h 1 ( x 1 , x 2 ) = ( 3 ( 1 − x 1 ) 2 1 ) , ∇ h 2 ( x 1 , x 2 ) = ( 0 − 1 ) \begin{aligned}
\nabla f(x_1,x_2) = \begin{pmatrix}
-1
\\
0
\end{pmatrix}, \nabla h_1(x_1,x_2) = \begin{pmatrix}
3(1 - x_1)^2
\\
1
\end{pmatrix}, \nabla h_2(x_1,x_2) = \begin{pmatrix}
0
\\
-1
\end{pmatrix}
\end{aligned}
∇ f ( x 1 , x 2 ) = ( − 1 0 ) , ∇ h 1 ( x 1 , x 2 ) = ( 3 ( 1 − x 1 ) 2 1 ) , ∇ h 2 ( x 1 , x 2 ) = ( 0 − 1 )
となる.しかしながら,解( x 1 ∗ , x 2 ∗ ) (x_1^*,x_2^*) ( x 1 ∗ , x 2 ∗ )
∇ f ( x 1 ∗ , x 2 ∗ ) + z 1 ∇ h 1 ( x 1 ∗ , x 2 ∗ ) + z 2 ∇ h 2 ( x 1 ∗ , x 2 ∗ ) = 0 \nabla f(x_1^*,x_2^*) + z_1 \nabla h_1(x_1^*,x_2^*) + z_2 \nabla h_2(x_1^*,x_2^*) = \mathbf{0}
∇ f ( x 1 ∗ , x 2 ∗ ) + z 1 ∇ h 1 ( x 1 ∗ , x 2 ∗ ) + z 2 ∇ h 2 ( x 1 ∗ , x 2 ∗ ) = 0
すなわち
( − 1 0 ) + z 1 ( 0 1 ) + z 2 ( 0 − 1 ) = ( 0 0 ) \binom{-1}{0} + z_1\binom{0}{1} + z_2\binom{0}{-1} = \binom{0}{0}
( 0 − 1 ) + z 1 ( 1 0 ) + z 2 ( − 1 0 ) = ( 0 0 )
を満たす非負の数z 1 , z 2 z_1,z_2 z 1 , z 2 ∇ h 1 ( x 1 ∗ , x 2 ∗ ) = ( 0 , 1 ) T , ∇ h 2 ( x 1 ∗ , x 2 ∗ ) = ( 0 , − 1 ) T \nabla h_1(x_1^*,x_2^*) = (0,1)^T, \nabla h_2(x_1^*,x_2^*) = (0,-1)^T ∇ h 1 ( x 1 ∗ , x 2 ∗ ) = ( 0 , 1 ) T , ∇ h 2 ( x 1 ∗ , x 2 ∗ ) = ( 0 , − 1 ) T
z 0 ( − 1 0 ) + z 1 ( 0 1 ) + z 2 ( 0 − 1 ) = ( 0 0 ) z_0\binom{-1}{0} + z_1\binom{0}{1} + z_2\binom{0}{-1} = \binom{0}{0}
z 0 ( 0 − 1 ) + z 1 ( 1 0 ) + z 2 ( − 1 0 ) = ( 0 0 )
はz 0 = 0 , z 1 = z 2 = 1 z_0 = 0, z_1 = z_2 = 1 z 0 = 0 , z 1 = z 2 = 1
定理5.4: 不等式制約付き問題の最適性条件:2次の必要条件
不等式制約付き問題の局所的最小解x ∗ \mathbf{x}^* x ∗ f , h i ( i = 1 , ⋯ , l ) f,h_i(i = 1,\cdots,l) f , h i ( i = 1 , ⋯ , l ) z ∗ \mathbf{z}^* z ∗ i ∈ I ( x ∗ ) i \in I(\mathbf{x}^*) i ∈ I ( x ∗ ) ∇ h i ( x ∗ ) T v = 0 \nabla h_i(\mathbf{x}^*)^T \mathbf{v} = 0 ∇ h i ( x ∗ ) T v = 0 v ∈ R n \mathbf{v} \in \mathbb{R}^n v ∈ R n ϕ : [ 0 , c ) → R n が存在して , ϕ ( 0 ) = x ∗ , h i ( ϕ ( τ ) ) = 0 ( ∀ i ∈ I ( x ∗ ) , ∀ τ ∈ ( 0 , c ) ) , lim τ → ∞ ϕ ( τ ) − ϕ ( 0 ) τ = β v \phi : [0,c) \rightarrow \mathbb{R}^n\text{が存在して},\phi (0) = \mathbf{x}^*, h_i(\phi(\tau)) = 0(\forall i \in I(\mathbf{x}^*), \forall \tau \in (0,c)),\lim_{\tau \rightarrow \infty} \frac{\phi(\tau) - \phi(0)}{\tau} = \beta \mathbf{v} ϕ : [ 0 , c ) → R n が存在して , ϕ ( 0 ) = x ∗ , h i ( ϕ ( τ ) ) = 0 ( ∀ i ∈ I ( x ∗ ) , ∀ τ ∈ ( 0 , c ) ) , lim τ → ∞ τ ϕ ( τ ) − ϕ ( 0 ) = β v β \beta β ∇ h i ( x ∗ ) T v = 0 ( ∀ i ∈ I ( x ∗ ) ) \nabla h_i(\mathbf{x}^*)^T \mathbf{v} = 0(\forall i \in I(\mathbf{x}^*)) ∇ h i ( x ∗ ) T v = 0 ( ∀ i ∈ I ( x ∗ ) ) v ∈ R n \mathbf{v} \in \mathbb{R}^n v ∈ R n
v T ∇ x 2 L ( x , z ) v ≥ 0 \mathbf{v}^T \nabla^2_\mathbf{x} L(\mathbf{x},\mathbf{z})\mathbf{v} \geq 0
v T ∇ x 2 L ( x , z ) v ≥ 0
となる.ただし,∇ x 2 L ( x , z ) \nabla_\mathbf{x}^2 L(\mathbf{x},\mathbf{z}) ∇ x 2 L ( x , z ) x \mathbf{x} x
∇ x 2 L ( x , z ) = ∇ 2 f ( x ) + ∑ i = 1 l z i ∇ 2 h i ( x ) \nabla_\mathbf{x}^2 L(\mathbf{x},\mathbf{z}) = \nabla^2 f(\mathbf{x}) + \sum_{i=1}^l z_i \nabla^2 h_i(\mathbf{x})
∇ x 2 L ( x , z ) = ∇ 2 f ( x ) + i = 1 ∑ l z i ∇ 2 h i ( x )
で表される.
最小解であるための2次の十分条件を述べるにあたって,次の集合を定義しておく.
I + ( x ∗ ) = { i ∣ z i ∗ > 0 } V ( x ∗ ) = { v ∈ R n ∣ ∇ h i ( x ∗ ) T v = 0 , i ∈ I + ( x ∗ ) , ∇ h i ( x ∗ ) T v ≤ 0 , i ∈ I ( x ∗ ) I + ( x ∗ ) } \begin{aligned}
I_+(\mathbf{x}^*) &= \lbrace i \ |\ z_i^* > 0 \rbrace
\\
V(\mathbf{x}^*) &= \lbrace \mathbf{v} \in \mathbb{R}^n \ |\ \nabla h_i(\mathbf{x}^*)^T \mathbf{v} = 0, i \in I_+(\mathbf{x}^*),\nabla h_i(\mathbf{x}^*)^T \mathbf{v} \leq 0, i \in \frac{I(\mathbf{x}^*)}{I_+(\mathbf{x}^*)} \rbrace
\end{aligned}
I + ( x ∗ ) V ( x ∗ ) = { i ∣ z i ∗ > 0 } = { v ∈ R n ∣ ∇ h i ( x ∗ ) T v = 0 , i ∈ I + ( x ∗ ) , ∇ h i ( x ∗ ) T v ≤ 0 , i ∈ I + ( x ∗ ) I ( x ∗ ) }
定理5.5: 不等式制約付き問題の最適性条件:2次の十分条件
x ∗ \mathbf{x}^* x ∗ f , h i ( i = 1 , ⋯ , l ) f,h_i(i = 1,\cdots,l) f , h i ( i = 1 , ⋯ , l ) z ∗ \mathbf{z}^* z ∗ v ∈ V ( x ∗ ) \mathbf{v} \in V(\mathbf{x}^*) v ∈ V ( x ∗ )
v T ∇ x 2 L ( x , z ∗ ) v > 0 \mathbf{v}^T \nabla_\mathbf{x}^2 L(\mathbf{x},\mathbf{z}^*) \mathbf{v} > 0
v T ∇ x 2 L ( x , z ∗ ) v > 0
が成り立つとする.この時,x ∗ \mathbf{x}^* x ∗ x ∗ \mathbf{x}^* x ∗ x ∗ \mathbf{x}^* x ∗
次の非線形最小化問題それぞれに対して,ラグランジュ関数を作り,最適解を求めよ.
(1)
min x 1 2 + x 2 2 + x 3 2 s . t x 1 + 3 x 2 + 4 x 3 = 61 \begin{aligned}
\min \quad &x_1^2 + x_2^2 + x_3^2
\\
s.t \quad &x_1 + 3x_2 + 4x_3 = 61
\end{aligned}
min s . t x 1 2 + x 2 2 + x 3 2 x 1 + 3 x 2 + 4 x 3 = 6 1
ラグランジュ関数は
L ( x 1 , x 2 , x 3 , y ) = x 1 2 + x 2 2 + x 3 2 + y ( x 1 + 3 x 2 + 4 x 3 − 61 ) L(x_1,x_2,x_3,y) = x_1^2 + x_2^2 + x_3^2 + y(x_1 + 3x_2 + 4x_3 - 61)
L ( x 1 , x 2 , x 3 , y ) = x 1 2 + x 2 2 + x 3 2 + y ( x 1 + 3 x 2 + 4 x 3 − 6 1 )
となる.等式制約付き問題の最適性条件:一次の必要条件より
∂ L ∂ x 1 = 2 x 1 + y = 0 , ∂ L ∂ x 2 = 2 x 2 + 3 y = 0 , ∂ L ∂ x 3 = 2 x 3 + 4 y = 0 ∂ L ∂ y = x 1 + 3 x 2 + 4 x 3 − 61 = 0 \begin{aligned}
&\frac{\partial L}{\partial x_1} = 2x_1 + y = 0, \frac{\partial L}{\partial x_2} = 2x_2 + 3y = 0, \frac{\partial L}{\partial x_3} = 2x_3 + 4y = 0
\\
&\frac{\partial L}{\partial y} = x_1 + 3x_2 + 4x_3 - 61 = 0
\end{aligned}
∂ x 1 ∂ L = 2 x 1 + y = 0 , ∂ x 2 ∂ L = 2 x 2 + 3 y = 0 , ∂ x 3 ∂ L = 2 x 3 + 4 y = 0 ∂ y ∂ L = x 1 + 3 x 2 + 4 x 3 − 6 1 = 0
で表される.ただし,
∇ f ( x ) = ( 2 x 1 2 x 2 2 x 3 ) , ∇ g ( x 1 , x 2 , x 3 ) = ( 1 3 4 ) \begin{aligned}
\nabla f(\mathbf{x}) = \begin{pmatrix}
2x_1
\\
2x_2
\\
2x_3
\end{pmatrix}, \nabla g(x_1,x_2,x_3) = \begin{pmatrix}
1
\\
3
\\
4
\end{pmatrix}
\end{aligned}
∇ f ( x ) = ⎝ ⎛ 2 x 1 2 x 2 2 x 3 ⎠ ⎞ , ∇ g ( x 1 , x 2 , x 3 ) = ⎝ ⎛ 1 3 4 ⎠ ⎞
である.これを解くと,y = − 61 13 y = -\frac{61}{13} y = − 1 3 6 1
( x 1 , x 2 , x 3 ) = ( 61 26 , 183 26 , 122 13 ) (x_1,x_2,x_3) = (\frac{61}{26}, \frac{183}{26}, \frac{122}{13})
( x 1 , x 2 , x 3 ) = ( 2 6 6 1 , 2 6 1 8 3 , 1 3 1 2 2 )
となる.
(2)
min x 1 2 − x 2 2 s . t x 1 2 + 4 x 2 2 = 1 \begin{aligned}
\min \quad &x_1^2 - x_2^2
\\
s.t \quad &x_1^2 + 4x_2^2 = 1
\end{aligned}
min s . t x 1 2 − x 2 2 x 1 2 + 4 x 2 2 = 1
ラグランジュ関数は
L ( x 1 , x 2 , y ) = x 1 2 + x 2 2 + y ( x 1 2 + 4 x 2 2 − 1 ) L(x_1,x_2,y) = x_1^2 + x_2^2 + y(x_1^2 + 4x_2^2 - 1)
L ( x 1 , x 2 , y ) = x 1 2 + x 2 2 + y ( x 1 2 + 4 x 2 2 − 1 )
となる.等式制約付き問題の最適性条件:一次の必要条件より
∂ L ∂ x 1 = 2 x 1 + 2 y x 1 = 0 , ∂ L ∂ x 2 = − 2 x 2 + 8 y x 2 = 0 ∂ L ∂ y = x 1 2 + 4 x 2 2 − 1 = 0 \begin{aligned}
&\frac{\partial L}{\partial x_1} = 2x_1 + 2yx_1 = 0, \frac{\partial L}{\partial x_2} = -2x_2 + 8yx_2 = 0
\\
&\frac{\partial L}{\partial y} = x_1^2 + 4x_2^2 - 1 = 0
\end{aligned}
∂ x 1 ∂ L = 2 x 1 + 2 y x 1 = 0 , ∂ x 2 ∂ L = − 2 x 2 + 8 y x 2 = 0 ∂ y ∂ L = x 1 2 + 4 x 2 2 − 1 = 0
で表される.ただし,
∇ f ( x ) = ( 2 x 1 − 2 x 2 ) , ∇ g ( x 1 , x 2 ) = ( 2 x 1 8 x 2 ) \begin{aligned}
\nabla f(\mathbf{x}) = \begin{pmatrix}
2x_1
\\
-2x_2
\end{pmatrix}, \nabla g(x_1,x_2) = \begin{pmatrix}
2x_1
\\
8x_2
\end{pmatrix}
\end{aligned}
∇ f ( x ) = ( 2 x 1 − 2 x 2 ) , ∇ g ( x 1 , x 2 ) = ( 2 x 1 8 x 2 )
である.これを解くと,y = − 1 , 1 4 y = -1, \frac{1}{4} y = − 1 , 4 1 y = − 1 y = -1 y = − 1 y = 1 4 y = \frac{1}{4} y = 4 1
( x 1 , x 2 ) = ( 0 , 1 2 ) (x_1,x_2) = (0, \frac{1}{2})
( x 1 , x 2 ) = ( 0 , 2 1 )
となる.
(3)
min x 1 + x 2 + ⋯ + x n s . t x 1 2 + x 2 2 + ⋯ + x n 2 = 1 \begin{aligned}
\min \quad &x_1 + x_2 + \cdots + x_n
\\
s.t \quad &x_1^2 + x_2^2 + \cdots + x_n^2 = 1
\end{aligned}
min s . t x 1 + x 2 + ⋯ + x n x 1 2 + x 2 2 + ⋯ + x n 2 = 1
ラグランジュ関数は
L ( x 1 , ⋯ , x n , y ) = x 1 + x 2 + ⋯ + x n + y ( x 1 2 + x 2 2 + ⋯ + x n 2 − 1 ) L(x_1,\cdots, x_n, y) = x_1 + x_2 + \cdots + x_n + y(x_1^2 + x_2^2 + \cdots + x_n^2 - 1)
L ( x 1 , ⋯ , x n , y ) = x 1 + x 2 + ⋯ + x n + y ( x 1 2 + x 2 2 + ⋯ + x n 2 − 1 )
となる.ただし,
∇ f ( x ) = ( 1 ⋮ 1 ) , ∇ g ( x ) = ( 2 x 1 ⋮ 2 x n ) \begin{aligned}
\nabla f(\mathbf{x}) = \begin{pmatrix}
1
\\
\vdots
\\
1
\end{pmatrix}, \nabla g(\mathbf{x}) = \begin{pmatrix}
2x_1
\\
\vdots
\\
2x_n
\end{pmatrix}
\end{aligned}
∇ f ( x ) = ⎝ ⎜ ⎜ ⎛ 1 ⋮ 1 ⎠ ⎟ ⎟ ⎞ , ∇ g ( x ) = ⎝ ⎜ ⎜ ⎛ 2 x 1 ⋮ 2 x n ⎠ ⎟ ⎟ ⎞
である.等式制約付き問題の最適性条件:一次の必要条件より方程式を解くと,
x i = ± n n ( i = 1 , ⋯ , n ) , y = − n 2 x_i = \pm \frac{\sqrt{n}}{n} (i = 1, \cdots, n), y = -\frac{\sqrt{n}}{2}
x i = ± n n ( i = 1 , ⋯ , n ) , y = − 2 n
となる.最適解は
( x 1 , ⋯ , x n ) = ( − n n , ⋯ , − n n ) (x_1,\cdots,x_n) = (-\frac{\sqrt{n}}{n}, \cdots, -\frac{\sqrt{n}}{n})
( x 1 , ⋯ , x n ) = ( − n n , ⋯ , − n n )
である.
次の非線形最小化問題のKKT条件を書き,さらにKKT条件を満たす( x ∗ , z ∗ ) (\mathbf{x}^*,\mathbf{z}^*) ( x ∗ , z ∗ )
min 1 2 ( ( x 1 − 2 ) 2 + ( x 2 − 4 ) 2 ) s . t x 1 + 3 x 2 ≤ 6 x 1 + 4 x 2 ≤ 4 x 1 ≥ 0 , x 2 ≥ 0 \begin{aligned}
\min \quad &\frac{1}{2}((x_1 - 2)^2 + (x_2 - 4)^2)
\\
s.t \quad &x_1 + 3x_2 \leq 6
\\
&x_1 + 4x_2 \leq 4
\\
&x_1 \geq 0,x_2 \geq 0
\end{aligned}
min s . t 2 1 ( ( x 1 − 2 ) 2 + ( x 2 − 4 ) 2 ) x 1 + 3 x 2 ≤ 6 x 1 + 4 x 2 ≤ 4 x 1 ≥ 0 , x 2 ≥ 0
ラグランジュ関数は
L ( x 1 , x 2 , z 1 , z 2 , z 3 , z 4 ) = 1 2 ( ( x 1 − 2 ) 2 + ( x 2 − 4 ) 2 ) + z 1 ( x 1 + 3 x 2 − 6 ) + z 2 ( x 1 + 4 x 2 − 4 ) − z 3 x 1 − z 4 x 2 \begin{aligned}
L(x_1,x_2,z_1,z_2,z_3,z_4) = &\frac{1}{2}((x_1 - 2)^2 + (x_2 - 4)^2)
\\
&+ z_1(x_1 + 3x_2 - 6) + z_2(x_1 + 4x_2 - 4) - z_3x_1 - z_4x_2
\end{aligned}
L ( x 1 , x 2 , z 1 , z 2 , z 3 , z 4 ) = 2 1 ( ( x 1 − 2 ) 2 + ( x 2 − 4 ) 2 ) + z 1 ( x 1 + 3 x 2 − 6 ) + z 2 ( x 1 + 4 x 2 − 4 ) − z 3 x 1 − z 4 x 2
となるので,KKT条件は次式で表される.
∇ x L ( x , z ) = ( x 1 − 2 x 2 − 4 ) + z 1 ( 1 3 ) + z 2 ( 1 4 ) + z 3 ( − 1 0 ) + z 4 ( 0 − 1 ) = ( 0 0 ) ∇ z L ( x , z ) = ( x 1 + 3 x 2 − 6 x 1 + 4 x 2 − 4 − x 1 − x 2 ) ≤ ( 0 0 0 0 ) z 1 , ⋯ , z 4 ≥ 0 , z 1 ( x 1 + 3 x 2 − 6 ) = 0 , z 2 ( x 1 + 4 x 2 − 4 ) = 0 , z 3 x 1 = 0 , z 4 x 2 = 0 \begin{aligned}
&\begin{aligned}
\nabla_\mathbf{x} L(\mathbf{x,z}) = &\binom{x_1 - 2}{x_2 - 4} + z_1\binom{1}{3} + z_2\binom{1}{4}
\\
& + z_3\binom{-1}{0} + z_4\binom{0}{-1} = \binom{0}{0}
\end{aligned}
\\
&\begin{aligned}
\nabla_\mathbf{z} L(\mathbf{x,z}) &= \begin{pmatrix}
x_1 + 3x_2 - 6
\\
x_1 + 4x_2 - 4
\\
-x_1
\\
-x_2
\end{pmatrix} \leq \begin{pmatrix}
0
\\
0
\\
0
\\
0
\end{pmatrix}
\end{aligned}
\\
&\begin{aligned}
&z_1,\cdots,z_4 \geq 0,
\\
&z_1(x_1 + 3x_2 - 6) = 0, z_2(x_1 + 4x_2 - 4) = 0, z_3x_1 = 0, z_4x_2 = 0
\end{aligned}
\end{aligned}
∇ x L ( x , z ) = ( x 2 − 4 x 1 − 2 ) + z 1 ( 3 1 ) + z 2 ( 4 1 ) + z 3 ( 0 − 1 ) + z 4 ( − 1 0 ) = ( 0 0 ) ∇ z L ( x , z ) = ⎝ ⎜ ⎜ ⎜ ⎛ x 1 + 3 x 2 − 6 x 1 + 4 x 2 − 4 − x 1 − x 2 ⎠ ⎟ ⎟ ⎟ ⎞ ≤ ⎝ ⎜ ⎜ ⎜ ⎛ 0 0 0 0 ⎠ ⎟ ⎟ ⎟ ⎞ z 1 , ⋯ , z 4 ≥ 0 , z 1 ( x 1 + 3 x 2 − 6 ) = 0 , z 2 ( x 1 + 4 x 2 − 4 ) = 0 , z 3 x 1 = 0 , z 4 x 2 = 0
最適解(20 17 , 12 17 \frac{20}{17}, \frac{12}{17} 1 7 2 0 , 1 7 1 2
− 46 17 z 1 = 0 , 0 ⋅ z 2 = 0 , 20 17 z 3 = 0 , 12 17 z 4 = 0 -\frac{46}{17}z_1 = 0, 0 \cdot z_2 = 0, \frac{20}{17}z_3 = 0, \frac{12}{17}z_4 = 0
− 1 7 4 6 z 1 = 0 , 0 ⋅ z 2 = 0 , 1 7 2 0 z 3 = 0 , 1 7 1 2 z 4 = 0
なので,z 1 = z 3 = z 4 = 0 z_1 = z_3 = z_4 = 0 z 1 = z 3 = z 4 = 0 ∇ x L ( x , z ) = 0 \nabla_\mathbf{x} L(\mathbf{x},\mathbf{z}) = \mathbf{0} ∇ x L ( x , z ) = 0
z 2 ( 1 4 ) = − ∇ f ( 20 17 , 12 17 ) = ( 14 17 56 17 ) z_2 \binom{1}{4} = -\nabla f(\frac{20}{17}, \frac{12}{17}) = \binom{\frac{14}{17}}{\frac{56}{17}}
z 2 ( 4 1 ) = − ∇ f ( 1 7 2 0 , 1 7 1 2 ) = ( 1 7 5 6 1 7 1 4 )
なので,z 2 = 14 17 > 0 z_2 = \frac{14}{17} > 0 z 2 = 1 7 1 4 > 0
z 0 ( − 14 17 − 56 17 ) + z 2 ( 1 4 ) = ( 0 0 ) z_0\binom{-\frac{14}{17}}{-\frac{56}{17}} + z_2\binom{1}{4} = \binom{0}{0}
z 0 ( − 1 7 5 6 − 1 7 1 4 ) + z 2 ( 4 1 ) = ( 0 0 )
はz 0 = 0 , z 2 = 14 17 z_0 = 0, z_2 = \frac{14}{17} z 0 = 0 , z 2 = 1 7 1 4
最適解( x 1 , x 2 ) = ( 20 17 , 12 17 ) (x_1,x_2) = (\frac{20}{17}, \frac{12}{17}) ( x 1 , x 2 ) = ( 1 7 2 0 , 1 7 1 2 )
等式制約付き問題と不等式制約付き問題のそれぞれの最適性条件をまとめると,一般の制約付き問題に対する最適性条件が得られる.すなわち,ラグランジュ関数を
L ( x , y , z ) = f ( x ) + y T g ( x ) + z T h ( x ) = f ( x ) + ∑ i = 1 n y i g i ( x ) + ∑ j = 1 l z j h j ( x ) \begin{aligned}
L(\mathbf{x}, \mathbf{y}, \mathbf{z}) &= f(\mathbf{x}) + \mathbf{y}^T \mathbf{g}(\mathbf{x}) + \mathbf{z}^T \mathbf{h}(\mathbf{x})
\\
&= f(\mathbf{x}) + \sum_{i = 1}^n y_i g_i(\mathbf{x}) + \sum_{j=1}^l z_j h_j(\mathbf{x})
\end{aligned}
L ( x , y , z ) = f ( x ) + y T g ( x ) + z T h ( x ) = f ( x ) + i = 1 ∑ n y i g i ( x ) + j = 1 ∑ l z j h j ( x )
と定義した時,制約付き問題を解くことは次の5つの条件を満足する点( x ∗ , y ∗ , z ∗ ) (\mathbf{x}^*,\mathbf{y}^*,\mathbf{z}^*) ( x ∗ , y ∗ , z ∗ )
∇ x L ( x , y , z ) = ∇ f ( x ) + ∑ i = 1 m y i ∇ g i ( x ) + ∑ j = 1 l z j ∇ h j ( x ) = 0 ∇ y L ( x , y , z ) = g ( x ) = 0 ∇ z L ( x , y , z ) = h ( x ) ≤ 0 z i ≥ 0 ( i = 1 , ⋯ , l ) z i h i ( x ) = 0 ( i = 1 , ⋯ , l ) \begin{aligned}
&\nabla_\mathbf{x} L(\mathbf{x},\mathbf{y},\mathbf{z}) = \nabla f(\mathbf{x}) + \sum_{i=1}^m y_i \nabla g_i(\mathbf{x}) + \sum_{j=1}^l z_j \nabla h_j(\mathbf{x}) = \mathbf{0}
\\
&\nabla_\mathbf{y} L(\mathbf{x},\mathbf{y},\mathbf{z}) = \mathbf{g}(\mathbf{x}) = \mathbf{0}
\\
&\nabla_\mathbf{z} L(\mathbf{x},\mathbf{y},\mathbf{z}) = \mathbf{h}(\mathbf{x}) \leq \mathbf{0}
\\
&z_i \geq 0 \quad (i = 1,\cdots,l)
\\
&z_i h_i(\mathbf{x}) = 0 \quad (i = 1,\cdots,l)
\end{aligned}
∇ x L ( x , y , z ) = ∇ f ( x ) + i = 1 ∑ m y i ∇ g i ( x ) + j = 1 ∑ l z j ∇ h j ( x ) = 0 ∇ y L ( x , y , z ) = g ( x ) = 0 ∇ z L ( x , y , z ) = h ( x ) ≤ 0 z i ≥ 0 ( i = 1 , ⋯ , l ) z i h i ( x ) = 0 ( i = 1 , ⋯ , l )
以上の5つの条件を改めてKarush-Kuhn-Tucker条件(KKT条件)と呼び,KKT条件を満足する点(x ∗ , y ∗ , z ∗ \mathbf{x}^*,\mathbf{y}^*,\mathbf{z}^* x ∗ , y ∗ , z ∗
定理:凸計画問題のKKT条件:Karush-Kuhn-Tuckerの最適性十分条件
点(x ∗ , y ∗ , z ∗ \mathbf{x}^*,\mathbf{y}^*,\mathbf{z}^* x ∗ , y ∗ , z ∗ f ( x ) , h i ( x ) ( i = 1 , ⋯ , l ) が x ∗ f(\mathbf{x}),h_i(\mathbf{x})(i = 1,\cdots,l) \text{が}\mathbf{x}^* f ( x ) , h i ( x ) ( i = 1 , ⋯ , l ) が x ∗ g i ( x ) ( i = 1 , ⋯ , m ) g_i(\mathbf{x})(i = 1,\cdots,m) g i ( x ) ( i = 1 , ⋯ , m ) x ∗ \mathbf{x}^* x ∗
この定理の仮定を満足するような制約付き問題を,特に凸計画問題(convex programming problem)と呼ぶ.
例題:線形計画問題のKKT条件
A ∈ R m × n , b ∈ R m , c ∈ R n A \in \mathbb{R}^{m \times n},\mathbf{b} \in \mathbb{R}^m,\mathbf{c} \in \mathbb{R}^n A ∈ R m × n , b ∈ R m , c ∈ R n x ∈ R n \mathbf{x} \in \mathbb{R}^n x ∈ R n
min c T x s . t A x = b ( x ≥ 0 ) \begin{aligned}
\min \quad &\mathbf{c}^T\mathbf{x}
\\
s.t \quad &A\mathbf{x} = \mathbf{b} \quad (\mathbf{x} \geq \mathbf{0})
\end{aligned}
min s . t c T x A x = b ( x ≥ 0 )
を考える.g ( x ) = b − A x , h ( x ) = − x \mathbf{g}(\mathbf{x}) = \mathbf{b} - A\mathbf{x},\mathbf{h}(\mathbf{x}) = -\mathbf{x} g ( x ) = b − A x , h ( x ) = − x
L ( x , y , z ) = c T x + y T ( b − A x ) − z T x L(\mathbf{x},\mathbf{y},\mathbf{z}) = \mathbf{c}^T\mathbf{x} + \mathbf{y}^T(\mathbf{b} - A\mathbf{x}) - \mathbf{z}^T\mathbf{x}
L ( x , y , z ) = c T x + y T ( b − A x ) − z T x
で定義される.また,KKT条件は次式で与られる.
c − A T y − z = 0 , A x = b x ≥ 0 , z ≥ 0 , z i x i = 0 ( i = 1 , ⋯ , n ) \begin{aligned}
&\mathbf{c}- A^T\mathbf{y} - \mathbf{z} = \mathbf{0}, \quad A\mathbf{x} = \mathbf{b}
\\
&\mathbf{x} \geq \mathbf{0},\quad \mathbf{z} \geq \mathbf{0}, \quad z_ix_i = 0(i = 1,\cdots,n)
\end{aligned}
c − A T y − z = 0 , A x = b x ≥ 0 , z ≥ 0 , z i x i = 0 ( i = 1 , ⋯ , n )
これらの条件式は3.8節の相補性定理で述べた最適性条件にほかならない
例題:凸2次計画問題のKKT条件
Q ∈ R n × n , A ∈ R m × n , b ∈ R m , c ∈ R n Q \in \mathbb{R}^{n \times n}, A \in \mathbb{R}^{m \times n},\mathbf{b} \in \mathbb{R}^m, \mathbf{c} \in \mathbb{R}^n Q ∈ R n × n , A ∈ R m × n , b ∈ R m , c ∈ R n x ∈ R n \mathbf{x} \in \mathbb{R}^n x ∈ R n
min 1 2 x T Q x + c T x s . t A x = b ( x ≥ 0 ) \begin{aligned}
\min \quad &\frac{1}{2}\mathbf{x}^TQ\mathbf{x} + \mathbf{c}^T\mathbf{x}
\\
s.t \quad &A\mathbf{x} = \mathbf{b} \quad (\mathbf{x} \geq \mathbf{0})
\end{aligned}
min s . t 2 1 x T Q x + c T x A x = b ( x ≥ 0 )
を考える.ただし,Qは半正定値対称行列である.線形計画問題の場合と同様に,ラグランジュ関数は
L ( x , y , z ) = 1 2 x T Q x + c T x + y T ( b − A x ) − z T x L(\mathbf{x},\mathbf{y},\mathbf{z}) = \frac{1}{2}\mathbf{x}^TQ\mathbf{x} + \mathbf{c}^T\mathbf{x} + \mathbf{y}^T(\mathbf{b} - A\mathbf{x}) - \mathbf{z}^T\mathbf{x}
L ( x , y , z ) = 2 1 x T Q x + c T x + y T ( b − A x ) − z T x
で定義され,KKT条件は次式で与られる.
Q x + c − A T y − z = 0 , A x = b x ≥ 0 , z ≥ 0 , z i x i = 0 ( i = 1 , ⋯ , n ) \begin{aligned}
&Q\mathbf{x} + \mathbf{c} - A^T\mathbf{y} - \mathbf{z} = \mathbf{0}, \quad A\mathbf{x} = \mathbf{b}
\\
&\mathbf{x} \geq \mathbf{0}, \mathbf{z} \geq \mathbf{0}, z_ix_i = 0(i = 1,\cdots,n)
\end{aligned}
Q x + c − A T y − z = 0 , A x = b x ≥ 0 , z ≥ 0 , z i x i = 0 ( i = 1 , ⋯ , n )
凸QPのKKT点は(比較的)簡単に求められる(数値解法あり,5.4節参照)
次の非線形最小化問題のKKT条件を記述し,さらに最適解を求めよ.
min x 1 log x 1 + x 2 log x 2 + ⋯ + x n log x n s . t x 1 + x 2 + ⋯ + x n = 1 x 1 , ⋯ , x n ≥ 0 \begin{aligned}
\min \quad &x_1\log x_1 + x_2\log x_2 + \cdots + x_n\log x_n
\\
s.t \quad &x_1 + x_2 + \cdots + x_n = 1
\\
&x_1,\cdots,x_n \geq 0
\end{aligned}
min s . t x 1 log x 1 + x 2 log x 2 + ⋯ + x n log x n x 1 + x 2 + ⋯ + x n = 1 x 1 , ⋯ , x n ≥ 0
なお,log 0 = − ∞ , 0 log 0 = 0 \log 0 = -\infty, 0\log 0 = 0 log 0 = − ∞ , 0 log 0 = 0
ラグランジュ関数は
L ( x , y , z ) = x 1 log x 1 + ⋯ + x n log x n + y ( x 1 + ⋯ + x n − 1 ) − z 1 x 1 − ⋯ − z n x n \begin{aligned}
L(\mathbf{x}, \mathbf{y}, \mathbf{z}) = x_1\log{x_1} + \cdots + x_n\log{x_n} + y(x_1 + \cdots + x_n - 1) - z_1x_1 - \cdots - z_nx_n
\end{aligned}
L ( x , y , z ) = x 1 log x 1 + ⋯ + x n log x n + y ( x 1 + ⋯ + x n − 1 ) − z 1 x 1 − ⋯ − z n x n
KKT条件より
∇ x L ( x , y , z ) = 0 ∇ y L ( x , y , z ) = x 1 + x 2 + ⋯ + x n − 1 = 0 ∇ z L ( x , y , z ) = − x ≤ 0 z i ≥ 0 ( i = 1 , ⋯ , n ) z i x i ( x ) = 0 ( i = 1 , ⋯ , n ) \begin{aligned}
&\nabla_x L(\mathbf{x}, \mathbf{y}, \mathbf{z}) = \mathbf{0}
\\
&\nabla_\mathbf{y} L(\mathbf{x},\mathbf{y},\mathbf{z}) = x_1 + x_2 + \cdots + x_n - 1 = \mathbf{0}
\\
&\nabla_\mathbf{z} L(\mathbf{x},\mathbf{y},\mathbf{z}) = -\mathbf{x} \leq \mathbf{0}
\\
&z_i \geq 0 \quad (i = 1,\cdots,n)
\\
&z_i x_i(\mathbf{x}) = 0 \quad (i = 1,\cdots,n)
\end{aligned}
∇ x L ( x , y , z ) = 0 ∇ y L ( x , y , z ) = x 1 + x 2 + ⋯ + x n − 1 = 0 ∇ z L ( x , y , z ) = − x ≤ 0 z i ≥ 0 ( i = 1 , ⋯ , n ) z i x i ( x ) = 0 ( i = 1 , ⋯ , n )
これを解くと,最適解は
( x 1 , ⋯ , x n ) = ( 1 n , ⋯ , 1 n ) (x_1,\cdots,x_n) = (\frac{1}{n}, \cdots, \frac{1}{n})
( x 1 , ⋯ , x n ) = ( n 1 , ⋯ , n 1 )
となり, 最小値は− log n -\log{n} − log n