Probability Theory and Mathematical Statistics

自然界和社会上发生的事件是多种多样的，有的是一定条件下必然发生的，还有的是在自然界和社会生活中大量存在着的随机现象，例如人的寿命，天气现象，金融市场等等。随机现象虽然存在不确定性，但还是有某些规律的。概率论与数理统计是研究和揭示随机现象统计规律性的一门数学学科。

概率论的基本概念

第1到第5章节为概率论的内容

从第6章节开始为数理统计内容

样本空间和随机事件

随机实验

在概率论中，满足以下三个特点的实验称为随机实验：

1. 可以在相同的条件下重复地进行
2. 每次实验地可能结果不止一个，并且能事先明确实验地所有可能结果
3. 进行一次实验之前不能确定哪一个结果会出现

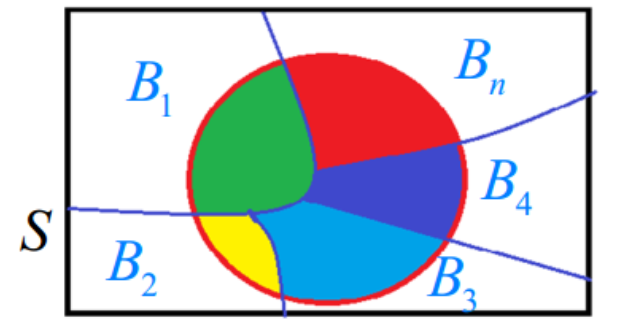
样本空间

随机事件

• 如果把S看作事件，则每次实验S总是发生，所以S称为必然事件
• 如果事件只含有一个样本点，称其为基本事件
• 如果事件是空集，里面不包括任何样本点，记为$\varnothing$，则每次实验$\varnothing$都不发生，称$\varnothing$为不可能事件

事件的相互关系与事件的运算

事件的相互关系有：

• 相等 $A \subset B$
• 和事件 $A \cup B$
• 积事件 $A \cap B$
• 差事件 $A - B$
• 互不相容，互斥的 $A \cap B = \varnothing$
• 逆事件，对立事件 $B \cup \overline{B} = S, \quad B \cap \overline{B} = \varnothing$

在进行事件运算时，常用以下定律，设A，B，C为事件，则有：

• 交换律：$A \cup B = B \cup A ; \quad A \cap B = B \cap A$
• 结合律：$A \cup (B \cup C) = (A \cup B) \cup C ; \quad A \cap (B \cap C) = (A \cap B) \cap C$
• 分配律：$A \cup (B \cap C) = (A \cup B) \cap (A \cup C) ; \quad A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$
• 德摩根律：$\overline{A \cup B} = \overline{A} \cap \overline{B} ; \quad \overline{A \cap B} = \overline{A} \cup \overline{B}$

频率与概率

频率

频率定义：$\color{blue}{f_n(A) = \frac{n_A}{n}}$

其中$n_A$是A发生的次数（频数），n是总试验次数，称$f_n(A)$为A在这n次试验中发生的概率

频率的基本性质：

1. $0 \leq f_n(A) \leq 1$
2. $f_n(S) = 1$
3. 若$A_1 \cdots A_k$是两两互不相容的事件，则$f_n(A_1 \cup \cdots \cup A_k) = f_n(A_1) + \cdots + f_n(A_k)$

概率

概率的统计性定义：当试验的次数增加时，随机事件A发生的频率的稳定值p称为概率，记为$P(A) = p$

概率的公理化定义：

设随机试验对应的样本空间为S，对每个事件A，定义P(A)，满足：

1. 非负性：$\color{blue}{P(A) \geq 0}$
2. 规范性：$\color{blue}{P(S) = 1}$
3. 可列可加性：$A_1, \cdots$两两互斥，即$A_iA_j = \varnothing, i \neq j$则，$\color{blue}{P(\bigcup_{i=1}^{\infty}) = \sum_{i=1}^{\infty} P(A_i)}$

称P(A)为事件A的概率

概率的性质：

1. $\color{blue}{P(\varnothing) = 0}$
2. $\color{blue}{P(A) = 1 - P(\overline{A})}$
3. $\color{blue}{A_1, \cdots, A_n, A_iA_j = \varnothing, i \neq j \Rightarrow P(\bigcup_{i=1}^n A_i) = \sum_{i=1}^{\infty} P(A_i)}$(有限可加性)
4. 若$\color{blue}{A \subset B}$，则有$\color{blue}{P(B - A) = P(B) - P(A)}$
5. 概率的加法公式：$\color{blue}{P(A \cup B) = P(A) + P(B) - P(AB)}$

等可能概型(古典概型)

定义：若试验满足：

• 样本空间S中样本点有限（有限性）
• 出现每一个样本点的概率相等（等可能性）

称这种试验为等可能概型（或古典概型）

条件概率

事件$A$发生的条件下事件$B$发生的条件概率

$$\begin{aligned} P(B \ |\ A) = \frac{P(AB)}{P(A)} \end{aligned}$$

• $P(B \ |\ A)$：事件$A$已经发生的条件下事件$B$发生的概率
• $P(AB)$：事件$A$与事件$B$同时发生的概率

条件概率本质上是把原来的样本空间S缩小到了现在的A的范围，所以它依然是概率，同样满足概率的性质：

• 非负性：对于每一个事件有$P(B \ |\ A) \geq 0$
• 规范性：对于必然事件$S$，有$P(S \ |\ A) = 1$
• 可列可加性：设$B_1,B_2,\cdots$是两两互不相容事件，则$P(\bigcup^\infty_{i=1} B_i \ |\ A) = \sum^\infty_{i=1}P(B_i \ |\ A)$

乘法公式

当下面的条件概率都有意义时：

• $\color{blue}{P(AB) = P(A) \cdot P(B \ |\ A) = P(B) \cdot P(A \ |\ B)}$
• $\color{blue}{P(ABC) = P(A) P(B \ |\ A) P(C \ |\ AB)}$
• $\color{blue}{P(A_1 A_2 \cdots A_n) = P(A_1) P(A_2 \ |\ A_1) P(A_3 \ |\ A_1A_2) \cdots P(A_n \ |\ A_1 \cdots A_{n-1})}$

全概率公式

定义：称$B_1, \cdots, B_n$为S的一个划分，若

1. 不漏 $B_1 \cup \cdots \cup B_n = S$
2. 不重 $B_iB_j = \varnothing, i \neq j$

定理：设$B_1, \cdots, B_n$为S的一个划分且$P(B_i) > 0$，则有全概率公式：

$$\begin{aligned} \color{blue}{P(A) = \sum_{J = 1}^n P(B_j) \cdot P(A \ |\ B_j)} \end{aligned}$$

贝叶斯公式

定理：设$B_1, \cdots, B_n$为S的一个划分且$P(B_i) > 0$。对$P(A) > 0$有Bayes公式：

$$\begin{aligned} \color{blue}{P(B_i \ |\ A) = \frac{P(B_i) P(A \ |\ B_i)}{\sum_{j=1}^n P(B_j) P(A \ |\ B_j)}} \end{aligned}$$

独立性

定义：设$A,B$是两随机事件，如果

$$\begin{aligned} \color{blue}{P(AB) = P(A)P(B)} \end{aligned}$$

则称$A,B$是相互独立

• 若$P(A) > 0, P(B) > 0$，则$A,B$相互独立与$A,B$互不相容不能同时成立
• 若$A,B$相互独立，则$P(B \ |\ A) = P(B)$
• 若$A,B$相互独立，则$A$与$\overline{B}$，$\overline{A}$与$B$，$\overline{A}$与$\overline{B}$也相互独立

随机变量及其分布

随机变量(Random Variable)

定义：设随机试验的样本空间为S，若

$$\begin{aligned} \color{blue}{X = X(e)} \end{aligned}$$

为定义在S上的实值单值函数，则称$X(e)$为随机变量，简写为X。

常见的两类随机变量：

• 离散型随机变量
• 连续性随机变量

离散型随机变量及其分布率

离散型随机变量的概率分布律（简称分布律）：

$X$	$x_1$	$x_2$	$\cdots$	$x_k$	$\cdots$
$P$	$p_1$	$p_2$	$\cdots$	$p_k$	$\cdots$

分布律的内容：

• 随机变量的所有可能取值
• 取每个可能取值对应的概率

分布律的性质：$\color{blue}{p_k \geq 0, \quad \sum_{k=1}^{+\infty} p_k = 1}$

分布律的另一表现形式：$P(X = x_k) = p_k, \quad k = 1, 2, \cdots$

下面介绍三种重要的离散型随机变量

(0-1)分布

定义：若X的概率分布律为

$X$	$0$	$1$
$P$	$1-p$	$p$

其中$0 < p < 1$，就称X服从参数为p的0-1分布（或两点分布），记为$\color{blue}{X \sim 0-1(p)}$ 或 $\color{blue}{X \sim B(1, p)}$

其分布律还可以写成：$P(X = k) = p^k(1 - p)^{1-k}, \quad k = 0,1$

伯努利试验，二项分布

设试验E只有两个可能的结果：$A$或$\overline{A}$，且$P(A) = p, \quad 0 < p < 1$。将E独立地重复进行n次，则称这一串重复地独立试验为n重伯努利试验

二项分布定义：若$X$地的概率分布律为：

$$\begin{aligned} \color{blue}{P(X = k) = C_n^k p^k (1 - p)^{n-k}, \quad k = 0, 1, \cdots, n} \end{aligned}$$

其中$n \geq 1,\quad 0 < p < 1$，就称$X$服从参数为$n,p$的二项分布(Binomial)，记为$\color{blue}{X \sim B(n, p)}$

• $E(X) = np$
• $V(X) = np(1 - p)$

例題

〇×で解答する試験において、気まぐれに解答する。10問ある時、正答の個数を $X$ として、$X$ の平均と分散を求めよ。また、$X \geq 8$ となる確率を求めよ

• $E(X) = np = 10 * 0.5 = 5$
• $V(X) = np(1 - q) = 10 * 0.5 * 0.5 = 2.5$
• $P(X \geq 8) = P(X = 8) + P(X = 9) + P(X = 10) = C_{10}^8 (\frac{1}{2})^8 (\frac{1}{2})^2 + C_{10}^9 (\frac{1}{2})^9 (\frac{1}{2}) + C_{10}^{10} (\frac{1}{2})^{10} (\frac{1}{2})^0 \simeq 0.0547$

泊松分布

定义：若$X$的概率分布律为

$$\begin{aligned} \color{blue}{P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}, \quad k = 0, 1, 2, \cdots} \end{aligned}$$

• $E(X) = \lambda$
• $V(X) = \lambda$

其中$\lambda > 0$，就称$X$服从参数为$\lambda$的泊松分布(Poisson)，记为$\color{blue}{X \sim \pi(\lambda)}$或$\color{blue}{X \sim P(\lambda)}$

泊松分布的用途：

• 某人一天内收到的微信的数量
• 来到某公交汽车站的乘客
• 某放射性物质发射出的粒子
• 显微镜下某区域中的白血球

如果某事件以固定强度 $\lambda$，随机且独立地出现，该事件在单位时间内出现地次数（个数）可以看成是服从泊松分布

二项分布与泊松分布有以下近似关系：

$$\begin{aligned} C_n^k p^k (1 - p)^{n - k} \simeq \frac{e^{-\lambda}\lambda^k}{k!}, \quad \lambda = np, n > 10, p < 0.1 \end{aligned}$$

例題

ある製品の製造工程では、微小領域に1万個の点にレーザーを当てていく。位置をずれるのは2万個に一つであるという。この工程ではずれが一つもないという確率を求めよ

• $\lambda = np = 10000 * \frac{1}{20000} = 0.5$
• $E(X) = \lambda = 0.5$
• $V(X) = \lambda = 0.5$
• $P(X = 0) = P(0, \lambda) = e^{-0.5} \cdot \frac{0.5^0}{0!} \simeq 0.606531$
• $B(n, p) = C_{10000}^0 (\frac{1}{20000})^0 (\frac{19999}{20000})^{10000} \simeq 0.606523$

几何分布

定义：若$X$的概率分布律为

$$\begin{aligned} P(X = k) = p(1 - p)^{k - 1}, \quad k = 1, 2, 3, \cdots, \end{aligned}$$

其中$0 < p < 1$，称$X$服从参数为$p$的几何分布(Geometric)，记为$\color{blue}{X \sim Geom(p)}$

几何分布的用途：在重复多次的伯努利实验中，实验进行到某种结果出现第一次为止，此时的试验总次数服从几何分布。如：射击，首次击中目标时射击的次数

• $E(X) = \frac{1}{p}$
• $V(X) = \frac{1 - p}{p^2}$

例題

合格率10%の試験を挑み、$X$ 回目で初めて合格する。$X$ の平均と分散を求めよ。また、$X = 3$ となる確率を求めよ

• $E(X) = \frac{1}{p} = \frac{1}{0.1} = 10$
• $V(X) = \frac{1 - p}{p^2} = \frac{1 - 0.1}{0.1^2} = 90$
• $P(X = 3) = 0.9^2 * 0.1 = 0.081$

随机变量的分布函数

定义：随机变量$X$，对任意实数$x$，称函数

$$\begin{aligned} F(x) = P(X \leq x) \end{aligned}$$

为$X$的概率分布函数，简称分布函数

分布函数用途：可以给出随机变量落入任意一个范围的可能性

$F(x)$的性质：

• $0 \leq F(x) \leq 1$
• $F(x)$单调不减
• $F(-\infty) = 0, F(+\infty) = 1$
• $F(x)$是右连续函数，即$F(x + 0) = F(x)$

连续型随机变量及其概率密度

对于随机变量$X$的分布函数$F(x)$，若存在非负函数$f(x)$，使对于任意实数$x$有：

$$\begin{aligned} \color{blue}{F(x) = \int_{-\infty}^x f(t) dt} \end{aligned}$$

则称$X$为连续型随机变量，其中$f(x)$称为$X$的概率密度函数，简称概率密度，有时也写为$f_X(x)$

$f(x)$性质：

• $f(x) \geq 0$
• $\int_{-\infty}^{+\infty} f(x) dx = 1$
• 对于任意的实数$x_1,x_2(x_1 < x_2)$，$P(x_1 < X \leq x_2) = \int_{X_1}^{X_2} f(t)dt$
• 若$f(x)$在点$x$处连续，则有$F'(x) = f(x)$

下面介绍3种重要的连续性随机变量

均匀分布

若 $X$ 的概率密度函数为

$$\begin{aligned} \color{blue}{f(x) = \begin{cases} \frac{1}{b-a}, \quad &x \in (a, b) \\ 0, \quad &\text{其他} \end{cases}} \end{aligned}$$

其中 $a < b$，就称 $X$ 服从$(a, b)$上的均匀分布(Uniform)，记为 $\color{blue}{X \sim U(a, b)}$ 或 $\color{blue}{X \sim \text{Unif}(a, b)}$

均匀分布的性质：均匀分布具有等可能性，即，服从 $U(a, b)$ 上的均匀分布的随机变量 $X$ 落入 $(a, b)$ 中的任意子区间上的概率只与其区间长度有关与区间所处的位置无关。即，$X$ 落入 $(a, b)$ 中的等长度的任意子区间上是等可能的。

• $E(X) = \frac{b + a}{2}$
• $V(X) = \frac{(b - a)^2}{12}$

例題

ある自動車のブレーキテストで時速50kmでブレーキをかけた時、とまるまでに要する距離 $X$ は区間 $(a, b)$ 上の一様分布に従うという。$b$ よりも $a$ に近いところで止まる確率を求めよ

$$P(a < X < \frac{a+b}{2}) = \int_a^{\frac{a+b}{2}} \frac{1}{b - a} dx = \frac{1}{2}$$

指数分布

若 $X$ 的概率密度函数为

$$\begin{aligned} \color{blue}{f(x) = \begin{cases} \lambda e^{-\lambda x}, \quad &x > 0 \\ 0, \quad &x \leq 0 \end{cases}} \end{aligned}$$

其中 $\lambda > 0$，就称 $X$ 服从参数为 $\lambda$ 的指数分布(Exponential)，记为 $\color{blue}{X \sim E(\lambda)}$ 或 $\color{blue}{X \sim \text{Exp}(\lambda)}$

• $E(X) = \frac{1}{\lambda}$
• $V(X) = \frac{1}{\lambda^2}$

随机变量 $X$ 的分布函数为：

$$\begin{aligned} \color{blue}{F(x) = \begin{cases} 1 - e^{-\lambda x}, \quad &x > 0 \\ 0, \quad &x \leq 0 \end{cases}} \end{aligned}$$

指数分布的性质：指数分布具有无记忆性

指数分布的用途：

• 指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔，中文维基百科新条目出现的时间间隔等等
• 在排队论中，一个旅客接受服务的时间长短也可以用指数分布来近似
• 无记忆性的现象（连续时）

正态分布

若 $X$ 的概率密度函数为

$$\begin{aligned} \color{blue}{f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x - \mu)^2}{2\sigma^2}}, \quad -\infty < x < +\infty} \end{aligned}$$

其中 $-\infty < \mu < +\infty, \sigma > 0$ ，就称 $X$ 服从参数为 $\mu, \sigma$ 的正态分布（或高斯分布），记为 $\color{blue}{X \sim N(\mu, \sigma^2)}$

• $E(X) = \mu$
• $V(X) = \sigma^2$

正态分布的特征：

• $f(x)$ 关于 $x = \mu$ 对称
• 当 $x \leq \mu$ 时，$f(x)$ 是严格单调递增函数
• $f_{max} = f(\mu) = \frac{1}{\sqrt{2\pi}\sigma}$
• $\lim_{|x - \mu| \rightarrow \infty} f(x) = 0$

正态分布的参数：

• $\mu$ 为位置参数，决定对称轴位置
• $\sigma$ 为尺度参数，决定曲线分散程度

正态分布的用途：

• 自然界和人类社会中很多现象可以看做正态分布
  • 例如：人的生理尺寸（身高，体重），医学检验指标（红细胞数，血小板），测量误差等等
• 多个随机变量的和可以用正态分布来近似
  • 例如：注册MOOC的某位同学完成所有作业的时间，二项分布等等

标准正态分布

若 $Z \sim N(0, 1)$，称 $Z$ 服从标准正态分布

• $Z$ 的概率密度函数：$\phi(z) = \frac{1}{\sqrt{2\pi}}e^{-\frac{z^2}{2}}$
• $Z$ 的分布函数：$\Phi(z) = \int_{-\infty}^Z \frac{1}{\sqrt{2\pi}} e^{-\frac{t^2}{2}} \, dt$

标准正态分布的分布函数有一个重要的性质：

$$\Phi(-z_0) = 1 - \Phi(z_0)$$

对于任意的实数 $z_0$ 都成立

此外，当 $X \sim N(\mu, \sigma^2)$ 时，$\frac{X - \mu}{\sigma} \sim N(0, 1)$，由此可知，当 $X \sim N(\mu, \sigma^2)$ 时，对于任意实数 $a$，有

$$\color{blue}{F_X(a) = P(X \leq a) = P(\frac{X - \mu}{\sigma} \leq \frac{a - \mu}{\sigma}) = \Phi(\frac{a - \mu}{\sigma})}$$

随机变量的函数的分布

在实际中，我们常对某些随机变量的函数更感兴趣，例如，我们能测量圆轴截面的直径 $d$，而关心的却是截面面积 $A$。这里随机变量 $A$ 是随机变量 $d$ 的函数。

一般，若已知 $X$ 的概率分布，$Y = g(X)$，求 $Y$ 的概率分布的过程为：先给出 $Y$ 的可能取值，再利用等价事件来给出概率分布

• 若 $X$ 为离散型随机变量，则先写出 $Y$ 的可能取值：$y_1, \cdots, y_j, \cdots$，再找出 $\lbrace Y = y_j \rbrace$ 的等价事件 $\lbrace X \in D \rbrace$，得 $P(Y = y_j) = P(X \in D)$
• 若 $X$ 为连续型随机变量，先根据 $X$ 的取值范围，给出 $Y$ 的取值范围，然后写出 $Y$ 的概率分布函数：$F_Y(y) = P(Y \leq y)$，找出 $\lbrace Y \leq y \rbrace$ 的等价事件 $\lbrace X \in D \rbrace$，得 $F_Y(y) = P(X \in D)$，再求出 $Y$ 得概率密度函数 $f_Y(y)$

定理：设随机变量 $X \sim f_X(x), -\infty < x < +\infty, Y = g(X), g'(x) > 0$ 或 $g'(x) < 0$，则 $Y$ 具有概率密度为：

$$\begin{aligned} f_Y(y) = \begin{cases} f_X(h(y)) \cdot |h'(y)|, \quad &\alpha < y < \beta \\ 0, \quad &\text{其他} \end{cases} \end{aligned}$$

注意：

• 这里 $(\alpha, \beta)$ 是 $Y$ 的取值范围，其中：$\alpha = g(-\infty), \beta = g(+\infty)$，当 $g'(x) < 0$ 时，$\alpha = g(+\infty), \beta = g(-\infty)$
• $h$ 是 $g$ 的反函数，即 $h(y) = x \Leftrightarrow y = g(x)$

一般的，若随机变量 $X \sim N(\mu, \sigma^2)$，则有 $Y = aX + b \Rightarrow Y \sim N(a\mu + b, a^2\sigma^2)$

多维随机变量及其分布

以上只限于讨论一个随机变量的情况，但在实际问题中，对于某些随机实验的结果需要同时用两个或两个以上的随机变量来描述。

二维随机变量

设 $E$ 是一个随机试验，样本空间 $S = \lbrace e \rbrace$，设 $X = X(e)$ 和 $Y = Y(e)$ 是定义在 $S$ 上的随机变量，由它们构成的向量 $(X, Y)$ 叫做二维随机向量或二元随机变量

二维随机变量分布函数

设 $(X,Y)$ 是二维随机变量，对于任意实数 $x,y$，二元函数

$$F(x,y) = P((X \leq x) \cap (Y \leq y)) =P(X \leq x, Y \leq y)$$

称为二维随机变量 $(X,Y)$ 的分布函数，或称为随机变量 $X$ 和 $Y$ 的联合分布函数

分布函数 $F(x, y)$ 的性质：

• $F(x,y)$ 关于 $x$ 和 $y$ 单调不减
• $0 \leq F(x,y) \leq 1, F(+\infty, +\infty) = 1$ 对任意 $x, y$ 有：$F(-\infty, y) = F(x, -\infty) = F(-\infty, -\infty) = 0$
• $F(x+0, y) = F(x,y), F(x, y+0)=F(x,y)$ 即$F(x,y)$ 关于 $x$ 右连续，关于 $y$ 也右连续
• 对于任意 $(x_1, y_1), (x_2, y_2), x_1 < x_2, y_1 < y_2$ 有：$F(x_2, y_2) - F(x_2, y_1) + F(x_1, y_1) - F(x_1, y_2) \geq 0$

二元离散型随机变量

若二元随机变量 $(X, Y)$ 全部可能取到的不同值是有限对或可列无限对，则称 $(X, Y)$ 是二元离散型随机变量

设二维随机变量 $(X,Y)$ 所以可能取到的值为 $(x_i, y_j),i,j=1,2,\cdots$，即 $P(X=x_i,Y=y_i)=p_{ij}$，则有

$$p_{ij} \geq 0 \qquad\sum^\infty_{i=1}\sum^\infty_{j=1}p_{ij} = 1$$

我们称 $P(X=x_i, Y=y_i) = p_{ij},i,j=1,2,\cdots$ 为二维离散型随机变量 $(X,Y)$ 的分布律，或随机变量 $X$ 和 $Y$ 的联合分布律

联合分布律的性质：

1. $p_{ij} \geq 0$
2. $\sum_{i=1}^{\infty} \sum_{j=1}^{\infty} p_{ij} = 1$
3. $P((X, Y) \in D) = \sum_{(x_i, y_j) \in D} p_{ij}$

二维连续型的随机变量

对于二维随机变量 $(X,Y)$ 的分布函数 $F(x,y)$，如果存在非负的函数 $f(x,y)$ 使对于任意 $x,y$ 有

$$\color{blue}{F(x,y) = \int^y_{-\infty}\int^x_{-\infty}f(u,v)du,dv}$$

则称 $(X,Y)$ 是二元连续型随机变量，函数 $f(x,y)$ 称为二维随机变量 $(X,Y)$ 的概率密度或联合概率密度

概率密度的性质：

• $f(x, y) \geq 0$
• $\int^\infty_{-\infty}\int^\infty_{-\infty}f(x,y)dxdy = F(\infty,\infty)= 1$
• 设 $D$ 是 $xoy$ 平面上的区域，点 $(X,Y)$ 落在 $D$ 内的概率为 $P((X,Y) \in D) = \iint_D f(x,y)dxdy$
• 若 $f(x)$ 在点 $x$ 处连续，则有 $\frac{\partial^2F(x,y)}{\partial x \partial y} = f(x,y)$

边缘分布

二维离散型随机变量边缘分布

二维随机变量 $(X, Y)$ 作为一个整体，具有分布函数 $F(x, y)$，而 $X$ 和 $Y$ 都是随机变量，各自也有分布函数，将他们分别记住 $F_X(x), F_Y(y)$，依次称为二维随机变量 $(X, Y)$ 关于 $X$ 和 $Y$ 的边缘分布函数

X\Y	$y_1$	$y_2$	$\cdots$	$y_j$	$\cdots$	$P(X = x_i)$
$x_1$	$p_{11}$	$p_{12}$	$\cdots$	$p_{1j}$	$\cdots$	$p_{1 \cdot}$
$x_2$	$p_{21}$	$p_{22}$	$\cdots$	$p_{2j}$	$\cdots$	$p_{2 \cdot}$
$\vdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\vdots$
$x_i$	$p_{i1}$	$p_{i2}$	$\cdots$	$p_{ij}$	$\cdots$	$p_{i \cdot}$
$\vdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\cdots$	$\vdots$
$P(Y = y_j)$	$p_{\cdot 1}$	$p_{\cdot 2}$	$\cdots$	$p_{\cdot j}$	$\cdots$	1

注：分别称 $p_{i \cdot}$ 和 $p_{\cdot j}$ 为 $(X,Y)$ 关于 $X$ 和关于 $Y$ 的边缘分布律

$$\begin{aligned} p_{i \cdot} &= \sum^\infty_{j=1}p_{ij} = P(X = x_i), \quad i=1,2,\cdots \\ p_{\cdot j} &= \sum^\infty_{i=1}p_{ij} = P(Y = y_j), \quad j=1,2,\cdots \end{aligned}$$

二维连续型随机变量边缘分布

对于连续型随机变量 $(X, Y)$，设它的概率密度为 $f(x, y)$

$$F_X(x) = F(x, \infty) = \int^x_{-\infty}\left [\int^\infty_\infty f(x,y)dy\right ]dx$$

可得

$$\begin{aligned} f_X(x) &= \int^\infty_{-\infty}f(x,y)dy \\ f_Y(y) &= \int^\infty_{-\infty}f(x,y)dx \end{aligned}$$

分别称 $f_X(x)$ 和 $f_Y(y)$ 为 $(X,Y)$ 关于 $X$ 和关于 $Y$ 的边缘概率密度

条件分布

二维离散型随机变量条件分布

由条件概率很自然地引出条件概率分布的概念

$(X,Y)$ 是二维离散型随机变量，其分布律为

$$P(X = x_i, Y = y_j) = p_{ij}, \quad i,j = 1,2,\cdots$$

$(X,Y)$ 关于 $X$ 和关于 $Y$ 的边缘分布律分别为

$$\begin{aligned} P(X = x_i) &= P_{i\cdot} = \sum^\infty_{j=1}p_{ij}, \quad i=1,2,\cdots \\ P(Y = y_j) &= P_{\cdot j} = \sum^\infty_{j=1}p_{ij}, \quad j=1,2,\cdots \end{aligned}$$

现在考虑在事件 $Y=y_j$ 已发生的条件下 $X=x_i$ 发生的概率，也就是求

$$P(X=x_i|Y=y_j) = \frac{P(X=x_i,Y=y_j)}{P(Y=y_i)} = \frac{p_{ij}}{p_{\cdot j}}, \quad i = 1,2,\cdots$$

由此引出以下定义：

设 $(X,Y)$ 是二元离散型随机变量，对于固定的 $y_j$，若 $P(Y = y_j) > 0$，则称

$$\color{blue}{P(X = x_i|Y = y_j) = \frac{P(X = x_i, Y = y_j)}{P(Y = y_j)} = \frac{p_{ij}}{p_{\cdot j}}, \quad i=1,2,\cdots}$$

为在 $Y = y_j$ 条件下随机变量 $X$ 的条件分布律；同样，对于固定的 $x_i$，若 $P(X = x_i) > 0$，则称

$$\color{blue}{P(Y = y_j|X = x_i) = \frac{P(X = x_i, Y = y_j)}{P(X = x_i)} = \frac{p_{ij}}{p_{i\cdot}}, \quad j=1,2,\cdots}$$

为在 $X = x_i$ 条件下随机变量 $Y$ 的条件分布律

二维连续型随机变量条件分布

设二元随机变量 $(X,Y)$ 的概率密度为 $f(x,y)$，$(X,Y)$ 关于 $Y$ 的边缘概率密度为 $f_Y(y)$，若对于固定的 $y$，$f_Y(y) > 0$，则称 $\frac{f(x,y)}{f_Y(y)}$ 为在 $Y=y$ 的条件下 $X$ 的条件概率密度，记为

$$f_{X|Y}(x|y) = \frac{f(x,y)}{f_Y(y)}$$

称

$$\int^x_{-\infty} f_{X|Y}(x|y)dx = \int^x_{-\infty}\frac{f(x,y)}{f_Y(y)}dx$$

为在 $Y=y$ 的条件下 $X$ 的条件分布函数，记为 $P(X \leq x | Y = y)$ 或 $F_{X|Y}(x|y)$
同理，称

$$\int^y_{-\infty} f_{Y|X}(y|x)dy = \int^y_{-\infty}\frac{f(y,x)}{f_X(x)}dy$$

为在 $X=x$ 的条件下 $Y$ 的条件分布函数，记为 $P(Y \leq y | X = x)$ 或 $F_{Y|X}(y|x)$

二元均匀分布

若二元随机变量 $(X, Y)$ 的概率密度在平面上的一个有界区域 $D$ 内是常数，而在其余地方取值为零，称 $(X, Y)$ 在 $D$ 上服从均匀分布，设

$$\begin{aligned} f(x, y) = \begin{cases} \frac{1}{A}, \quad &(x, y) \in D \\ 0, \quad & (x, y) \notin D \end{cases} \end{aligned}$$

其中 $A$ 为区域 $D$ 的面积

二元正态分布

设二元随机变量 $(X, Y)$ 的概率密度为：

$$\begin{aligned} f(x, y) = \frac{1}{2\pi \sigma_1 \sigma_2 \sqrt{1 - \rho^2}} \times \exp \lbrace \frac{-1}{2(1-\rho^2)} [\frac{(x - \mu_1)^2}{\sigma_1^2} - 2\rho \frac{(x - \mu_1)(y - u_2)}{\sigma_1 \sigma_2} + \frac{(y - u_2)^2}{\sigma_2^2}] \rbrace \end{aligned}$$

其中，$\mu_1, \mu_2, \sigma_1 > 0, \sigma_2 > 0, -1 < \rho < 1$ 都是常数，称 $(X, Y)$ 为服从参数为 $\mu_1, \mu_2, \sigma_1, \sigma_2, \rho$ 的二元正态分布，记为：$\color{blue}{(X, Y) \sim N(\mu_1, \mu_2, \sigma_1^2, \sigma_2^2, \rho)}$

二元正态分布的两个边际分布都是一元正态分布，并且都不依赖于参数$\rho$

相互独立的随机变量

本节讲利用两个事件相互独立的概念引出两个随机变量相互独立的概念

设 $F(x,y)$ 是二元随机变量 $(X, Y)$ 的分布函数，$F_X(x),F_Y(y)$ 分别是 $X, Y$ 的边际分布函数，若对所有 $x,y$ 有

$$P(X \leq x, Y \leq y) = P(X \leq x)P(Y \leq y)$$

即

$$\color{blue}{F(x,y) = F_X(x)F_Y(y)}$$

称随机变量 $X, Y$ 相互独立

离散型随机变量相互独立

设 $(X, Y)$ 是离散型随机变量，$P(X = x_i, Y = y_j)$，$P(X = x_i)$，$P(Y = y_j)$ 分布为 $(X, Y)$ 的联合分布律和边缘分布律，则 $X$ 和 $Y$ 相互独立的条件为

$$\color{blue}{P(X = x_i, Y = y_j) = P(X = x_i) P(Y = y_j)}$$

需要检验所有等式成立才能得独立结论

连续型随机变量相互独立

设 $(X, Y)$ 是连续型随机变量，$f(x, y)$，$f_X(x)$，$f_Y(y)$ 分布为 $(X, Y)$ 的概率密度和边缘概率密度，则 $X$ 和 $Y$ 相互独立的条件为

$$\color{blue}{f(x, y) = f_X(x) f_Y(y)}$$

连续型变量独立，其联合密度函数一定能分解成 $x$ 的函数与 $y$ 的函数的乘积，即 $f(x, y) = g(x)h(y)$

随机变量的数字特征

上一章介绍了随机变量的分布函数，概率密度，分布律，它们都能完整地描述随机变量，但在某些实际或理论问题中，人们感兴趣于某些能描述随机变量某一种特征地常数

本章介绍随机变量几个重要地数字特征：

• 数学期望
• 方差
• 协方差与相关系数
• 其他数字特征
• 多元正态分布的性质

数学期望

一元离散型随机变量

定义：设离散型随机变量 $X$ 的分布律为：$P(X = x_k) = p_k, k = 1, 2, \cdots$ 若级数 $\color{blue}{\sum_{k=1}^{+\infty}} x_k p_k$ 绝对收敛，则称级数 $\sum_{k=1}^{+\infty} x_k p_k$ 的值为随机变量 $X$ 的数学期望，记为 $E(X)$，即

$$\color{blue}{E(X) = \sum_{k=1}^{+\infty}} x_k p_k$$

• $p_k$ 可以理解成为加权平均中 $x_k$ 的权重。数学期望简称为期望，又称均值(mean)

定理：设 $Y$ 是随机变量 $X$ 的函数：$Y = g(X)$，若 $X$ 是离散型随机变量，它的分布律为：$P(X = x_k) = p_k, k = 1, 2, \cdots$，若 $\sum_{k=1}^{\infty}g(x_k)p_k$ 绝对收敛，则

$$\color{blue}{E(Y) = E[g(X)] = \sum_{k=1}^{\infty}} g(x_k) p_k$$

一元连续型随机变量

定义：设连续型随机变量 $X$ 的概率密度函数为 $f(x)$，若积分 $\int_{-\infty}^{+\infty} xf(x) dx$ 绝对收敛（即 $\int_{-\infty}^{+\infty} |x|f(x) dx < +\infty$），则称积分 $\int_{-\infty}^{+\infty} xf(x) dx$ 的值为随机变量 $X$ 的数学期望，即

$$\color{blue}{E(X) = \int_{-\infty}^{+\infty} xf(x) dx}$$

定理：设 $Y$ 是随机变量 $X$ 的函数：$Y = g(X)$，若 $X$ 是连续型随机变量，它的概率密度函数为：$f(x)$，若 $\int_{-\infty}^{+\infty} g(x) f(x) dx$ 绝对收敛，则

$$\color{blue}{E(Y) = E(g(X)) = \int_{-\infty}^{+\infty} g(x) f(x) dx}$$

数学期望的性质

• $E(c) = c$
• $E(cX) = cE(X)$
• $E(X + Y) = E(X) + E(Y)$
• $E(XY) = E(X) E(Y) \quad X, Y\text{相互独立}$

条件期望的性质

• $E[a∣Y] = a$
• $E[aX + bZ|Y] = aE[X|Y] + bE[Z|Y]$
• $E[X|Y] = E[X](\text{独立})$
• $E[E[X|Y]] = E[X]$
• $E[Xg(Y)|Y] = g(Y)E[X|Y]$
• $E[X|Y,g(Y)] = E[X|Y]$
• $E[E[X|Y,Z]] = E[X|Y]$

方差

设 $X$ 是一个随机变量，若 $E \lbrace [X - E(X))]^2 \rbrace$ 存在，则称其为 $X$ 的方差，记为 $\color{blue}{D(X)}$ 或 $\color{blue}{\text{Var}(X)}$，即

$$\color{blue}{D(X) = E \lbrace[X - E(X)]^2 \rbrace}$$

• $\sqrt{D(X)}$ 记为 $\color{blue}{\sigma(X)}$，称为 $X$ 的标准差或均方差

一元离散型随机变量

对于离散型随机变量 $X$，其分布律为 $P(X = x_k) = p_k, k = 1, 2, \cdots$，则

$$\color{blue}{D(X) = \sum_{k=1}^\infty[x_k - E(X)]^2 p_k}$$

一元连续型随机变量

对于连续型随机变量 $X$，其概率密度函数为 $f(x)$，则

$$\color{blue}{D(X) = \int_{-\infty}^\infty[x - E(X)]^2 f(x)dx}$$

方差的性质

• $D(c) = 0$
• $D(cX) = c^2D(x)$
• $D(X) = E(X^2) - E(X)^2$
• $D(X \pm Y) = D(X) + D(Y) \pm 2Cov(X,Y)$
  • $Cov(X,Y) = E \lbrace [X - E(X)][Y - E(Y)] \rbrace$
  • 特别的，若 $X, Y$ 相互独立，则有 $D(X + Y) = D(X) + D(Y)$
• $D(X) = 0 \Leftrightarrow P(X = c) = 1$ 且 $c = E(X)$

条件方差的性质

• $\text{Var}[Y∣X] = E[Y - E[Y∣X]2∣X]$
• $E[\text{Var}[Y|X]] = E[E[Y^2|X]] - E[E[Y|X]^2] = E[Y^2] - E[E[Y|X]^2]$
• $\text{Var}[E[Y|X]] = E[E[Y|X]^2] - E[E[Y|X]]^2 = E[E[Y|X]^2] - E[Y]^2$
• $E[\text{Var}[Y|X]] + \text{Var}[E[Y|X]] = E[Y^2] - E[Y]^2 = \text{Var}[Y]$

协方差及其相关系数

上一节中方差性质3：

设 $X,Y$ 是两个随机变量，则有

$$D(X + Y) = D(X) + D(Y) + \color{blue}{2E \lbrace [X - E(X)] [Y - E(Y)] \rbrace }$$

特别地，若 $X$ 和 $Y$ 相互独立时，则有 $D(X + Y) = D(X) + D(Y)$。即，若 $X$ 和 $Y$ 相互独立时，则有 $\color{blue}{E \lbrace [X - E(X)] [Y - E(Y)] \rbrace } = 0$

这意味着当 $E \lbrace [X - E(X)] [Y - E(Y)] \rbrace \neq 0$ 时，$X$ 和 $Y$ 不相互独立，而是存在着一定的关系。

定义：数值 $E \lbrace [X - E(X)] [Y - E(Y)] \rbrace$ 为随机变量 $X$ 与 $Y$ 的协方差，记作 $Cov(X, Y)$，即

$$Cov(X, Y) = E \lbrace [X - E(X)] [Y - E(Y)] \rbrace$$

协方差 $Cov(X, Y)$ 反应了随机变量 $X$ 与 $Y$ 的线性相关性：

• 当 $Cov(X, Y) > 0$，称 $X$ 与 $Y$ 正相关
• 当 $Cov(X, Y) < 0$，称 $X$ 与 $Y$ 负相关
• 当 $Cov(X, Y) = 0$，称 $X$ 与 $Y$ 不相关

由于

$$\begin{aligned} &E \lbrace [X - E(X)] [Y - E(Y)] \rbrace \\ = &E \lbrace XY - XE(Y) - YE(X) + E(X)E(Y) \rbrace \\ = &E(XY) - E(X)E(Y) - E(Y)E(X) + E(X)E(Y) \\ = &E(XY) - E(X)E(Y) \end{aligned}$$

• 协方差的计算公式：

$$\color{blue}{Cov(X, Y) = E(XY) - E(X)E(Y)}$$

协方差的性质

1. $Cov(X, Y) = Cov(Y, X)$
2. $Cov(X, X) = D(X)$
3. $Cov(aX, bY) = ab \cdot Cov(X, Y)$，其中 $a, b$ 为两个实数
4. $Cov(X_1 + X_2, Y) = Cov(X_1, Y) + Cov(X_2, Y)$

例题：

(1)

$$\begin{aligned} &Cov(3X + 2Y, X) \\ = &Cov(3X, X) + Cov(2Y, X) \\ = &3Cov(X, X) + 2Cov(Y, X) \\ = &3D(X) + 2Cov(X, Y) \end{aligned}$$

(2)

$$\begin{aligned} &D(3X - 2Y) \\ = &D(3X + (-2Y)) \\ = &D(3X) + D(-2Y) + 2Cov(3X, -2Y) \\ = &9D(X) + 4D(X) - 12Cov(X, Y) \end{aligned}$$

相关系数

协方差是有量纲的数字特征，为了消除其量纲的影响，引入一个新概念：

定义：数值 $\rho_{XY} = \frac{Cov(X, Y)}{\sqrt{D(X)D(Y)}}$ 称为随机变量 $X$ 与 $Y$ 的相关系数，是没有量纲的

若记作标准化变量

$$\begin{aligned} X^* = \frac{X - E(X)}{\sqrt{D(X)}}, \qquad Y^* = \frac{Y - E(Y)}{\sqrt{D(Y)}} \end{aligned}$$

则，$\rho_{XY} = Cov(X^*, Y^*)$

相关系数的性质

1. $|\rho_{XY}| \leq 1$
2. $|\rho_{XY}| = 1 \Leftrightarrow$ 存在常数 $a, b$, 使 $P(Y = a + bX) = 1$，特别的，$\rho_{XY} = 1$ 时， $b > 0$， $\rho_{XY} = -1$ 时， $b < 0$

上面性质也可以写为：

当 $D(X)D(Y) \neq 0$ 时，有 $(Cov(X, Y))^2 \leq D(X)D(Y)$，其中等号当且仅当 $X$ 与 $Y$ 之间有严格的线性关系，即存在常数 $a, b$，使 $P(Y = a + bX) = 1$

相关系数是一个用来表征两个随机变量之间线性关系密切程度的特征数，有时也称为”线性相关系数“。

• 当 $|\rho_{XY}|$ 较大时，表明 $X$ 与 $Y$ 的线性关系程度较好
• 当 $|\rho_{XY}|$ 较小时，表明 $X$ 与 $Y$ 的线性关系程度较差
• 当 $|\rho_{XY}| = 1$ 时，表明 $X$ 与 $Y$ 之间以概率1存在线性关系
• 当 $|\rho_{XY}| = 0$ 时，表明 $X$ 与 $Y$ 之间没有线性关系，成两个变量不相关

矩、协方差矩阵

矩

本节先介绍随机变量的另外几个数字特征，设 $(X, Y)$ 是二维随机变量

定义1.1：若 $E(X^k), k = 1, 2, \cdots$ 存在，则称之为 $X$ 的 $\color{blue}{k\text{阶(原点)矩}}$

定义1.2：若 $E \lbrace [X - E(X)]^k \rbrace, k = 1, 2, \cdots$ 存在，则称之为 $X$ 的 $\color{blue}{k\text{阶中心矩}}$

之前提到的随机变量的期望和方差就是其1阶原点矩和2阶中心矩

定义2.1：若 $E(X^k Y^l), k,l = 1, 2, \cdots$ 存在，则称之为 $X$ 与 $Y$ 的 $\color{blue}{k+l\text{阶混合(原点)矩}}$

定义2.2：若 $E \lbrace [X - E(X)]^k [Y - E(Y)]^l \rbrace, k,l = 1, 2, \cdots$ 存在，则称之为 $X$ 与 $Y$ 的$\color{blue}{k+l\text{阶混合中心矩}}$

之前提到的随机变量的协方差就是其1 + 1阶混合中心矩

多元随机变量的数字特征(数学期望与协方差矩阵)

定义3：设 $n$ 元随机变量 $\tilde{X} = (X_1, X_2, \cdots, X_n)^T, n \geq 1$，若其每一分量的数学期望都存在，则称

$$E(\tilde{X}) = (E(X_1), E(X_2), \cdots, E(X_n))^T, n \geq 1$$

为 $n$ 元随机变量 $\tilde{X}$ 的数学期望(向量)

定义4：设 $n$ 元随机变量 $\tilde{X} = (X_1, X_2, \cdots, X_n)^T, n \geq 1$，若 $Cov(X_i, X_j), i,j = 1, 2, \cdots, n$ 都存在，则称

$$\begin{aligned} C = Cov(\tilde{X}) = \begin{pmatrix} D(X_1) & Cov(X_1, X_2) & \cdots & Cov(X_1, X_n) \\ Cov(X_2, X_1) & D(X_2) & \cdots & Cov(X_2, X_n) \\ \vdots & \vdots & \ddots & \vdots \\ Cov(X_n, X_1) & Cov(X_n, X_2) & \cdots & D(X_n) \end{pmatrix} \end{aligned}$$

为 $n$ 元随机变量 $\tilde{X}$ 的协方差矩阵(是对称非负定矩阵)

即：$\mathbf{C} = (c_{ij})_{n \times n}, c_{ij} = Cov(X_i, X_j), i,j = 1, 2, \cdots, n$

多元正态分布的概率密度

• $n$ 元正态随机变量的联合概率密度的矩阵表示

引入列向量 $\tilde{\mathbf{x}} = (x_1, \cdots, x_n)^T, \tilde{\mathbf{\mu} = (E(X_1), \cdots, E(X_n))^T}$，协方差矩阵为 $\mathbf{C} = (c_{ij})_{n \times n}, c_{ij} = Cov(X_i, X_j), i,j = 1, \cdots, n$。则 $n$ 元正态随机变量 $\tilde{X} = (X_1, \cdots, X_n)^T, n \geq 1$，其联合概率密度为

$$\begin{aligned} f(x_1, \cdots, x_n) = \frac{1}{(2\pi)^{\frac{n}{2}} |\mathbf{C}|^{\frac{1}{2}}} \exp \lbrace -\frac{1}{2}(\tilde{\mathbf{x}} - \tilde{\mathbf{\mu}})^T \mathbf{C}^{-1} (\tilde{\mathbf{x}} - \tilde{\mathbf{\mu}}) \rbrace \end{aligned}$$

多元正态分布的四条性质

1. $n$ 元正态随机变量 $\tilde{X} = (X_1, X_2, \cdots, X_n)^T, n \geq 1$，其任意子向量 $(X_{i1}, \cdots, X_{ik})^T (1 \leq k \leq n)$ 均服从 $k$ 元正态分布。特别地，其中每一个分量 $X_i, i = 1, \cdots, n$ 都是一元正态变量。反之，若 $X_i, i = 1, \cdots, n$ 均为一元正态变量，且相互独立，则 $\tilde{X} = (X_1, \cdots, X_ n)^T, n \geq 1$ 是 $n$ 元正态随机变量

例如：$\tilde{X} = (X_1, X_2, X_3)^T$ 为3元正态随机变量，则 $(X_1,X_2)^T, (X_1, X_3)^T, (X_2, X_3)^T$ 均为二元正态变量

2. $n$元随机变量$\tilde{X} = (X_1, X_2, \cdots, X_n)^T, n \geq 1$服从$n$元正态分布$\Leftrightarrow X_1, \cdots, X_n$的任意线性组合$l_0 + l_1X_1 + \cdots + l_nX_n$均服从一元正态分布，其中$l_1, \cdots, l_n$不全为0

例如：$\tilde{X} = (X_1, X_2, X_3)^T$ 为3元正态随机变量，则 $3X_1 - X_2, 2X_1 + 4X_3 + 1, X_2 - 3X_1 - X_3 - 2$ 均为一元正态变量

3. $n$ 元正态随机变量 $\tilde{X} = (X_1, X_2, \cdots, X_n)^T, n \geq 1$，若 $Y_1, \cdots, Y_k, k \geq 1$均为 $X_i, i = 1, 2, \cdots, n$ 的线性函数，则 $(Y_1, \cdots, Y_k)^T$ 也服从 $k$ 元正态分布。

这一性质称为$\color{blue}{\text{正态变量的线性变换不变性}}$

例如：$\tilde{X} = (X_1, X_2, X_3)^T$ 为3元正态随机变量，则 $(3X_1 - X_2, 2X_1 + 4X_3 + 1, X_2 - 3X_1 - X_3 - 2, X_2)^T$ 服从4元正态分布

4. 设 $\tilde{X} = (X_1, X_2, \cdots, X_n)^T, n \geq 1$ 服从 $n$ 元正态分布，则 $X_1, \cdots, X_n$ 相互独立$\Leftrightarrow X_1, \cdots, X_n$ 两两不相关 $\Leftrightarrow \tilde{X}$ 的协方差矩阵为对角矩阵

$$\begin{aligned} \mathbf{C} = \begin{pmatrix} D(X_1) & 0 & \cdots & 0 \\ 0 & D(X_2) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & D(X_n) \end{pmatrix} \end{aligned}$$

---

常用公式：

• $Cov(\mathbf{X}, \mathbf{Y}) = E(\mathbf{X}\mathbf{Y}^T) - E(\mathbf{X})E(\mathbf{Y})^T$
• $Cov(\mathbf{X}, \mathbf{X}) = E(\mathbf{X}\mathbf{X}^T) - E(\mathbf{X})E(\mathbf{X})^T$
• $Cov(\mathbf{AX}, \mathbf{BY}) = \mathbf{A}Cov(\mathbf{X}, \mathbf{Y})\mathbf{B}^T$
• $Cov(\mathbf{AX}, \mathbf{AX}) = \mathbf{A}Cov(\mathbf{X}, \mathbf{X})\mathbf{A}^T$
• $E(\mathbf{X}^T\mathbf{AX}) = tr \mathbf{A} Cov(\mathbf{X}, \mathbf{X}) + E(\mathbf{X})^T\mathbf{A}E(\mathbf{X})$

补充矩阵的迹的性质：

$\mathbf{A},\mathbf{B}$ 是 $n \times n$ 的正方矩阵

• $tr(\mathbf{A} + \mathbf{B}) = tr(\mathbf{A}) + tr(\mathbf{B})$
• $tr \mathbf{AB} = tr \mathbf{BA}$
• $tr \mathbf{A}(\mathbf{A}^T\mathbf{A})^{-1}\mathbf{A}^T = tr \mathbf{A}^T \mathbf{A} (\mathbf{A}^T \mathbf{A})^{-1} = tr \mathbf{I}_n = n$ ($\mathbf{A}$ 是 $m \times n$ 的矩阵且 $rank(\mathbf{A}) = n$)
• $\mathbf{x}^T \mathbf{Ax} = tr \mathbf{Axx}^T$ ($\mathbf{x}$是 $n$ 维的列向量)

依概率收敛，切比雪夫不等式

大数定律及中心极限定理

大数定律

贝努里大数定律：记 $n_A$ 为 $n$ 重贝努里实验中事件 $A$ 发生的次数，并记事件 $A$ 在每次试验中发生的概率为 $p(0 < p < 1)$，则对于 $\forall \epsilon > 0$，有

$$\lim_{n \rightarrow +\infty} P \lbrace |\frac{n_A}{n} - p| \geq \epsilon \rbrace = 0$$

即，$\frac{n_A}{n} \rightarrow p$，当 $n \rightarrow +\infty$

贝努里大数定律的重要意义：

• 提供了用大量重复独立试验中事件出现的频率的极限值来确定概率的理论依据，使得概率才有严格的意义
• 提供了通过试验来确定事件的概率的方法：可以通过做试验确定某事件发生的概率并把它作为相应的概率估计。例如：想估计某产品的不合格频率 $p$，可以随机抽取 $n$ 件（$n$ 较大），将 $n$ 件产品的不合格的比例作为 $p$ 的估计

大数定律(Laws of Large Numbers)：设 $X_1, X_2, \cdots, X_n, \cdots$ 是一列随机变量，则在一定条件下，随机变量序列 $Y_n = \frac{X_1 + X_2 + \cdots + X_n}{n}$，收敛到 $\mu$，当 $n \rightarrow \infty$

• 随机变量序列 $Y_n$ 收敛到 $\mu$ 的含义：依概率收敛
• $\mu$ 是：当 $X_i$ 期望相同时，$\mu = E(X_i)$
• 在不一样的条件下得到不同的大数定律

切比雪夫大数定律的推论：设 $X_1, X_2, \cdots, X_n, \cdots$ 为相互独立的随机变量，且具有相同的期望 $\mu$，相同的方差 $\sigma^2$，那么 $\frac{1}{n} \sum_{i=1}^n X_i \rightarrow \mu$，当 $n \rightarrow \infty$

前面的定理要求随机变量的方差存在，但当随机变量服从相同分布时，就不需要这一要求

辛钦大数定律：$X_1, X_2, \cdots, X_n, \cdots$ 为独立同分布的随机变量，且其期望存在，记为 $\mu$，那么 $\frac{1}{n} \sum_{i=1}^n X_i \rightarrow \mu$，当 $n \rightarrow \infty$

辛钦大数定律的意义：

• 提供了求随机变量 $X$ 的数学期望 $E(X)$ 的近似值的方法：将随机变量 $X$ 独立重复地观察 $n$ 次，记第 $k$ 次观测值为 $X_k$，则 $X_1, X_2, \cdots, X_n$ 相互独立，且与 $X$ 具有同样的分布。那么，当 $E(X)$ 存在时，由辛钦大数定律，可知当 $n$ 充分大时，可将 $n$ 次的平均 $\frac{1}{n} \sum_{i=1}^n X_i$ 作为 $E(X)$ 的近似
• 其目的是寻求 $X$ 的期望，则这样做可以不必考虑 $X$ 的分布！

中心极限定理

问题的提出：有许多随机变量，它们是由大量的相互独立的随机变量的综合影响所形成的，而其中每个个别的因素作用都很小，这种随机变量往往服从或近似服从正态分布，或者说它的极限分布是正态分布，中心极限定理正是从数学上论证了这一现象，它在长达两个世纪的时期内曾是概率论研究的中心课题

独立同分布的中心极限定理(CLT)：设随机变量 $X_1, \cdots, X_n, \cdots$，相互独立且同分布，$E(x_i) = \mu, D(X_i) = \sigma^2, i = 1, 2, \cdots$，则对于充分大的 $n$ 有 $\sum_{i=1}^n X_i \sim N(n \mu, n \sigma^2)$。此时，$P(a < \sum_{i=1}^n X_i \leq) \simeq \Phi(\frac{b - n\mu}{\sqrt{n} \sigma}) - \Phi(\frac{a - n\mu}{\sqrt{n} \sigma})$

德莫弗-拉普拉斯中心极限定理：记 $n_A$ 为 $n$ 重贝努里实验中事件 $A$ 发生的次数，并记事件 $A$ 在每次试验中发生的概率为 $p(0 < p < 1)$，则对于充分大的 $n$ 有 $n_A \sim N(np, np(1 - p))$。即，对于二项分布 $B(n, p)$，当 $n$ 充分大时，可用正态分布来近似

样本及抽样分布

从本章节开始为数理统计内容，在前述的概率论中，我们所研究的随机变量，它的分布都是假设已知的，在这一前提下去研究它的性质，特点和规律性，例如求出它的数字特征，讨论随机变量函数的分布，介绍常用的各种分布等

在数理统计中，我们研究的随机变量，它的分布是未知的，或者是完全不知道的，人们是通过对所研究的随机变量进行重复独立的观察，得到许多观察值，对这些数据进行分析，从而对所研究的随机变量分布做出种种推断的

本章介绍总体，随机样本及统计量等基本概念，并着重介绍几个常用统计量及抽样分布

随机样本

直方图和箱线图

抽样分布

参数估计

点估计

基于截尾样本的最大似然估计

估计量的评选标准

区间估计

正态总值均值与方差的区间估计

(0-1)分布参数的区间估计

单侧置信区间

假设检验

假设检验

正态总体均值的假设检验

正态总体方差的假设检验

置信区间与假设检验之间的关系

样本容量的选取

分布拟合检验

秩和检验

假设检验问题的p值检验法

方差分析及回归分析

单因素试验的方差分析

双因素试验的方差分析

一元线性回归

多元线性回归

Gauss-Markov定理

在统计学中，高斯－马尔可夫定理(Gauss-Markov Theorem)陈述的是：在线性回归模型中，如果误差满足零均值、同方差且互不相关，则回归系数的最佳线性无偏估计(BLUE, Best Linear unbiased estimator)就是普通最小二乘法估计。

• 这里最佳的意思是指相较于其他估计量有更小方差的估计量，同时把对估计量的寻找限制在所有可能的线性无偏估计量中
• 值得注意的是这里不需要假定误差满足独立同分布(iid)或正态分布，而仅需要满足零均值、不相关及同方差这三个稍弱的条件

总结-统计分布

分布	参数	符号	分布律/概率密度函数	期望	方差
$0-1$分布	$0<p<1$	$\color{red}{X \sim{} 0 - 1(p)}$	$P(X=k) = p^k(1-p)^{1-k}$	$p$	$p(1-p)$
二项分布	$\begin{aligned}n \geq 1\quad\\0<p<1\end{aligned}$	$\color{red}{X \sim{} b(n, p)}$	$P(X=k) = \binom{n}{k}p^k(1-p)^{n-k}$	$np$	$np(1 - p)$
几何分布	$0<p<1$	$\color{red}{X \sim{} G(p)}$	$P(X=k) = (1-p)^{k-1}p \quad k=1,2,\cdots$	$\frac{1}{p}$	$\frac{1-p}{p^2}$
超几何分布	$\begin{aligned}N,M,n\\(M \leq N)\\(n \leq N)\end{aligned}$	$\color{red}{X \sim{} H(n, K, N)}$	$P(X=k, n, K, N) = \frac{\binom{M}{k}\binom{N-M}{n-k}}{\frac{N}{k}}$	$\frac{nM}{N}$	$n\frac{M}{N}(1 - \frac{M}{N})(1 - \frac{n-1}{N-1})$
泊松分布	$\lambda > 0$	$\color{red}{X \sim{} \pi(\lambda)}$	$P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!}$	$\lambda$	$\lambda$
均匀分布	$a<b$	$\color{red}{X \sim{} U(a, b)}$	$f(x) =\begin{cases}\frac{1}{b-a} \quad & a < x < b\\0 \quad & \text{其他}\end{cases}$	$\frac{a+b}{2}$	$\frac{(b-a)^2}{12}$
指数分布	$0<\lambda<1$	$\color{red}{X \sim{} Exp(\lambda)}$	$f(x) =\begin{cases}\lambda{}e^{-\lambda{}x} \quad & x \geq 0\\0 \quad & x < 0\end{cases}$	$\frac{1}{\lambda}$	$\frac{1}{\lambda^2}$
正态分布	$u.\sigma>0$	$\color{red}{X \sim{} N(\mu, \sigma^2)}$	$f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-u)^2}{2\sigma^2}} \quad -\infty < x < \infty$	$\mu$	$\lambda$
Gamma分布	$x \geq 0, \alpha > 0, \lambda > 0$	$\color{red}{X \sim{} \Gamma(\alpha, \frac{1}{\lambda})}$	$f_X(x) = \frac{\lambda^{\alpha}}{\Gamma(\alpha)} x^{\alpha - 1}e^{-\lambda x} (\Gamma(\alpha) = \int_0^{\infty} e^{-t} t^{\alpha - 1} dt)$	$\frac{\alpha}{\lambda}$	$\frac{\alpha}{\lambda^2}$

总结-随机变量

	离散型随机变量	连续型随机变量
概率	$P(X = x_k) = p_k, \quad k =1,2,\cdots$	$f(x)$
(分布/概率密度)函数	$F(x) = P(X \leq x), \quad \infty < x < \infty$	$F(x) = \int^x_{-\infty}f(t)dt$

	离散型二维随机变量	连续型二维随机变量
联合(分布/概率)函数	$F(x,y) = P((X \leq x) \cup (Y \leq y)) =P(X \leq x, Y \leq y)$	$F(x,y) = \int^y_{-\infty}\int^x_{-\infty}f(u,v)du,dv$
边缘分布函数	$\begin{aligned}p_{i \cdot} = \sum^\infty_{j=1}p_{ij} = P(X = x_i), \quad i=1,2,\cdots\\p_{\cdot j} = \sum^\infty_{i=1}p_{ij} = P(Y = y_j), \quad j=1,2,\cdots\end{aligned}$	$\begin{aligned}f_X(x) = \int^\infty_{-\infty}f(x,y)dy\\f_Y(y) = \int^\infty_{-\infty}f(x,y)dx\end{aligned}$
条件分布	$\begin{aligned}P(X = x_i\vert Y = y_j) = \frac{P(X = x_i, Y = y_j)}{P(Y = y_j)} = \frac{p_{ij}}{p_{\cdot j}}, \quad i=1,2,\cdots\\P(Y = y_i\vert X = x_i) = \frac{P(X = x_i, Y = y_j)}{P(X = x_i)} = \frac{p_{ij}}{p_{i\cdot}}, \quad j=1,2,\cdots\end{aligned}$	$\begin{aligned}\int^x_{-\infty} f_{X\vert Y}(x\vert y)dx = \int^x_{-\infty}\frac{f(x,y)}{f_Y(y)}dx\\\int^y_{-\infty} f_{Y\vert X}(y\vert x)dy = \int^y_{-\infty}\frac{f(y,x)}{f_X(x)}dy\end{aligned}$
相互独立	$\begin{aligned}P(X=x_i, Y=y_j) = P(X=x_i)P(Y=y_i)\end{aligned}$	$f(x,y) = f_X(x)f_Y(y)$

参考文献

• 《概率论与数理统计》浙大版(第四版)
• 高斯－马尔可夫定理 以及为什么最小二乘法是最佳线性无偏估计