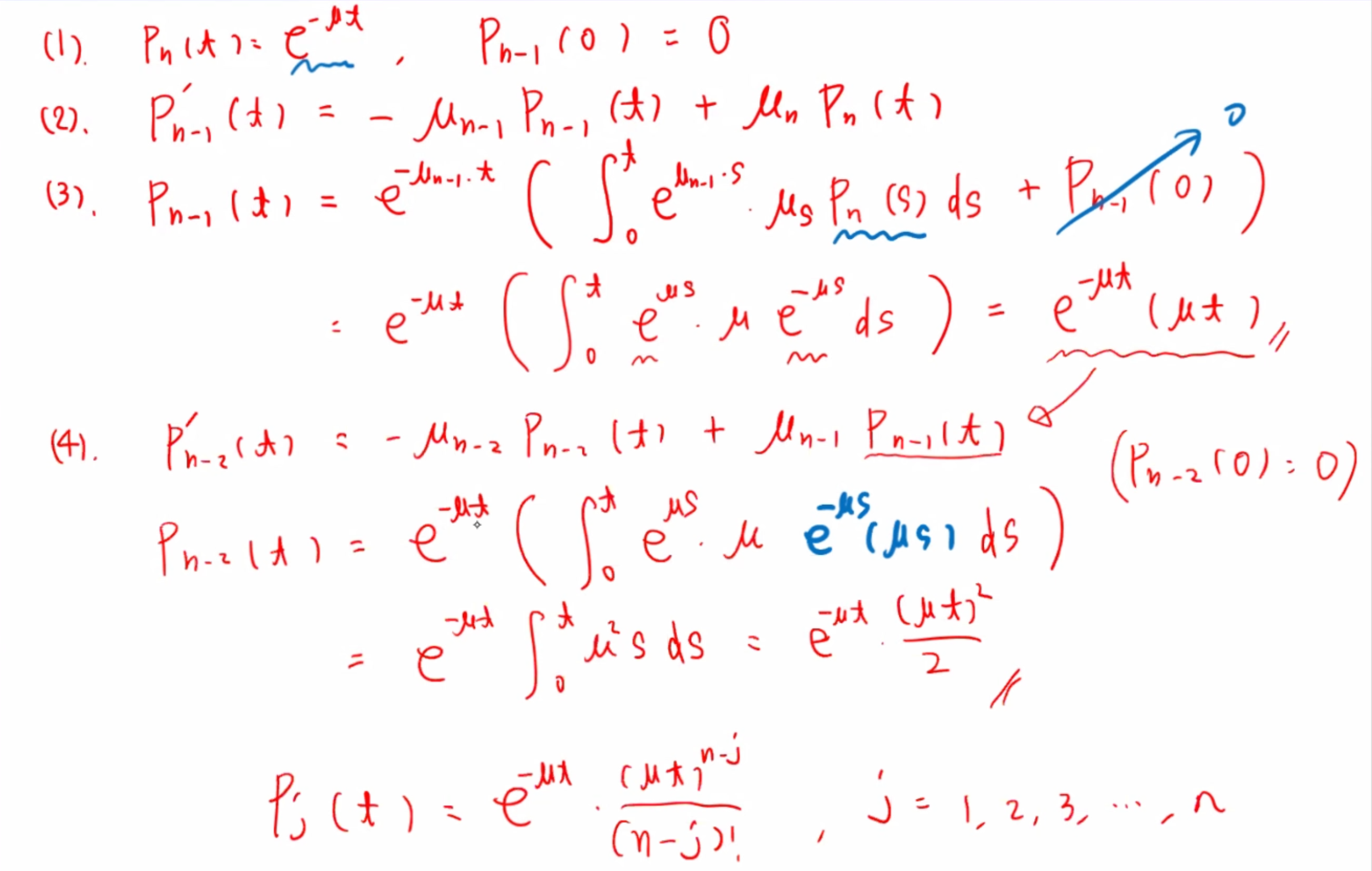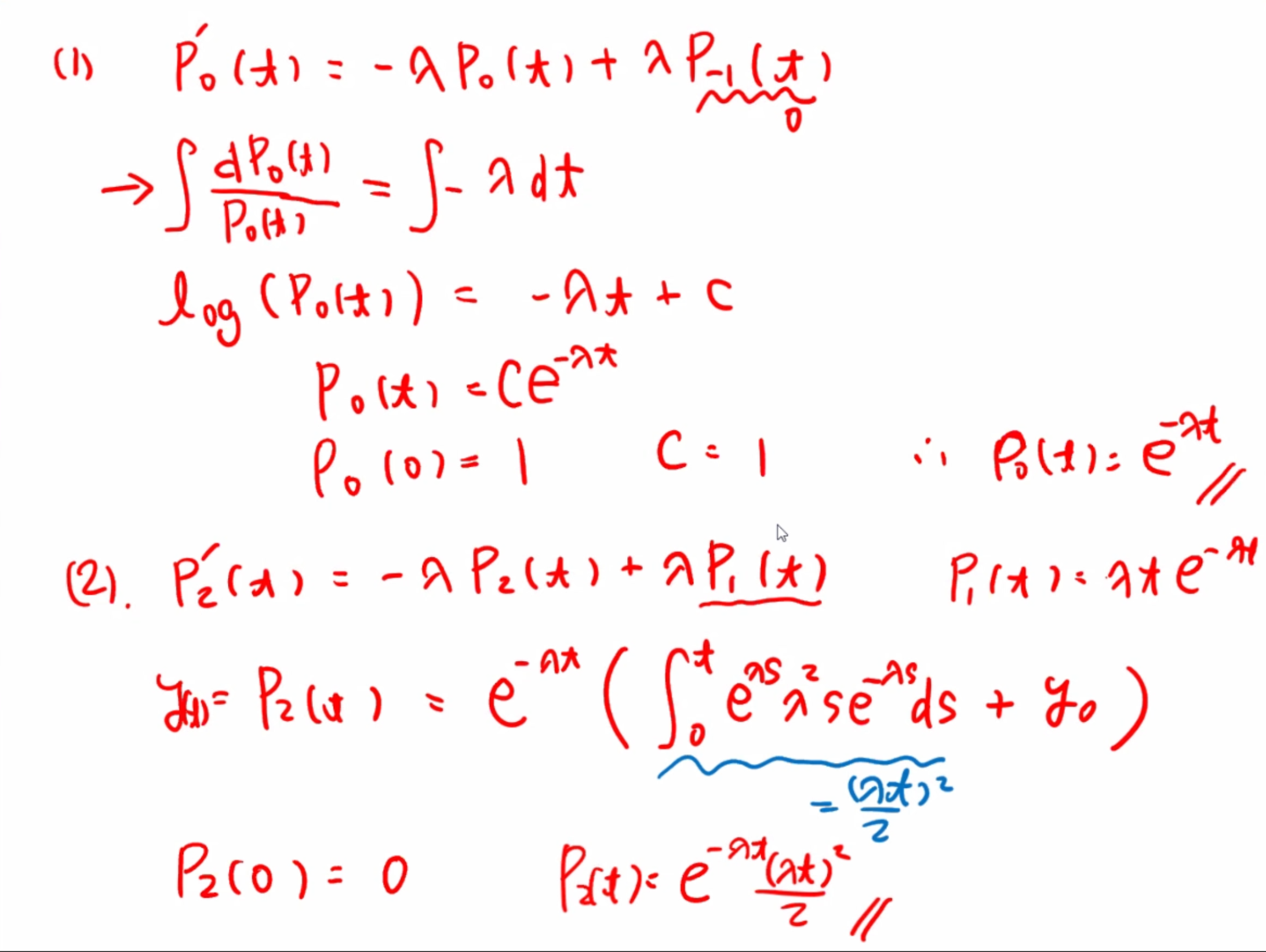CS专业课学习笔记
確率分布
(0-1)分布
定义:若X的概率分布律为
| X |
0 |
1 |
| P |
1−p |
p |
其中0<p<1,就称X服从参数为p的0-1分布(或两点分布),记为X∼0−1(p) 或 X∼B(1,p)
其分布律还可以写成:P(X=k)=pk(1−p)1−k,k=0,1
伯努利试验,二项分布
设试验E只有两个可能的结果:A或A,且P(A)=p,0<p<1。将E独立地重复进行n次,则称这一串重复地独立试验为n重伯努利试验
二项分布定义:若X地的概率分布律为:
P(X=k)=Cnkpk(1−p)n−k,k=0,1,⋯,n
其中n≥1,0<p<1,就称X服从参数为n,p的二项分布(Binomial),记为X∼B(n,p)
- E(X)=np
- V(X)=np(1−p)
例題
〇×で解答する試験において、気まぐれに解答する。10問ある時、正答の個数を X として、X の平均と分散を求めよ。また、X≥8 となる確率を求めよ
- E(X)=np=10∗0.5=5
- V(X)=np(1−p)=10∗0.5∗0.5=2.5
- P(X≥8)=P(X=8)+P(X=9)+P(X=10)=C108(21)8(21)2+C109(21)9(21)+C1010(21)10(21)0≃0.0547
泊松分布
定义:若X的概率分布律为
P(X=k)=k!λke−λ,k=0,1,2,⋯
- E(X)=λ
- V(X)=λ
其中λ>0,就称 X 服从参数为 λ 的泊松分布(Poisson),记为X∼π(λ)或X∼P(λ)
泊松分布的用途:
- 某人一天内收到的微信的数量
- 来到某公交汽车站的乘客
- 某放射性物质发射出的粒子
- 显微镜下某区域中的白血球
如果某事件以固定强度 λ,随机且独立地出现,该事件在单位时间内出现地次数(个数)可以看成是服从泊松分布
二项分布与泊松分布有以下近似关系:
Cnkpk(1−p)n−k≃k!e−λλk,λ=np,n>10,p<0.1
例題
ある製品の製造工程では、微小領域に1万個の点にレーザーを当てていく。位置をずれるのは2万個に一つであるという。この工程ではずれが一つもないという確率を求めよ
- λ=np=10000∗200001=0.5
- E(X)=λ=0.5
- V(X)=λ=0.5
- P(X=0)=P(0,λ)=e−0.5⋅0!0.50≃0.606531
- B(n,p)=C100000(200001)0(2000019999)10000≃0.606523
几何分布
定义:若 X 的概率分布律为
P(X=k)=p(1−p)k−1,k=1,2,3,⋯
其中 0<p<1,称 X 服从参数为 p 的几何分布(Geometric),记为 X∼Geom(p)
几何分布的用途:在重复多次的伯努利实验中,实验进行到某种结果出现第一次为止,此时的试验总次数服从几何分布。如:射击,首次击中目标时射击的次数
- E(X)=p1
- V(X)=p21−p
例題
合格率10%の試験を挑み、X 回目で初めて合格する。X の平均と分散を求めよ。また、X=3 となる確率を求めよ
- E(X)=p1=0.11=10
- V(X)=p21−p=0.121−0.1=90
- P(X=3)=0.92∗0.1=0.081
均匀分布
若 X 的概率密度函数为
f(x)={b−a1,0,x∈(a,b)其他
其中 a<b,就称 X 服从 (a,b) 上的均匀分布(Uniform),记为 X∼U(a,b) 或 X∼Unif(a,b)
均匀分布的性质:均匀分布具有等可能性,即,服从 U(a,b) 上的均匀分布的随机变量 X 落入 (a,b) 中的任意子区间上的概率只与其区间长度有关与区间所处的位置无关。即 X 落入 (a,b) 中的等长度的任意子区间上是等可能的。
- E(X)=2b+a
- V(X)=12(b−a)2
例題
ある自動車のブレーキテストで時速50kmでブレーキをかけた時、止まるまでに要する距離 X は区間 (a,b) 上の一様分布に従うという。b よりも a に近いところで止まる確率を求めよ
P(a<X<2a+b)=∫a2a+bb−a1dx=21
指数分布
若 X 的概率密度函数为
f(x)={λe−λx,0,x>0x≤0
其中 λ>0,就称 X 服从参数为 λ 的指数分布(Exponential),记为 X∼E(λ) 或 X∼Exp(λ)
- E(X)=λ1
- V(X)=λ21
随机变量 X 的分布函数为:
F(x)={1−e−λx,0,x>0x≤0
指数分布的性质:指数分布具有无记忆性
指数分布的用途:
- 指数分布可以用来表示独立随机事件发生的时间间隔,比如旅客进机场的时间间隔,中文维基百科新条目出现的时间间隔等等
- 在排队论中,一个旅客接受服务的时间长短也可以用指数分布来近似
- 无记忆性的现象(连续时)
正态分布
若 X 的概率密度函数为
f(x)=2πσ1e−2σ2(x−μ)2,−∞<x<+∞
其中 −∞<μ<+∞,σ>0 ,就称 X 服从参数为 μ,σ 的正态分布(或高斯分布),记为 X∼N(μ,σ2)
- E(X)=μ
- V(X)=σ2
正态分布的特征:
- f(x) 关于 x=μ 对称
- 当 x≤μ 时,f(x) 是严格单调递增函数
- fmax=f(μ)=2πσ1
- lim∣x−μ∣→∞f(x)=0
正态分布的参数:
- μ 为位置参数,决定对称轴位置
- σ 为尺度参数,决定曲线分散程度
正态分布的用途:
- 自然界和人类社会中很多现象可以看做正态分布
- 例如:人的生理尺寸(身高,体重),医学检验指标(红细胞数,血小板),测量误差等等
- 多个随机变量的和可以用正态分布来近似
- 例如:注册MOOC的某位同学完成所有作业的时间,二项分布等等
标准正态分布
若 Z∼N(0,1),称 Z 服从标准正态分布
- Z 的概率密度函数:ϕ(z)=2π1e−2z2
- Z 的分布函数:Φ(z)=∫−∞Z2π1e−2t2dt
标准正态分布的分布函数有一个重要的性质:
Φ(−z0)=1−Φ(z0)
对于任意的实数 z0 都成立
此外,当 X∼N(μ,σ2) 时,σX−μ∼N(0,1),由此可知,当 X∼N(μ,σ2) 时,对于任意实数 a,有
FX(a)=P(X≤a)=P(σX−μ≤σa−μ)=Φ(σa−μ)
マルコフ連鎖(Markov chain)
马尔可夫过程是研究信号多级传输,分子的布朗运动,顾客服务,计算机网络流量等诸多问题时使用的经典模型
確率過程
時間 t に応じて偶然に変化する結果を X(t) とする
- X(t):確率変数
- {X(t);t≥0}:確率過程
例:
- t 時に届くemailの数
- t 日の株価の終値
- コイン投げ t 回における表の出現回数
マルコフ過程:ある時点における現象の確率が直前の結果だけで決まる確率過程
- マルコフ連鎖:離散時間 {t=0,1,2,⋯}、離散値 {i;i=0,1,2,⋯} をとるマルコフ過程
- ポアソン過程:連続時間 t≥0、離散値をとるマルコフ過程
マルコフ連鎖の例
0, 1のラベルがついた球が入っている箱A, 箱Bを考える
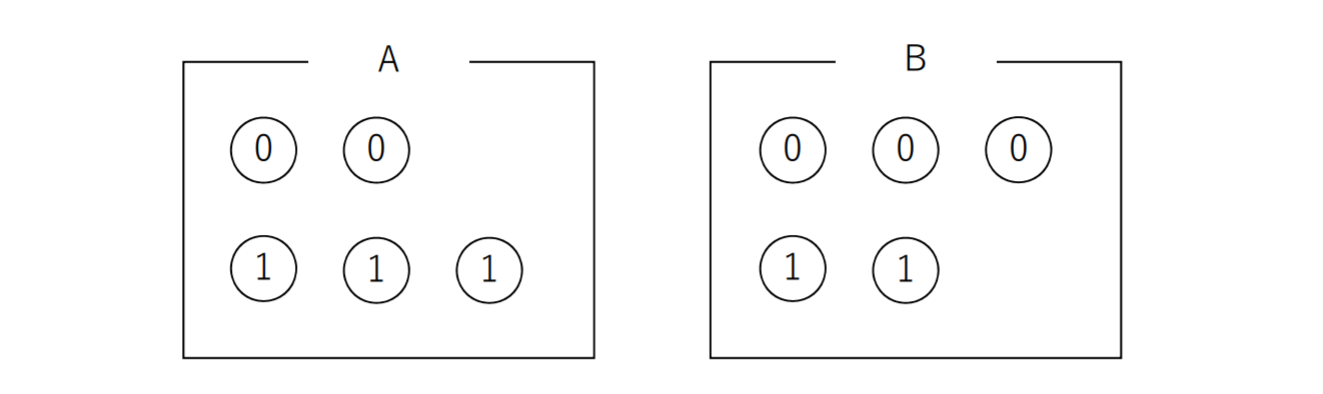
初めにどちらかの箱から球を取り出し、玉のラベルを書き出す。次にラベルに応じて次に取り出す箱を決める。球はその都度元の箱へ戻す

マルコフ連鎖の定義
Xn;n=0,1,2,⋯ が任意の n≥0 と、任意の S の要素 x0,x1,⋯,i,j について次のような性質を持つとき、マルコフ連鎖という
P(Xn+1=j ∣ X0=x0,X1=x1,⋯,Xn=i)=P(Xn+1=j ∣ Xn=i)

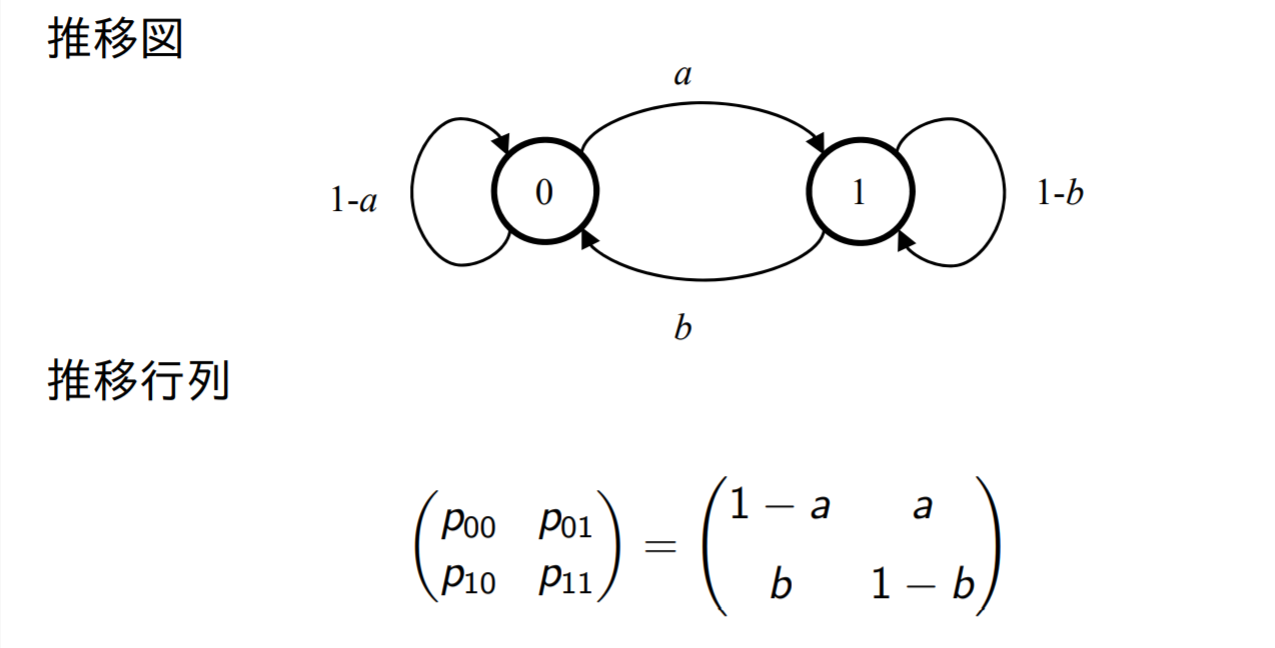
2状態マルコフ連鎖
ある学習モデルを考える。一連の実験において正答した次は確率 a で誤答し、誤答した次は確率 b で正答する。このマルコフ連鎖の推移図と推移行列を求めよ。(ただし、正答の状態を0、誤答の状態を1とおく)
マルコフ連鎖の時間ダイナミクス
- pij は状態 i から状態 j へ一段階で推移する確率
- 状態 i から状態 j へちょうど n 段かかって推移する確率を pij(n) とおく (n 段階の推移確率)
- 時間に一様な場合なので m に無関係
pij(n)=P(Xm+n=j ∣ Xm=i)
查普曼-柯尔莫格洛夫方程(Chapman-Kolmogorov equation,C-K equation)
チャップマン・コルモゴロフの等式(Chapman–Kolmogorov equation):一般に (n+m) 段階では
pij(n+m)=pi0(n)p0j(m)+pi1(n)p1j(m)+⋯+pik(n)pkj(m)+⋯=k∑pik(n)pkj(m)
n 段階の推移確率 pij(n) を (i,j) 成分とする行列を P(n) (n 段階の推移行列)と書く
P(n+m)=P(n)P(m)
- P(1)=P
- P(2)=P(1+1)=PP=P2
- P(3)=P(2+1)=P2P=P3
- P(n)=Pn
初期確率 αi (状態 i から始まる確率)が次のように与えられているとする
αi=P(X0=i),i=0,1,2,⋯(i∑αi=1)
マルコフ連鎖が n 段階後に状態 j にある確率 P(Xn=j) は、
P(Xn=j)=i∑αipij(n)
したがって、初期確率ベクトル α=(α0,⋯,αi,⋯) とおくと P(Xn=j) は αPn の (i,j) 成分である
例題2.1

α=(0,0,1)
と置く
αP2=⎝⎛0.50.30.20.40.40.30.40.30.5⎠⎞⎝⎛0.50.30.20.40.40.30.40.30.5⎠⎞=(0.29,0.35,0.36)
状態の分類
ある整数 n≥0 に対し、pi,j(n)>0 の時、状態 j は状態 i から到達可能であるといい、i→j と表す。i,j が互いに到達可能であるとき、i↔j と表す
関係 ↔ は次の同値関係を満たす
- i↔j:反射法則
- i↔j ならば j↔i:対称法則
- i↔j および j↔k ならば、i↔k:推移法則
状態の全体は、同値な組に分割することができる(同値な組に含まれる状態は互いに到達可能)
同値な組がただ一つなとき、そのマルコフ連鎖は既約であるという
例題2.2

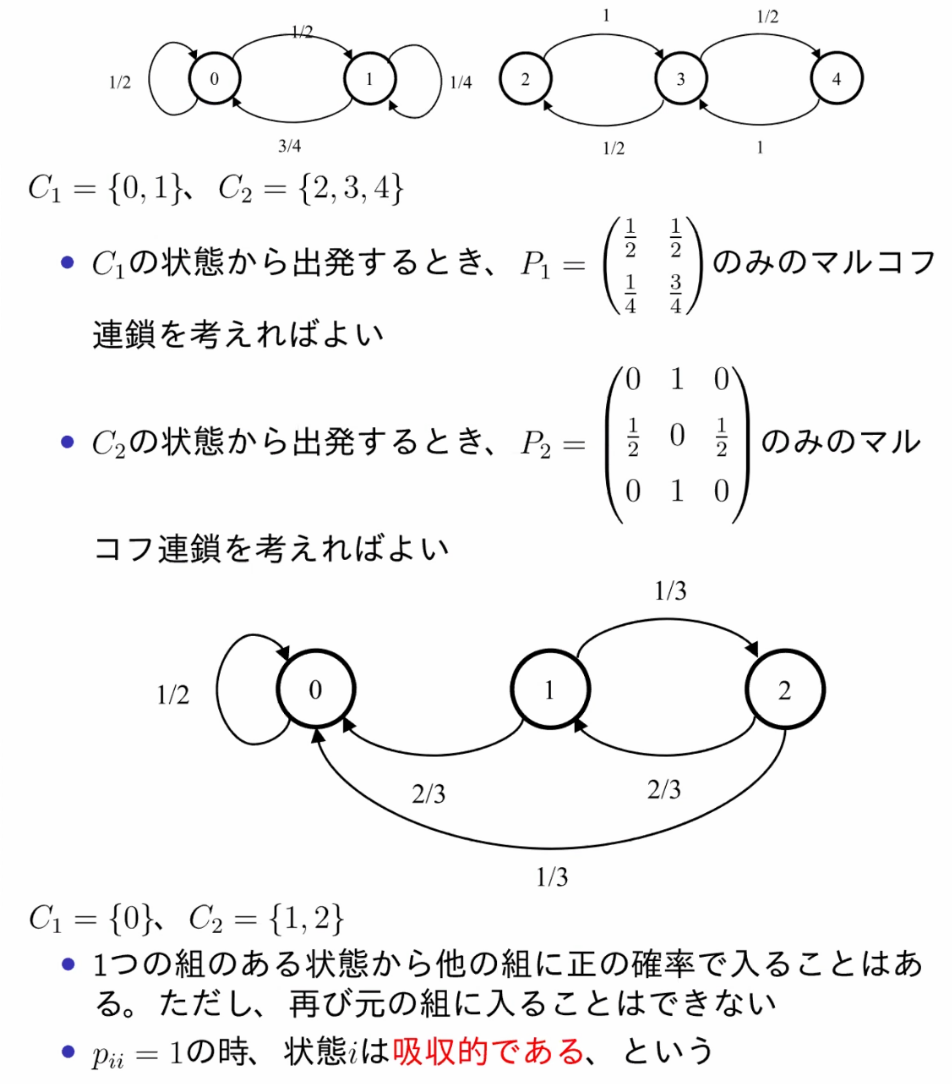
pii=1 の時、状態 i は吸収的である
第一个状态转移图有错(41,43 颠倒),图片待修改!!!
第二个状态转移图也有错,p00=1 ,图片待修改!!!
状態 i から出発するマルコフ連鎖が状態 i へ初めて戻るまでに要する時間(段階数)を τi とする。すなわち
τi=min{n≥1;Xn=i}
この時、τi が有限となる確率が1の時、状態 i は再帰的であるという。一方、1よりも小さい時、状態 i は一時的であるという
- 状態 i が再帰的、状態 i と状態 j は互いに到達可能 → 状態 j も再帰的
- 状態 i が一時的、状態 i と状態 j は互いに到達可能 → 状態 j も一時的
再帰的、一時的の性質:
- 規約なマルコフ連鎖においては全ての状態は再帰的か一時的かのどちらか
- 有限マルコフ連鎖(有限個の状態からなる連鎖)においては、状態 i が一時的であるための必要十分条件は、i→j であるが i⇍j となる j があることである
- 有限マルコフ連鎖の一時的な組は"閉じてない"
- 少なくとも一つの再帰的な状態が存在する(規約なら再帰的)
- 状態 i が再帰的であれば、i から出発すると何回も i に戻ってくる。したがって、状態 i が再帰的であるための必要十分条件は、i から出発して i へ戻る回数の平均が無限大になることである
式で書くと
ln={1,Xn=10,Xn=1T=n=1∑∞ln
とおき、マルコフ連鎖が状態 i から出発するときの条件的確率で測った T の期待値を求めると、
Ei[T]=n=1∑∞Ei[ln]=n=1∑∞1×P(Xn=i ∣ X0=i)=n=1∑∞pii(n)
となる。したがって、状態 i は
- ∑n=1∞pii(n)=∞ ならば再帰的
- ∑n=1∞pii(n)<∞ ならば一時的
別の表現として
状態 i から出発して、n 段階目ではじめて j に到達する確率を fij(n)(初到達確率)とおく
fij(1)=pij
fij=n=1∑∞fij(n):最終到達確率
- ∑n=1∞fii(n)=∞ ならば再帰的
- ∑n=1∞fii(n)<∞ ならば一時的
例題2.3
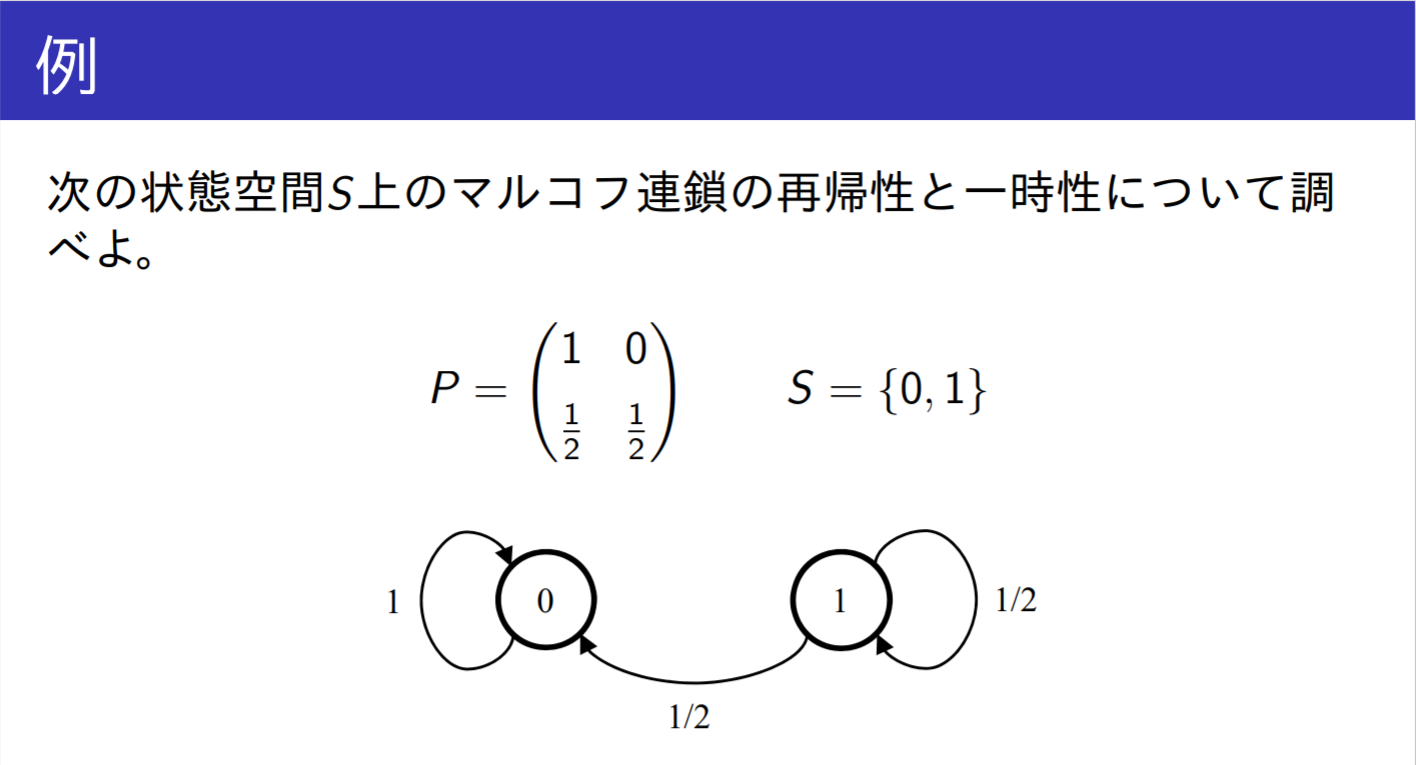
マルコフ連鎖の再帰性と一時性
思路:求解 ∑n=1∞pii(n) 即可
- p00(n)=1→∑n=1∞p00(n)=∞:状態 0 は再帰的
- ∑n=1∞p11(n)=∑n=1∞(21)n=1−1−221=1:状態 1 は一時的
进入0的话一直循环,如果是1的话,只会进入1次0,一旦进入0的话就出不来了
状態 i が再帰的なとき、τi の平均値
μi=n=1∑∞nfii(n)
を平均再帰時間といい、μi<∞,μi=∞ に応じて i をそれぞれ正状態、零状態という
状態 i に対して、pii(n)>0 を満たす整数 n≥1 の全体の最大公約数を状態 i の周期といい、di で表す。di=1 の時、i は非周期的であるという。また、全ての n に対して pii(n)=0 の時は di=1 とする。非周期的、再帰的、正状態をエルゴード状態という
例題2.4


マルコフ連鎖の周期
对于状态 i,满足 pii(n)>0 的整数 n≥1 的所有最大公约数为状态 i 的周期,di=1 的时候,i 是非周期。
第二个周期为2的例子,是以01循环,故周期为2
例題2.5

今日の天気が晴れなので
α=(1,0,0)
- αP=(0.4,0.6,0)
- αP2=(0.28,0.54,0.18)
マルコフ連鎖の定常分布
マルコフ連鎖が既約でエルゴード状態である場合,推移行列の極限値が存在する
πj=n→∞limpij(n)
これは状態 i に無関係であり、
πj=μj1,j=0,1,2,⋯
μj は状態 j の平均再帰時間、この πj は次の方程式を解いて得られ,解は正の値としてただ一通りに決まる
πP=π,π=(π0,π1,⋯),j=0∑∞πj=1
時間が経過しても確率分布が変化しない場合,その分布を定常分布という
πP=π↔i=0∑∞πipij=πj,j=0,1,2,⋯
この方程式の解 π をマルコフ連鎖の定常分布という
確率分布 π が存在するための必要十分条件はマルコフ連鎖が再帰的で正状態であること
既約なマルコフ連鎖のすべての状態は再帰的な正状態、再帰的な零状態、一時的のいずれかである
既約な有限マルコフ連鎖は再帰的な正状態
例題2.6

πP=π
を解くと
π=(8519,8548,8518)
设 π=(a,b,c) 计算即可,注意 a+b+c=1
吸収マルコフ連鎖
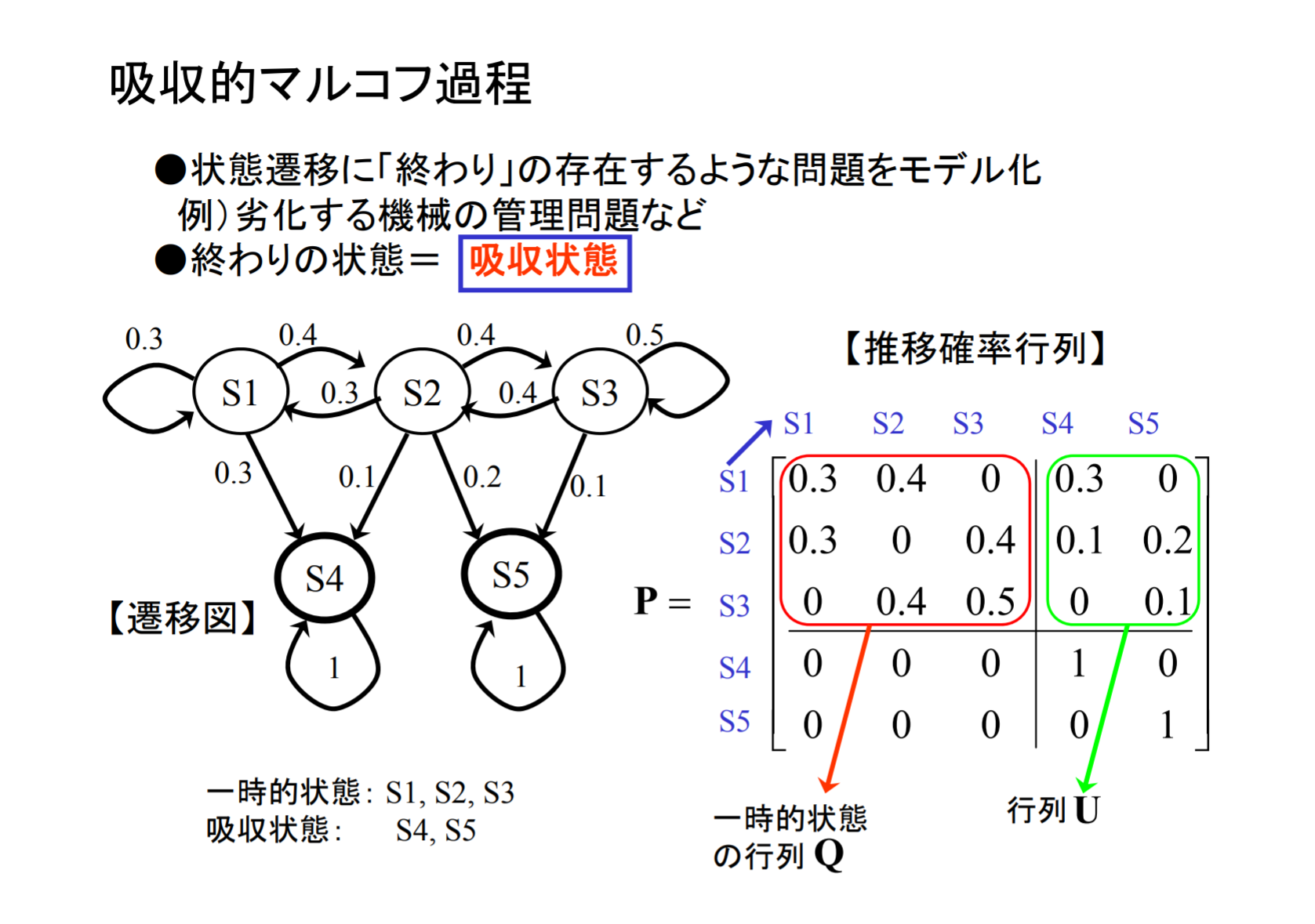
吸収マルコフ連鎖:状態空間が一時的もしくは吸収的な状態からなるマルコフ連鎖
k 個の吸収状態,n−k 個の一時状態がある吸収マルコフ連鎖
P=(IR0Q)
- I:k×k の単位行列
- R:一時状態から吸収状態への推移に関する (n−k)×k 行列
- Q:一時状態から一時状態への推移に関する (n−k)×(n−k) 行列
- 0:ゼロ行列
Pn=(IRn0Qn)
ただし、
Rn=(I+Q+⋯+Qn−1)R=(I−Qn)(I−Q)−1R
Q は非負行列で,行の和は1以下であるため、limn→∞Qn=0 より
n→∞limRn=(I−Q)−1R=MR
P∞=(IMR00)
- M:基本行列
- MR:吸収確率
状態 i,j が一時状態の時、i から出発して吸収状態に達するまでの間に j を訪問する平均回数を mij とする
mij は,一時状態 i から出発して吸収状態に達するまでに平均何時間(何段階)を一時状態 j で過ごすかを表している
mij=δij+t∑pitmtj
状態 i から一段階で吸収状態に達するか、途中の一時状態 t を経て最終的に吸収状態に達するかのどちらか
M=(mij) と置いて上式を行列で表せば、平均滞在時間(平均訪問回数)の行列 M は次式で表される
M=I+QM↔M=(I−Q)−1
例題2.7

吸収マルコフ連鎖
先按照吸収マルコフ連鎖定义将推移矩阵分为4部分,并通过 M=(I−Q)−1 求解 M 和 MR
与单位矩阵同一列的矩阵是表示从一时状态到吸收状态
从一时状态到吸收状态所需平均时间看矩阵 M。例如状态2到吸收状态的平均时间记为矩阵 M 中表示状态2的那一行加起来即可
到吸收状态的概率看吸收概率矩阵 MR
1次元ランダム・ウォーク
数直線上を確率 p で右へ1だけ移動するか,確率 q=1−p で左へ1だけ移動する粒子の運動
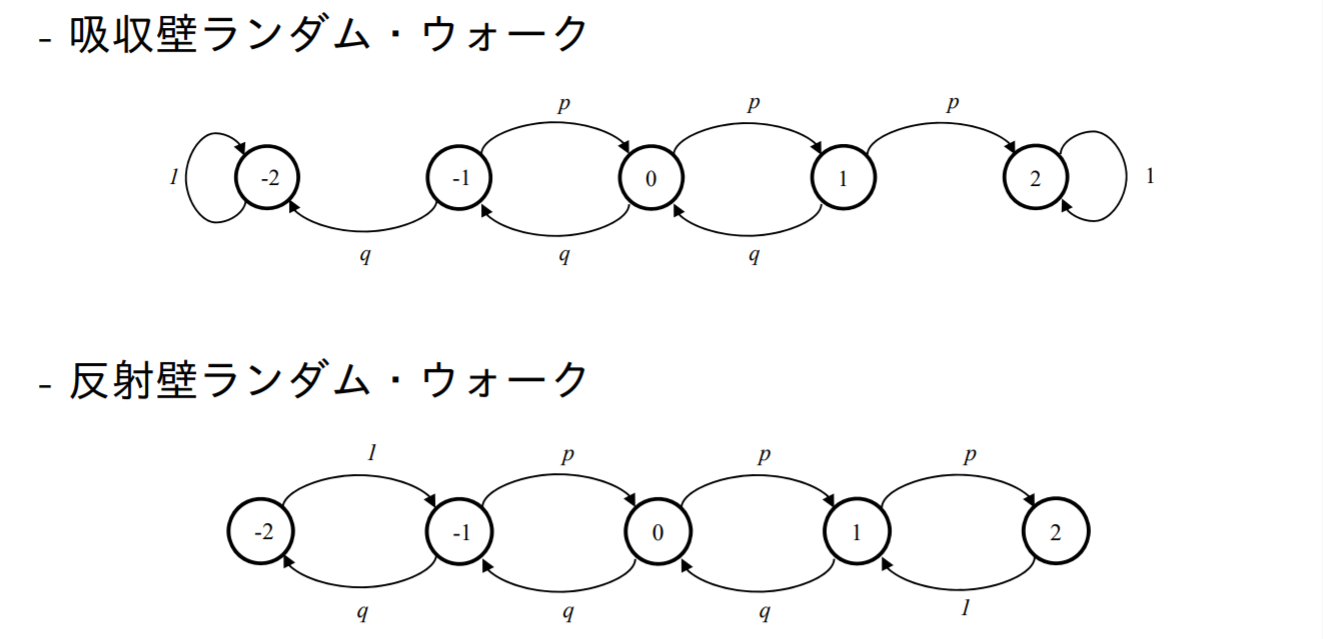
状態 i から状態 i に戻る推移確率を考える
- 奇数ステップ (2n−1) で戻る確率:pii(2n−1)=0,n=1,2,⋯
- 偶数ステップ (2n) で戻る確率:pii(2n)=n!n!(2n)!(p(1−p))n
スターリングの公式
n!≃2πn(en)n
より、p=21 の時
n=1∑∞pii(2n)=n=1∑∞πn(4p(1−p))n=n=1∑∞πn1>π1n=1∑∞n1=∞
よって,再帰的
p=21 の時、r=4p(−1p),(∣r∣<1) と置くと
n=1∑∞pii(2n)=n=1∑∞πnrn<π1n=1∑∞rn=π11−rr<∞
よって,一時的
左右等確率で移動する場合を、1次元の対称なランダム・ウォークという
1次元と2次元の対称な (p=1/2) ランダム・ウォークは再帰的、3次元以上の対称なランダム・ウォークは一時的である
- 原点回りをうろつくよりも、一方の側に偏っていることが多い。原因:原点右側にいる割合を x,左側にいる割合を 1−x とすると、その確率密度関数 f(x) は f(x)=πx(1−x)1 となることが知られている(逆正弦法則)
例題2.8

P=⎝⎛1033210731⎠⎞
定常分布:πP=π
例題2.9

ポアソン過程
泊松过程是一种典型的独立增量过程,它具有连续参数 t 与分离散状态取值,因而也是连续参数马尔科夫链。在通信,交通,日常零售业务等各个领域的研究中,泊松过程是各类问题建模时最常用的一种输入模型
e-mailの着信数,交通事故の発生数,新築の住宅数,外国人の流入数,機械の修理数,サービス窓口の行列人数などの事象を考える
t=0 で観測を始め,時間 t までに起こる発生数を N(t) とすると、N(t) はどのような性質を持つ?
時間10までに起こる交通事故の発生数 N(10) は、時間10と15の間に起こる交通事故の発生数 N(15)−N(10) とは無関係
独立増分:互いに排反な時間区分に起こる事象の発生数が独立
N(15)−N(10) は時間の幅 15−10=5 のみにより定まる確率変数
定常増分:時間 s と t(s<t) の間に起こる事象の発生数の分布が時間の幅 (t−s) のみに依存して決まる
ポアソン過程の定義
連続時間 t≥0 で離散値 {i;i=0,1,2,⋯} を取るマルコフ過程のうち、次のような性質を持つものをポアソン過程という
- N(0)=0
- N(t) は定常独立増分を持つ
- 十分小さい時間の幅 h に対して,P(N(h)=1)=λh+o(h).ただし λ>0
- 十分小さい時間の幅 h に対して,P(N(h)≥2)=o(h)
ここで,limh→0=hf(h)=0 が成り立つとき,f(h)=o(h) と表す h が十分小さいとき,o(h) は無視できる
P(N(h)=1)≃λhP(N(h)≥2)≃0
ポアソン過程の性質
- 観測開始時点 t=0 では事象の発生はない
- t0<t1<⋯<tn の時,確率変数 N(ti)−N(ti−1) と N(tj)−N(tj−1) は独立 (i=j) (独立増分)
- 確率変数 N(t2+h)−N(t1+h) と N(t2)−N(t1) は,任意の h>0 に対し同じ分布を持つ(定常増分)
- 十分小さい時間幅 h の間に発生する事象の数が1回である確率は h に比例
- h の間に発生する事象の数が2回以上発生する確率は0
- h の間に事象が発生しない確率は 1−λh
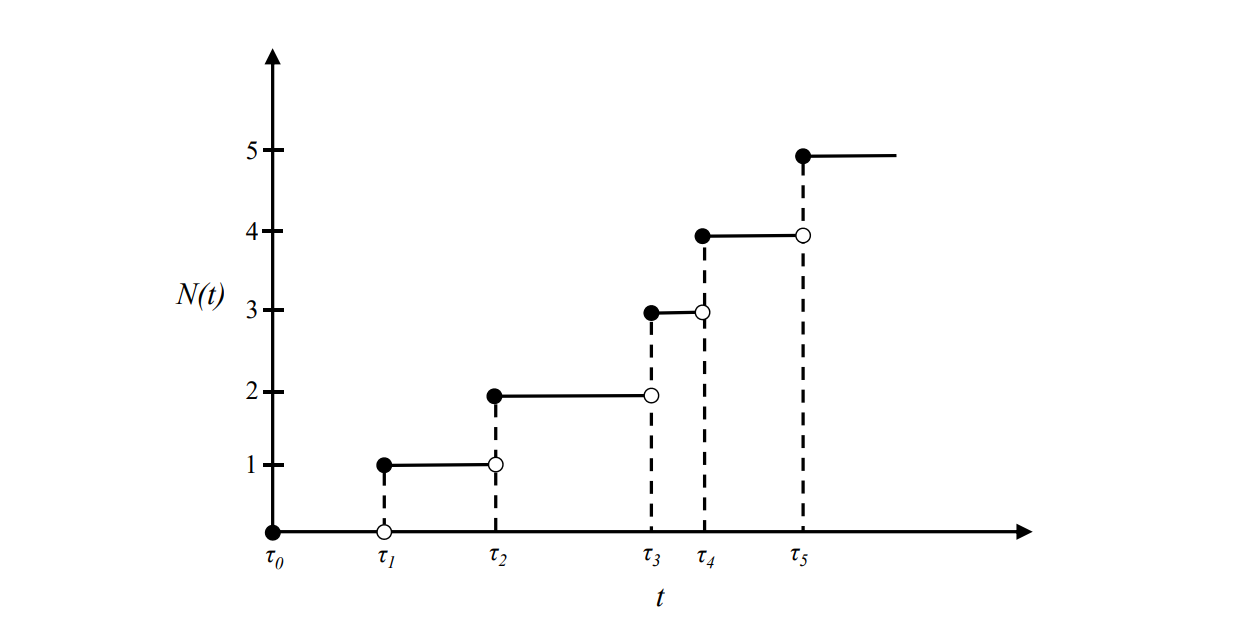
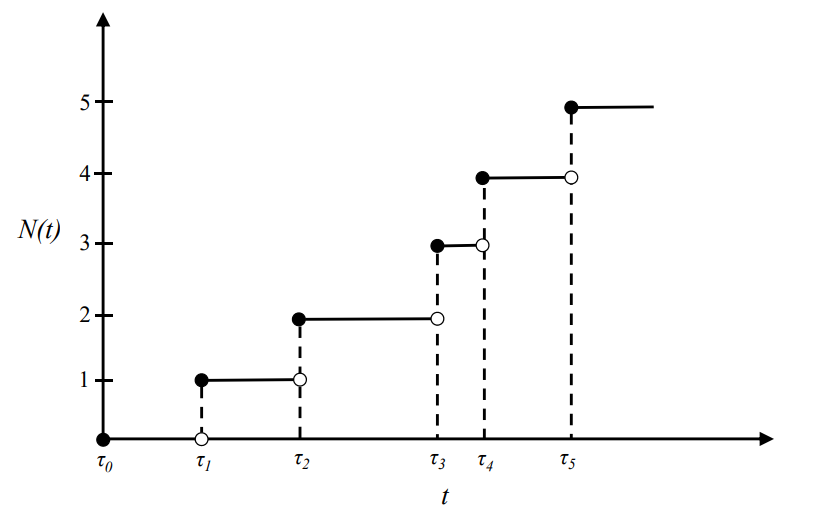
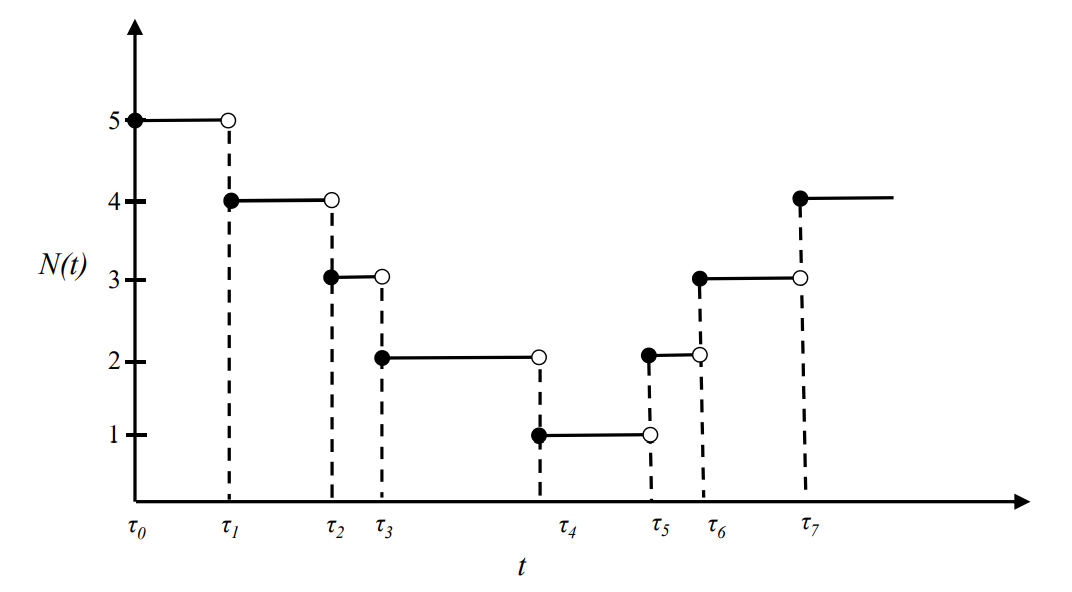
y=N(t) は,高さ1で飛躍する階段状の関数となる.τi は確率変数である
ポアソン分布
時間 t 内に事象が k 個発生する確率 Pk(t)
N(t) は平均 λt のポアソン分布をしている
Pk(t)=e−λtk!(λt)k,k=0,1,2,⋯
- E[N(t)]=V[N(t)]=λt
例題3.1

事象の発生確率–ポアソン分布
アクセス数は λ=0.5 のポアソン過程をなすと考える
Pk(t)=e−λtk!(λt)k,k=0,1,2,⋯
(1) 丁度3
P3(2)=e−13!1=0.0613
(2) 3以下
P0(2)+P1(2)+P2(2)+P3(2)=e−1(1+1!1+2!1+3!1)=0.981
(3) 3以上
1−(P0(2)+P1(2)+P2(2))=1−0.9197=0.0803
事象の発生時間間隔の分布
発生時間間隔 Ti は独立,かつ,パラメータ λ の指数分布に従う
E[Ti]=λ1,V[Ti]=λ21
P(Ti>t)=e−λt
指数分布の無記憶性
P(X>t+s ∣ X>s)=P(X>t)
を満たす確率分布は指数分布のみ
事象の発生確率がポアソン分布、事象の発生時間間隔は指数分布

例題3.2
事象の発生時間間隔–指数分布
P(Ti>t)=e−λt
(1) 2分以上
P(T≥2)=1−P(T<2)=1−(1−e−1)=0.3679
(2) 4分以内
P(T≤4)=1−P(T>4)=1−e−2=0.8647
n番目の事象が起こるまで時間 Sn が従う分布
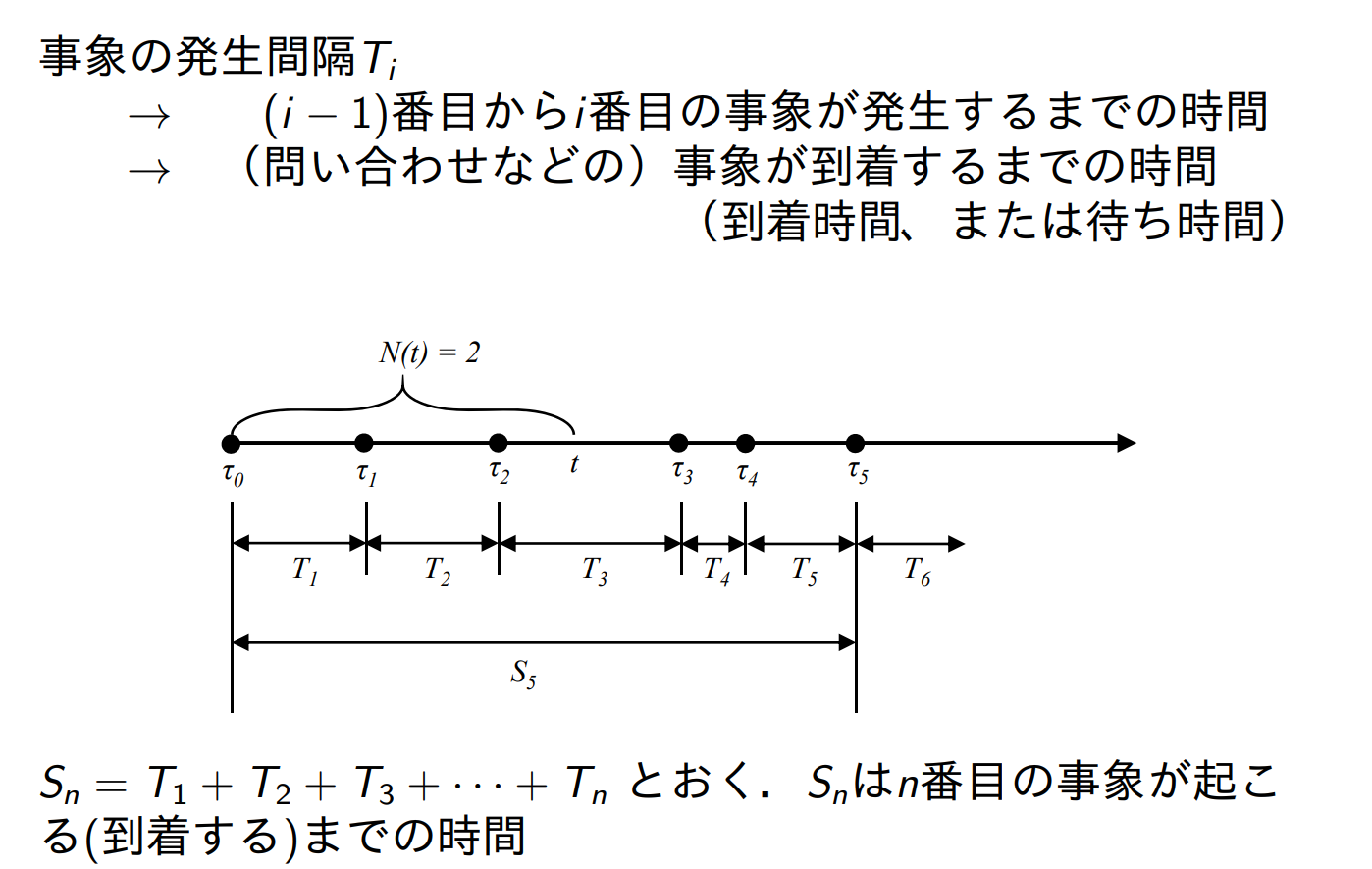
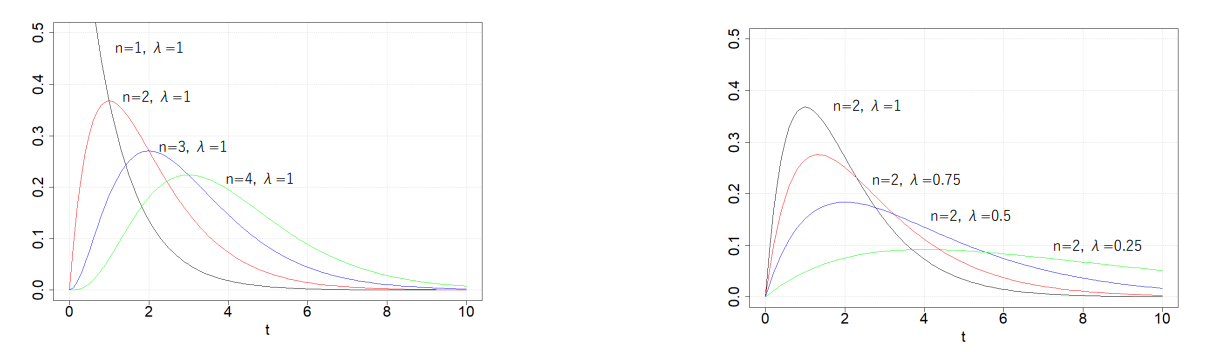
Sn はパラメータ n,λ のガンマ分布 gn,λ に従う
gn,λ(t)=λe−λt(n−1)!(λt)n−1,t≥0
E[Sn]=λn,V[Sn]=λ2n
例題3.3

(1) E[Sn]=λn より
E[S100]=1100=100
(2) P(Ti>t)=e−λt より
P(T101>2)=e−λt=e−2=0.1353
(3) Pk(t)=e−λtk!(λt)k,k=0,1,2,⋯ より
P(N(6)=0)=P0(6)=e−6=0.0025
例題3.4

[1] ポアソン分布
(1)
Pn(t)=e−λt⋅n!(λt)n
(2)
P0(T)=e−λt
[2] 一時間あたり受け取るメール数は λ=2448=2
(1) 事象の発生確率がポアソン分布に従う。
P3(6)=e−2∗6⋅3!(2∗6)3=0.00177
(2) 事象の発生時間間隔は指数分布に従う。P(Ti>t)=e−λt より
P(T≥2)=e−2∗2=0.01832
(3) 事象の発生確率がポアソン分布に従う。E[N(t)]=V[N(t)]=λt より
E[N(t)]=λt=E[N(3)]=2∗3=6
純出生過程
ポアソン過程の最も簡単な拡張を考える
- 独立性の仮定の除外
- 時間 t 内に起こる事象の発生数が j (状態 j )のとき、引き続く微小区間で新た1つ発生する確率が j に依存する場合を考える
状態遷移が隣り合う状態だけで起きる
に分けて考える
純出生過程
時刻 t で状態 j の時
- 十分小さい時間幅 h で j→j+1 に変わる確率 λjh+o(h)
- 十分小さい時間幅 h で j→j+1 以外に変わる確率 o(h)
- 変化しない確率 1−λjh+o(h)
ただし,各 λj は正数(出生率に相当)
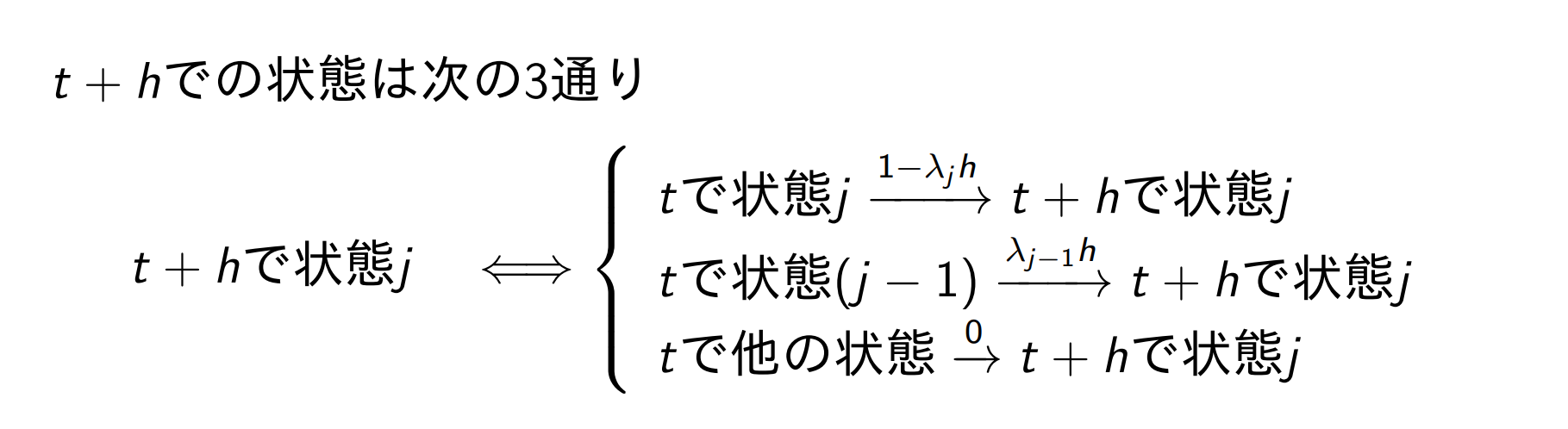
Pj′(t)=−λjPj(t)+λλj−1Pj−1(t),j=1,2,⋯P0′(t)=−λ0P0(t)
初期条件 P0(0)=1,Pj(0)=0,j=1,2,⋯ を用いて,
P0(t)=e−λ0t
となり,P1(t),P2(t) を順に求めることができる
ユール・ファーリ過程
λj=jλ,(λ>0) とすると,初期条件
Pj(0)=1,j=1Pj(0)=0,j=1
のもとで,Pj(t) は次式で表される.
Pj(t)=e−λt(1−eλt)j−1,j≥1
P0(t)=0. 線形出生過程ともいわれる
j=1∑∞Pj(t)=j=1∑∞e−λt(1−eλt)j−1=e−λt{1−(1−e−λt)1}=1
純死滅過程
時刻 t で状態 j の時
- 十分小さい時間幅 h で j→j−1 に変わる確率 μjh+o(h)
- 十分小さい時間幅 h で j→j−1 以外に変わる確率 o(h)
- 変化しない確率 1−μjh+o(h)
ただし,各 μj は正数(死亡率に相当)
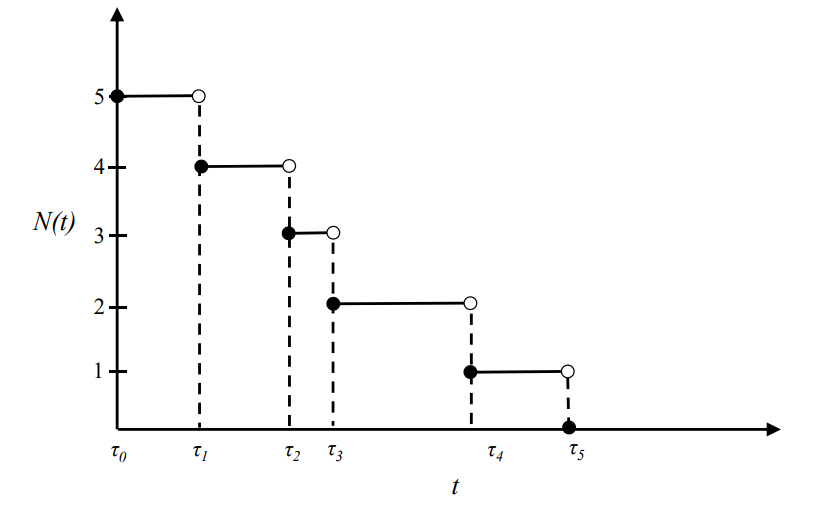

Pj′(t)=−μjPj(t)+μμj+1Pj+1(t),j=1,2,⋯Pn′(t)=−μnPn(t)P0′(t)=μ1P1(t)
初期条件 Pn(0)=1,Pj(0)=0,j=1,2,⋯ を用いて,
Pn(t)=e−μnt
となり,Pn−1(t),Pn−2(t),⋯,P0(t) を順に求めることができる
例題3.5

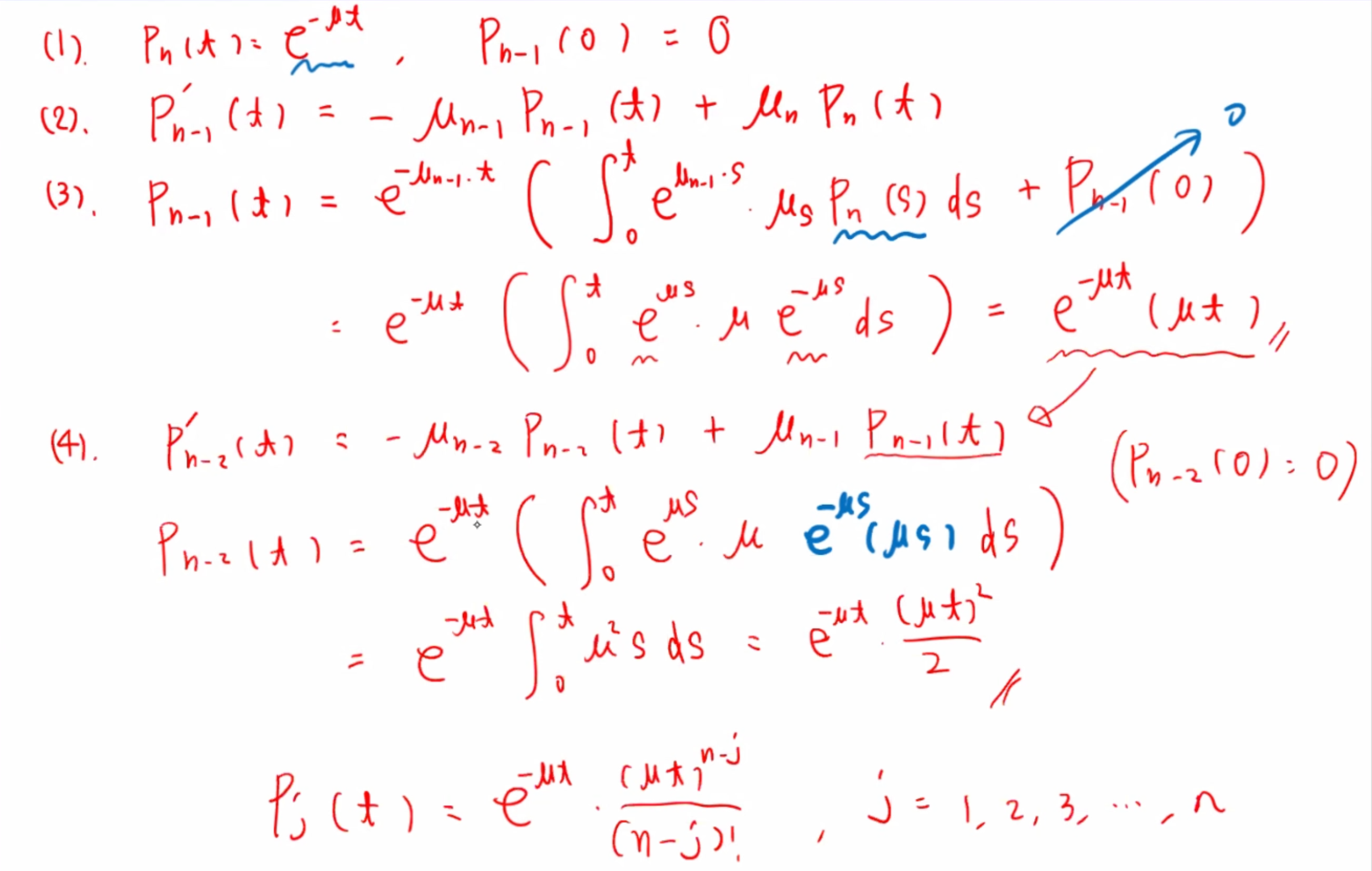
- 時刻0は Pn(0) 以外は全部0
- 通式:Pj(t)=e−μt⋅(n−j)!(μt)n−j,j=1,2,⋯,n
出生死滅過程
- 純出生過程では状態数の増加のみが発生
- 純死滅過程では状態数の減少のみが発生
実際のシステムでは,出生と死滅がランダムに発生する場合が多い
時刻 t で状態 j の時
- 十分小さい時間幅 h で j→j+1 に変わる確率 λjh+o(h)
- 十分小さい時間幅 h で j→j−1 に変わる確率 μjh+o(h)
- 隣以外に変わる確率 o(h)
- 変化しない確率 1−(λj+μj)h+o(h)

時間 t で状態 j にある確率を Pj(t) とおくと,次式を得る
dtdPj(t)=−(λj+μj)Pj(t)+λj−1Pj−1(t)+μj+1Pj+1(t)
t=0 で状態 i にあるとする.この時,初期条件は
Pj(0)=δij,δij={1,j=i0,j=i
に従う Pj(t) を Pi,j(t) とする
dtdPi,0(t)=−λ0Pi,0(t)+μ1Pi,1(t)dtdPi,j(t)=−(λi+μj)Pi,j(t)+λj−1Pi,j−1(t)+μj+1Pi,j+1(t)Pi,j(0)=1,j=iPi,j(0)=0,j=i
パラメータ {λj>0,μj+1>0.j=0,1,2,⋯} の出生死滅過程において,極限の推移確率
pj=t→∞limPi,j(t),i,j=0,1,2,⋯
が初期状態 i と独立に存在するための必要十分条件は
j=0∑∞aj<∞,aj=μjμj−1⋯μ1λj−1λj=2⋯λ0,a0=1
この時,極限の推移確率は次式となる
p0=(j=0∑∞)−1,pj=ajp0
例題3.6

(1) n 番目の事象が起こるまで時間 Sn が従う分布はガンマ分布なので
E[Sn]=λn=E[S180]=3180=60[min]
(2) P(Sn≤t)=P(N(t)≥n)=∑j=1∞e−λtj!(λt)j
P(S5>2)=1−P(S5≤2)=e−6(1+6+2!62+3!63+4!64)=0.2851
(3) 事象の発生時間間隔–指数分布
P(T4≤0.5)=1−P(T4≥0.5)=1−e−3∗0.5=0.7769
例題3.7

待ち行列
待ち行列理論の発展
- 1838: ポアソン分布 ランダムに発生するイベントの統計分布
- 1900前半: アーランの計算 ポアソン分布を電話の呼び出しが発生する確率に応用し,電話がつながらない確率などを計算(待ち行列理論の始まり)
- 1953: ケンドールの記号 ケンドールの記号を導入し,待ち行列理論を分類・整理
- 1957: ジャクソンによるネットワーク問題の解析 待ち行列理論を組み合わせたネットワークの問題を解析(空港の手続きのようにチェックインで並び,セキュリティ検査で並び,というような引き続き起こる待ち行列モデルの解析)
- 1961: リトルの公式 リトルが待ち行列,待ち時間に関する一般的な公式を導出
待ち行列モデル
待ち行列理論(Queueing Theory):不確定な需要と供給という両面から待ちができる行列モデルを数学モデルとして扱う
- スーパーのレジ台
- 到着する客が支払いサービスを受ける
- サービスが終わると出ていく
- 順番を待っている次の客がサービスを受ける
- 情報処理センターのスパコン
- 到着するジョブが処理のサービスを受ける
- 終わって空きができると次のジョブが処理を受ける
客、ジョブの到着、支払い/処理のサービス時間は偶然に変化する.どのようにシステムを設計する?
- 客:サービスを受けようとする個々の要求
- 窓口:サービスを提供するもの
- 待ち行列:サービス中の客を除いた実際の待ち行列
- システム:サービス中の人も含めた全体の待ち行列
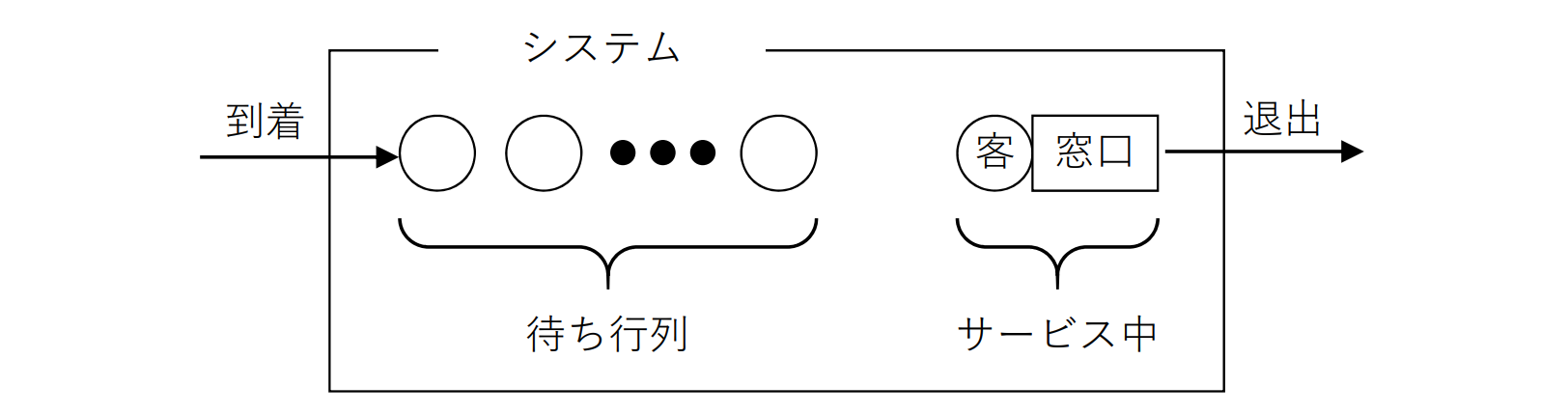
行列が一つでサービス窓口が一つの場合を単一待ち行列という(行列が一つで窓口が複数の場合は複数待ち行列)
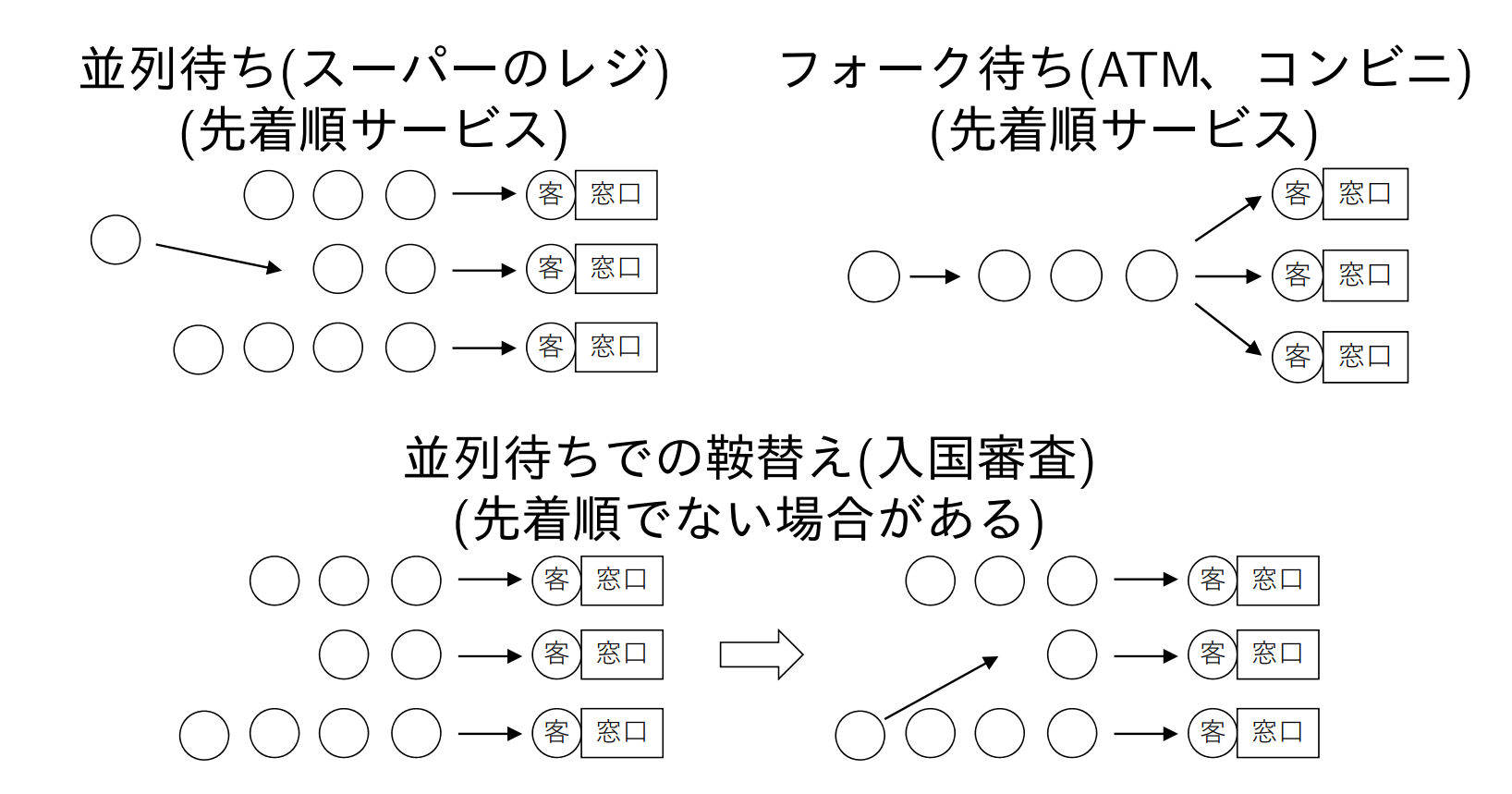
ケンドールの記号
- A:客はどれくらいの間隔で到着する?
- B:サービスの時間はどれくらいばらつく?
- C:窓口の数?
- K:行列の上限は?
ケンドールの記号: A/B/C/K もしくは A/B/C(K)
この表記の場合,
- 母集団(システムに来る客の数)は ∞(=m)
- 待ち行列のルールは先着順(First Come, First Served) (=Z)
全て書き出す場合は,
A/B/C/K/m/Z
と表される
客の到着(A)/サービス時間(B)
ポアソン到着(記号:M)
- 到着がパラメータ λ のポアソン過程に従う
- 到着時間間隔は指数分布に従う
F(t)=1−e−λt,t>0
一定分布(記号:D)
- 到着間隔が t=λ で一定
F(t)={0,t≤λ11,t≥λ1
一般分布(記号:G)
- 到着間隔は独立で同一の分布 F(t) に従う
単一待ち行列モデル
M/M/1(INF)
- 客の到着:パラメータ λ のポアソン分布
- サービス時間:パラメータ μ の指数分布
- 窓口の数:1つ
- 行列の上限:制限なし
客の到着を個体の出生,サービスを受けて退出することを死亡とすると,M/M 型待ち行列モデルは
λi=λ,μi+1=μ(i=0,1,2,⋯)
の出生死滅過程で定式化でき,極限の推移確率 pj を求めることができる
極限の推移確率が存在するための必要十分条件は
j=0∑∞aj<∞,aj=μjμj−1⋯μ1λj−1λj=2⋯λ0=(μλ)j,a0=1
ρ=μλ とおくと,∑j=0∞ρj<∞ であるから,ρ<1 でなければならない.この時,
j=0∑∞ρj=1−ρ1<∞
これは,到着率(=出生率) λ がサービス率(=死亡率) μ より小さいときである
ρ<1 の時,極限の推移確率は,
pj=ajp0=ρjp0,p0=(j=0∑∞aj)−1=(j=0∑∞ρj)−1=1−ρ
これはシステム内に j 人の客(1人のサービス中の客 +(j−1) 人の待ち行列の客)がいる確率を表している.ここで,
ρ=μλ=サービス率到着率=1/λ1/μ=平均到着時間間隔平均サービス時間
はトラフィック密度もしくは利用率と呼ばれる
システム内のいる客の平均値および分散は,
L=E(X)=j=0∑∞j×pj=1−ρρ
Var(X)=E(X2)−E(X)2=(1−ρ)2ρ
待ち行列の平均の長さは,サービス中の客を除いた平均の待ち行列の長さであるから,
Lq=j=1∑∞(j−1)×pj=L−(1−p0)=L−ρ=1−ρρ2
リトルの公式
待ち人数 = 待ち時間 × 到着率
システム内の客の平均待ち時間を W,待ち行列での客の平均待ち時間を Wq とすると,
L=λWLq=λWq
が成り立つ.したがって
W=λ1L=μ(1−ρ)1(平均系内時間)Wq=λ1Lq=μ(1−ρ)ρ(平均待ち時間)
待ち行列で用いられる特性値

注:7的待ち行列での客の平均待ち時間为 Wq
M/M/1(N)
パラメータ λi=λ,μi+1=μ,有限状態 i=0,1,⋯,N からなる出生死滅過程を考える.
j=1,2,⋯,N−1 においては,
dtdPi,0(t)=−λPi,0(t)+μPi,1(t)dtdPi,j(t)=−(λ+μ)Pi,j(t)+λPi,j−1(t)+μPi,j+1(t)Pi,j(0)=1,j=iPi,j(0)=0,j=i
が成り立つ.j=N における境界条件を考えると
dtdPi,N(t)=λPi,N−1(t)−μPi,N(t)
が成り立つ.
出生死滅過程の極限の推移行列が存在するための条件は,
j=0∑∞aj<∞,aj=μjμj−1⋯μ1λj−1λj=2⋯λ0=(μλ)j,a0=1
であるが,有限状態の出生死滅過程では常に満足することが明らか ∑j=0Naj<∞ である.従って,
pj=ρjp0
ただし,
p0+p1+⋯+pN=j=0∑Npj=1
需要注意的是,与 M/M/1(∞) 不同的是,M/M/1(N) 并没有 ρ<1 的条件
ρ=1 の時,
p0(1+N)=1↔p0=1+N1
ρ=1 の時,
p0(1+ρ+⋯+ρN)=ρ(1−ρ1−ρN+1)=1↔p0=1−ρN+11−ρ
よって
pj=⎩⎪⎪⎨⎪⎪⎧1+N1,1−ρN+11−ρρj,ρ=1ρ=1
pN=1−ρN+11−ρρN呼損率(棄損率)
システム内にいる客の平均値は ρ=1 に対して,
L=j=0∑Nj×pj=1−ρρ1−ρN+11−(N+1)ρN+NρN+1
ρ が十分小さく ρN≃0,ρN+1≃0 とできる場合は,
L=1−ρρ1−01−(N+1)0+N0
となり近似的に M/M/1(∞) モデルの L と同じになる.
待ち行列の平均長さは,
Lq=j=1∑N(j−1)×pj=1−ρρ21−ρN+11−NρN−1+(N−1)ρN
ρ=1 に対しては,
L=j=0∑Nj×pj=1+N12N(N+1)=2N
Lq=j=1∑N(j−1)×pj=L−(1−p0)=2(N+1)N(N−1)
M/M/1(N) 待ち行列モデルでもリトルの公式は成り立つ.ただし,システムに N 人の客がいるとき,新たに待ち行列に加わることができないため,実質到着率 λa は
λa=j=0∑N−1pjλ=(1−PN)λ=1−ρN+1λ1−ρN,ρ=1
システム内の客の平均待ち時間を W,待ち行列での客の平均待ち時間を Wq とすると,
W=λa1L=μ(1−ρ)11−ρN1−(N+1)ρN+NρN+1(平均系内時間)Wq=λa1Lq=μ(1−ρ)ρ1−ρN1−NρN−1+(N−1)ρN(平均待ち時間)
例題4.1

複数待ち行列モデル
M/M/s(INF)
- 客の到着:パラメータ λ のポアソン分布
- サービス時間:パラメータ μ の指数分布
- 窓口の数:s(s=2,3,⋯)
- 行列の上限:制限なし
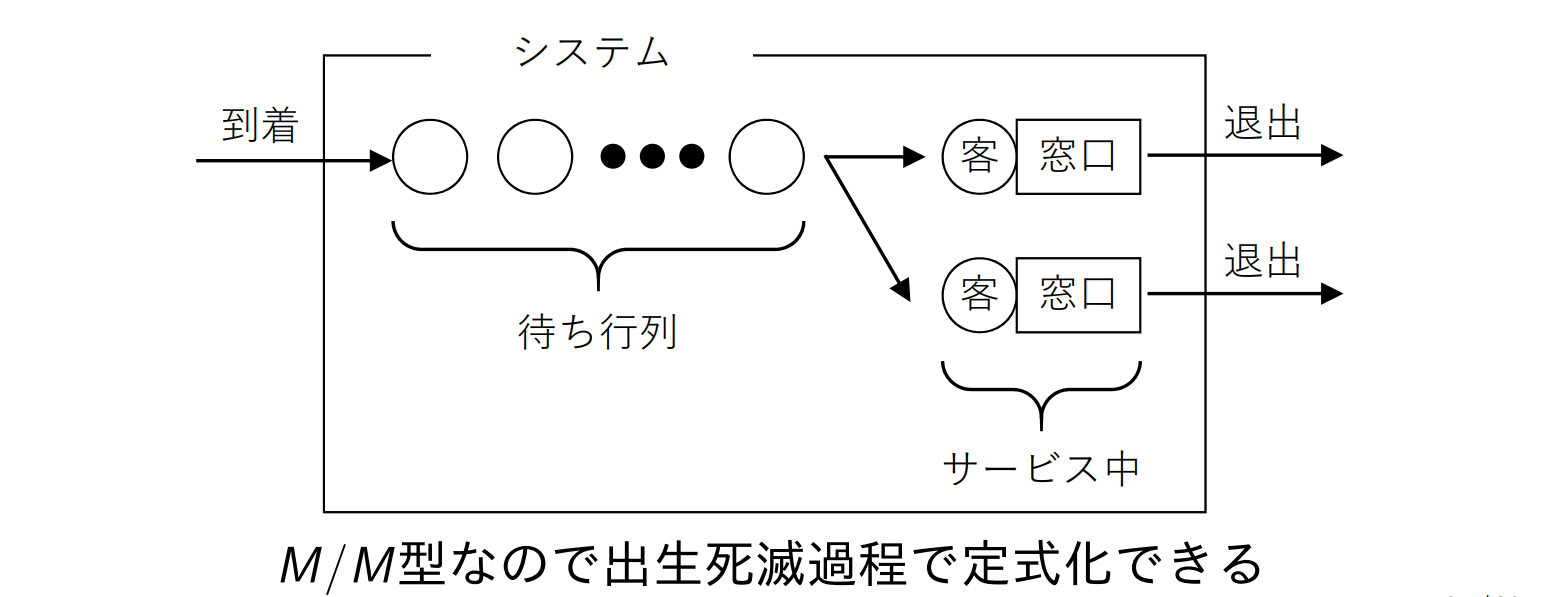
サービス率 μk は,窓口の数によって異なる.システム内に k 人の客がいた場合,
μk={kμ,k≤ssμ,k>s
となり,客の数が窓口数よりも多いか少ないかでサービス率が異なる
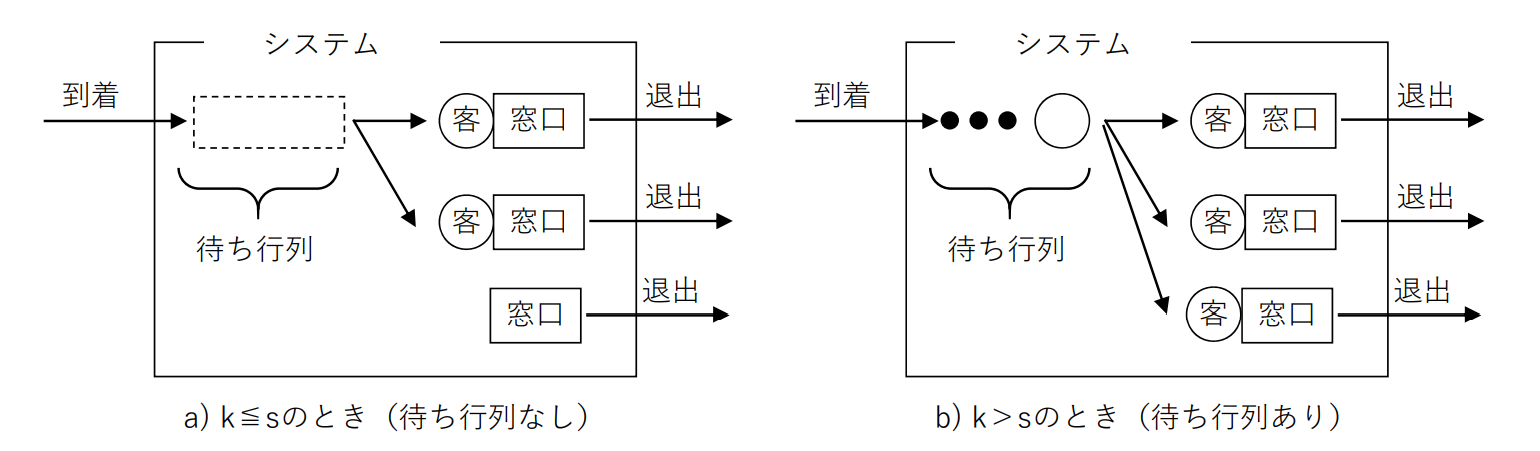
極限の推移確率が存在するための必要十分条件は
j=0∑∞aj=j=0∑∞k=1∏jμkλk−1=j=0∑s−1j!uj+s!usn=0∑∞ρn<∞,u=μλ,ρ=sμλ
であるから,ρ<1 でなければならない.この時,極限の推移確率は,
pj=⎩⎪⎪⎨⎪⎪⎧j!ujp0,j≤ss!us(su)j−sp0,j>s
p0=[j=0∑s−1j!uj+s!(1−ρ)us]−1
待ち行列の平均の長さ Lq は,窓口の個数が s であるから,
Lq=j=s∑∞(j−s)pj=p0s!us(0+1ρ+2ρ2+⋯)=s!(1−ρ)2p0usρ
システム内にいる客の平均値 L は
L=j=0∑∞jpj=j=0∑s−1j!ujp0+j=s∑∞s!us(su)j−sp0=u+Lq
実質到着率 ∑k=0∞λkpk=λ より,リトルの公式から
W=λ1L(平均系内時間)Wq=λ1Lq(平均待ち時間)
M/M/s(N)
- 客の到着:パラメータ λ のポアソン分布
- サービス時間:パラメータ μ の指数分布
- 窓口の数:s(s=2,3,⋯)
- 行列の上限:N−s
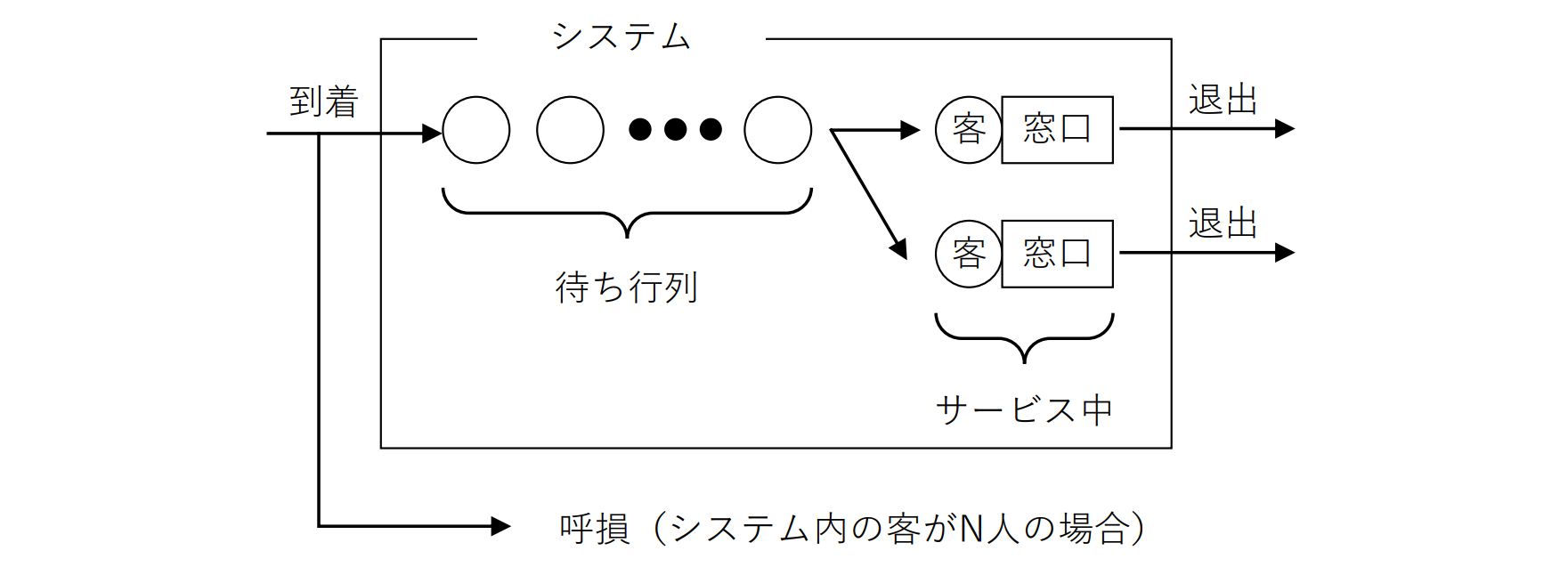
1≤j<s のとき
pj=j!ujp0,u=μλ
s≤j≤N のとき
pj=s!us(su)j−sp0
p0=[j=0∑s−1j!uj+s!us((1−ρ)1−ρN−s+1)]−1
待ち行列の平均の長さ Lq は,窓口の個数が s であるから,
Lq=j=s∑∞(j−s)pj=s!us(1−ρ)2ρp0{1−[(N−s)(1−ρ)+1]ρN−s}
システム内にいる客の平均値 L は,
L=j=0∑∞jpj=Lq+μλPN
リトルの公式から
W=λ1L(平均系内時間)Wq=λ1Lq(平均待ち時間)
例題4.2

例題4.3

平均サービス率を固定して,平均到着率を変化させる. ρ が大きくなるにつれて待ち行列は長くなる.特に0.9を超えると急激に増加する
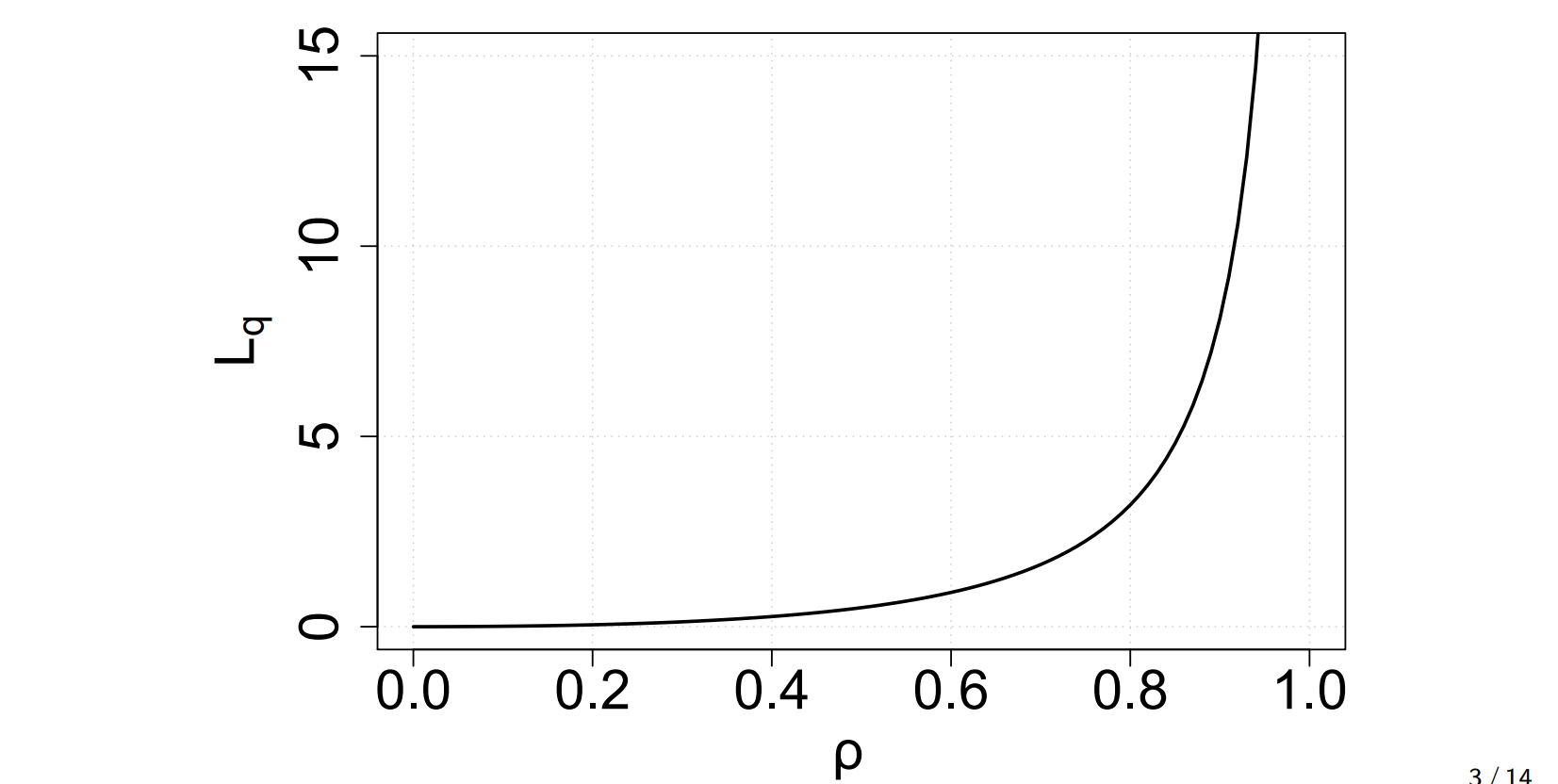
例題4.4

乱数
エージェントモデルシミュレーション
参考