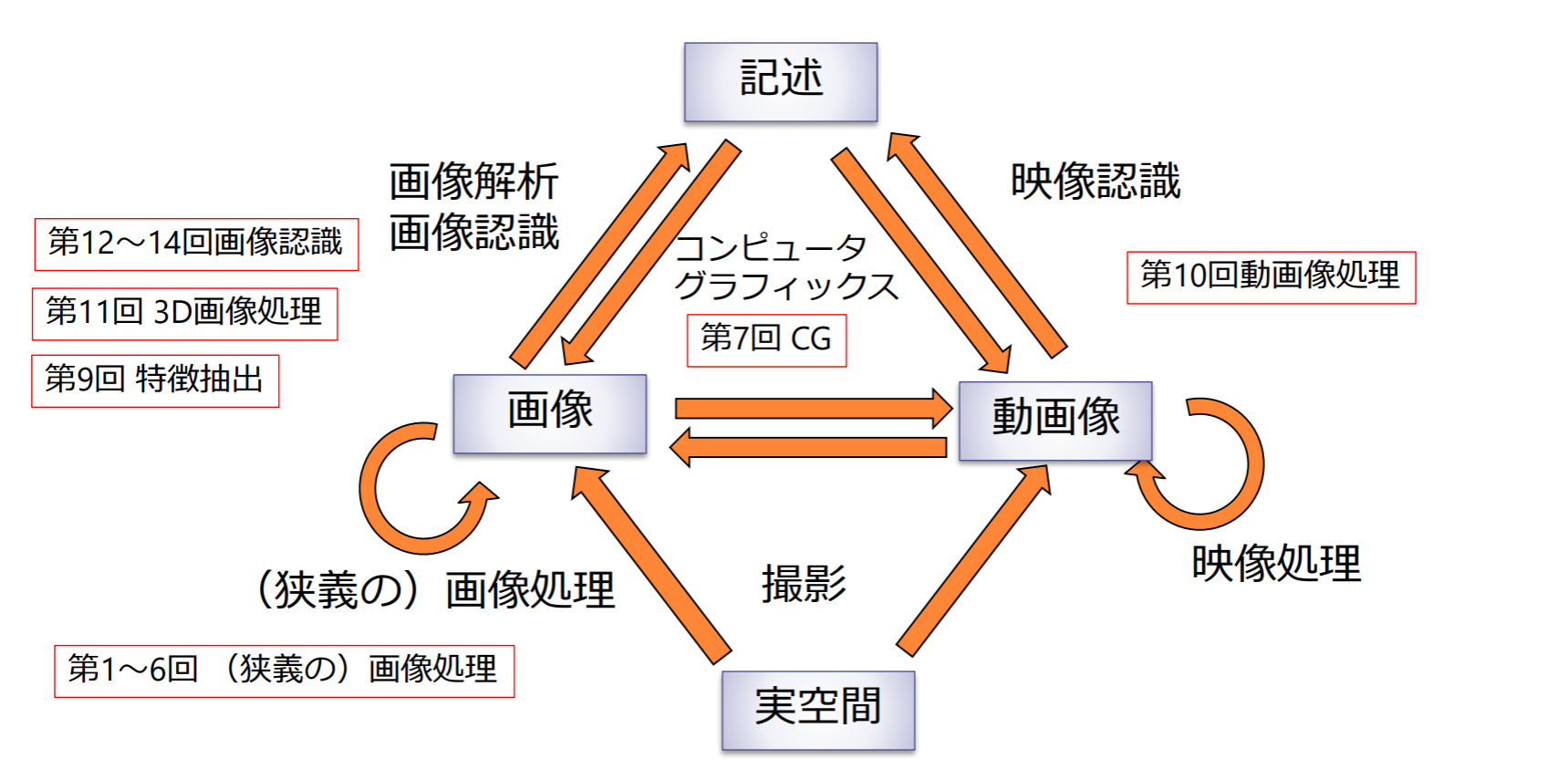
- 1. 画像処理紹介
- 2. デジタル画像
- 3. 空間フィルタリング(spatial filtering)
- 4. 二値画像処理
- 5. 画像の空間周波数解析
- 6. 画像の幾何変換
- 7. CGの基礎
- 8. 特徴抽出
- 9. 動画像処理
- 10. 3次元画像処理
- 11. 画像分類
- 12. 物体検出
- 13. 深層学習
CS专业课学习笔记
画像処理紹介
目とカメラの類似性
| 機能 | 眼 | カメラ |
|---|---|---|
| 光を集める | 水晶体 | レンズ |
| 光量の調節 | 虹彩(瞳孔) | 絞り・シャッター |
| 光センサー | 網膜 | 撮像素子 フィルム |
| ピント調節 | 水晶体の厚みを変える | レンズと撮像素子の距離を変える |
視野角と画角
- 視野角 (viewing angle):一度に見ることができる範囲(両眼を使うことで180度程度あると言われている)
- 画角 (field of view):カメラはレンズを変えることで視野角を変える
- 広角レンズ,魚眼レンズ,360度カメラ
絞りとシャッター
- 露出:レンズを通る光の量
- 絞り:光の通る孔の大きさを調整する機構
- シャッター:光センサーへの照射時間を調整する機構
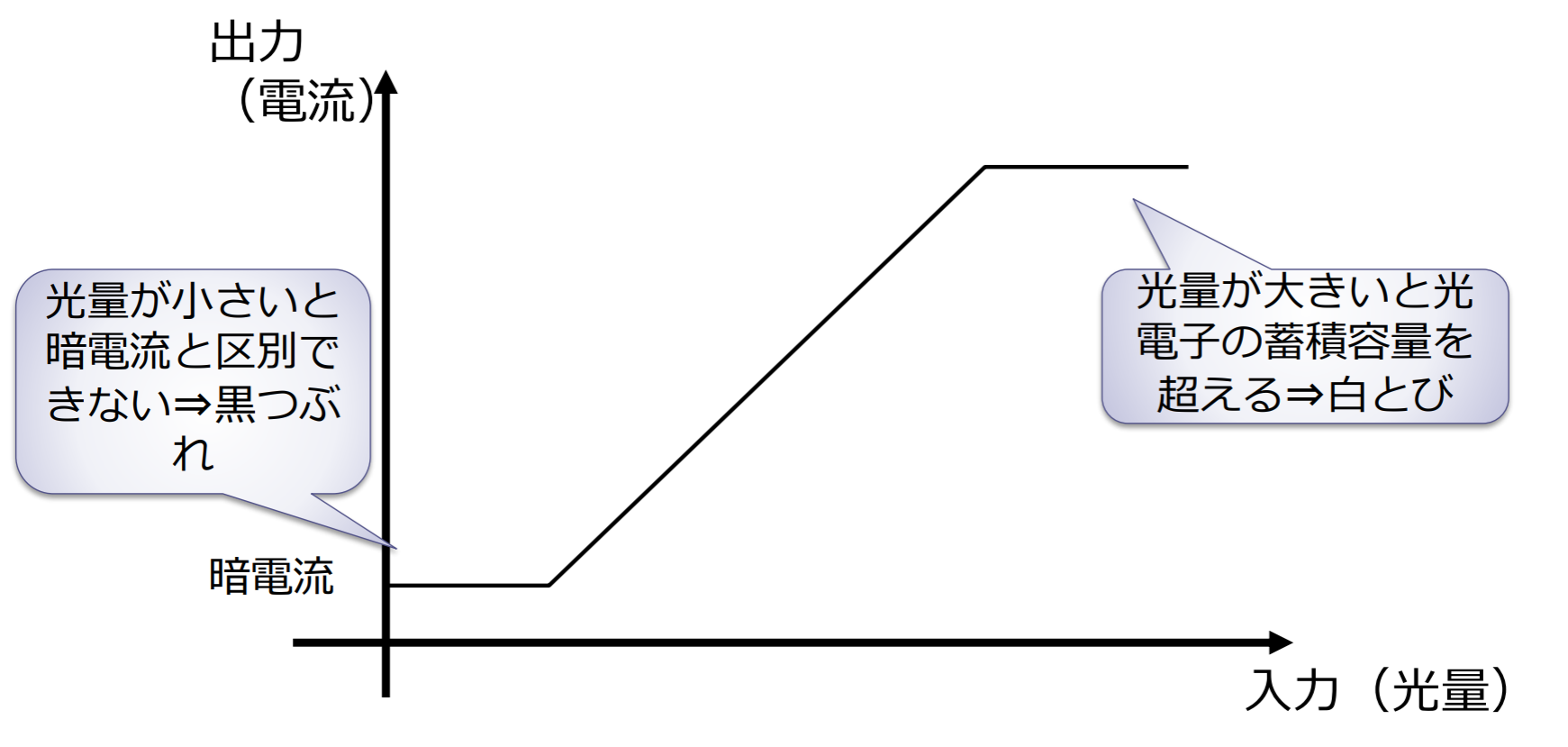
- 露出制御
- 「黒つぶれ」:写真の中にある暗い部分が真っ黒になる現象
- 「白とび」:明るい部分を真っ白になる現象
イメージセンサ
- CCD (Charge Coupled Device)イメージセンサ:光強度を電圧に変換する受光素子(フォトダイオード) を格子状に配置した撮像素子
- 単板式カラーCCD:1枚のCCDでカラー画像を撮像する方式.各画素毎に異なる色フィルタを配置する
加法混色と減法混色
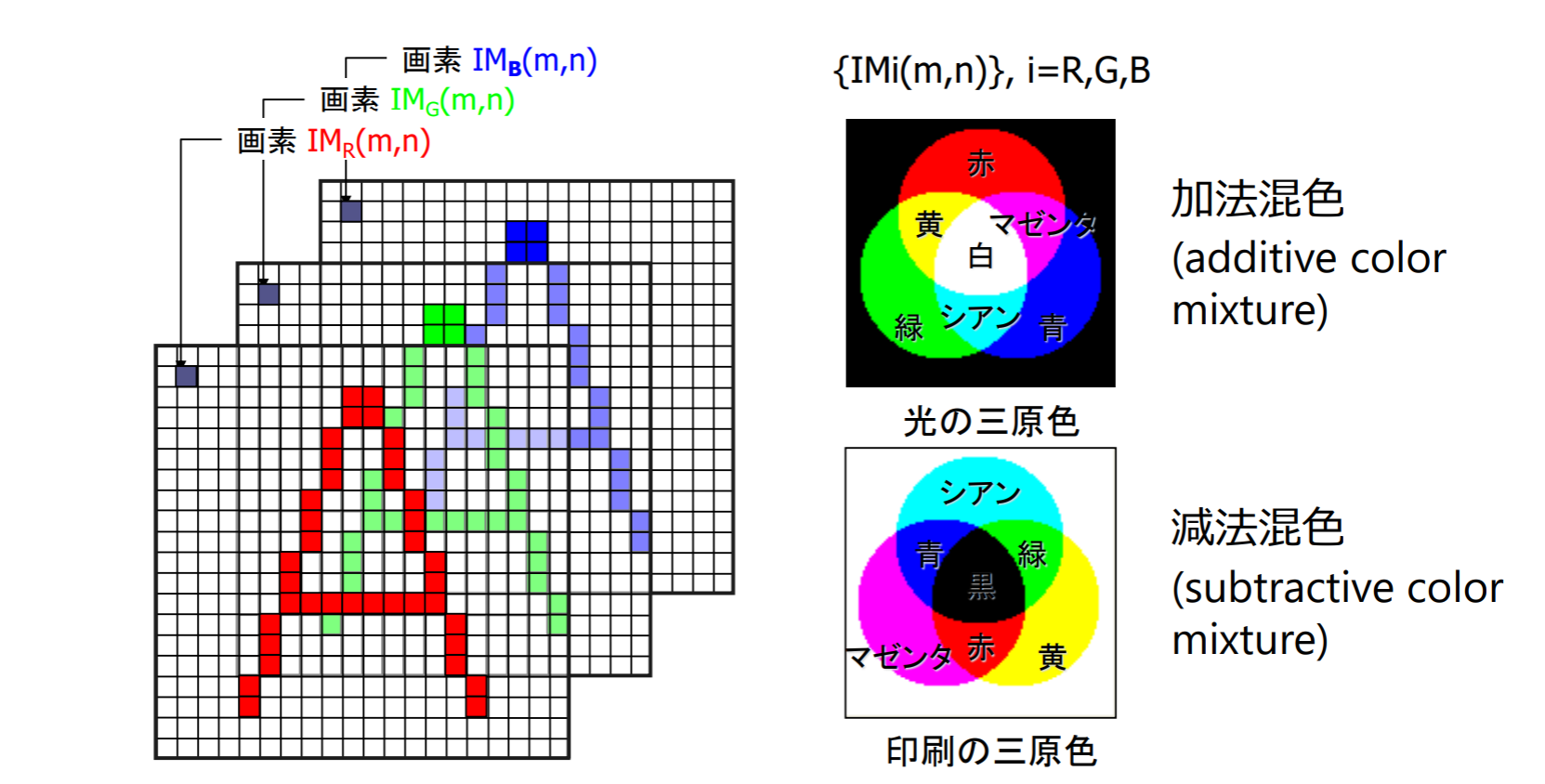
- プリンタ等で用いられる色:CMY
- 三原色を混合することで様々な色を合成できるのは、赤・緑・青の各波長に感度を持つ錐体と呼ばれる3種類の視細胞が人にはあるからである
白いスクリーン上に異なる色の光を重ねて投影することで,別の色を作るような混色を加法混色(additive color mixture)という.この混色における代表的な三原色が赤, 緑,青である
白い紙の上で絵の具を混ぜ合わせて別の色を作るような混色や,色付きフィルタを通して白色光を見せるような混色を減法混色(subtractive color mixture)という.この混色における代表的な三原色はシアン, マゼンタ,黄色である
画像処理の三つの役割
- 人間の視覚機能を拡大する
- 肉眼では見にくいもの,見えないものを見えるようにする
- eg. X線画像,CT画像による体の内部の可視化
- 人間の視覚機能を代行する
- 人間ができることをコンピュータに代行させて省力化する
- eg. 防犯カメラの不審者検知
- 人間の視覚機能に訴える
- 言葉で表現するのが難しいことを画像・映像を使って分かり易く伝える,魅力的に見せる,楽しく伝える
- eg. SNSにおける写真加工・画像共有
デジタル画像
コンピュータ内部データ表現
コンピュータ内部表現: 数値を要素としてもつ2次元配列

グレースケール画像(濃淡画像)は,明るさを持つ点(画素またはピクセル(pixel)とよぶ)から構成される
- グレースケール画像: 一つの画素に一つの数値が対応

- 二値画像: 一つの画素が一つの数値に対応
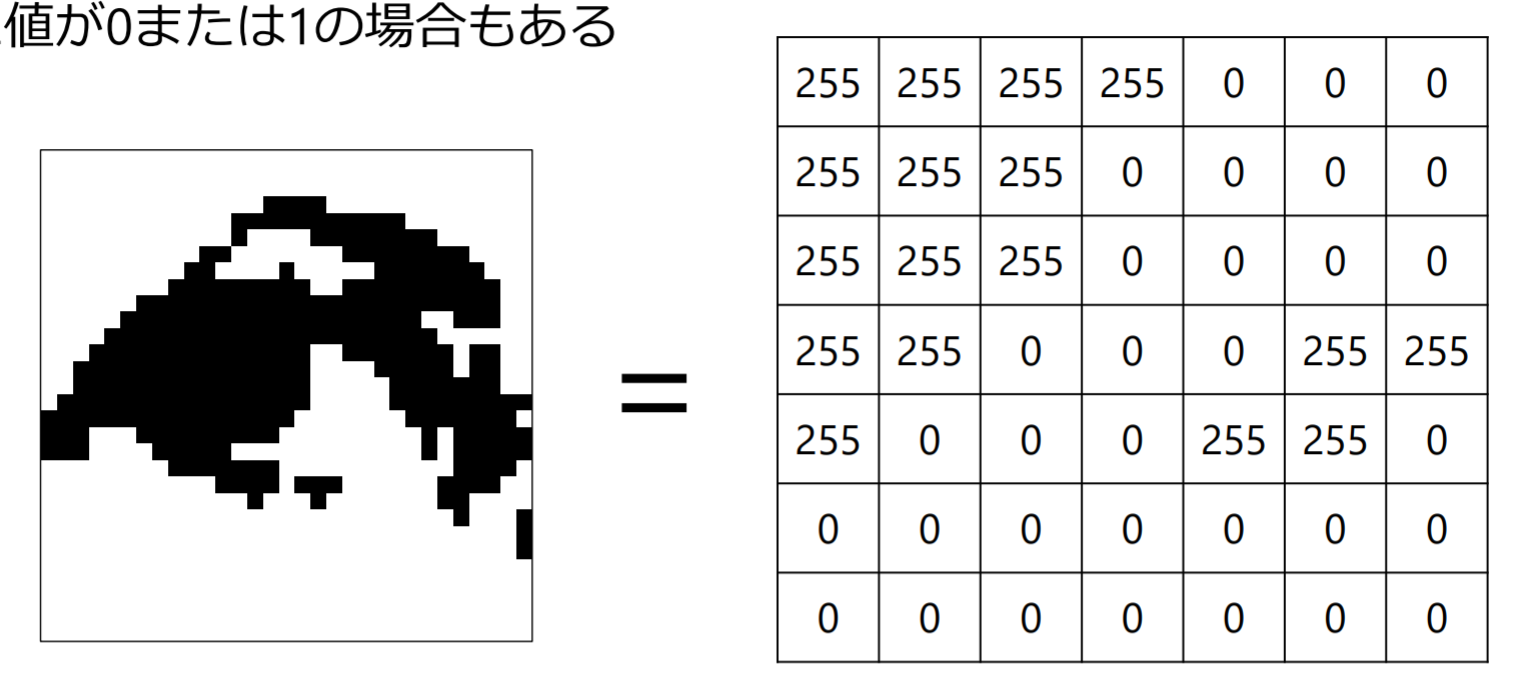
- カラー画像: 一つの画素に三つの値(R, G, B)が対応する
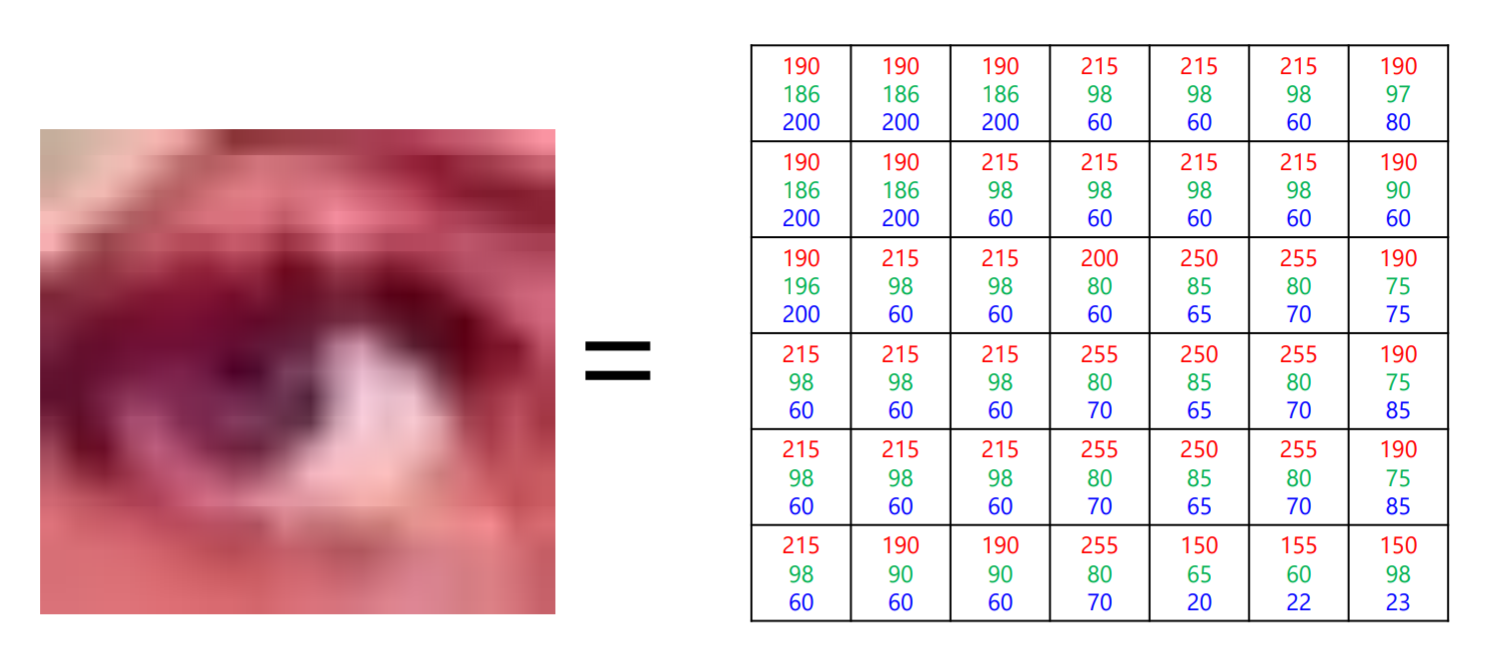
画像座標系
- グレースケール画像:2次元配列
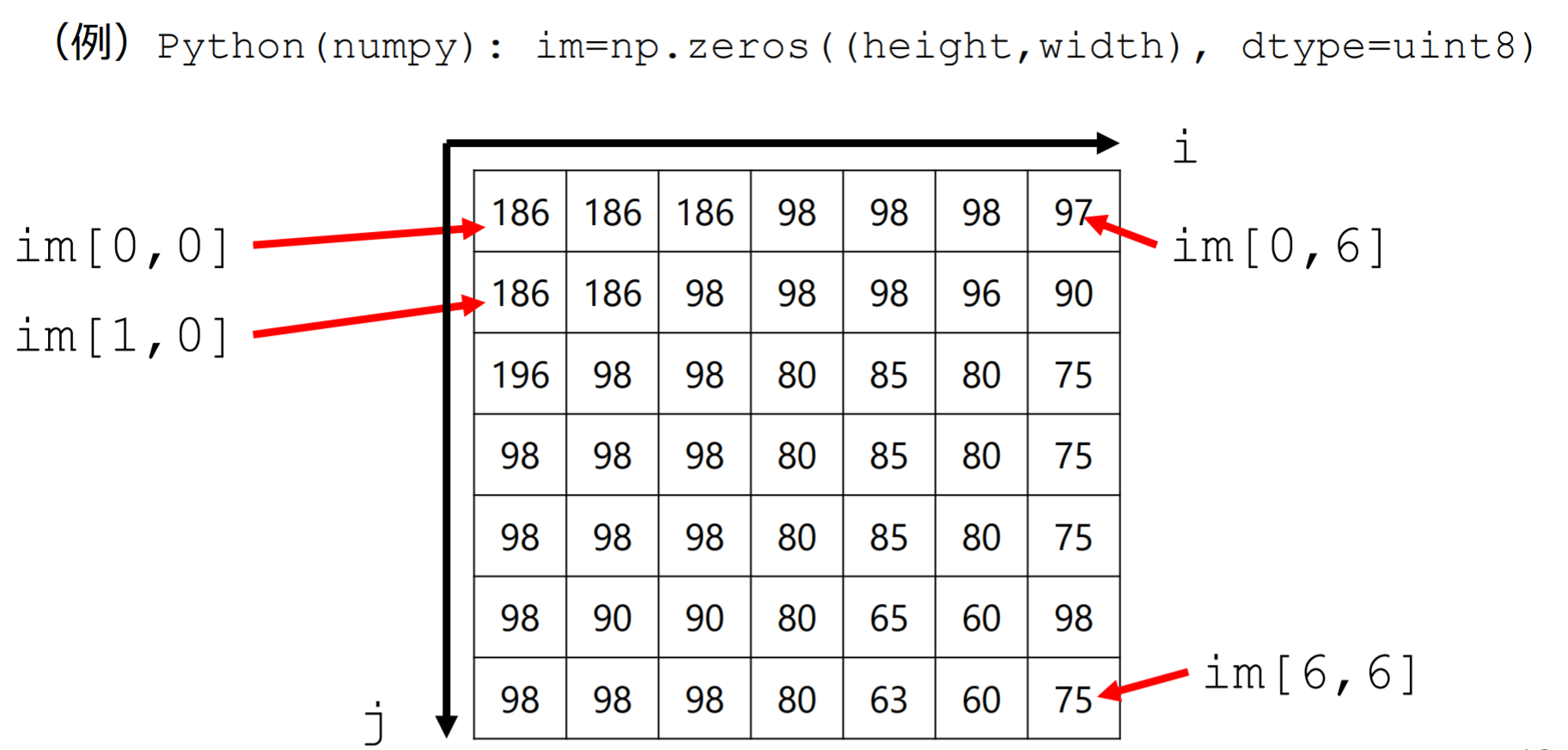
特别需要注意:(height, width)
- カラー画像

色の配列順序はライブラリやOS依存
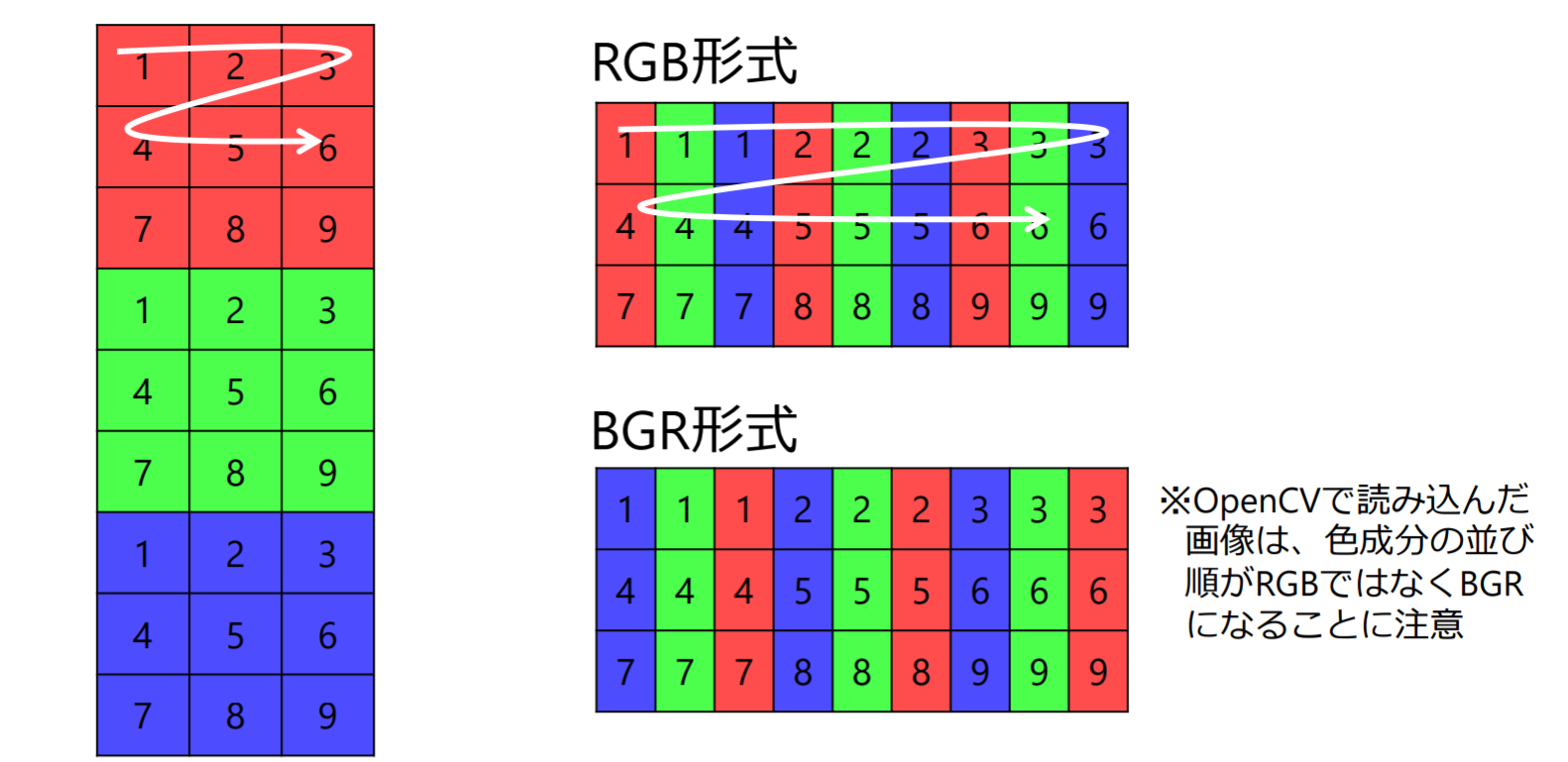
代表的な画像ファイルフォーマット
- ファイル保存:多次元の配列のままで良い?
- 縦・横の画素数,ビット数などが不明 ヘッダにメタデータを記録
- データ量が大きい 冗長性を削減して圧縮
- 画像ファイルフォーマット
- BMP – Microsoft Windows Bitmap Image
- GIF – Graphics Interchange Format
- JPEG, JPG – Joint Photographic Expert Group
- PNG – Portable Network Graphics
- TIFF, TIF – Tagged Image File Format
例題2.1
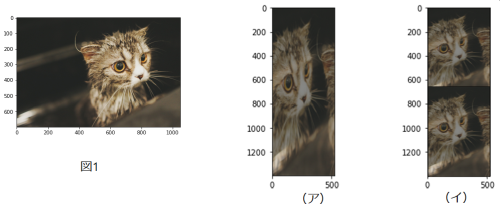
画像の幅・高さを とする。画素の並びを変えないで、配列のサイズを としたときに生成される画像は(ア)、(イ)のいずれか?
- (ア),从 (height, width) 即可判断
画像のデジタル化
標本化と量子化
- 離散化(discretization):連続量であるアナログ信号を離散的な値にする
- 標本化(sampling):離散的な位置(標本点)における明るさ(アナログ値)を取り出す処理
- 量子化(quantization):明るさ(アナログ値)を離散化する処理
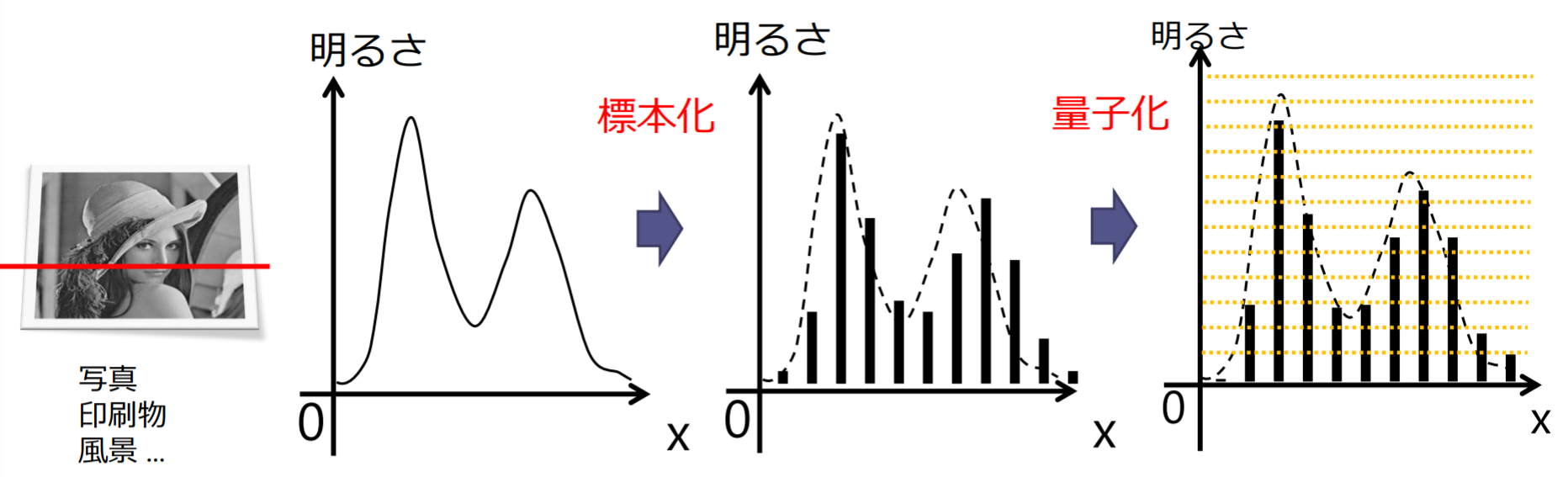
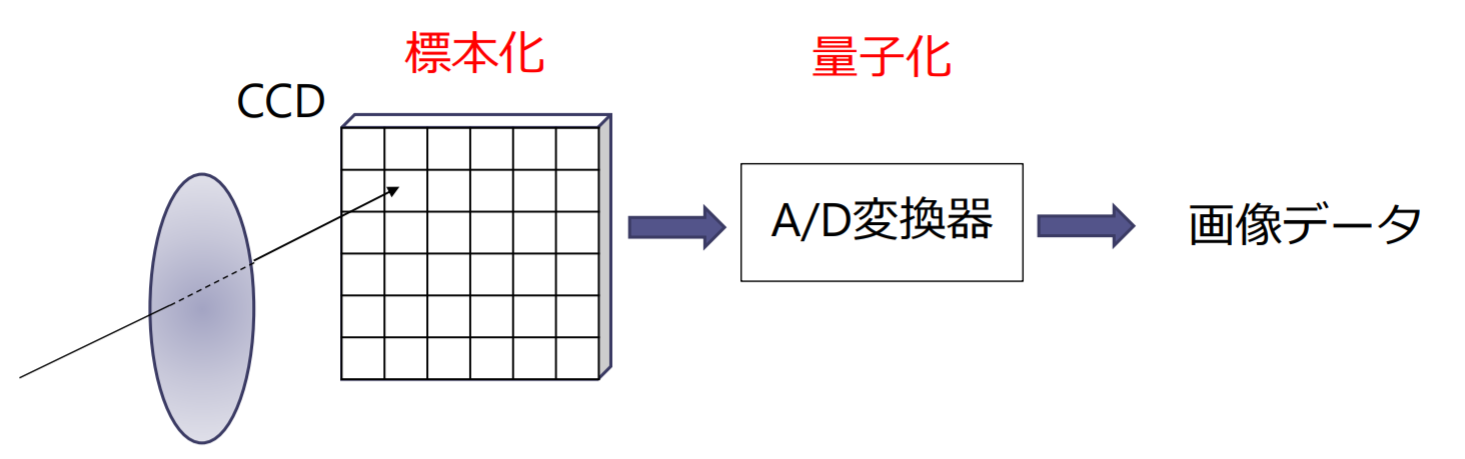
デジタルカメラにおける画像の標本化と量子化:
- 標本化:撮像素子(CCD)に受光素子(フォトダイオード)が離散的な位置における光強度を電圧に変換する
- 量子化:撮像素子が出力する電圧信号をA/D(Analog to digital)変換器が離散化し画素値を出力する
解像度と画像品質
解像度(resolution):画像を構成する格子の細かさ(標本点の数)デジタルカメラ画像の場合は縦横の画素数
- 標本化間隔を広げると,格子の数が減り,画素数が減る

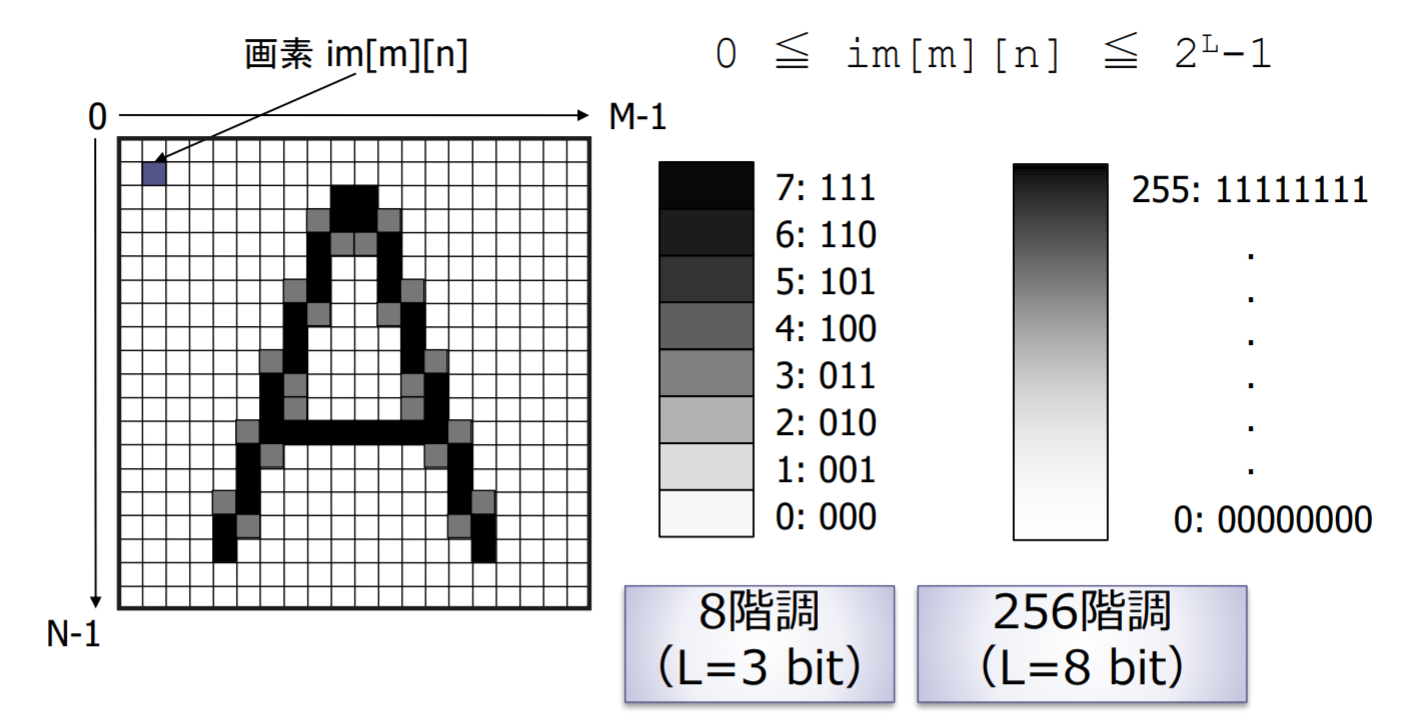
階調数と画像品質
階調:明るさ(色)の量子化のレベル数。この数が大きいほど細かな色や明るさの違いを表現できるが、画素あたりのデータ量は増大する

画像の性質を表す諸量
| 諸量 | 意味 |
|---|---|
| 最小値(minimum)・最大値(maximum) | ある画像の画素値のなかで,最小と最大の値.ヒストグラムを調べることで取得できる |
| 平均値(mean) | |
| 中央値(median) | ヒストグラムを求め,画素値の小さい方から 番目の画素値 |
| 最頻値(mode) | ヒストグラムを求め,最も頻度が高い画素値 |
| 分散(variance) |
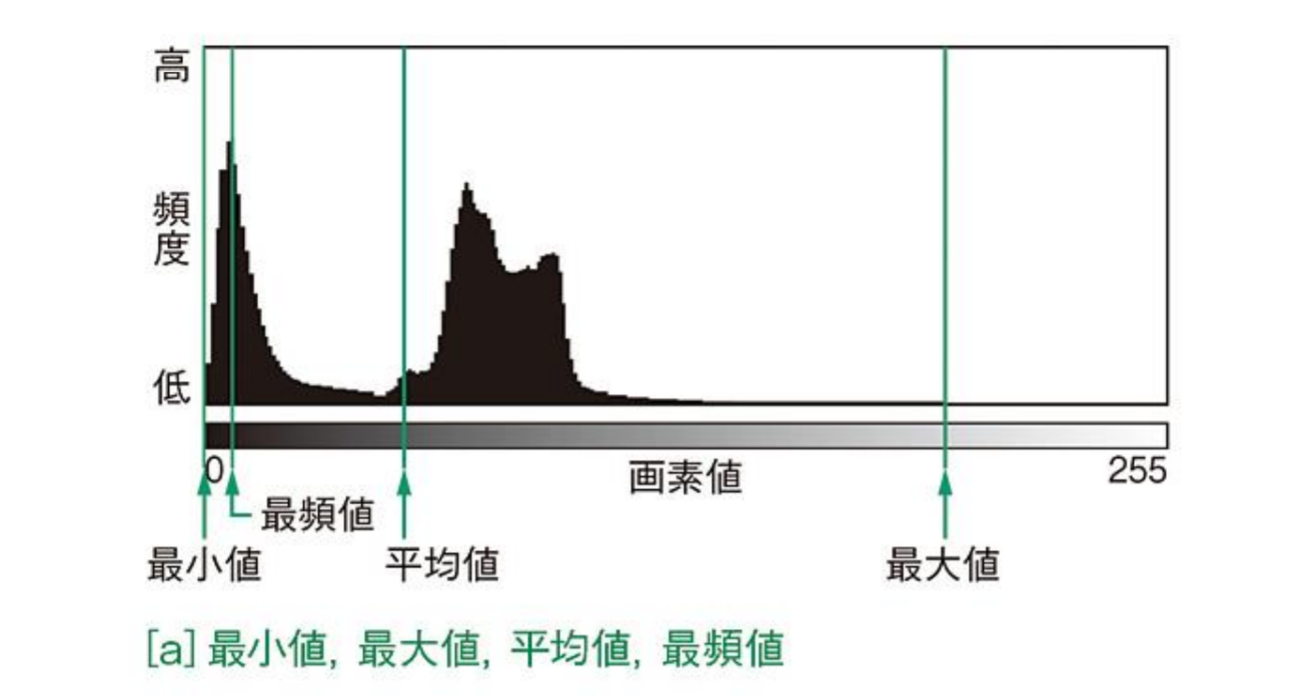
輝度(濃度)ヒストグラム
ヒストグラム(histogram):横軸に画素値を,縦軸にそれぞれの輝度値を持つ画素の数をとったグラフ
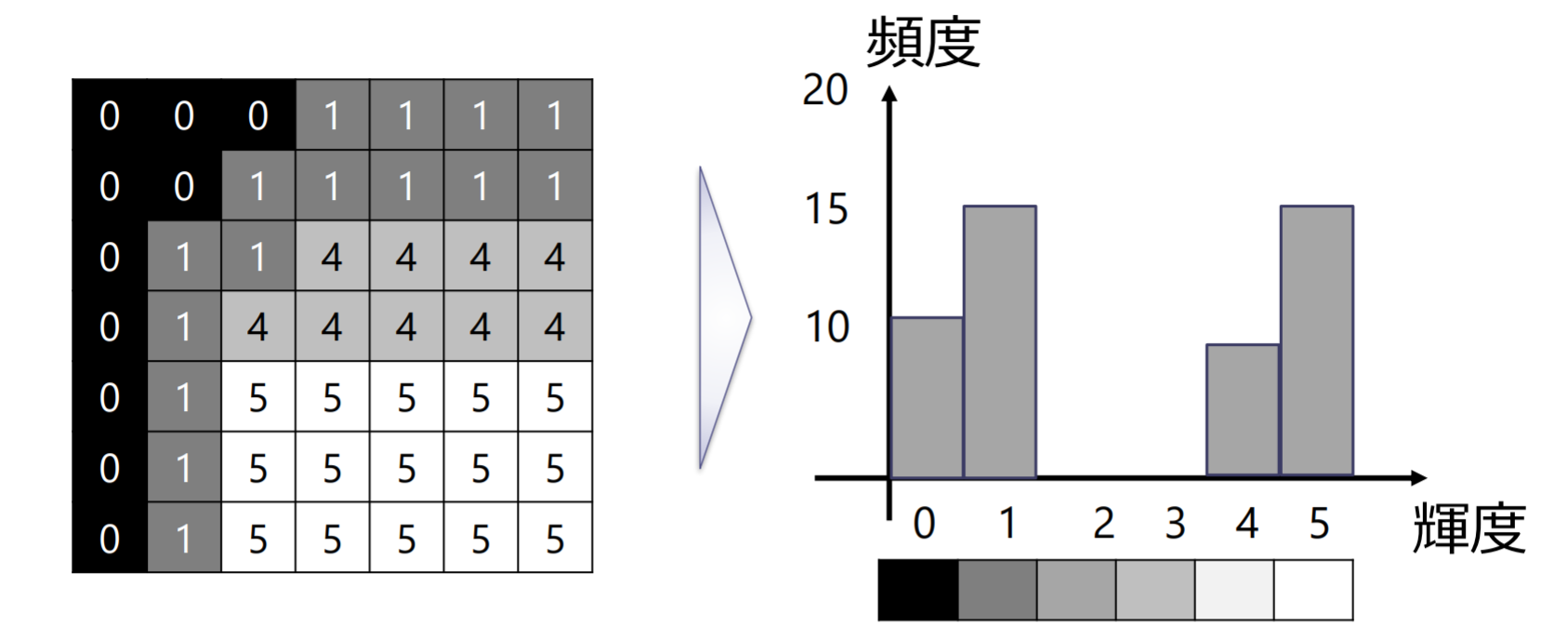
コントラスト
コントラスト(contrast):画像のヒストグラムの分布の広がり
- ヒストグラムが広い範囲に分布し,画像中の明暗差が大きな画像をコントラストが高い画像と呼ぶ
- 尺度の例:

シャープネス
シャープネス(sharpness):画像を見たときに感じる鮮鋭感を表す尺度.鮮鋭度が高い画像は,エッジ付近の画素値変化が急激で,細かな部分まで鮮明に観察できる
- エッジ部分の画素値変化を調べる方法と,空間周波数に対する振幅の変化を計測する方法がある

例題2.2
以下の画像 に対応する輝度ヒストグラムを(ア),(イ),(ウ)から選びなさい

- は夜景で黒に近い画素が多いので(ア)と判断できる
- はホワイトボードの面が大きな面積を占めており,光の反射で明るくなったり,黒い文字が見えるが,画素値の変動幅は に比べて小さいので(ウ)が適切と考えられる
- :(イ)
階調変換(濃淡変換)
- 階調変換関数h: 入力画像の画素値 を出力画像の画素値 に変換する関数
- トーンカーブ(tone curve): 階調変換関数をグラフであらわしたもの
ネガ・ポジ反転
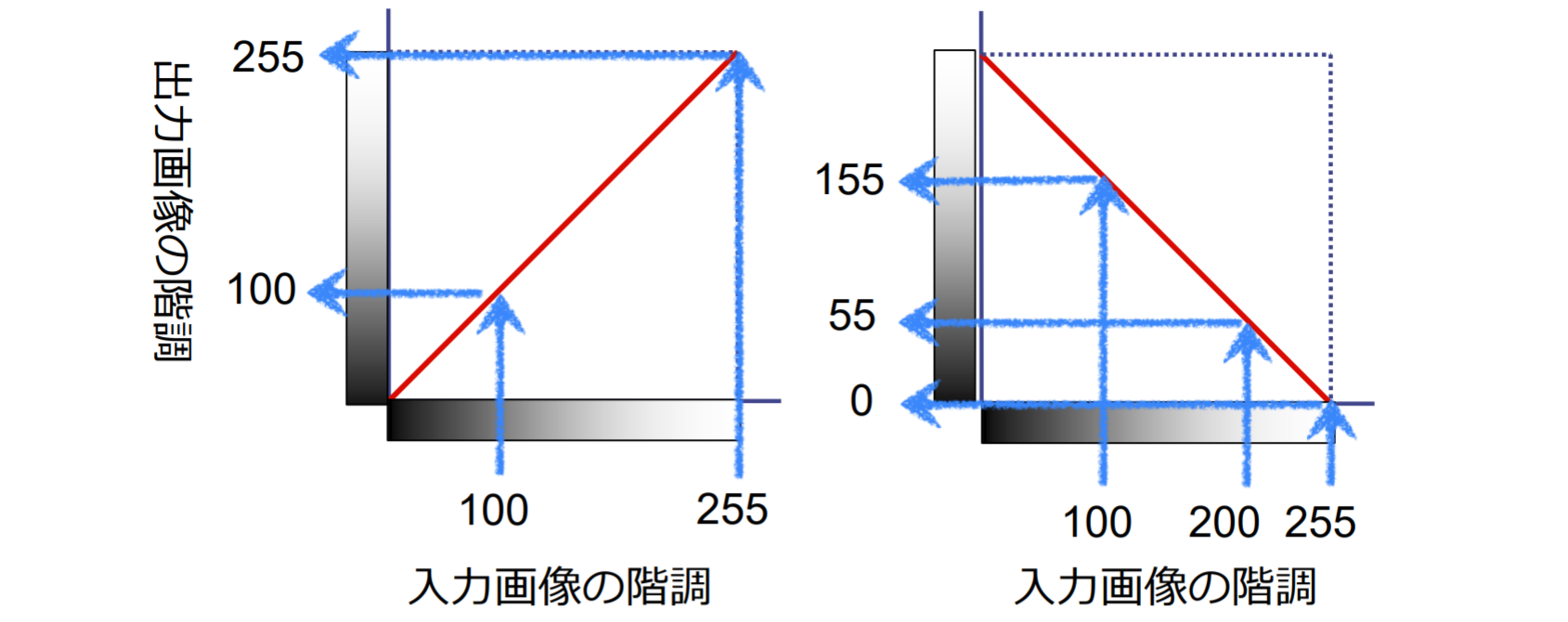
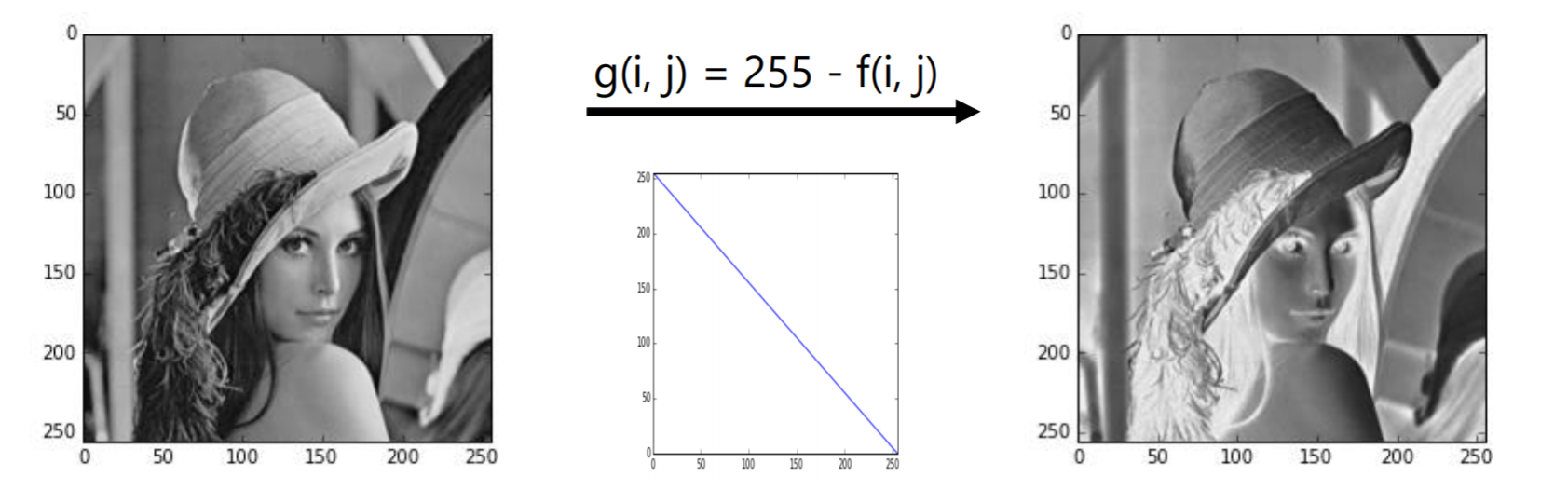
ポスタリゼーション
ポスタリゼーション(posterization):階段状のトーンカーブによる変換.トーンカーブが水平な部分では出力画素値が同じ値になるため,出力画素値が数段階に制限される
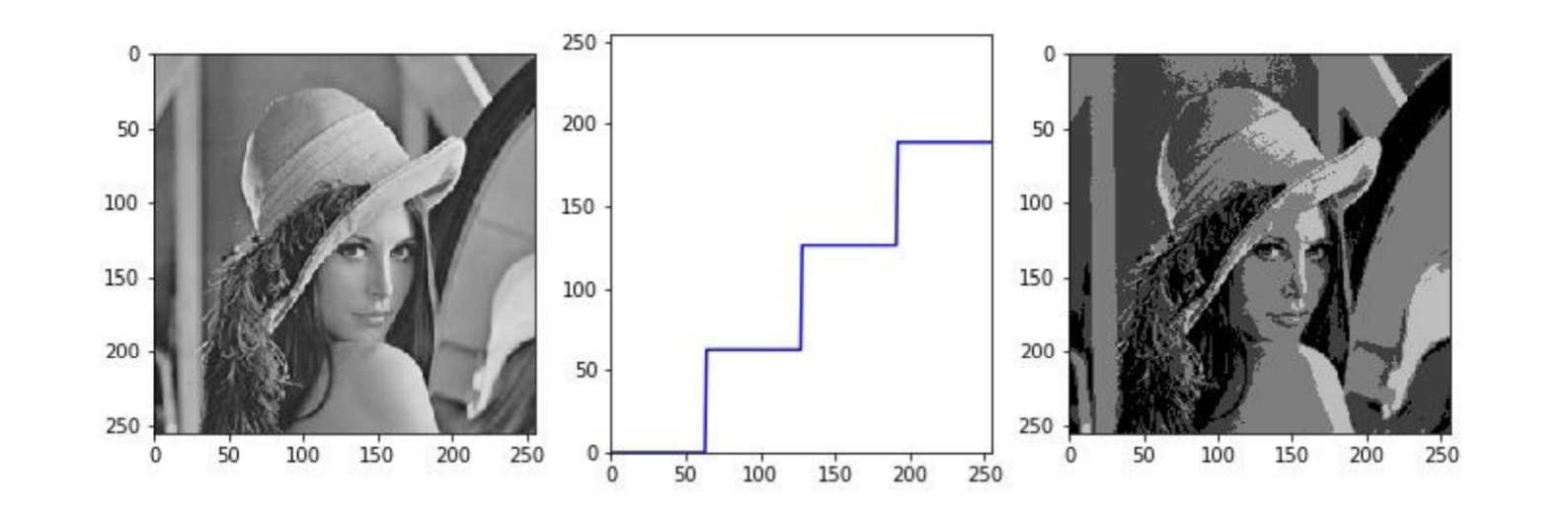
二値化
二値化 (binarization):階調を2段階に制限することで二値画像に変換
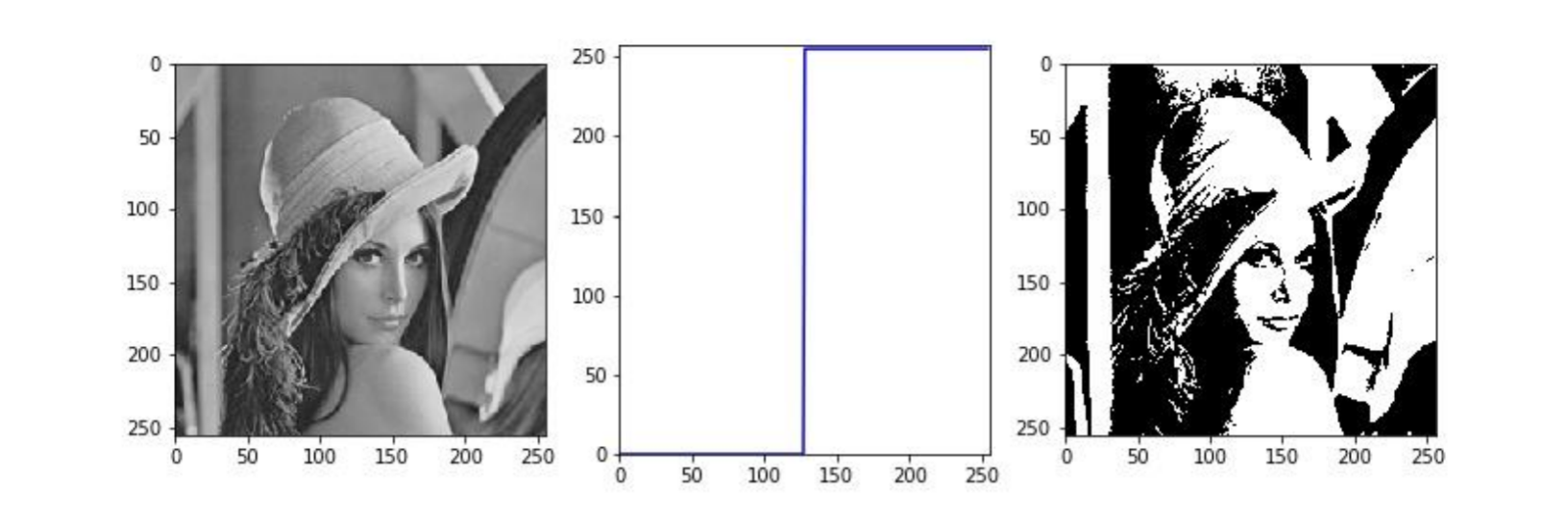
ソラリゼーション
ソラリゼーション(solarization):非単調なトーンカーブによる階調変換.元は写真制作時の暗室テクニック
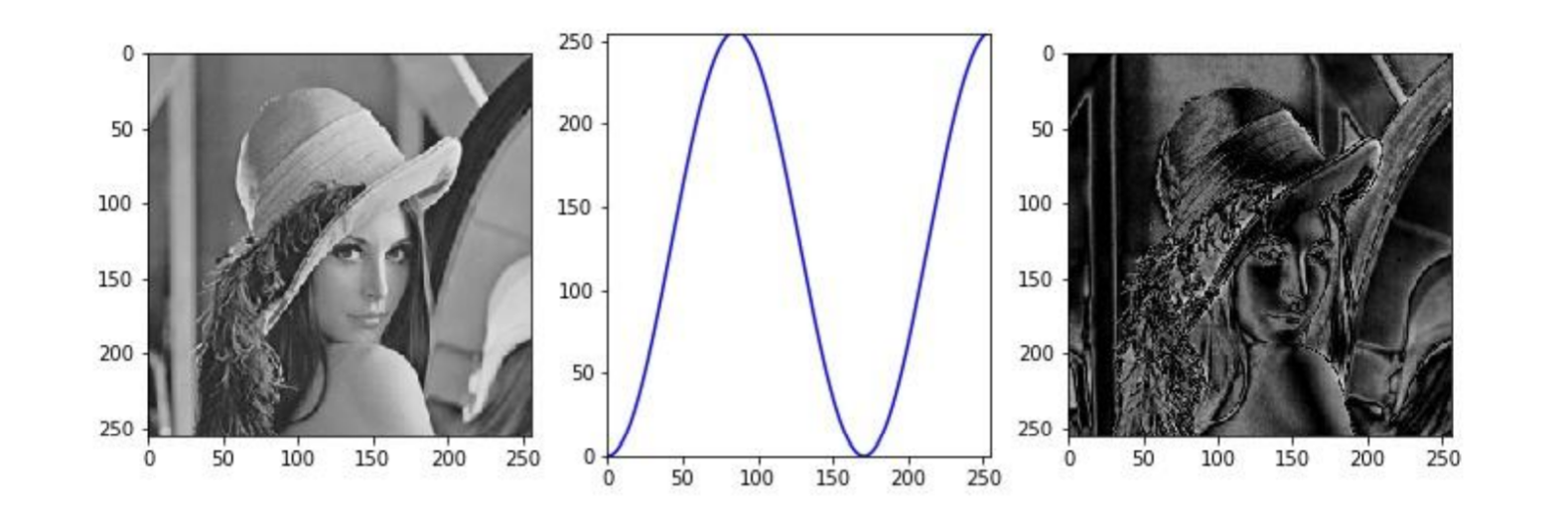
コントラストを改善する
コントラスト:画像のヒストグラム分布の広がり(画像中の明暗差)を改善する
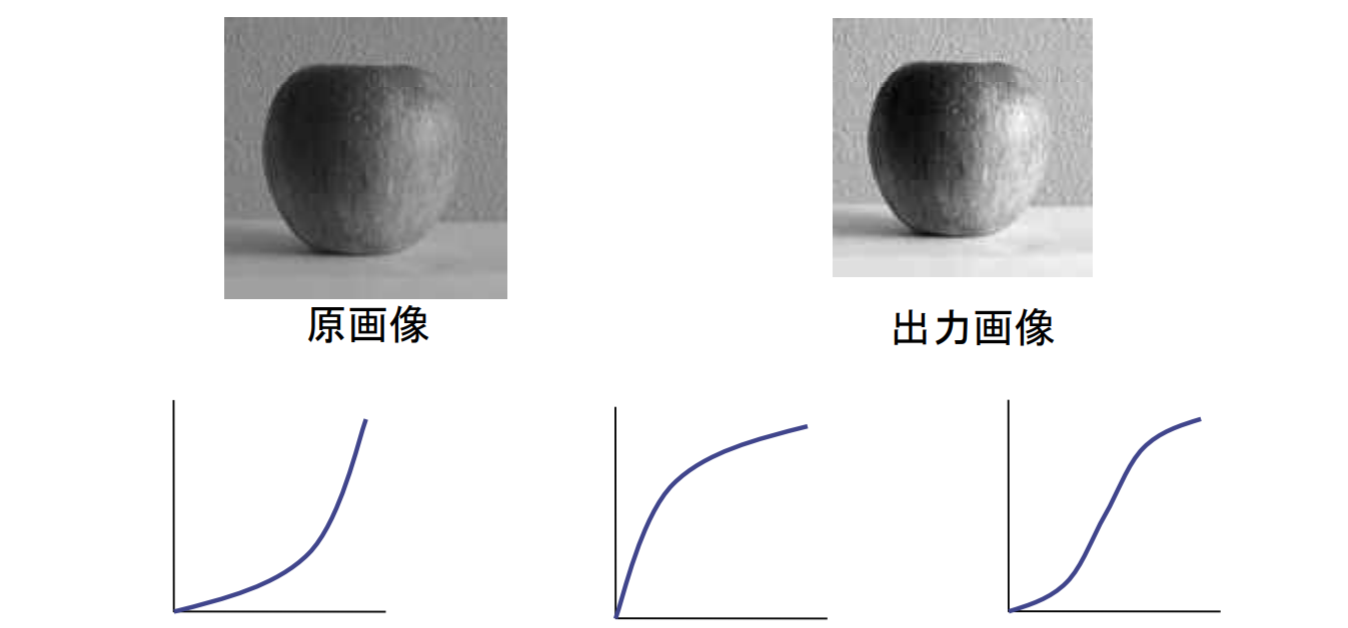
ガンマ補正
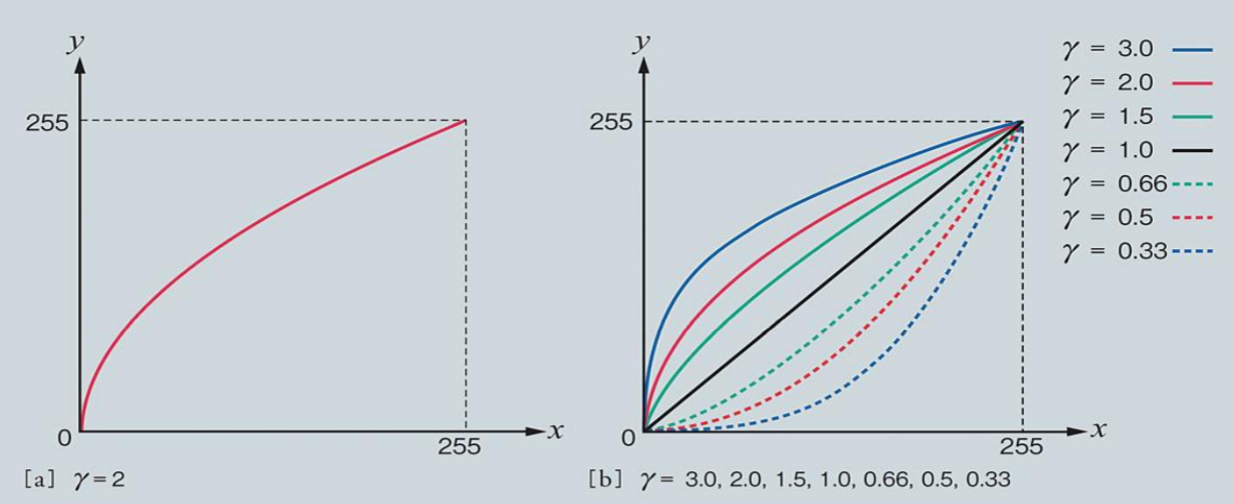

例題2.3
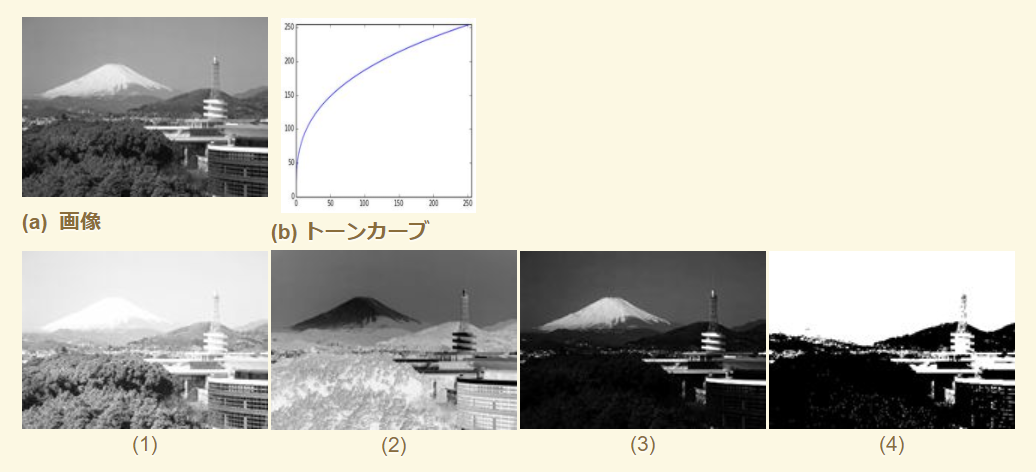
- (b)に示すトーンカーブは上に凸の関数なので,入力画像の画素値が引き上げられ,全体的に明るくなるため、以下に示す画像(a) を,(b) に示すトーンカーブを用いて階調変換した結果の画像は(1)
- 二値化画像は(4)
- ネガ・ポジ反転は,明るい領域が暗くなる.富士山の頂が暗くなっているため、(2)がネガ・ポジ反転
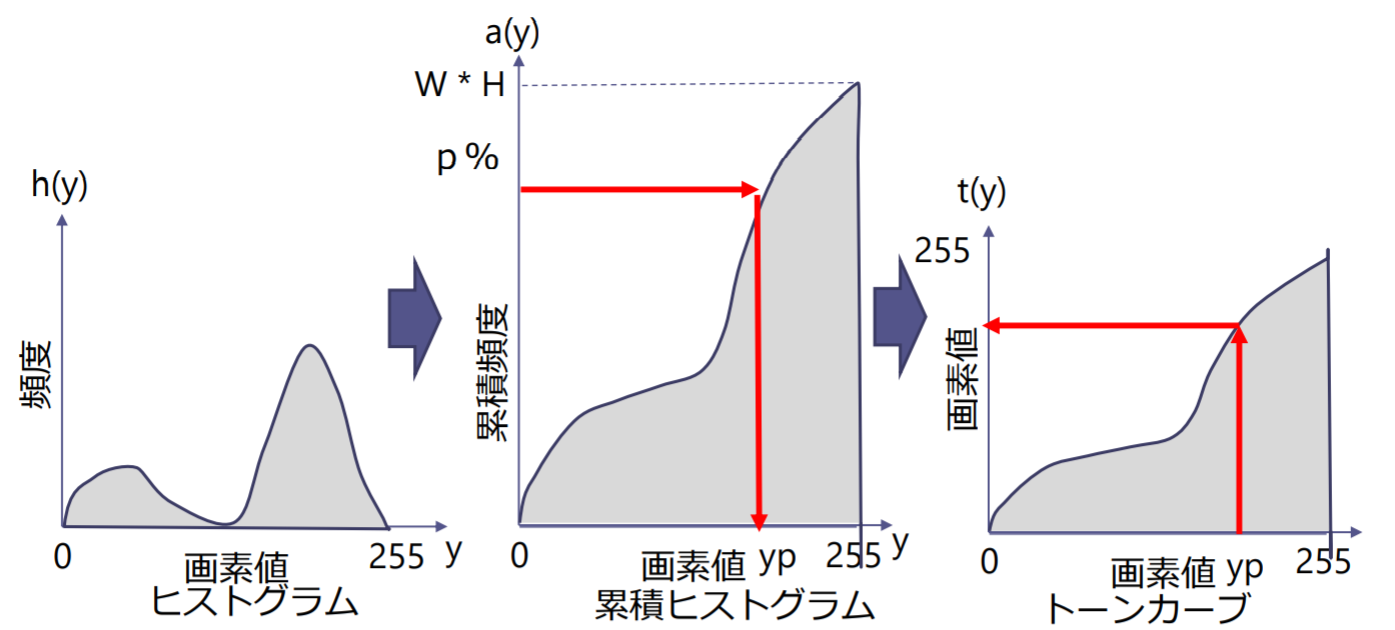
ヒストグラム平坦化
ヒストグラム平坦化(histogram equalization):ヒストグラムが画素値の全域にわたって均等に分布するように変換する濃淡変換
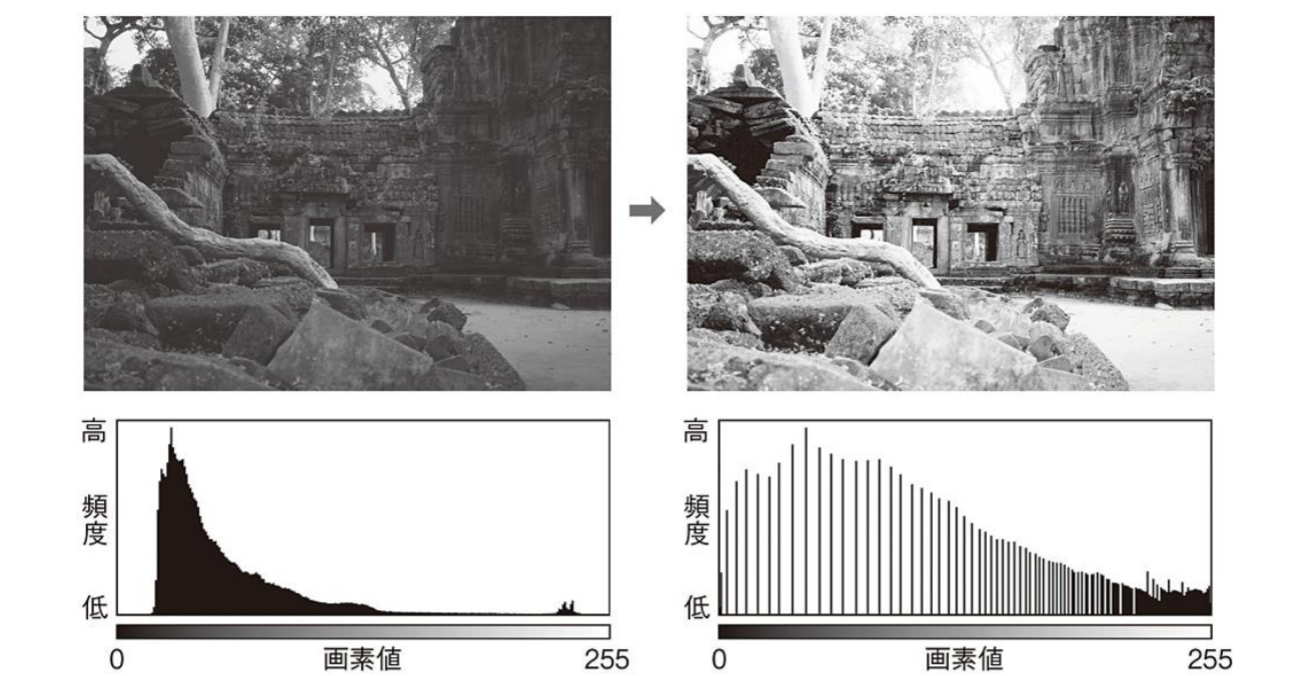
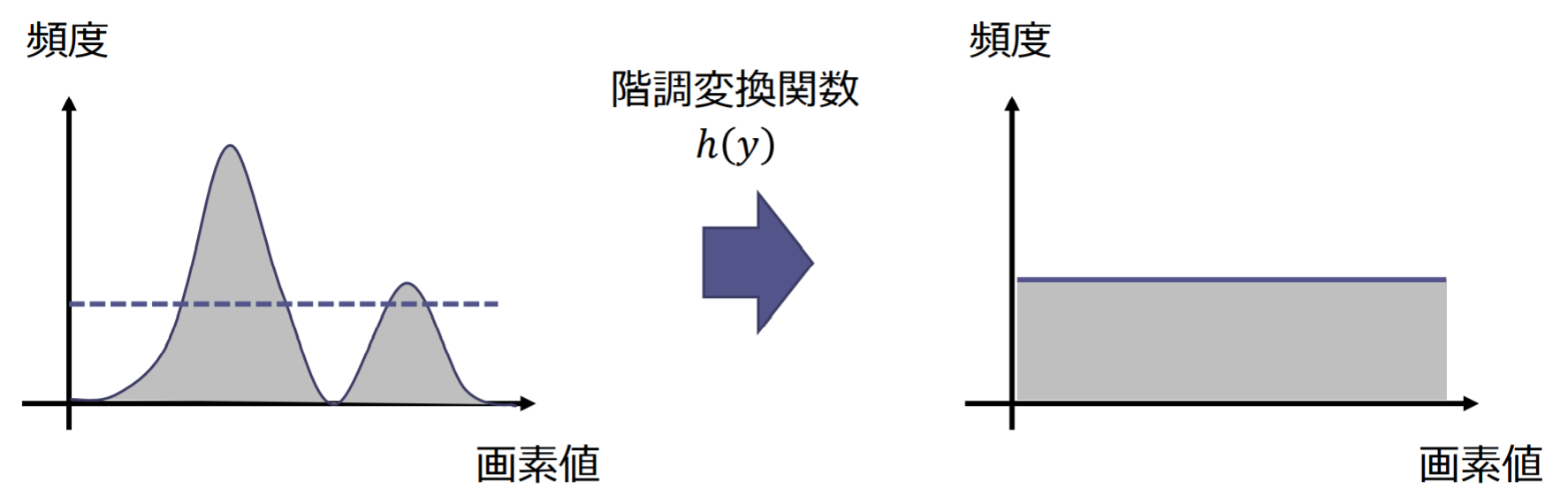
ヒストグラム平坦化の処理概要:
- 入力画像の輝度ヒストグラムを とする
- 累積ヒストグラム を求める
- 累積ヒストグラムの最大値を とする( は縦横の画素数)
- 階調変換関数 を求める:
空間フィルタリング(spatial filtering)
空間フィルタの種類
- ノイズ除去(平滑化)
- 移動平均フィルタ
- ガウシアンフィルタ
- メディアンフィルタ
- バイラテラルフィルタ
- エッジ検出・強調
- 微分フィルタ
- ラプラシアンフィルタ
- 別の分類
- 線形フィルタ
- 非線形フィルタ
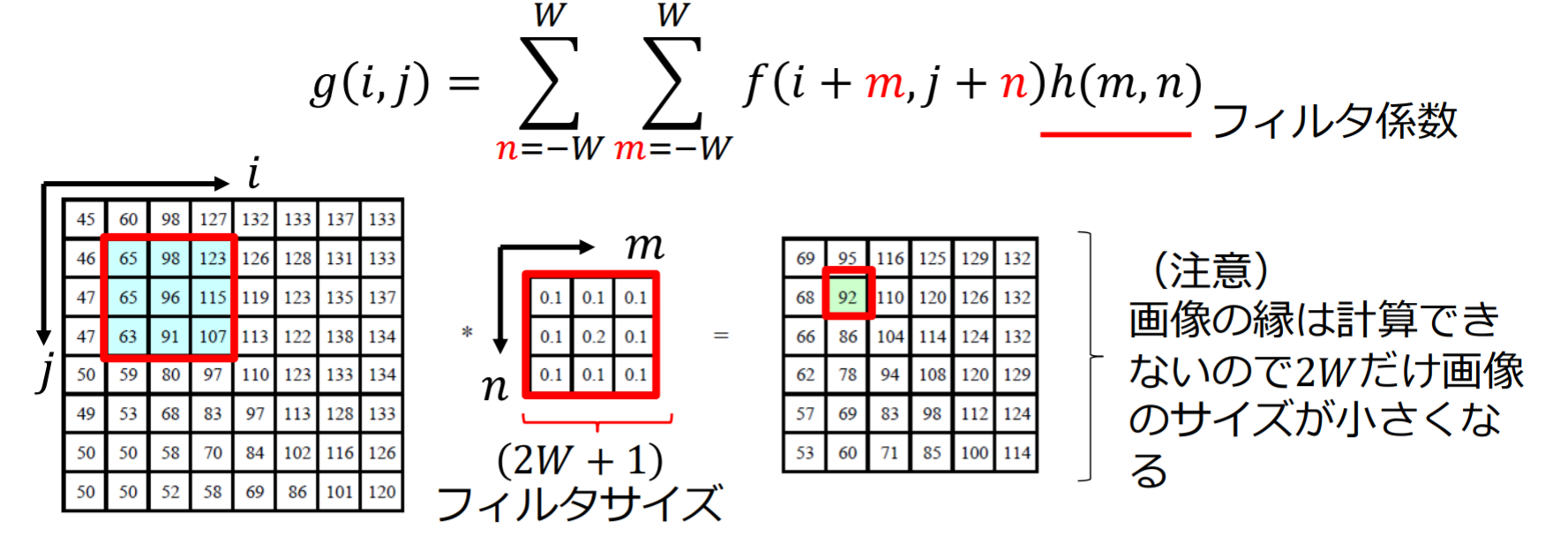
線形フィルタリング
線形フィルタリング(linear filtering):注目画素 の近傍画素の重み付き和で出力画素値 を算出する。畳み込み演算(convolution)とも呼ぶ
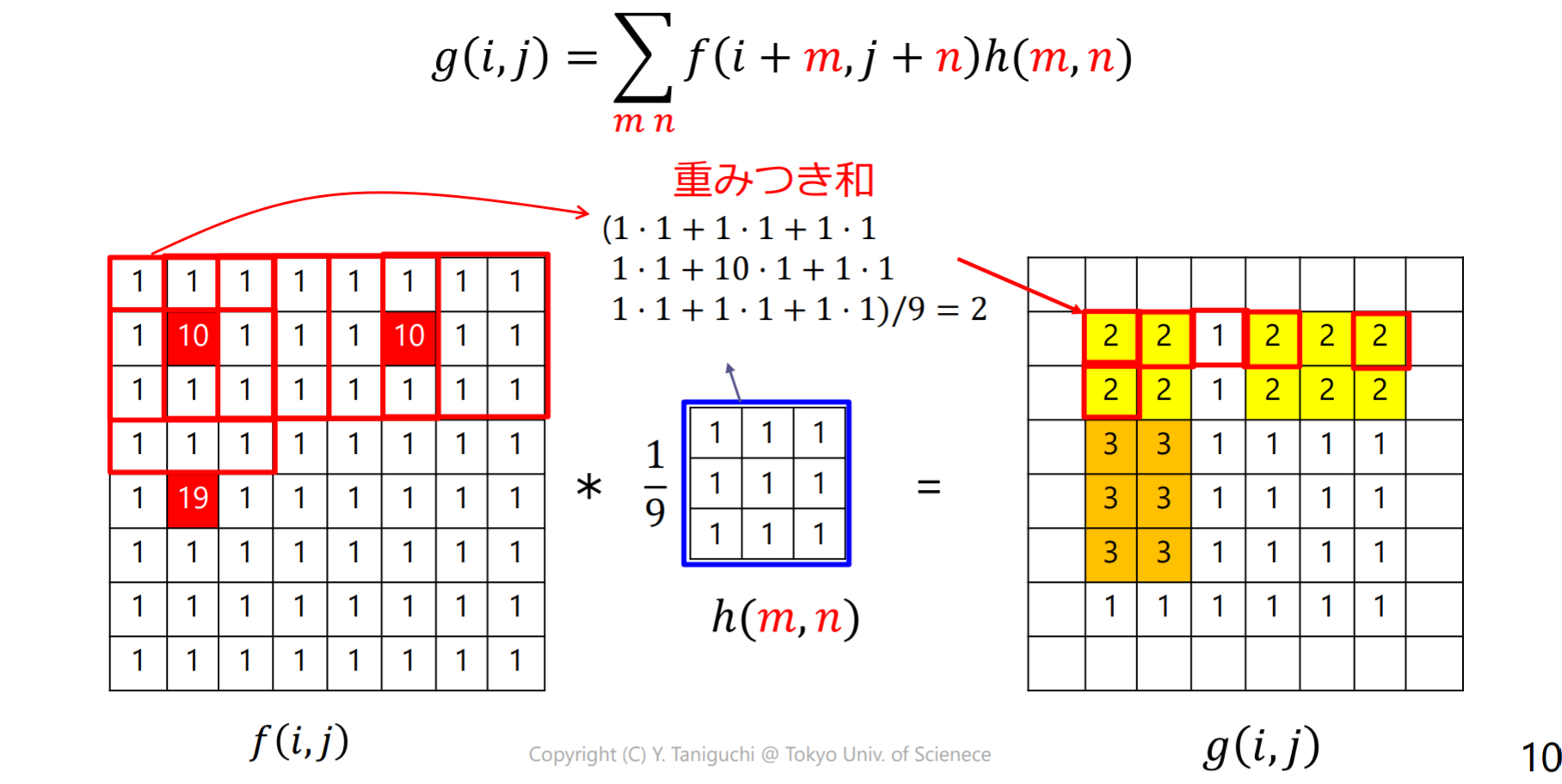
移動平均フィルタ
移動平均フィルタ(moving average filter):注画素の近傍画素の平均値を出力する。ボックスフィルタ(box filter)とも呼ぶ
- ノイズ除去(noise removal),平滑化(smoothing)の効果がある
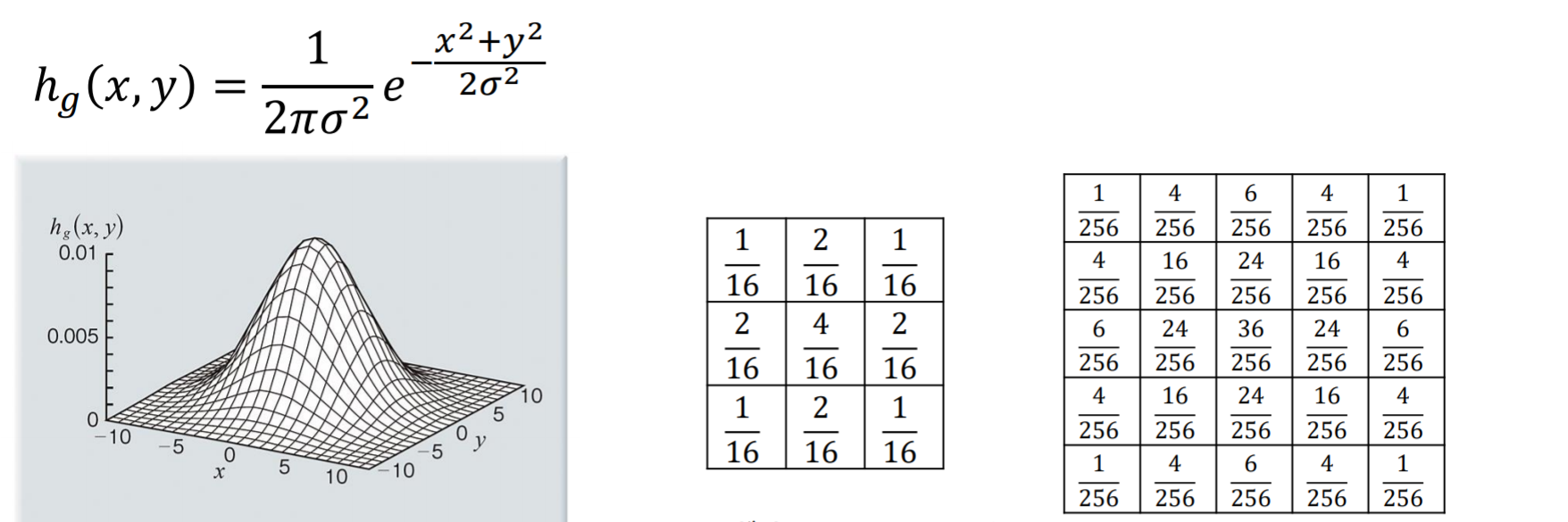
ガウシアンフィルタ(Gaussian filter)
加重平均化フィルタ(weighted averaging filter): 単純な平均ではなく(通常は,フィルタの原点に近いほど大きな)重みを付けたフィルタ
ガウシアンフィルタ:重みをガウス分布に近づけたもの
例題3.1
図1の画像に対して,以下の線形フィルタ の畳み込み演算の結果は1-4のいずれか?
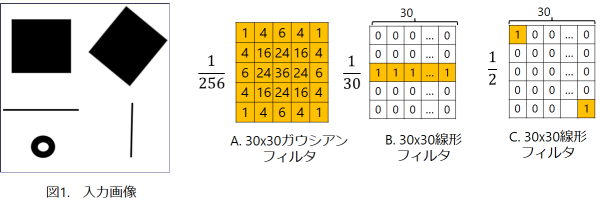
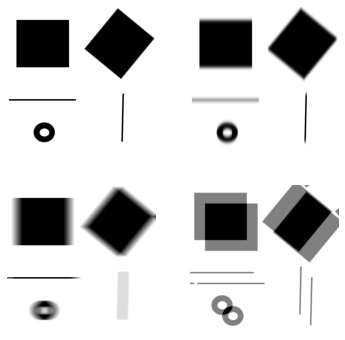
- フィルタ :(1)
- フィルタ :(3)
- フィルタ は水平方向に画素を平均しているので、水平方向に動く物体をカメラで撮影したときの動きボケと似た画像が得られる
- フィルタ :(4)
- フィルタ は画像を平行移動して重ね合わせたような画像が得られる
積分画像
移動平均化フィルタの高速化
積分画像(integral image):矩形領域 で画素値 を積分してできる画像

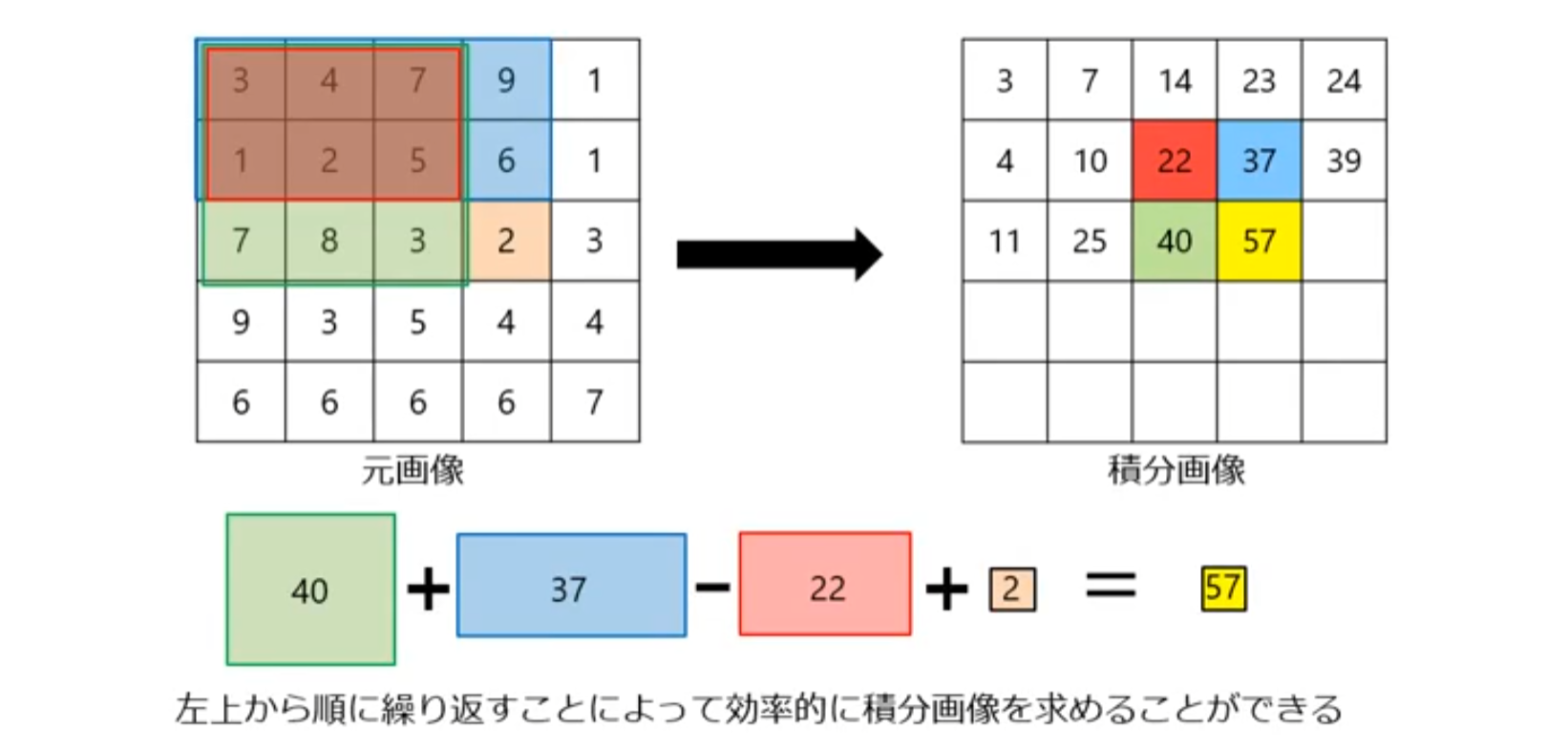
例題3.2
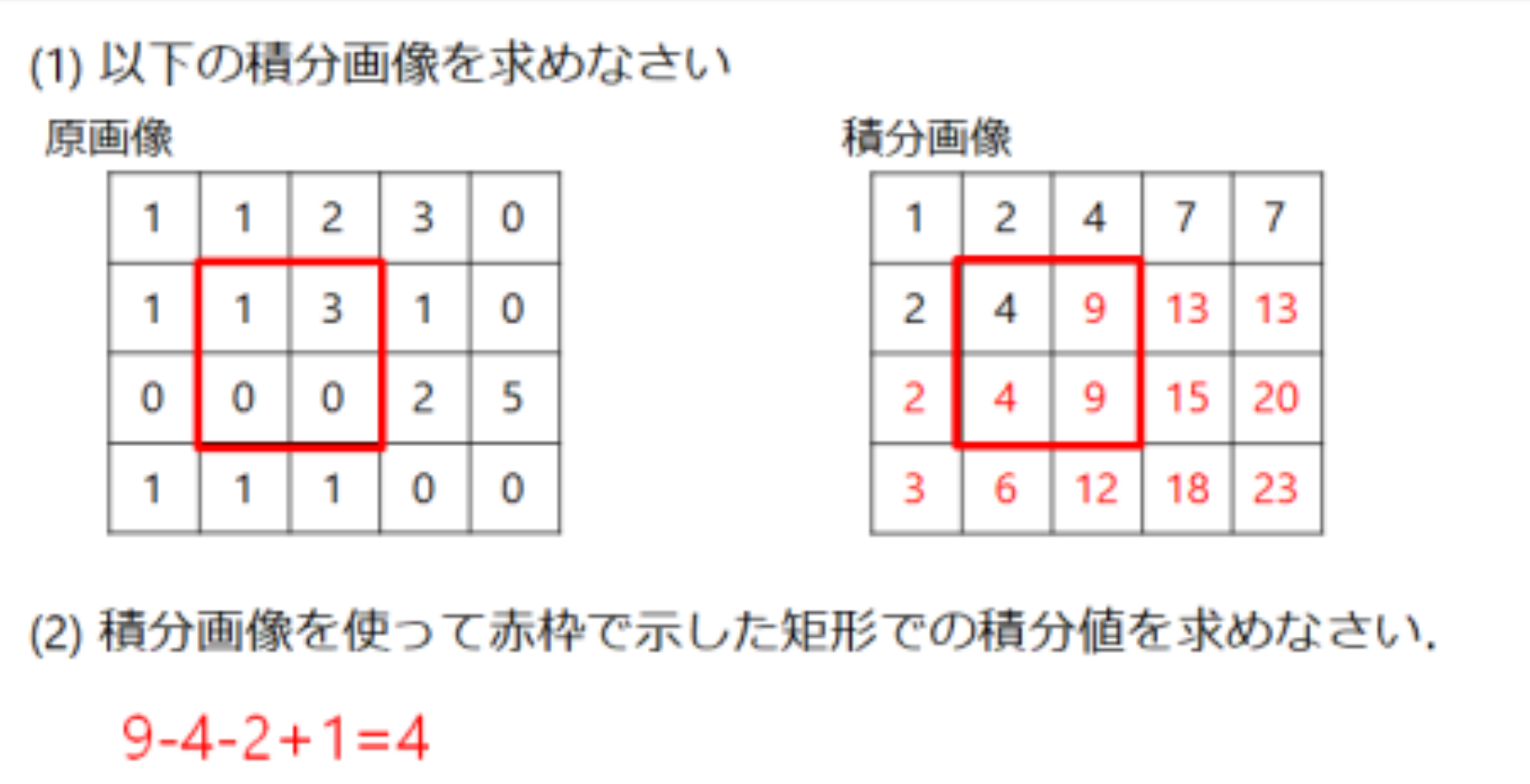
- (2):右下角(9) - 右上角(4) - 左下角(2) + 左上角(1) = 4
エッジ検出
- 画像中で画素値が急激に変化する部分
- 画像 の微分係数が大きな値をとる点
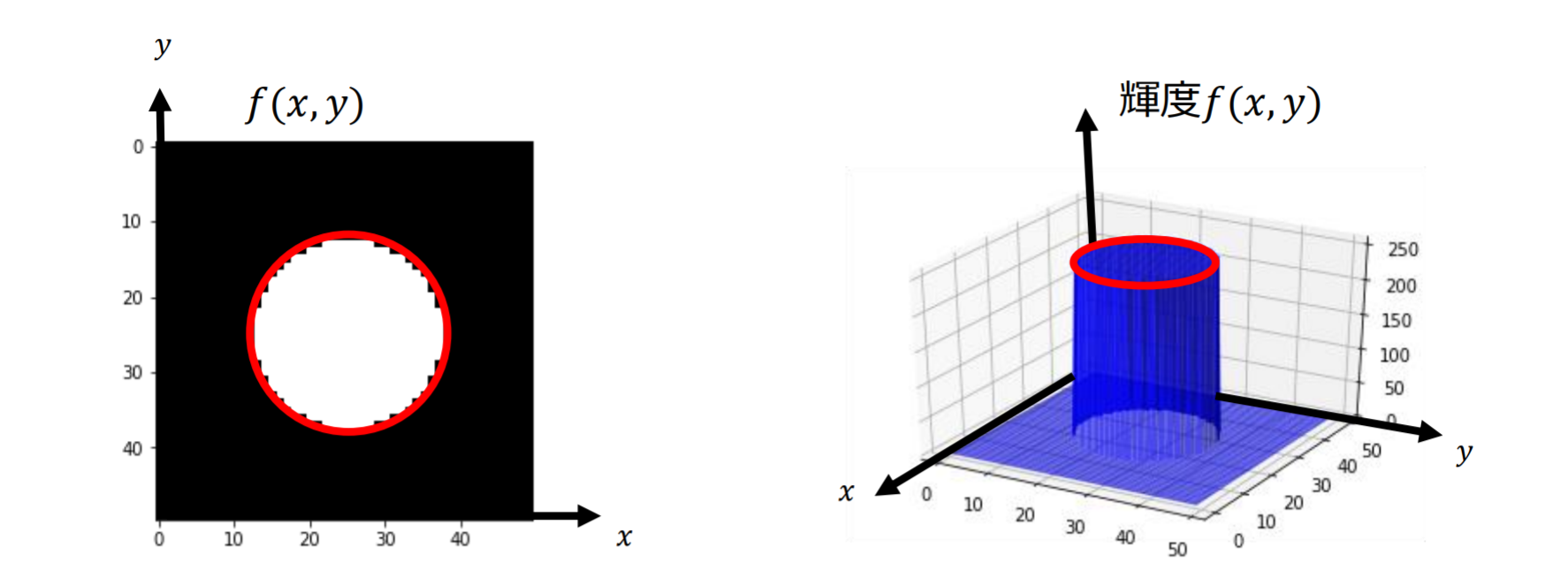
微分フィルタ:明るさが急に変化するエッジ部分を検出
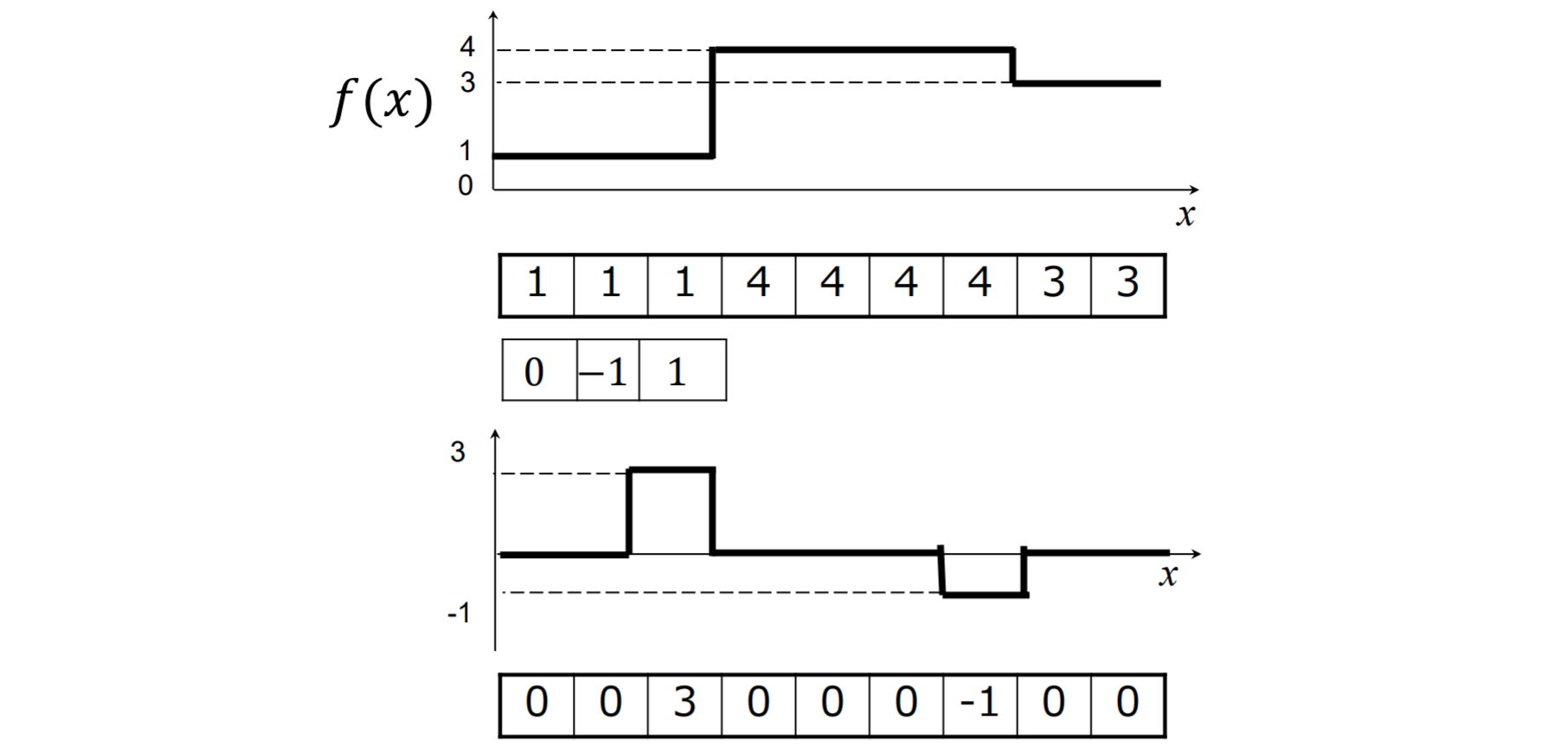
勾配 (gradient)とエッジ強度
- 勾配(gradient):
- 勾配の大きさ(エッジ強度):
- 勾配の方向:
「勾配の大きさ」が大きい画素をエッジとみなす
Prewittフィルタ,Sobelフィルタ
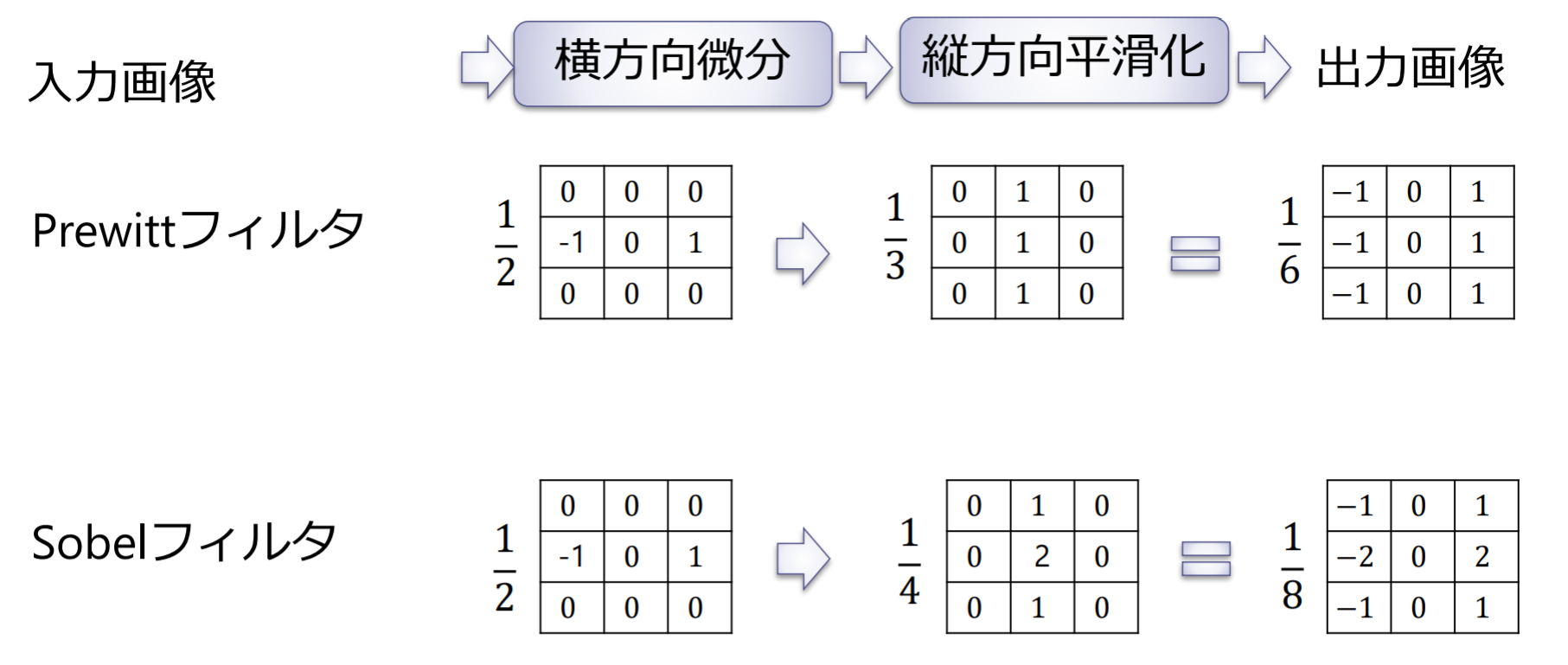
微分フィルタとSobelフィルタの違い:Sobelフィルタの結果は微分フィルタに比べてノイズが抑えられ,より滑らかにエッジが検出されている
ラプラシアン
関数 のラプラシアン(Laplacian)
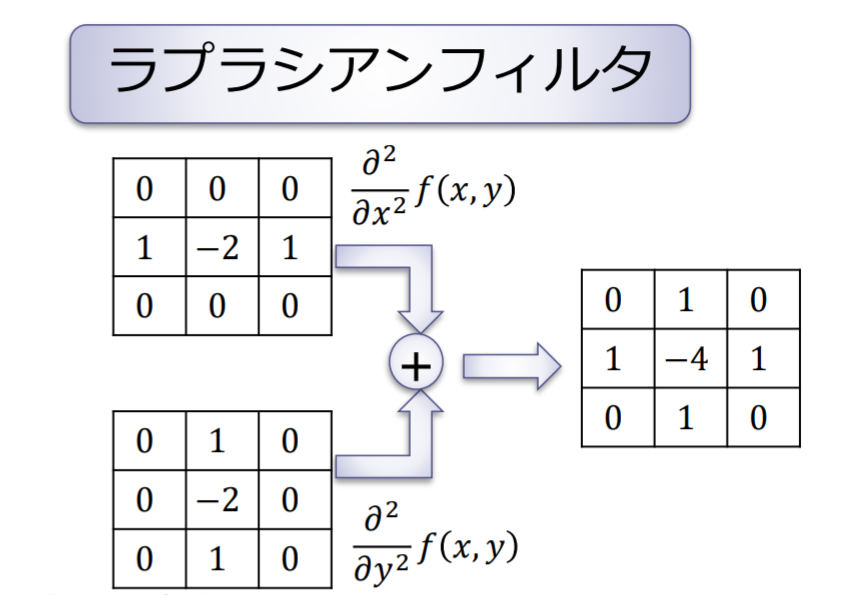
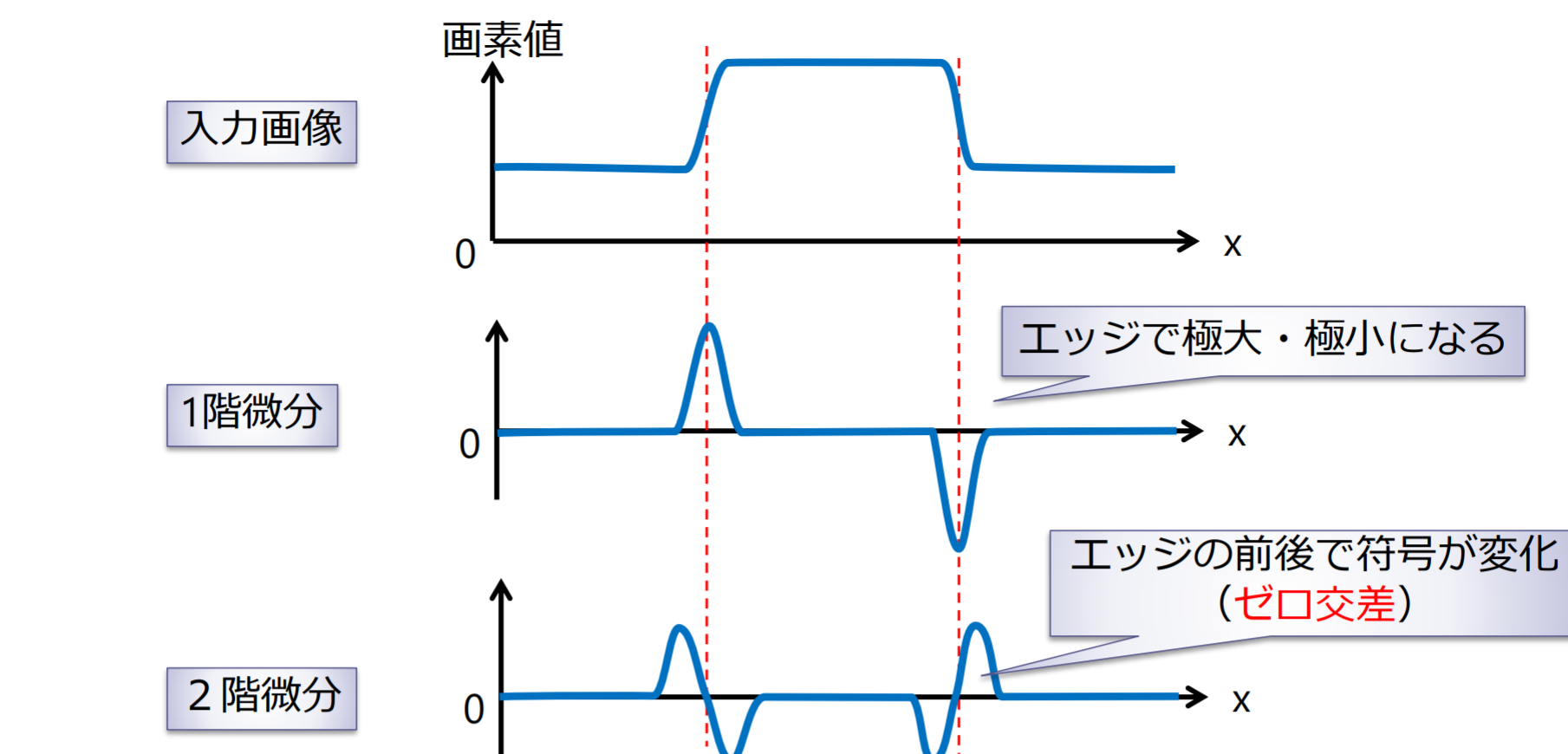
ラプラシアンフィルタを使って、符号の変換を見ることでエッジを検出することができる
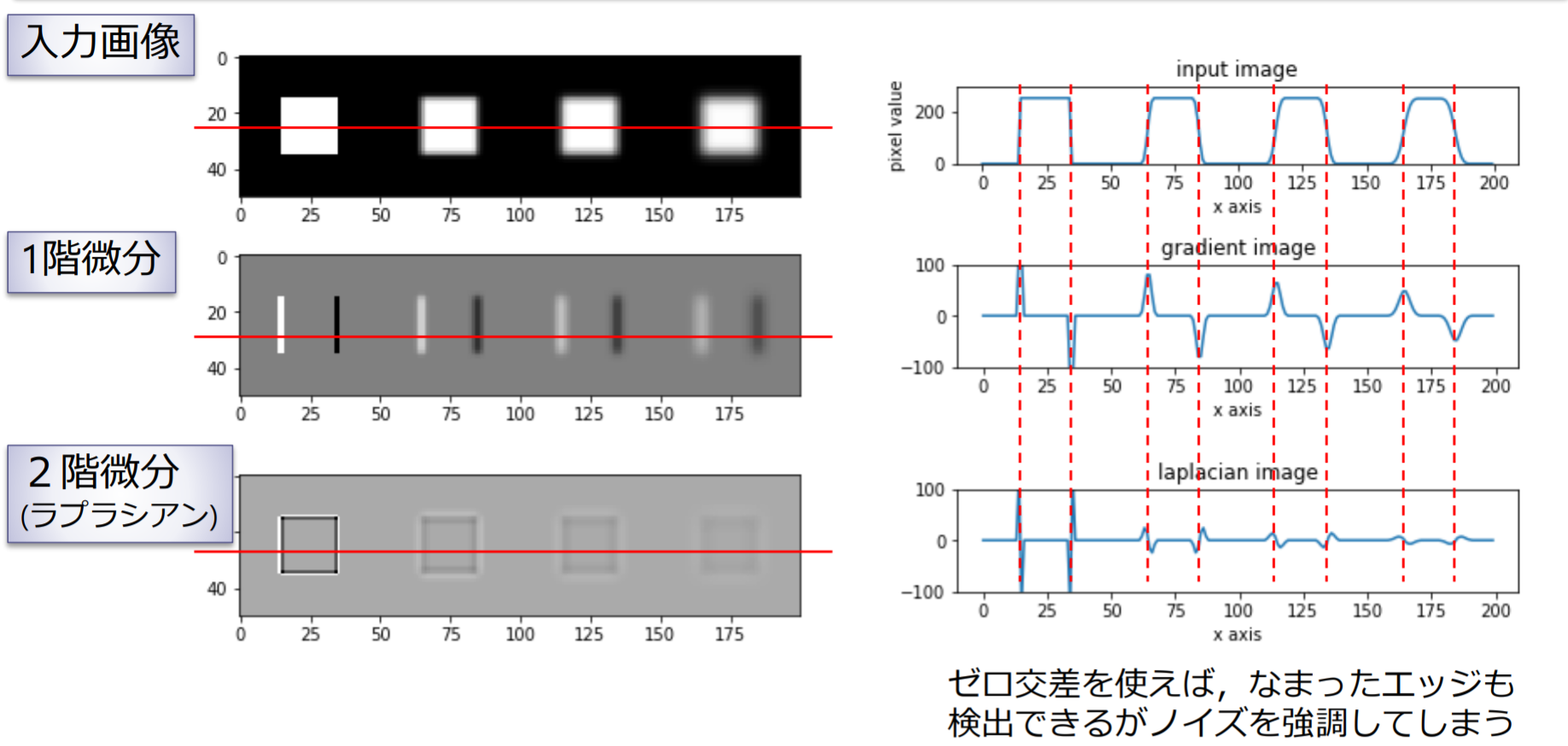
LoGフィルタ
ラプラシアンは微分を繰り返すためノイズを強調してしまうという欠点がある
LoG(Laplacian of Gaussian)フィルタ:ガウシアンフィルタで平滑化したのちラプラシアンフィルタを適用
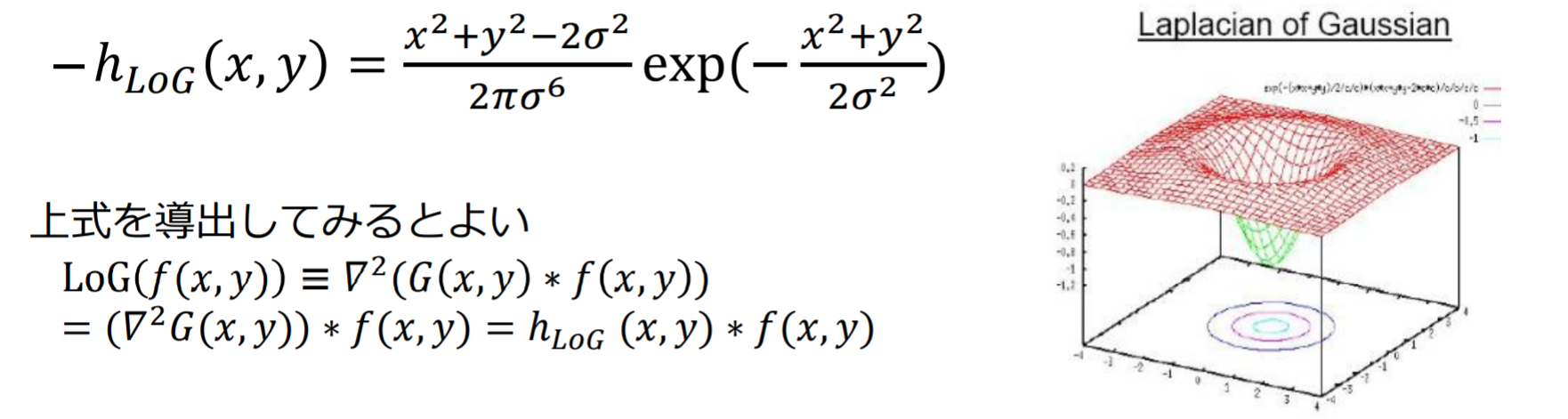
例題3.3
灰色の画素の画素値が0に対応し、白色は正、黒色は負の値をとる
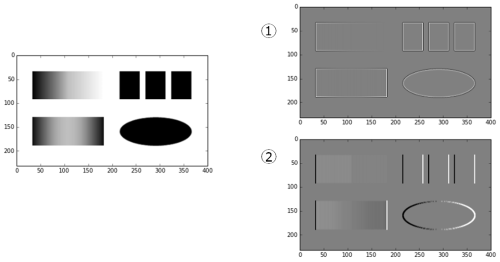
- Sobelフィルタは:(2)
- ラプラシアンフィルタ:(1)
Sobelフィルタの結果は微分フィルタに比べてノイズが抑えられ,より滑らかにエッジが検出されている
先鋭化フィルタ
鮮鋭化フィルタ(sharpening filter)
鮮鋭化フィルタ(sharpening filter):入力画像から2階微分した画像(ラプラシアン)を引くと,エッジが強調された(鮮鋭化された)画像が得られる
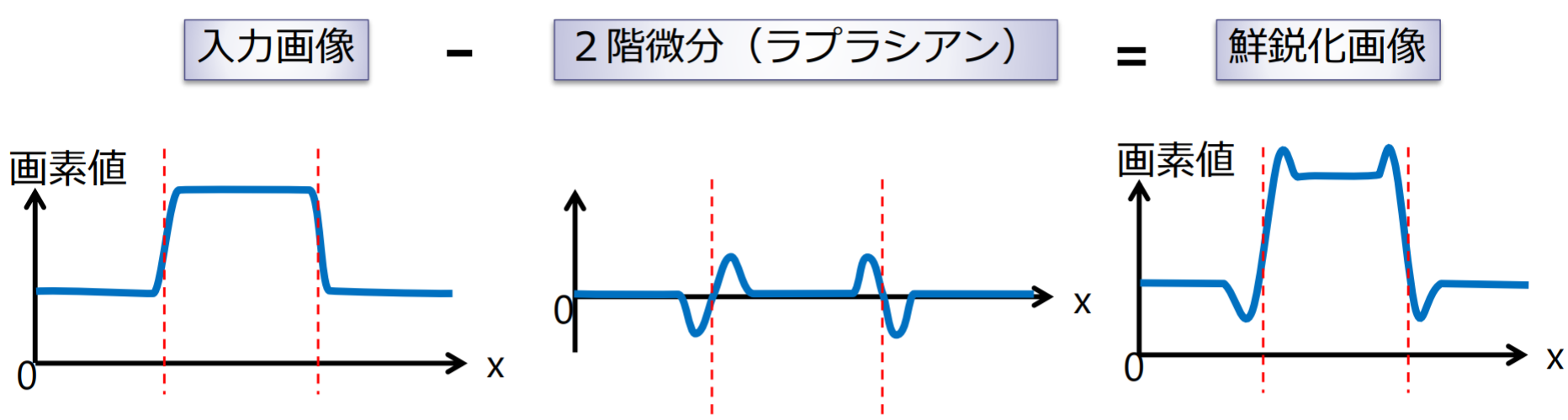

を大きくするとより鮮鋭化された画像が得られる
非線形フィルタ
メディアンフィルタ、バイラテラルフィルタはいずれも、エッジを保存しながら、ノイズを除去(平滑化)する効果がある
メディアンフィルタ
メディアンフィルタ(median filter): 近傍画素の画素値の中央値を出力画像の画素値として設定
- ごま塩ノイズの除去
- エッジがなまりにくい


メディアンフィルタはエッジを強調する効果がない
バイラテラルフィルタ
バイラテラルフィルタ(bilateral filter):エッジを保存しながらノイズを除去
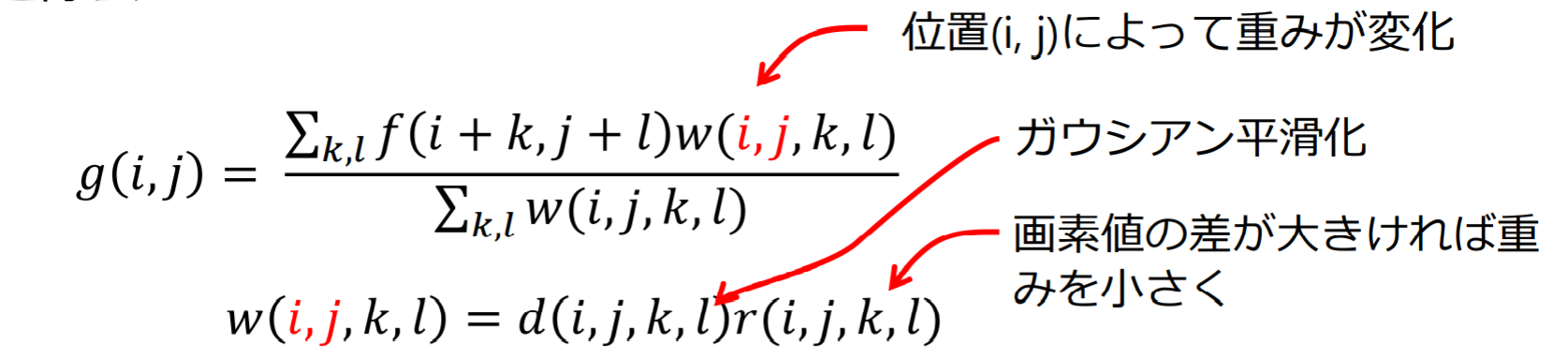
- データ非依存:
- データ依存:

繰り返し適用すると,ある領域の画素値の近いものどおしが同じ画素値をもつようにまとめられ,イラスト風の画像ができる

例題3.4

例題3.5

- 図1の入力画像からラプラシアンフィルタの出力画像を引き算した画像は[エ]
- 入力画像からラプラシアンフィルタの出力画像を引き算するとエッジが強調され画像が鮮鋭化される
二値画像処理
二値画像(Binary image)
二値画像とは、各ピクセルの取り得る値が2種類のみのデジタル画像である。一般的に、二値画像に使用される2つの色は白と黒であるが、これら以外の任意の色の組み合わせも使用することができる
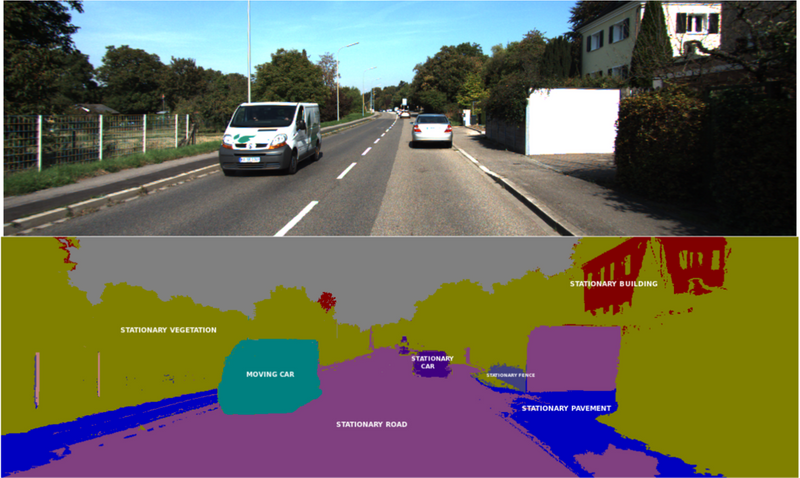
セマンティックセグメンテーション(Semantic Segmentation)
- 二値ではなく複数種類の領域に分割した多値画像もある
- 処理方法は二値画像と同じ
閾値の設定法
画素値(輝度)が閾値以上の時に"1", 閾値未満のときに"0"
- モード法:ヒストグラムに双峰性が仮定できる場合
- Pタイル法:前景画素の割合が予測できる場合
- 判別分析法(大津法):前景画素と背景画素の分離度(=クラス間分散とクラス内分散の比)を最大化
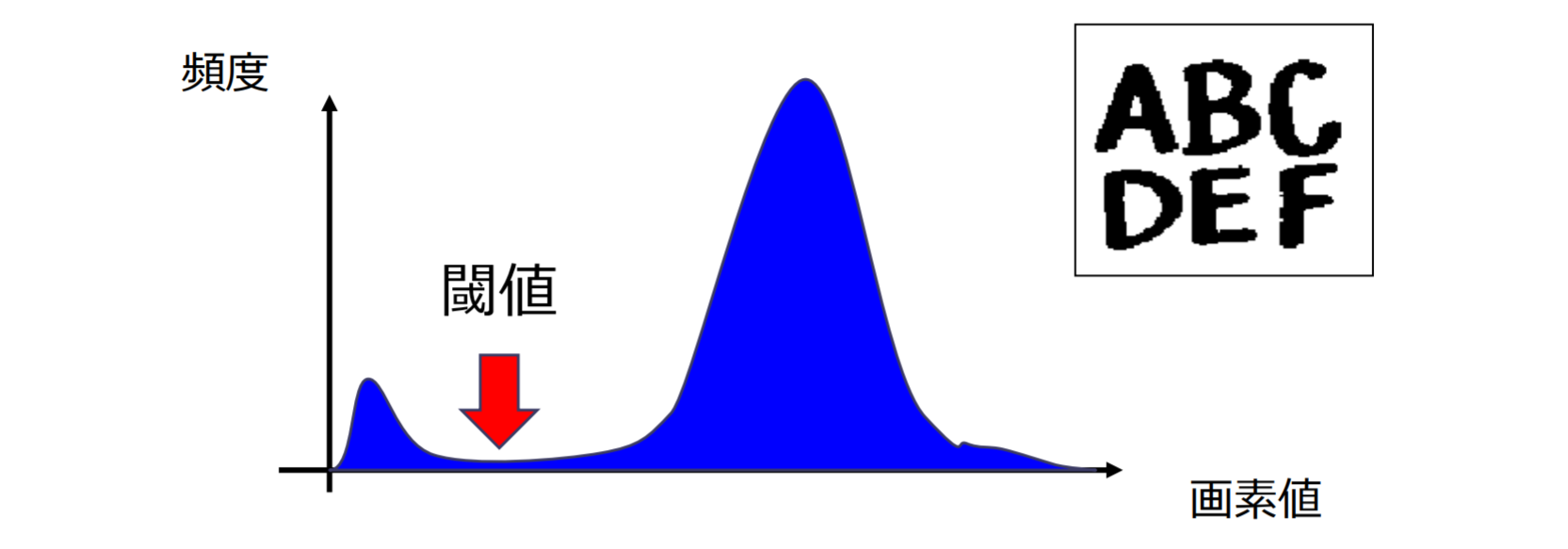
モード法
モード法(mode method):輝度ヒストグラムの谷の位置を示す画素値を閾値と設定
- 2つの山(双峰性)を持つ場合に適用可能
Pタイル法
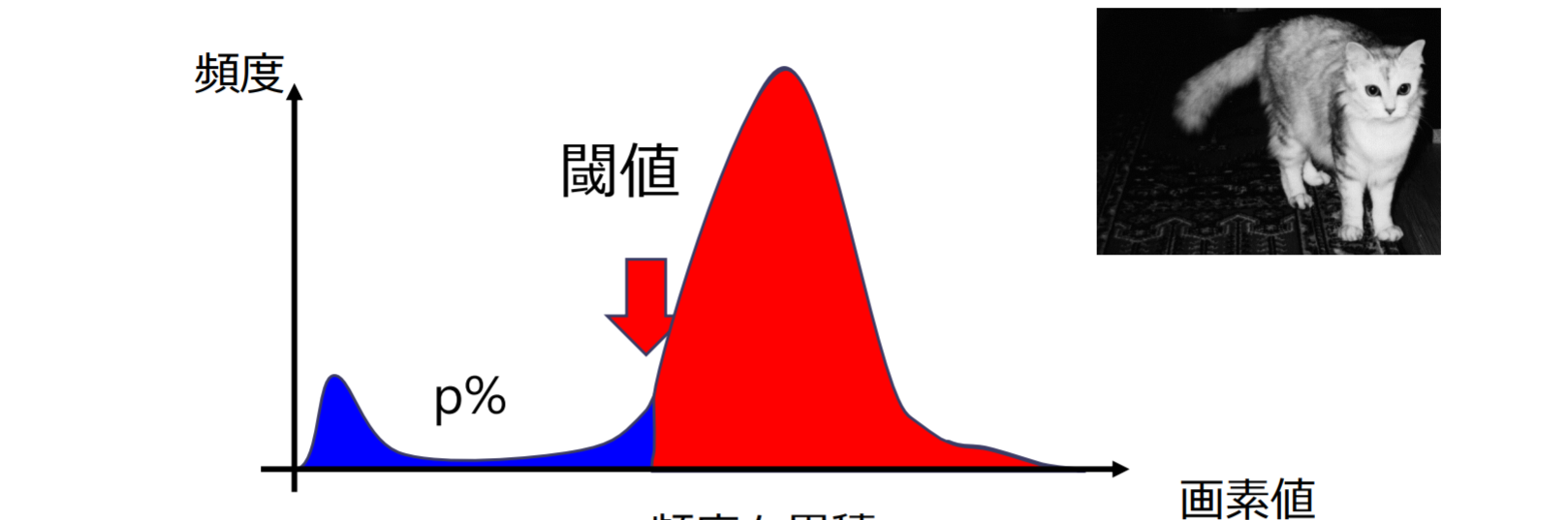
P-タイル法(p-tile method):画素値が低いところから頻度を累積していき,累積頻度が となる画素値を閾値と設置
- 切り出したい図形が占める面積の割合 が分かっている場合に適用可能
判別分析法(大津法)
判別分析法(discriminant analysis method):閾値で二つのクラスに分割したとき,二つのクラスが最もよく分離するように閾値を設定
- クラス間分散 とクラス内分散 の比(分離度) を最大にする
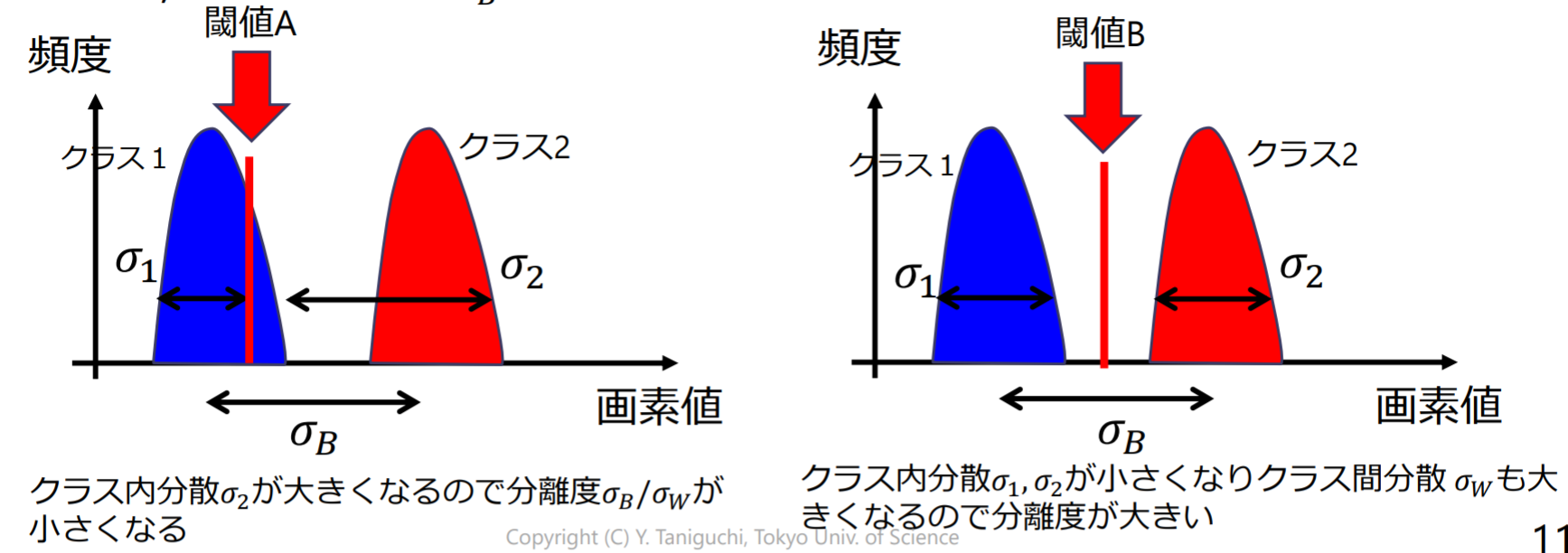
クラス内分散(within-class variance)
- :クラス の画素数
- :平均輝度値
- :分散
クラス間分散(between-class variance)
- :全画素の平均輝度
全分散 とクラス内,クラス間分散 の間には の関係があるから
閾値によらず全分散 は一定.分離度を最大化するためにはクラス間分散 が最大になるように閾値 を決めればよい
モルフォロジ演算(morphology)

モルフォロジ演算(morphological operation):(一般的には)二値画像の形状を変化させるような演算
近傍(neighbor)
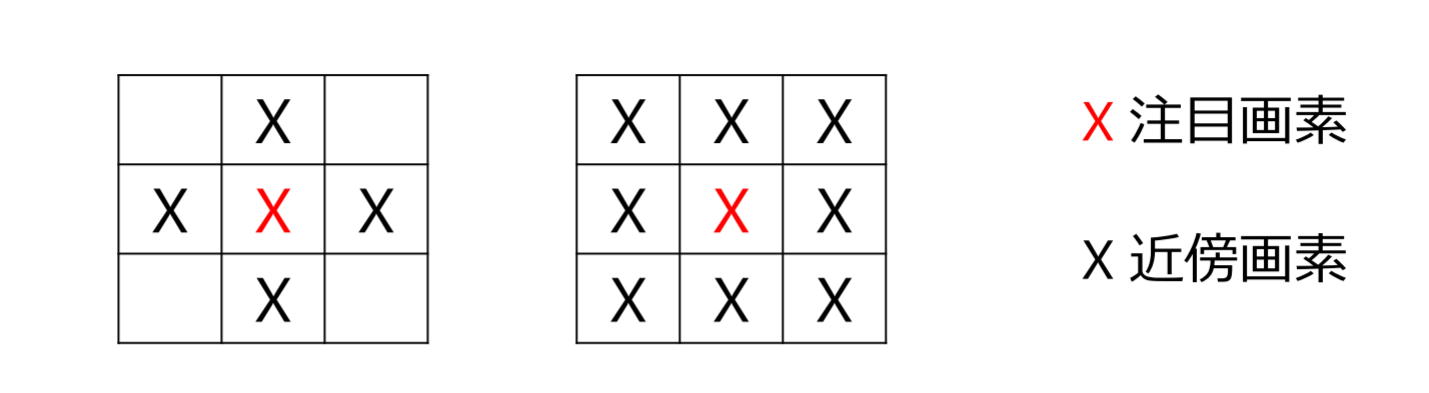
連結性(connectivity)
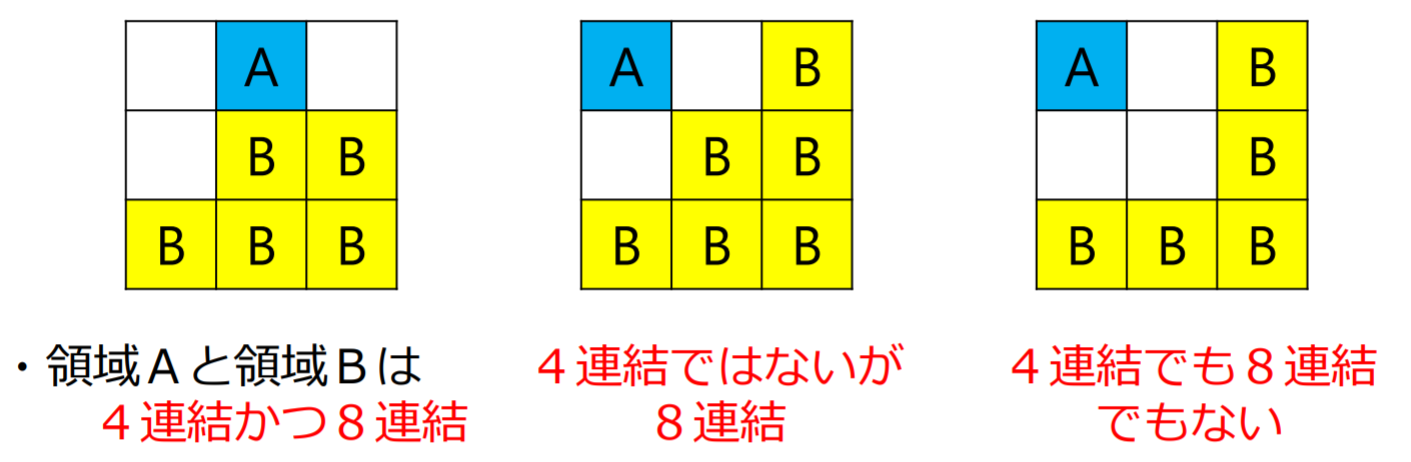
- 連結成分(connected components):連結している画素の集合
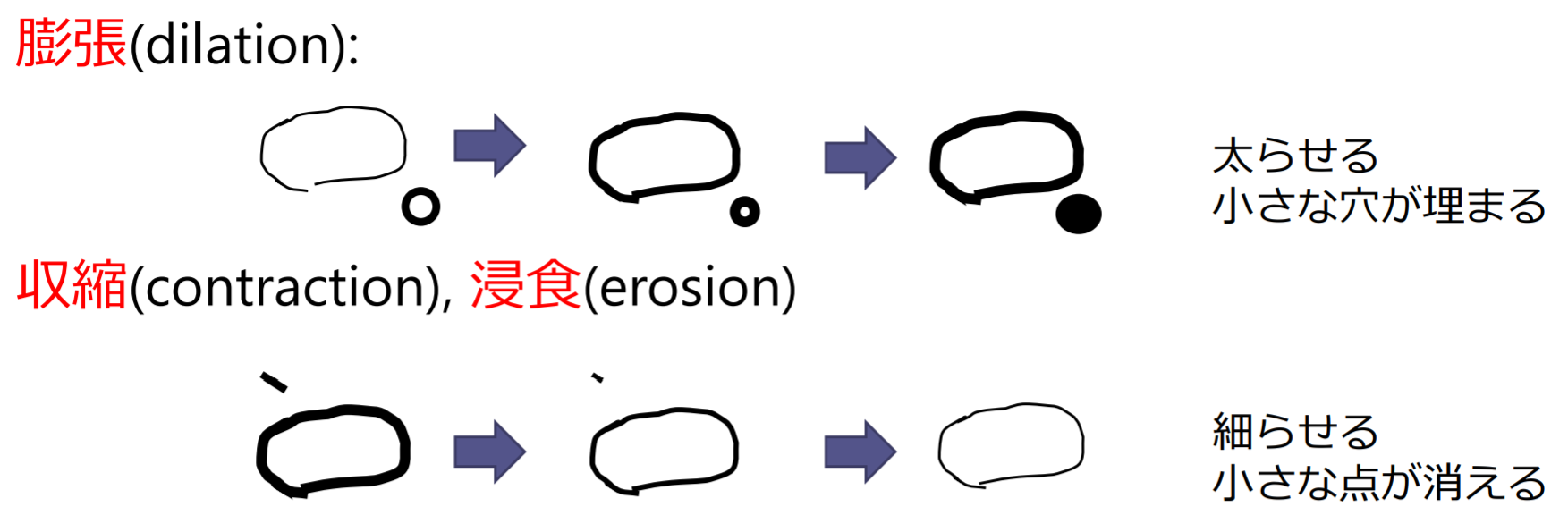
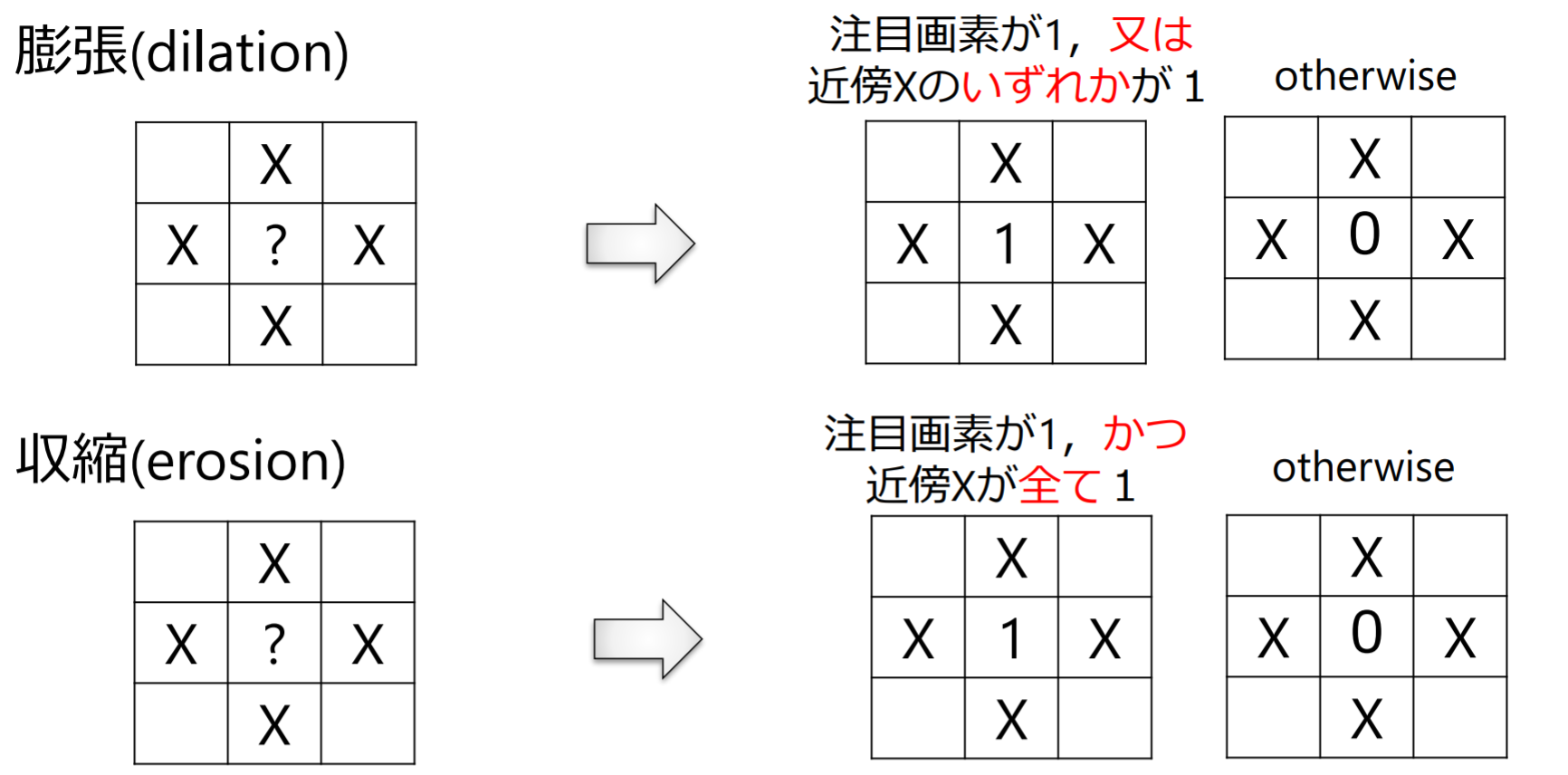
膨張と収縮
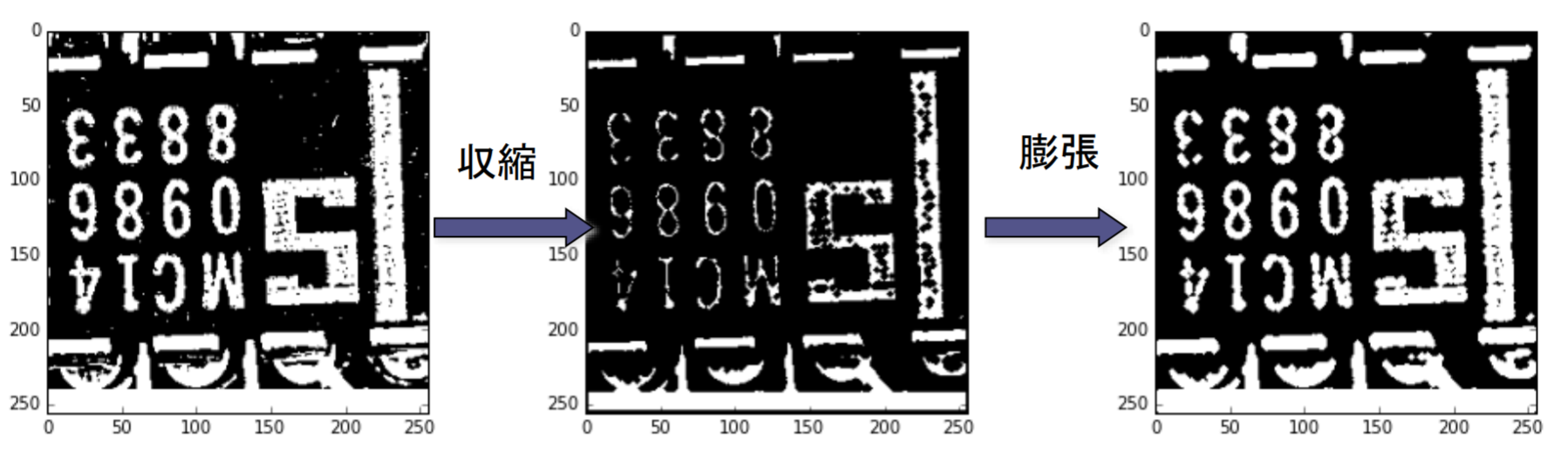
オープニング演算とクロージング演算
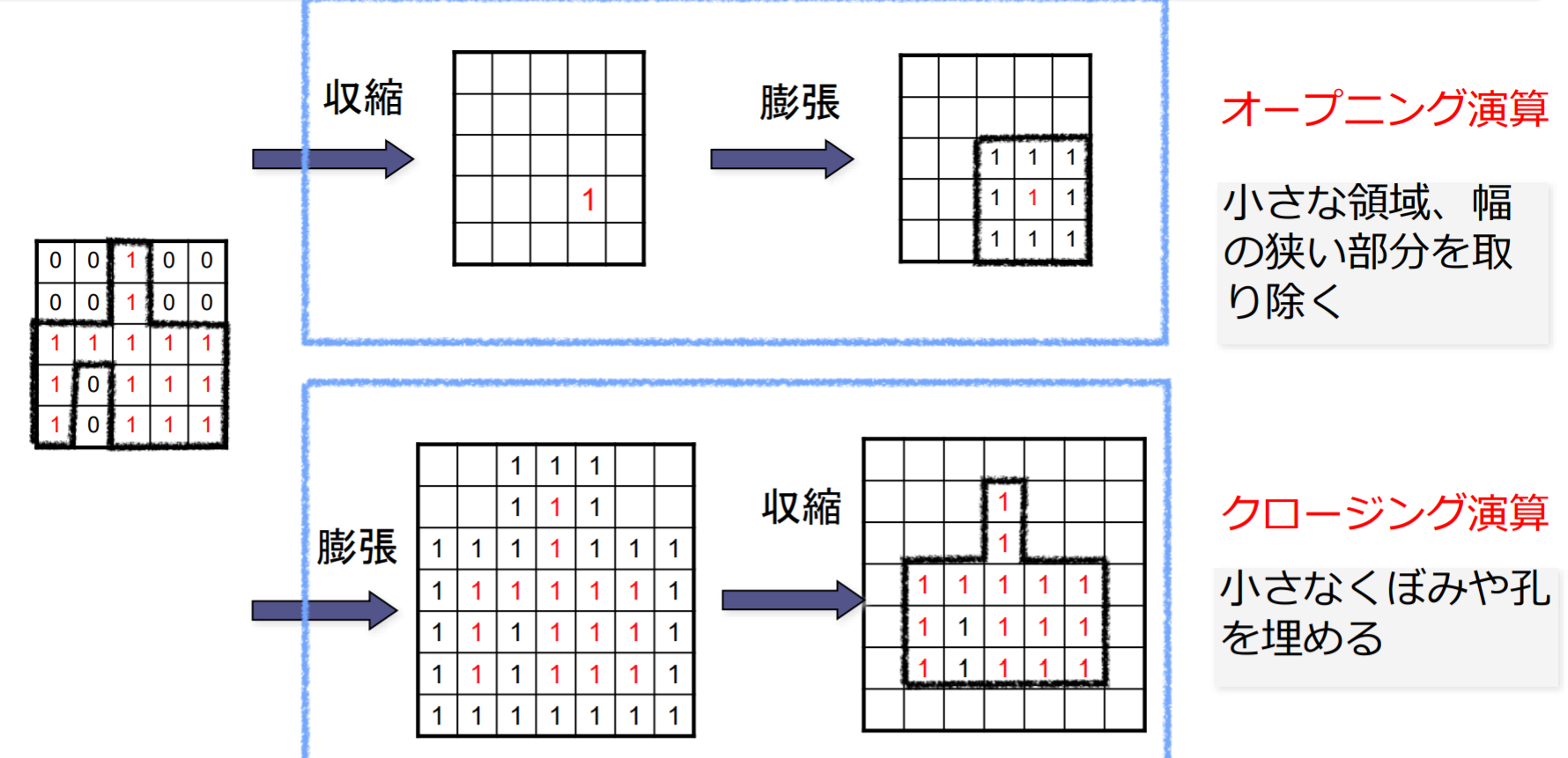
- オープニング:収縮してから膨張
- クロージング:膨張してから収縮
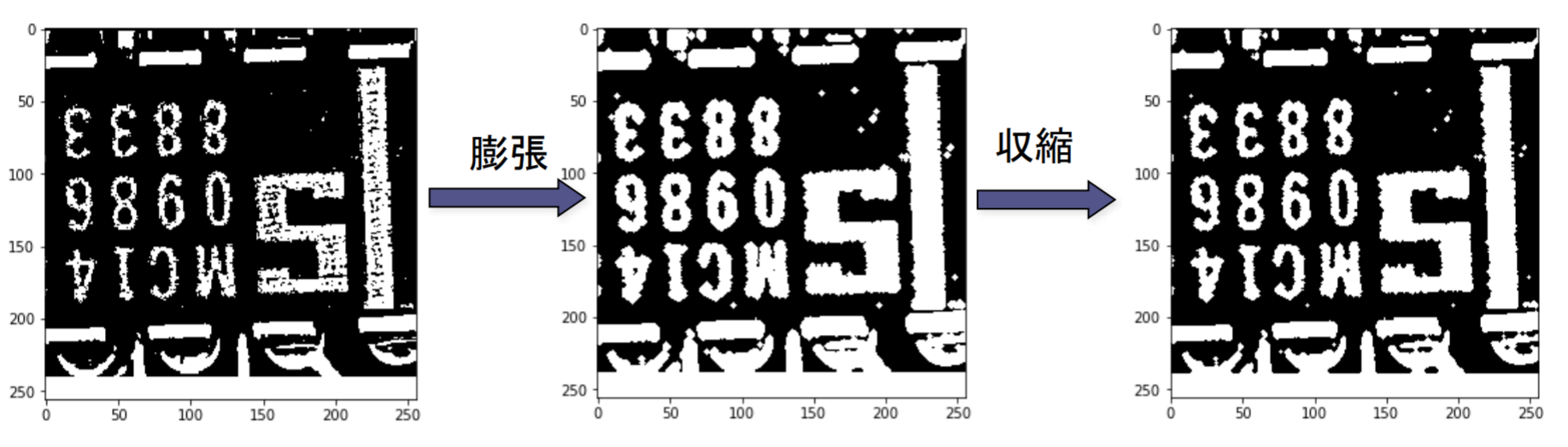
例題4.1
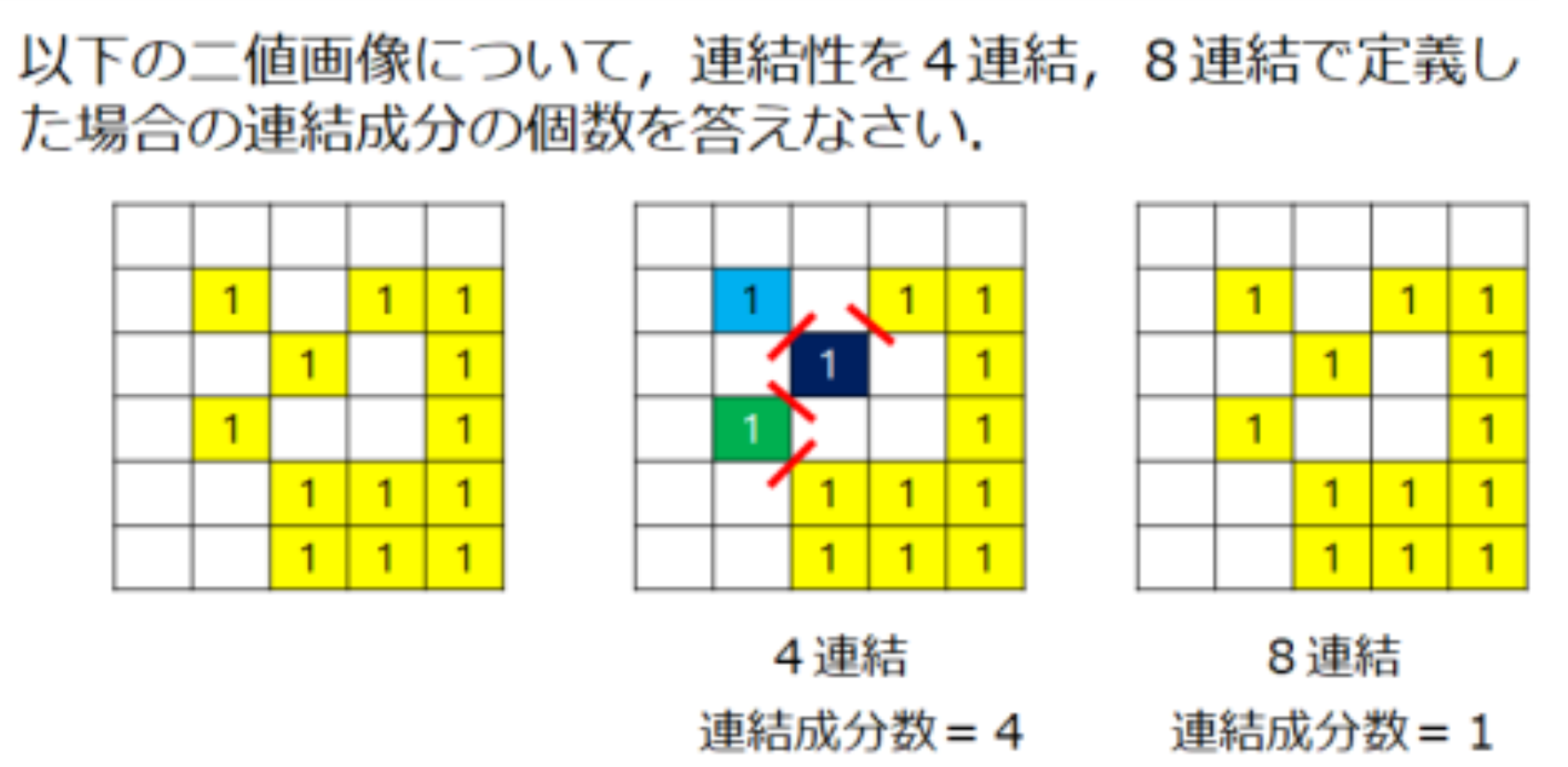
- 4連結で定義した場合:4
- 8連結で定義した場合:1
距離変換(distance transform)
2値画像 を多値画像 へ変換
- は画素 から黒画素 までの最短距離
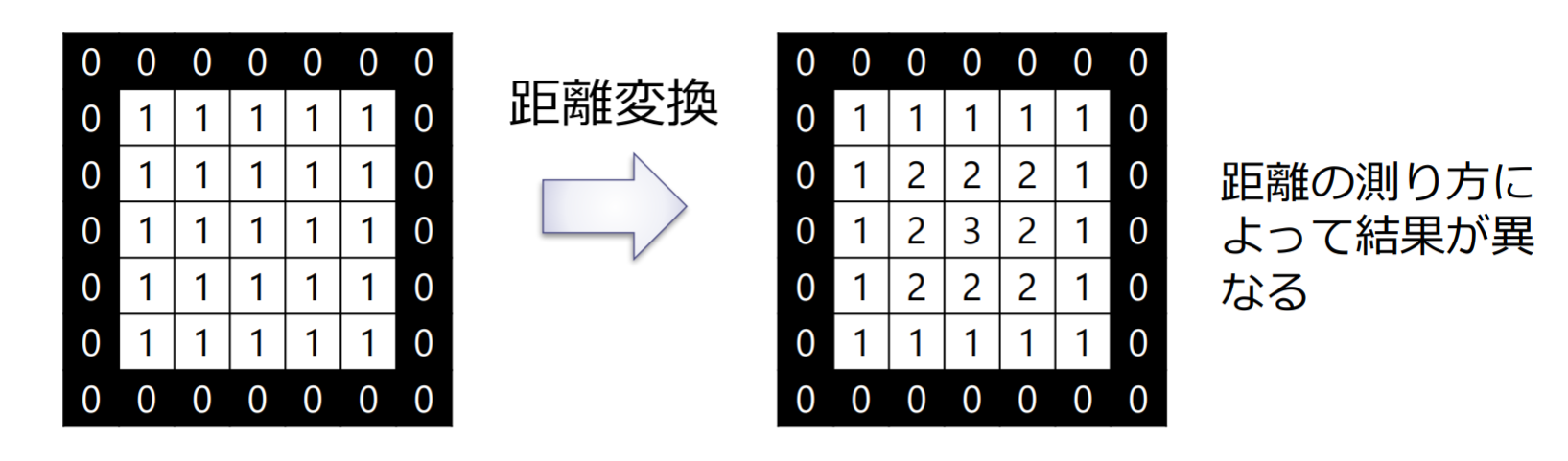
画素 と画素 の間の距離の定義
- ユークリッド距離( 距離)
- 4近傍距離(市街地距離,マンハッタン距離, 距離)
- 8近傍距離(チェス盤距離,チェビシェフ距離, 距離)
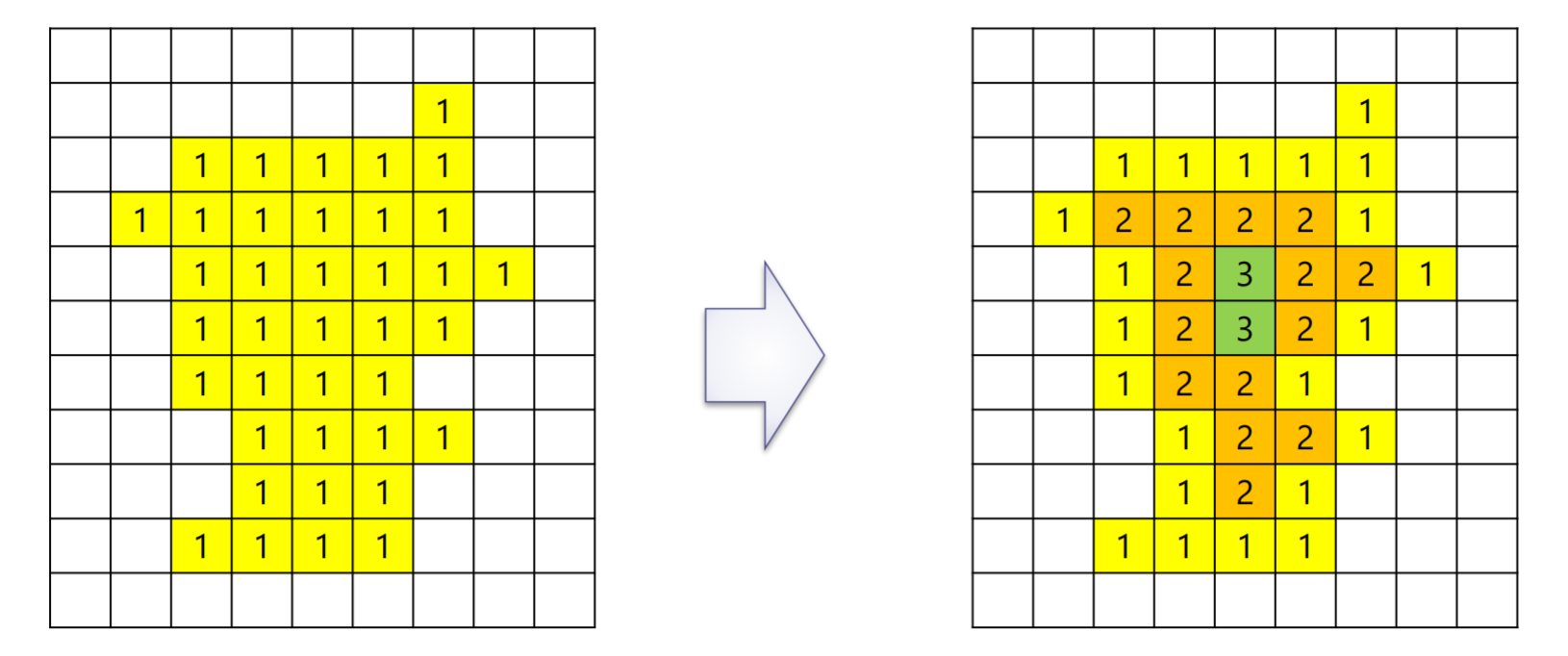
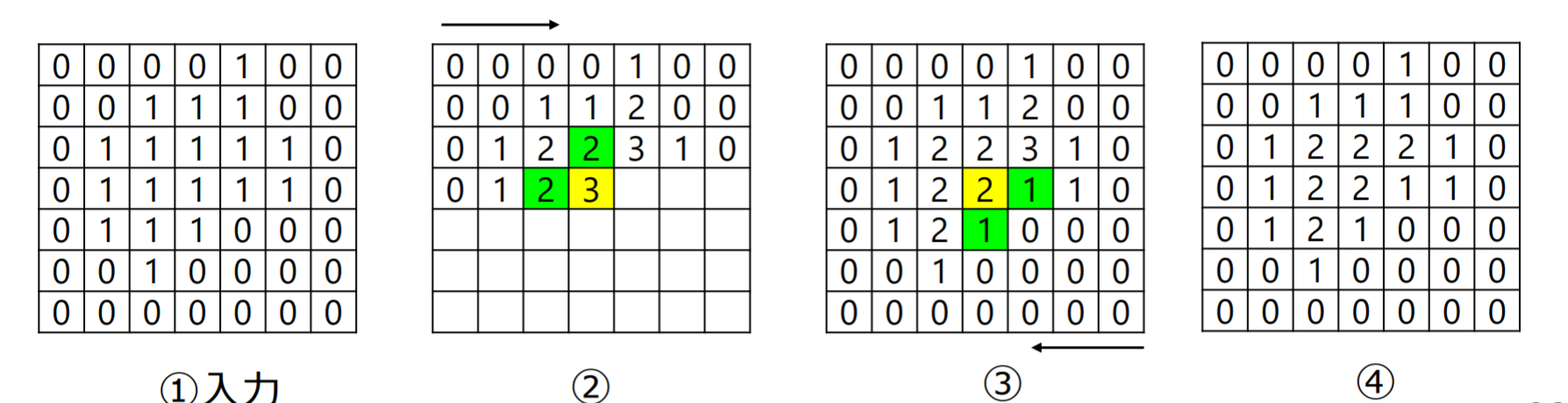
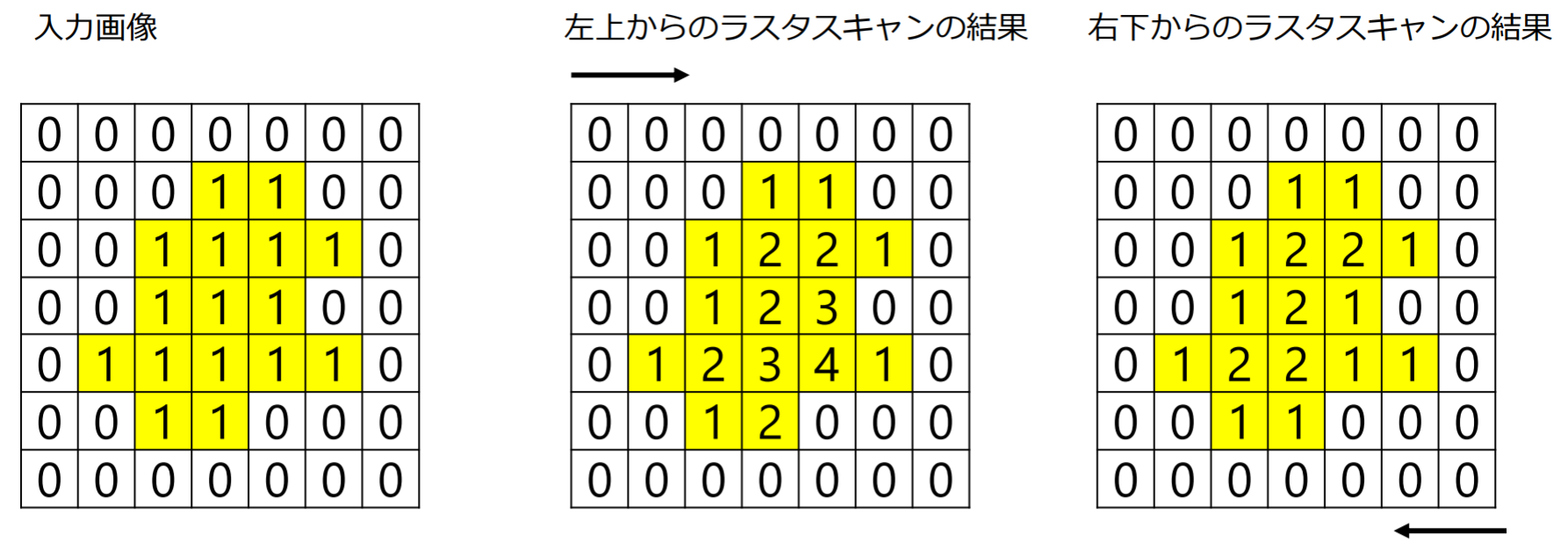
ラスタスキャンを用いた距離変換処理
- 入力画像
- 左上からラスタスキャン:緑色の値から黄色の値を算出(緑セルの値に1足した値の小さい方を黄色セルの値とする)
- 右下からラスタスキャン:緑色の値から黄色の値を算出(緑セルの値に1足した値と黄色セルの値の最小値を黄色セルの値とする)
注意:有黄色的地方才需要看上述算法,没有黄色的格子直接为0
- 左上方开始的扫描是取有黄色格子的 (左边+1,上方+1) 的最小值
- 右下方开始的扫描是取 (下方+1,右方+1,左上扫过后格子的值) 中最小的值
- 距離変換の応用例: Chamfer matching
連結成分のラベリング
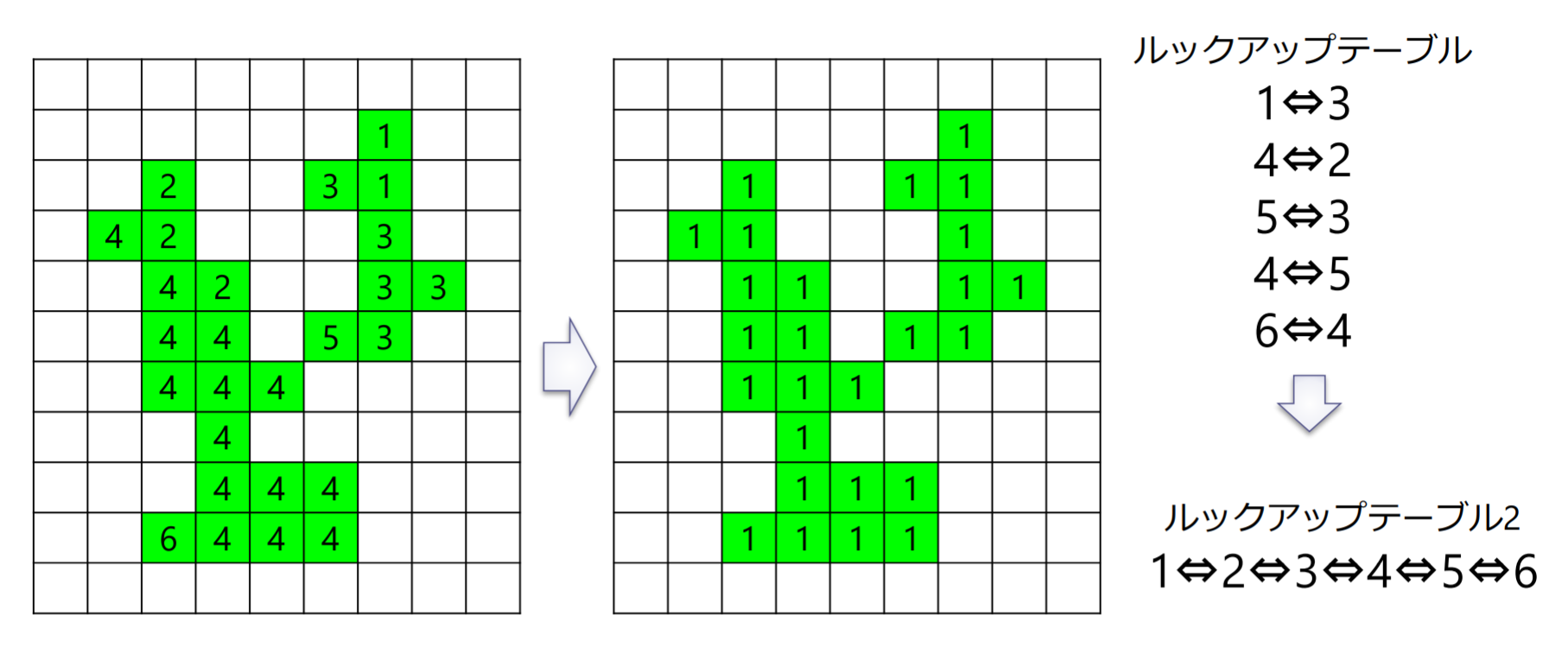
連結している画素の集合である連結成分に番号(ラベル)を付与
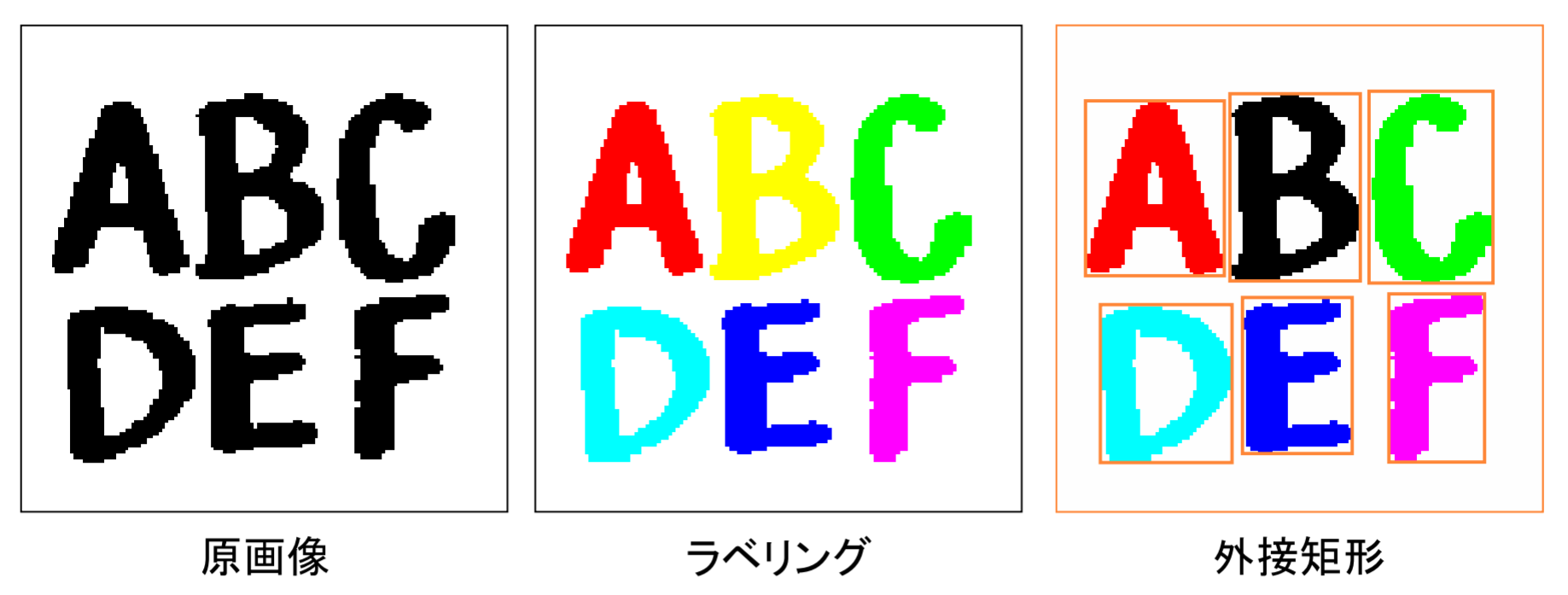
4連結を用いたラベリングの手順
- 左上画素からラスタスキャンを行い,ラベルの付いていない黒画素が見つかったら注目画素とする
- if (注目画素の上の画素がラベルを持つ) then 上の画素のラベルを注目画素に付ける
- if (左の画素がラベルを持つ) and (注目画素のラベルと異なる) then ルックアップテーブルにそれらのラベルが同一連結成分に属することを記録する
- else if (左の画素がラベルを持つ) then 左の画素のラベルを注目画素に付ける
- else 新しいラベルを注目画素に付ける
- 走査する画素がなくなるまで1から繰り返す
- 再度,ラスタスキャンを行い,ルックアップテーブルを参照しながら,同一の連結成分に属するラベル群から最も小さいラベルを選んで付け直す
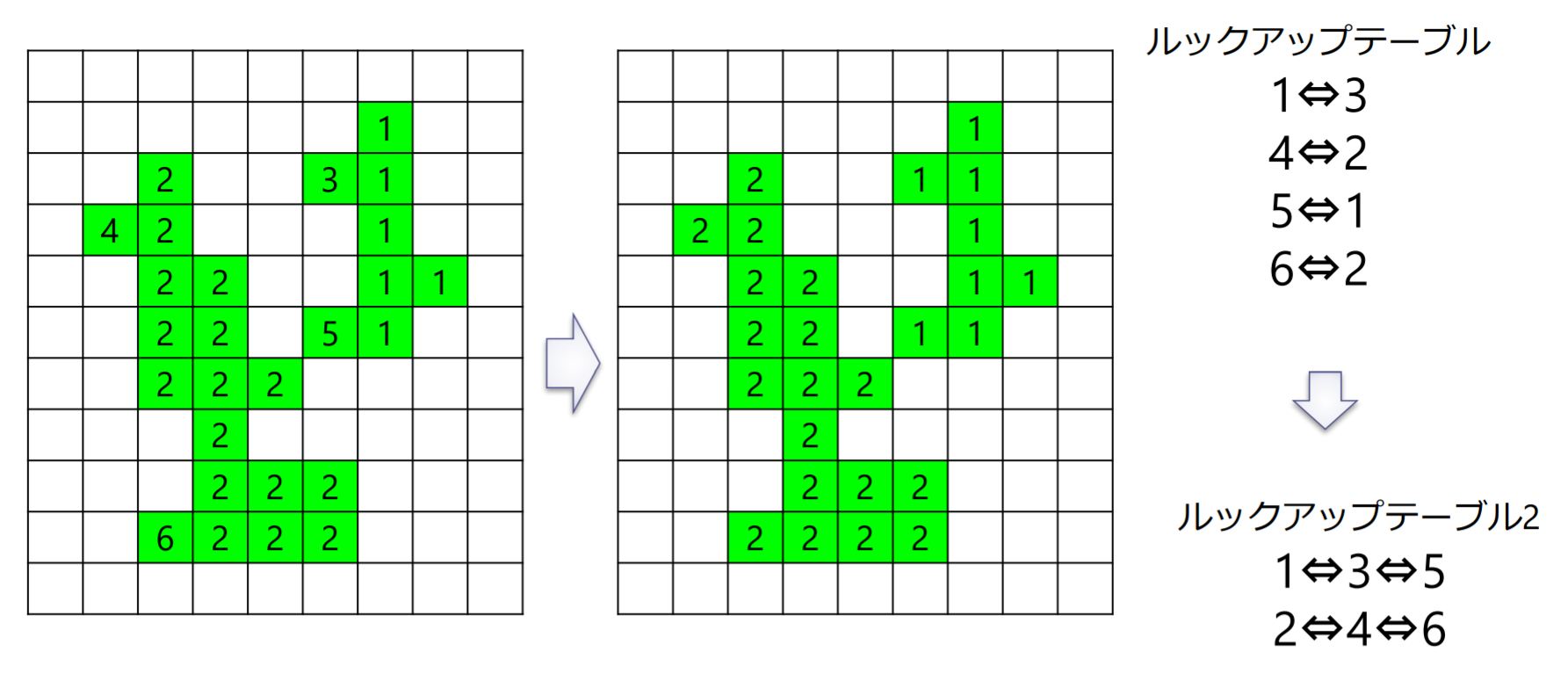
8連結を用いたラベリング
二値画像の形状特徴パラメータ
- 形状特徴パラメータ:二値画像中の連結成分の形状特徴を数値化したもの
- 面積(area):連結成分を構成する画素の数
- 周囲長(perimeter):輪郭追跡し一周する移動量
- 円形度(roundness):図形がどれだけ円に近いかを表す尺度
- モーメント特徴(moment feature)
画像の空間周波数解析
一次元フーリエ変換
連続関数 を正弦波の重ね合わせ(フーリエ級数)として表現
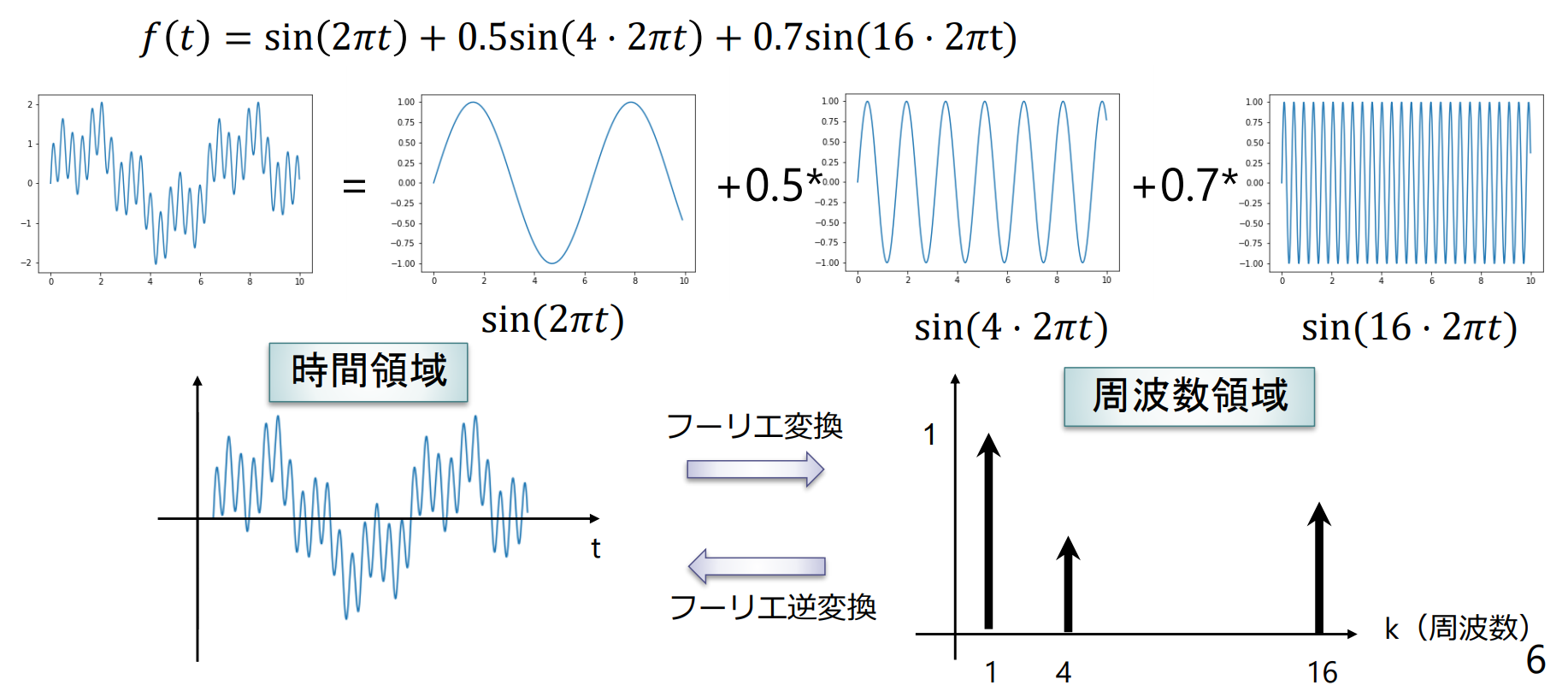
フーリエ級数展開
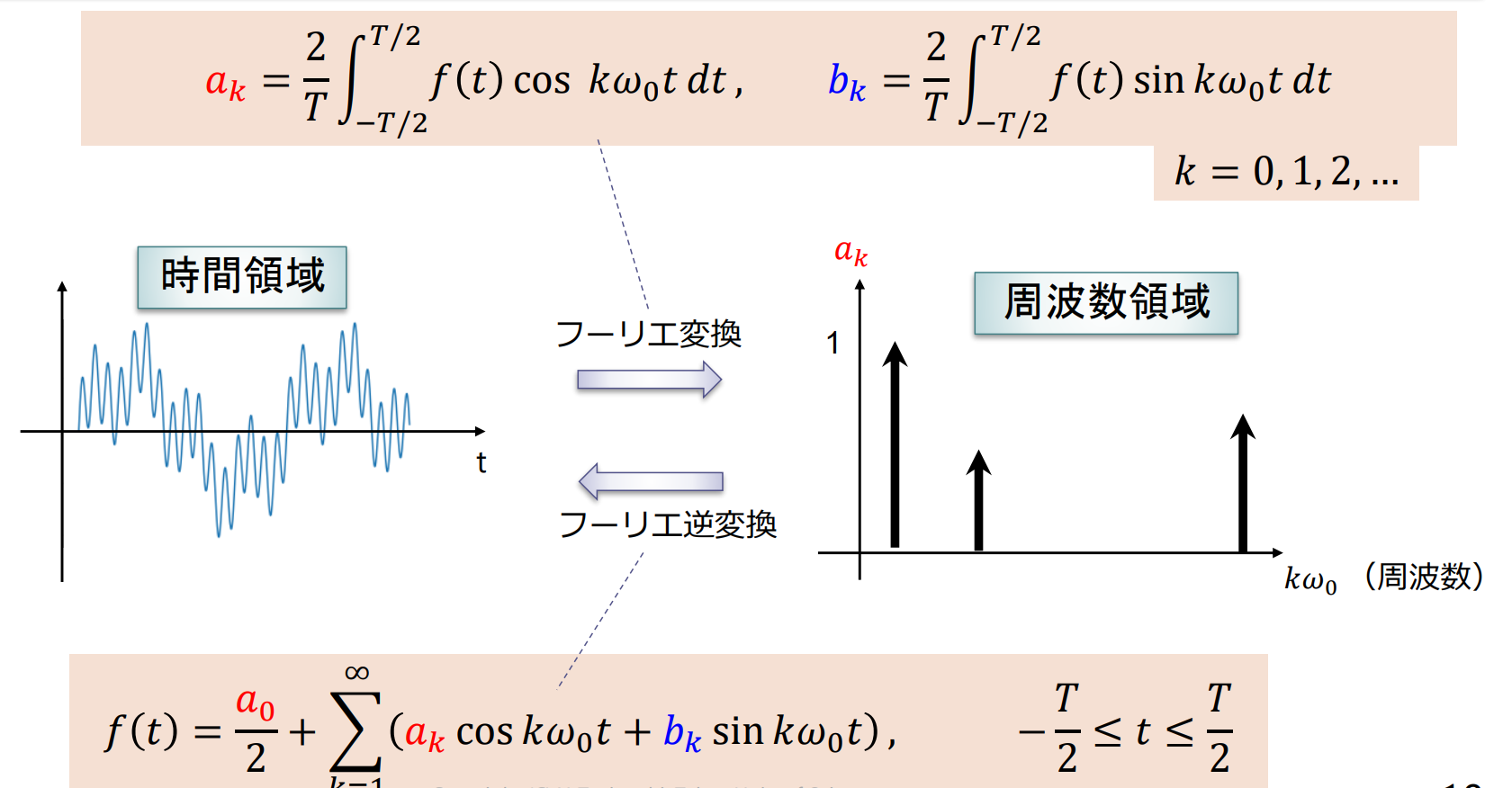
周期 の連続関数 は以下のようにフーリエ級数に展開できる( 関数の重ね合わせで表現できる)

フーリエ変換とフーリエ逆変換
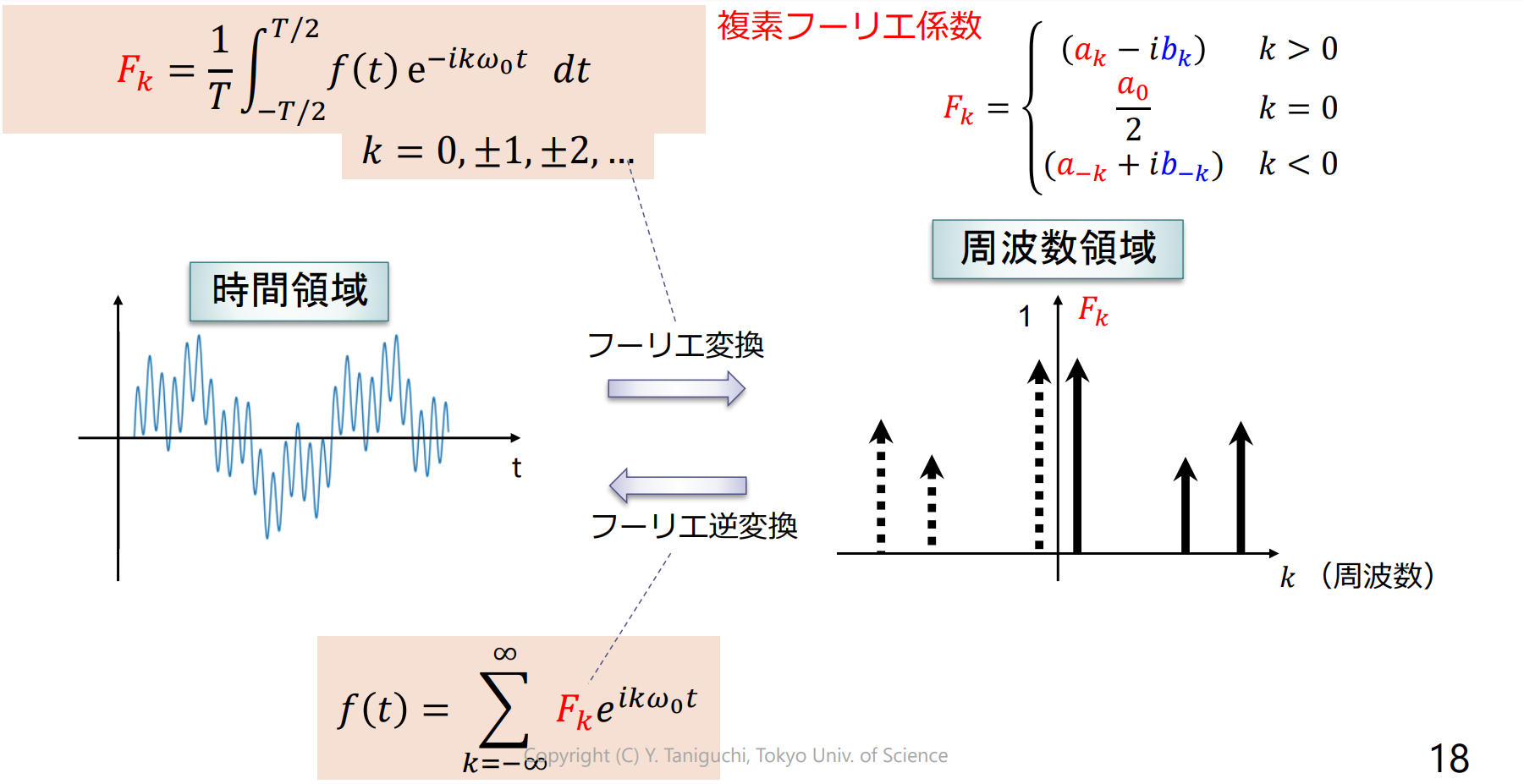
フーリエ級数の複素数表示
パワースペクトル
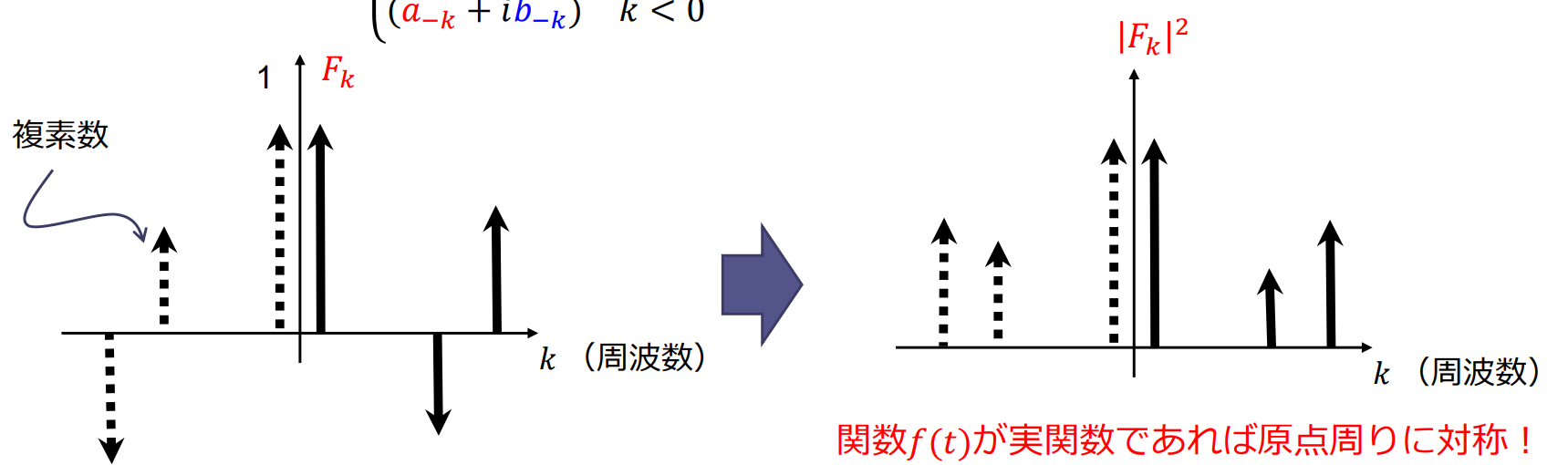
複素フーリエ級数 は複素数なので棒グラフで表せない パワースペクトルで可視化
パワースペクトル (power spectra):縦軸に複素フーリエ係数の絶対値の二乗 をプロット
- 振幅スペクトル: をプロット
離散フーリエ変換
区間 を間隔 で 分割して標本化するので とおく
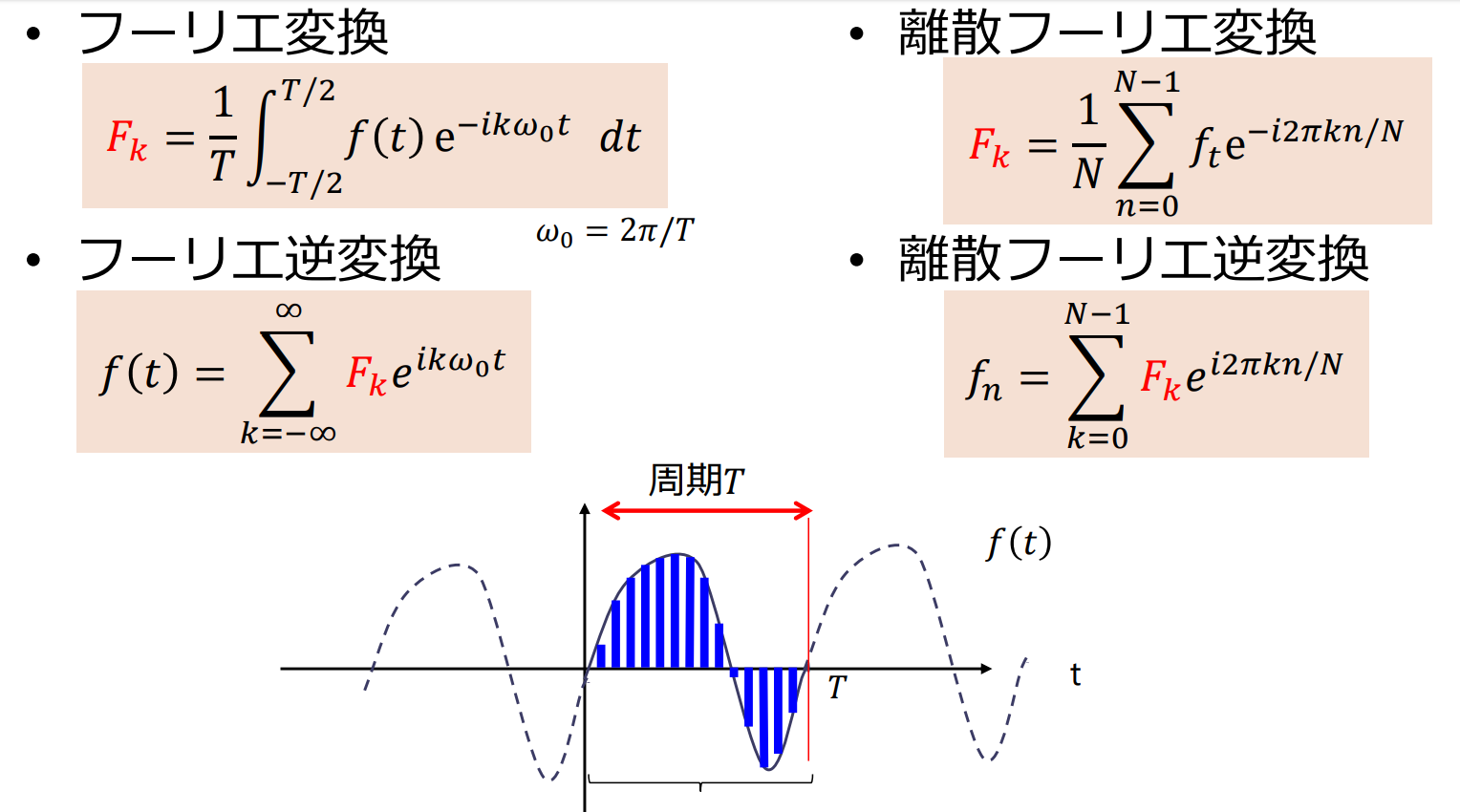
高速フーリエ変換
高速フーリエ変換(Fast Fourier Transform; FFT):離散フーリエ変換(Discrete Fourier Transform; DFT)を高速に計算するアルゴリズム
- 標本点の数が の場合,素朴にフーリエ変換すると計算量は
- 高速フーリエ変換を使用すると で計算できる( が2のべき乗のとき)
2次元フーリエ変換
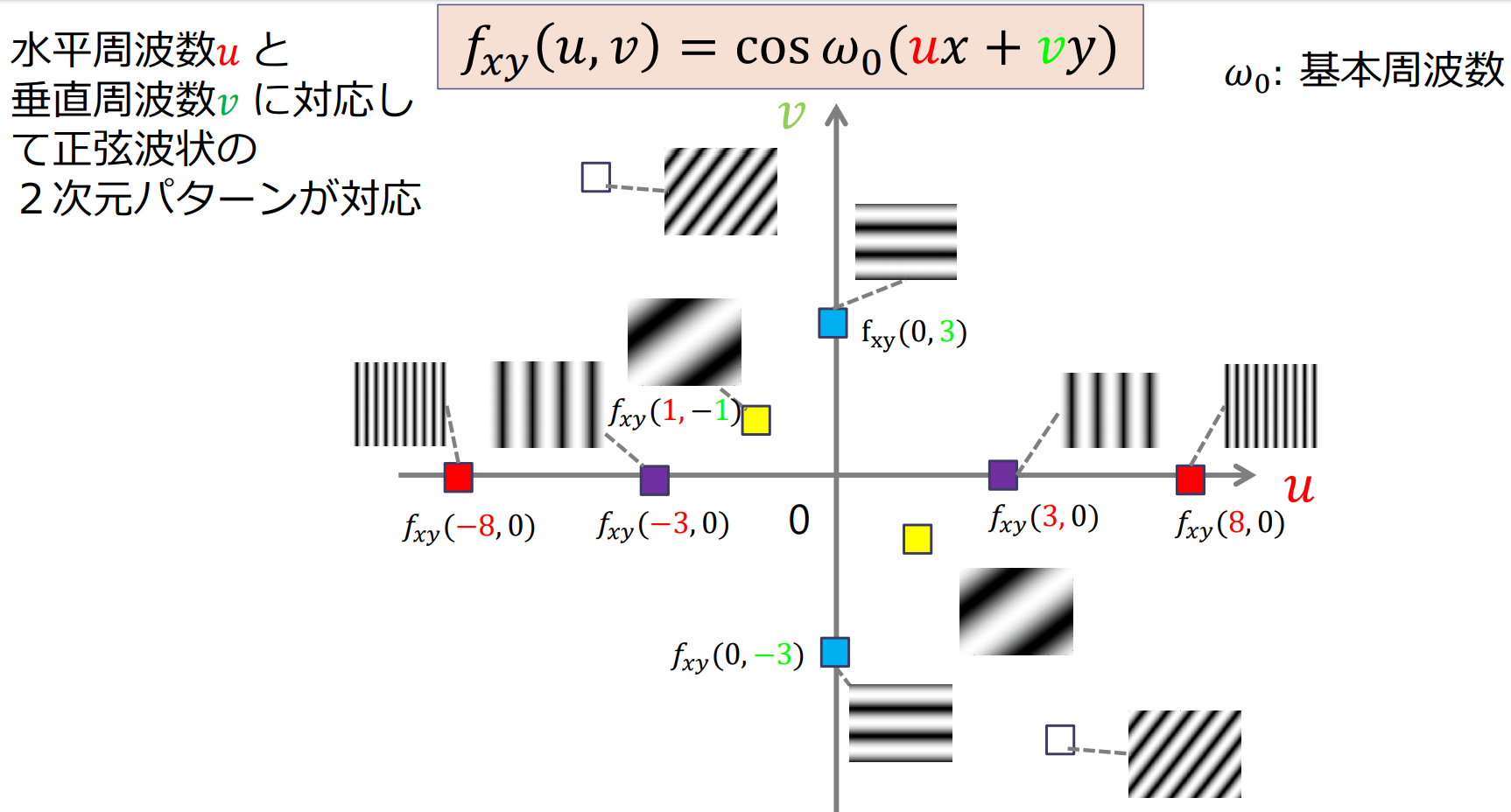
画像 は2次元正弦波の重ね合わせとして表現できる
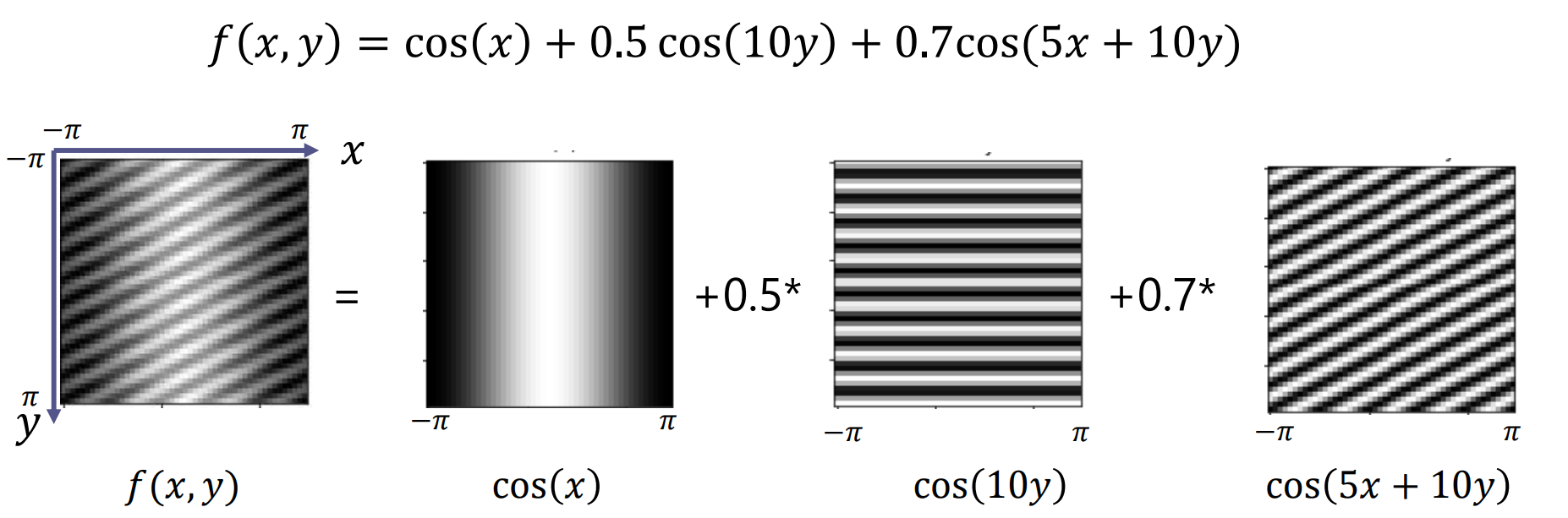
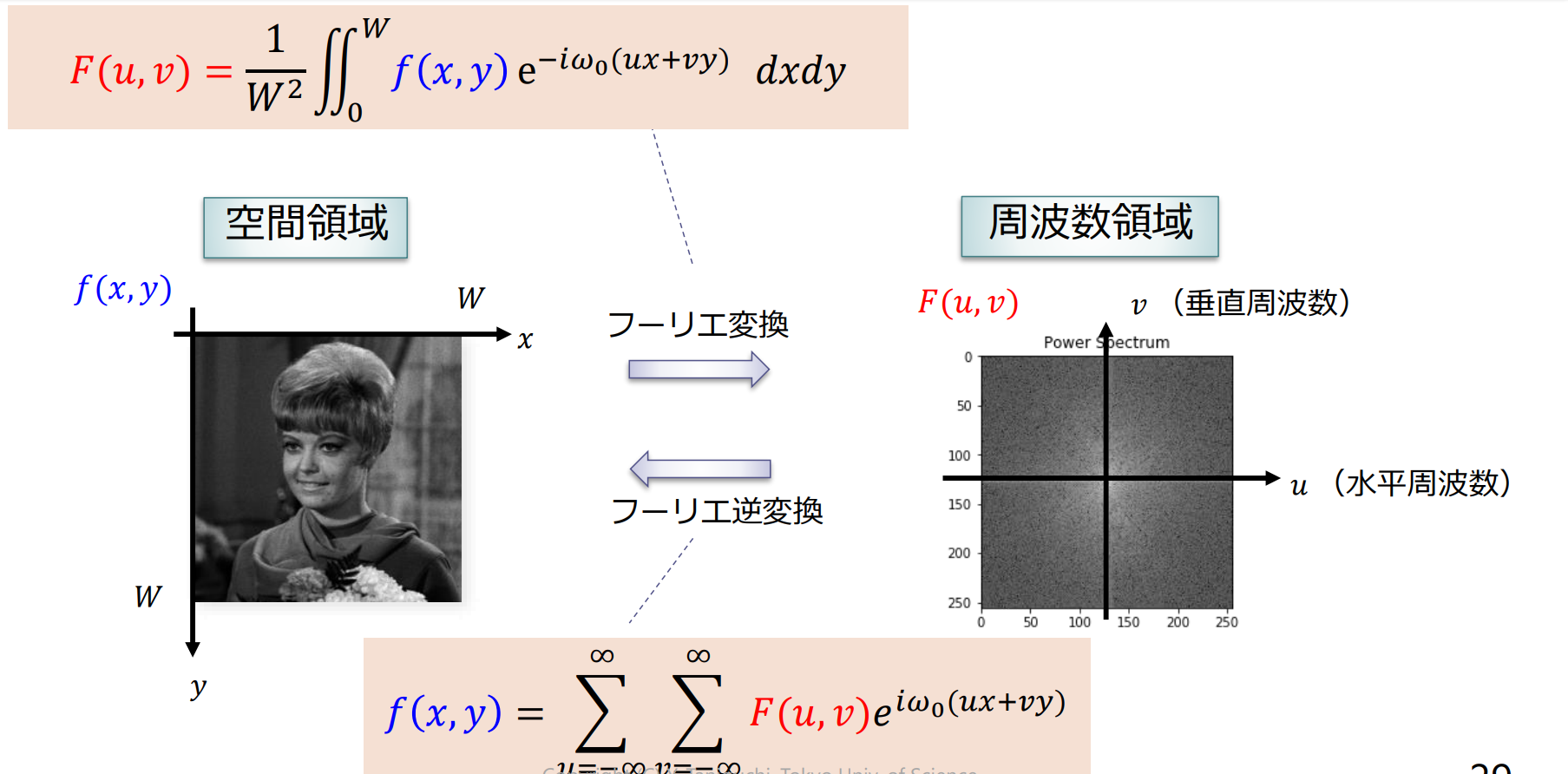
2次元正弦波と画像の関係
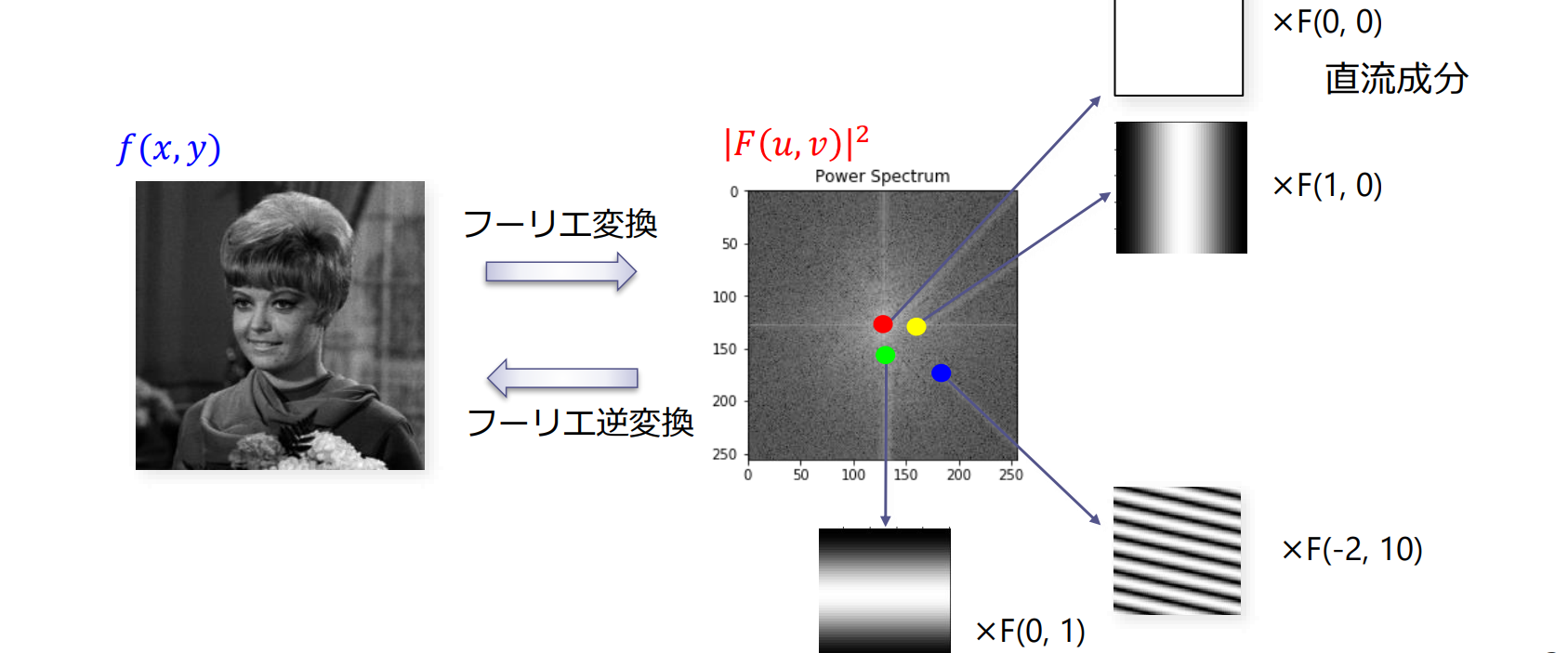
パワースペクトルと画像の関係
(複素)フーリエ係数は正弦波状の2次元パターンを合成する際の大きさ(重み)と位相に対応
例題5.1

- (1)は,エッジや細かなテクスチャがないので,低周波領域にエネルギーが集中するので
- (2)は,細かなテクスチャを持つので高周波領域にもエネルギーが分散する.縦方向,横方向の明確なエッジはないので に対応する
- (3)は,小さな文字を含むので高周波領域にもエネルギーが分散する.横方向に文字が並んでいるので,パワースペクトル画像に縦方向の筋が見えるAが対応する((2),(3)の区別は難しい)
- (4)は,建物に斜めに延びるエッジを含むので,パワースペクトル画像に斜めの筋がみえるDが対応する
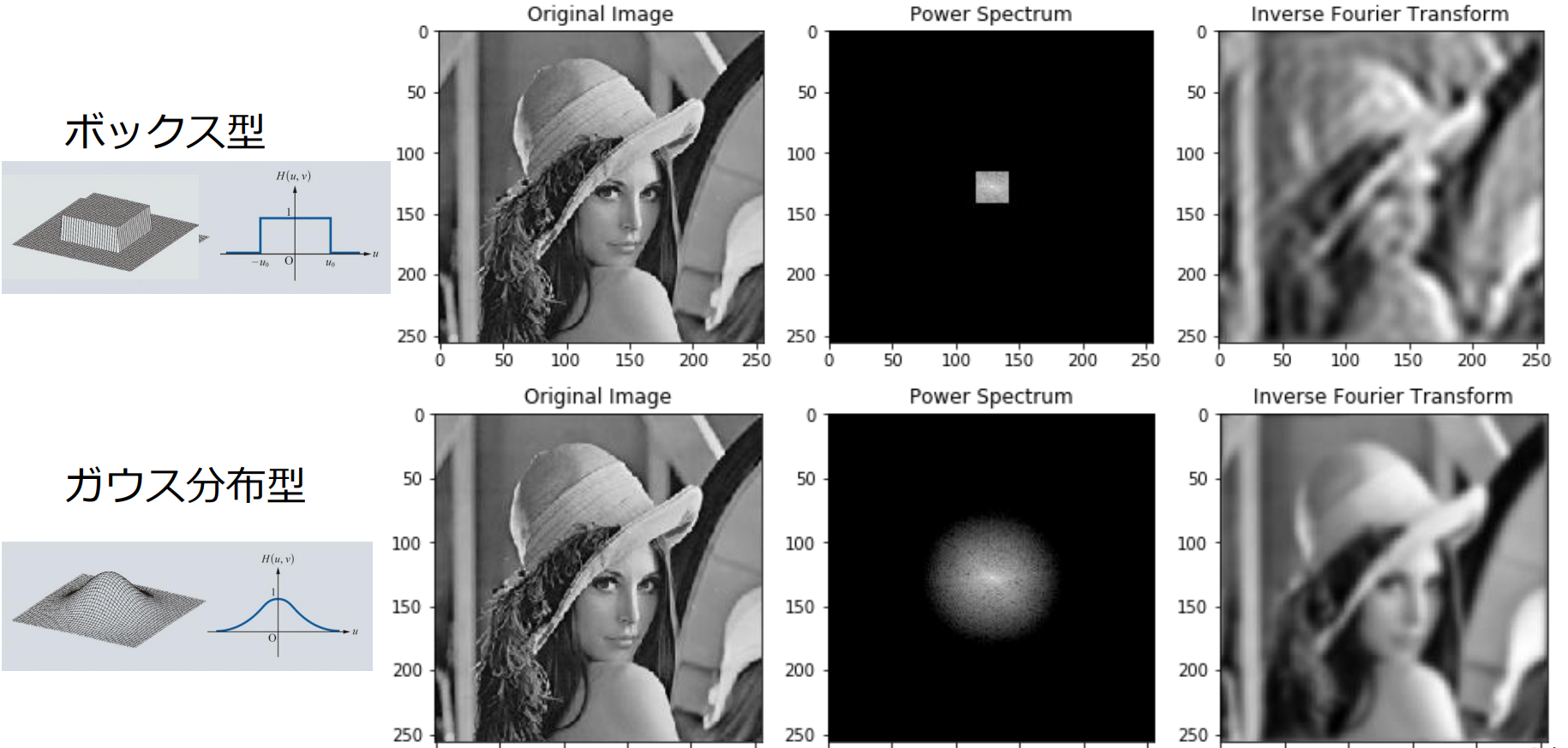
周波数領域でのフィルタ処理
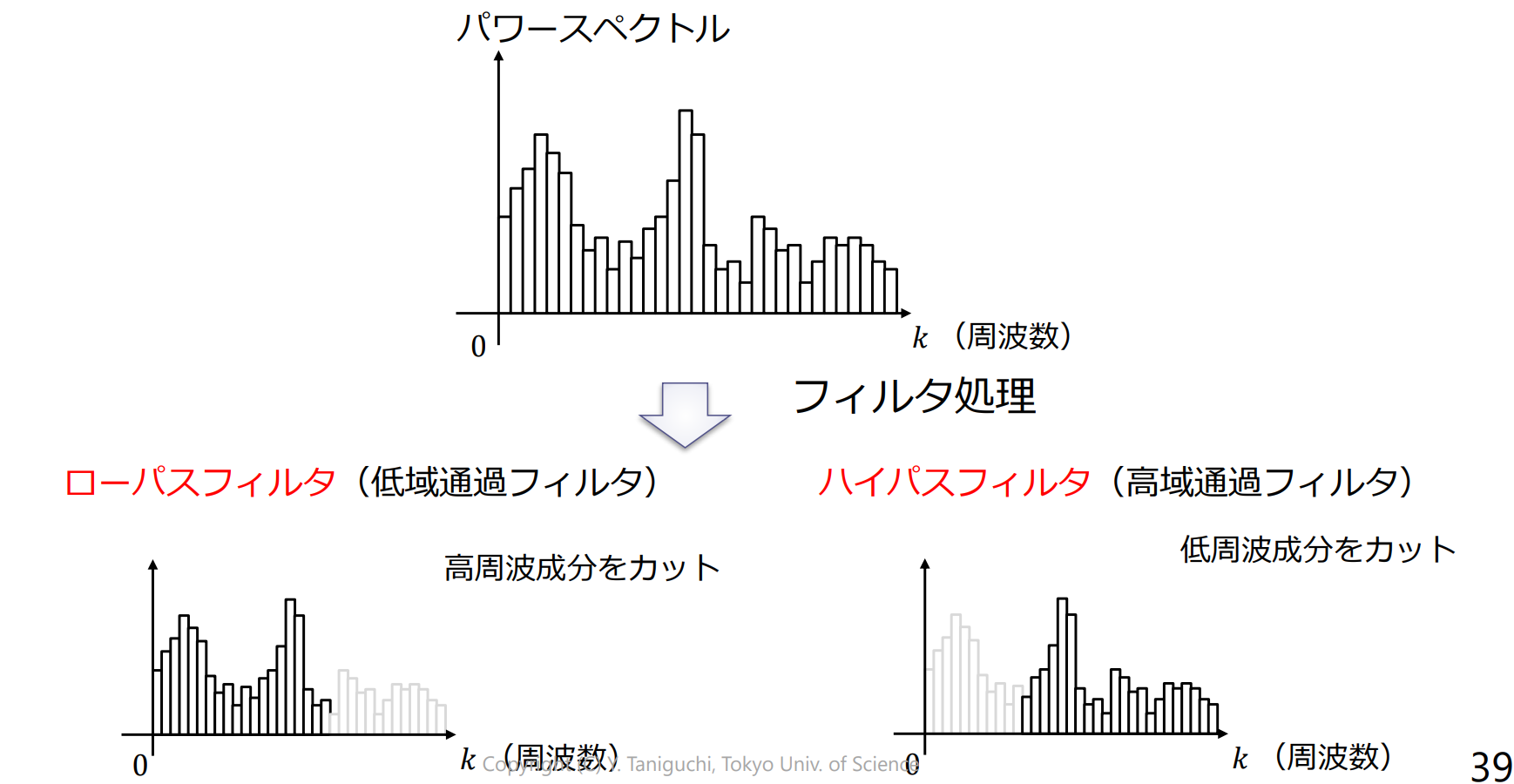

ローパスフィルタ
ハイパスフィルタ
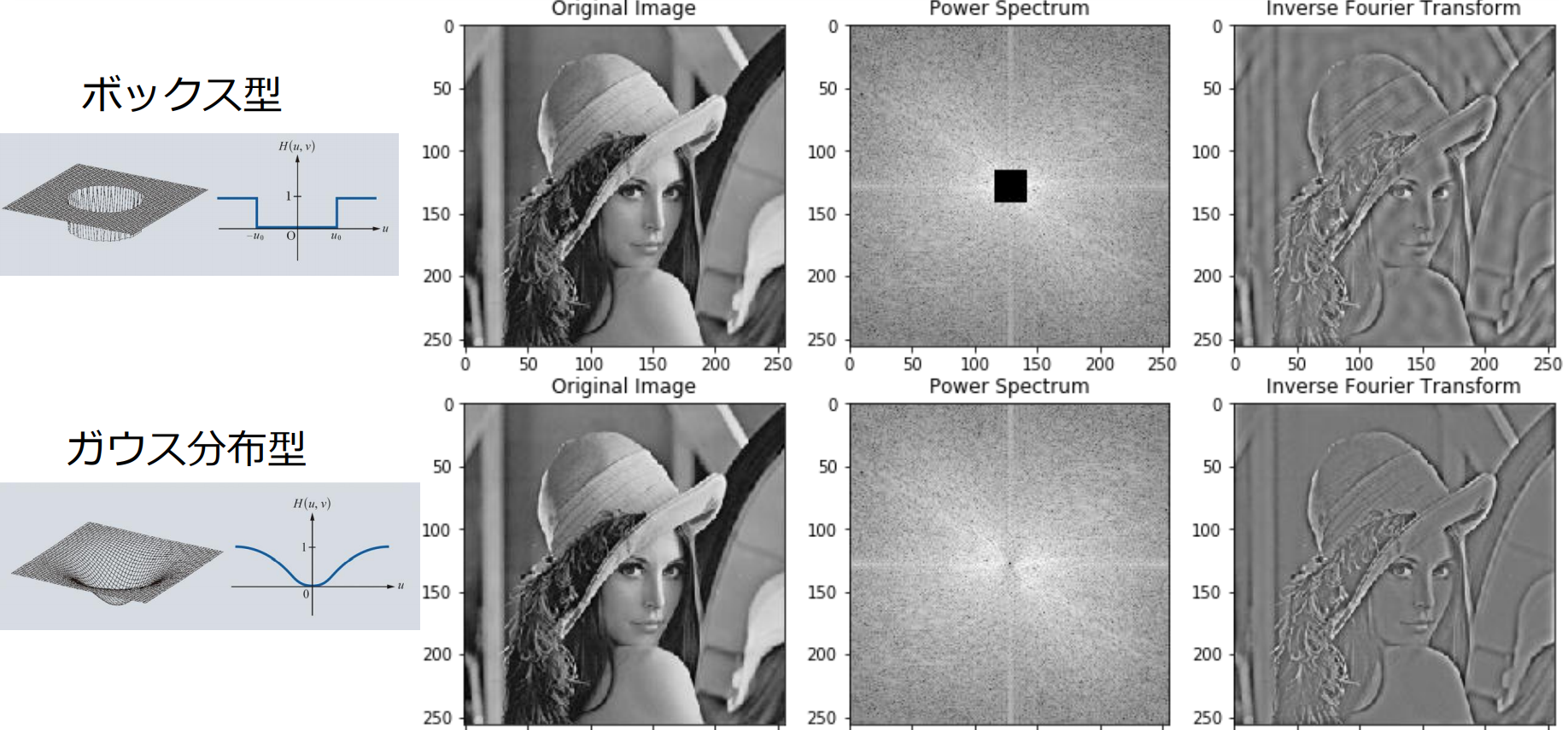
畳み込み定理(convolution theorem)
畳み込み定理(convolution theorem):空間領域の畳み込み演算 は,周波数領域の積演算 と等しい

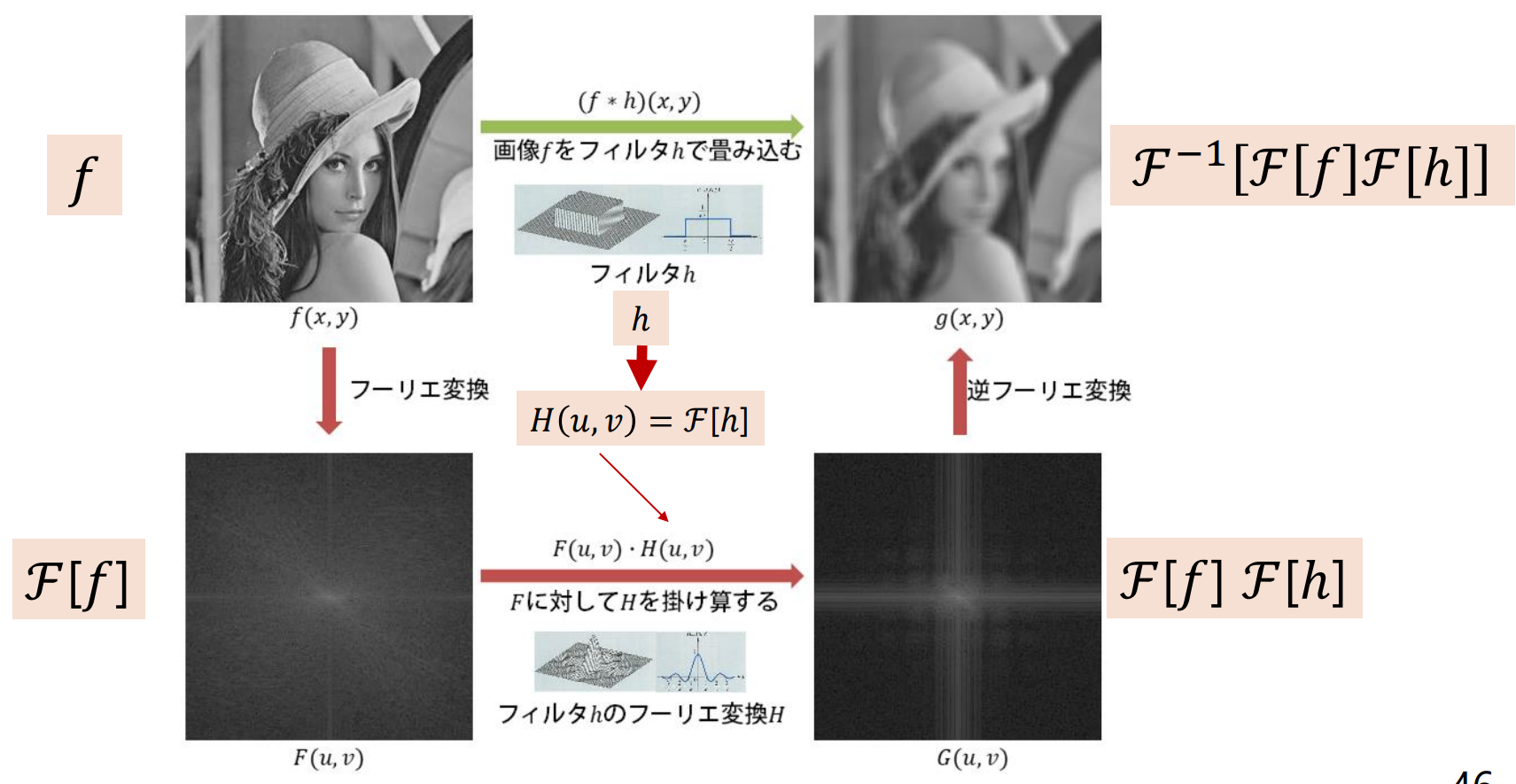
フーリエ変換の画像応用
フーリエ変換の利用分野:
- 画像情報の圧縮(符号化)-- 離散コサイン変換(DCT: discrete cosine transform)
- テクスチャ解析
- 空間フィルタ処理の高速計算
- 計算機ホログラム
離散コサイン変換(DCT)
DCTは連続関数をcos関数の重ね合わせで表現

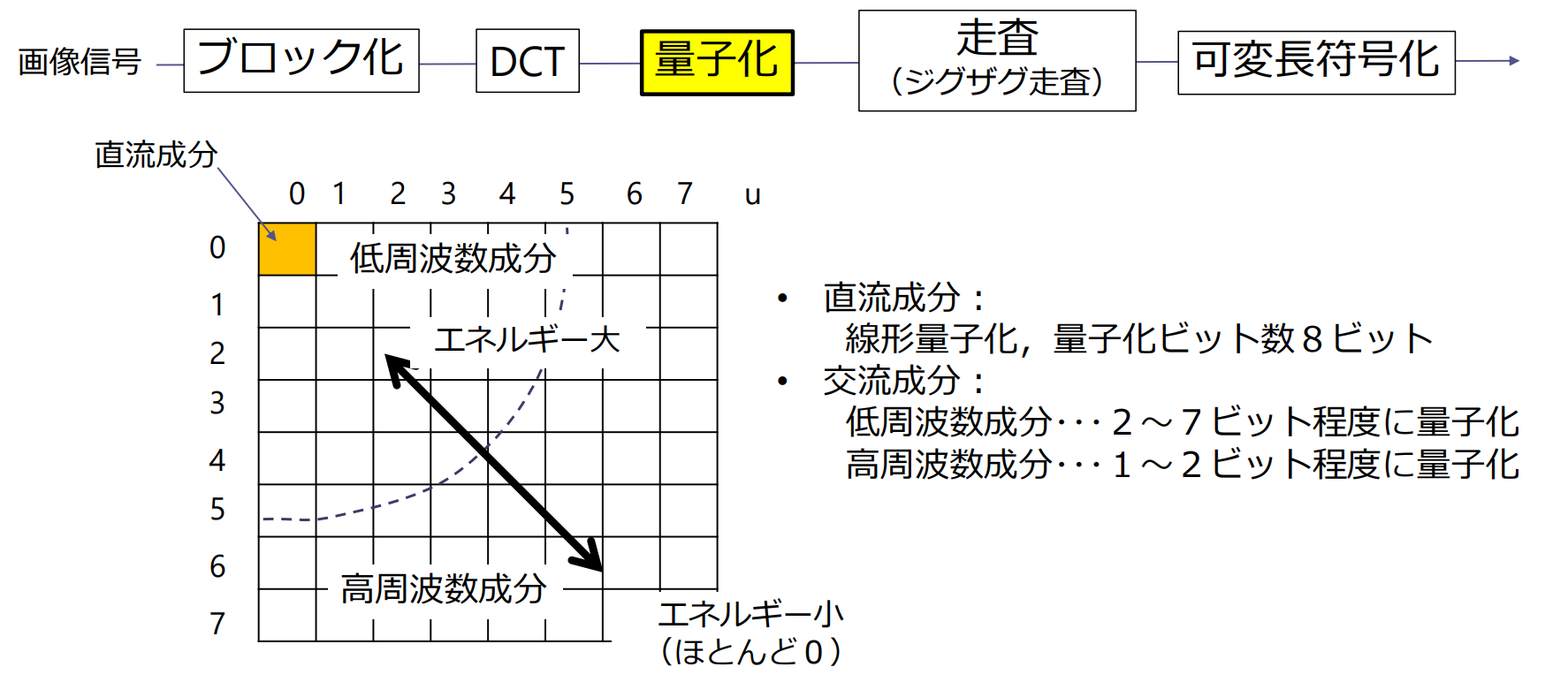
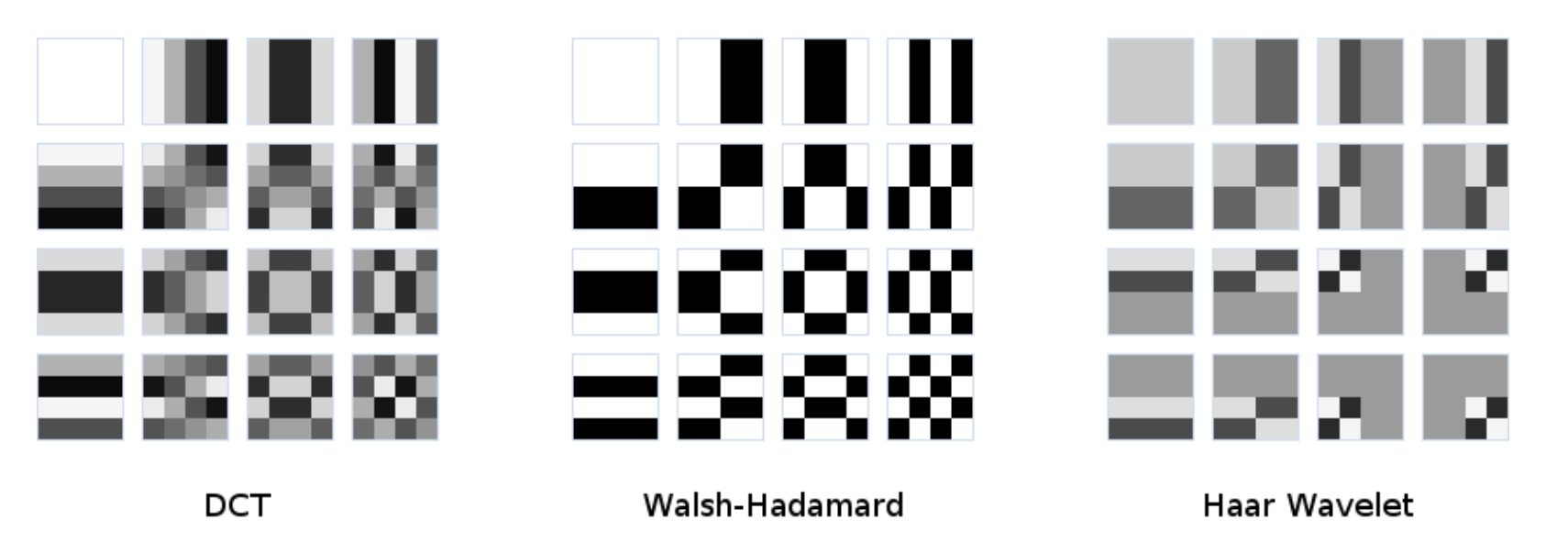
Haarウェーブレット
特徴抽出に利用(Viola & Johnes 顔検出)
MOSSE filter
MOSSE filter:周波数フィルタの物体トラッキングへの応用

例題5.2
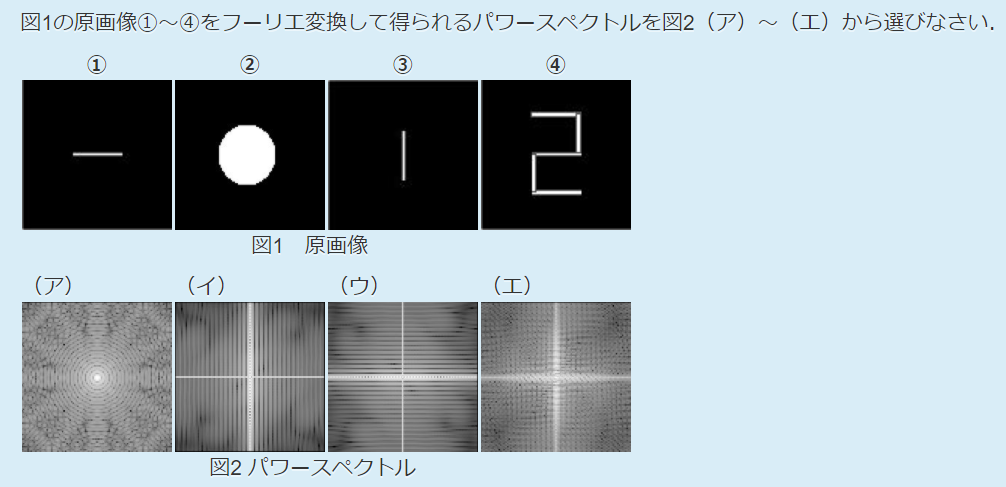
- 原画像1に対応するパワースペクトル:イ
- 原画像2に対応するパワースペクトル:ア
- 原画像3に対応するパワースペクトル:ウ
- 原画像4に対応するパワースペクトル:エ
例題5.3
- 畳み込み定理によれば,空間領域の畳み込み演算(convolution)は,周波数領域における積演算に対応する(等価である)
- 1次元フーリエ変換は,連続関数 を正弦波(sin波とcos波)の重ね合わせることで表現する
- 元の信号 が実関数であれば,そのフーリエ変換のパワースペクトルは原点まわりに対称になる
- ガウス関数のフーリエ変換はガウス関数,一様関数のフーリエ変換はデルタ関数,矩形関数のフーリエ変換はsinc関数となる
- フーリエ変換を高速に計算するアルゴリズムをFFTとよぶ
- 高域周波数をカットした画像(ローパスフィルタ後の画像)は,原画像に対して平滑化する効果があり,低域周波数をカットした画像(ハイパスフィルタ後の画像)は,原画像に対してエッジ検出する効果がある
画像の幾何変換
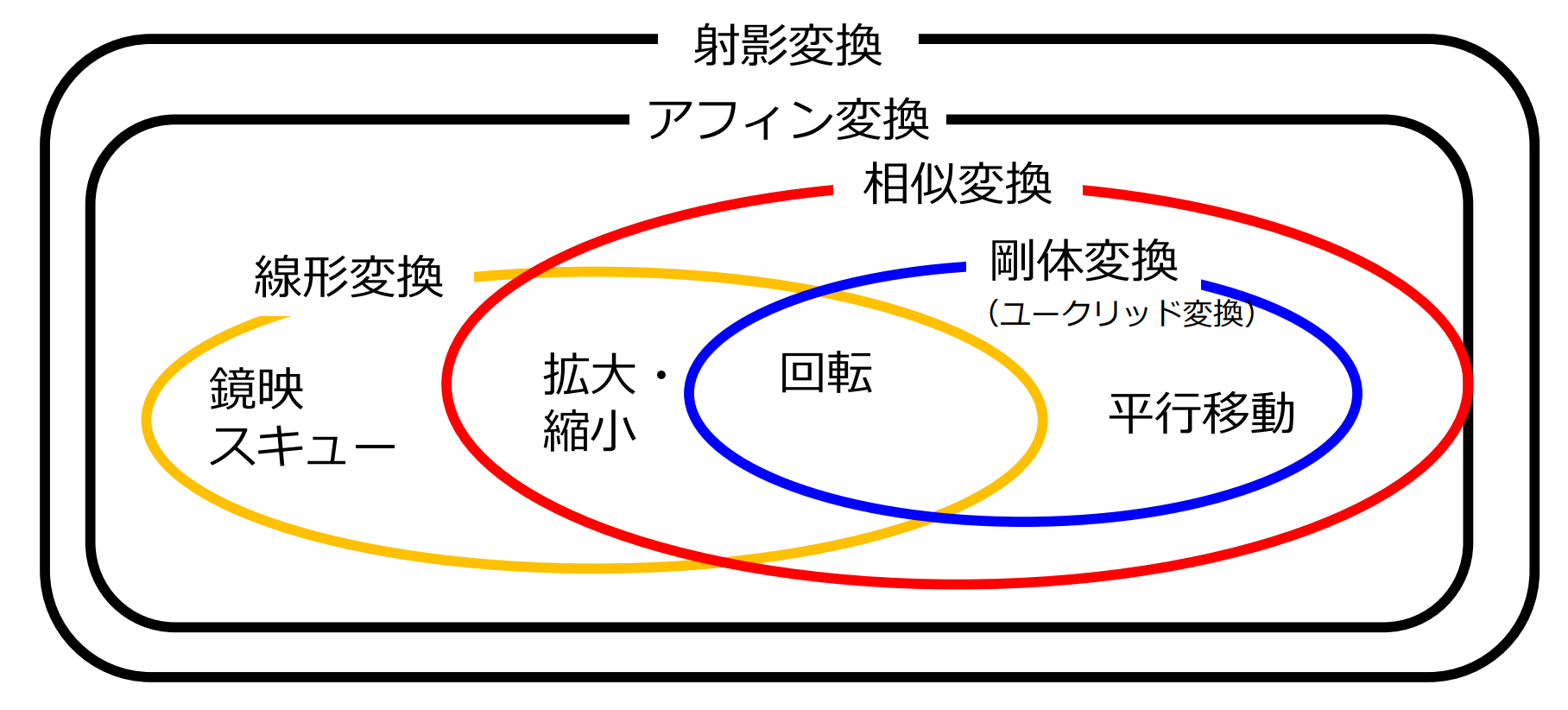
線形変換(linear transformation)
入力画像上の点 が出力画像上の点 に移動
線形変換の具体例:
- 拡大・縮小
- 回転
- 反転(鏡映)
- スキュー(せん断)
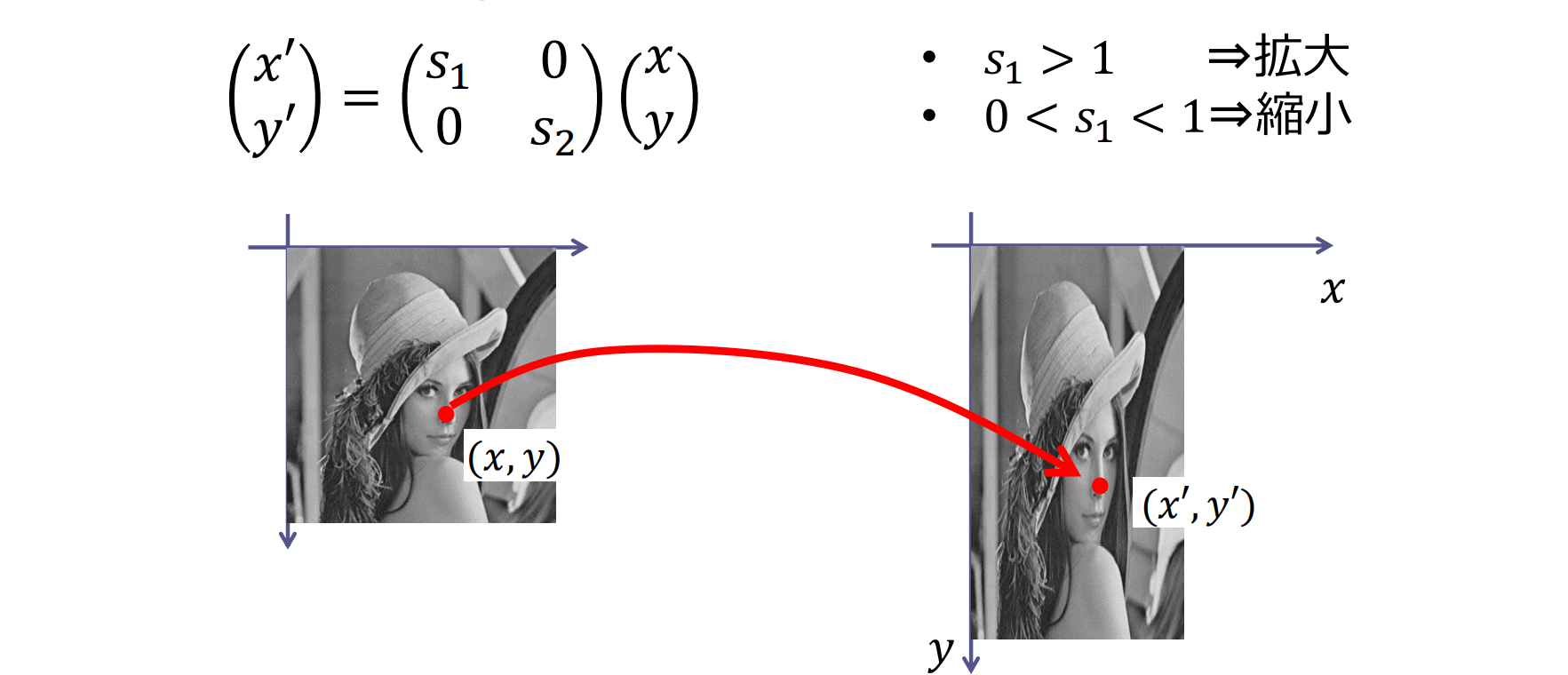
拡大・縮小
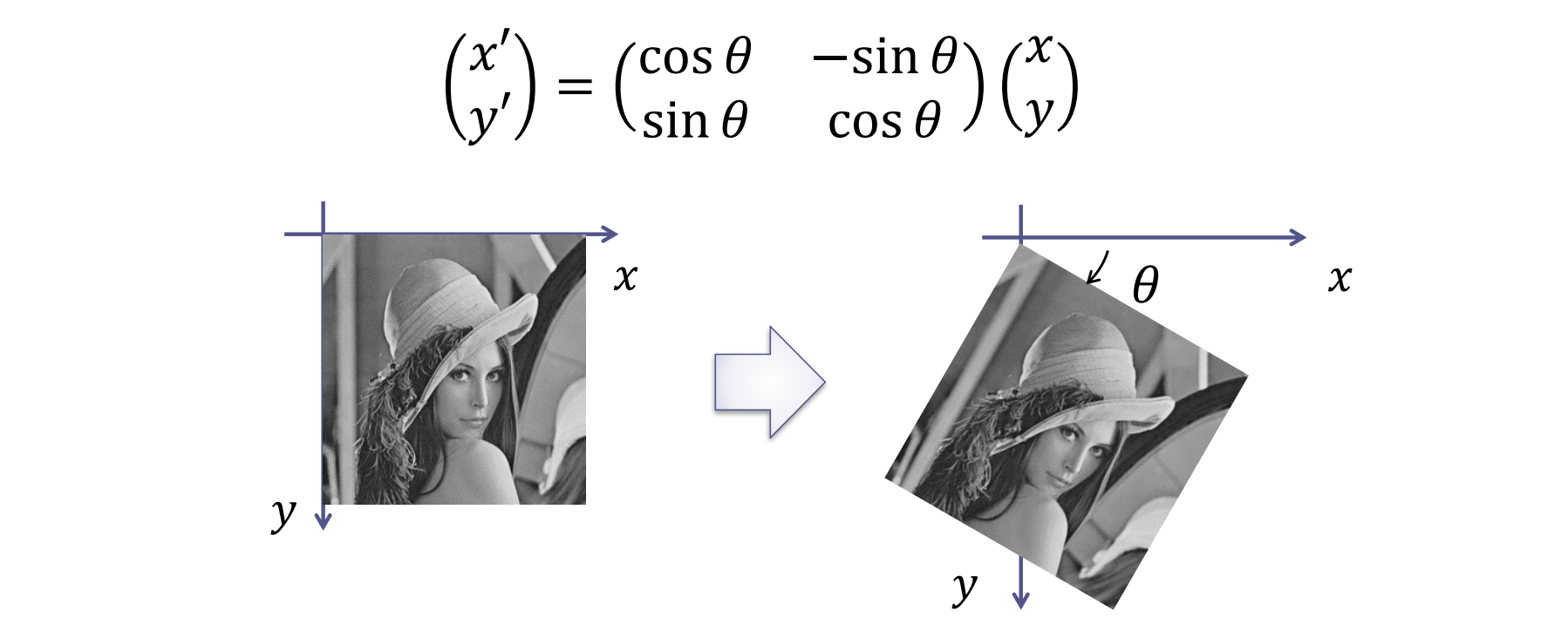
回転
角度 の回転(rotation)
反転(鏡映)
直線や点について対称な位置に移動する変換を反転(inverse)
- 直線に関する反転を鏡映(reflection)
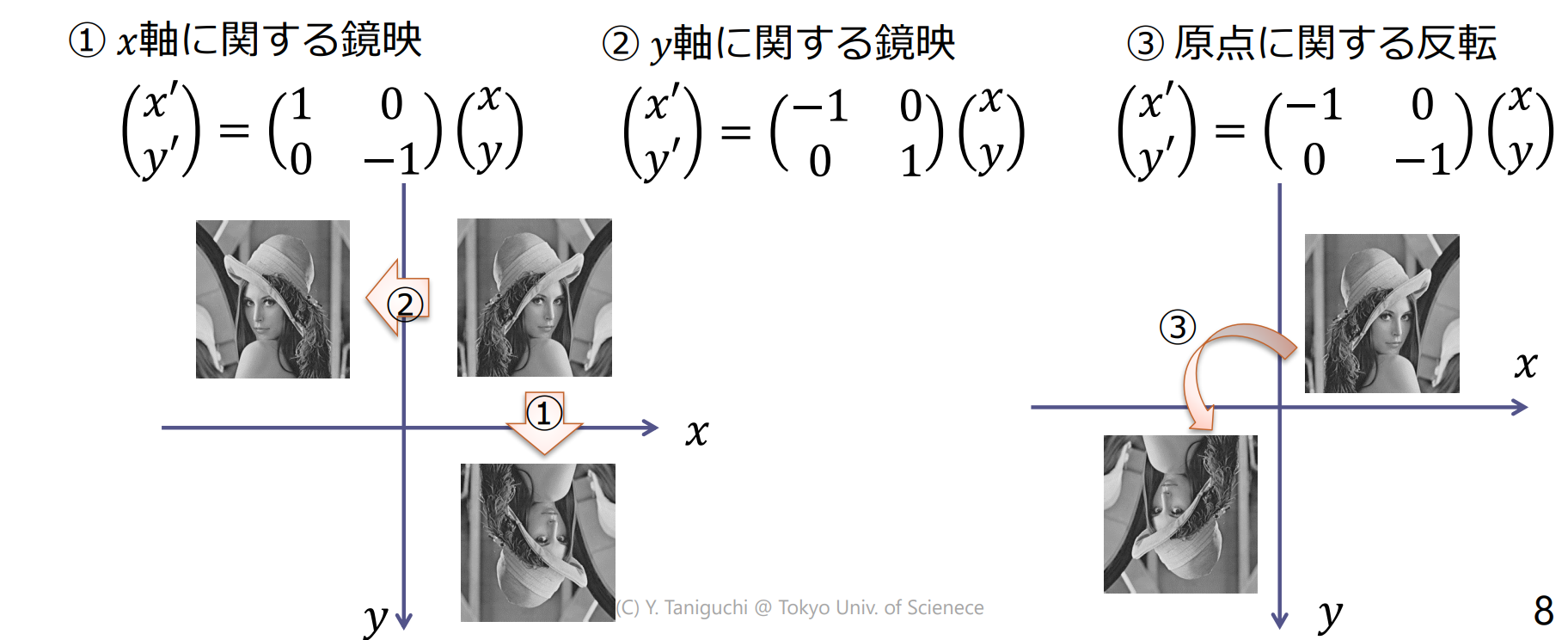
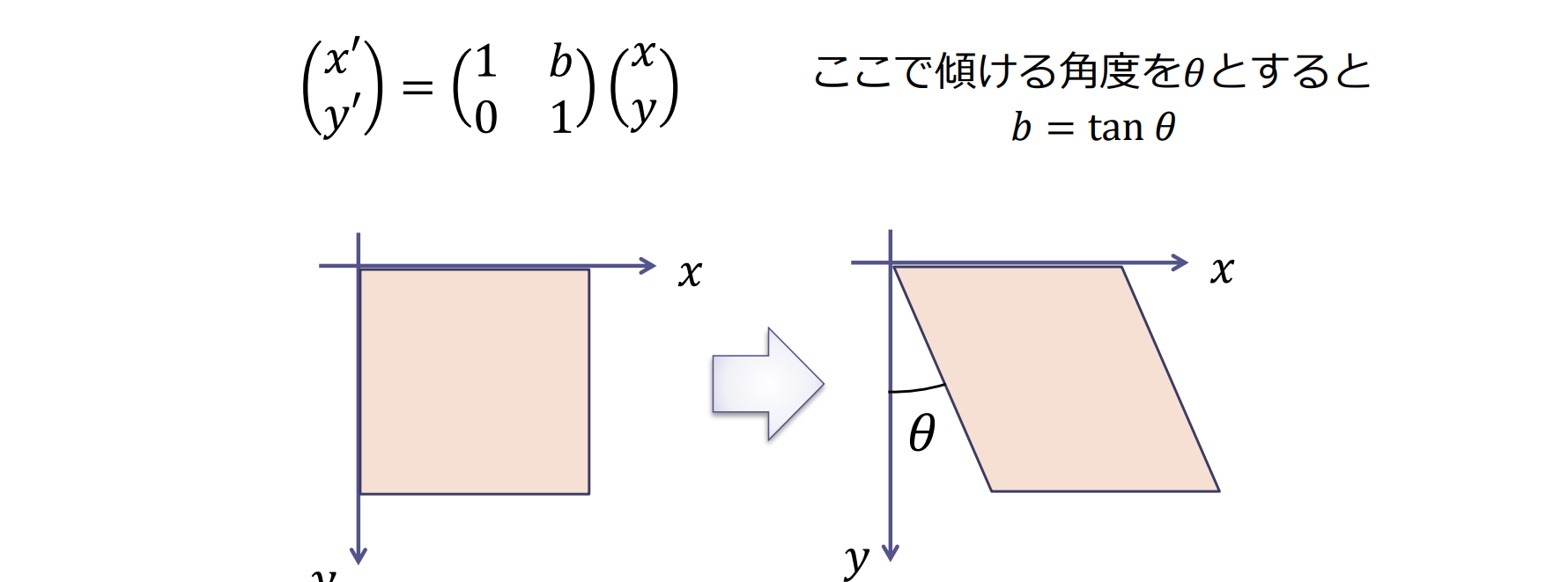
スキュー(せん断)
長方形を傾けて平行四辺形にするような変換をスキュー(skewing),あるいはせん断(shearing)
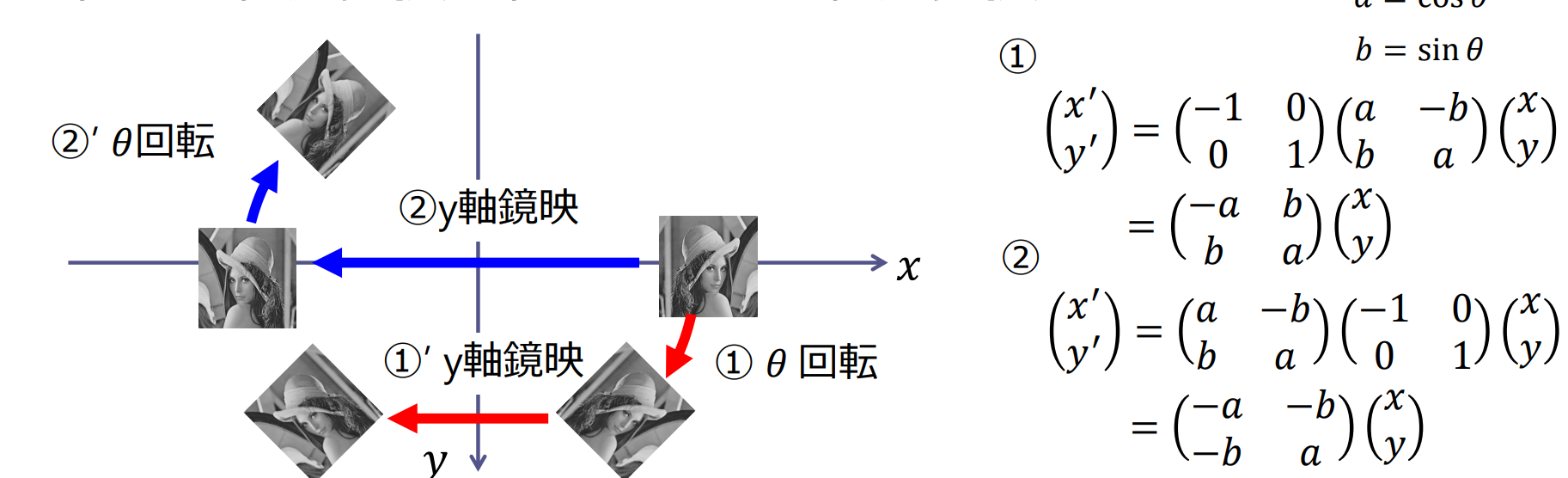
合成変換
合成変換(composite transformation)を表す行列は,個々の変換行列の積となる
- 任意の線形変換の組み合わせは線形変換
変換の順序を変えると結果が変わる
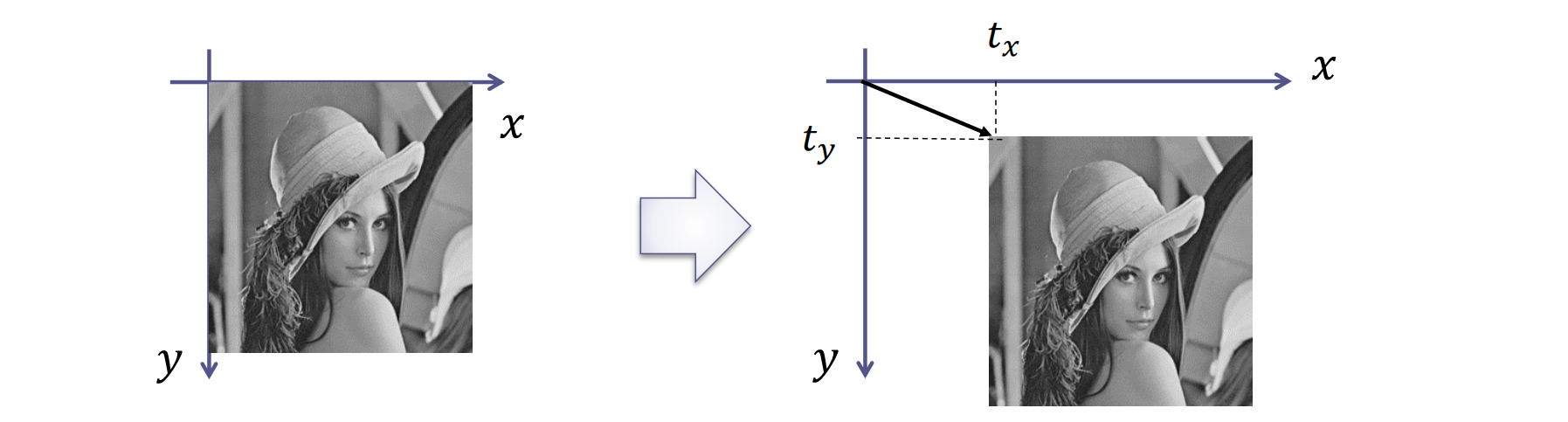
並行移動
平行移動(translation)
平行移動は線形変換ではない
アフィン変換
アフィン変換(affine transformation):任意の線形変換と平行移動を組み合わせた変換
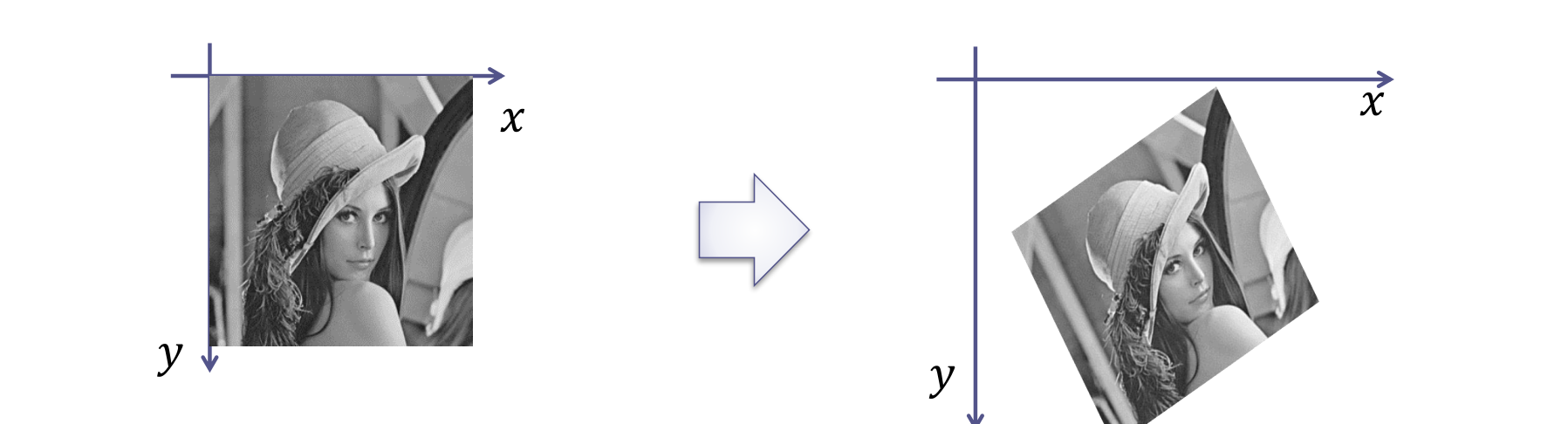
例題6.1
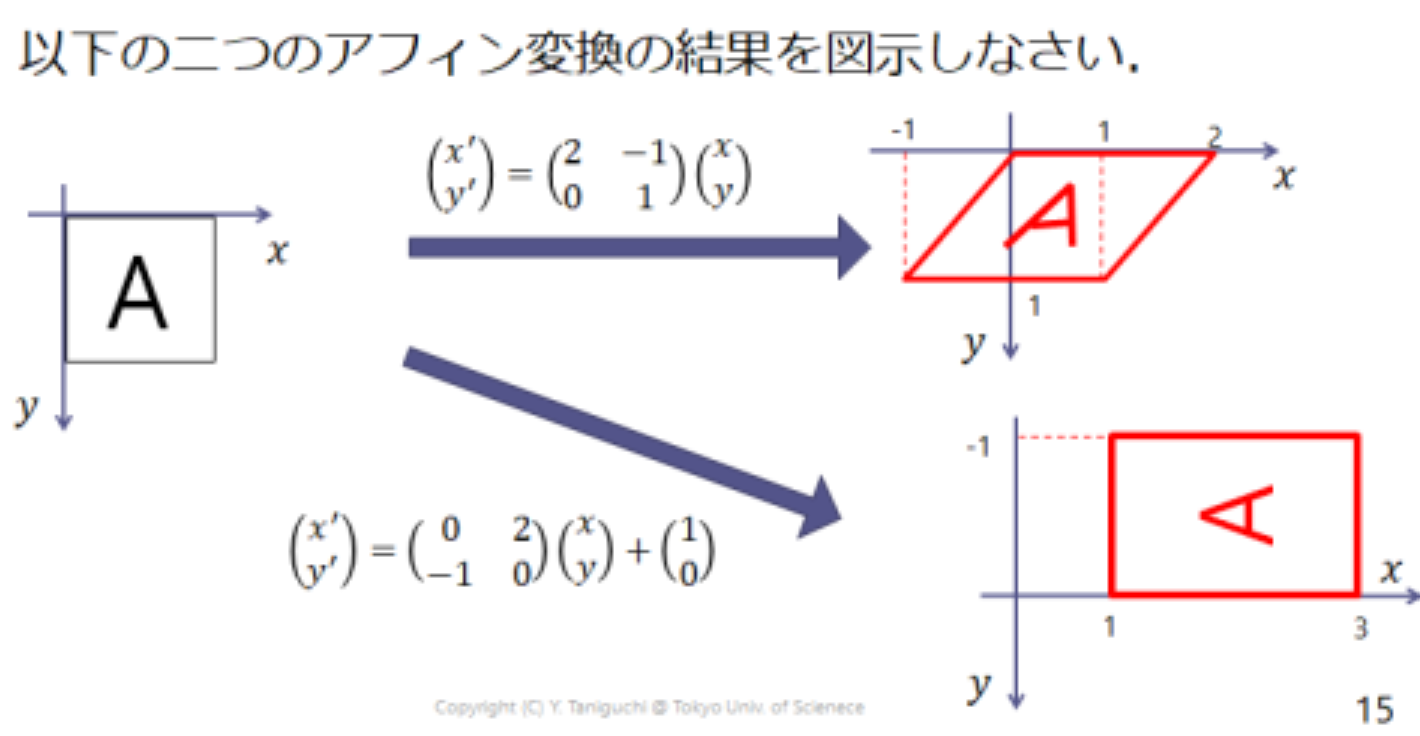
同次座標を用いた幾何変換の表現
アフィン変換の合成変換
二つのアフィン変換の合成:
デカルト座標と同次座標
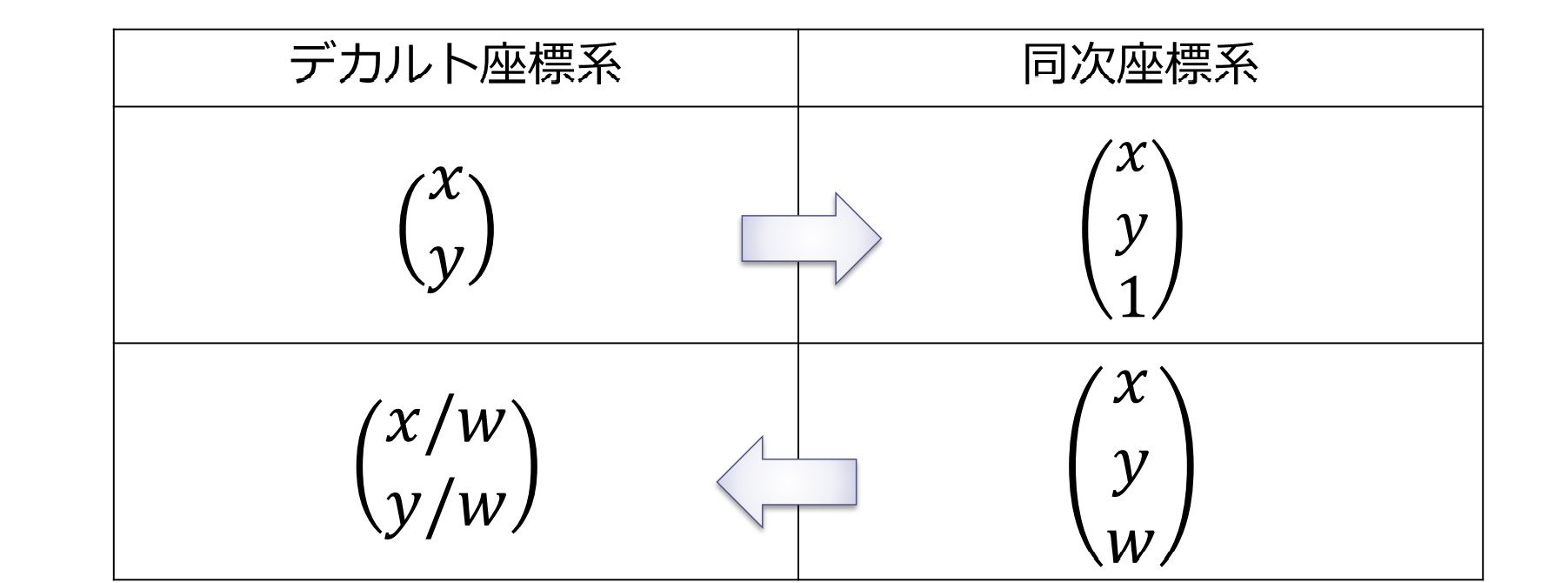
同次座標を用いたアフィン変換
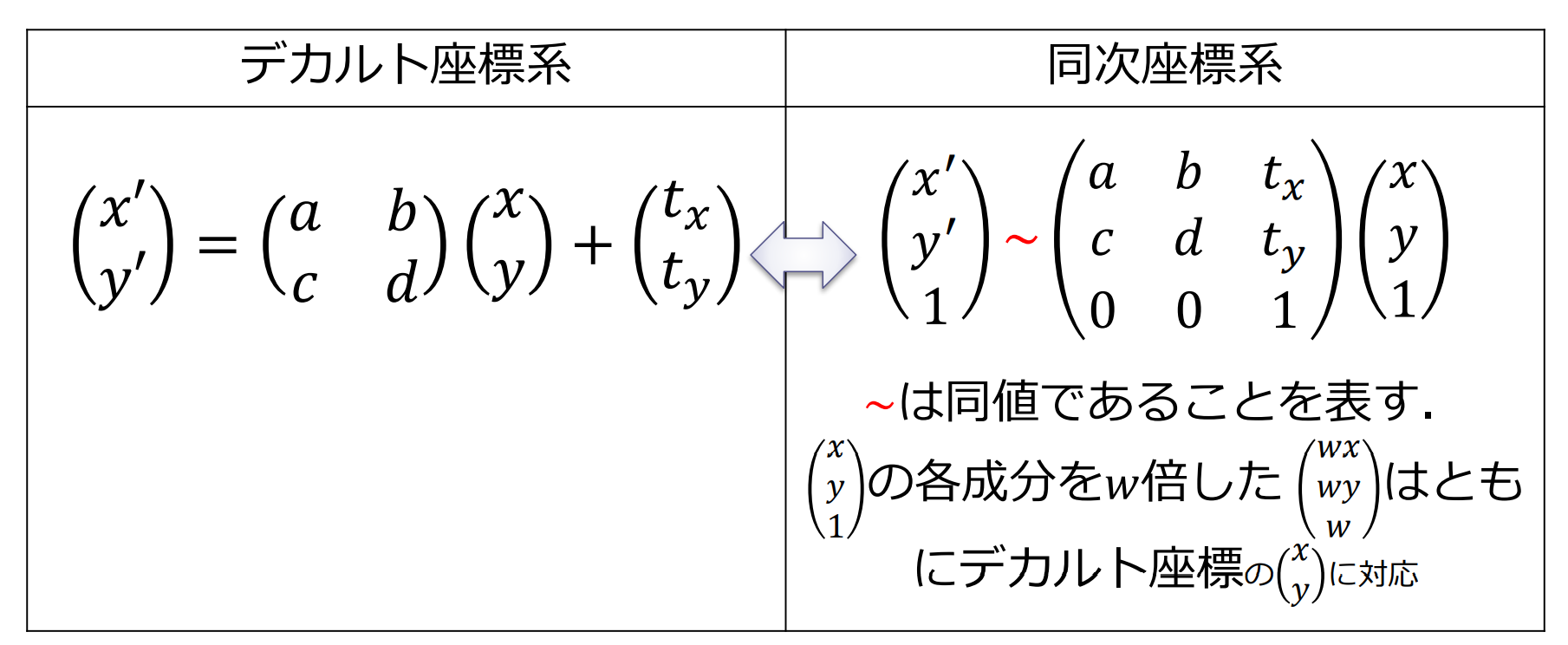
アフィン変換の合成変換
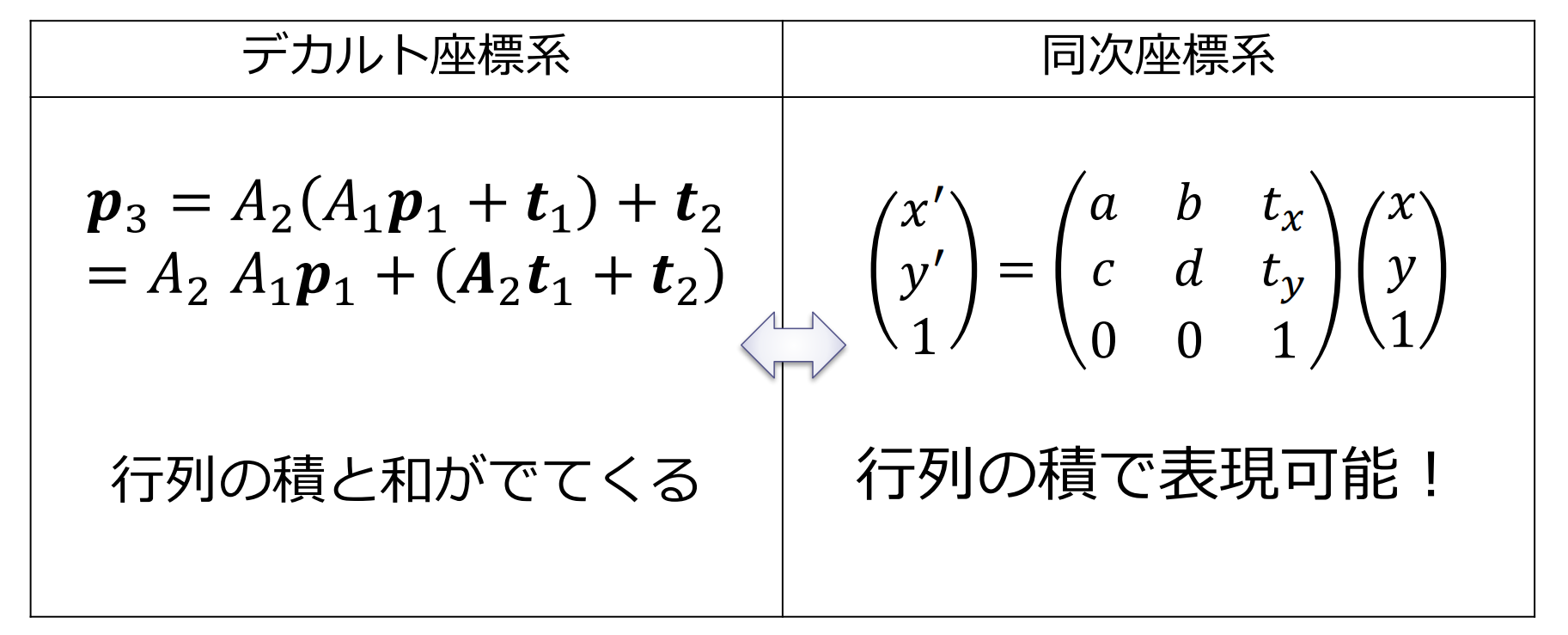
同次座標による幾何変換の表示

同次座標を用いたアフィン変換の合成変換
変換行列 によって が に変換される式は
変換行列 によって が に変換される式は
- :合成変換行列

例題6.2

平面射影変換
- 透視変換(perspective transform), ホモグラフィー(homography)とも呼ばれる
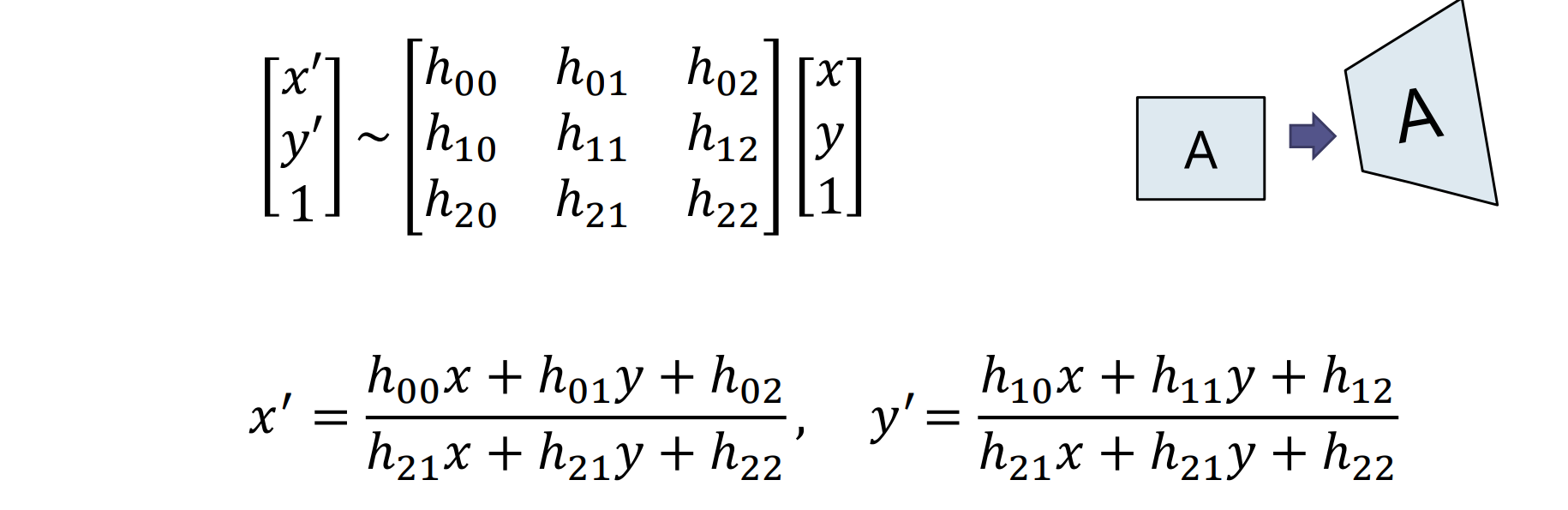
注意:上图中 的分母
2次元幾何変換のまとめ
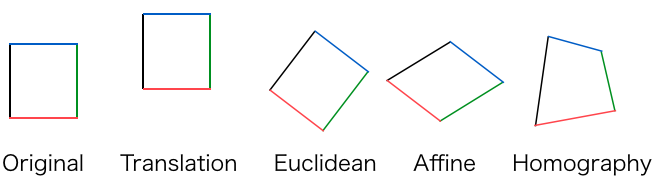
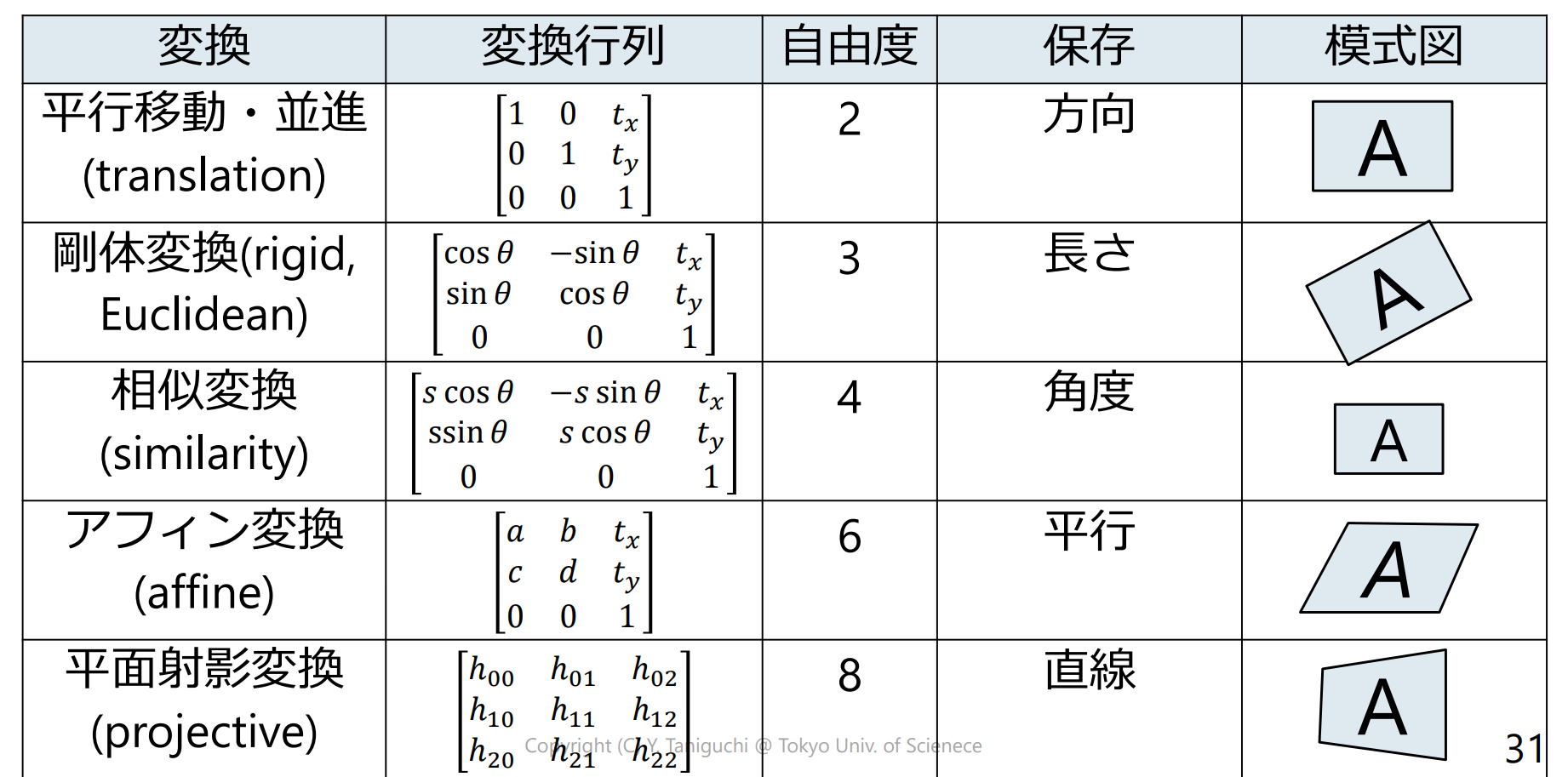
順変換
平面幾何変換の計算法:順変換
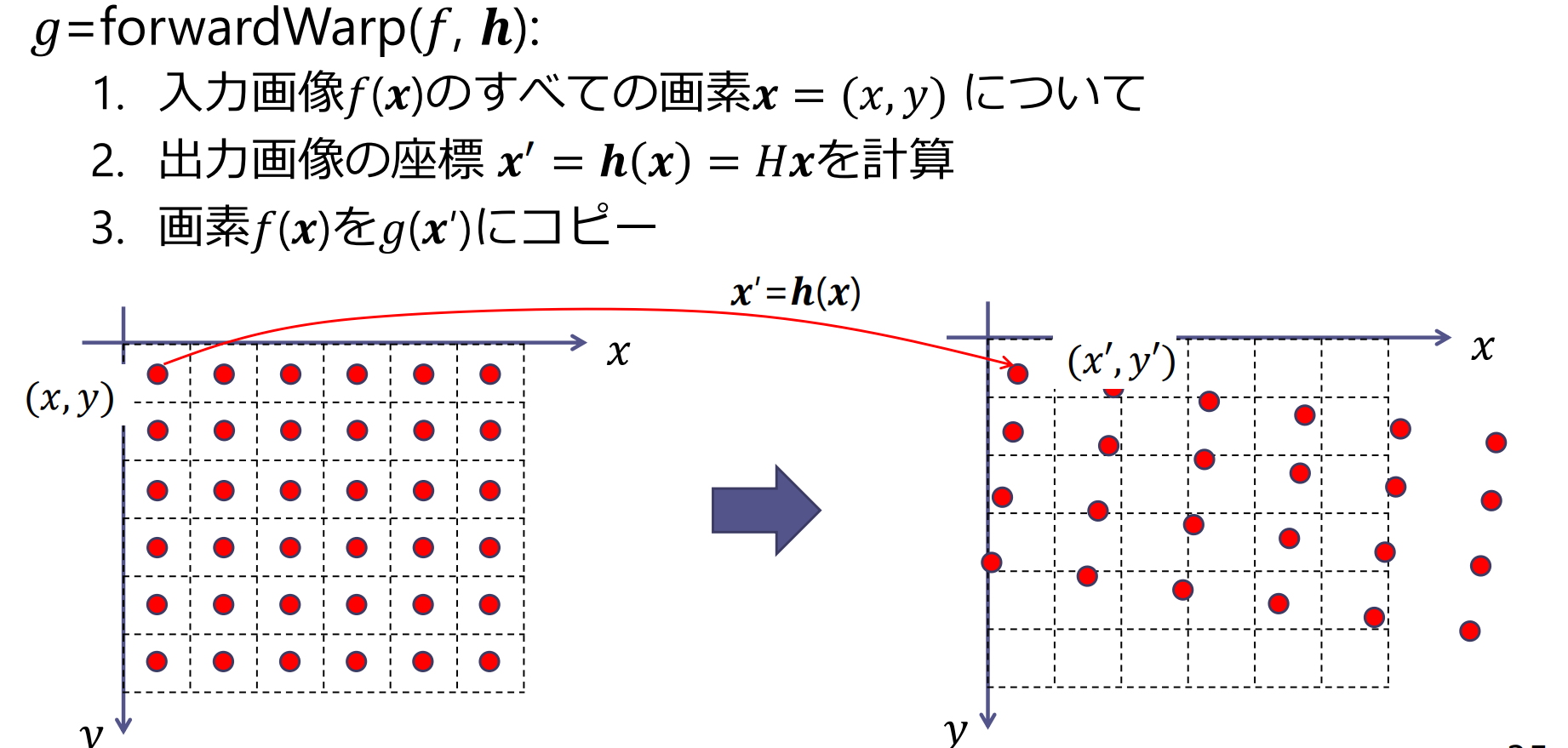
順変換を用いた場合の問題点:
- エイリアシング(aliasing)による縞模様(モアレ)が表れる
- 対応づけできない画素に穴があく

逆変換
平面幾何変換の計算法:逆変換
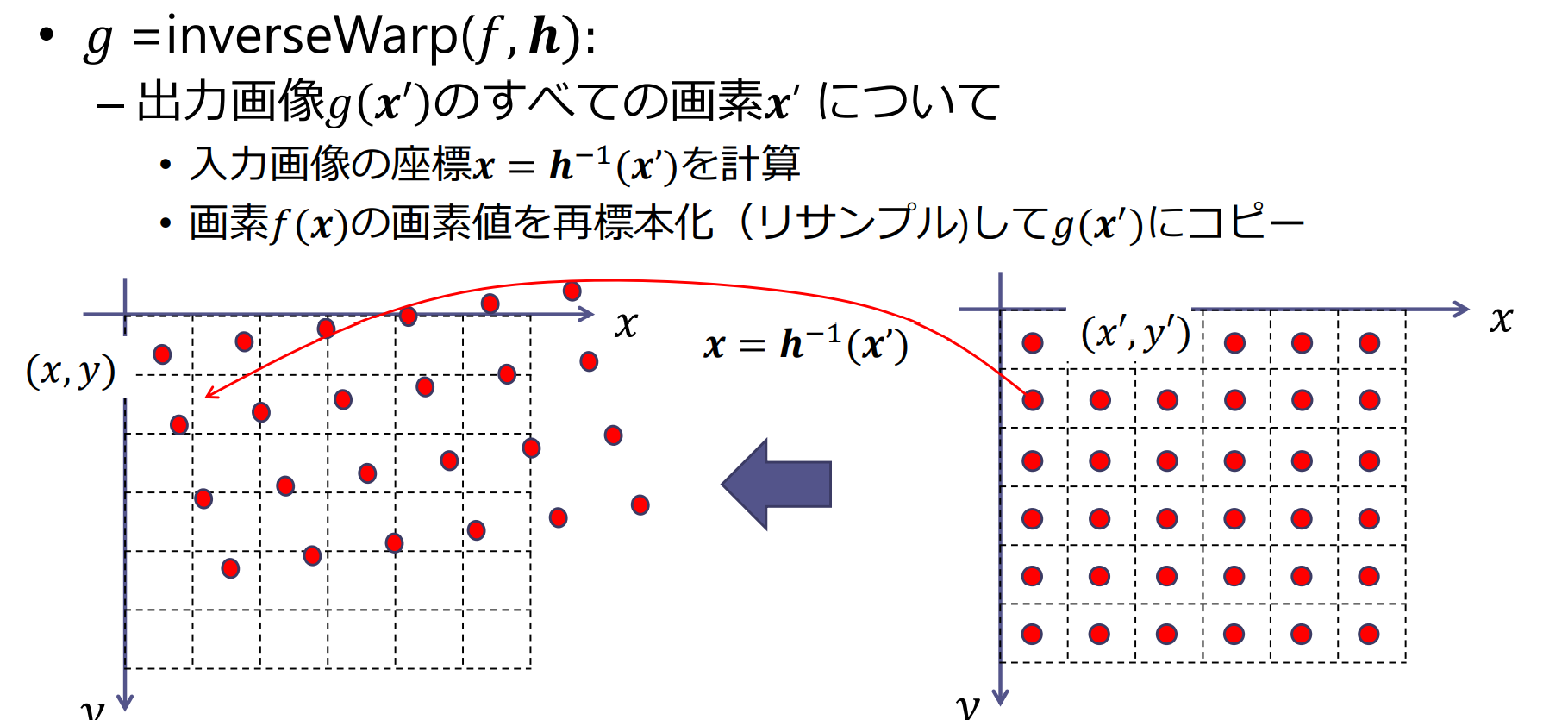
逆変換を用いた場合の問題点:
- 穴があく問題は解決したが,モアレの問題は解決していない

再標本化
再標本化(resampling):入力画像の画素値を用いて,変換後の画素値(標本点の値)を求める補間処理のこと
- 最近傍内挿法(ニアレストネイバー法)
- バイリニア補間法
- バイキュービック補間法
最近傍内挿法
最近傍内挿法(ニアレストネイバー法):求めたい位置に最も近い画素の画素値をそのまま利用する方法
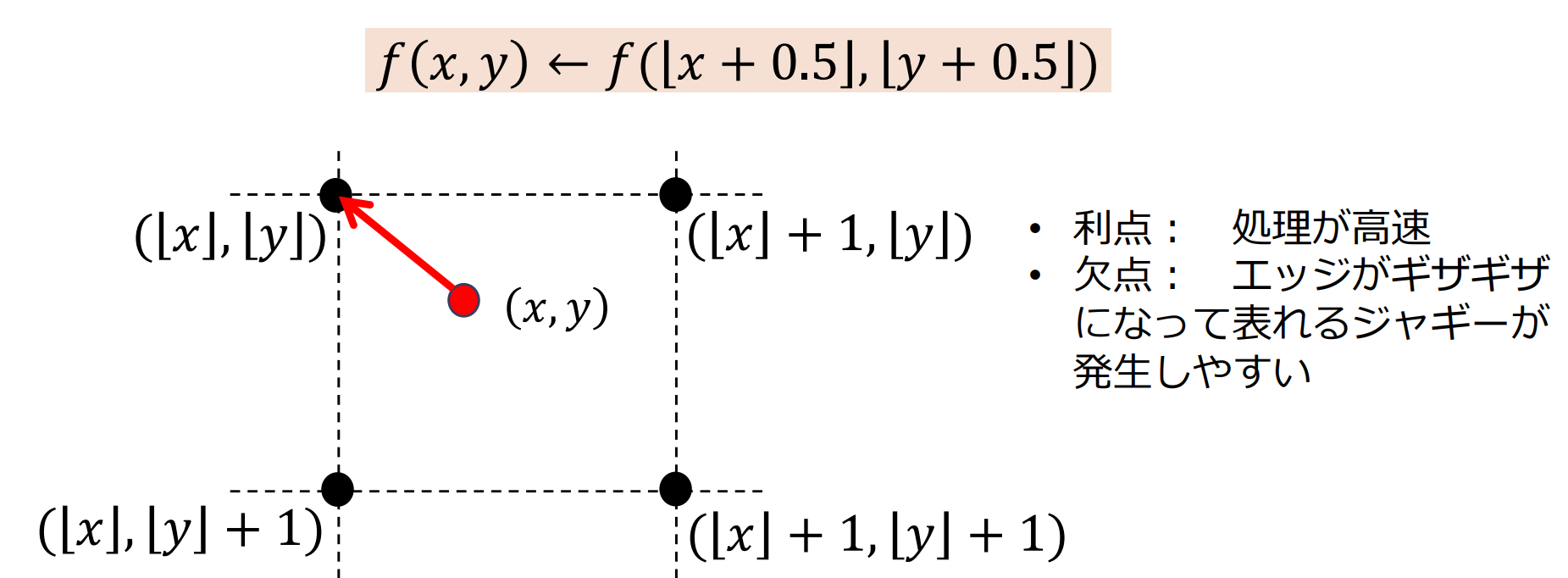
バイリニア補間法
バイリニア補間法(bilinear interpolation):周りの4点の画素値を用いて補間
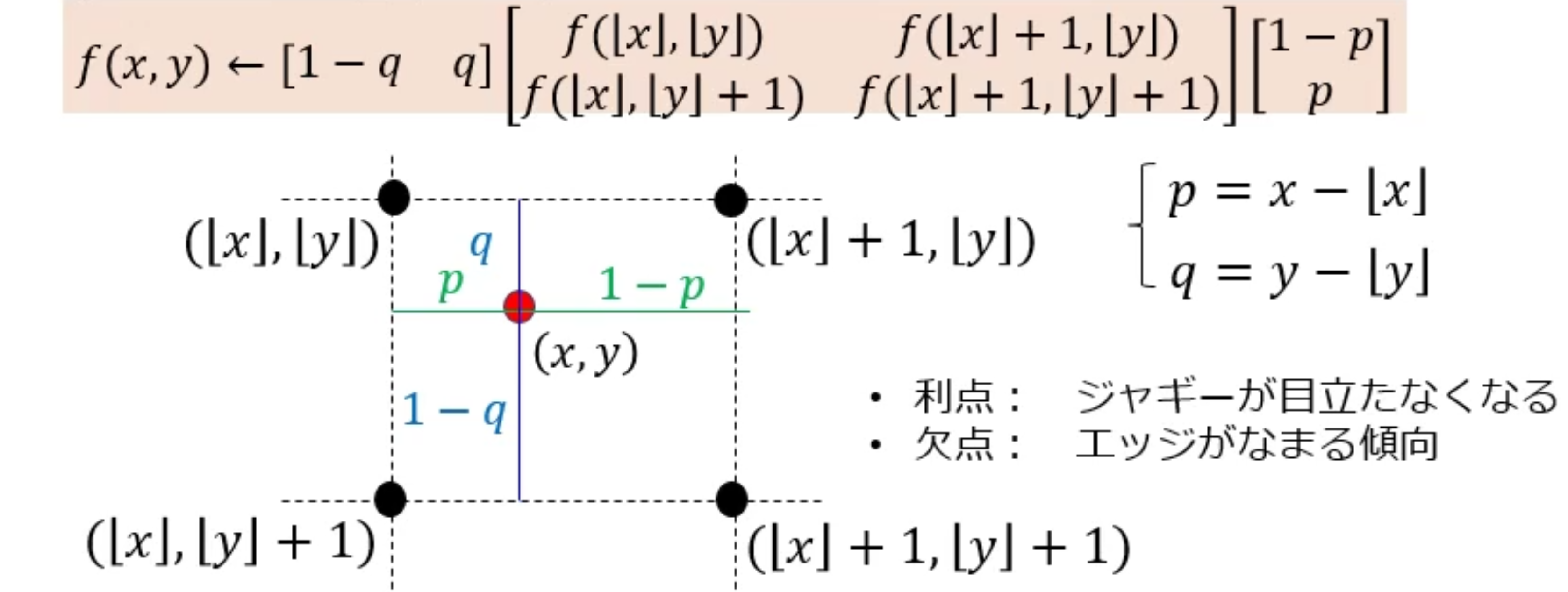
バイキュービック補間
バイキュービック補間(bicubic interpolation):周りの16点の画素値を用いて補間
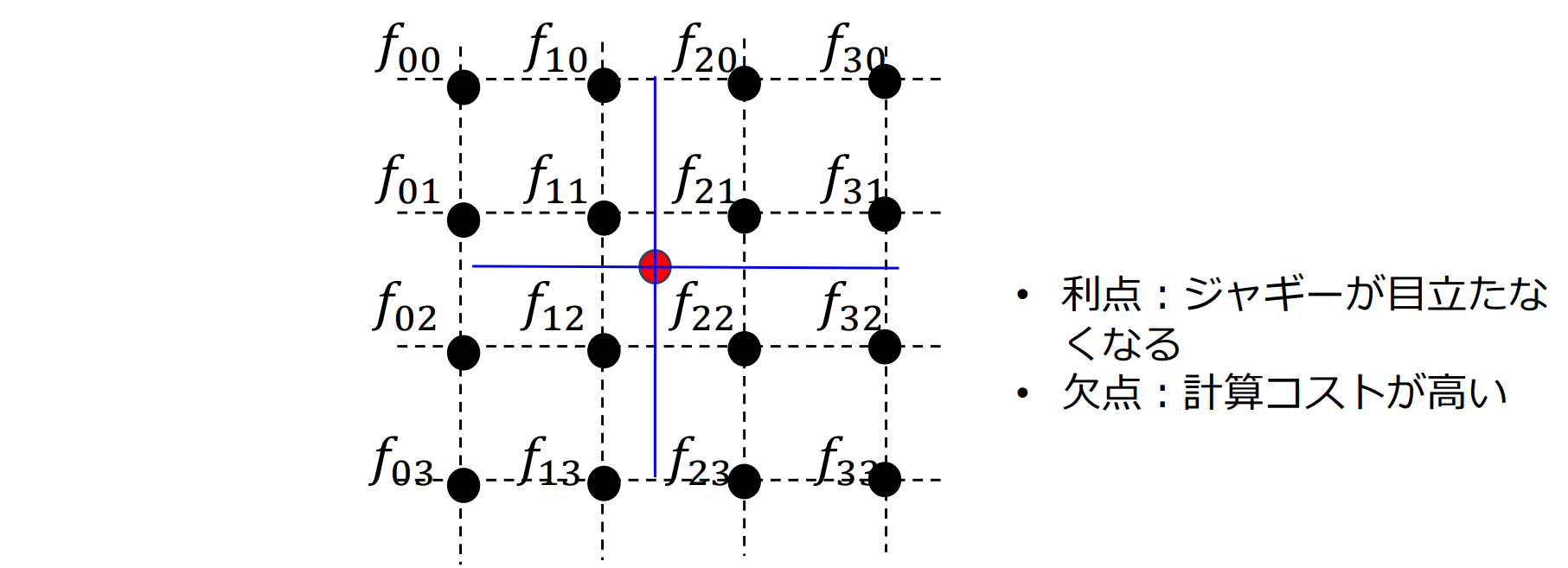
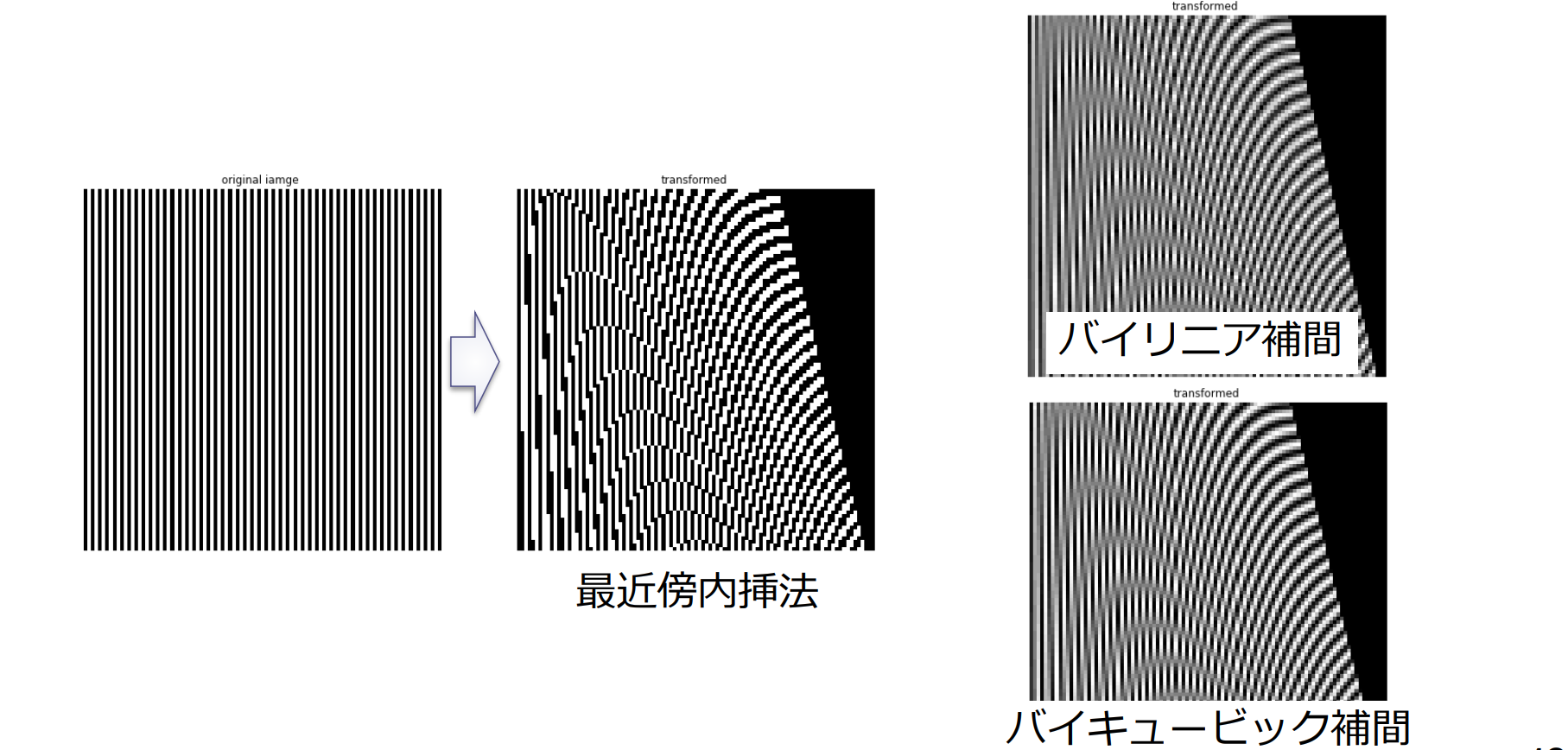
画像の再標本化(resampling)
小数点位置の画素値を周りの画素値から補間して求める
- 最近傍内挿(nearest neighbor)
- バイリニア補間(bilinear interpolation)
- バイキュービック補間(bicubic interpolation)
OpenCVのresize関数にも再標本化のオプションがある

CGの基礎
モデリング(形状の表現)
3次元モデルとデータ表現
- ワイヤーフレームモデル:直線や曲線で構成された線のみのデータ
- サーフェスモデル:ワイヤーフレームに面の情報を付加
- ソリッドモデル:体積を持つ立体として形状表現
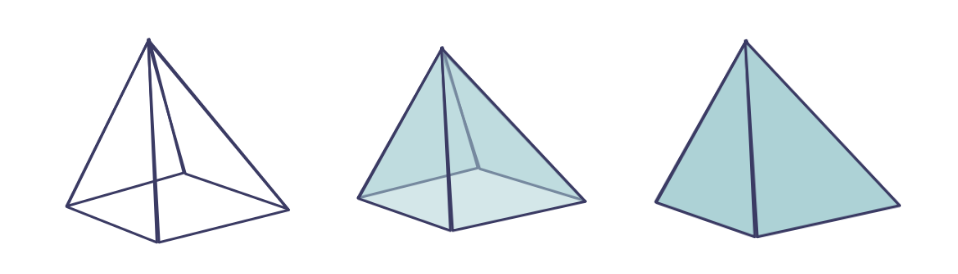
サーフェスモデル
平面や曲面から構成されるサーフェスで形状を表現。立体の内と外を区別できない
- ポリゴン(多面体データ):各多角形の頂点列で表現
- 関数曲面:2次元空間内に定義されたスカラ関数 で曲面を定義
- 陰関数曲面:3次元空間内に定義されたスカラ関数 で以下の式を満たす点の集合として曲面を定義
- eg.メタボール
- パラメトリック曲面:2次元空間内に定義された3次元ベクトル関数 によって定義される曲面
- eg.ベジェ曲面

自由曲面モデル
- 空間に制御点を設定し,高次方程式で制御点を補間
- 単純な数式で表現できない,滑らかな曲面を少ないデータで表現可能
- 代表的な自由曲面:ベジェ曲面、B-スプライン曲面、NURBS
ベジェ曲線(Bézier Curve):制御点 とする
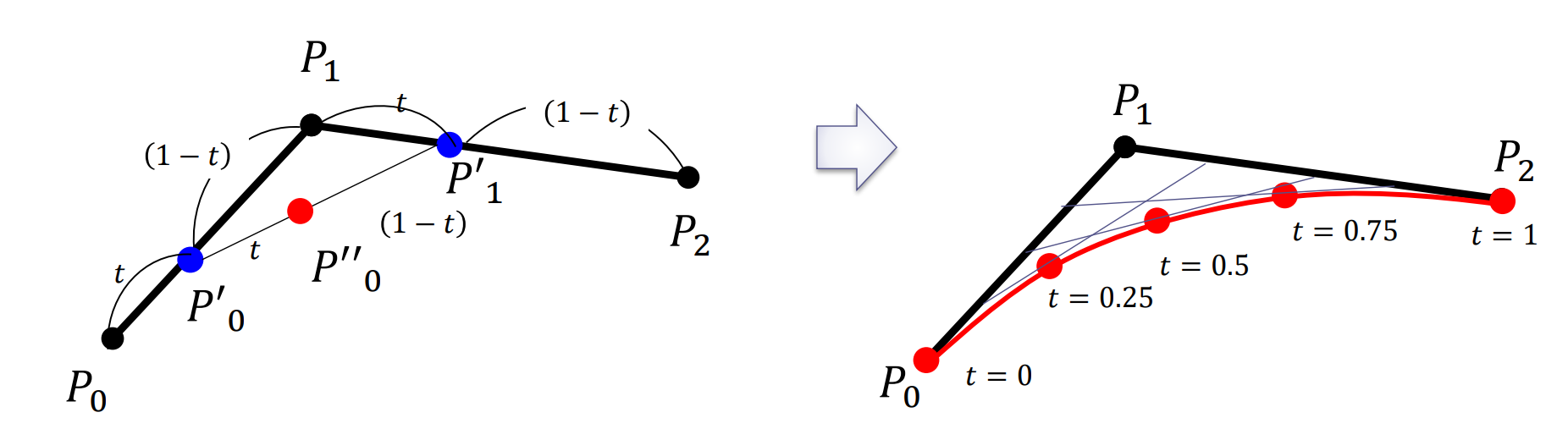
次のベジェ曲線: 個の制御点
但し、バーンスタイン多項式(Bernstein polynomial)は
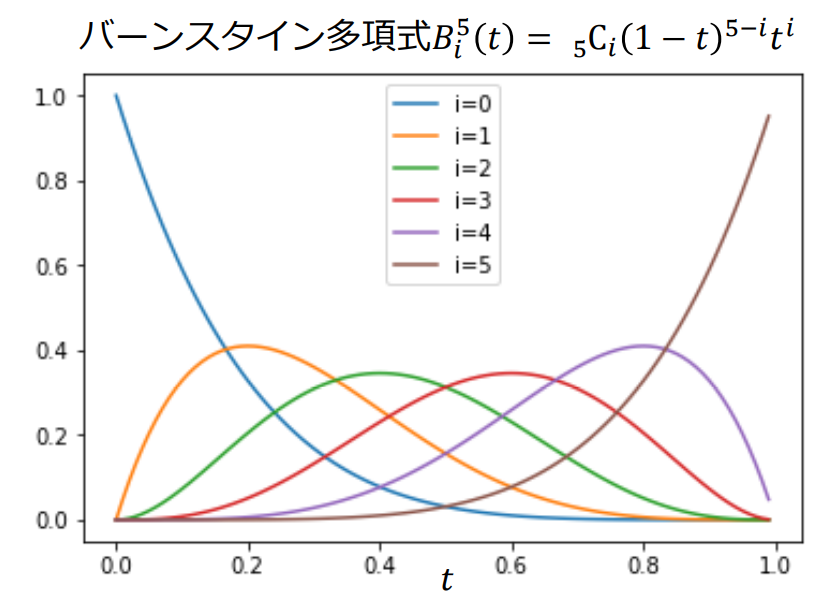
ベジェ曲面:格子状に配置された制御点 を与え,以下で定義
NURBS:非均一有理Bスプライン曲面

- 制御点を与えることによって、描かれる曲線を表す
- 対話的に制御点を動かすことで任意の曲面を表現できる
ソリッドモデル
体積を持つ立体として3次元形状を表現
- 立体の内側と外側の区別がある
- 干渉計算や集合演算ができる
ソリッドモデリングの手法:
- CSG (constructive solid geometry)表現
- 境界表現 B-rep(メッシュモデル, サブディビジョンサーフェスモデル)
- メタボール
CSGモデル(constructive solid geometry):比較的簡単な3次元形状である基本形状要素(プリミティブ)と集合演算(ブール演算)、座標変換の組み合わせで立体形状を表現
- メリット: データ構造が簡単でやり直し操作などの履歴管理が可能
- デメリット:局所的な自由変形が困難

境界表現 B-rep (Boundary Representation):立体形状をその境界である面の組み合わせとして表現(ウイングドエッジ構造ともよばれる)
- 幾何情報:多角形や曲面形状、頂点の座標
- 位相情報:面と面の隣接関係
- メリット:局所的な変形が比較的容易
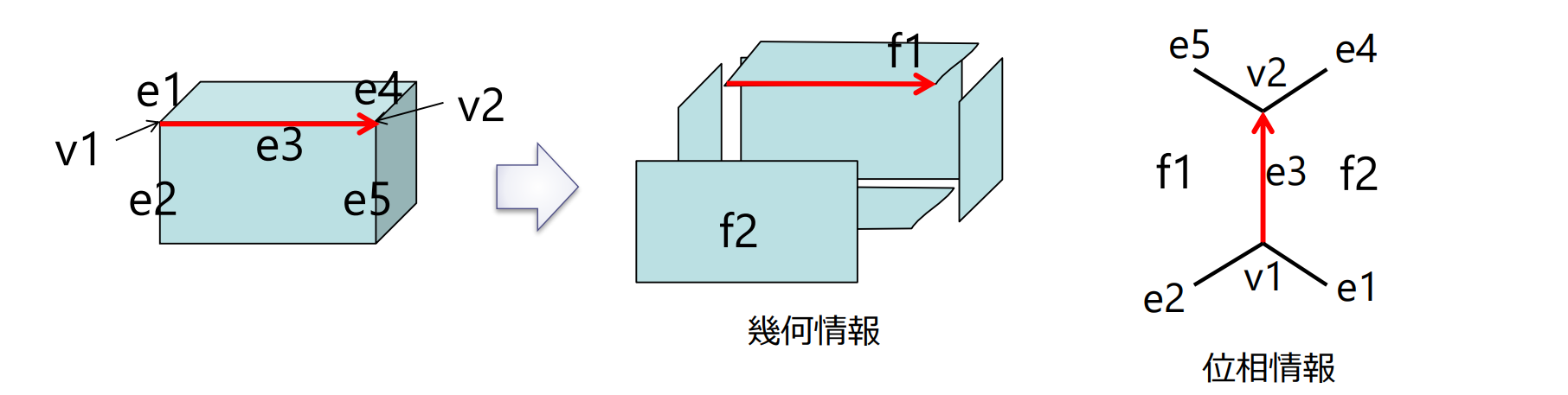
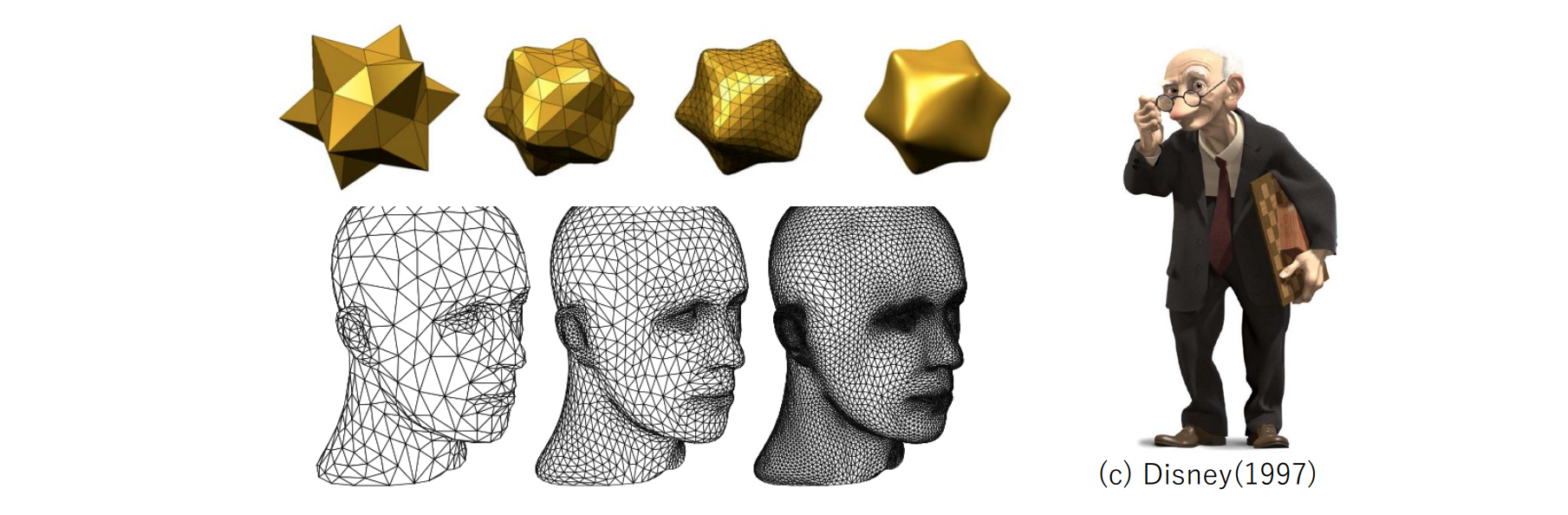
メッシュモデル:全ての面が多角形(三角形等)で表現されるポリゴンの集合として立体形状を表現

サブディビジョンサーフェス(細分割曲面)モデル:
- 多面体を分割していくことで滑らかな形状を表現
- 多面体をどんどん分割していくため、複雑な形状を一つのモデルで表現できる
- 必要に応じて分割数を変えることも可能
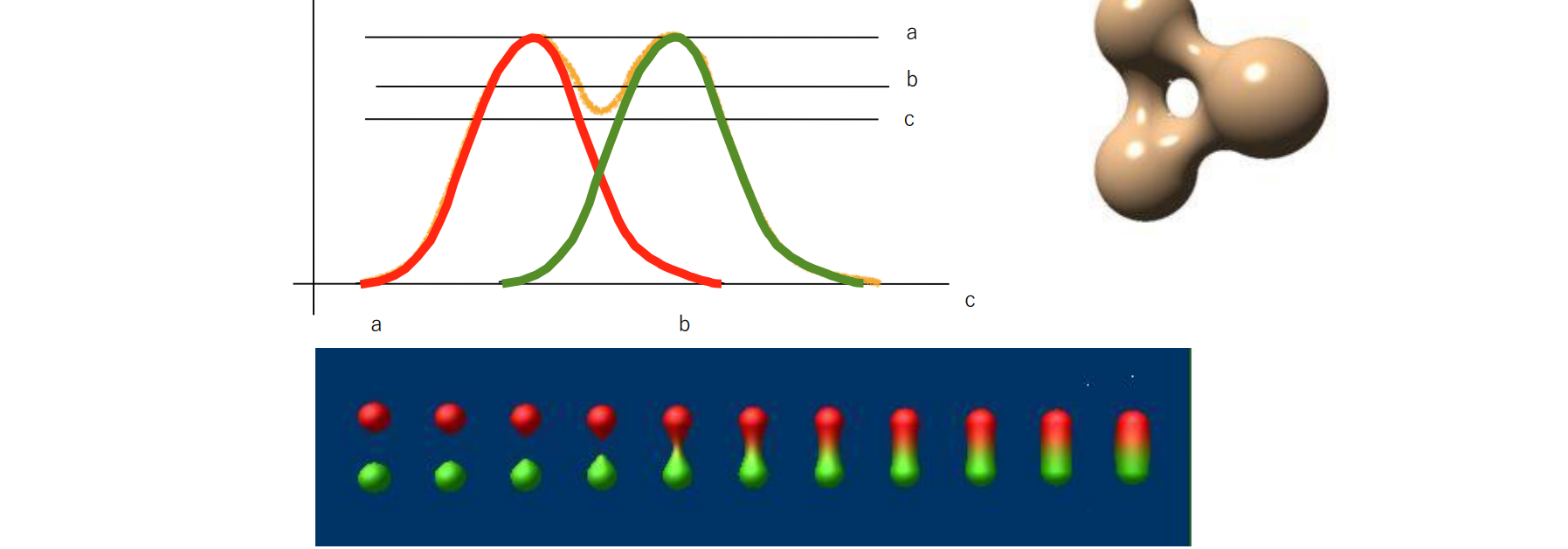
メタボール(陰関数曲面の例):
- 球の集まりで立体形状を表現
- 距離とともに減衰する影響力(関数)を定義し, その重ね合わせで形状を表現 雲,人体の表現
レンダリング(光の表現)
- 光線追跡法(レイトレーシング法)
- 目から画素を通過してシーンに至る光線を投影
- 反射や屈折による光線を再帰的に生成していく手法
- ラジオシティ法
- 世界が小さな拡散面の集合で構成されると仮定し、それぞれの微小面に到達する光の量を求めていく
- 光の相互反射を厳密に計算
- フォトンマッピング法
- 間接照明を効率的かつ確実に計算可能な大域照明手法
- 光源からフォトンをばらまき、それを追跡。反射・透過・吸収 したフォトンの分布を利用し、光・陰影の描画を効率よく実施
光線追跡法
- 視点からスクリーンのすべての画素に向けて光線をのばす
- 光線が物体に衝突したら、屈折光と反射光に分岐する
- 反射光の輝度はPhongの反射モデル等で計算
- 衝突しなければ背景色とする
- 以上を再帰的に繰り返す
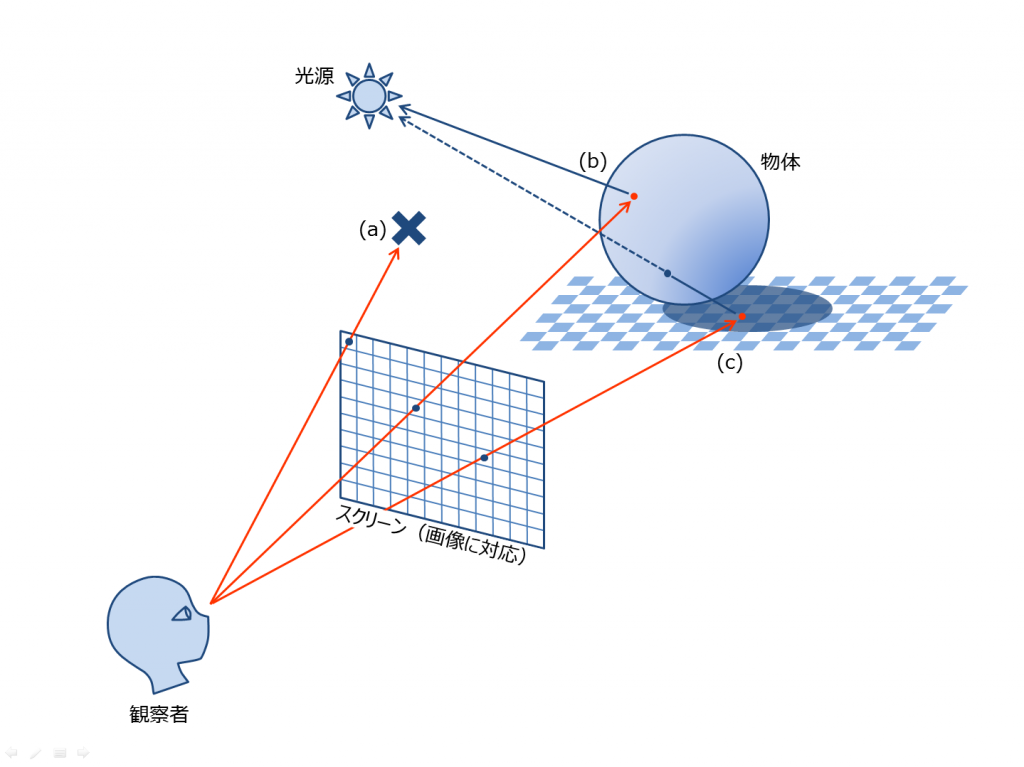
- メリット:鏡面反射や屈折透過光の効果が得られる
- デメリット
- 計算に時間がかかる
- 間接反射によって作られる薄明るい影やレンズなどによって光が集まったり分散したりする効果は得られない
物体の反射特性
拡散反射(diffuse reflection):物体に入射した光があらゆる方向に均等に拡散.石膏のようなざらざらした表面からの反射
- ランバート反射(Lambertian reflection)
鏡面反射(specular reflection):物体に入射した光が一方向に反射.鏡やつるつるした表面からの反射
- 光沢,ハイライト
フォン(Phong)の反射モデル
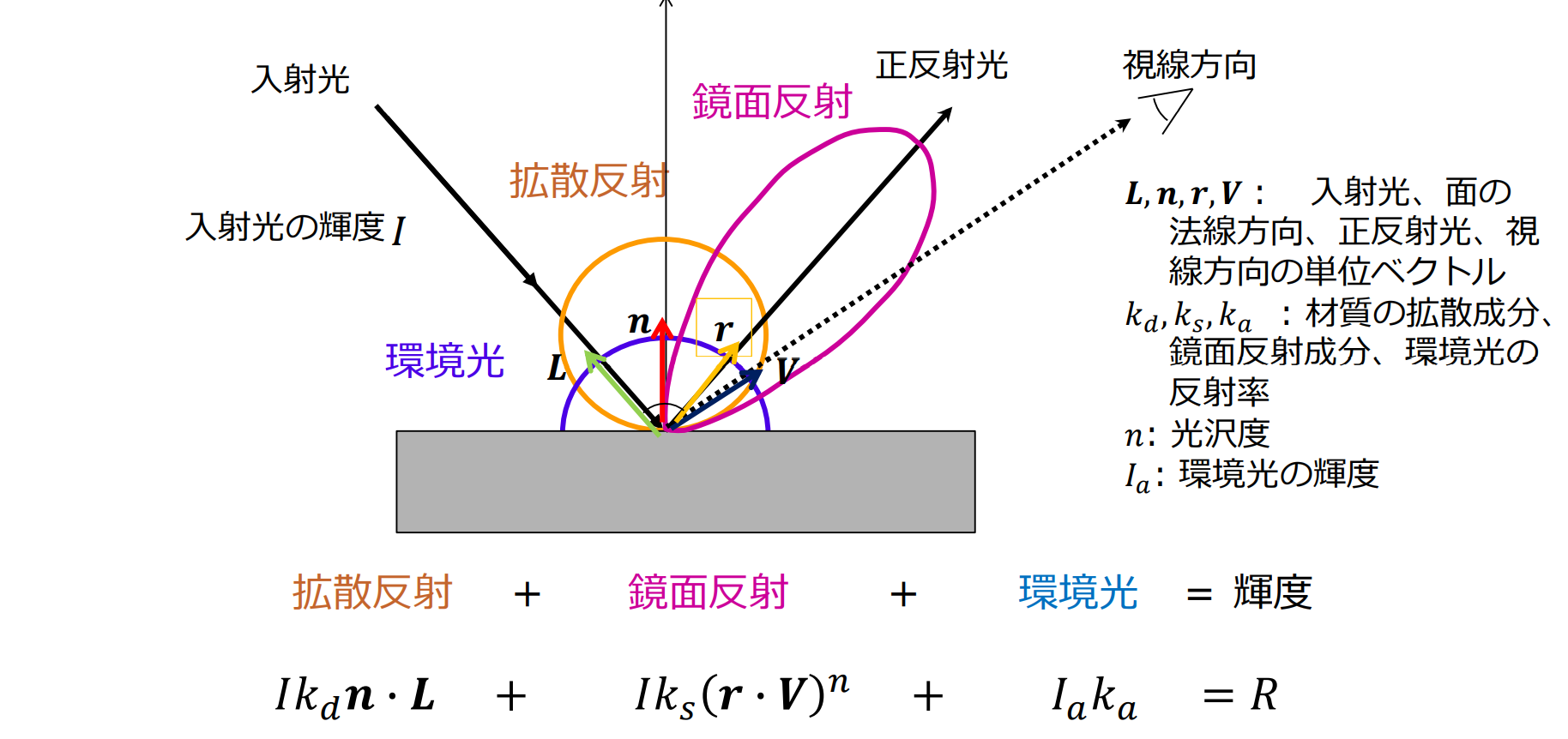
- 石膏のような拡散反射面に入射した光はあらゆる方向に均等に拡散する
- シーン全体を照らす環境反射光は、あらゆる方向に均等に拡散する
- 拡散反射光の強度は、物体表面に垂直に入射する場面に最大になる
フォトンマッピング
光源からフォトンをばらまき、それを追跡する。反射・透過・吸収 したフォトンの分布の可視化によって光・陰影の描画
を効率よく実施

- 物体表面において反射や屈折を繰り返す光
- 雲や煙などの媒質の中で散乱・吸収を繰り返す光
- 素材の透明感や質感
イメージベースドレンダリング
- 正確な3Dモデル(形状・素材・反射特性など)を画像から取得
- レンダリングには一般的な3Dグラフィックスの手法を使用
- 画像をそのまま使用して物体を描画
- 画像を使ったレンダリングに特化したモデル表現,レンダリング手法を用いる
テクスチャマッピング
複雑な表面属性を計算することなく、テクスチャ(2次元画像)を3次元空間内の面に貼り込む方法
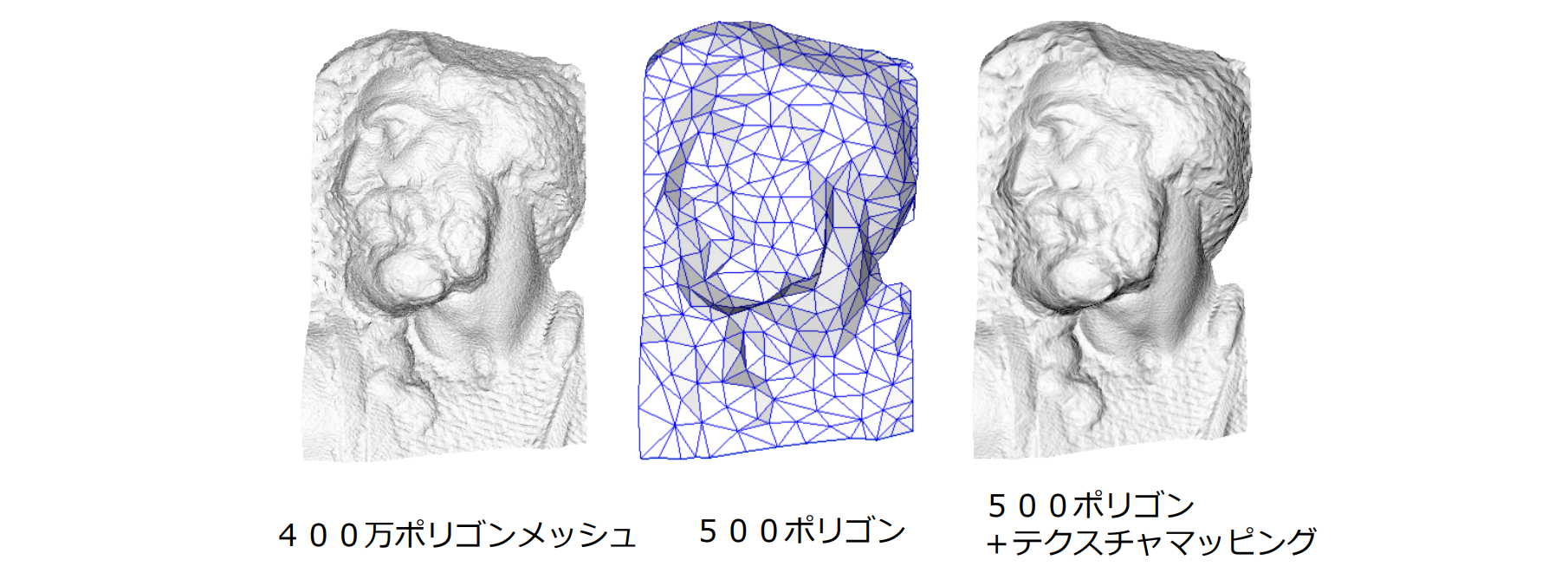
Photo Tourism
画像検索技術と3次元復元技術を組み合わせることで、あたかもその場に行って移動するかのように、インターネット上の写真を鑑賞

画像検索に基づく画像合成
インターネットにある何百枚もの写真を使って、自分の写真の気に入らない部分を自由に消す

特徴抽出
特徴(feature):画像の対応づけや識別・認識の手がかりとなる画像要素

特徴点とパッチ
画像から特徴点を検出し2枚の画像の間で対応付ける
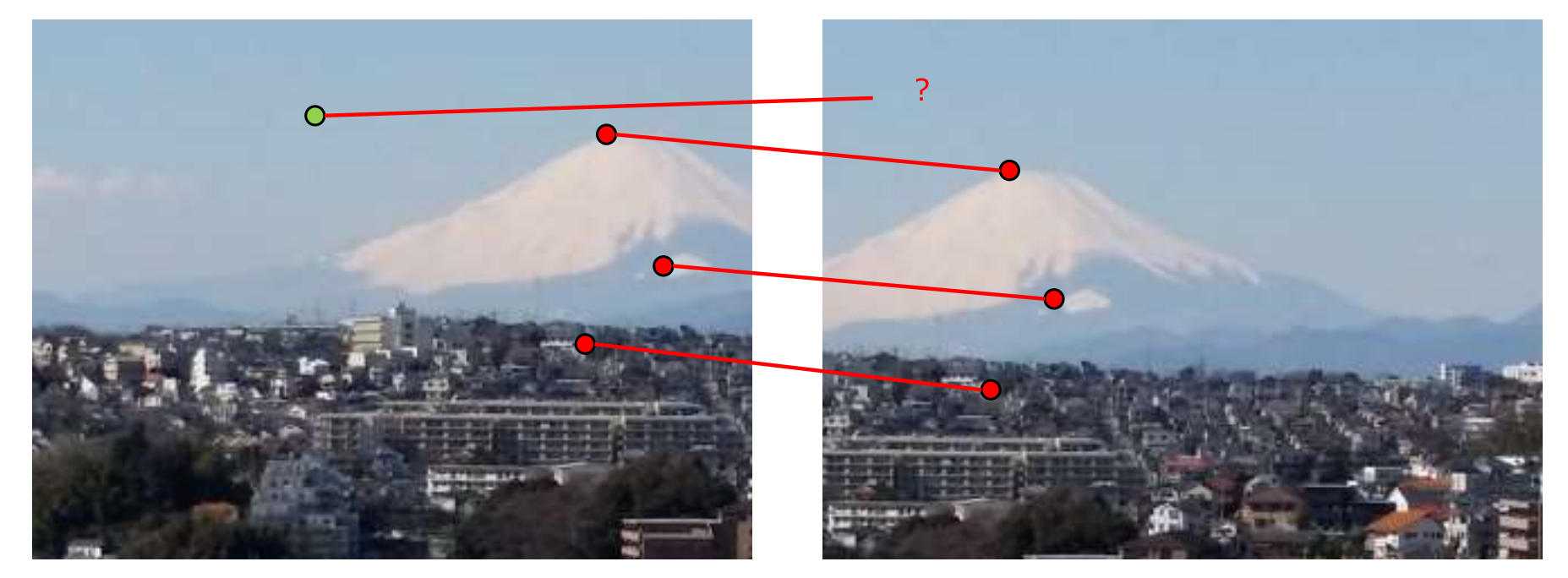
特徴点マッチングの流れ
- 特徴点検出(feature detection): 画像から特徴的な点(キーポイントともいう)を検出
- 特徴記述(feature description): 特徴点の周辺領域(局所パッチ)を抽出し,その輝度パターンを特徴記述子(feature descriptor)に変換
- 特徴マッチング(feature matching):画像間で対応する特徴点を特定する.特徴記述子の間の距離を測る
graph LR
detector --> descriptor
descriptor --> matching
望ましい特徴点(キーポイント):
- 対応が一意に決まる
- 撮影条件に依らず安定に検出できる
- スケール不変性(拡大・縮小に対する不変性)
- 回転不変性
- アフィン不変性
どのような特徴点なら安定して対応が求まる:
- コーナ:画像間の対応付けに有効
- ブロブ:画像間の対応付けに有効
- 平坦な領域:対応付けの手がかりがない
- エッジ:一つの方向にのみに輝度変化がある エッジのどこと対応すればいいかわからない(開口問題)
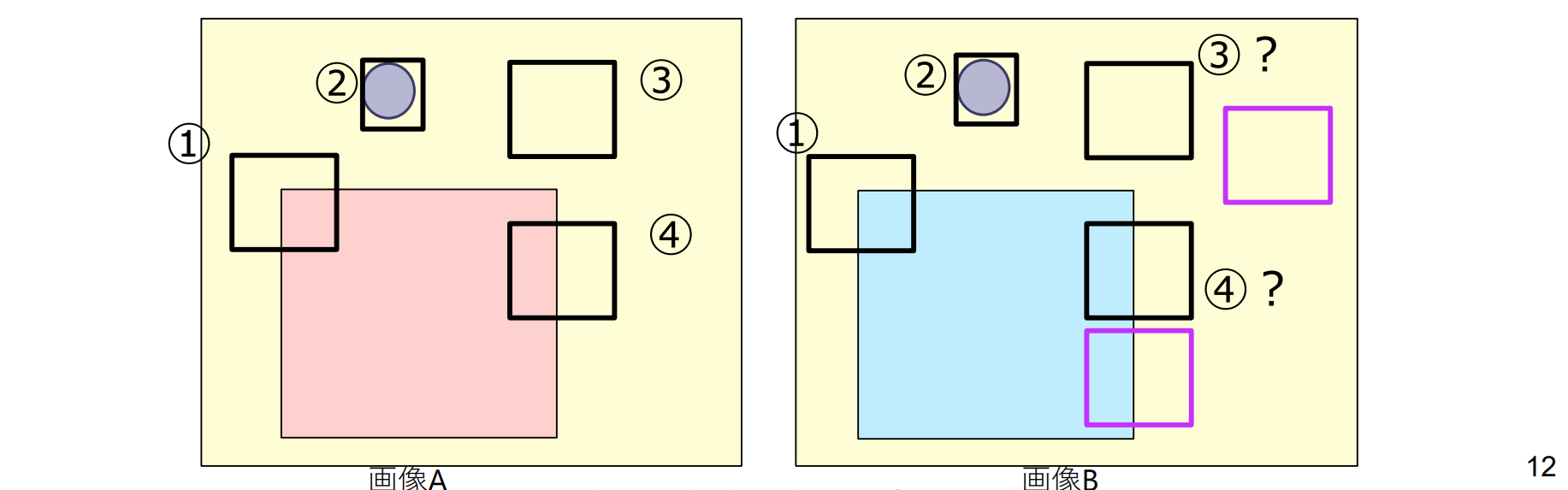
開口問題(アパチャー問題)
コーナーとブロブにいては、対応が一意に決まるが、それ以外の点は、一般的に近傍だけ見えても唯一には決まらない
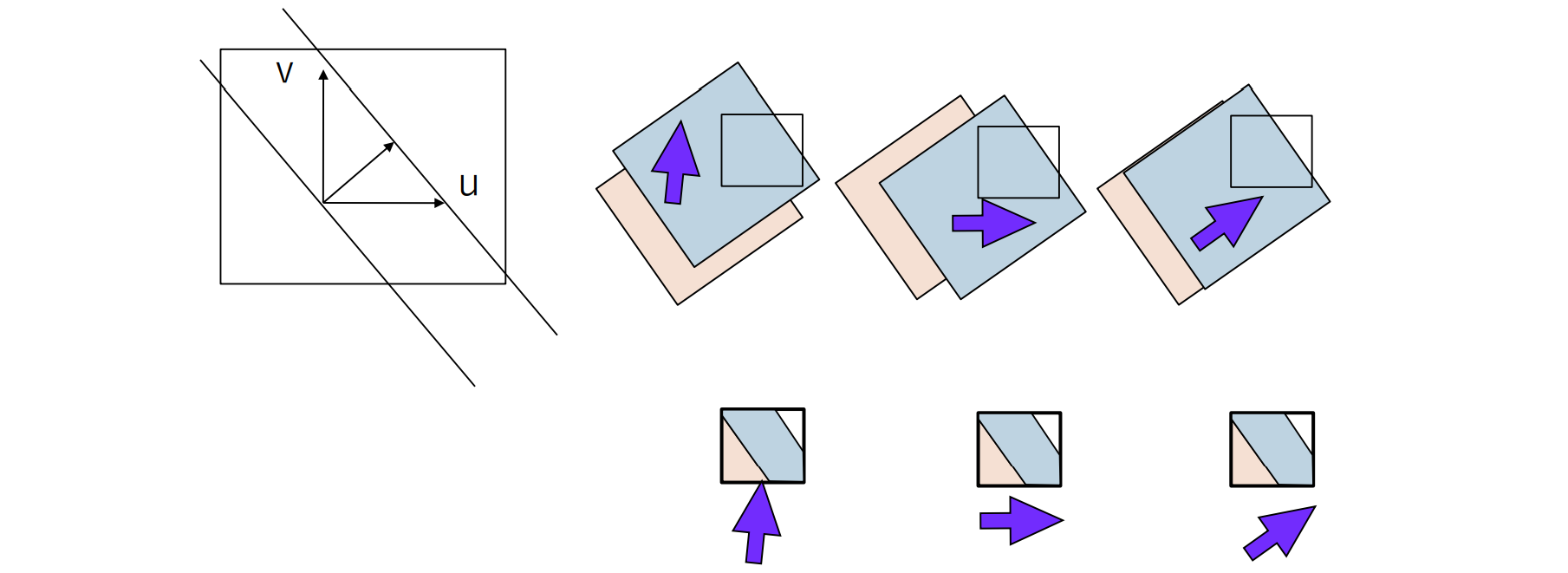
特徴点検出
特徴点検出の手法:
- コーナー検出[Harris(1988)]
- ブロブ検出 (Blob detection)
- Laplacian of Gaussian (LoG) [Lindeberg(1993)]
- Difference of Gaussian (DoG) filters[Lowe(2004)]
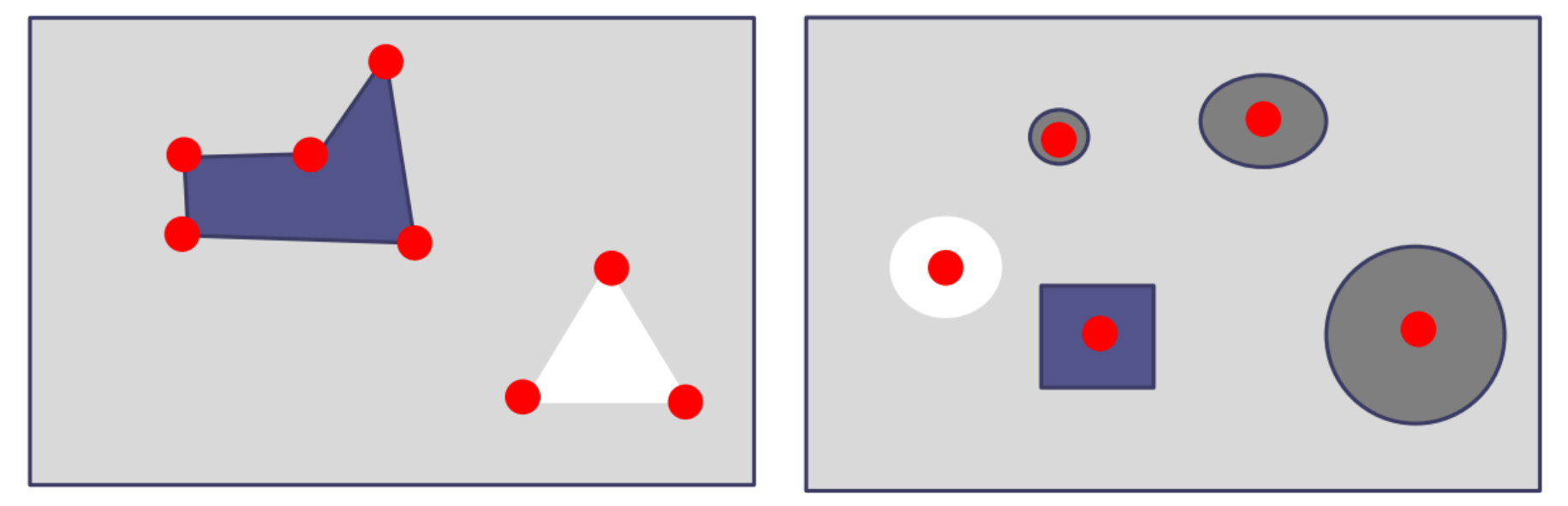
コーナ検出とブロブ検出

コーナ検出の原理
パッチの位置を微小変化 させたとき,画素値の変化が大きい点をコーナとして検出

自己相関関数の近似
テーラー展開 を用いて式を変形

ハリスのコーナ検出(Harris corner detector)


コーナ検出関数
画像の全ての点でコーナ検出関数の値を計算し,(1) 予め定めたしきい値を越え,かつ,(2) 局所的に最大値となる点をコーナとして検出
- Harris and Stephens(1988)
- Shi and Tomasi(1994)
- Harmonic mean, Brown, Szeliski, and Winder(2005)
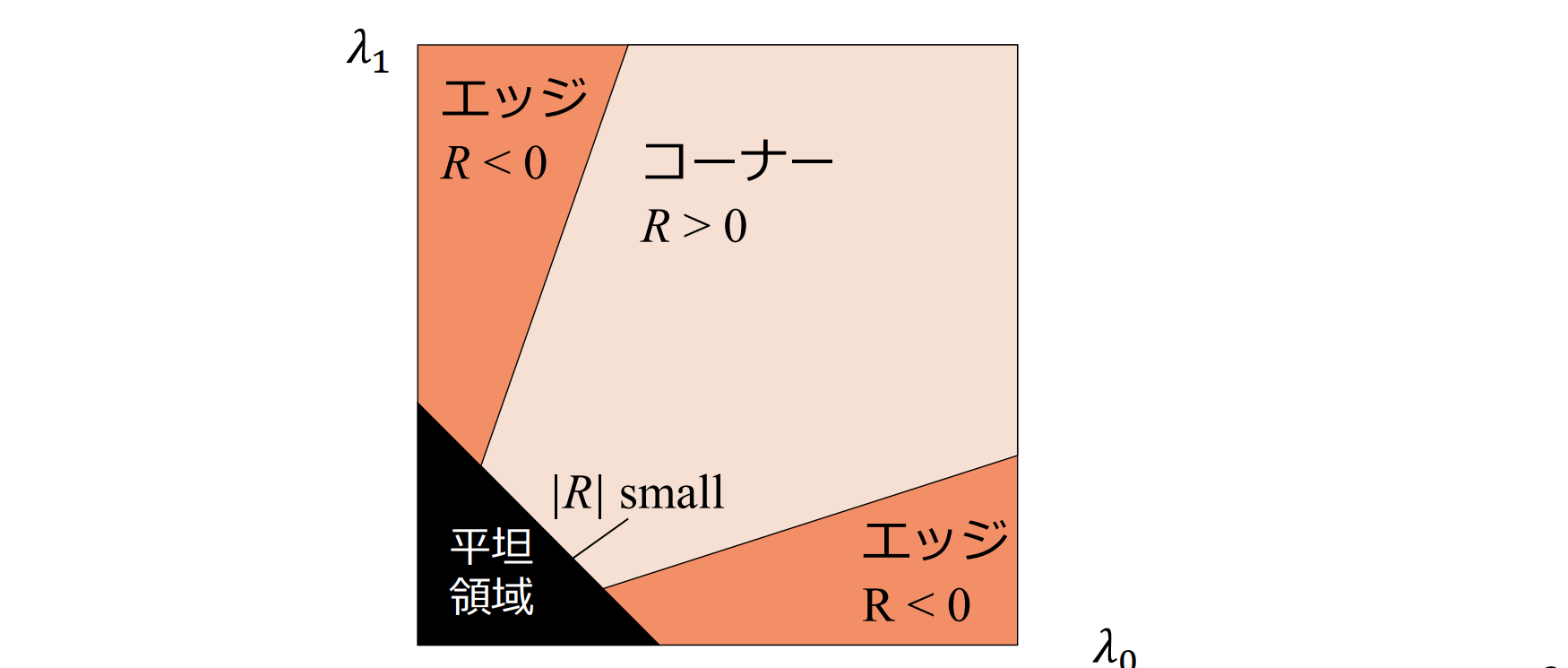
ブロブ検出(blob detector)
特徴点検出の課題:スケール不変性。拡大するとコーナと判定されないが,縮小して見るとコーナー
ブロブ検出(blob detector):特徴点とスケール(ブロブの径)を同時に求める手法
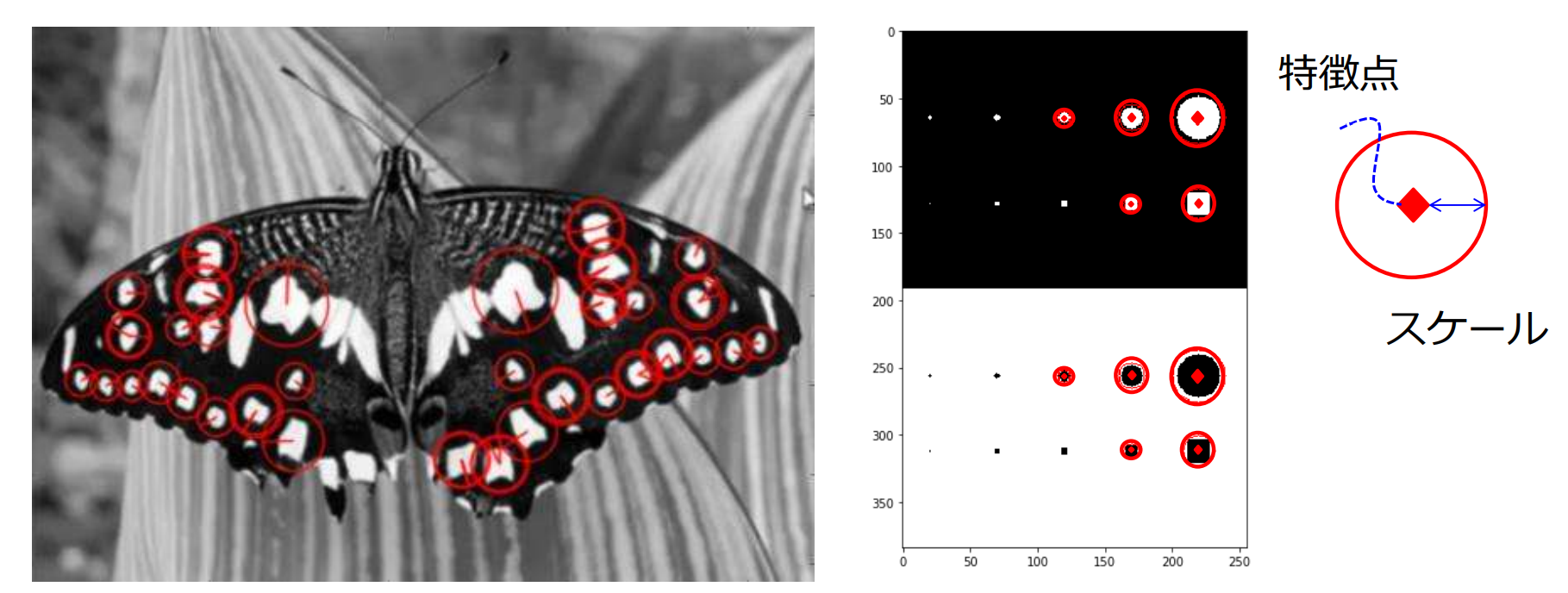
Difference of Gaussian(DoG)
DoG画像:異なる で平滑化した2枚の平滑化画像 の差分
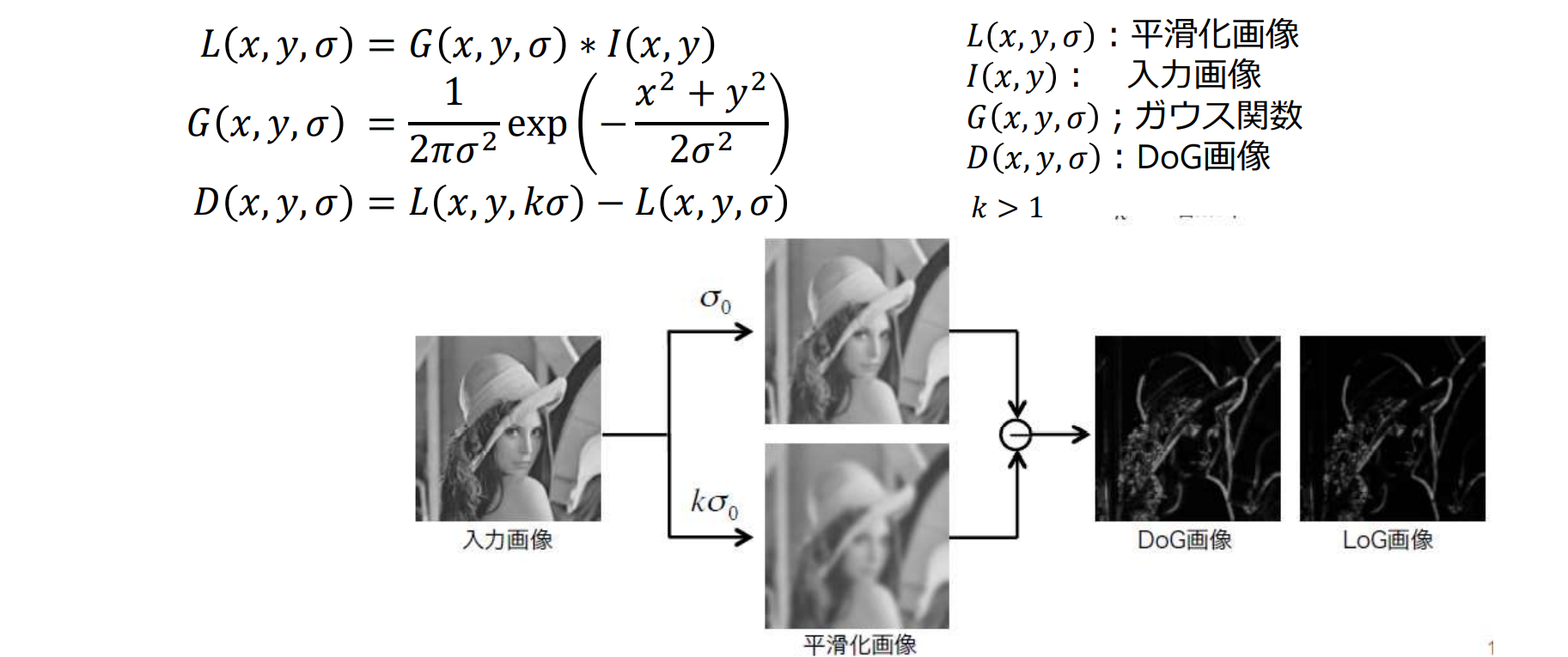
DoGは逆Mexican hat型の空間フィルタの畳み込みと等価

ブロブ検出とスケール推定
異なるスケール のDoGフィルタを畳み込み,極大値・極小値をとる点を探索することで,ブロブのサイズ(スケール)を推定
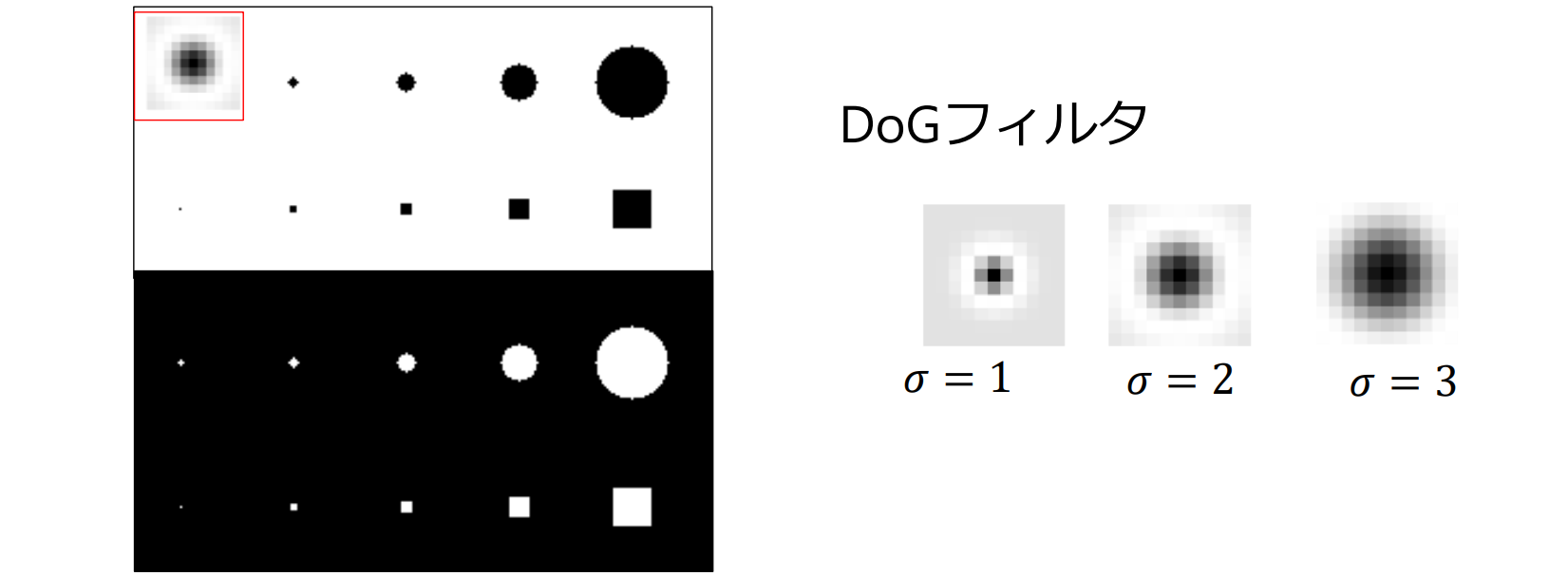
高速化テクニック:DoGによるスケールスペースの構築
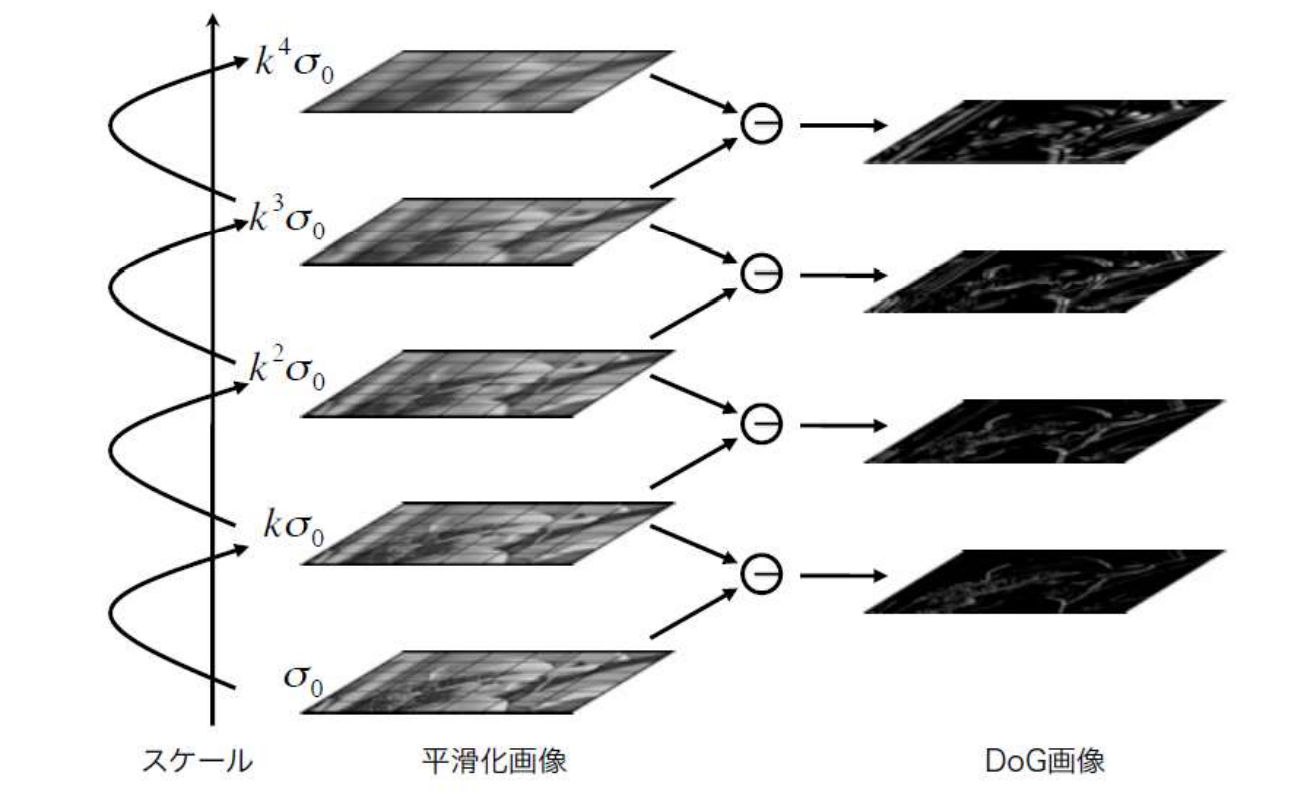
高速化テクニック:極値探索
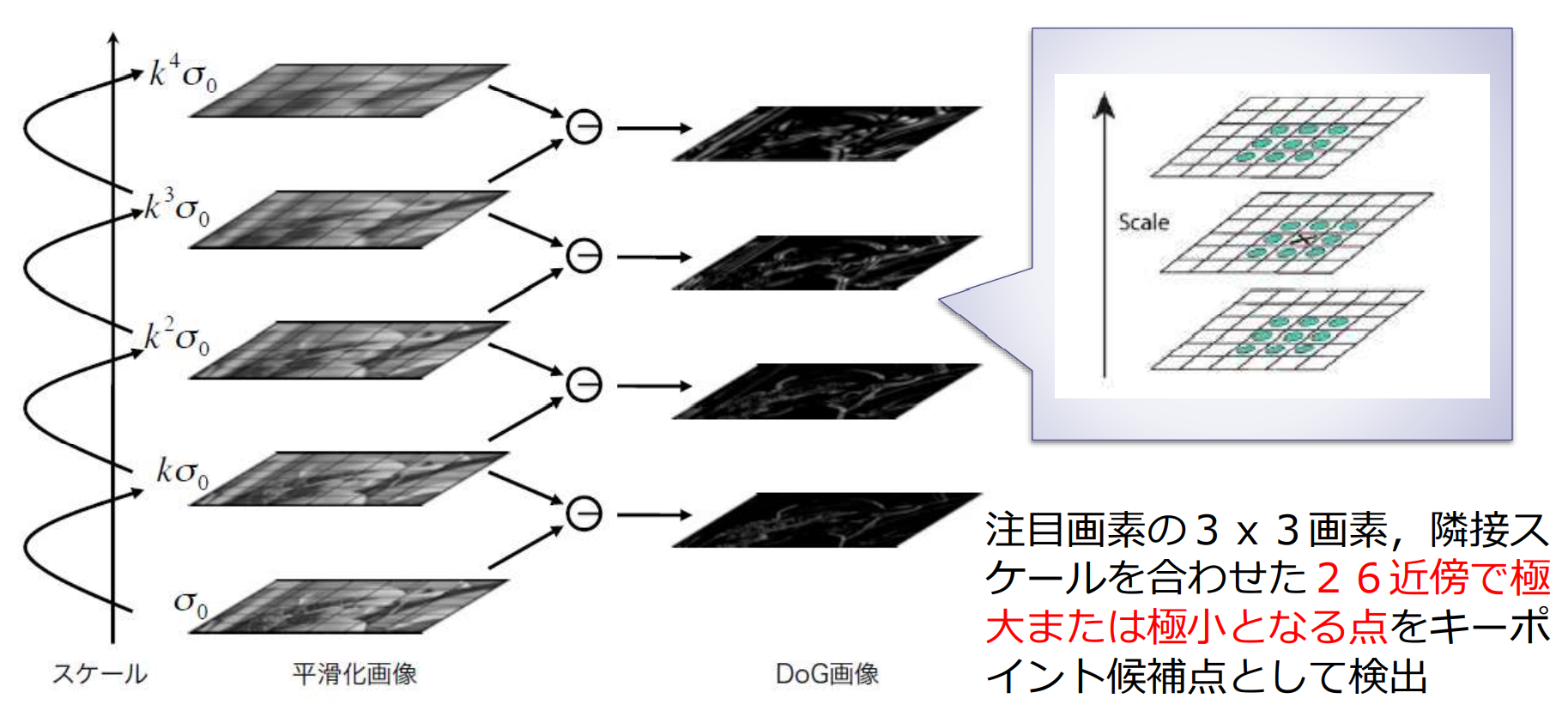
特徴点の絞り込み
エッジ上の点やコントラストが低い点を削除

特徴記述
画像局所特徴量:SIFT
スケールと回転に対して不変(invariant)な特徴記述(特徴記述(descriptor):局所的な輝度バターンを数値化する処理)
- 特徴点(キーポイント)検出と絞り込み
- DoG画像を用いてキーポイント(ブロブ)を検出
- 特徴を最も多く含むスケールを自動決定
- 特徴記述
- 選択された特徴点(領域)の輝度変化の方向性(オリエンテーション)を求める
- 128次元の特徴量(SIFT特徴量)で記述
オリエンテーションの算出
回転に不変な特徴量を算出するために特徴の“方向性”を算出
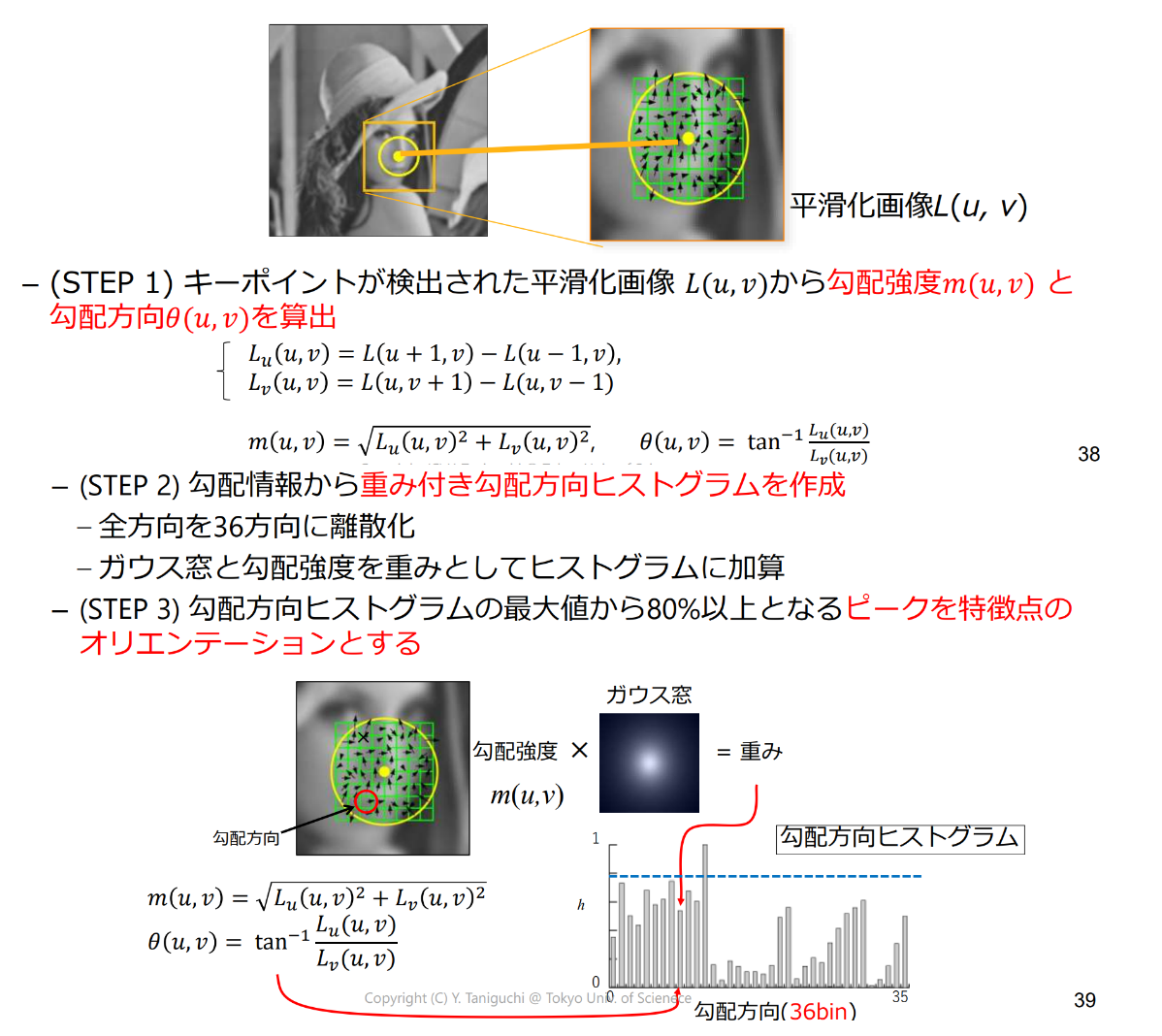
記述領域の方向の正規化
特徴量を記述する領域をキーポイントが持つオリエンテーションに合わせて回転させる
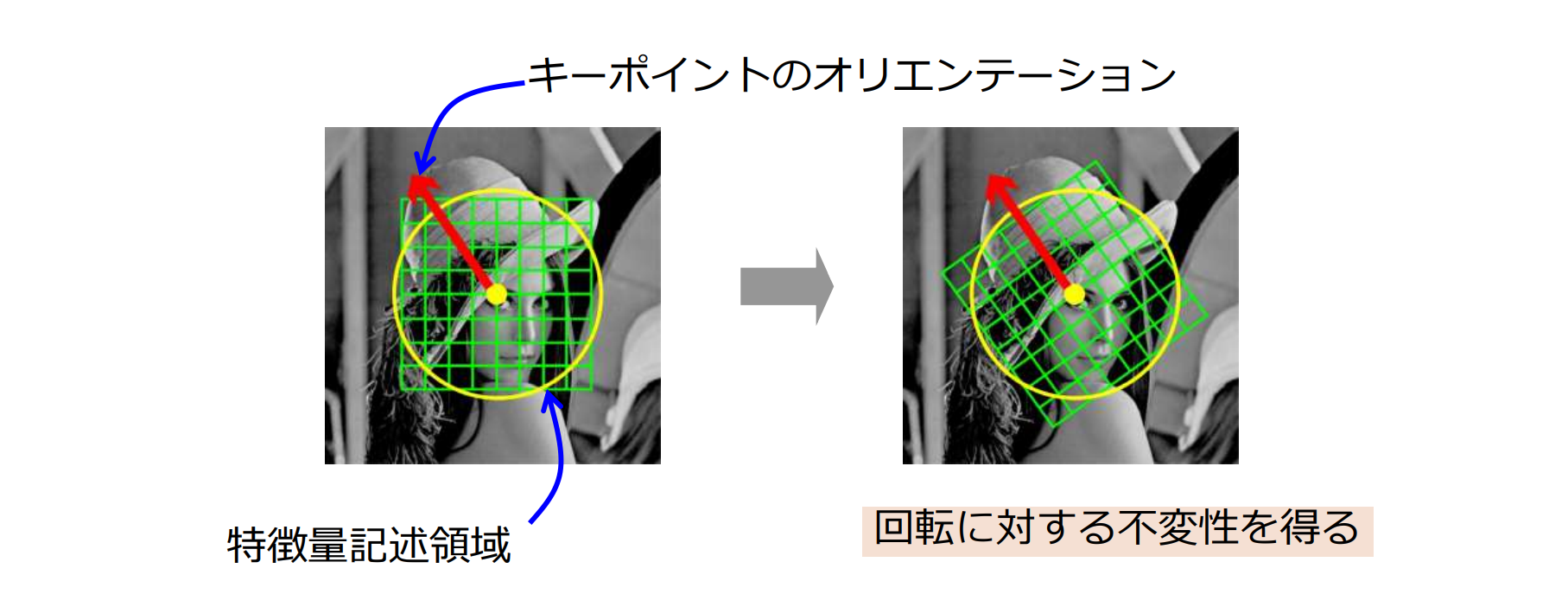
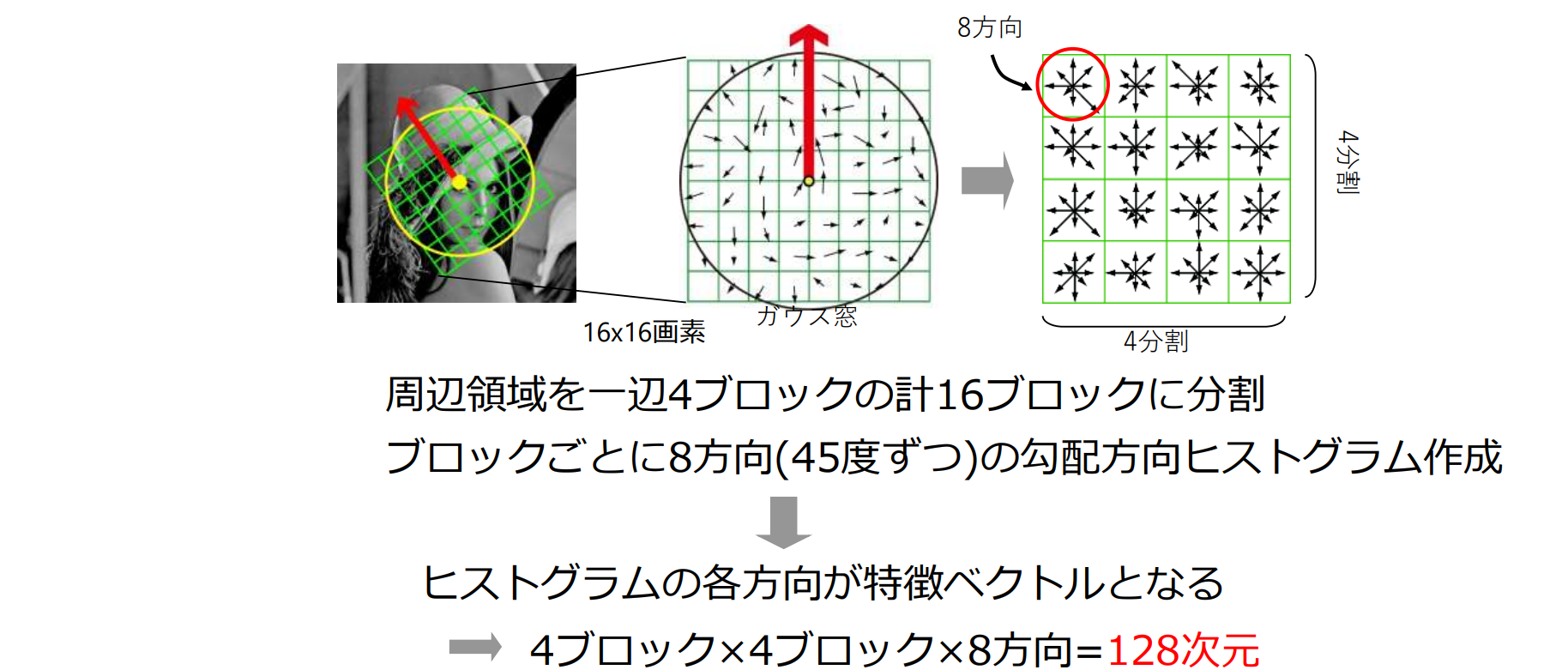
特徴ベクトル算出
特徴ベクトルを算出
SURF(Speed-up Robust Feature)
| SIFT | SURF | |
|---|---|---|
| 特徴点検出 | DoGによるブロブ検出 | ボックスフィルタ(積分画像を使用すると高速に計算可能) |
| 特徴記述 | 勾配方向ヒストグラム(128次元=4x4ブロックx8方向) | Harr waveletの一次応答の総和(64次元=4x4ブロックx4つの値) |
局所特徴量のバリエーション
- SIFT(Scale-Invariant Feature Transform)
- PCA-SIFT: PCAで次元削減
- GLOH(Gradient Location and Orientation)
- SURF(Speeded-Up Robust Features)
- FAST, ORB, BRISK, KAZE, AKAZE
特徴点検出器(ディテクタ)と特徴記述(デスクリプタ)の組み合わせ
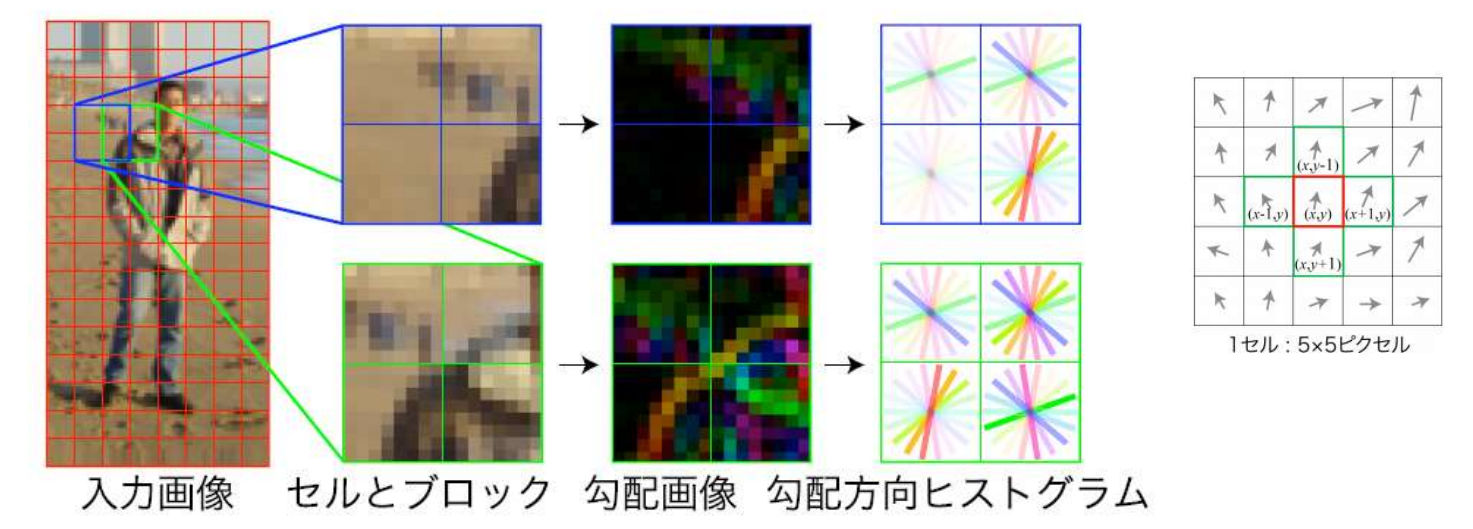
HOG(Histogram of Oriented Gradients)
局所領域に含まれる勾配分布を捉える特徴
- 服の色や背景の明るさによってエッジの方向は“符号”は変化するので区別せずヒストグラムを計算
- SIFTでオリエンテーションによる正規化を行わない場合に近い(回転不変ではないから)
特徴点マッチング
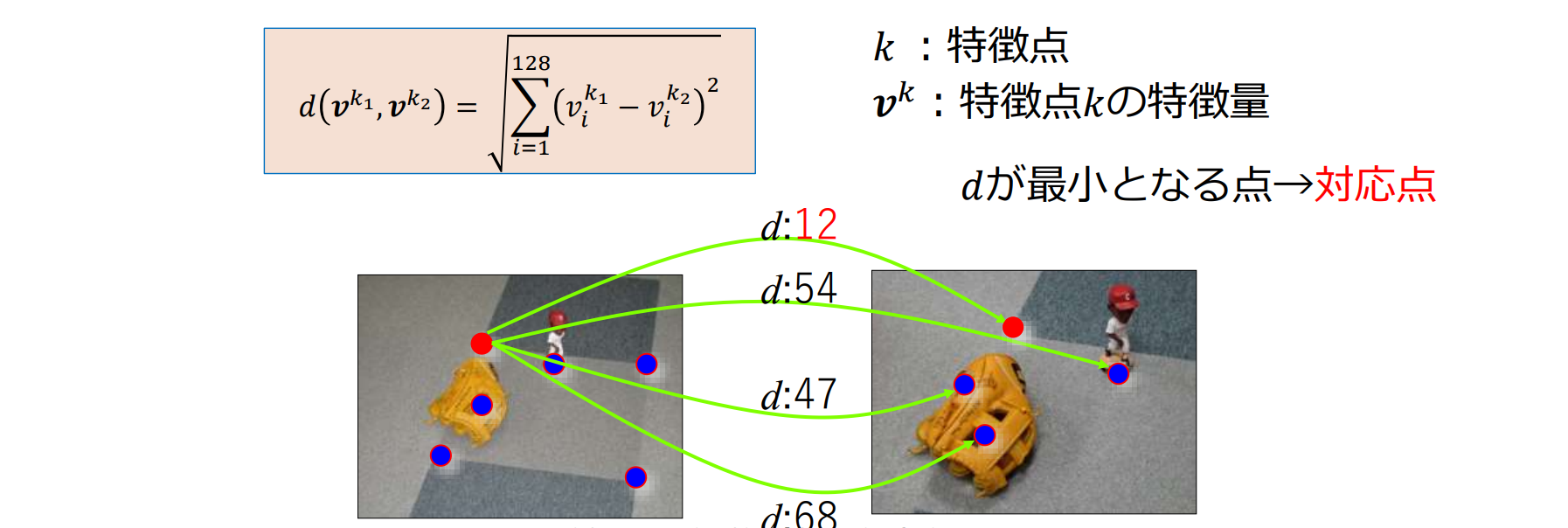
SIFTの対応点探索による画像のマッチング
画像1の特徴点 に対して,画像2のすべての特徴点 との距離を計算,最も距離が小さい特徴点を対応点とする
- 128次元のSIFT特徴ベクトル間のユークリッド距離

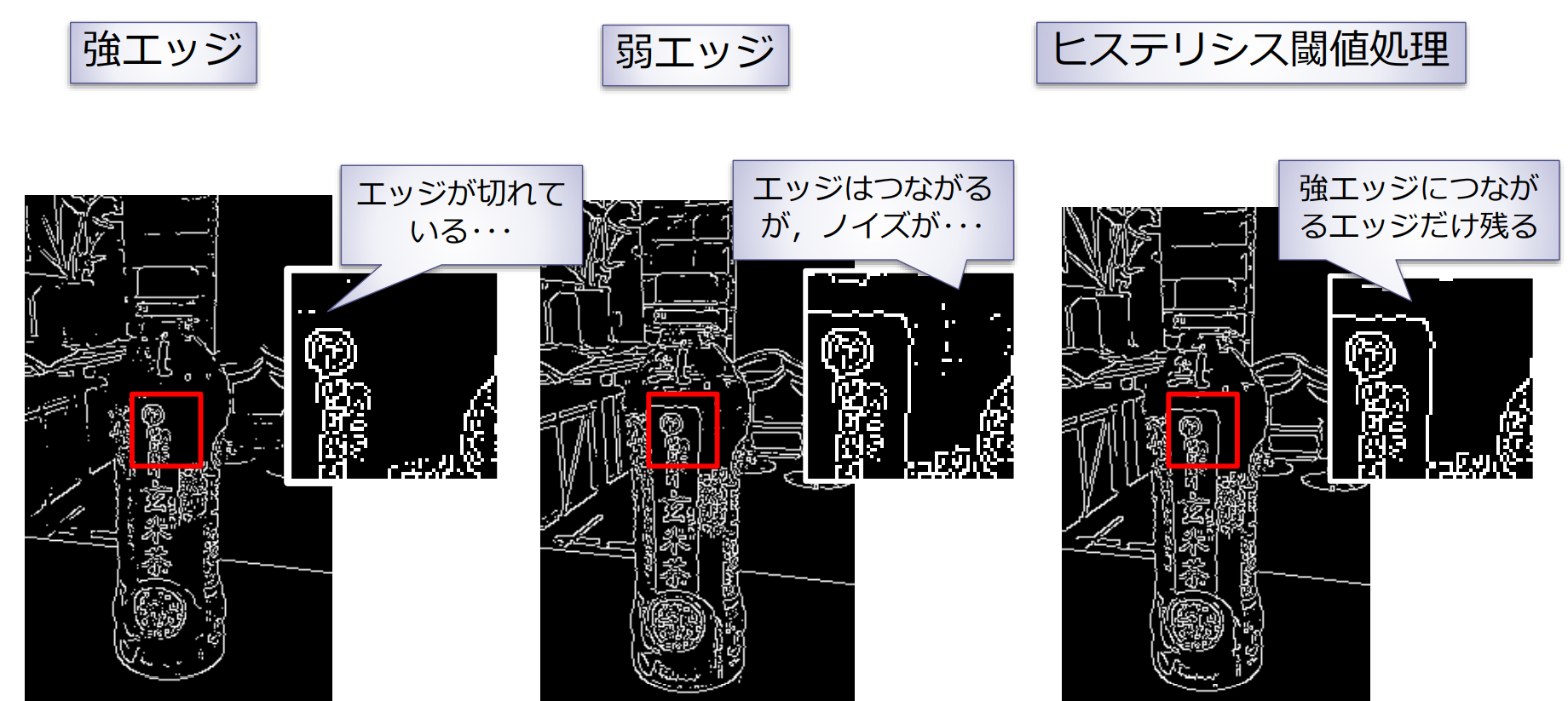
Cannyエッジ検出アルゴリズム(1986)
今でも最もよく使われているエッジ検出アルゴリズム

ヒステリシス閾値処理(hysteresis threshold):2つの閾値を用意する.大きい方の閾値で検出されたエッジ点(強エッジ)から追跡し始めたら,小さい方の閾値より小さくなるまで追跡し続ける
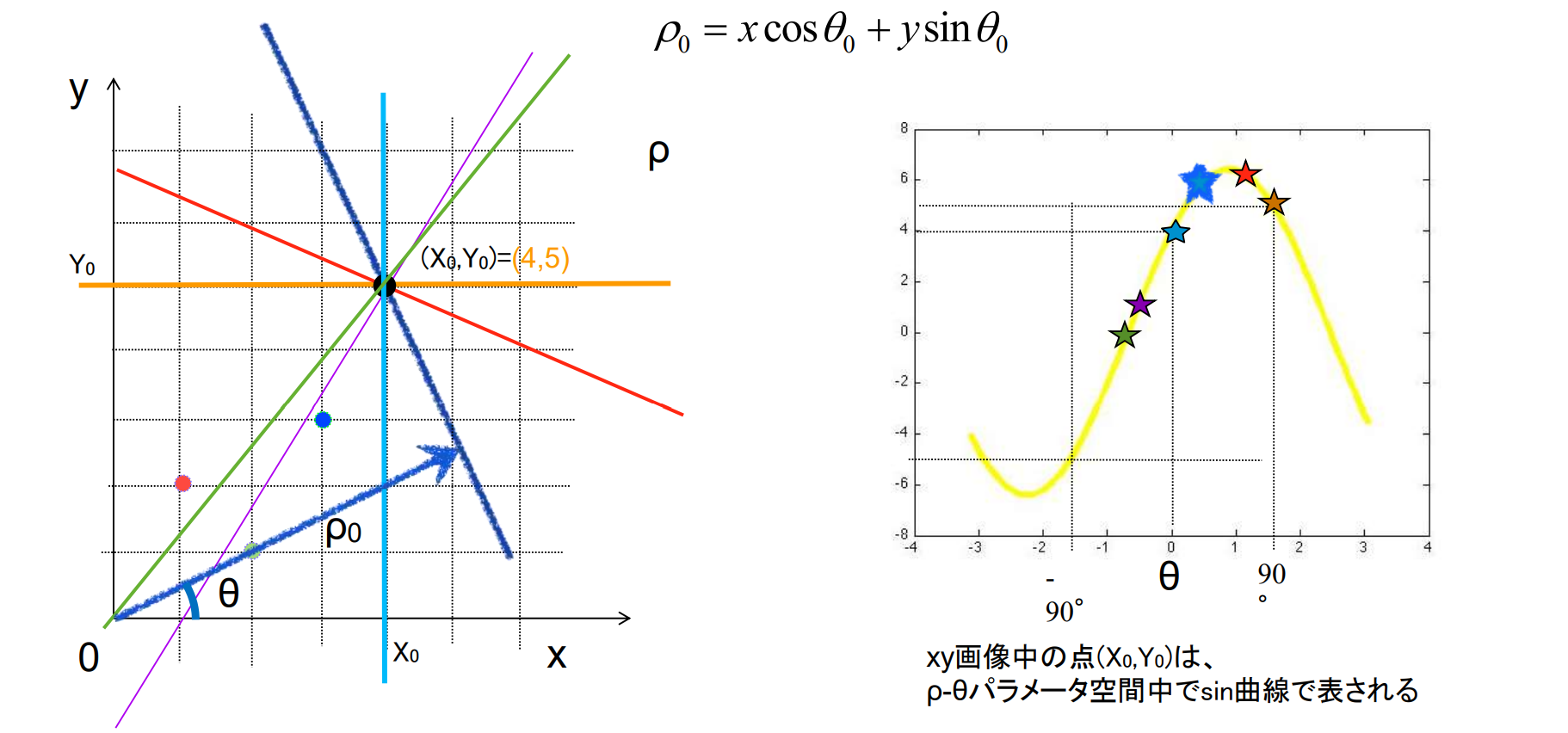
線の抽出(ハフ変換)
目的:エッジ点をつなげて直線を抽出したい
ハフ変換(Hough transform):Hough(1962)が提案.確からしい直線の位置へエッジ点を投票(voting)

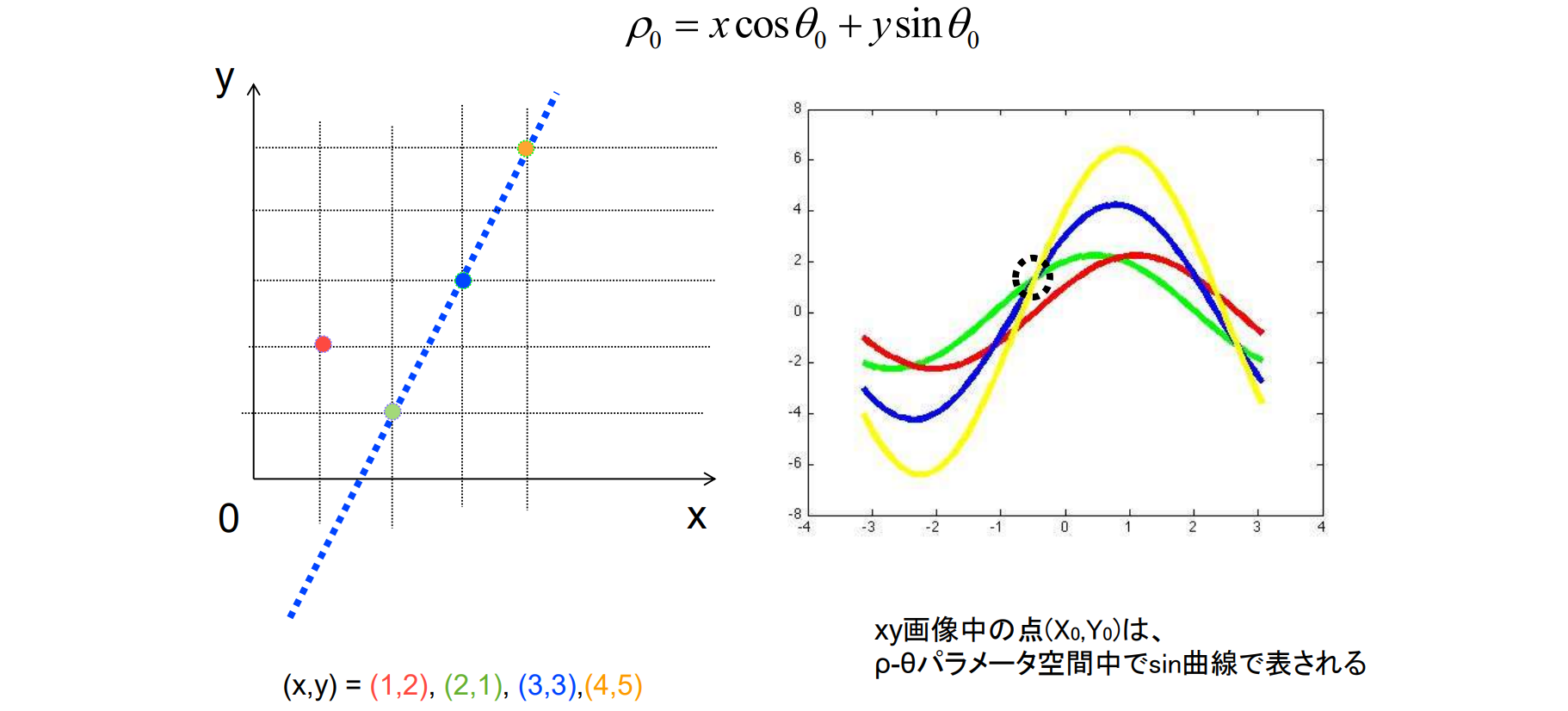
RANSACに基づく直線検出
エッジ点をランダムに二つ選び出して直線の候補(line hypothesis)を作り,エッジ点がこの直線上にどれだけ存在するか検証するという処理を繰り返す
- エッジ点と直線の距離が閾値以下であれば,直線上に存在する(インライア)と判定
- 十分な数のインライア(inlier)があれば直線を出力
動画像処理
動画像(moving picture, motion picture):短い時間間隔(例えば1/30秒)で連続的に取り込まれた静止画像の集合
- 3次元配列 で表現される(色を入れると4次元配列)
- フレーム(frame):動画像を構成する個々の静止画像
オプティカルフロー
オプティカルフロー (optical flow):異なる時間に撮影された2枚の画像間で同じ対象の対応付けを行い,その移動量をベクトルとして表現したもの
オプティカルフローの応用例:
- 撮影した物体の移動速度を測定
- 監視カメラで撮影した移動物体の振る舞いを把握
- 複数枚の画像の位置合わせ(手ぶれ補正)
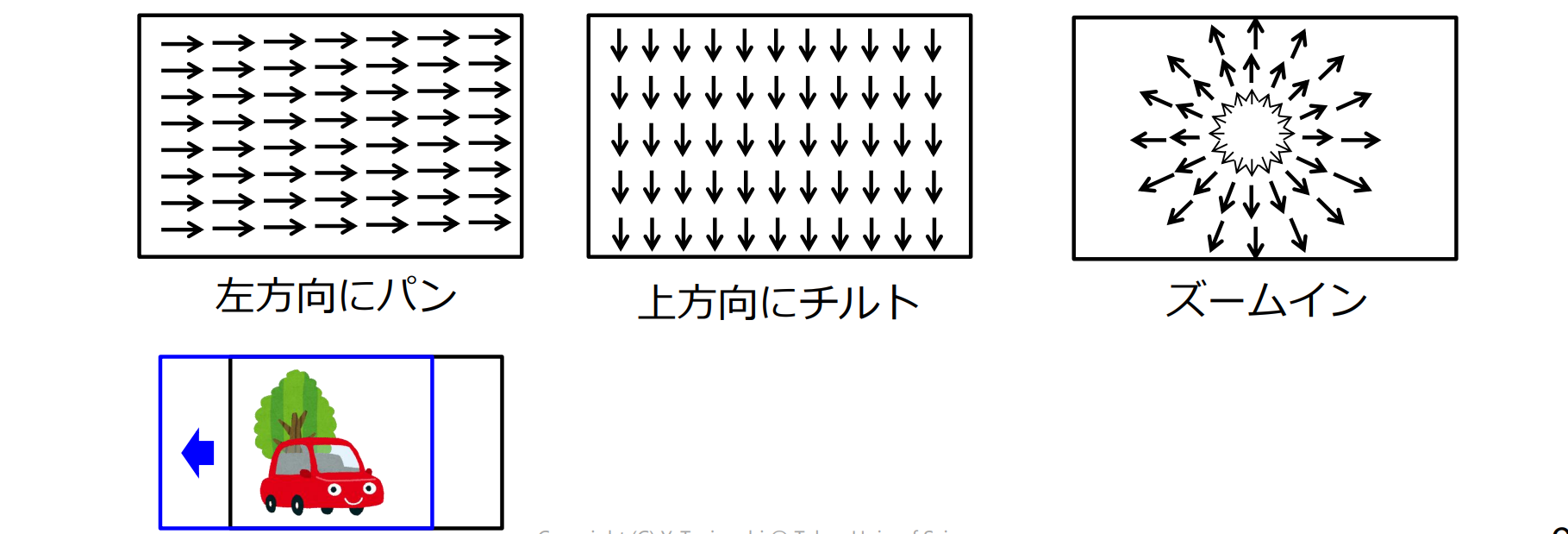
カメラの動きとオプティカルフローの関係
- パン(pan):カメラを左右に振る
- チルト(tilt):カメラを上下に振る
- ズーム(zoom):カメラの焦点距離を変化させる
ブロックマッチング法
ブロックマッチング法(block matching method):注目点の近傍(ブロック)では,対象物が平行移動すると仮定、次のフレームで,注目ブロックに最も類似するブロックを探索して移動量を求める方法
- 時刻tのフレームにおける座標 の画素を注目点とするとき,この画素を中心とした 画素のブロックを考える
- 時刻 のフレームから,このブロックに最も類似する同サイズのブロックを求める
- 最も類似していると評価されたブロックの中心画素を,注目点に対する対応点とする
非類似度の指標
残差(差分)絶対値和(sum of absolute difference; SAD)
- 完全一致するときに0,値が大きいほど二つのブロックは類似度が低い
残差(差分)2乗和(sum of squared difference; SSD)
類似度の指標
正規化相関係数:1以上1以下の値をとり値が大きいほどブロックは類似
探索範囲
- 探索範囲(search area):類似するブロックを探索する範囲
- 全探索(full search):探索範囲内に存在する全ての同サイズのブロックに対して類似度(非類似度)の評価をすること
残差逐次検定法
残差逐次検定法(sequential similarity detection algorithm):計算量を削減しながらも,全探索と同じ結果が得られる
1 | d_min := ∞ // 残差絶対値和の最小値を記録する変数 |
勾配法
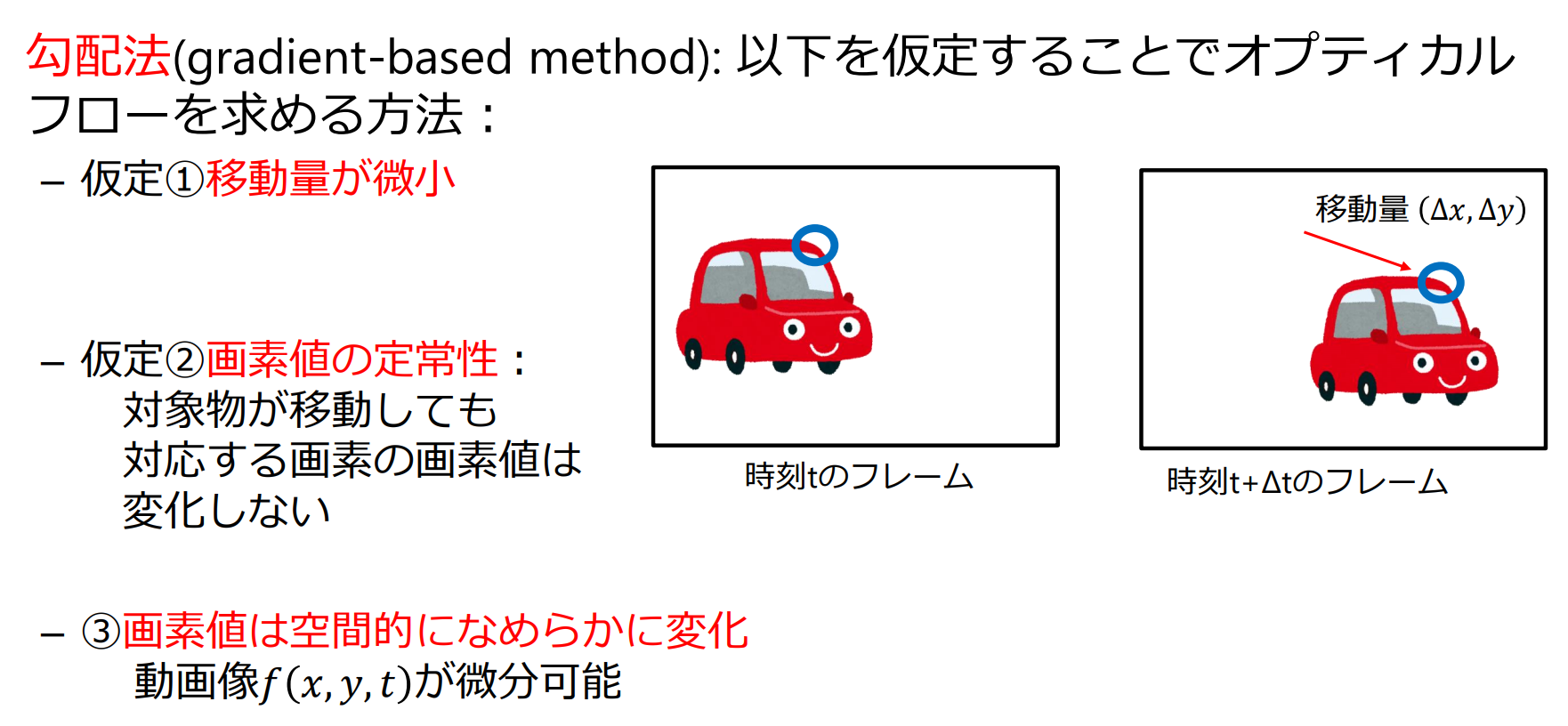
オプティカルフローの拘束条件式:
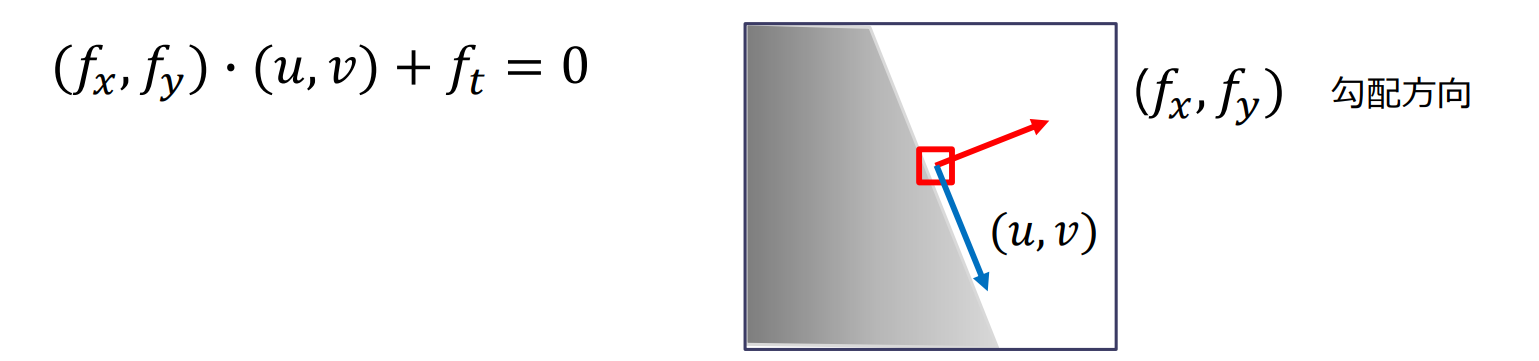
- 変数が の二つで式が一つなので値が一意に決まらない
- 条件を追加することで を求める
- Horn Schunck法
- Lucas Kanade(LK)法
Horn-Schunck法
Horn-Schunck法:オプティカルフローが空間的に滑らに変化することを仮定し,画像全体のオプティカルフローを求める方法

Lucas-Kanade法(LK法)

- 微小な移動を前提としているため,移動量が大きい場合はNG
KLT tracker(Kanade Lucas Tomasi)
- Harrisコーナ検出器で特徴点(good feature to track)を求める
- 画像ピラミッドを作成し,最も縮小率の低い画像対に対してLK法によりオプティカルフローを求める.段階的に,縮小率を下げながら,LK法を適用することで精度の高いオプティカルフローを推定
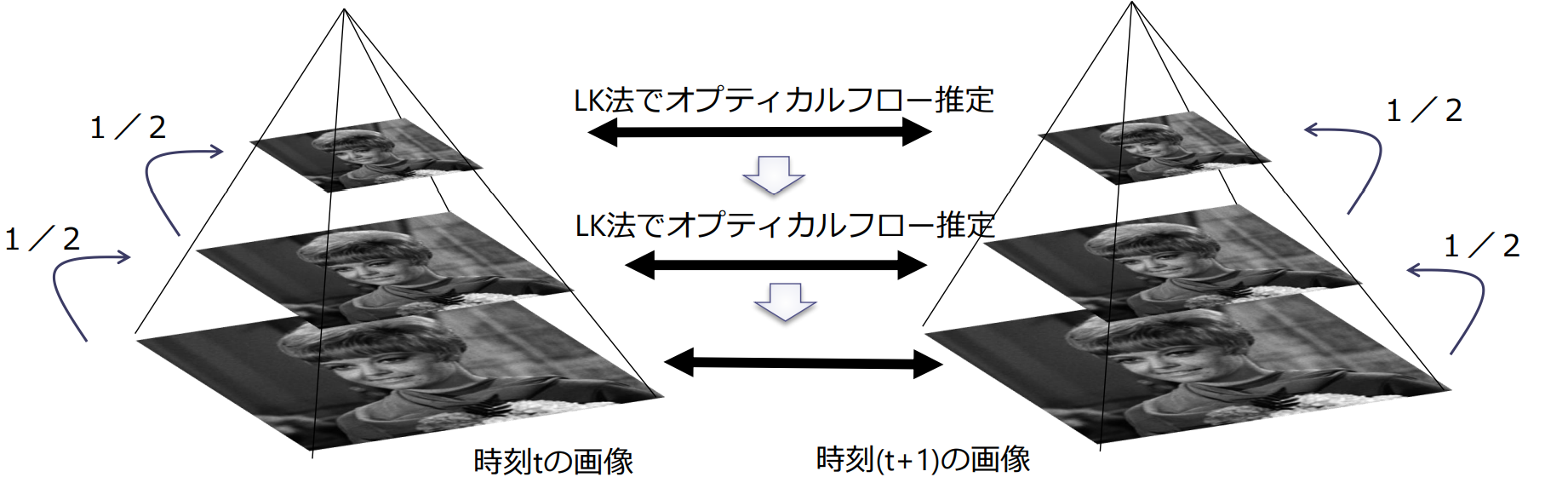
- 人物の後ろ側の輪郭付近では隠れていた部分が現れるため,対応する画素がなく,正しくオプティカルフローを求めることができない
移動物体領域の抽出
差分画像(subtraction image)
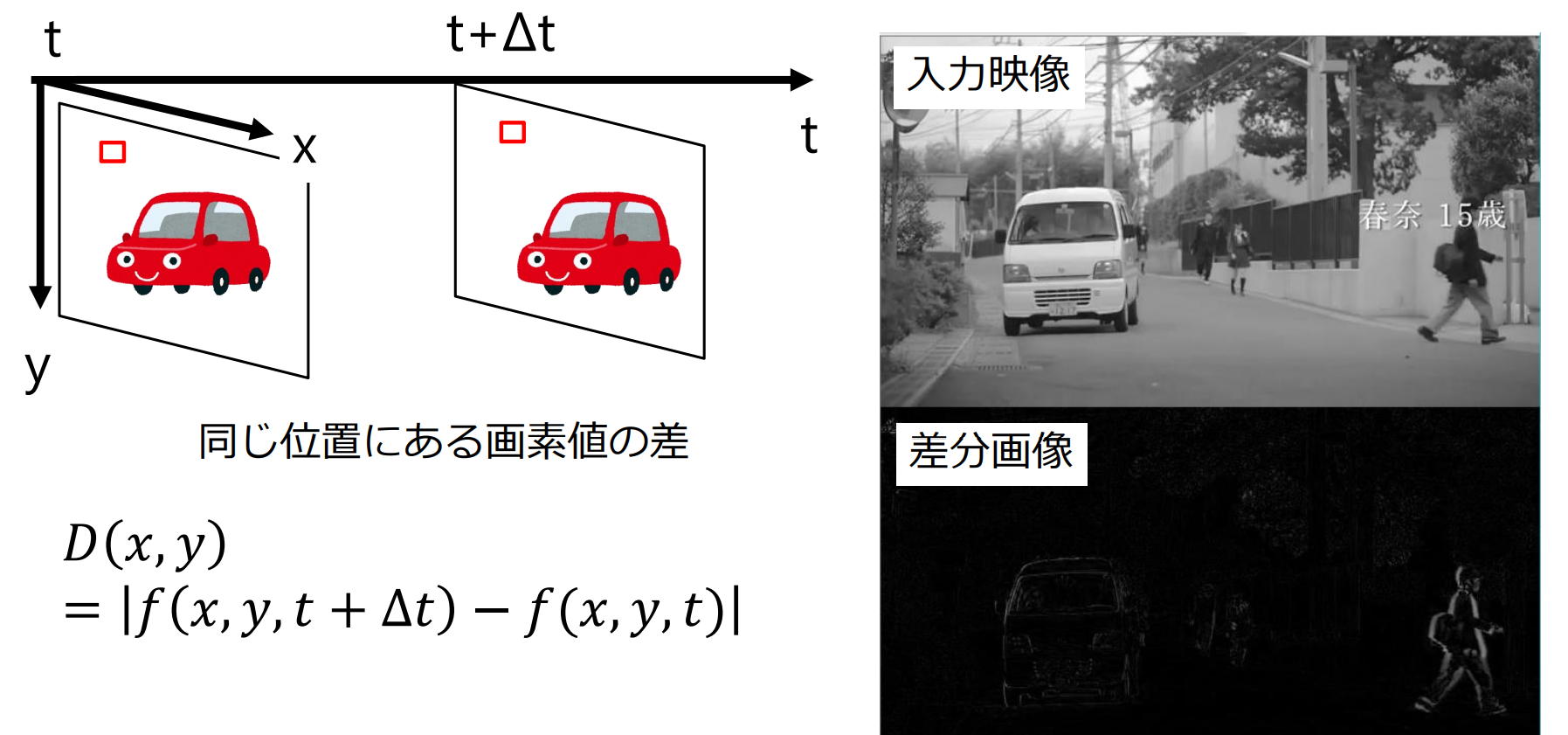
背景差分法(background subtraction method)
移動物体が無い状態の背景画像(background image)を何らかの方法で取得しておく
背景画像 と動画像 の差分画像を求める
差分画像 を2値化することで移動物体領域を求める
フレーム間差分法(frame subtraction method)
移動物体がない理想的な背景画像を取得できない場合、移動物体を撮影した異なる時刻の3枚の画像を用いて移動物体領域を切り出す
フレーム と の差分画像を求める
差分画像 を2値化する
時刻 の移動物体領域を,2値画像 の積集合として求める
統計的背景差分法
画素値の定常的な変動を考慮して移動物体を検出
- 樹木部分:時間変動大
- 道路部分:時間変動小
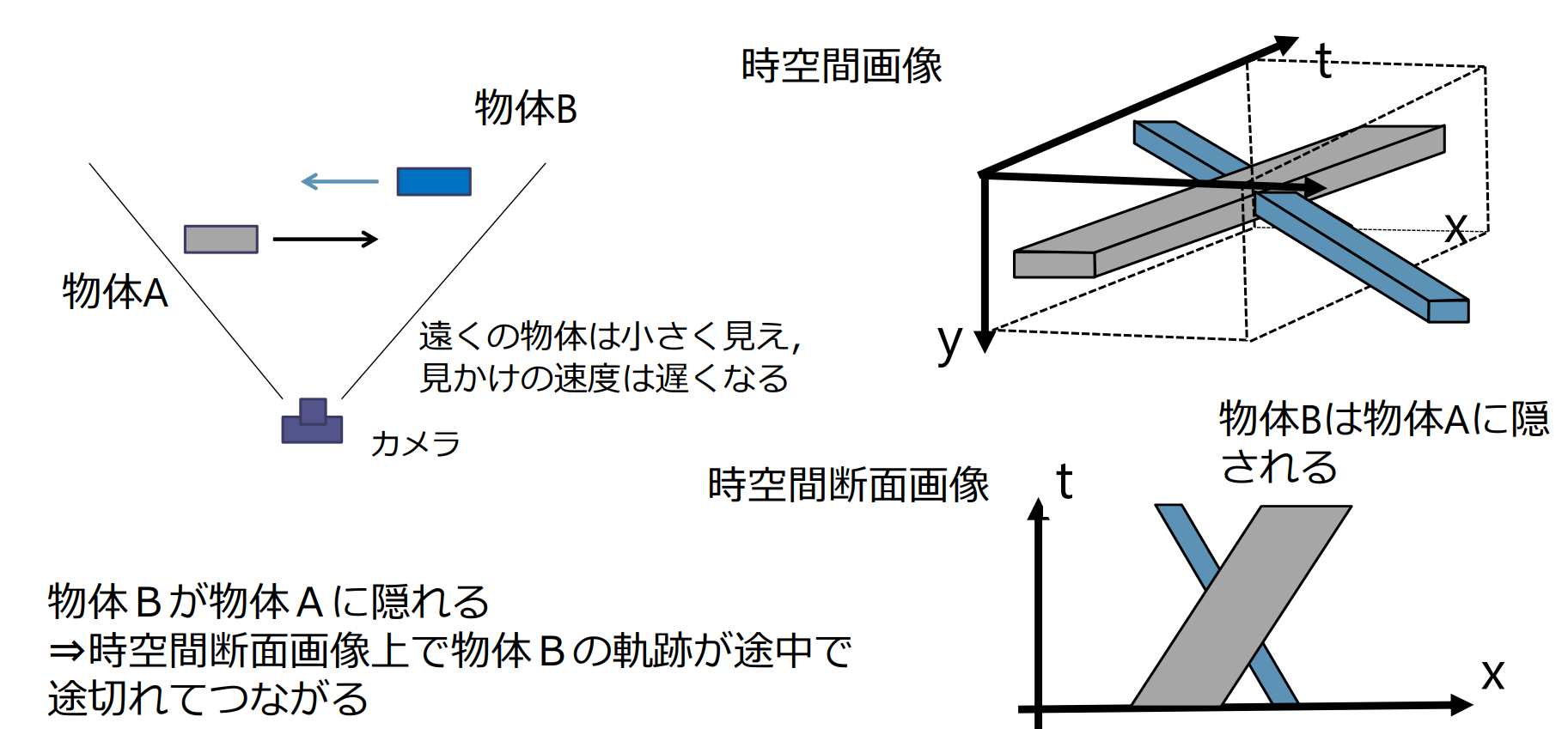
時空間画像
時空間画像(spatio-tempral image):動画像を構成するフレームの画素を下図のように水平・垂直軸,時間軸の3次元信号として扱うこと
時空間断面画像
時空間断面画像:時空間画像を切断した断面