查尔斯·达尔文的这句话就是整个进化算法的核心思想
简介
进化算法(演化算法:Evolutionary Algorithms)包括遗传算法(Genetic Algorithms),遗传规划(Genetic Programming),进化策略(Evolution Strategies)和进化规划(Evolution Programming)4种典型方法。第一类方法比较成熟,现已广泛应用,进化策略和进化规划在科研和实际问题中的应用也越来越广泛
为什么要学习进化计算?进化计算的作用:
- 做优化Optimization
- 可以用这个算法反过来去模拟自然界变化
最重要的是做优化,那么什么是优化?
The process of searching for the optimal solution from a set of candidates to the problem of interest based on certain performance criteria
进化计算的关键概念:
- Population-Based Stochastic Optimization Methods:与BP算法不同(从一点开始梯度求导,慢慢收敛),它不是单点的,进化计算是多点的;梯度下降每一步是确定的,但Stochastic是随机的,每次运行结果不完全一样
- Inherently Parallel:并行的好处是不容易陷入局部最优解
- A Good Example of Bionics in Engineering
- Survival of the Fittest
- Chromosome, Crossover, Mutation
- Metaheuristics
- Bio-/Nature Inspired Computing
EA Family:不止一个算法,包括经典的GA,GP,ES,EP,以及:
- EDA:分布估计算法(Estimation of Distribution Algorithm)
- PSO:粒子群优化算法(Particle Swarm Optimization)
- ACO:蚁群算法(Ant Colony Optimization)
- DE:差分进化算法(Differential Evolution)
遗传算法(GA)
遗传算法模拟一个人工种群的进化过程,通过选择(Selection)、交叉(Crossover)以及变异(Mutation)等机制,在每次迭代中都保留一组候选个体,重复此过程,种群经过若干代进化后,理想情况下其适应度达到近似最优的状态
自从遗传算法被提出以来,其得到了广泛的应用,特别是在函数优化、生产调度、模式识别、神经网络、自适应控制等领域,遗传算法发挥了很大的作用,提高了一些问题求解的效率
遗传算法的基本组成
- Representation
任何一个问题,首先必须要进行编码(encode)表示,才能在计算机上计算,有的时候会用二进制(例如属性选择,选择为1,没选为0),而有些问题可能天生就是连续型的,是一个函数,有若干个函数,每个值 这样表示出来
- Genetic Operators
表示完后要进行操作,要进行各种各样的运算来生成新的个体,有两种:杂交(Crossover)和变异(Mutation),杂交就是把两个染色体中间某些基因交换
- Selection Strategy
"适者生存"说的就是选择,我们有很多个体parent,到底哪些可以用来繁殖后代,这需要选择;生成的后代offspring,哪些可以生存又需要选择
Representation
- Individual(Chromosome)
表达其实就是所谓的个体Individual,生物学上一般称为染色体,在计算机当中一般称为Individual,就像一串项链,有多少个输入就一一对应,若为100维的函数,那就是个100维的向量,每一维对于一个可行的参数取值
- Population
很多个Individual合在一起就是Population,GA一直在维持maintain,例如100,1000个Individual同时在搜索,好处就是parallel search,有助于提高全局最优解。若只有一个点在搜索,运气差的时候就会掉入局部最优解,但是如果有100,1000个点同时搜索,而且通过Crossover,点之间可以互相交换信息,会提高发现全局最优解的可能性
- Offspring
通过杂交和编译,生成的新的向量,Hopefully contain better solutions
- Encoding
表示成01不一定只有二进制,还有一种编码方式叫格雷码(Gray),还有例如TSP问题,我们怎么编码
| Decimal | Binary | Gray |
|---|---|---|
| 0 | 000 | 000 |
| 1 | 001 | 001 |
| 2 | 010 | 011 |
| 3 | 011 | 010 |
| 4 | 100 | 110 |
| 5 | 101 | 111 |
| 6 | 110 | 101 |
| 7 | 111 | 100 |
Selection
我们把每一个个体都打一个分,根据这个分数来选择
最原始的方法就是Roulette Wheel Selection,值越大给的面积越大,然后扔飞镖,扎到哪个个体就选择哪个,当然也有缺点,比如负值的情况,或者有某个值特别高的情况
所以提出了第二种方法Rank Selection,给分数排序,类比于大学成绩90分到100分都给S评定
第三种方法叫做Tournament Selection,假设从100个学生中选择好的学生,每次挑出2人PK,选择赢的一方。但是选择几个人PK是个问题,所以PK人数越多,水平越高才能被选中
第四种方法叫做Elitism Selection,类比于考试的保送生,我们知道进化不能保证每一次都比上一次好,有可能杂交后还不如原来的好,这会造成收敛,不稳定,所以说精英主义就是把原来最好的复制到下一代
还有一种是Offspring Selection,就是生出的子代怎么选择,通常有2种做法:把子代完全作为新代替换父代;还有一种就是 即100个新代和原来100个合在一起,从这200个里面选100个
Crossover
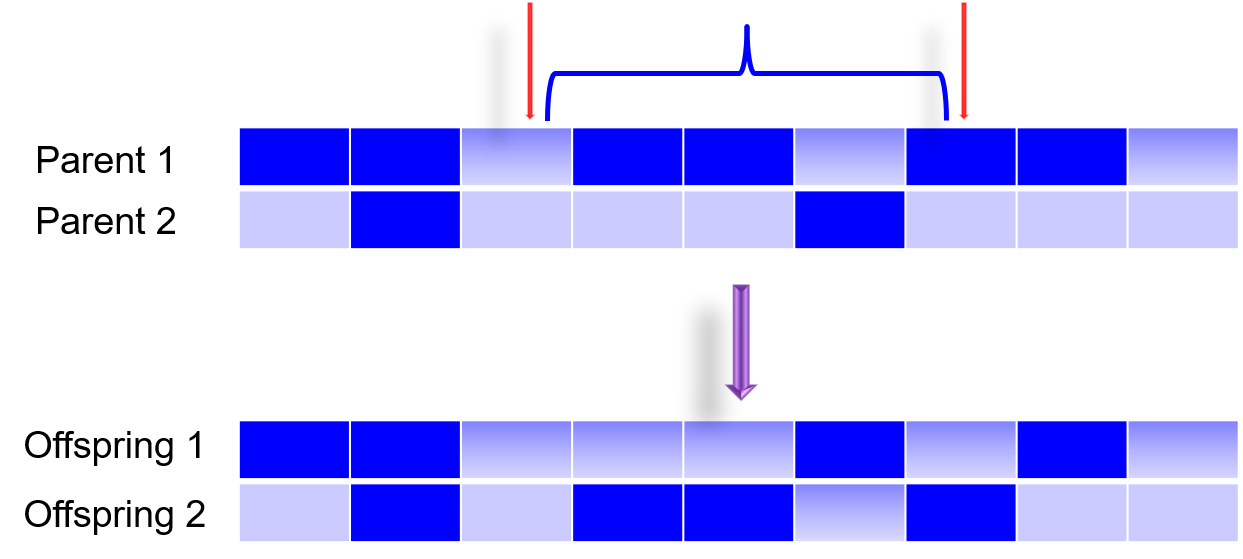
最简单的方法是一点杂交(One Point Crossover),简单的说就是选一个点,从这个点以后所有的遗传物质进行交换
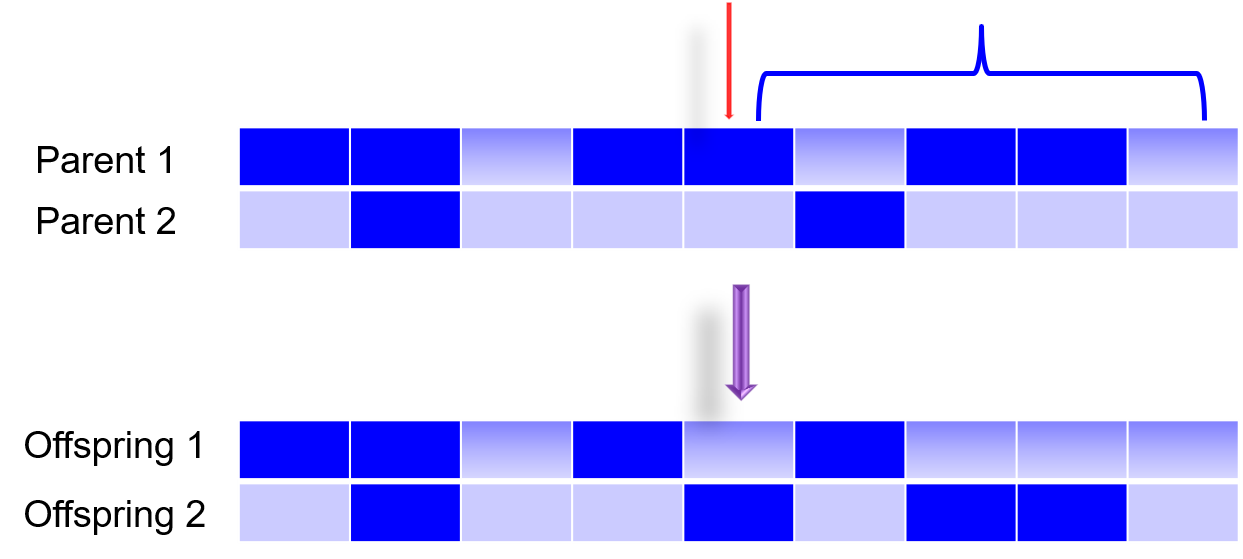
第二种方法是两点杂交(Two Point Crossover),简单的说就是选两个点,把这两个点之间的所有的遗传物质进行交换
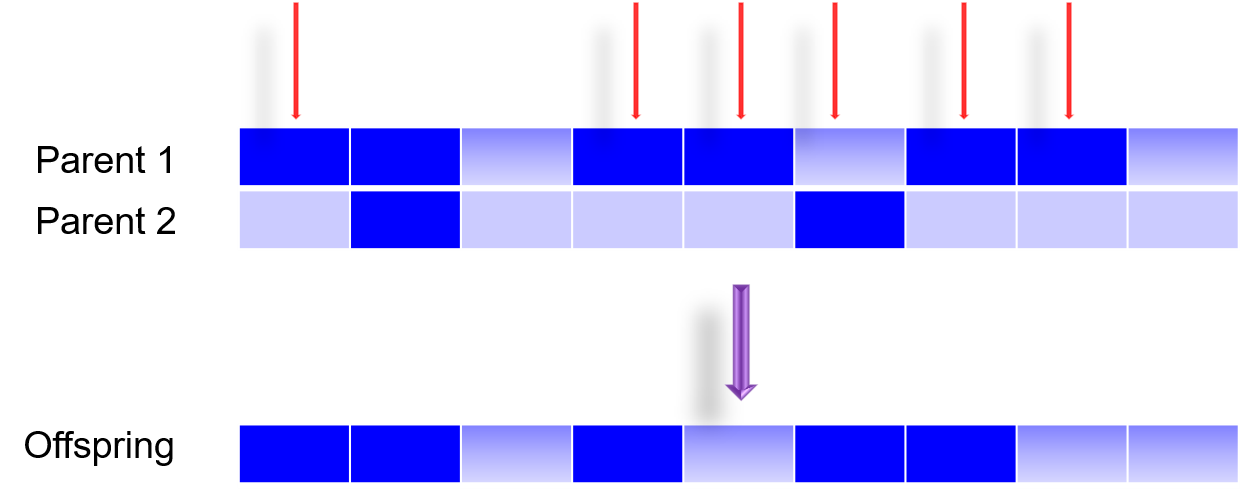
还有一种方法是 Uniform Crossover,即各个点都可以杂交
看似杂交只需要交换一下那么简单,但实际上并非如此。例如 Crossover of Two Individuals for TSP 问题中,用数字代表访问 city 的顺序,然后杂交,有时就会产生不合法的数字出现情况。一般来说有2种解决方法,第一,修复不合法的数字,第二,设计新的杂交,使得杂交出来是合法的 tour
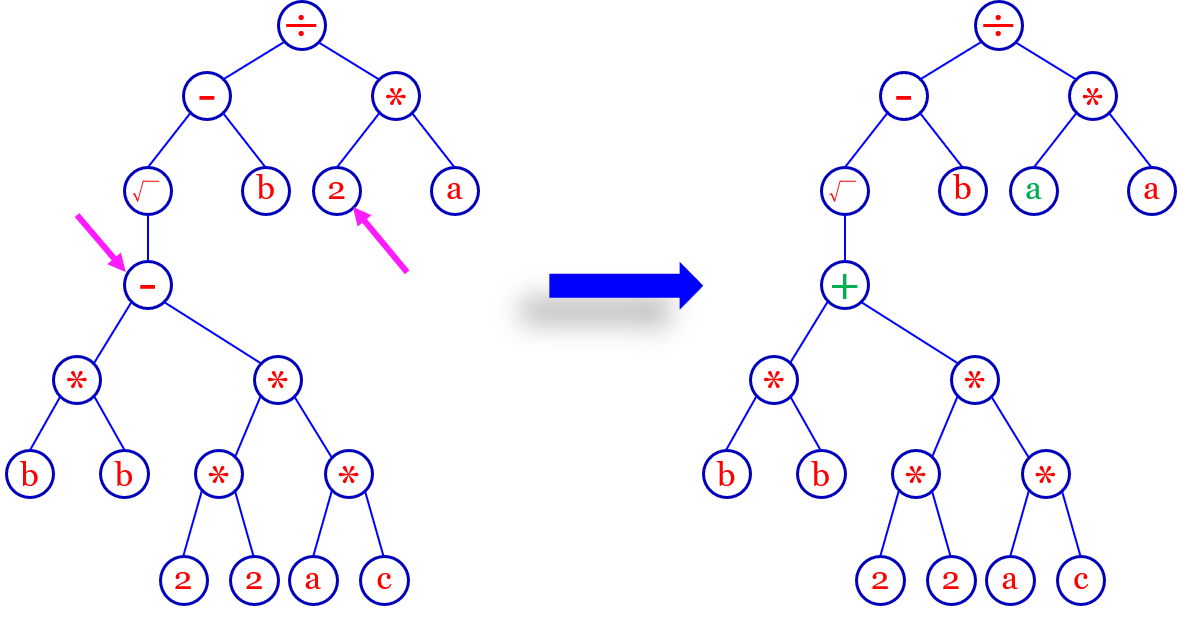
Mutation
一般随机选几个位置,不会选很多,变异太多搜索会变成随机性的,0变1,1变0;如果是连续值得话,会加上高斯,例如原来是0,加高斯在-0.1到-0.2之间取值
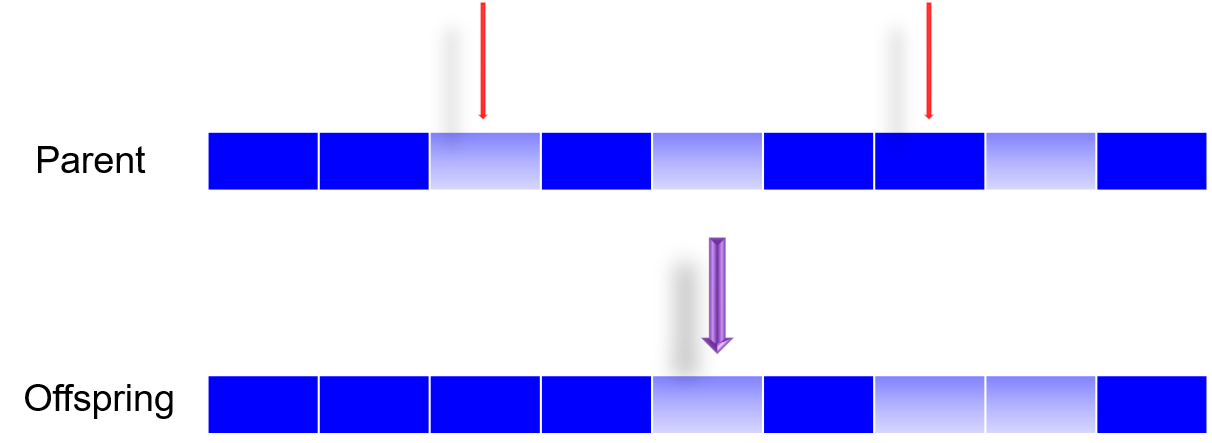
Mutation is mainly used to maintain the genetic diversity
下图就是一个例子,如果你的基因多样性损失的太快,太早,就会导致不成熟收敛,应该收敛到图中笑脸的位置,真正的算法虽然最后一定要收敛,但是如果收敛错了地方也是不对的
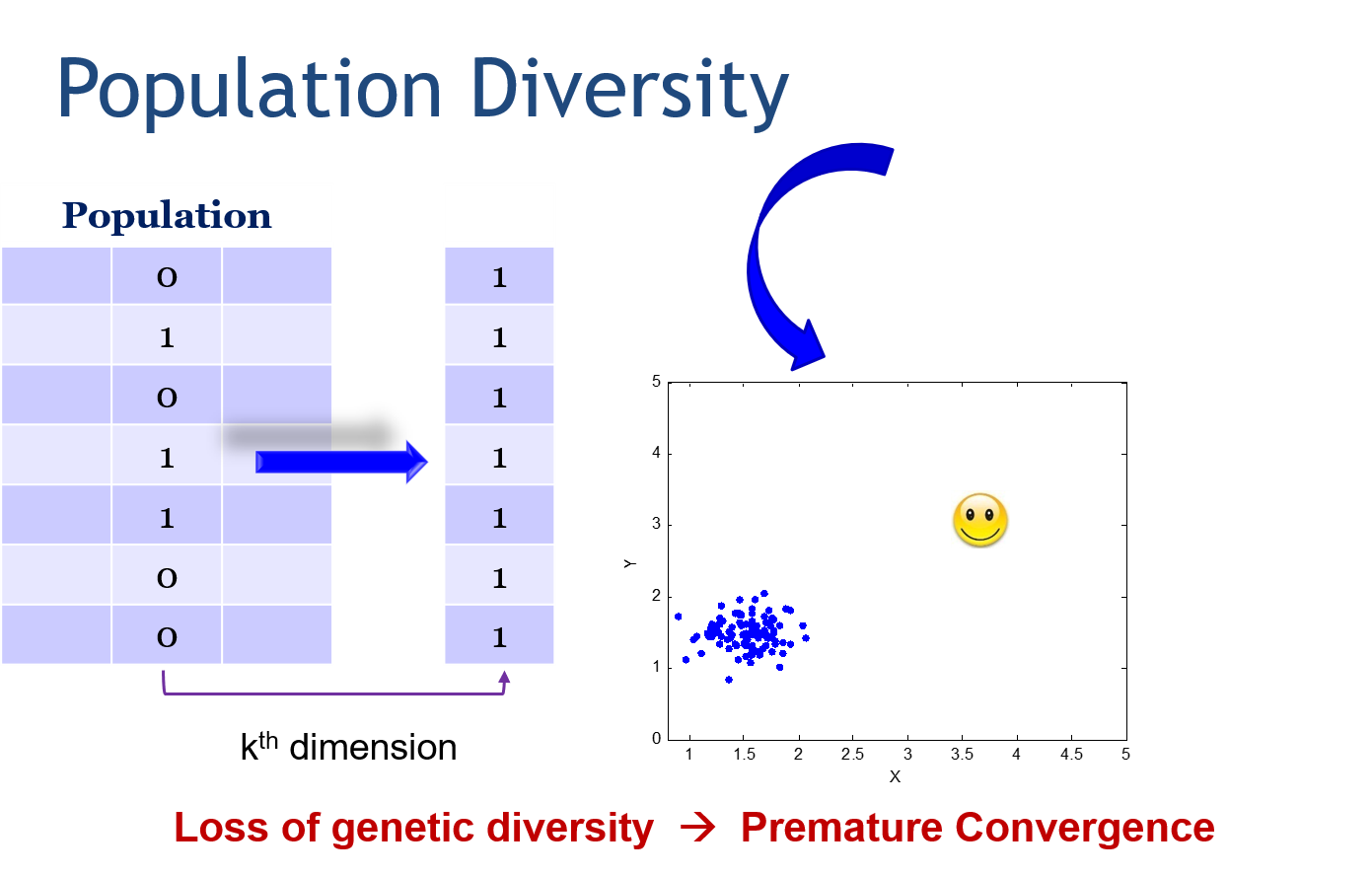
总结
Selection vs. Crossover vs. Mutation:
Selection是给最有希望的个体多一些资源,但是可能会造成基因多样性的损失,有一些个体就会被从种群中移除,它们所带的基因就会消失
Crossover是杂交,交换一些遗传信息,它的主要目的是希望让杂交出的子代更好;杂交对基因多样性没有影响,原来有什么基因杂交后还是那些基因
而Mutation是专门生成新的基因,保持种群的基因多样性,从搜索的角度看是让种群到别的地方搜索,不要集中在一个地方
这三个合在一起,体现了一个重要的思想:Exploration vs. Exploitation:
Exploration是指100个人满校园去找,把搜索资源用于广度优先,各个地方各个角落都去找一找;而Exploitation是指有人说钱包是都在3楼的某一间教室,然后大家一起拉网式在这个教室搜索
Exploration一开始是非常重要的,但是也不能总是在特别广的范围搜索,搜索效率太低,这里有个平衡
整个遗传算法的框架:
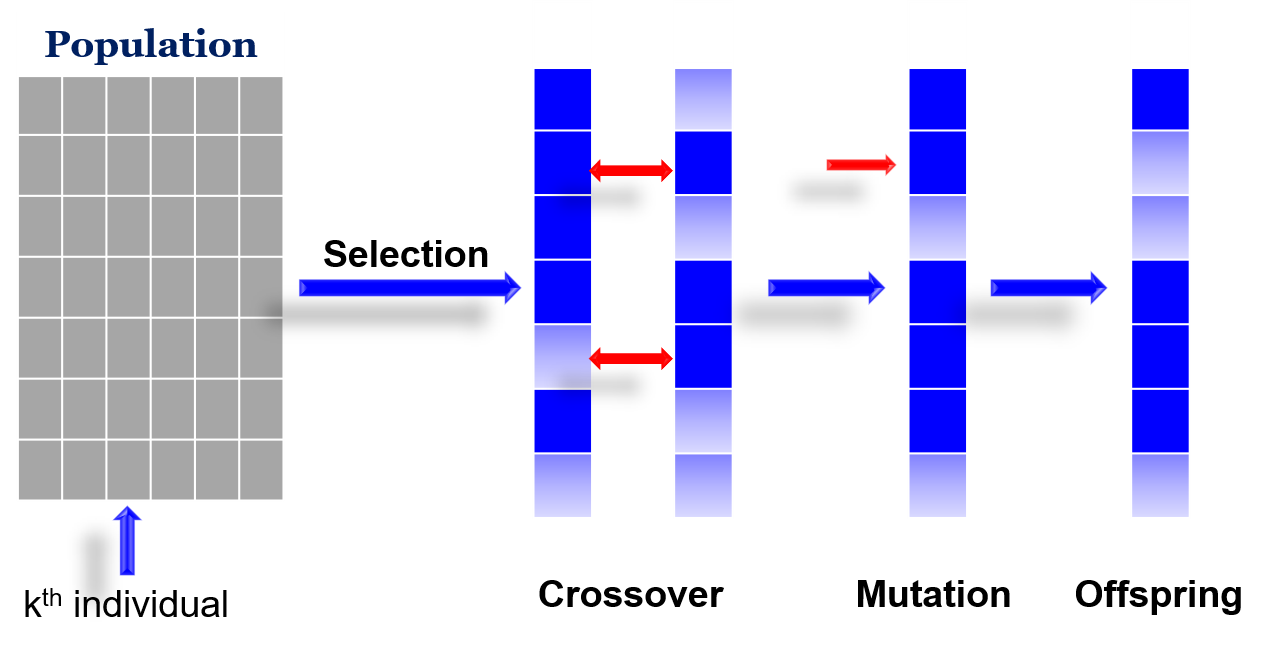
从一个population的某一列,适应度大的个体就有大的概率被选择,选择后让他们杂交生成一个新的个体,让他在变异,当然变异的地方很少,最后生成一个真正的子代

首先是Initialization:生成一个初始的种群,比如说生成100个个体。然后对每一个个体的适应度进行一个Evaluate
接下来是两层循环:外面的循环就是一代一代的循环,从父代到子代一代代循环;里面的循环是生成population中的每一个个体,比如说从当前的种群中用某种选择方法挑选2个个体出来,让他们杂交,变异,再评估,这算是生成了2个新个体,然后再重复,直到把100个个体都生成完毕,这算是一代内部的循环结束
遗传算法在使用的时候有很多参数(Parameters)需要调整:
Population Size到底要多大?太大会很慢,就像管理国家有10亿人一样,当然太小也一样,相当于2个人去矿山找金子一样
Crossover Rate推荐值是0.8,80%的杂交,剩下20%就复制到个体中
Mutation Rate推荐值是 ,假设你有100位,那么概率就是1%,一次就只有1位变异。如果太大会造成搜索在空间中到处跳,就像随机搜索一样,但是太小的话,如果收敛的很快,收敛到一个错误的地方后,变异率太小不足以把它拉回到其他区域
Selection Strategy是非常重要的,如果一开始就给相对比较好的个体太多优先权,那么后面的population里面很可能都是他们的孩子,就相当于过度繁殖了,生出的孩子很他们特别像,这会导致这个种群很快的收敛到某个特点的点。当然这个选择有很多方法:
- Tournament Selection:可以选两两PK,也可以三个三个PK
- Truncation Selection (Select top T individuals):类比高考画分数线,通常选top30%
归根到底就是selection pressure,到底给好的个体多大的选择权,同时兼顾好的和不好的个体
整个遗传算法GA其实就是各种参数的选择来控制搜索过程,到底是Exploration还是Exploitation
特征选择
特征选择可以降低维度,减小问题规模提高分类的精确度,那么如何用特征选择来解决遗传算法的问题呢?通常接近问题选择有2种策略:
- Filter Method:不考虑使用哪个分类器,只是单纯分析属性
- Wrapper Method:是需要考虑使用的SVM还是神经网络,将这些也包含在属性当中,也就是说针对SVM的特征选择,针对神经网络的特征选择,针对KNN的特征选择是不一样的
遗传算法做特征选择
Representation:Binary strings,前面说过,选择为1,没选择就是0
Fitness Function:Classification errors (KNN, SVM, ANN etc.),目标函数即分类器用什么,比如说选了5个属性,放在SVM当中,训练一下看看准确度多高,就拿这个作为适应度,误差越小,适应度越高
Evolve a population of candidate subset of features,很多个体,其中一个个体选5个属性,另一个个体选8个属性,无论选几个,放进去跑一下好的就留下
主要的问题是维度不能太高,维度太高会导致计算复杂度太高,可能会需要用一些方法先降维到几十维,然后挑几个可能用GA比较好
聚类(Clustering)
聚类就是把没有标签的数据分成 组的过程
聚类有很多算法,K-Means是其中最经典的算法:
- 选择初始化的 个样本作为初始聚类中心
- 针对数据集中每个样本 计算它到 个聚类中心的距离并将其分到距离最小的聚类中心所对应的类中
- 针对每个类别 ,重新计算它的聚类中心 ,即属于该类的所有样本的质心
- 重复上面2,3步操作,直到达到某个中止条件(迭代次数,最小误差变化等)
K-Means算法也存在一些问题:如果 的初始值选的不好,收敛会收敛错地方,所以说用遗传算法做聚类,就是去寻找这K个中心点
GAs & Clustering
Representation:
- A string of K centres
- Length: K·D (D is the data dimensionality)
Fitness Evaluation:给你 个中心点,把数据归类,重新计算每一个class的中心点,最后使用 来衡量一下 个中心点好不好,理论上讲这个值越小越好
评价之后就可以选择,杂交,变异
遗传算法待决的问题
遗传算法还有一些待决的问题:
比如说Parameter Control,它有很多参数,比如种群大小,杂交率,变异率,Selection Strategy,这些都需要决定,有时是在运行之前就把参数设置好了(Parameter Tuning);而有的时候需要在进化的过程中,根据它的进化情况,来动态调整参数
同样还有Constraint Handling问题,实际上问题都是有各种各样边界限制条件的,这些问题怎么把他融合到现有的遗传算法当中
也有多目标优化Multi-Objective Optimization问题,人都是贪心的,在真正的优化时很少只优化一个目标,很多时候目标是矛盾的,这会导致一个经典问题:Pareto Front,想让目标函数 同时取最小值
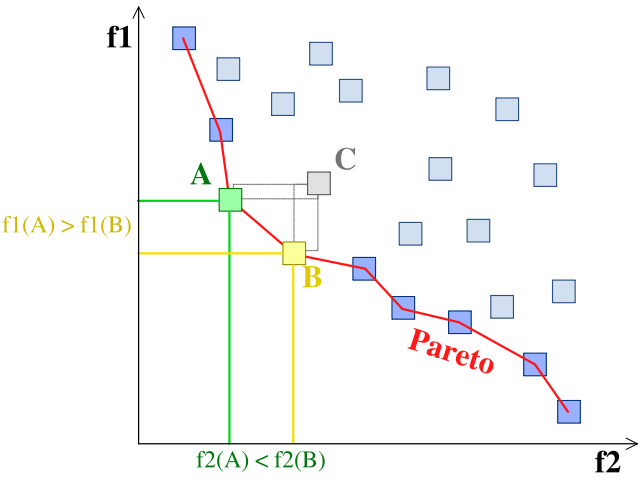
从图中可以看出所有边上的点都满足条件,任何两个点都是各有千秋,实际上我们会把这个面,二维是个曲线,把上面所有的解都返回,让用户自己挑选
遗传算法还有一个缺点:运算量大,比如同时搜索1000个点,可以想象复杂度很高。但是好处是可以是Parallel Computing
遗传编程(GP)
遗传编程,或称基因编程/GP ,是一种从生物进化过程得到灵感的自动化生成和选择计算机程序来完成用户定义的任务的技术。从理论上讲,人类用遗传编程只需要告诉计算机"需要完成什么",而不用告诉它"如何去完成",最终可能实现真正意义上的人工智能:自动化的发明机器
GA vs. GP
- GP is a branch of GAs
- Crossover/Mutation/Selection
- Representation
- GA:Strings of numbers (0/1)
- GP:Computer programs in tree structure (LISP)
- Output
- GA:A set of parameter values optimizing the fitness function
- GP:A computer program (Yes, a computer program!)
Functions & Terminals
GP是一个程序,所以需要Terminal Set:变量,常量,还需要Function Set:加减乘除等
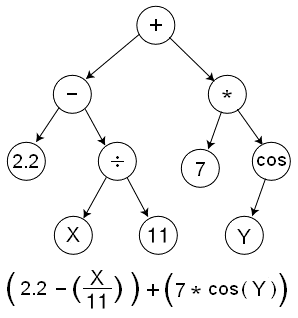
Crossover
这个树也是可以杂交变异的,在一棵树上选择子树,在另一颗树上选择子树,然后交换就会生成两棵新的子树,可以发现,杂交后的树深度可能会变长

在GA当中两个100维向量杂交后一定是100维的,而GP当中非常灵活
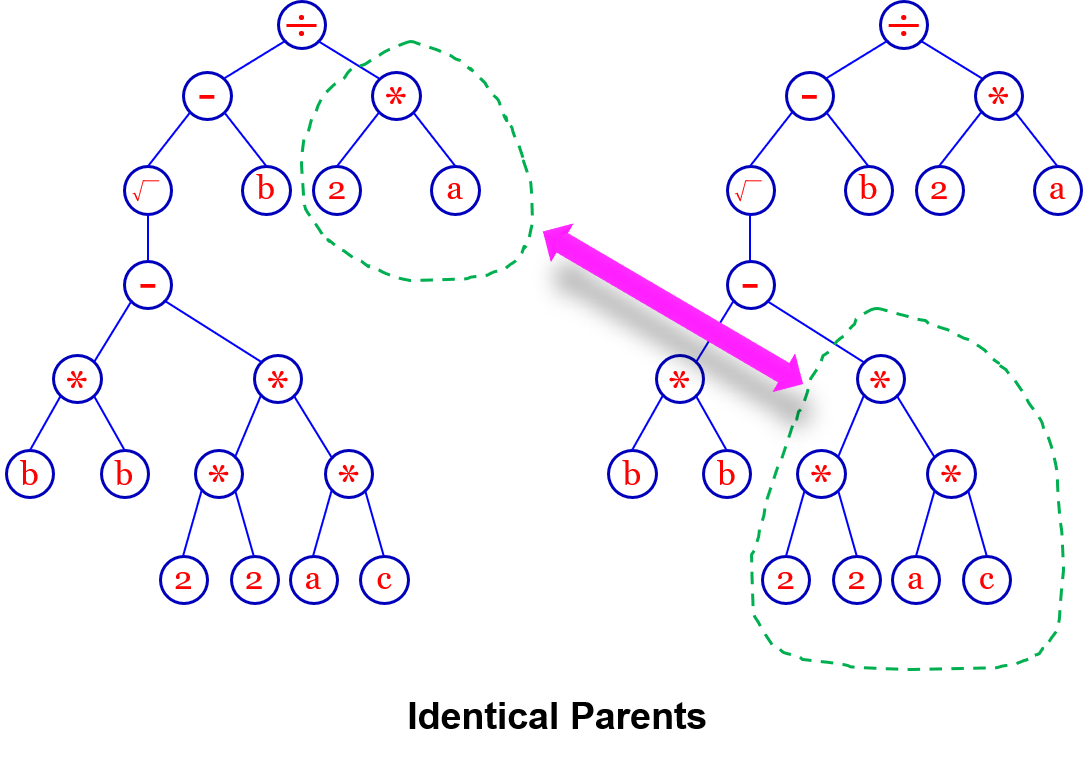
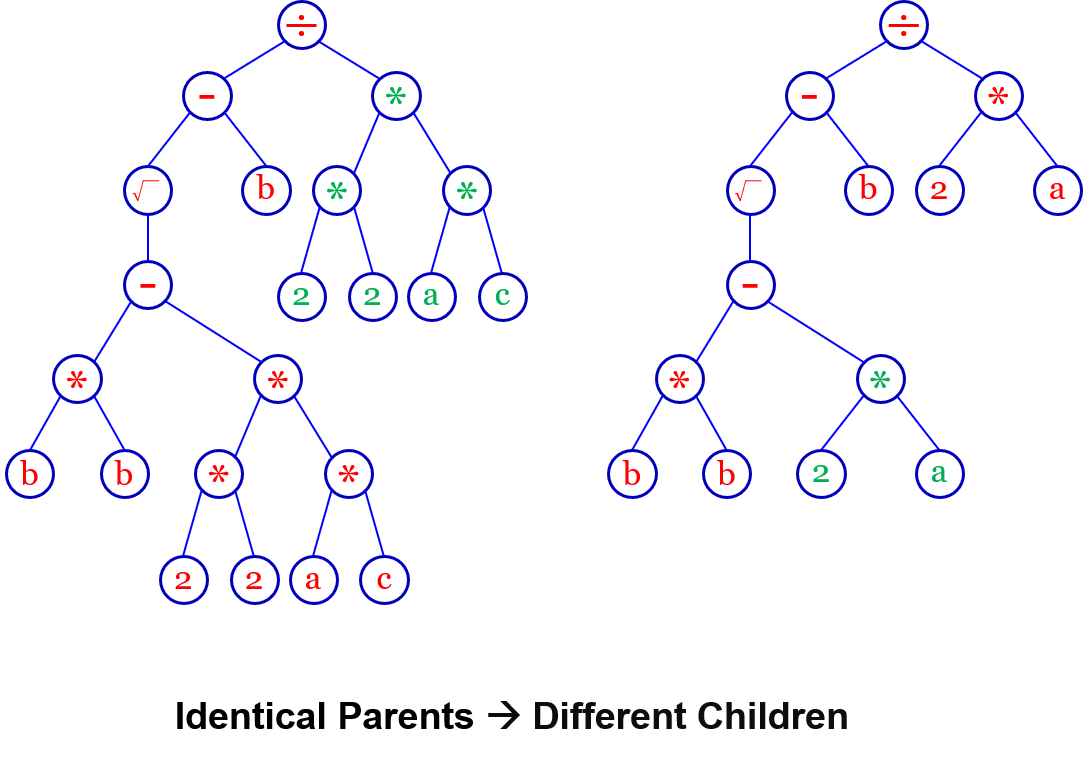
还有更为神奇的,在GA中,如果两个父代完全一样,它们之间杂交是没有意义的,但是在GP当中是不一样的,例如下图一元二次方程求根公式的例子:
Mutation
GP的应用
- Regression problem
- Control problem
- Classification
万物皆可进化
- Evolvable Circuits
- Antenna for NASA
- Car Design
- Artificial Life
- Evolutionary Arts
- Evolving Mona Lisa