CS专业课学习笔记
计算理论用来研究计算的过程与功效的数学理论
导引
自动机, 可计算性与复杂性
计算理论的三个传统的核心领域: 自动机, 可计算性和复杂性.
计算复杂性理论
复杂性理论的一个重要成果是,发现了一个按照计算难度给问题分类的完美体系。
可计算性理论
可计算性理论与复杂性理论是密切相关的。在复杂性理论中,目标是把问题分成容易的和困难的;而在可计算理论中,是把问题分成可解的和不可解的。
自动机理论
自动机理论论述计算的数学模型的定义和性质。这些模型在计算机科学的若干应用领域中起着作用。可计算性理论和复杂性理论需要给计算机下一个精确的定义。自动机理论允许在引入与计算机科学的其他非理论领域有关的概念时使用计算的形式定义。
数学概念和术语
集合
集合是一组对象,把它作为一个整体。集合中的对象称作它的元素或成员。
集合与描述它时元素的排列顺序无关,也不考虑元素的重复。{57,7,7,7,21}和{7,21,57}表示同一个集合。如果要考虑元素出现的次数,则把它称作多重集合。例如,{7}和{7,7}作为多重集合时不相同的,而作为集合是相同的。
- 子集 A⊂B
- 真子集 A⊆B
- 自然数集 N{1,2,3,...}
- 整数集 Z{...,−2,−1,0,1,2,...}
- 空集 ∅
- 并集 A∪B
- 交集 A∩B
- 补集 A
序列和多元组
对象的序列是这些对象按某种循序排列成一列。通常把它写在一对圆括号内指明这是一个序列。在集合中不靠路元素的顺序,而在序列中要考虑。因此,(7,21,57)和(57,7,21)是不相同的。在集合中不允许重复,而在序列中允许重复,从而(7,7,21,57)与前两个都不相同,而集合{7,21,57}与{7,7,21,57}相同。
- 多元组: 有穷序列
- k元祖: k个元素的序列
- A{0,1}的幂集是A的所有子集的集合: {∅,{0},{1},{0,1}}是A的幂集。
- 笛卡尔积或叉积: 第一个元素为A的成员,第二个元素为B的成员的所有有序对组成的集合,记作A×B。
例
AA×B={1,2}B={x,y,z}={(1,x),(1,y),(1,z),(2,x),(2,y),(2,z)}
函数和关系
函数建立一个输入-输出的关系。设f是一个函数,当输入值为a时它的输出值为b,则记作
f(a)=b
函数又称作映射,并且若f(a)=b,则说f把a映射到b。
-
定义域: 函数的所有可能的输入组成的集合
-
值域: 函数的输出取自于一个集合,这个集合称作它的值域。记号f:D→R
-
k元函数: k个自变量的函数
-
元数: k称作函数的元数
-
一元函数: k等于1时,f有一个自变量,称作一元函数
-
二元函数: k等于2时,f是二元函数
-
谓词或性质: 值域为{TRUE,FALSE}的函数。例:even是一个谓词,当输入是偶数时为TRUE;当输入是奇数时为FALSE。
- 定义域为Ak的谓词称作关系,k元关系或A上的k元关系。通常用的是二元关系
-
等价关系:是一种特殊类型的二元关系,它抓住了用某种特征把两个对象等同起来的想法。如果二元关系R满足下述3个条件:
- R是自反的,即对每一个x,xRx。
- R是对称的,即对每一个x和y,xRy当且仅当yRx。
- R是传递的,即对每一个x,y和z,xRy和yRz蕴含xRz。
则R是一个等价关系。
图
无向图又简称为图: 是一个点的集合和连接其中的某些点的线段。这些点称作顶点,线段称作边,顶点的度数是以这个顶点为端点的边的数目。
- 子图: 如果图𝐺的顶点集是图𝐻的顶点集,则𝐺是𝐻的子图
- 路径: 由边连接的顶点序列
- 简单路径: 没有顶点重复的路径
- 简单圈: 只有最后一个点和第一个的重复的圈
- 树: 连通且没有简单圈的图
有向图: 箭头代替线段。用有序对(i,j)表示从i到j的边。一个有向图G的形式描述是(V,E),其中V是顶点集,E是边集。
- 出度: 从一个顶点引出的箭头数是这个顶点的出度
- 入度: 指向一个顶点的箭头数是这个顶点的入度
- 有向路径: 所有箭头的方向都与其前进的反向一致的路径
- 强连通(strongly connection): 从每一个顶点到另一个顶点都有一条有向路径
字符串和语言
字母表是任意一个有穷集合。字母表的成员是该字母表的符号。字母表上的字符串是该字母表中符号的有穷序列。字符串的字典序只是短的字符串排在长的字符串的前面。语言是字符串的集合。
布尔逻辑
布尔逻辑是建立在两个值TRUE和FALSE上的数学体系。
定义,定理和证明
定义描述我们使用的对象和概念。
证明是一种逻辑论证,它使人们确信一个命题是真的。
定理是被证明为真的数学命题。通常只对特别感兴趣的命题使用这个词。有时,有兴趣证明某些命题只是因为他们有助于证明另一个更有意义的命题,这样的命题叫做引理。有时,一个定理或它的证明可以使我们容易得出另外一些有关的命题为真的结论,这些命题叫做这个定理的推论。
寻找证明:
- P仅当Q: 若P为真,则Q为真,写作P⇒Q
- P当Q:若Q为真,则P为真,写作P⇐Q
- P当且仅当Q:写作P⇔Q
证明的类型
构造性证明
许多定理说明存在一种特定类型的对象。证明这种定理的一个方法是说明如何构造这样的对象。这种技术就是构造型证明。
反证法
证明定理的一种通用的论证形式是,假设这个定理为假,然后证明这个假设导致一个明显的错误结论,叫做矛盾。
归纳法
归纳法是证明无穷集合的所有元素都有一种特定性质的高级方法。每一个归纳证明由两部分组成:归纳步骤和归纳基础。
正则语言
计算理论的第一个问题是:什么是计算机?现实的计算机相当复杂,很难直接对它们建立一个易于处理的数学理论。于是我们采用称作计算模型的理想计算机。
有穷自动机
有穷自动机是关于储存量及其有限的计算机的很好的模型.
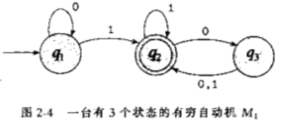
图2-4叫做有穷自动机M1的状态图
- 它有3各状态,记作q1,q2,q3。起始状态q1,用一个指向它的无出发点的箭头表示,接收状态q2带有双圈
- 从一个状态指向另一个状态的箭头叫做转移
- 当这个自动机接到输入串(eg.1101)它处理这个字符串并且产生一个输出。输出是接收或者拒绝。
我们将只考虑这种是非型的输出,以使事情维持简单。处理开始时M1处于起始状态q1。自动机从左至右一个接一个地接收输入串的所有符号。读到一个符号之后,M1沿着标有该符号的转移从一个状态已移动到另一个状态。当读到最后一个符号时,M1产生出它的输出。如何M1现在处于一个接收状态,则输出为接收;否则接收为拒绝。
例如,把输入串1101提供给图2-4中的有穷自动机M1,处理如下进行:
- 开始时处于状态q1
- 读到1,沿着转移从q1到q2
- 读到1,沿着转移从q2到q2
- 读到0,沿着转移从q2到q3
- 读到1,沿着转移从q3到q2
- 输出接收,因为在输入串的末端M1处于接收状态q2。
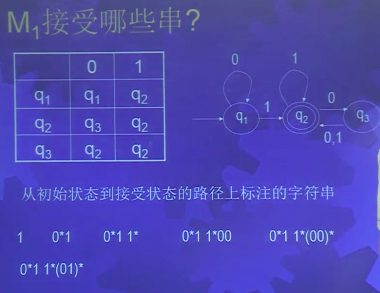
如图,这个有穷自动机可以接受的序列:0∗1等.这里的星号表示若干个0.
DFA的形式定义
- 形式定义是精确的
- 形式定义提供一种表述方法,而好的表示方法有助于思考和精确地表达你的思想
- 形式定义把一台有穷自动机描述成以下5部分的表:状态集,输入字母表,动作规则,起始状态以及接收状态集。用数学语言表达,5个元素的表经常叫做5元组。因此,我们定义有穷自动机是由这5部分组成的5元组。
- 用转移函数定义动作规则,常记作δ。如果有穷自动机有从状态x到状态y标有输入符号1的箭头,这表示当它处于状态x时读到1,则转移到状态y。记作δ(x,1)=y
定义(2.1)
有穷自动机是一个5元组(M=(Q,Σ,δ,q0,F))其中
- Q是一个有穷集合,记作有穷状态集
- Σ是一个有穷集合,叫做输入字母表
- δ:Q×Σ→Q是转移函数(意思是根据当前所处的状态和当前的符号进入下一个状态)(δ:Q×Σ∗→Q, 扩展转移函数)
- q0∈Q是起始状态
- F⊆Q是接收状态集
没有接收状态:F等于空集∅
设A是机器M接收的全部字符串集,称A是机器M的语言,记作L(M)=A。又称M识别A或M接受A。
例
A={w ∣ w至少有一个1并且在最后的1后面有个偶数个0}那么,L(M1)=A,或者等价地说,M1识别A。
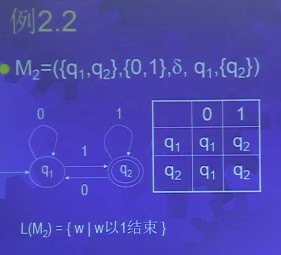
如图,一个有穷自动机用两种方式表示,一个是状态表示图,一个是状态转移表,他们是等价的。有两个状态q1,q2,这个就是状态集Q.有两个符号0,1,转移函数δ就是通过转移图和转移表来描述。初始状态q1,接受状态这里只有一个{q2}。注意接受状态是个集合,有可能有若干个。
DFA计算的形式定义
- M=(Q,Σ,δ,q0,F)
- 输入w1,w2,⋯,wn
- 计算:状态系列r0,r1,⋯,rn
- r0=q0
- δ(ri,wi+1)=ri+1;(i=0,1,⋯,n−1)
- 接受计算:M接受w
- M识别(接受)的语言:
- L(M)={x ∣ M接受x}
一个有穷自动机是个元祖,它拿到一个字符串假设有n个符号.
它的计算就是它的一个序列r0直到rn,r0是初始状态,初始状态下读的第一个符号w1之后,进入一个状态叫做r1,等等等等,最后在rn−1状态下读的输入符号wn进入状态rn.每一个后续状态都是ri以及输入的相应的那一位wi+1来共同决定的.
如果最后rn是一个接受状态,就说这个计算是一个接受计算.
有穷自动机举例
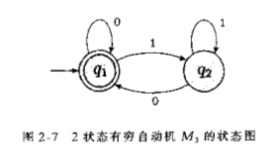
如图,M3接受所有读完之后停留在接受状态的字符串。因为起始状态又是接受状态,所以M3接受空串ϵ。只要机器一开始读空串,处理就结束了。因此,如果起始状态是接受状态,则ϵ被接受。除空串之外,这台机器接受任何以0结束的字符串。从而
L(M3)={w∣w是空串ϵ或以0结束}
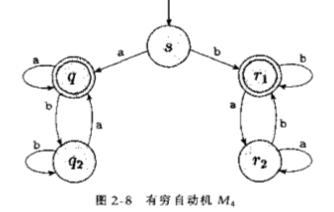
如图,M4有两个接受状态q1和r1,试验表明它接受字符串a,b,aa,bb,bab,但是不接受字符串ab,ba,bbba。如果输入串的第一个符号是a,那么它向左走并且当输入串以a结束时接受。类似的,如果输入串的第一个符号是b,那么它向右走并且当输入串以b结束时接受。所以,M4接受开头和结尾都是以a或者开头和结尾都是b的所有字符串。换句话说,M4接受开头和结尾符号相同的所有字符串。
设计有穷自动机
- 状态:需要记住的东西
- 转移:根据输入符号,从一种状态到另一种状态

如图,这个自动机也是分两个阶段来设计,先确定状态集,再确定转移函数,最后表示上起始状态和终止状态。
正则运算
在算术中,基本对象是术,工具是处理数的运算,如+和×。在计算理论中,对象是语言,工具包括为处理语言专门设计的运算。
设A和B是两个语言,定义正则运算并,连结和星号如下:
- 并:A∪B={x ∣ x∈A或x∈B}
- 连结: AB={xy ∣ x∈A且y∈B}
- 星号: A∗={x1x2⋯xk ∣ k≥0且每一个xi∈A}
例 设字母表Σ是标准的26个字母{a,b,⋯,z}。又设A={good,bad},B={boy,girl},则
A∪BA⋅BA∗={good,bad,boy,girl},={goodboy,goodgirl,badboy,badgirl}={ϵ,good,bad,goodgood,goodbad,badgood,badbad,goodgoodgood,goodgoodbad,goodbadgood,goodbadbad,⋯}
正则语言类在并运算下封闭,换句话说,如果A1和A2是正则语言,则A1∪A2也是正则语言。
正则语言类在连结运算下封闭,换句话说,如果A1和A2是正则语言,则A1⋅A2也是正则语言。
非确定型(nondeterminism)
- 确定型计算
- 非确定型计算
- 下一个状态可以不唯一确定
- ϵ移动,多种选择(含0种选择)产生不同备份
- 无法移动时,该备份就消失
- 有一个备份接受,整个计算就接受
注意:这里ϵ移动的意思是我不需要读任何输入符号,就能从一个状态转移到另一个状态。
非确定型是一个有用的概念,已经对计算理论产生巨大的影响。当机器处于给定的状态读下一个输入符号时,我们知道机器的下一个状态是什么–它是确定的。我们称这是确定型(deterministic)计算。在非确定型机器中,在任何一点,下一个状态可能存在若干个选择。
确定型有穷自动机(DFA)和非确定型有穷自动机(NFA)之间的区别:
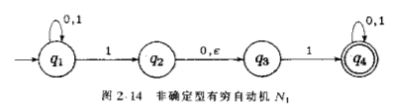
- 第一,DFA的每一个状态对于字母表中的每一个符号总是恰好又一个转移箭头射出。图中给出的非确定型自动机打破了这条规则。状态q1对于0有一个射出的箭头,而对于1有2个射出的箭头;q2对于0有一个箭头,而对于1没有箭头。在NFA中,一个状态对于字母表中的每一个符号可能有0个,1个或多个射出的箭头。
- 第二,在DFA中,转移箭头上的标号是取自字母表的符号。N1有一个带有标号ϵ的箭头。一般来说,DFA的箭头可以标记字母表中的符号或ϵ。从一个状态可能射出0个,1个或多个带有标号ϵ的箭头。
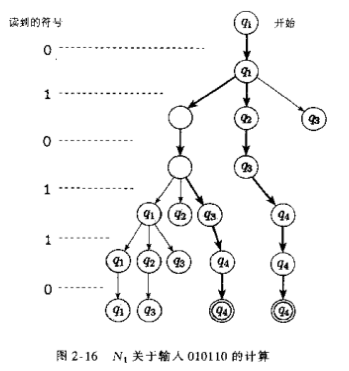
继续考虑如图2-14给出的NFAN1的运行。对于输入010110,从起始状态q1开始,读第一个符号0。对于0,从q1出发只有一个地方能去,即回到q1,所以保持不动。
接着读第2个符号1。对于1,q1有两种选择:或者停留在q1,或者移到q2。对非确定型(NFS),机器分裂成两个,分头追踪每一种选择。为了记住可能处于哪些状态,在机器的每一个可能的状态上放一个手指。因此现在把手指的状态q1和q2上。有一个ϵ箭头离开状态q2,故机器再次分裂:一个手指留在q2,另一个手指移到q1。现在在q1,q2和q3上都有手指。
当读到第三个符号0时,返回来看每一个手指,q1上的手指保持不动,q2上的手指移到q3,并且把原来在q3上的手指拿掉。原来在q3上的手指没有0箭头能沿着走,这对应一个完全“死掉”的过程。此时,在状态q1和q3上都有手指。
最后N1接受了这个字符串。图2-16描绘了N1关于输入010110的计算。
NFA的形式定义
- N=(Q,Σ,δ,q0,F)
- Q:有穷状态集
- Σ:输入字母表;(Σϵ=Σ∪{ϵ})
- δ:Q×Σϵ→P(Q),转移函数
- qo∈Q:初始状态
- F⊂Q:接受状态(终结状态)
NFA计算的形式定义
- N=(Q,Σ,δ,q0,F)
- 输入W=w1w2⋯wm
- 计算:状态系列r0,r1,⋯,rm
- r0=q0
- ri+1∈δ(ri,wi+1)(i=0,1,⋯,m−1)
- 接受计算:M接受w
- M识别(接受)的语言:存在接受计算
- L(M)={x ∣ M接受x}
NFA与DFA的等价性
证明思路:
- 给定NFA,构造等价DFA
- 用DFA模拟NFA
- DFA记住NFA的所有分支
- 设NFA有k个状态,则共有2k个不同状态子集合
- ϵ闭包:
- 对每个状态子集合,经ϵ移动可到达的新状态子集合
推论:一个语言是正则的,当且仅当有一台NFA识别它
对正则运算的封闭性
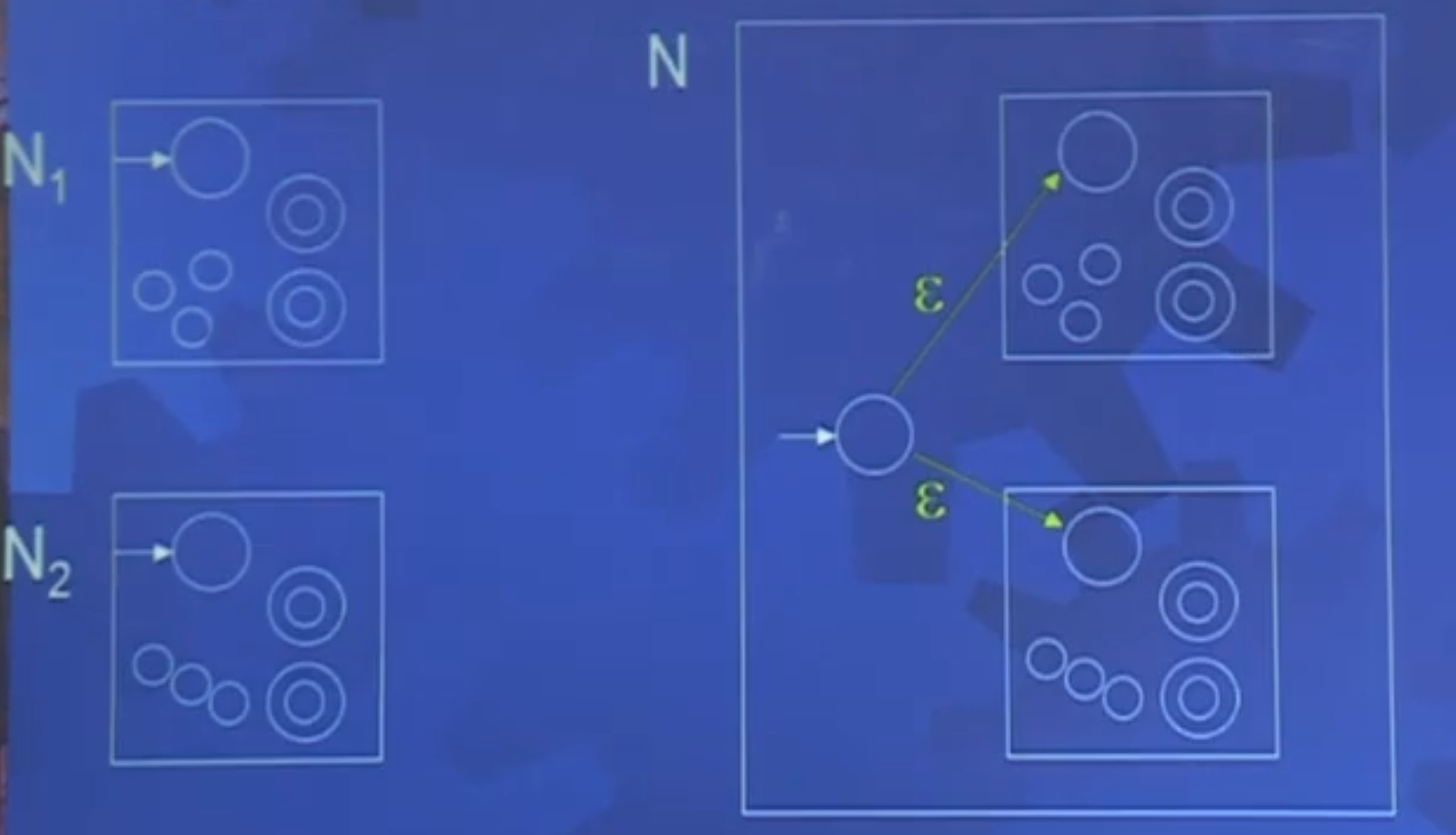
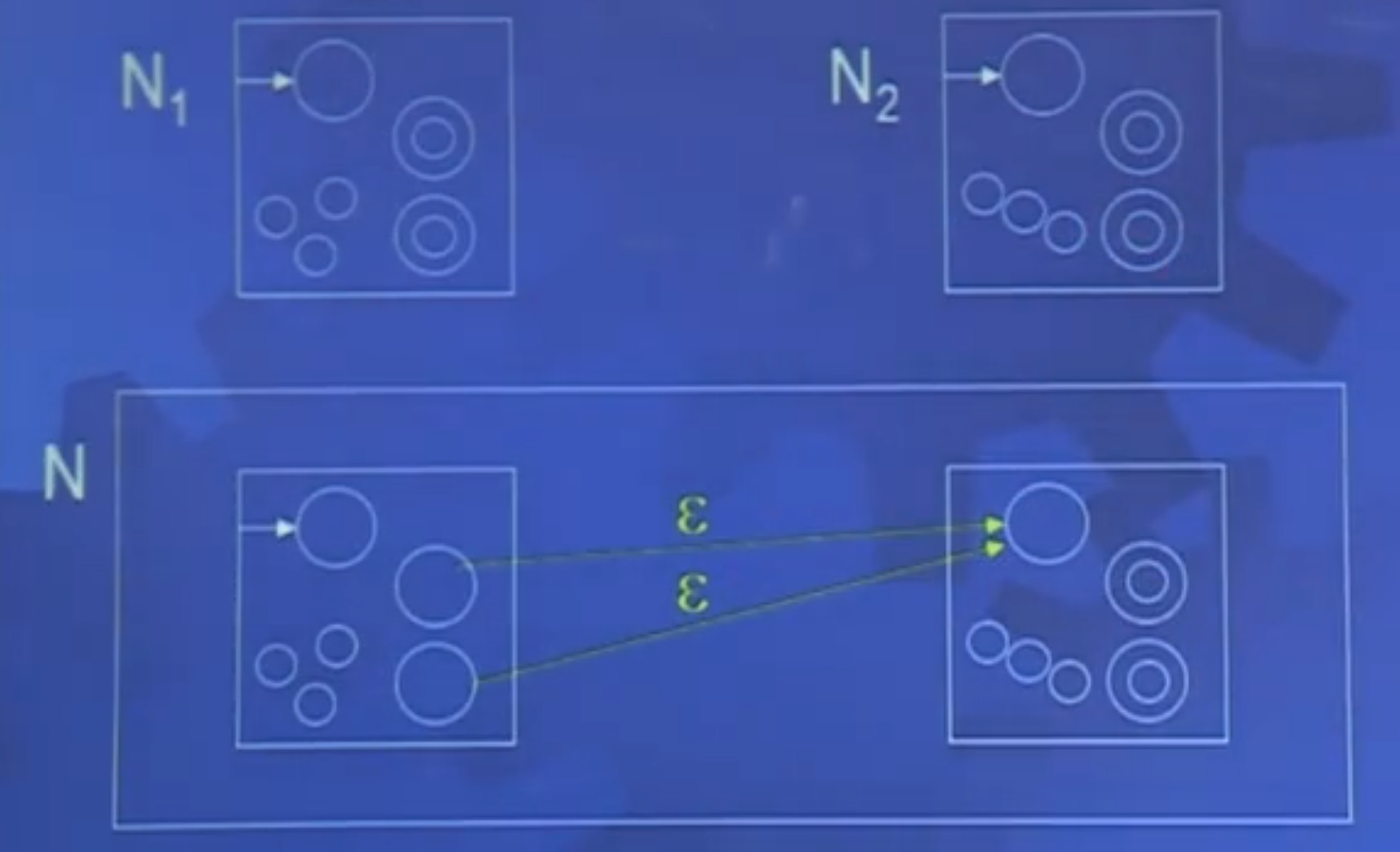
证明:
设NFA Ni=(Qi,Σ,δi,qi,Fi)识别Ai,i=1,2.
构造NFA N=(Q,Σ,δ,q0.F)识别A1∪A2
令Q=Q1∪Q2∪{q0};F=F1∪F2
δ(q,a)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧δ1(q,a)δ2(q,a){q1,q2}∅,若q∈Q1,若q∈Q2,若q=q0且a=ϵ,若q=q0且a=ϵ
证明:
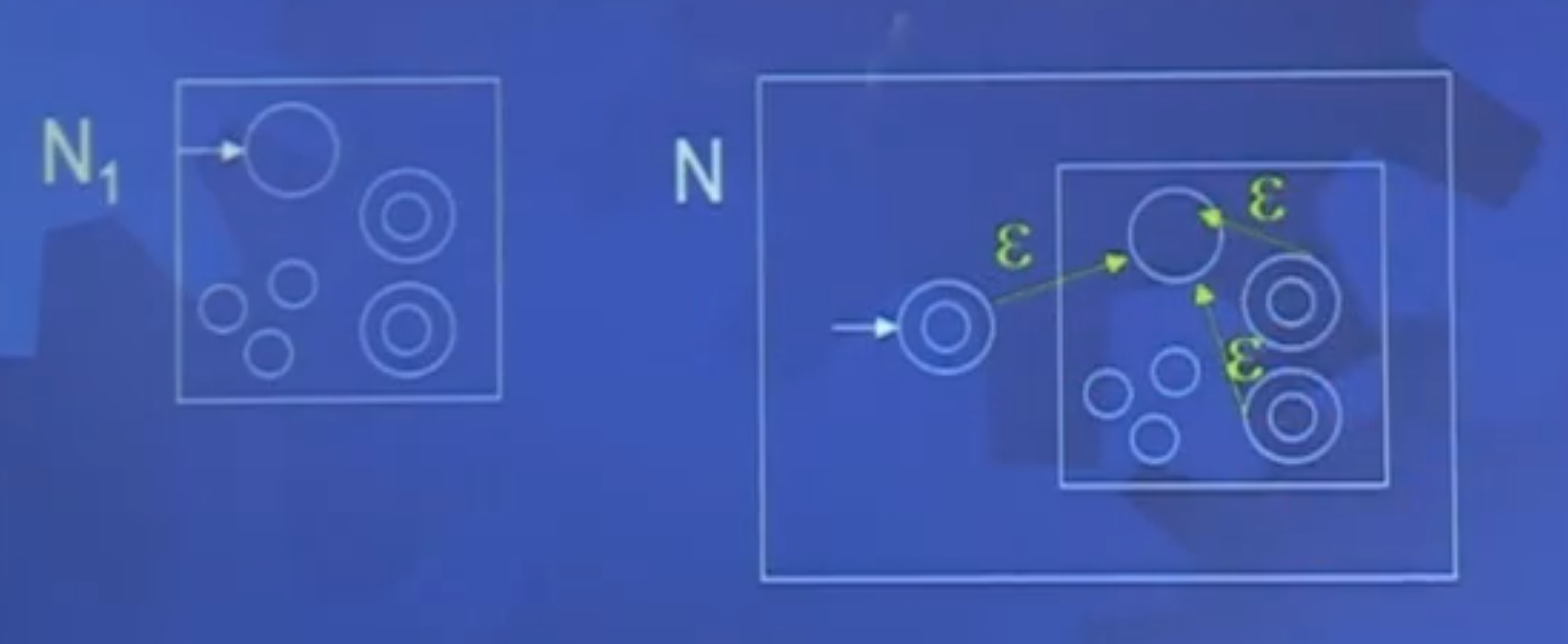
设NFA Ni=(Qi,Σ,δi,qi,Fi)识别Ai,i=1,2.
构造NFA N=(Q,Σ,δ,q0.F)识别A1A2
令Q=Q1∪Q2;
δ(q,a)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧δ1(q,a)δ1(q,a)δ1(q,a)∪{q2}δ2(q,a),若q∈Q1且q∈/F1,若q∈F1且a=ϵ,若q=F1且a=ϵ,若q∈Q2
证明:
设A1=L(N1),A1∗=L(N), NFA N1=(Q1,Σ,δ1,q1,F1)
构造NFA N=(Q,Σ,δ,q0.F)
令Q=Q1∪{q0};F=F1∪{q0};
δ(q,a)=⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧δ1(q,a)δ1(q,a)δ1(q,a)∪{q1}{q1}∅,若q∈Q1且q∈/F1,若q∈F1且a=ϵ,若q=F1且a=ϵ,若q∈q0且a=ϵ,若q=q0且a=ϵ
正则表达式
正则表达式是描述模式的一种手段
例:
(0∪1)0∗=({0}∪{1}){0}∗={0,1}{0}∗
这个集合就是表示0或者1开头后面跟着若干个0这样的字符串构成的集合,这就是正则表达式.
例:
- Σ={0,1}
- (0∪1)∗={0,1}∗=Σ∗
- Σ是任意字母表
- Σ表示所有长为1的串组成的语言
- Σ∗表示所有串组成的语言
- Σ∗1表示所有以1结尾的串组成的语言
- (0Σ∗)∪(Σ∗1)表示所有以0开头或以1结尾的串组成的语言
正则表达式的形式定义
定义:R是正则表达式当且仅当R是
- a,a∈Σ; (表示{a})
- ϵ; (表示{ϵ})
- ∅; (表示∅)
- (R1∪R2),R1和R2都是正则表达式;
- (R1R2),R1和R2都是正则表达式;
- (R1∗),R1是正则表达式;
当想要明显地区分正则表达式R和它表示的语言时,把R表示的语言写成L®.
归纳定义:用较小的表达式定义较大的表达式.
表达式中的括号可以略去,如果省略括号,计算按照优先级:星号 > 连接 > 并.
例:
- 设Σ={0,1}
- 0∗10∗={w ∣ w恰好有一个1}
- Σ∗1Σ∗={w ∣ w至少有一个1}
- Σ∗001Σ∗={w ∣ w含有子串001}
- (ΣΣ)∗={w ∣ w为偶数长度}
- 01∪10={01,10}
- 0Σ∗0∪1Σ∗1∪0∪1={w ∣ w首尾符号相同}(后面这两种情况表示只有0和只有1)
- (0∪ϵ)1∗=01∗∪1∗(表示有1个0或者没有0后面跟着若干个1)
- (0∪ϵ)(1∪ϵ)={ϵ,0,1,01}(注意连接运算不可换顺序,并运算可以交换顺序)
- 1∗∅=∅(空语言跟别的语言做连接出来一定是空语言,因为它里面不能提供任何字符串)
- ∅∗={ϵ}
注意:空串本身不属于空语言,空语言里面什么都没有,但是对它做了星号运算之后就会产生一个空串,得到空串语言。
下面是几个恒等式:
- R∪∅=R
- Rϵ=R (ϵ代表由空串组成的语言,空串跟别的串连接还是别的串)
- 一般R∅=R,R∪ϵ=R
- R∪ϵ=R∪{ϵ}(可能不等于,R=0)
- R∅=∅(可能不等于,R=0)
正则表达式与有穷自动机的等价性
定理
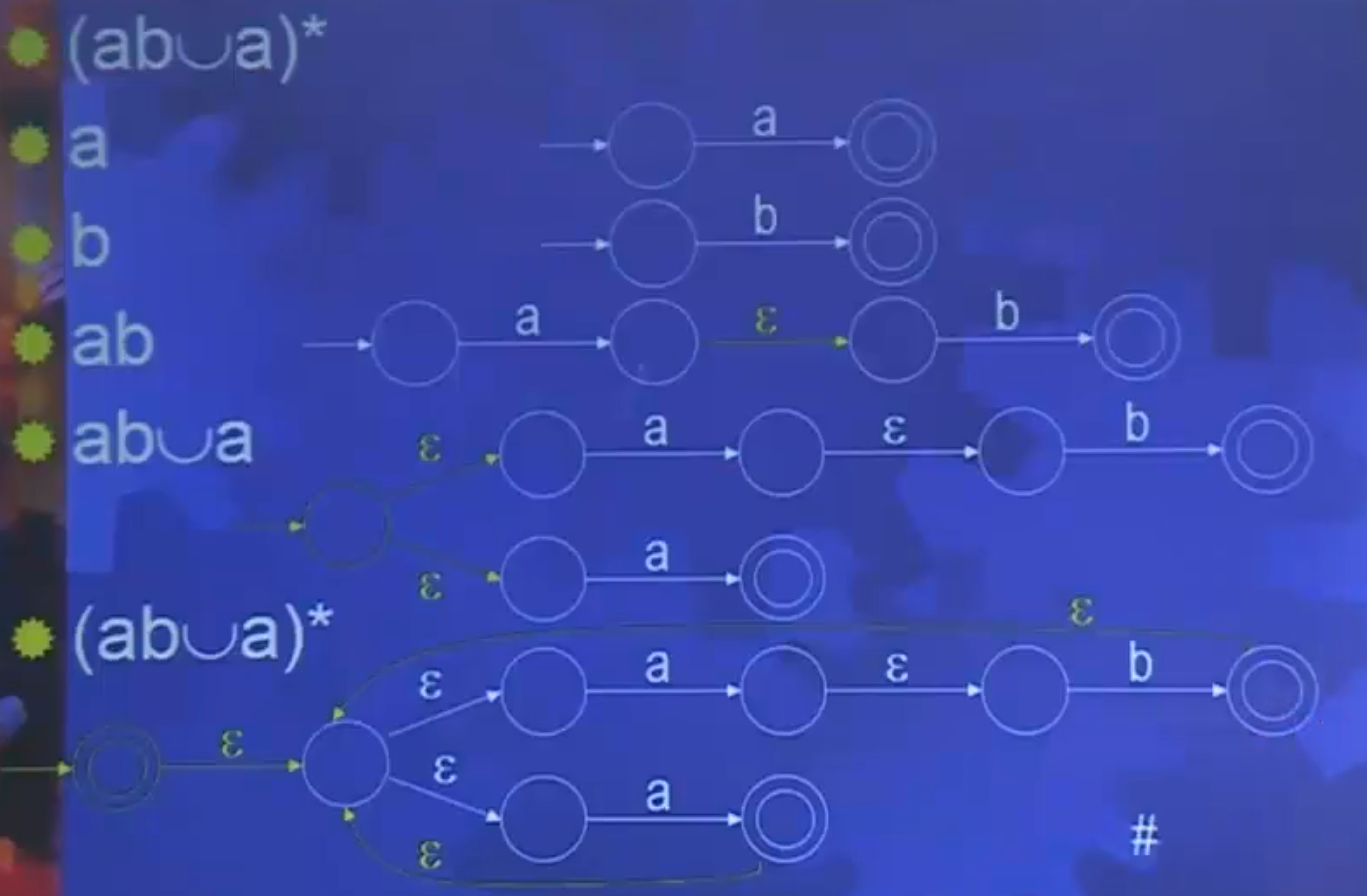
一个语言是正则的当且仅当可用正则表达式描述这个语言
给一个正则表达式我们要构造一个有穷自动机,识别这个正则表达式所产生的串。给定一个自动机我们要构造一个正则表达式,使得这个正则表达式描述的串正好就是那个自动机所识别的串。
例:
例:
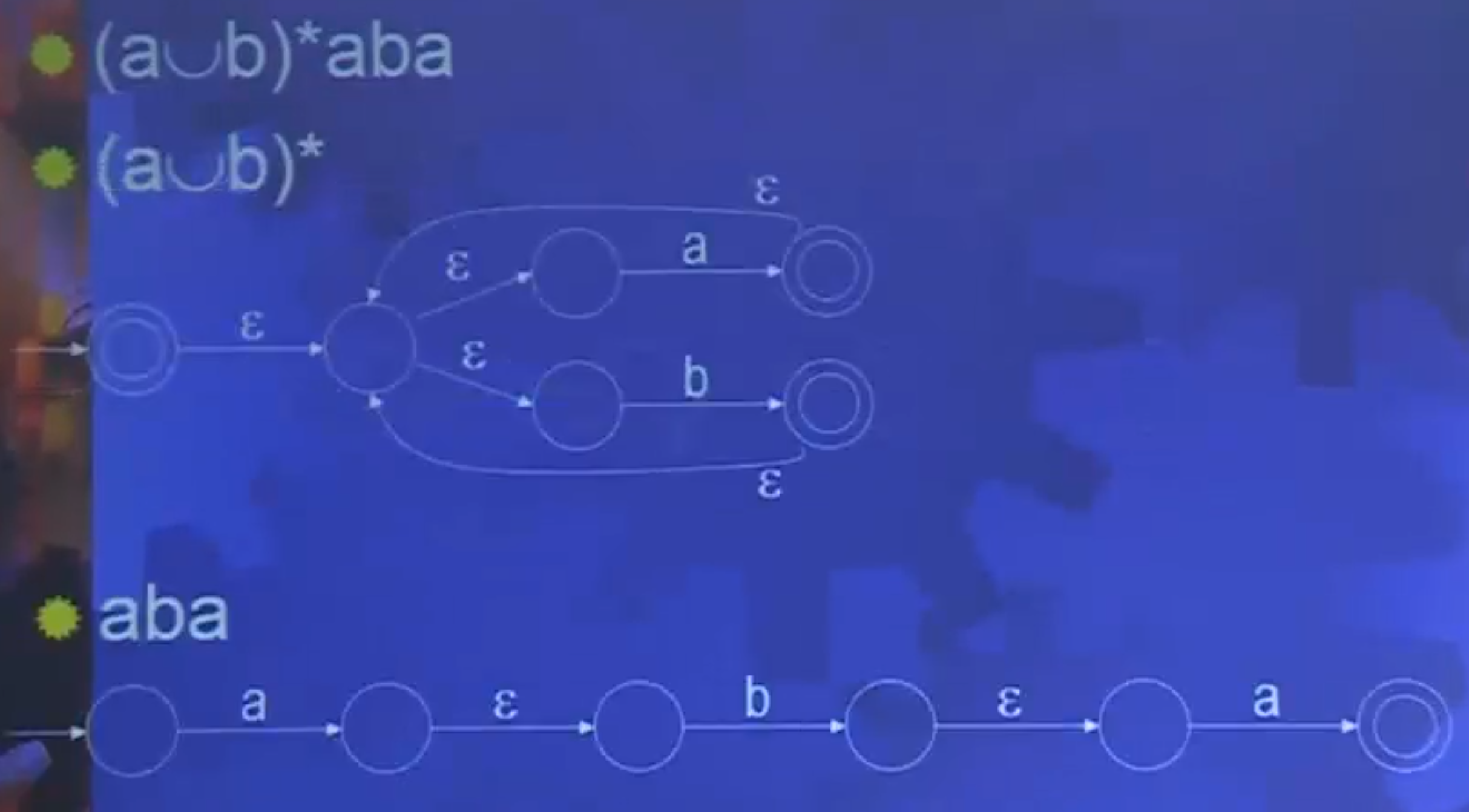
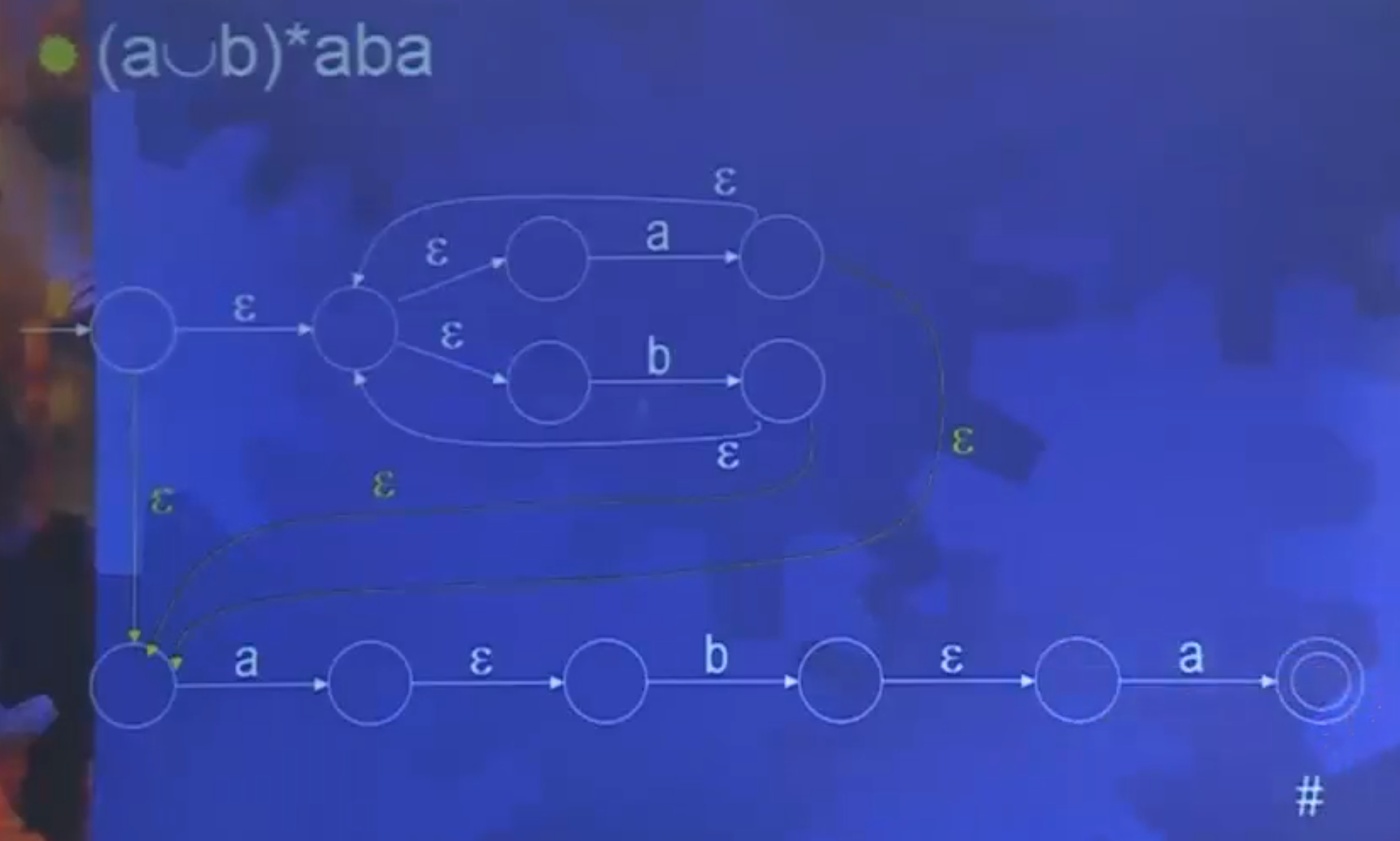

例题:

例题:

证明思路:
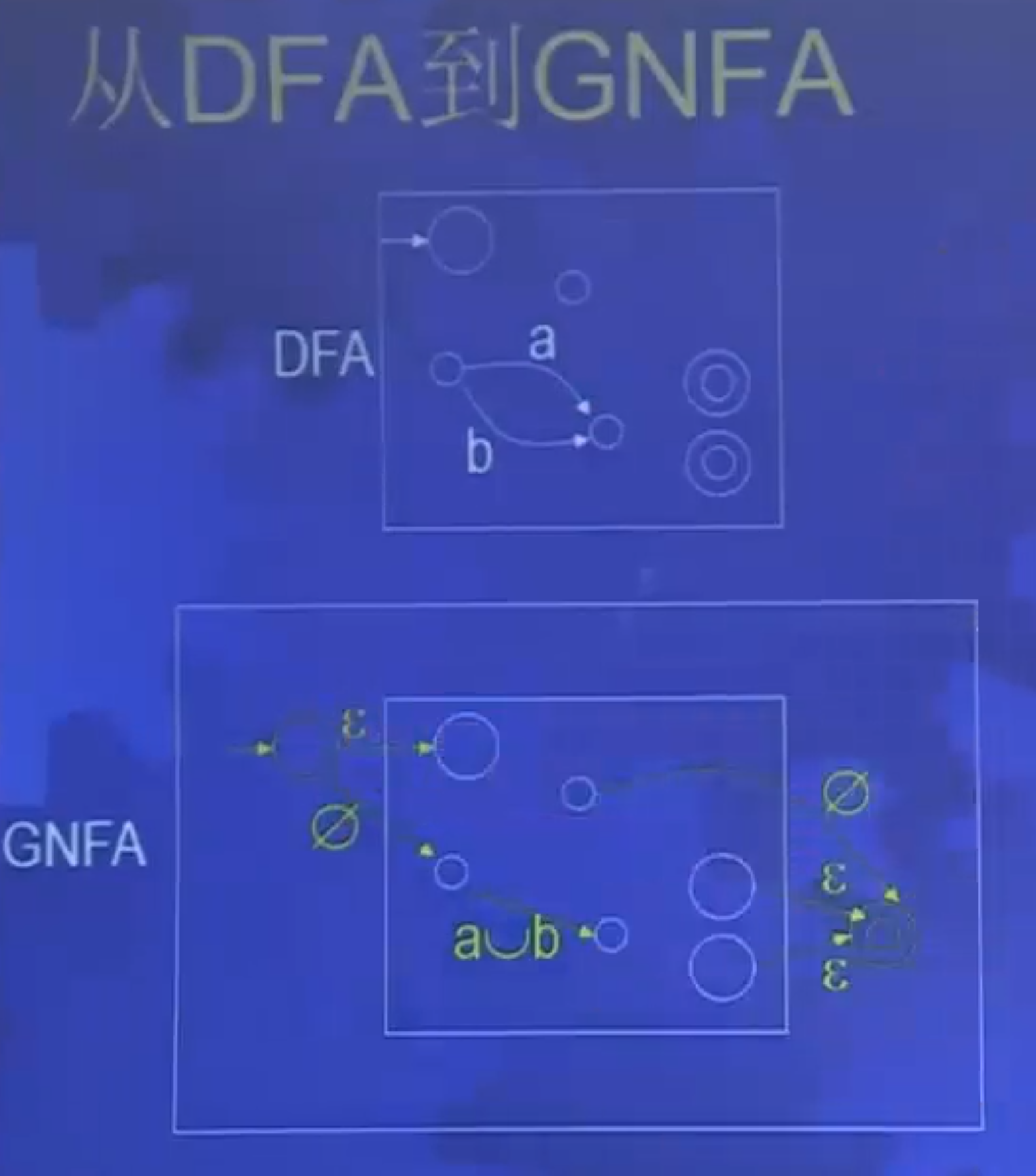
- 广义非确定型有穷自动机(GNFA)
- 从DFA构造等价的GNFA
- 从GNFA构造等价的正则表达式
GNFA的特殊形式
- 初始状态
- 有到所有其他状态的箭头
- 所有其他状态都没有到它的箭头
- 接受状态
- 唯一,且与初始状态不同
- 没有到任何其他状态的箭头
- 所有其他状态都有到它的箭头
- 其他每个状态
GNFA的形式定义
- GNFA是5元祖(Q,Σ,δ,qstart,qaccept)
- Q是有穷状态集
- Σ是输入字母表
- δ:(Q−{qaccept})×(Q−{qstart})→R是转移函数 (R是字母表Σ上全体正则表达式的集合)(表示这两个状态之间箭头上面的正则表达式是R)
- qstart是初始状态
- qaccept是接受状态
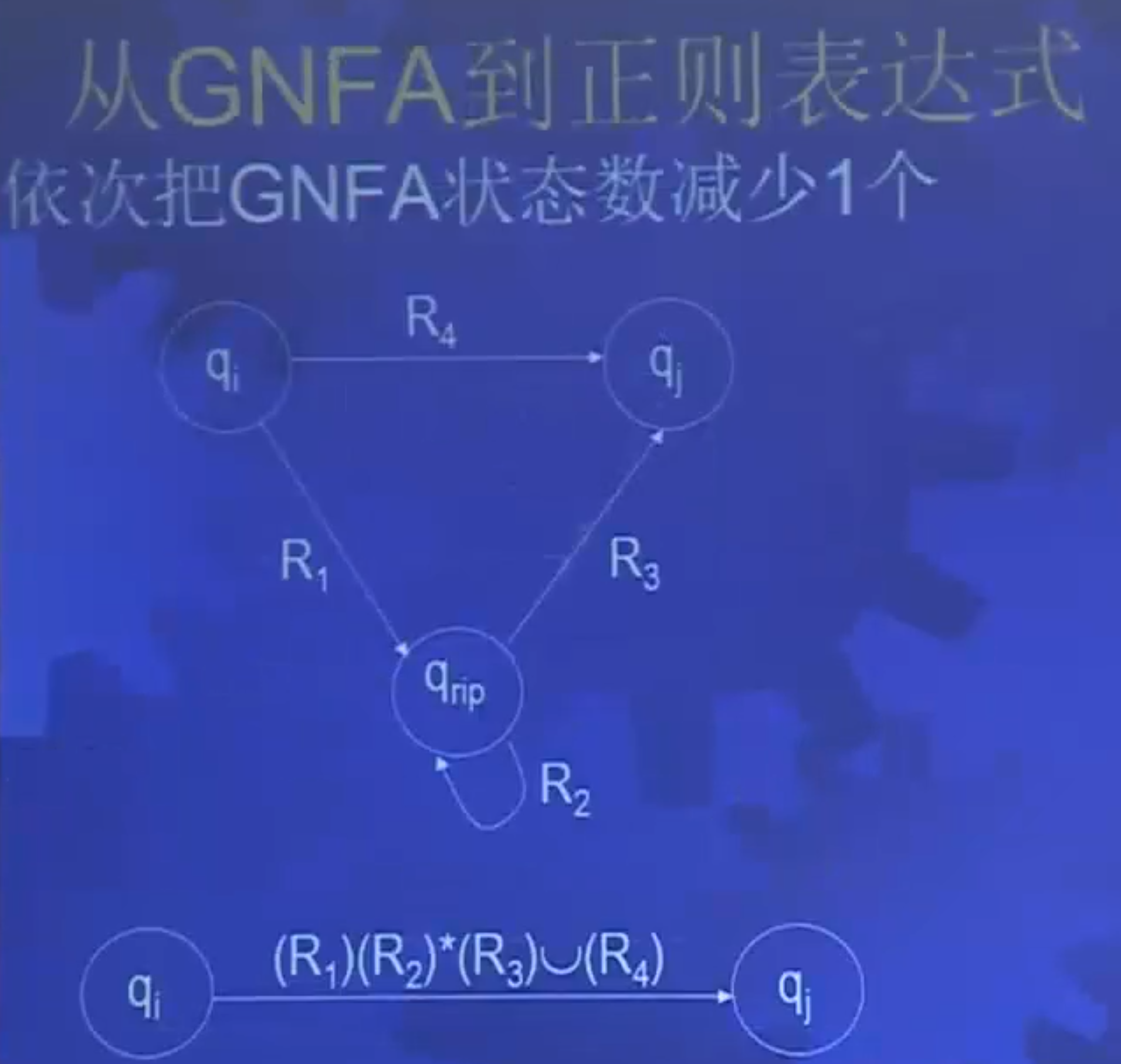
GNFA计算的形式定义
- 输入w=w1w2⋯wk,wi∈Σ∗
- 计算:状态序列q0,q1,⋯,qk
- q0=qstart是初始状态
- ∀i,wi∈L(Ri),Ri=δ(qi−1,qi)
- 接受计算:
- qk=qaccept是接受状态
非正则语言
B={0n1n ∣ n≥0}
C={w ∣ w中0和1一样多}
D={w ∣ w中字串01和10一样多}
这里面D中正则的,因为01最多比10多一个,有穷自动机可以记录。相反,B,C这两个有穷自动机是做不到的,无法精确记录这个n,所以无法跟后面的1进行匹配,所以B,C是非正则语言。
泵引理
该定理指出所有的正则语言都有一条特殊的性质,如果能证明一个语言没有这种性质,则保证它不是正则的。这条性质是:语言中所有字符串只要它的长度不小于某个特定的值——泵长度,就可以被“抽取”。
定理
设A是正则语言,则存在常数p(称为泵长度),使得若s∈A且∣s∣≥p,则s=xyz,并且满足下述条件:
- ∀i≥0,xyiz∈A;(y可以重复若干次)
- |y| > 0;(y不能是空串)
- |xy| ≤ p;(xy串总长度不超过p)
通常会取一个特殊的s,然后这么一泵,让y增加或减少,按照泵引理出来的串仍然还在这个语言里面,如果出现了矛盾,就说明原来的语言不是正则语言。
泵引理的应用
证明上述B不是正则的
-
反证法:假设B是正则的,设p是泵长度
-
取s∈B,∣s∣≥p
-
根据泵引理,s=xyz,
- ∀i≥0,xyiz∈B
- ∣xy∣≤p
- ∣y∣>0
-
证明∃i≥0,使得xyiz∈/B,矛盾。
假设B是正则的,设p泵长度,令s=0p1p,则s=xyz,对任意∀i≥0,xyiz∈B。
下面分3种情况:
- y∈0∗0,则xy2z中0比1多,矛盾
- y∈1∗1,则xy2z中1比0多,矛盾
- y∈0∗011∗,则xy2z∈/0∗1∗,矛盾
上下文无关语言
在第2章中,我们介绍了描述语言的两种不同,但却等价的方法;有穷自动机和正则表达式。证明许多语言可以用它们描述,但是还有一些简单的语言不能用它们描述,比如{0n1n ∣ n≥0}。
本章介绍上下文无关文法,这是一种能力更强的描述语言的方法。这种方法能够描述某些具有递归结构的特征。与上下文无关文法有关的一类语言叫做上下文无关语言。它们包括所有的正则语言以及许多新添加的语言。还要介绍下推自动机,这是一类识别上下文无关语言的机器。下推自动机是有用处的,它使我们能够更进一步了解上下文无关文法的能力。
上下文无关文法(CFG)
AAB→0A1→B→#
AAB→0A1,→B,→#
- 变元(非终结符): A, B
- 终结符: 0, 1, #
- 终结符类似于输入符号,通常用小写字母,数字或特殊符号表示
- 初始符(起始变元): A
- 派生: A ⇒ 0A1 ⇒ 00A11 ⇒ 000A111 ⇒ 000B111 ⇒ 000#111
- 语法分析树

L(G1)={0n#1n ∣ n≥0}
AB→0A1 ∣ B→#
这里这个竖线代表了缩写,表示A既能够派生出0A1也能够派生出B.
CFG的形式定义
定义:上下文无关文法G=(V,Σ,R,S)
- V: 有穷变元集
- Σ: 有穷终结符集
- R: 有穷规则集 (规则形如A→w,w∈(V∪Σ)∗)
- S∈V: 初始变元
- 一步生成(派生,推导):
- uAv⇒uwv (A→w是产生式)
实际上这里u,v构成A的上文和下文,这个文法是上下文无关文法,也就是不用考虑u和v对A的约束,任何情况下都能把A换成w。
在上下文无关文法中,左侧永远是单个符号,所以被称为上下文无关的。
- 任意步生成(派生,推导):
- u⇒∗v: u⇒u1⇒u2⇒⋯⇒uk⇒v 或 u=v
- 文法(生成)的语言:
- L(G)={w∈Σ∗ ∣ S⇒∗w}
- 上下文无关语言(CFL): CFG生成的语言
例:
G1=({A,B},{0,1,#},{A→0A1,A→B,B→#},A)
上下文无关文法举例
文法G3=({S},{a,b},R,S)其中R为{S→aSb ∣ SS ∣ ϵ}
下面是几条派生:
SSS⇒SS⇒aSbS⇒abS⇒∗abab⇒aSb⇒aaSbb⇒∗aaabbb⇒aSb⇒aSSb⇒∗aababb
这个文法表示的是括号的配对,a代表左括号,b代表右括号
- L(G3)包含所以匹配的括号串或空串
设计CFG
例如:要得到语言{0n1n ∣ n≥0}∪{1n0n ∣ n≥0}的文法
首先构造语言{0n1n ∣ n≥0}的文法
S1→0S11 ∣ ϵ
和语言{1n0n ∣ n≥0}的文法
S2→1S20 ∣ ϵ
然后加上规则S→S1 ∣ S2,得到所求的文法:
S→S1 ∣ S2S1→0S11 ∣ ϵS2→1S20 ∣ ϵ
合并
- 一般情况: 增加S→S1 ∣ S2 ∣ ⋯ ∣ Sk
- S是新的起始变元
- S1,S2,⋯,Sk是原来的初始变元
正则
- 为正则语言设计CFG
- 把DFA转换成等价地CFG
- 设DFA M=(Q,Σ,δ,q0,F)
- Q={q0,q1,⋯,qk}
- δ(qi,a)=qj
- qi∈F
- 则CFG G=(V,Σ,R,R0)
- V={R0,R1,⋯,Rk}
- Ri→aRj
- Ri→ϵ
匹配
- 0n1n
- R→0R1,R→ϵ
- 0000011111
- wwR
- 倒置: w=11010,wR=01011
- 可用上下文无关文法生成
- ww
- 非正则,非上下文无关(因为前后要一样,是上下文有关)
- 非ww
递归

CFL to CFG
- L1={aib2i ∣ i≥0}
我们首先试着代入i的值,看一下上下文无关语言L
L1={a0b0,a1b2,a2b4,⋯}L1={ϵ,abb,aabbbb,⋯}
观察abb和aabbbb,我们发现后者在前者基础上中间加上了abb,所以我们可以写出CFG
S→aSbb ∣ ϵ
- L2={anbm ∣ n,m≥1}
S→ABA→aA ∣ aB→bB ∣ b
小技巧:最后写S→AB
- L3={anbncm ∣ n,m≥1}
S→ABA→aAb ∣ abB→cB ∣ c
- L4={ancmbn ∣ n,m≥1}
S→aSb ∣ aAbA→cA ∣ c
小技巧:可以尝试画个树状图,例如当n=2,m=1的时候,从S→aSb→aaAbb→aacbb
歧义性
G5:<EXPR>→<EXPR>+<EXPR> ∣ <EXPR>×<EXPR> ∣ (<EXPR>) ∣ a
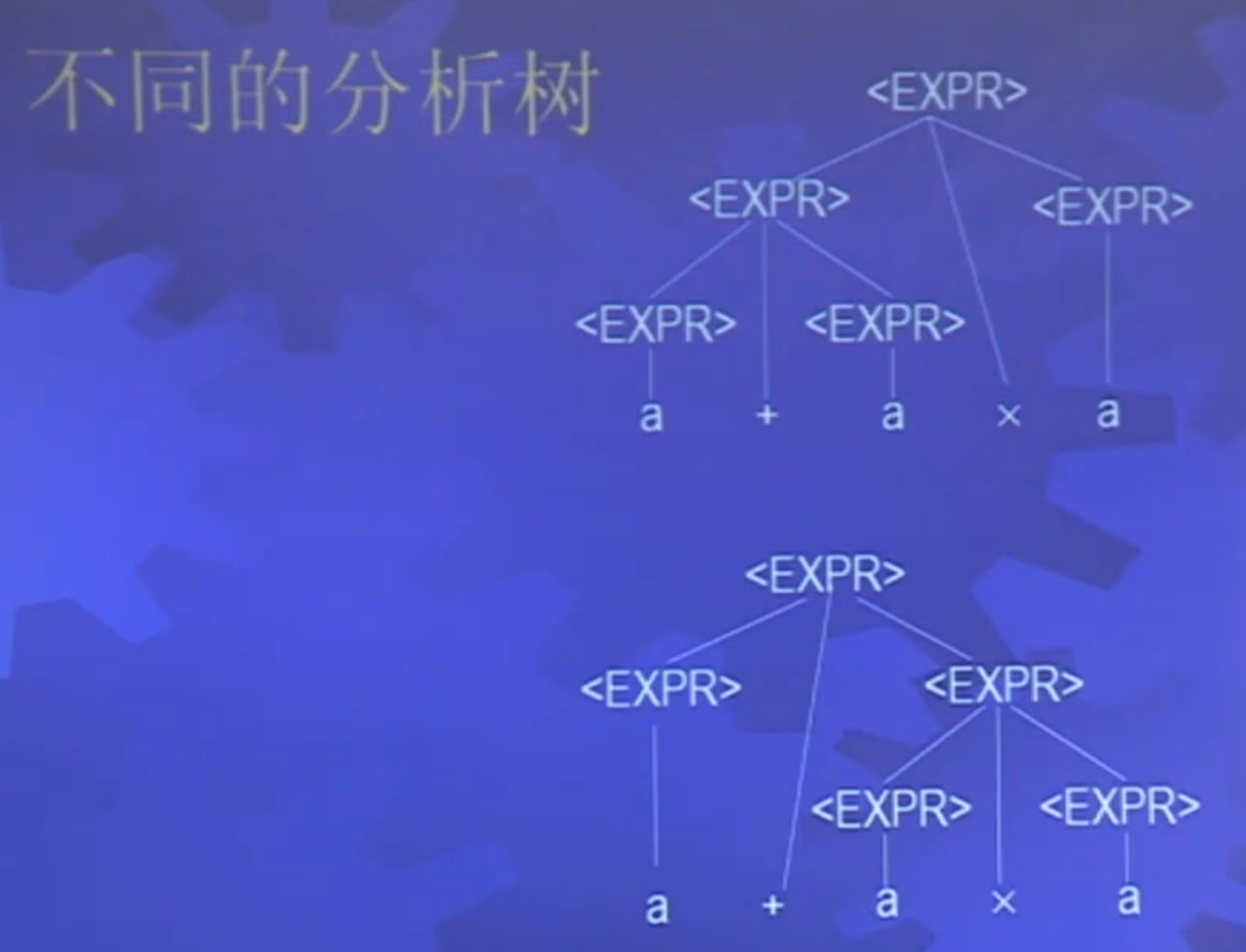
这个文法没有抓住通常的优先关系,其他歧义地产生了字符串a+a×a.
G2:the_girl_touches_the_boy_with_flower
同样的这个文法G2也会产生歧义
例:
<EXPR><EXPR>⇒<EXPR>+<EXPR>⇒a+<EXPR>⇒a+<EXPR>×<EXPR>⇒a+a×<EXPR>⇒a+a×a⇒<EXPR>×<EXPR>⇒<EXPR>+<EXPR>×<EXPR>⇒a+<EXPR>×<EXPR>⇒a+a×<EXPR>⇒a+a×a
乔姆斯基范式(CNF)
当使用上下文无关文法时,如果它们时简化的形式,常常时方便的。一种最简单,最有用的形式叫做乔姆斯基范式。
CNF: 只允许如下形式的规则
SAA→ϵ→BC→a
其中:
- A,B,C是任意变元
- B,C不是初始变元(初始变元不能在右方出现)
- a是任意终结符
求乔姆斯基范式的算法
- 证明思路: 下列算法:
- 添加新的初始变元
- 处理A→ϵ (ϵ规则)
- 处理A→B (单一规则)
- 处理A→u1u2⋯uk (k≥3)
- 处理A→aiaj,A→aiB,A→Bai
(1)添加新初始变元
添加新初始变元S0和规则S0→S.其中S是旧初始变元.
(2)考虑所有ϵ规则
若A不是初始变元,则删除A→ϵ,以各种可能的方式删除其他规则右边的A,添加新的规则,例如
由B→uAv由B→uAvAw由B→A添加B→uv添加B→uvAw ∣ uAvw ∣ uwv添加B→ϵ(除非已删除过B→ϵ)
直到删除所以ϵ规则(S0→ϵ除外)为止.
(3)处理所有单一规则
删除A→B,
若有规则B→u,则添加规则A→u,除非A→u是已删除过的单一规则.
重复上述步骤, 直到删除所有单一规则为止.
(4)处理A→u1u2⋯uk规则
把每一条规则A→u1u2⋯uk换成
AA1A2Ak−2→u1A1→u2A2→u3A3⋯→uk−1uk(k≥3)
(5)处理终结符
对每个终结符ai,引入变元Ui和规则Ui→ai.
把A→aiaj换成A→UiUj把A→aiB换成A→UiB把A→Bai换成A→BUi
例题:
G6:S→ASA ∣ aB,A→B ∣ S,B→b ∣ ϵ求等价CNF
(1)
S0SAB→S→ASA ∣ aB→B ∣ S→b ∣ ϵ
(2a)处理ϵ规则,删除B→ϵ,同时把右边出现B的所有地方都替换成空.
S0SAB→S→ASA ∣ aB ∣ a→B ∣ S ∣ ϵ→b
(2b)这是又出现了ϵ,同样的删除A→ϵ,同时A在右边出现的地方也要修改.
S0SAB→S→ASA ∣ aB ∣ a ∣ SA ∣ AS ∣ S→B ∣ S→b
(3a)处理单一规则.删除S→S
S0SAB→S→ASA ∣ aB ∣ a ∣ SA ∣ AS→B ∣ S→b
(3b)处理单一规则.删除S0→S,把S直接换上去即可
S0SAB→ASA ∣ aB ∣ a ∣ SA ∣ AS→ASA ∣ aB ∣ a ∣ SA ∣ AS→B ∣ S→b
(3c)处理单一规则.删除A→B,同时将有B的地方换成B右边的值b
S0SAB→ASA ∣ aB ∣ a ∣ SA ∣ AS→ASA ∣ aB ∣ a ∣ SA ∣ AS→S ∣ b→b
(3d)处理单一规则.删除A→S,同时将有S删掉并把S右边的值替换到A这里.
S0SAB→ASA ∣ aB ∣ a ∣ SA ∣ AS→ASA ∣ aB ∣ a ∣ SA ∣ AS→b ∣ ASA ∣ aB ∣ a ∣ SA ∣ AS→b
(4)处理常规则(ASA),添加新的变元和规则
S0SABA1→AA1 ∣ aB ∣ a ∣ SA ∣ AS→AA1 ∣ aB ∣ a ∣ SA ∣ AS→b ∣ AA1 ∣ aB ∣ a ∣ SA ∣ AS→b→SA
(5)处理常规则(aB),添加新的变元和规则
S0SABA1U→AA1 ∣ UB ∣ a ∣ SA ∣ AS→AA1 ∣ UB ∣ a ∣ SA ∣ AS→b ∣ AA1 ∣ UB ∣ a ∣ SA ∣ AS→b→SA→a
到这里已经满足乔姆斯基范式的要求了,变元生成单个的终结符,或者右边都是两个变元.
下推自动机(PDA)
下推自动机跟有穷自动机不同的地方是,下推自动机多了一个栈。
- {0n1n ∣ n≥0}
- {anbncm,anbmcn ∣ m,n≥0}
- 一般来说PDA指的是非确定型PDA
下推自动机的形式定义
PDA M=(Q,Σ,Γ,δ,q0,F),其中
- Q: 有穷状态集
- Σ: 输入字母表,Σϵ=Σ∪{ϵ}
- Γ: 栈字母表,Γϵ=Γ∪{ϵ}
- δ:Q×Σϵ×Γϵ→P(Q×Γϵ),转移函数
- q0∈Q: 初始状态
- F⊆Q: 接受状态(终结状态)集
PDA计算的形式定义
- M=(Q,Σ,Γ,δ,q0,F);输入w=w1w2⋯wm,wi∈Σϵ
- 计算:状态-栈符号串序列(r0,s0),(r1,s1),⋯,(rm,sm), 其中ri∈Q,si∈Γ∗,满足
- (r0,s0)=(q0,ϵ);(栈开始是空的,所以是ϵ)
- (rr+1,b)∈δ(ri,Wi+1,a);其中si=at;si+1=bt,a,b∈Σϵ,t∈Γ∗
- 接受计算:
- rm∈F(或者同时要求sm=ϵ)
- M接受w:
- M(识别,接受)的语言:
- L(M)={x ∣ M接受x}
下推自动机举例


跟有穷自动机不一样的地方是标记,有穷自动机是读一个符号从一个状态进入下一个状态,现在PDA同时处理输入符号和栈.
如图,q1指向q2的箭头意思是读输入符号ϵ,把栈里的ϵ符号换成$,同时从状态q1进入状态q2.用一个逗号隔开,逗号前面是输入符号,逗号后面是栈的替换符号,在q1状态下,不读输入符号把栈顶换成$符号,也就是$入栈。
在q2状态下,如果读0,就让0入栈,把栈顶的ϵ换成0,实际上就是0入栈。如果读1,就把栈顶的0弹出,变成ϵ就相当于弹出了。然后进去q3,q3就记住1了。
在q3状态下,每读一个1就把栈顶的0弹出,这个时候就是在做匹配。当1读完以后,就是ϵ然后看到$符号并把$符号弹出,进入状态q4。
q1,q4都是接受状态,q1代表接受空串,q4代表接受0n1n。如果输入串不是0n1n那么他就不接受,一定会在图中某个地方终止。比如说你在q3状态下又看到0,它就不走了,这样保证它不会接受。
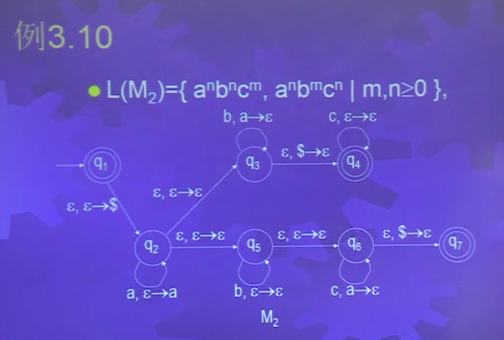
思考方法:
- 先读a,并且把a推入堆栈
- 利用非确定型,猜想a是与b匹配还是与c配肥
- 与b匹配
- 每读到一个输入符号b,就从堆栈中弹出一个a,若从输入中读b结束时堆栈排空,则读若干个c后接受,否则拒绝
- 与c匹配
- 读若干个b后,每读到一个输入符号c,就从堆栈中弹出一个a,若输入结束时堆栈排空,否则拒绝
如图,从初始状态q1出发,把$押入栈,在q2状态下读a就把a押入栈,然后分支。先看上面,q3是跟b匹配,每读一个b,把栈顶的a弹出。等到b读完之后,如果栈顶空了说明ab数量一样,进入q4,然后找c。注意如果在q3状态下读a就不走了,只有输入符号是b和空才能走。

- 开始时把读到的符号推入堆栈中
- 在每一步,非确定型地猜测已到达字符串的中点,然后变成把读到的每一个符号弹出堆栈,检查在输入中和在堆栈顶读到的符号是否一样
- 如果它们总是一样的,并且输入结束时堆栈同时排空,则接受,否则拒绝
PDA与CFG的等价性
定理
定理:一个语言是CFL,当且仅当存在PDA识别这个语言
引理2:如果一个语言被PDA识别,则这个语言是CFL
从CFG构造PDA的算法
引理1:如果一个语言是CFL,则存在PDA识别这个语言
- 证明思路
- CFG通过派生来产生串
- PDA如何识别这个串?
- PDA在堆栈中模拟派生过程
- 让栈顶的终结符与输入进行匹配
- 栈顶是终结符,就进行匹配
- 如何把栈顶换成一串符号?
q↓ra,s→xyz⇒q↓q1↓q2↓ra,s→zε,ε→yε,ε→x
如果要从状态q进入状态r,输入带读的符号是a,栈顶的符号s然后把s换成xyz。
通过中间状态来做:引入两个中间状态q1,q2。
- 首先在状态q下读输入符号a,在栈顶把栈顶符号s换成z同时进入状态q1。
- 其次,在状态q1下,不读输入符号(ϵ),同时栈顶不弹出就是ϵ空串,然后y进入,相当于把y直接押入栈,进入状态q2。
- 然后,在状态q2下,不读输入符号(ϵ),同时栈顶不弹出就是ϵ空串,然后x进入,相当于把x直接押入栈,进入状态r。
这样就实现了从状态q到状态r同时把x,y,z押入栈这个过程。所以右端的自动机与左边的自动机是等价的。右端的自动机更加符合下推自动机的定义。
- 证明:设A是CFL,根据定义,存在产生A的CFG G=(V,Σ,R,S)。下面构造识别A的PDA
P=({qstart,qloop,qaccept}∪E,Σ,V∪Σ,δ,qstart,{qaccept})
- PDA是一个6元组,首先是状态集合。在我们设计的自动机里有三个特殊的状态:qstart是初始状态,qloop是循环状态,qaccept是唯一的接受状态,还有一些其他的状态E。E实际上就是刚才所说的中间状态。当把一串符号押入栈时,需要引入一些中间状态来实现一次只押入一个符号。
- Σ就是终结符的集合。也就是输入带的字母表。
- 堆栈里放的符号可以是变元,可以是终结符。
- δ是转移函数
- 初始状态是qstart
- 唯一的接受状态是qaccept
剩下的就是如何构造转移函数。这个转移函数就是在堆栈中去模拟派生过程,然后让栈顶跟输入符号进行匹配,如果栈顶是终结符,就跟输入终结符进行匹配,匹配上就弹出,匹配不上这个非确定型分支就拒绝。如果栈顶是个变元,就进行产生式的替换。
设P在状态q下读a,把栈顶s换成u=u1,u2,⋯,uk,进去状态r。则引入新状态q1,q2,⋯,qk−1。
令转移函数
δ(q,a,s)δ(q1,ϵ,ϵ)δ(q2,ϵ,ϵ)δ(qk−1,ϵ,ϵ)包含(q1,uk),={(q2,uk−1)},={(q3,uk−2)},⋯={(r,u1)}.
把这些动作记为(r,u)∈δ(q,a,s)(状态q下读a把栈顶s换成u同时进入状态r)。所以这类新状态的集合记为E。
说明:注意下推自动机是非确定型的,所以转移函数出来是一个集合,是所以可能的新的状态和栈顶的符号都在里面。δ(q,a,s)={(q1,uk)}意思是在状态q下,读输入带上的符号a,栈顶是s。可以把栈顶符号s换成uk,然后进入状态q1。现在第一个符号uk已经进栈了。本来是把s换成u1u2⋯,现在是先把s换成uk,下面再让其他的依次进栈。
转移函数δ如下规定:
- 从初始化栈开始,把符号$和初始变元S押入栈。形式描述是:δ(qstart,ϵ,ϵ)={(qloop,S,$)}
- 如果栈顶是变元A,则非确定地选择一个A的规则,并且把A替换成这条规则右边的字符串。形式描述:δ(qloop,ϵ,A)={(qloop,w) ∣ A→w是R中规则}
- 如果栈顶是终结符a,则读输入中的下一个符号,并且把它与a进行比较。如果它们匹配,则重复,如果它们不匹配,则这个非确定型分支拒绝。形式描述:δ(qloop,a,a)={(qloop,ϵ)}
- 如果栈顶符号是$,则进入接受状态。如果此时输入已经读完,则接受这个输入串。形式描述:δ(qloop,ϵ,$)={(qaccept,ϵ)}
→qstart↓ε,ε→S$qloop⇌{ε,A→wa,a→ε↓ε,$→εqaccept
从CFG构造PDA的例子
把以下CFG G转化成等价的PDA P1:
S→aTb ∣ b,T→Ta ∣ ϵ
→qstart↓ε,ε→S$qloop⇌⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧ε,S→aTbε,T→Taε,S→bε,T→εa,a→εb,b→ε↓ε,$→εqaccept
但是问题是这里面有长串S→aTb,T→Ta
非上下文无关语言
- B={anbncn ∣ n≥0} 非CFL(只有一个栈,无法匹配c)
- C={ww ∣ w∈{0,1}∗} 非CFL(典型的上下文有关语言)
- Cc={x ∣ x=ww,w∈{0,1}∗} 是CFL
上下文无关语言的泵引理(Pumping Lemma)
定理
设A是上下文无关语言,则存在常数p(泵长度)使得,若x∈A且∣s∣≥p,则s=uvxyz,满足以下条件:
- ∀i≥0,uvixyiz∈A;
- ∣vy∣>0;
- ∣vxy∣≤p;
丘奇-图灵论题
在计算理论的介绍中,已经给出计算设备的一些模型。又穷自动机对小存储量设备是较好的模型。下推自动机对无限存储设备是较好的模型,但无限存储设备只能以“先进后出”的栈方式使用。还证明了这些模型就连有些非常简单的任务都完不成。所以它们太过于局限,不能作为计算机的通用模型。
单带图灵机™
图灵机与有穷自动机的区别
- 图灵机在带子上既能写也能读
- 读写头既能向左移也能向右移
- 带子是无限长的
- 进入拒绝和接受状态将立即停机
单带图灵机的形式定义
定义
定义:TM M=(Q,Σ,Γ,δ,q0,qacc,qrej)
- Q是有穷状态集
- Σ是输入字母表,空格符B∈/Σ
- Γ是带字母表,Σ∪{B}⊆Γ
- δ:Q×Γ→Q×Γ×{L,R}是转移函数(L表示向左移动,R表示向右移动)
- q0∈Q是初始状态
- qacc∈Q是停机接受状态
- qrej∈Q是停机拒绝状态,qacc=qrej
单带图灵机的格局
- 格局:uqav
- 当前状态:q
- 当前带内容:uav(u,v都是串,a是一个符号,正在读a)
- 当前扫描符号:a
- 初始格局:q0w,w是输入串
- 接受格局:uqaccav
- 拒绝格局:uqrejav
- 停机格局:uqaccav,uqrejav
单带图灵机的格局的例子
101101111↑q7
这个图灵机当前状态是q7,正在读的字符是0。0的左端是1011,右端是1111。所以这个图灵机当前的格局是1011q701111。
我们给了一个图灵机能写出它的格局,反之给了一个格局,就知道这个图灵机当前的情况。所以格局包含了这个图灵机某一时刻的所有信息在内。
单带图灵机格局的产生
- C1产生C2:
- 如果δ(qi,b)=(qj,c,L),则uaqibv产生uqjacv,qibv产生qjcv(在带的左端不能向左移)
- 如果δ(qi,b)=(qj,c,R),则uaqibv产生uacqjv
如果在状态qi下读的符号b能够进入状态qj,同时把b改写成c而且带头向左移动。
单带图灵机的计算
- M接受输入w:存在格局序列C1,C2,⋯,Ck,使得
- C1=q0w是初始格局
- 每个Ci产生Ci+1(i=1,⋯,k−1)
- Ck是接受格局
- M(识别,接受)的语言:
- L(M)={x ∣ M接受x}
图灵机的计算结果:
图灵可识别,图灵可判定
- 图灵可识别:A=L(M)
- x∈A时,M在x上停机接受
- x∈/A时,M在x上停机拒绝或不停机
- 补图灵可识别:A=L(M)
- x∈/A时,M在x上停机拒绝
- x∈A时,M在x上停机接受或不停机
- 图灵可判定:A=L(M)
- x∈A时,M在x上停机接受
- x∈/A时,M在x上停机拒绝(处处停机)
对于有穷自动机而言,有穷自动机识别一个串和接受一个串是一样的意思。但是对于图灵机而言,要做区分。图灵可识别指的是可以不停机,对于图灵可判定是处处停机。
一些等价术语
- 图灵可识别 = 递归可枚举 = 计算可枚举 = 半可判定 = 半可计算
- 图灵可判定 = 递归 = 可解 = 能行 = 可判定 = 可计算
- 下一章证明:图灵可识别=图灵可判定
图灵机判定语言的例子
A={02n ∣ n≥0}
表示了1, 2, 4, 8, ⋯个0。这个语言不是正则的,也不是上下文无关的。因为正则语言和上下文无关语言有泵引理,泵引理里要求它是个等差序列都在这个语言里面,而这个语言显然它的间隔越来越大。也就是用有穷自动机和下推自动机都无法识别这个语言,但是图灵机就能识别这个语言。
- M2=(Q,σ,Γ,δ,q1,qacc,qrej)
- Q={q1,q2,q3,q4,q5,qacc,qrej}
- σ={0}
- Γ={0,X,B}
- δ如图所示
- 用空白符B作为左端点定界符
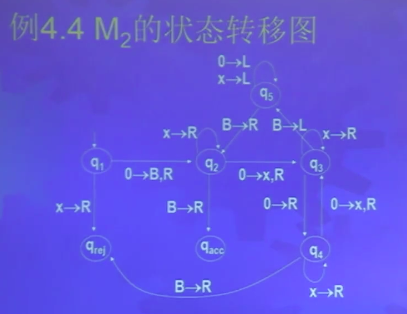
q10000,BX0Xq3B,q5BX0XB,BXXXq3B,q5BXXXB,BXXXq2B,Bq2000,BX0q5XB,Bq2X0XB,BXXq5XB,Bq2XXXB,BXXXqaccBXq300,BXq50XB,BXq20XB,BXq5XXB,BXq2XXB,BX0q40,Bq5X0XB,BXXq3XB,Bq5XXXB,BXXq2XB,
图灵机的变形
- 双向无穷带
- 多维带
- 多带
- 多头
- 非确定型
- ⋯
- TM概念有很强的稳健型
多带图灵机
- 多带图灵机的转移函数:
- δ:Q×Γk→Q×Γk×{L,R}k
- δ(qi,ai,⋯,ak)=(qj,b1,⋯,bk,L,R,⋯,L)
- “分道”:每道模拟一条带(改变字母表)
- “分段”:每段模拟一条带(加上#分隔开,还有虚拟读写头)
非确定型图灵机(NTM)
跟非确定型有穷自动机和非确定型下推自动机一样,区别在于转移函数。
δ:Q×Γ→P(Q×Γ×{L,R,S})
根据当前状态和当前转移符号,决定进入下一个状态和下一个符号以及带头如何移动(向左移动,向右移动,停止移动)。而且有不止一种选择,所以右边是一个幂集合的形式,是它的一个子集。可以是空集合,表示没有选择,可以是只有一个,表示只有一个选择,可以用多个表示多种选择。
同样,NTM的计算用一个计算树表示。(非确定型分支)
- 分析:DTM“遍历”NTM计算树
- 先深搜索(×)
- 先宽搜索(✓)
证明:用DTM D来模拟NTM N

D = “对于输入w”:
- 开始时,第一个带包含w,其余两个带为空
- 把第一个带复制到第二个带上
- 在第二个带上模拟N在输入w上的某个非确定型计算分支,这个分支由第三个带指定。若遇到接受格局,则接受。否则进入第4步
- 在第三个带上,用字典序下的下一个串来替代原用的串(一层一层),转到第2步
注意:识别指的是可以不停机,当输入串不在这个语言里就可以不停机。判定指的是无论是接受还是拒绝一定是停机的。
非确定型图灵机的工作方式:如果用它作识别,那么有些分支可以不停机,如果用它来作判定,那么它所有的分支都要求它要停机。当然有的分支停机之后是接受或者拒绝,只要有一个是接受就说它总的是接受。当所有的分支都停机拒绝,就说它拒绝。
枚举器和识别器
枚举器
- 计算装置的工作方式:
- 识别器:输入x,输入0/1/?(0:停机拒绝,1:停机接受,?:不停机)
- 判定器:输入x,输出0/1(一定是停机的,要么拒绝要么接受)
- 转换器:输入x,输出y
- 产生器:输入0n,输出xn
- 枚举器:输入ϵ,输出x1,x2,x3,⋯
可识别的意思是说:对于每一个输入要么停机接受,要么停机拒绝,或者不停机。
可枚举的意思是说:把语言的每一个串依次列出来,不讲究顺序没有遗漏可以重复。
计算模型的等价性
- 计算模型
- 图灵机(及其变种)
- λ-演算
- 0型文法
- ⋯
- 这些模型彼此等价
- 你的经验
算法的定义
希尔伯特问题
描述图灵机的术语
可判定性
首先我们看一下算法可解性的局限性
- 算法可解
- 按照算法可解性给问题分类
- 证明有些问题能用算法求解
- 证明另一些问题不能用算法求解
- 研究不可解性的意义
- 避免做无用功
- 激发想象力,全面透彻地理解什么是计算
可判定语言
与正则语言相关的可判定性问题
- DFA接受性问题
- NFA接受性问题
- 正则表达式派生性问题
- DFA空性问题
- DFA等价性问题
DFA接受性问题
DFA接受性问题是检测一个给定的确定性有穷自动机是否接受一个给定的串
ADFA={<B,w> ∣ DFAB接受串w}
DFA B接受串w ⇔<B,w>∈ADFA
- 证明思路:设计一个判定ADFA的TM M。M模拟B在w上的计算
- 证明:设计一个判定ADFA的TM M
M="对输入<B,w>,其中B是DFA,w是串:1)在输入w上模拟B.2)若模拟以结束状态结束,则接受;若模拟以非接受状态结束,则拒绝."
TM M首先检查输入<B,w>,若w不是字符串,或B不是(Q,σ,δ,q0,F)形式,则拒绝。然后M执行模拟,M通过在带上写下信息,来跟踪B在w上运行时当前状态和当前位置。状态和位置的更新由B的转移函数确定。当M处理完w最后一个符号时,如果B处于接受状态,则M接受,否则拒绝。
NFA接受性问题
NFA接受性问题是检测一个给定的非确定性有穷自动机是否接受一个给定的串
ANFA={<B,w> ∣ NFAB接受串w}
- 证明思路:
- 证法1:用NTM N模拟B在w上的计算
- 证法2:先把NFA B转化为等价的DFA C,再用TM M模拟C在w上计算
- 证明:构造判定ANFA的TM N
N="对输入<B,w>,其中B是NFA,w是串:1)把NFAB转化成等价DFAC.2)在输入<C,w>上运行TMM.3)如果M接受,则接受,否则拒绝."
正则表达式派生性问题
正则表达式派生性问题是一个正则表达式是否派生一个给定的串
AREX={<R,w> ∣ 正则表达式R派生串w}
- 证明:下面的TM P判定AREX
N="对于输入<R,w>,其中R是正则表达式,w是串:1)把REXR转化成等价DFAA.2)在输入<A,w>上运行TMM.3)如果M接受,则接受,否则拒绝."
注意:对于可判定性问题把DFA,NFA,REX提供给TM都是等价的,因为TM能在三种编码之间进行互相转换
DFA空性问题
DFA空性问题是一个DFA是否根本不接受任何串
EDFA={<A> ∣ A是DFA且L(A)=∅}
- 证明思路:逐个检查所有的串(有无穷多个串),DFA接受一个串当且仅当:从初始状态出发,沿着此DFA的箭头方向,能够到达一个接受状态
- 证明:
TMT="对于输入<A>,其中A是DFA:1)标记初始状态.2)重复下列步骤,直到所有状态都被标记.3)对于一个状态,如果有一个到达它的转移是从某个已经标记过的状态出发的,则将它标记4)如果没有接受状态被标记,则接受,否则拒绝."
DFA等价性问题
DFA等价性问题是检查两个DFA是否识别同一个语言
EQDFA={<A,B> ∣ A和B是DFA且L(A)=L(B)}
定理
EQDFA是可判定语言
- 证明思路:正则语言对于布尔运算封闭,因此对于对称差运算封闭。两个语言相等当且仅当其对称差为空语言。正则语言是否为空,这是可判定的。
- 证明:
TMF="对于输入<A,B>,其中A和B都是DFA:1)构造DFAC使得L(C)=L(A)⊕L(B).2)在输入<C>上运行TMT.3)如果T接受,则接受,否则拒绝."
与上下文无关语言相关的可判定性问题
- CFG派生性问题
- CFG空性问题
- CFG等价性问题
- 上下文无关语言
CFG派生性问题
CFG派生性问题是检查一个CFG是否派生一个特定的串
ACFG={<G,w> ∣ CFGG派生串w}
- 证明思路:
- 让G遍历所有的派生,以确定哪一个是w的派生。(如果G产生w,这个过程将终止,如果G不产生w,这个过程将不终止,这样只能证明ACFG是图灵可识别语言。)
- 采用CNF,派生长度为n的串恰好需要2n-1步,先把G转换成等价的CNF,在检查所有长度为2n-1的派生
- 证明:
TMS="对输入<G,w>,其中G是CFG,w是串:1)把G转化成等价的CNF.2)列出max{1,2∣w∣−1}步的所有派生3)如果这些派生中有一个产生w,则接受,否则拒绝."
CFG空性问题
CFG空性问题数检查一个CFG是否不派生任何串
ECFG={<G> ∣ G是CFG且L(G)=∅}
- 证明思路:
- 让TM S逐个检查所有可能的w,w有无限多个,这个过程将不终止。这样不可行,换一个办法,检查变元
- 检查初始变元是否产生一个终结符串(这是最终目的,如果初始变元能够产生出一个终结符串,那么它一定是非空的,它能够产生串)
- 那么怎么检查初始变元呢?检查每个变元是否产生一个终结符串,类似于DFA的标记算法
- 证明:
TMR="对输入<G>,其中G是CFG:1)将G中所有终结符做上标记;2)重复下列步骤,直到找不到可以做标记的变元3)如果G有规则A→U1U2⋯Uk,且U1U2⋯Uk都已经做过标记,则将初始变元A做上标记4)如果初始变元没有被标记,则接受,否则拒绝."
CFG等价性问题
CFG等价性问题是两个CFG是否派生同一个语言
EQCFG={<G,H> ∣ G和H都是CFG且L(G)=L(H)}
注意
EQCFG是不可判定语言!(下一章)
- 证明思路:
- 设A是CFL,把A的PDA转化成NTM,PDA某些计算分支可能不停机,NTM的计算分支也可能不停机,所以不是判定器(判定器要求处处停机)。
- 使用判定ACFG的TM S
- 证明:设A是CFL,G是A的CFG,下面设计判定A的TM MG.(其中G是给定的,w是任意的)
MG="对输入w:1)在输入<G,w>上运行TMS;2)如果这个机器接受,则接受,否则拒绝."
语言类间的关系
到目前为止,一共学习了4个主要语言类,正则的,上下文无关的,可判定的和图灵可识别的。下面是它们之间的关系图。
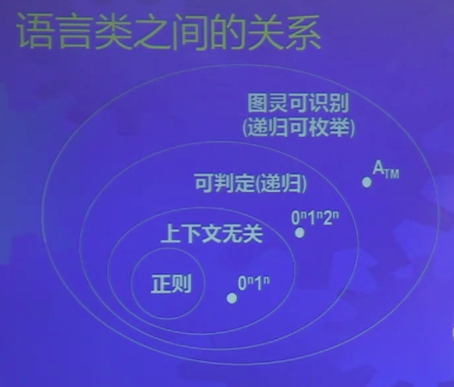
- 可判定由叫递归语言或叫可计算语言
- 图灵可识别又叫递归可枚举或叫半可计算语言。比如图灵机接受性问题,给一个图灵机给一个串,问这个图灵机接受不接受这个串。如果这个图灵机接受这个串,进行模拟最后一定会停下来,但是图灵机不接受这个串,就是死循环的情况下进行模拟,也就会陷入死循环,无法停机。所以说半可判定。也就是当输入在这个语言里的时候会停机,当输入不在这个语言里的时候就不停机。这种情况就叫图灵可识别或半可计算或半可判定。
如上图,问题是在图灵可识别之外还没有。下面通过计数法证明存在非图灵可识别语言。
一些计数结论
- 有理数集可数(楔形过程)
- 定理:实数集不可数(对角化)
- 推论:存在非图灵可识别语言
- 证明:全体图灵可识别语言构成可数集,全体语言是非可数集(这是因为每一个图灵可识别语言是由图灵机识别的,我们可以通过对图灵机进行编码,让每个图灵机变成一个字符串,我们又可以对字符串进行编码,让字符串对应一个自然数,自然数是有理数的子集合,有理数是可数的,所以自然数也是可数的,所以字符串是可数的,图灵机个数也是可数的,所以全体图灵可识别语言是可数集。但是全体语言是非可数集,与实数一样多)
停机问题
本节将证明算法上不可解的问题是存在的。本节和第6章都将介绍一些不可解问题,目的是帮助你了解这类不可解问题,和学习证明不可解性的技巧。
现在介绍第一个不可解性定理。下面的语言是不可解的:检查一个图灵机是否介绍一个给定的串的问题。类似于ADFA,ACFG,记为ATM,但ADFA,ACFG是可判定的,ATM却是不可判定的。
对角化方法
图灵机接受性问题
TM接受性问题是检查一个图灵机是否接受一个给定的串
ATM={<M,w> ∣ M是一个TM,且接受w}
- 证明思路:
- ATM={<M,w> ∣ TMM接受串w}
- DTM={<M> ∣ TMM接受串<M>}
- DTM是ATM的特例
- 用对角化方法证明DTM不可判定
- 证明:(反证法)假设TM H判定ATM,则
H(<M,w>)={接受若M接受w拒绝若M不接受w
利用H,构造TM D
D="对输入<M>,M是TM:1)在输入<M,<M>>上运行H;2)如果H接受,则拒绝,若H拒绝,就接受."则
D(<M>)={接受若M不接受<M>拒绝若M接受<M>
那么,D在输入<D>上结果怎么样?
D(<M>)={接受若M不接受<M>拒绝若M接受<M>D(D)={接受若D不接受<D>拒绝若D接受<D>
这时我们发现D(<D>)=接受⇔D(<D>)=拒绝,这是矛盾的。也就是前面假设的TM H和TM D都是不存在的。
回顾以下上述证明步骤。先假设TM H判定ATM,然后用H来构造一个TM D,它接受输入<M>,当且仅当M不接受输入<M>,最后在D自身上运行D。这些机器发生下列动作;
- H接受<M,w>当且仅当M接受w
- D拒绝<M>当且仅当M接受<M>
- D拒绝<D>当且仅当D接受<D>
最后一行是矛盾的。
上述定理的证明中,什么地方有对角化呢?
- U(<M,w>)结果(可能不停机)
| U |
<M1> |
<M2> |
<M3> |
<M4> |
<M5> |
<M6> |
⋯ |
| M1 |
接受 |
|
接受 |
|
接受 |
接受 |
⋯ |
| M2 |
|
接受 |
|
|
接受 |
|
⋯ |
| M3 |
|
|
|
|
|
|
⋯ |
| M4 |
接受 |
|
接受 |
|
接受 |
|
⋯ |
| M5 |
接受 |
接受 |
接受 |
接受 |
接受 |
接受 |
⋯ |
| M6 |
|
接受 |
|
|
|
接受 |
⋯ |
| ⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
我们把所有的图灵机列成一个表,前面讲过图灵机是可数的,每一个图灵机在每一个输入上运行有各种各样的可能。可能是停机接受,可能是停机拒绝,也可能是不停机。我们把停机接受的情况全部列出来。U是前面讲的通用机,它能够模拟任何其他的图灵机,只要直到描述即可。有可能不停机。
- H(<M,w>)结果(处处停机)
| H |
<M1> |
<M2> |
<M3> |
<M4> |
<M5> |
<M6> |
⋯ |
| M1 |
接受 |
拒绝 |
接受 |
拒绝 |
接受 |
接受 |
⋯ |
| M2 |
拒绝 |
接受 |
拒绝 |
拒绝 |
接受 |
拒绝 |
⋯ |
| M3 |
拒绝 |
拒绝 |
拒绝 |
拒绝 |
拒绝 |
拒绝 |
⋯ |
| M4 |
接受 |
拒绝 |
接受 |
拒绝 |
接受 |
拒绝 |
⋯ |
| M5 |
接受 |
接受 |
接受 |
接受 |
接受 |
接受 |
⋯ |
| M6 |
拒绝 |
接受 |
拒绝 |
拒绝 |
拒绝 |
接受 |
⋯ |
| ⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
我们假设H是判定这个接受性问题,那么H就一定是处处停机的。
- H(<M,<M>>)结果(处处停机)
| H |
<M1> |
<M2> |
<M3> |
<M4> |
<M5> |
<M6> |
⋯ |
| M1 |
|
拒绝 |
接受 |
拒绝 |
接受 |
接受 |
⋯ |
| M2 |
拒绝 |
|
拒绝 |
拒绝 |
接受 |
拒绝 |
⋯ |
| M3 |
拒绝 |
拒绝 |
|
拒绝 |
拒绝 |
拒绝 |
⋯ |
| M4 |
接受 |
拒绝 |
接受 |
|
接受 |
拒绝 |
⋯ |
| M5 |
接受 |
接受 |
接受 |
接受 |
|
接受 |
⋯ |
| M6 |
拒绝 |
接受 |
拒绝 |
拒绝 |
拒绝 |
|
⋯ |
| ⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
我们定义的H(<M,<M>>)实际考虑的是对角线的结果。
- D(<M>)=¬H(M,<M>)(处处停机)
| D |
<M1> |
<M2> |
<M3> |
<M4> |
<M5> |
<M6> |
⋯ |
| M1 |
|
拒绝 |
接受 |
拒绝 |
接受 |
接受 |
⋯ |
| M2 |
拒绝 |
|
拒绝 |
拒绝 |
接受 |
拒绝 |
⋯ |
| M3 |
拒绝 |
拒绝 |
|
拒绝 |
拒绝 |
拒绝 |
⋯ |
| M4 |
接受 |
拒绝 |
接受 |
|
接受 |
拒绝 |
⋯ |
| M5 |
接受 |
接受 |
接受 |
接受 |
|
接受 |
⋯ |
| M6 |
拒绝 |
接受 |
拒绝 |
拒绝 |
拒绝 |
|
⋯ |
| ⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
⋯ |
这里的D(<M>)把对角线的结果反过来了。现在我们就说D是不可计算的,因为会产生矛盾。如果D是可计算的,一定会出现在某一行,对应这图灵机D。那么问题来了,这一行在交叉点会产生矛盾。
- D(<D>)结果(矛盾)
| D |
<M1> |
<M2> |
<M3> |
<M4> |
⋯ |
D |
⋯ |
| M1 |
|
拒绝 |
接受 |
拒绝 |
⋯ |
接受 |
⋯ |
| M2 |
拒绝 |
|
拒绝 |
拒绝 |
⋯ |
拒绝 |
⋯ |
| M3 |
拒绝 |
拒绝 |
|
拒绝 |
⋯ |
拒绝 |
⋯ |
| M4 |
接受 |
拒绝 |
接受 |
|
⋯ |
拒绝 |
⋯ |
| ⋮ |
⋮ |
⋮ |
⋮ |
⋮ |
⋱ |
⋮ |
⋯ |
| D |
|
|
|
|
⋯ |
? |
⋯ |
| ⋮ |
⋮ |
⋮ |
⋮ |
⋮ |
⋯ |
⋮ |
⋱ |
所以这个D不可能是任意一个图灵机。这就是矛盾,这个证明方法就是对角化方法。
非图灵可识别语言
上一节介绍了不可判定的语言:ATM。现在介绍另一个语言,此语言甚至是不可识别的。注意,ATM还不是这样的语言,因为已经证明ATM是图灵可识别的。
定理
一个语言是可判定的,当且仅当它和它的补都是图灵可识别的
- A的补:Ac=Σ∗−A(课本记作A)
- A可判定⇔ A和Ac图灵可识别
- 证明:
- (⇒)设A是可判定的,可判定语言对布尔运算封闭,所以Ac是可判定的。可判定语言都是图灵可识别的,所以A和Ac都是图灵可识别的。
- (⇐)设A和Ac都是图灵可识别的。设TM M1识别A,TM M2识别Ac。下面构造TM M判定A。
M="对输入w:1)在输入w上并行运行M1,M2,M有两个带,一个模拟M1,一个模拟M2,M交替地模拟两个机器的一步,直到其中一个停机2)如果M1接受,则接受,如果M2接受,就拒绝."
下面证明M确实判定A(正确性)
- 任何一个串w要么在A中,要么在Ac中。所以M1,M2必有一个接受w。因为当M1或M2接受时,M就停机,所以M总会停机
- M接受所有A中的串,拒绝所有不在A中的串,所以,M判定A。
推论:ATM不是图灵可识别的
- 证明:(反证法)
- 假设ATM是图灵可识别的
- 因为ATM是图灵可识别的(引理)
- 所以ATM是可判定的(定理)
- 但是ATM是不可判定的(定理以及对角化证明)
- 矛盾!
现在可以完善刚才语言类之间的关系图了
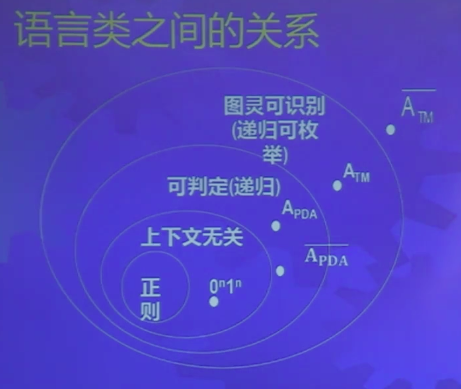
- 下推自动机的接受性问题是可判定的
- 它的补语言也是可判定的,因为可判定语言对于补是封闭的
(不)可判定性总结
|
DFA |
CFG |
TM |
| 接受性 |
|
|
|
| 空性 |
|
|
× |
| 等价性 |
|
× |
× |
- 用对角化法证明不可判定语言
- 通过定理,一个语言是可判定的,当且仅当它和它的补都是图灵可识别的语言
- 非图灵可识别语言
- 有一个语言:TM的接受性语言ATM,它本身是图灵可识别的,但是ATM不是图灵可判定的,所以ATM就不是图灵可识别的语言了。
- 因为如果ATM也是图灵可识别的语言的话,ATM就会成图灵可判定的了(矛盾)
可归约性
第5章介绍了几个在图灵机可解的问题,也给出了一个计算上不可解的问题,即ATM。本章讨论另外几个不可解问题。在讨论过程中,将介绍一个基本方法,可用来证明问题是计算上不可解的,这个方法称为可归约性。
规约就是将一个问题转化为另一个问题的方法,使得可以用第二个问题的解来解第一个问题。
- 在后面的复杂性理论中,当A可归约到B是,解A不可能比解B更难,因为B的一个解给出了A的一个解
- 根据可计算理论,如果A可归约到B,且B是可判定的,则A也是可判定的。等价地,如果A是不可判定的,且可归约到B,则B是不可判定的。后者在证明许多问题的不可判定性时起着关键作用
- 简单的说,下面方法可用来证明一个问题是不可解的:先证明另外一个问题是不可判定的,再将此问题归约到它
语言理论中不可判定问题
一个简单的不可判定问题
映射可归约性
可计算函数
映射可归约性的形式定义
可计算性理论的高级专题
递归定理
逻辑理论的可判定性
图灵可归约性
时间复杂性
如果求解一个问题需要过量的时间或存贮量,那么即使它可判定从而在理论上用计算机可解,在实际中他还是不可解的。
本书最后一部分介绍计算复杂性理论–一门研究求解计算问题所需要的时间,存贮量,或者其他资源的理论。
本章目的是给出时间复杂性理论的基础知识。
- 首先介绍一种度量求解问题所耗费时间的方法
- 然后介绍怎样根据所需要的时间来给问题分类
- 最后讨论某些可判定问题需要耗费极大量时间的情况,以及碰到这样的问题时该怎样识别它们
度量复杂性
big-O
设f和g是函数,f,g:N→R+。若∃c,n0,∀n≥n0,f(n)≤cg(n),则说f(n)=O(g(n)),或g是f的(渐进)上界。
例题8.3:设f(n)=5n3+2n2+22n+6,则
(1) f(n)=O(n3)
(2) f(n)=O(n4)
(3) f(n)=O(n2)
例题8.4:f(n)=3nlog2n+5nlog2(log2(n+2)),则
f(n)=O(nlogn)
small-o记号
- f(n)=o(g(n)):limn→∞g(n)f(n)=0
例题8.6:
- n=o(n)
- n=o(nloglogn)
- nloglogn=o(nlogn)
- nlogn=o(n2)
- n2=o(n3)
多项式界, 指数界
- 多项式界:nO(1)
- n0.1,n0.99,n1.1,n2,n2.57,n10,n100,⋯
- 指数界:2nα(1)
- 2n0.1,2n0.5,2n,22n,2n2,n!
多项式与指数的区别
- 多项式与指数在增长率上有巨大差异,当n=1000时,n3=10亿(尚可处理),2n>宇宙中的原子数。
- 多项式有稳定性,对加,减,乘,除,合成封闭,计算模型互相模拟的开销是多项式的
分析算法
DTM运行时间
我们先看DTM运行时间
设M是处处停机的DTM。
- timeM:Σ∗→N,timeM(x)=M在输入x上的运行步数。(M是有限长度的字符串的集合到自然数集合的映射,对每个串x有一个运行步数,是自然数),所以运行时间是由输入确定
- timeM:N→N,timeM(n)=M在长度为n的输入上的运行步数,运行时间由输入长度确定
所以timeM(n)是M的时间复杂性(度)
这时候我们要区分两种情况:最坏情形和平均情形
- 最坏情形复杂性:timeM(n)=M在长度为n的输入上的最大运行步数
- 平均情形复杂性:timeM(n)=M在长度为n的输入上的平均运行步数
这里只讨论最坏情形复杂性
- 输入长度与编码有关
- 输入规模(问题中的自然参数)与编码无关
- 要求二者是多项式相关的
有了计算复杂性的概念后,现在可以来看算法分析了
算法分析就是确定算法的(时间)复杂性
例题:A={0k1k ∣ k≥0}
我们知道这个串不是正则的,是上下文无关的。下面讲3个算法:
- 单带DTM M1:O(n2)
- 单带DTM M2:O(nlogn)
- 单带DTM在o(nlogn)时间内只能识别正则语言
- 单带DTM M3:O(n)
M1="对输入串w:1)扫描带,若在1右边发现0,就拒绝;2)若0和1都在带上,就重复下一步;3)扫描带,删除一个0和一个1;4)若所有1被删除后还有0,或所有0被删除后还有1,就拒绝;否则,带上没有留下1和0,接受."时间:2n+n∗2n+n=O(n2)
M2="对输入串w:1)扫描带,若在1右边发现0,就拒绝;2)若0和1都在带上,就重复下一步;3)扫描带,检查剩余的0和1总数,若总数是奇数,就拒绝;4)再次扫描带,从第一个0开始,隔一个删除一个0,然后从第一个1开始,隔一个删除一个15)若带上没有留下1和0,接受;否则,拒绝."时间:n+n∗(1+log2n)+n=O(nlogn)
M3="对输入串w:1)扫描带,若在1右边发现0,就拒绝;2)扫描带1上的0,把每个0复制到带2上,直到第一个1为止;3)扫描带1上的1直到输入结尾,每次从带1上读到一个1,就在带2上删除,若在读完1之前删除了所有的0,就拒绝;4)若所有0都被删除,就接受;否则,拒绝."时间:n+n+n+n=O(n)
时间复杂类TIME(t(n))
TIME(t(n))={L ∣ 某个O(t(n))时间的单带DTM判定语言L
例:A={0k1k ∣ k≥0}
- A∈TIME(nlogn)
- A∈TIME(n2)
模型间的复杂性关系
- 时间复杂性与模型有关
- 多带与单带:平方
- 非确定型与确定型:指数
定理
定理8.8:设函数t(n)≥n,则每个t(n)时间多带TM都与某个O(t2(n))时间单带TM等价
- 证明思路:分析定理4.8的证明,每步模拟需要O(t(n))时间,总共模拟t(n)步
NTM运行时间
判定机NTM N的运行时间是函数f:N→N,f(n)在长度n的输入上所有计算分支的最大步数。因为是判定机,每一条分支都是要停机的。
定理
定理8.10:设函数t(n)≥n,则每个t(n)时间单带NTM都与某个2O(t(n))时间单带DTM等价
- 证明思路:分析定理4.10的证明,每个分支模拟需要O(t(n))时间,总共模拟bt(n)个分支,b是所有节点的最大分支数
P类
P=UkTIME(nk)={L ∣ 某个多项式时间单带DTM判定语言L}
- P的重要性:对于所有与单带DTM多项式时间等价的计算机模型来说,P是不变的
- P大致对应于在计算机上实际可解的问题类,实际算法往往是O(n),O(n2),O(n3),几乎没有O(n100)
路径问题
给定一个有向图,一个起点和一个终点,确定是否存在从一个起点到终点的有向路径
PATH={<G,s,t> ∣ 有向图G有从s到t的有向路径}
- 分析:
- 输入规模:顶点数m
- 蛮力(brute-force)搜索:O(mm)
- 宽度优先搜索(标记算法):O(m)
互素问题
确定两个自然数是否互素
RELPRIME={<x,y> ∣ x与y互素}
- 分析:
- 输入规模:数的二进制表示的长度n
- 蛮力(brute-force)搜索:O(2n)
- 辗转相除:O(n2)
上下文无关语言问题
- 分析:
- 输入规模:串长度n=∣w∣
- 蛮力(brute-force)搜索:CNF,O(22n−1)
- 动态规划:O(n3)
NP类
刚才的P类问题是确定型的在多项式里求出解,NP类问题不能在多项式里求出解,但是可以在多项式时间内验证它的解
哈密顿路径问题
HAMPATH={<G,s,t> ∣ (有向)图G包含从s到t的哈密顿路径}
- (有向)哈密顿路径问题:给定一个有向图,一个起点,一个终点,确定是否存在从起点到终点的哈密顿路径
- (有向)哈密顿路径:(有向)图G中经过每个顶点恰好一次的(有向)路径
- 判定问题:有没有哈密顿路径
- 搜索问题:求出哈密顿路径
验证机
语言A={w ∣ ∃字符串c,算法V接受<w,c>}
- 算法V是语言A的验证机
- c称为w是A的成员的资格证书
- |c|是|w|的多项式(“短证明”)在|w|的多项式时间内运行(“容易验证”),若A有多项式时间验证机,则称A为多项式可验证的
合数问题
确定给定的自然数是否合数(两个大于1的自然数的乘积)
COMPOSITES={x ∣ x=pq,整数p,q>1}
NP类问题定义
NP={L ∣ 语言L有多项时间验证机}
- 解的长度是输入规模的多项式
- 验证解所花费时间是输入规模的多项式
- 候选解个数是输入规模的指数
- NP类问题指的就是多项式时间内可验证的内容问题类,解可以在多项式时间内可验证
刚才上述举例的问题中:
- HAMPATH ∈ NP
- <G,s,t>的证书是一条从s到t的哈密顿路径
- COMPOSITES ∈ NP
- HAMPATH的补问题 ∈? NP
- COMPOSITES的补问题 ∈ NP
定理
定理8.17:
NP={L ∣ 某个多项式时间NTM判定语言L}
- 分析:
- 多项式时间验证机⇔非确定型多项式时间判定机
定义8.18:
NTIME(t(n))={L ∣ 某个O(t(n))时间NTM判定语言L
推论8.19:
NP=UkNTIME(nk)
复习
进入NP完全问题之前先复习一下之前的内容
- TIME多带(t) ⊆ TIME(t2)
- 多带图灵机转化为单带图灵机的时候,时间复杂度要平方
- NTIME(t) ⊆ TIME(2O(t))
- P = UkTIME(nk)=多项式时间类
- NP = UkNTIME(nk)=非确定型多项式时间类 = 多项式时间可验证类
- EXP = ⋃kTIME(2nk) = 指数时间类
它们之间的关系可以表示为下面的图

- L是确定型对数空间
- NL是非确定型对数空间,它对于补是封闭的,所以NL = coNL
- 然后是多项式时间P,非确定型时间NP,以及它的补coNP,中间是NP∩coNP
- 再往上是PSPACE和NPSPACE,把非确定性空间转化为确定型空间开销是平方一下,因为多项式平方还是平方,所以PSPACE = NPSPACE
- 再往外是确定型指数时间
- 根据时间层次定理,P = EXP;根据空间层次定理,L = PSPACE
- 此外,其他的包含关系都是未知的。比如说L是不是等于NL,L是不是等于P,P是不是等于NP,NP是不是等于coNP不知道,P是不是等于PSPACE也不知道。
NP完全性
NP完全问题内容提要:
- 多项式时间m-归约
- NP完全性
- 库克定理:第一个NP完全问题SAT
- 其他NP完全问题:
- 3SAT,CLIQUE,VEXTER-COVER,(U)HAMPATH,SUBSET-SUM
多项式时间归约
- A≤mpB via f(p表示多项式时间,m表示映射归约)
- x∈A⇔f(x)∈B(A可以多项式时间归约到B)
- f是多项式时间可计算函数,计算f(x)所需时间是O(∣x∣k),k是与x无关的常数
多项式时间归约的性质
- 传递性
- 若A≤mpB,且B≤mpC,则A≤mpC
- P对≤mp封闭性
- 若A≤mpB,且B∈P,则A∈P
- NP对≤mp封闭性
- 若A≤mpB,且B∈NP,则A∈NP
可满足性问题
给定一个布尔公式,确定这个公式是否可满足
SAT={<ϕ> ∣ ϕ是可满足布尔公式}
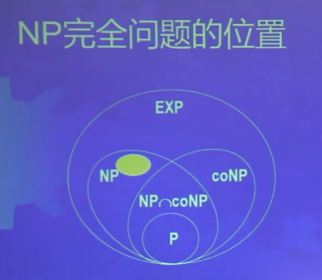
- NP完全问题在NP问题里,但是不在P问题中
- 证明一个问题是NP完全的,是一个很强的证据支持说这个问题不在P问题里,可能没有多项式时间的算法
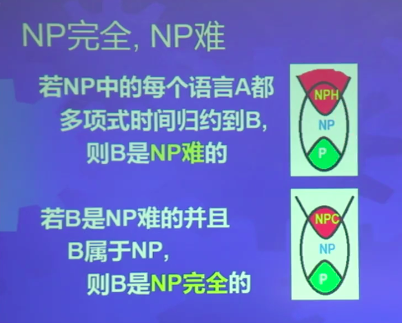
几个NP完全问题
空间复杂性
难解性
复杂性理论高级专题
参考文献
计算理论导引 | (美) Michael Siper
北京大学“理论计算机科学基础”课程
































