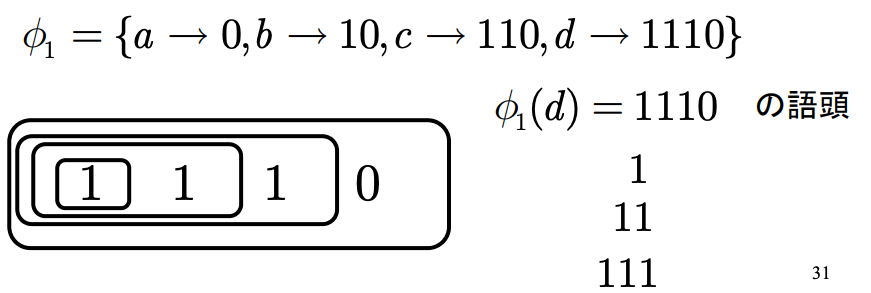CS专业课学习笔记
情報理論の概要、情報の表現
情報理論とは
- 情報通信の基礎となる学問,研究分野
- 1948 年の(C. E. Shannon)シャノンの論文 “A Mathematical Theory of Communication” に端を発する.
- 情報の保存: zip, lzh, DVD, CD…
- 情報の伝送: 衛星通信,携帯電話,ファクシミリ…
- 人工知能や暗号技術にも多大な影響
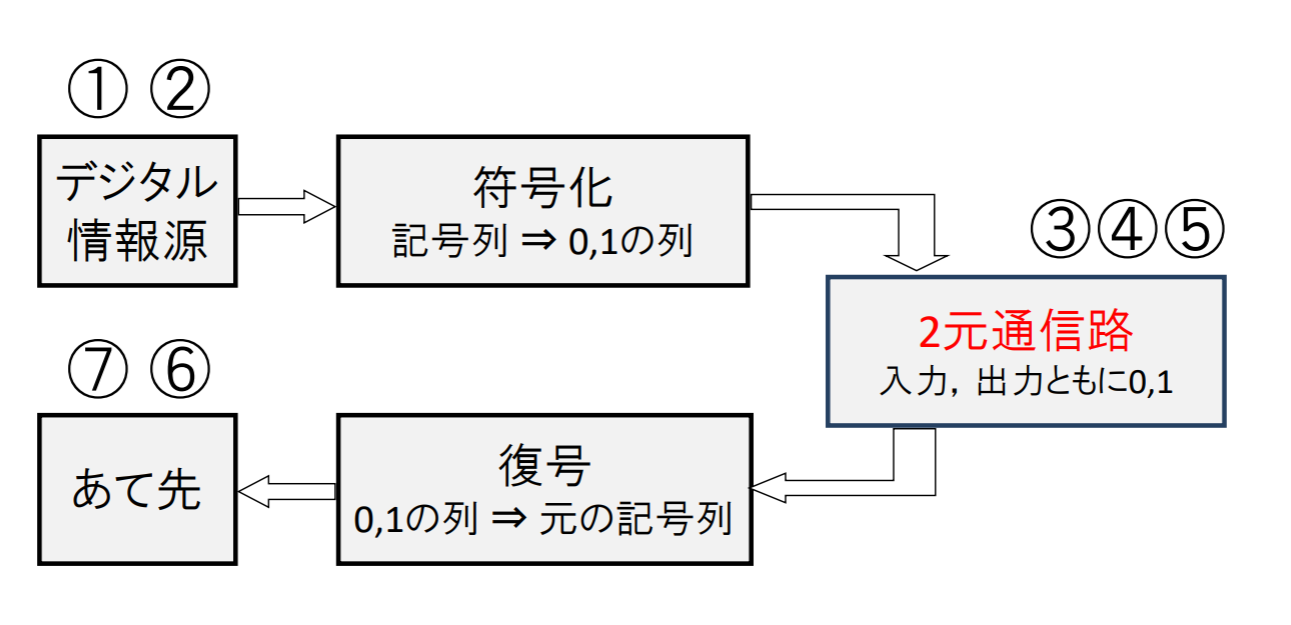
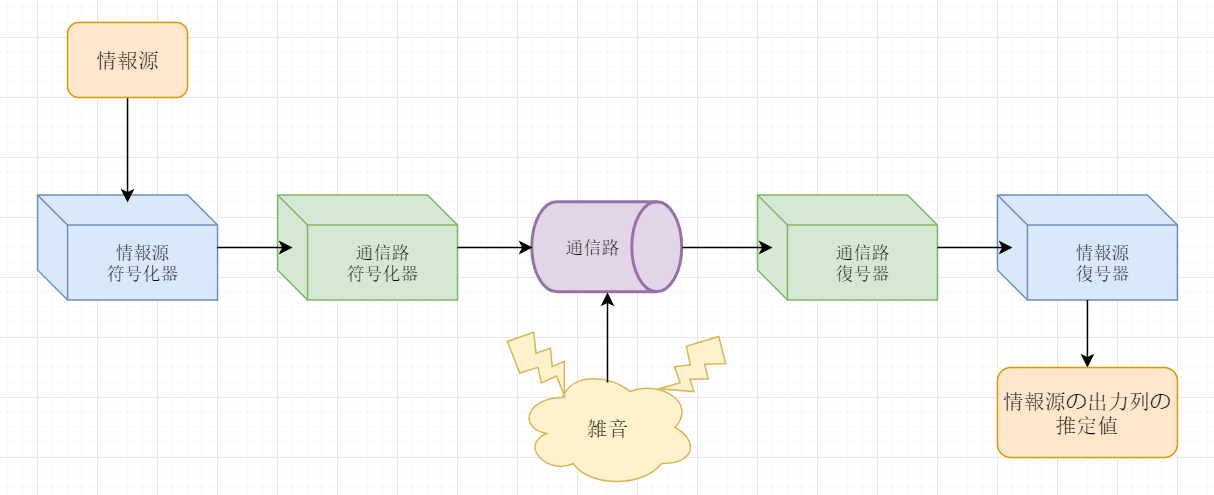
通信システムのモデル
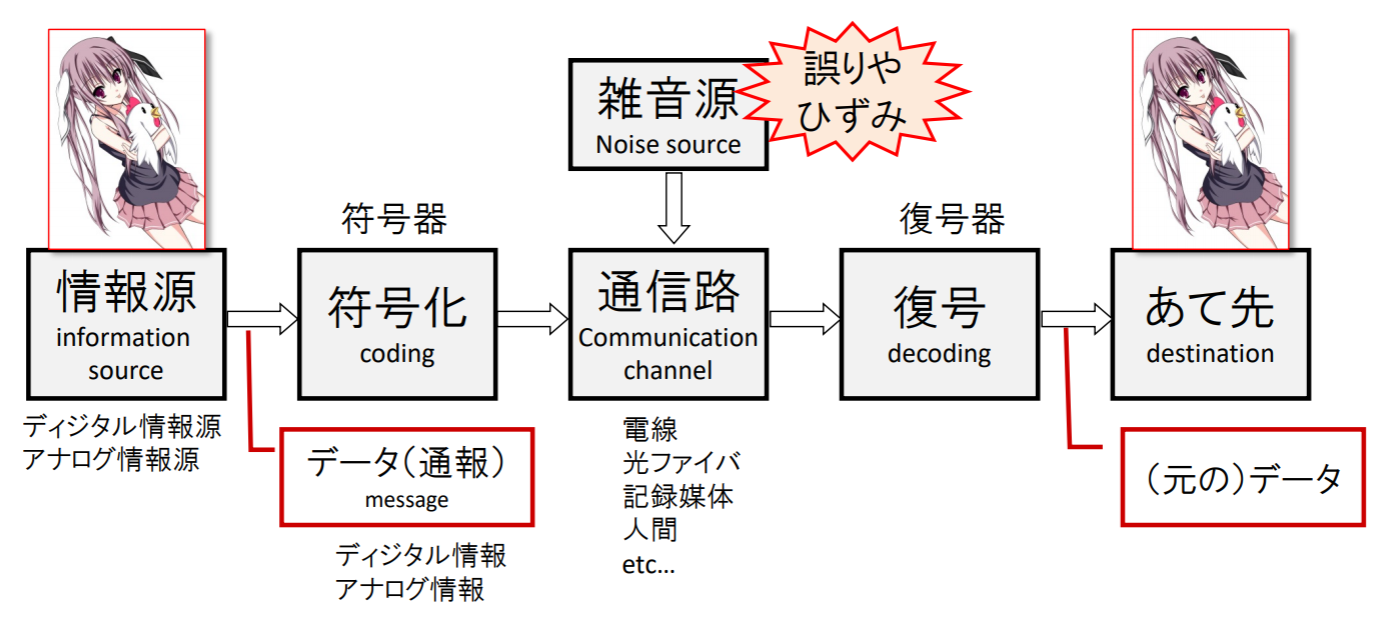
情報源が発する通報を,通信路を通して宛先へ伝達する際,情報伝達の効率や信頼性について考える
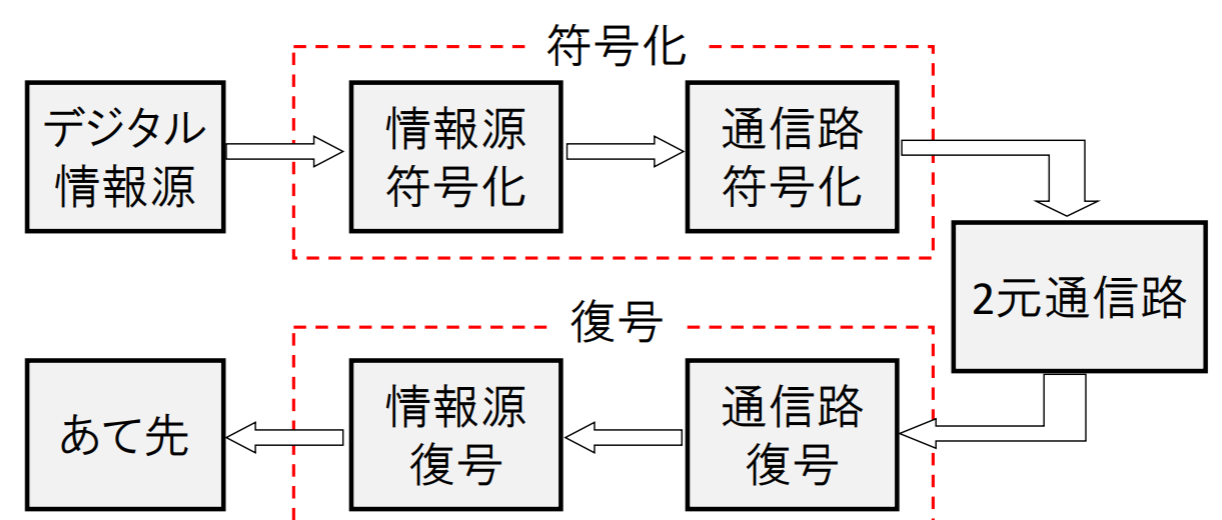
実際の情報源⋅通信路とモデルの対応
実際の通信システムを考えるとき,前述のモデルにどのように当てはめるかは,一意には定まらない
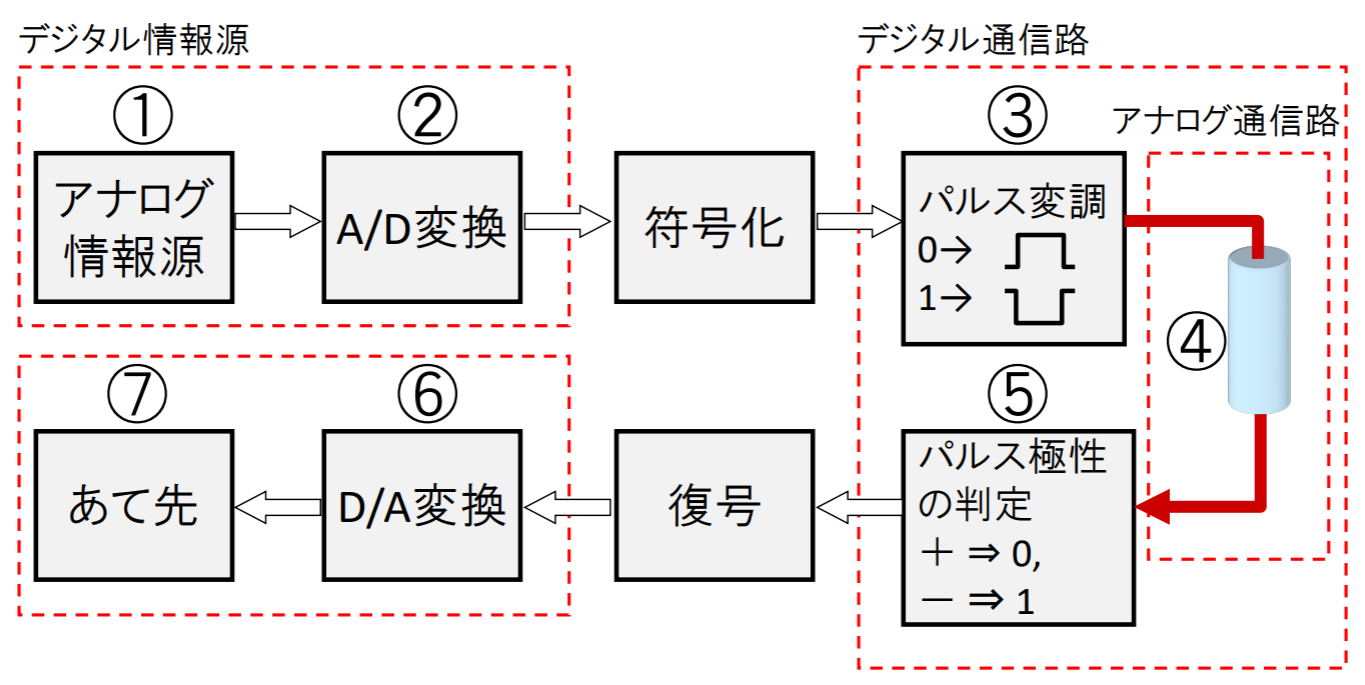
本科目の主題: デジタル情報源の符号化
- 情報源は記号列を出力する(デジタル情報源)
- 通信路は記号列を伝搬する(デジタル通信路)
情報理論の問題
次の二つを達成する具体的な符号化の方法とそれによってどこまで改善できるかの理論的限界を探る
- 通信路使用の効率(efficientcy)の向上
- 信頼性(reliability)の向上
情報理論が取り組む4つの問題
- 【問題1】 できるだけよい情報源符号化と復号の方法を見出す
- 1情報源記号あたりの符号系列の長さの平均値(平均符号長という)ができるだけ小さいことが望ましい
- 装置化が簡単で,符号化・復号による遅延が小さいほどよい
- 【問題2】情報源符号化の限界を知ること
- 1情報源記号あたりの平均符号長をどこまで小さくできるか?
- 【問題3】できるだけよい通信路符号化と復号の方法を見出す
- 付け加えた冗長性を信頼性向上に可能な限り有効に活用できる符号化が望ましい
- 復号した後の記号の誤り率・冗長度の最小化
- 【問題4】通信路符号化の限界を知ること
- 復号後の記号の誤り率をある値以下に抑えたとき,付加すべき冗長度をどこまで小さくできるか?
情報量による定量的な評価
対数をとることで情報の価値をうまく表現できる.
S=log2W
情報理論における主要な結果
-
情報源の符号化
- データ圧縮の理論
- zip, lzh などに応用
- 情報源の導入
- 平均符号長 (圧縮率),エントロピー(entropy)による定量的な評価
-
通信路の符号化
- 誤り訂正符号の理論
- CD, DVD, 携帯電話, 地上波デジタル TV 放送などに応用
- 通信による雑音の影響 = 通信路 (確率モデル) の導入
- 伝送速度,通信路容量による定量的な評価
重要な結果: 情報源符号化定理, 通信路符号化定理
情報源符号化: 平均符号長を小さくできる(エントロピーまで圧縮可能)
通信路符号化:
- 送信者が受信者へ0,1の情報を送る
- 途中の通信路で誤りが混入する(例:0→1,1→0のように誤る))
- 元のデータに対して冗長データを追加し,雑音に対する耐性をつける
情報理論における確率の役割
情報理論では,情報の"符号化"の可能性と限界について,定量的に明らかにすることをその主な目標としている.
⇒現実の情報源や通信路を"確率モデル"として抽象化し,その確率モデルの数理的な性質を調べる.
確率の基礎
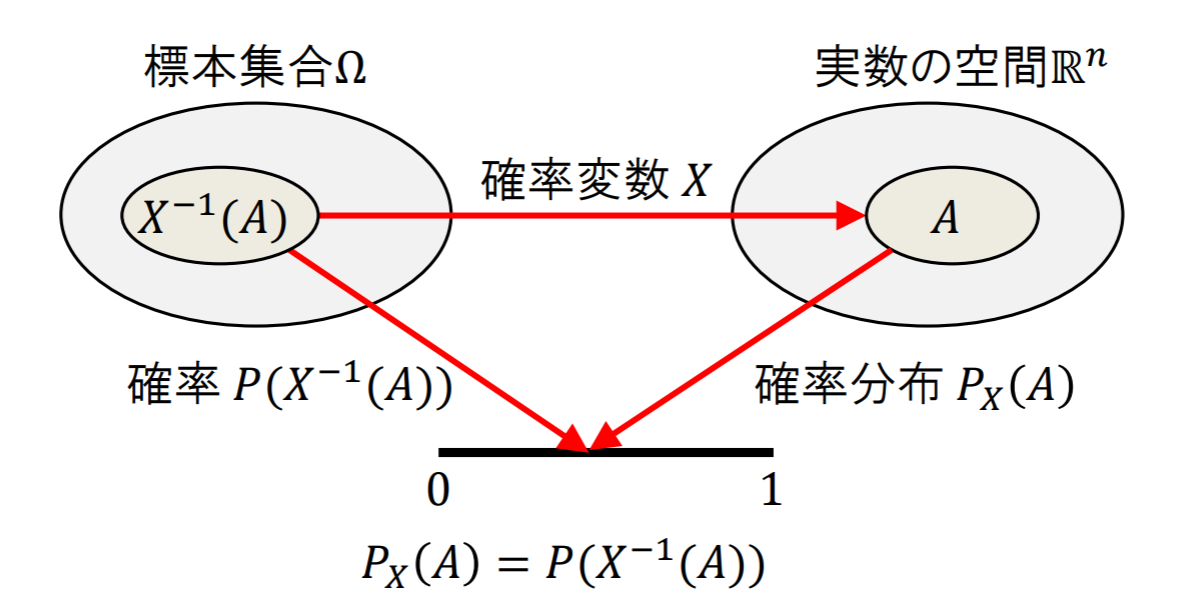
確率変数と確率分布
- 確率変数Xとは,標本集合Ωから実数空間R(Rn)への(確率と関連付いた)写像である
- 確率変数Xがある値になる確率を確率分布という
サイコロを振る,あるいはコインを投げる,等のように結果の集合は分かっているが,実際に行動するまでどの結果が得られるかは事前に分からない.このような行動を「確率的試行」と呼ぶ.
- 変数X: ある確率的試行の結果 (確率変数)
- χ:Xの取りうる範囲 = 標本空間
- x:実際の試行で確率変数がとった値 (標本値,実現値)
- Pr(X=x):確率変数Xがxを取る確率
- 定義: 次の性質を満たす量Pr(X=x)を確率と呼ぶ
- ∀x∈χ,0≤Pr(X=x)≤1
- Σx∈χPr(X=x)=1
Xに関するn個の事象A1,A2,...,Anを考える.このと
きAi∩Aj=ϕ(∀i=j)であれば
Pr(∪i=1nAi)=i=1∑nPr(Ai)
が成り立つ.
条件付き確率と独立性
P(A)>0のとき,
P(B ∣ A)=P(A)P(A∩B)
を,事象Aが起こったもとでの事象Bの条件付き確率と定義する.
このとき,明らかに次式が成り立つ
P(A∩B)=P(A)P(B ∣ A)
事象Bの起こる確率が事象Aの生起に無関係な場合,すなわち
P(B ∣ A)=P(B)
が成り立つとき,事象Aと事象Bは独立であるという.
このとき,明らかに次式が成り立つ
P(B ∣ A)=P(A)P(B)
情報量とエントロピー
情報量
情報には量がある
- 確率が高いことを知らされても,そのニュースは価値が低い
確率1の結果が知らされる⇒得られる情報量は0
- 確率が低いことを知らされたら,そのニュースは価値が高い

確率が0に近い事柄を知らされる⇒情報量は大!
一つの結果を知ったときの情報量
確率pの事象の生起を知ったときに得られる情報量をI(p)とするとI(p)は次のような性質を満たすべき
- I(p)は0<p≤1で単調減少な関数である
- 確率p1,p2で起こる二つの互いに独立な事象が同時に起こる確率p1,p2についてI(p1,p2)=I(p1)+I(p2)
- I(p)は0<p≤1で連続な関数である
これらを満たす関数I(p)は
I(p)=−logap
という形しかありえない(ただしa>1)
情報量の定義
確率pで生起する事象が起きたことを知ったときに得られる情報I(p)を自己情報量と呼び
I(p)=−logap
と定義する.ただし,aはa>1の定数とする
- a=2の場合,単位はビット(bit)という(確率1/2で生じる結果を知ったときの情報量 = 1 [bit])
- 自然対数で計るときはナット(nat) 1 nat ≈ 1.443 bit
- 10を底とする対数で計るときはハートレー(Hartley)
- もしくはディット(dit)またはデシット(decit) 1 Hartley ≈ 3.322 bit
平均情報量
M個の互いに排反な事象a1,a2,⋯,aMが起こる確率をp1,p2,⋯,pMとする(ただし,p1+p2+⋯+pM=1).このうち1つの事象が起こったことを知ったときに得る情報量は−log2piであるから,これを平均した期待値Iは
I=p1(log2p1)+p2(log2p2)+⋯+pM(log2pM)=−i=1∑Mpilog2pi
となる.これを平均情報量(単位はビット)という
エントロピー
確率変数Xがとりうる値がx1,x2,⋯,xMとし,Xがそれぞれの値をとる確率がp1,p2,⋯,pM(ただし,p1+p2+⋯+pM=1)であるとき,確率変数Xのエントロピーを
H(X)=−i=1∑Mpilog2pi
ビットと定義する.
エントロピーの性質
M個の値をとる確率変数XのエントロピーH(X)は次の性質を満たす.
- 0≤H(X)≤log2M
- H(X)が最小値0となるのは,ある値をとる確率が1で,他のM−1個の値をとる確率がすべて0のときに限る.すなわち,Xのとる値が初めから確定している場合のみである.
- H(X)が最大値log2Mとなるのは,M個の値がすべて1/Mで等しい場合に限る
エントロピー関数
エントロピー関数とは,0≤x≤1で定義される関数
H(X)=−xlog2x−(1−x)log2(1−x)
のことをいう.

結合エントロピー
二つの情報を一度に聞いたときの情報量は?果たしてH(X,Y)=H(X)+H(Y)だろうか?
二つの確率変数X,Yを考える.Xはx1,x2,⋯,xMXの値をとり,Yはy1,y2,⋯,yMYの値をとるものとする.確率変数の組(X,Y)の値が(x,y)となる結合確率分布をP(x,y)と書く.
確率変数XとYの結合エントロピーH(X,Y)は
H(X,Y)=−i=1∑MXj=1∑MYP(xi,yj)log2P(xi,yj)
により定義される.これを結合エントロピーと呼ぶ.ただし,{x1,x2,⋯,xMX}および{y1,y2,⋯,yMY}は,それぞれXとYが取りうる値の集合とする.
例題: ある日の天気Xとコンビニのアイスクリームの売上高Yの結合確率分布P(x,y)
| P(x,y) |
Y(1万円以上) |
Y(1万円未満) |
P(x) |
| X(晴) |
0.5 |
0.1 |
0.6 |
| X(雨) |
0.2 |
0.2 |
0.4 |
| P(y) |
0.7 |
0.3 |
- |
(X,Y)の結合エントロピーは,
H(X,Y)=−0.5×log20.5−0.1×log20.1−0.2×log20.2−0.2×log20.2≈1.76(bit)
結合エントロピーの性質
確率変数XとYの結合エントロピーH(X,Y)に対し,
0≤H(X,Y)≤H(X)+H(Y)
が成り立つ.またH(X,Y)=H(X)+H(Y)となるのは,XとYが独立のときのみである.
条件付きエントロピー
関連情報を事前に知っていた時の情報量は?

関連する情報が既知だと,驚きは少なくなる ⇒ エントロピーは小さくなっているはず!
確率変数Yで条件を付けたXの条件付きエントロピーH(X ∣ Y)は,
H(X ∣ Y)=−j=1∑MYP(yj)i=1∑MXP(xi ∣ yj)log2P(xi ∣ yj)
により定義される.ただし,{x1,x2,⋯,xMX}および{y1,y2,⋯,yMY}は,それぞれXとYが取りうる値の集合とする.
結合エントロピーと条件付きエントロピーの関係
{x1,x2,⋯,xMX}および{y1,y2,⋯,yMY}をとりうる値の集合とする確率変数XおよびYに関し,以下が成り立つ.
- H(X ∣ Y)=−∑i=1MX∑j=1MYP(xi,yj)log2P(xi ∣ yj)
- H(X,Y)=H(X)+H(Y ∣ X)=H(Y)+H(X ∣ Y)
- 0≤H(X ∣ Y)≤H(X)
- H(X ∣ Y)=H(X)はXとYが独立の時のみ成立
- 0≤H(Y ∣ X)≤H(Y)
- H(Y ∣ X)=H(Y)はXとYが独立の時のみ成立
別の情報を得ると,エントロピーは変化しないか減少する
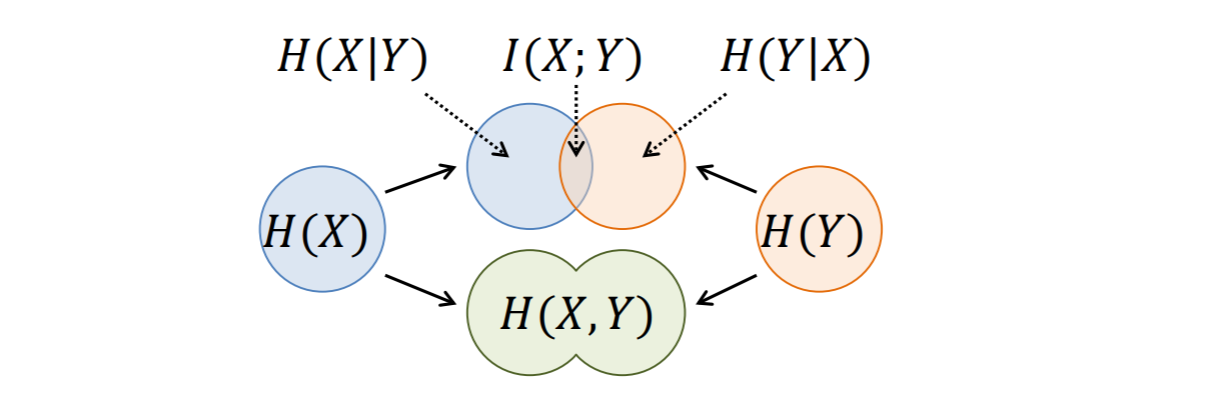
相互情報量の定義
I(X;Y)=H(X)−H(X ∣ Y)
と,先ほどの結合エントロピーと条件付きエントロピーの関係
H(X,Y)=H(X)+H(Y ∣ X)=H(Y)+H(X ∣ Y)
から,
I(X;Y)=H(X)−H(X ∣ Y)=H(X)+H(Y)−H(X,Y)=H(Y)−H(Y ∣ X)=I(Y;X)=i∑j∑p(xi,yj)logp(xi)p(yj)p(xi,yj)
が成り立つ.
- I(X;Y)の範囲は0≤I(X;Y)≤min{H(X),H(Y)}
まとめ
- 情報量
- 確率pで起こる事象の自己情報量I(p)=−logap
- エントロピー
- 確率変数Xの平均情報量H(X)=−∑i=1Mpilog2pi
- エントロピーの性質
- 0≤H(X)≤log2M
- 結合エントロピーH(X,Y)
- H(X,Y)=−∑i=1MX∑j=1MYP(xi,yj)log2P(xi,yj)
- H(X,Y)=H(X)+H(Y ∣ X)=H(Y)+H(X ∣ Y)
- XとYが独立のとき: H(X,Y)=H(X)+H(Y)
- 条件付きエントロピーH(X∣Y),H(Y∣X)
- H(X ∣ Y)=−∑j=1MYP(yj)∑i=1MXP(xi ∣ yj)log2P(xi ∣ yj)
- H(X,Y)=H(X)+H(Y ∣ X)=H(Y)+H(X ∣ Y)
- XとYが独立のとき:
- H(X ∣ Y)=H(X)
- H(Y ∣ X)=H(Y)
- 相互情報量I(X;Y)
- I(X;Y)=H(X)−H(X ∣ Y)
- I(X;Y)=H(X)+H(Y)−H(X,Y)
- I(X;Y)=H(Y)−H(Y ∣ X)
- I(X;Y)=I(Y;X)
例題(3.1)
X={x1,x2},Y={y1,y2}に対し以下の表に示すような同時確率に従う確率変数PXY(xi,yj)を考える.
| X/Y |
y1 |
y2 |
| x1 |
81 |
83 |
| x2 |
82 |
82 |
(1) エントロピーH(X),H(Y)を求めよ
XとYの周辺確率をそれぞれPxとPyとすれば,Px(x1)=21,Px(x2)=21,Py(y1)=83,Py(y2)=85となる.従って,
H(X)H(Y)=−21log21−21log21=1=−83log83−85log85≃0.9544
(2) 条件付きエントロピーH(X∣Y),H(Y∣X)を求めよ
P(X∣Y)P(Y∣X)=−81log8381−83log8583−82log8382−82log8582≃0.9512=−81log8481−82log8482−83log8483−82log8482≃0.9056
(3) 同時エントロピーH(X,Y)を求めよ
エントロピーの加法性より,
H(X,Y)=H(X)+H(Y∣X)≃1+0.9056≃1.9056
(4) 相互情報量I(X;Y)を求めよ
相互情報量とエントロピーの関係より,
I(X;Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)≃0.0488
情報源のモデル
情報源の数学モデル
通報集合 (message set): 伝送したい情報の集合.名前のついた離散的な概念.{表,裏},{晴,雨,曇,雪},{a,b,c,...,z}等.M個の要素を持つ集合として次の様に書く:
A={a1,a2,...,aM}
情報源 (source): 通報を定められた時点ごとに確率的に出力する.特に通報集合の大きさ(要素の個数)がMのときM元情報源という.
このとき時点iの情報源の出力をXi(i=1,2,...)で表す.Xiはa1,a2,...,aMのいずれかであるが,どれであるかは確率的に定まる,すなわち確率変数である.
結合確率分布(Joint distribution)
時点1からnまでの出力
X1,X2,...,Xn
を考えることが多い(これを長さnの情報源系列などという).この情報源系列の統計的性質はX1,X2,...,Xnの結合確率分布(同時確率分布ともいう)
PX1X2...Xn(x1,x2,...,xn)=[X1=x1,X2=x2,...,Xn=xnとなる(結合)確率]
で完全に定まる.PX1X2...Xn(x1,x2,...,xn)は省略してP(x1,x2,...,xn)と書かれることもある.
2元情報源{0,1},n=3の例
X1,X2,X3の結合確率分布
| x1 |
x2 |
x3 |
PX1X2X3(x1,x2,x3) |
| 0 |
0 |
0 |
0.648 |
| 0 |
0 |
1 |
0.072 |
| 0 |
1 |
0 |
0.032 |
| 0 |
1 |
1 |
0.048 |
| 1 |
0 |
0 |
0.072 |
| 1 |
0 |
1 |
0.008 |
| 1 |
1 |
0 |
0.048 |
| 1 |
1 |
1 |
0.072 |
一般に,結合確率P(x1,x2,⋅⋅⋅,xn)からX1の確率 P(x1)を求めるには
P(x1)=x2∈A∑...xn∈A∑P(x1,x2,...,xn)
を計算すればよい.これを周辺確率という.(周辺確率とは,ただ一つだけの事象が起きる確率である.)
P(x1,x2)なども同様に求められる.
P(x1,x2)=x3∈A∑...xn∈A∑P(x1,x2,...,xn)
となる.
結合確率分布が与えられれば,これに基づき様々な計算を行うことができる.例えばX1=0となる確率PX1(0)は
PX1(0)=x2=0∑1x3=0∑1PX1X2X3(0,x2,x3)=0.648+0.072+0.032+0.048=0.8
となることがわかる.もちろんPX1(1)=1−PX1(0)=0.2である.
周辺確率(Marginal distribution)
- 結合確率分布が与えられれば各時点の(周辺)確率分布を求めることができる.
- しかしながらnが大きくなると結合確率の数は爆発的に増加していく(その数はMn).これら全てを考えることは現実的ではない.
- 通常は確率分布にある制約を課した情報源を考えることが多い.
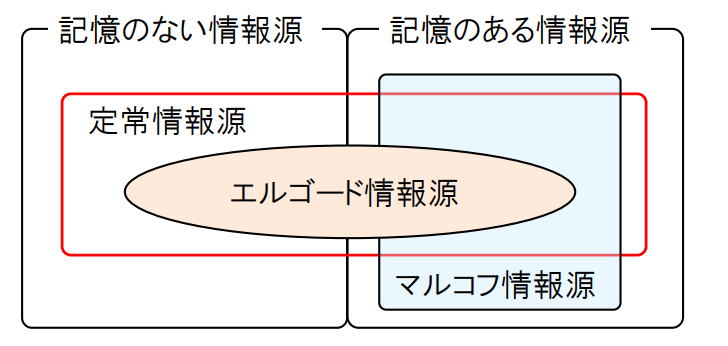
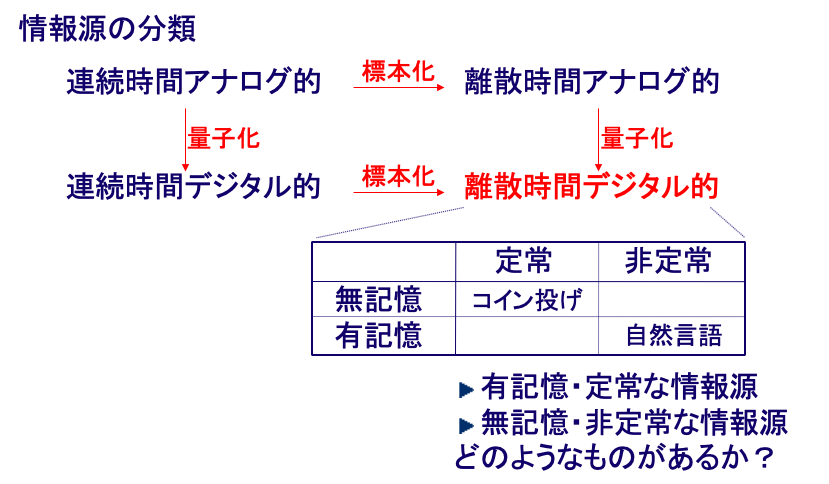
情報源の分類
定常無記憶情報源 (stationary memoryless source):各時点iにおける通報の発生が同一の確率分布に従う情報源. i.i.d. (independently and identically distributed)情報源ともいう.任意のnについて
PX1X2...Xn(x1,x2,...,xn)=i=1∏nPX(xi)
と書ける.この性質によりnが大きくなり通報の数が爆発的に増加しても,その結合確率は簡単な計算により求めることができる.
定常無記憶情報源は最も簡単な情報源のモデルである. 一方現実の情報源は記憶のある情報源が多いであろう. 例えば英文を発生する情報源を考えると各時点におけるアルファベットの出現確率は独立ではない. たとえばTが現れればその次にはHの出現する確率が他の場合よりも高くなる. また,QのあとにはUの現れる確率が著しく高くなる. このように連続して発生する文字の間には相関がみられ, 独立ではない.
しかしながら, 記憶のない定常情報源を考えることは, より複雑な情報源を扱う際の基本となる. この意味で極めて重要である.
確率過程
- 確率変数の列X1,X2,⋯,Xn,Xi∈A
- 情報源記号A
(x1,x2,⋯,xn)∈Anに対して同時確率を次式で定める.
P((X1,X2,⋯,Xn)=(x1,x2,⋯,xn))=P(x1,x2,⋯,xn)
このような確率変数の列を確率過程と呼ぶ.
例: 10回のコイン投げ
A={0,1}(0:表,1:裏),P(Xi=0)=21,P(Xi=1)=21とし,コイン投げの表裏は各時点で独立が決まる.
P((X1,X2,⋯,X10)=P(X1=x1)P(X2=x2)⋯P(X10=x10)=(21)10
定常情報源
確率変数列の同時確率が時刻のシフトに対して変化しないとき, すなわち任意の正整数n,kならびに(x1,x2,⋯,xn)∈Anに対して
P(X1=x1,X2=x2,⋯,Xn=xn)=P(X1+k=x1,X2+k=x2,⋯,Xn+k=xn)
が成り立つとき, この情報源を「定常である」あるいは「定常情報源」であると呼ぶ.
- 系列x1,x2,⋯,xnの発生する確率が時刻に応じて変化しないことを意味する.
定常無記憶情報源
コイン投げのように, 記号Aの値をとる確率変数の列X1,X2,⋯,Xnが互いに独立で, 同一の確率分布Qにしたがう場合
P(X1=x1,X2=x2,⋯,Xn=xn)=Q(x1)Q(x2)⋯Q(xn)
が成り立つとき, この情報源を「定常情報無記憶源」であると呼ぶ.
- Xi=xとなる確率は時刻によらずQ(x)のみによって決まる
- それ以前の系列X1,X2,⋯,Xkには依存しない(右辺も各時点のxiのみによって決まる)
- 定常情報無記憶源は「定常」である
マルコフ情報源
過去に出現したアルファベットに依存して,いま出現するアルファベットの確率が決まる. このような情報源をマルコフ (Andrei Andreyevich Markov, 1856-1922)情報源という.
任意の正整数nに対し, 記号Aの値をとる確率変数列X1,X2,⋯,Xnが全ての (x1,x2,⋯,xn)∈An について
P(Xn=xn∣Xn−1=xn−1,⋯,X1=x1)=P(Xn=xn∣Xn−1=xn−1)
を満足するとき, この情報源をマルコフ情報源という. さらに任意の正整数nならびに任意のx,x′∈Aに対して,
P(Xn=x)=P(X1=x)P(Xn=x′∣Xn−1=x)=P(X2=x′∣X1=x)
が成り立つとき, この情報源を定常マルコフ情報源という.
マルコフ情報源では同時確率は条件付き確率の積で表すことができる.
例: 2元定常マルコフ情報源
記号A={0,1}をもつ2元のマルコフ情報源を考える.ある記号が出現したときに次の記号が出現する確率を以下のように定める.
P(0∣0)P(0∣1)=1−a=bP(1∣0)P(1∣1)=a=1−b
また時刻n=1における確率変数X1の分布を
P(X1=0)=wP(X1=1)=1−w
と定める.以上によって定めた確率から確率変数の列X1,X2,⋯,Xn,Xi∈Aが発生する.
状態遷移図
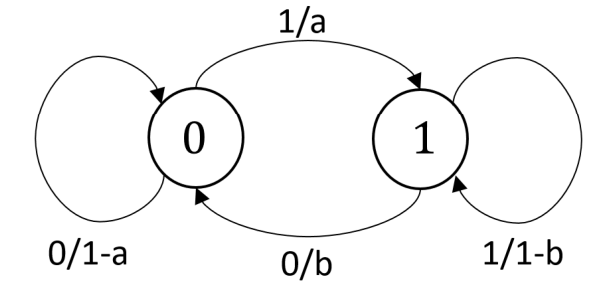
- 数字の○は状態とその番号を表す
- 矢印は状態から状態への遷移を表す
- 矢印のラベル’0/a’は記号0を確率aで出力
初期状態と定常確率分布
最初の時点の確率分布(初期状態の分布)P(X1)=wを定める.
- 2状態の場合ではP(X1=0)=w,P(X1=1)=1−w
- P(X1=0)=P(Xn=0)=w,P(X1=1)=P(Xn=1)=1−wがn=2,3,⋯で成りたつ必要ある.
- 以下のようにP(X1=0)=wを導出すればよい.
P(X2=0)=r=0∑1P(X2=0,X1=r)=r=0∑1P(X2=0∣X1=r)P(X1=r)=(1−a)w+b(1−w)
P(X2=0)=wを利用するとw=a+bbが得られる.このようなP(X1=0)=a+bb,P(X1=1)=a+baを定常確率分布と呼ぶ.
非定常マルコフ情報源
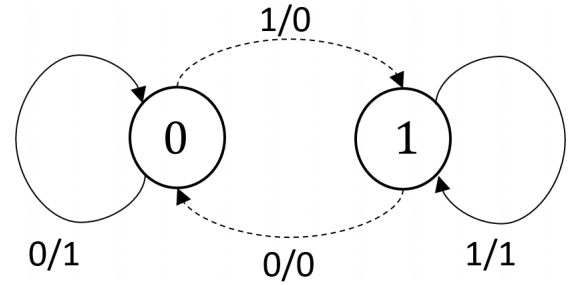
- a=b=0だとP(X1=0)=wが一意に定まらない
- 常に状態0もしくは状態1に滞在し続ける
まとめ
- 情報源に記憶がない(memoryless): ある時刻の通報が, それ以前の通報とは無関係に選ばれる.
- 定常(stationary)情報源: 時刻をシフトしても, 通報の確率分布が変わらない情報源
遷移確率行列(∏)
N個の状態s0,s1,⋯,sN−1を持つ正規マルコフ情報源を考える.状態遷移の仕方は,状態siにあるとき,次の時点で状態sjに遷移する確率pi,j=P(sj∣si)により決まる.これを遷移確率という.遷移確率pi,jを(i,j)要素とするN×N行列を遷移確率行列と呼ぶ.(状態数N個,行ごとに総合が1)
∏=⎝⎜⎜⎛p0,0⋮pN−1,0⋯⋱⋯p0,N−1⋮pN−1,N−1⎠⎟⎟⎞
遷移確率行列によるt時点後の遷移確率


正規マルコフ情報源の定常分布
十分時間が経過すれば,初期分布がどうであれ,状態分布は定常的な確率分布(定常分布)に落ち着く.
正規マルコフ情報源が落ち着く定常分布を
w=(w0,w1,⋯,wN−1)
とする.wiは確率なので,当然ながら
w0+w1+⋯+wN−1=1
ある時点の状態分布が定常的でwであるとすれば,次の時点の状態分布もwでなければならないので,wは
w∏=w
を満たさなければならない.
正規マルコフ情報源の遷移確率行列∏に対しては,この式を満たすwが唯一存在し,極限分布と一致する.


情報源符号
情報源符号化
- いかに効率よく圧縮するか
- データを小さくして保持できるか = データ圧縮
情報源符号の例(m = 4)
| ai |
PX(ai) |
C1 |
C2 |
| a1 |
0.6 |
00 |
0 |
| a2 |
0.25 |
01 |
10 |
| a3 |
0.1 |
10 |
110 |
| a4 |
0.05 |
11 |
1110 |
- 符号化: 記号aiを対応する符号語へ変換する.
- 復号化: 符号語から元の通報へ復元する.
- 符号C1: 符号語は{00,01,10,11}
- 符号C2: 符号語は{0,10,110,1110}
- 符号C1,C2どちらが良い? ⇒ 平均符号語長で符合を評価する.
平均符号語長
L(C)=E[l(X)]=i=1∑mPX(ai)l(ai)
l(ai):通報aiから得られる符号語の符号語長とする.
例(1)
符号C1,C2について平均符号語長を計算しなさい.
| ai |
C1 |
l(ai) |
PX(ai) |
| a1 |
00 |
2 |
0.6 |
| a2 |
01 |
2 |
0.25 |
| a3 |
10 |
2 |
0.1 |
| a4 |
11 |
2 |
0.05 |
L(C1)=2.00(bits/symbol)
| ai |
C2 |
l(ai) |
PX(ai) |
| a1 |
0 |
1 |
0.6 |
| a2 |
10 |
2 |
0.25 |
| a3 |
110 |
3 |
0.1 |
| a4 |
1110 |
4 |
0.05 |
L(C2)=1.60(bits/symbol)
例(2)
| ai |
PX(ai) |
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
| a1 |
0.6 |
00 |
0 |
0 |
0 |
0 |
0 |
| a2 |
0.25 |
01 |
10 |
10 |
01 |
10 |
10 |
| a3 |
0.1 |
10 |
110 |
110 |
011 |
11 |
11 |
| a4 |
0.05 |
11 |
1110 |
111 |
111 |
01 |
0 |
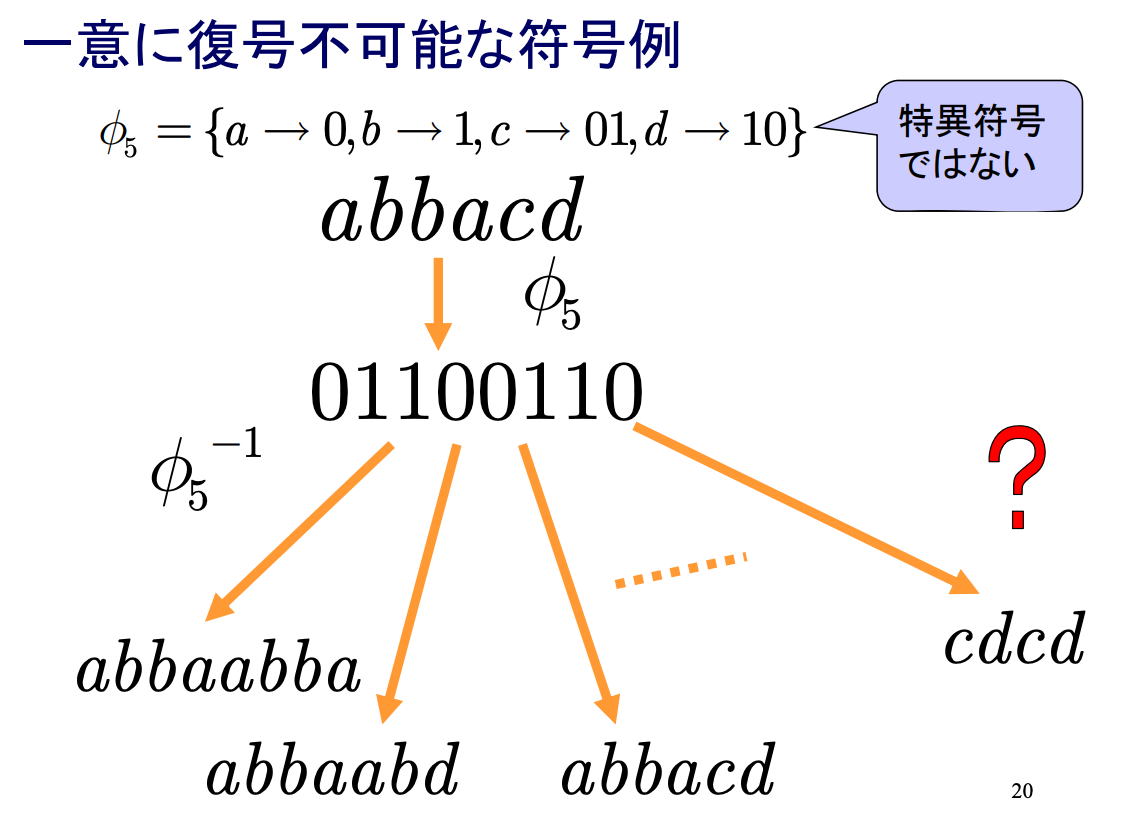
符号C1,⋯,C6についてそれぞれ復号して元通りに復元できるか?

情報源符号の種類
- 非特異符号: 異なる記号には異なる符号語を割り当てる.
- 一意復号可能符号: 対応する符号語から記号へ符号語の列が一意に復号できる符号.
- 語頭符号(または自己区切り符号): どの符号語も他の符号語の先頭部分と一致しない.

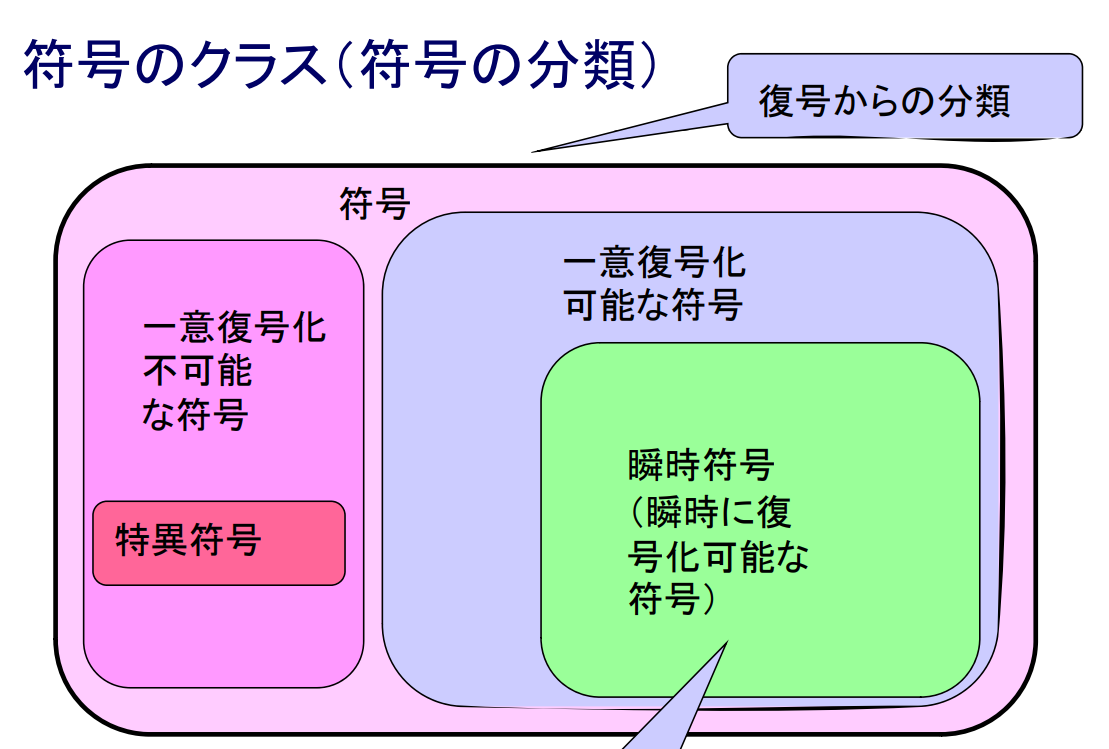
- 符号の包含関係:非特異符号 ⊇ 一意復号可能符号 ⊇ 語頭符号
語頭(prefix)
符号語Ci=x1ix2i⋯xlii∈Cに対して,x1ix2i⋯xji1≤j<liを(符号語ciの)語頭という.
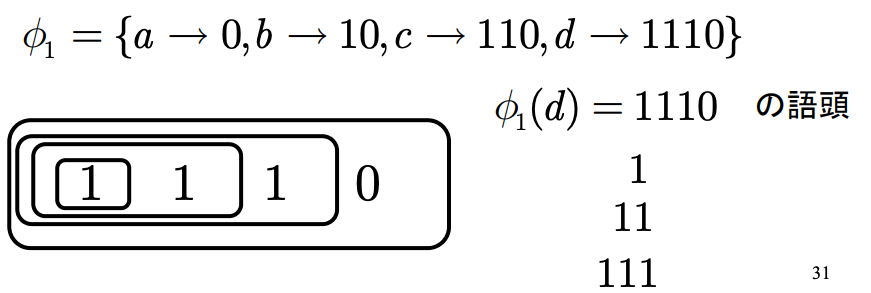
情報源符号化の満たすべき条件
情報源符号化の満たすべき条件:
- 一意復号可能であること, 瞬時符号が望ましい.
- 平均符号語長が短いこと.
- 瞬時符号でないと,n文字目以降を受け取るまで,最初の復号結果すら確定できない ⇒ 復号器内に大きなバッファが必要,大きな復号遅延の発生
- これら条件から上の6つの符号の中ではC3が望ましい.
瞬時復号可能性と語頭条件
符号Cが瞬時復号可能となる ⇔ Cのどの符号語も,他の符号語の語頭とならないこと(語頭条件, prefix condition)
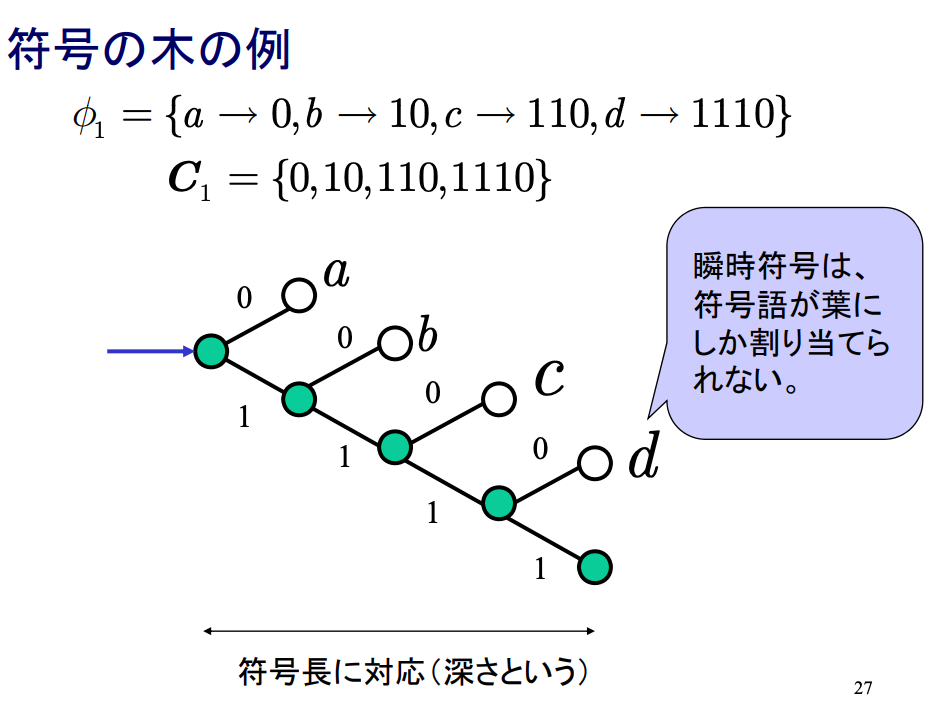
符号の木
接点(符号記号の区切り),枝(符号記号)として,各接点から2分岐(r元の場合はr分岐)させた木を符号の木という.各符号語は根から対応する接点までの経路上の符号記号の系列として求められる.
語頭条件は木で表せる
- 各符号語から枝が伸びていない = 語頭条件を満たす
- 逆に語頭条件を満たさないのは,符号語にあたる接点からさらに枝が伸びている場合
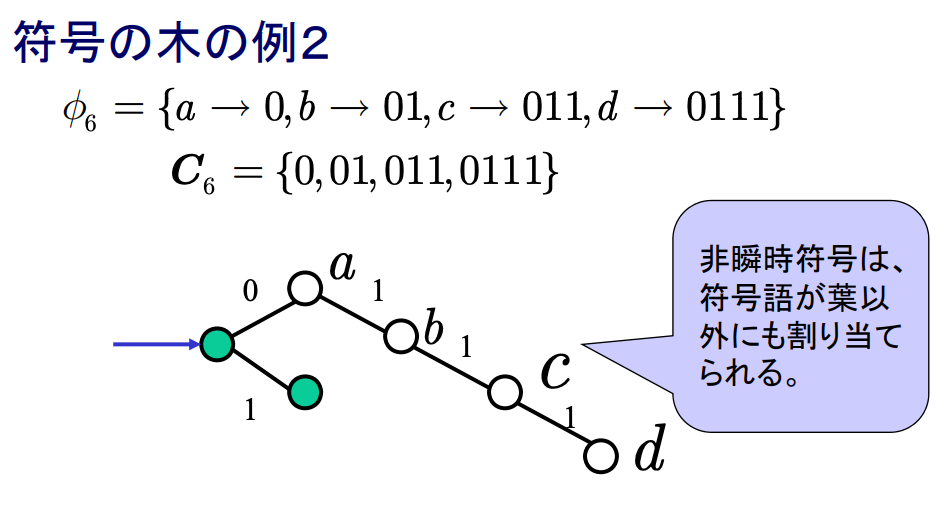
瞬時符号であるための必要十分条件:
- 符号の木として表現したとき全ての符号語が葉に割り当てられていることである.
- 各符号が他の符号の語頭になっていない.
クラフトの不等式(Kraft’s inequality)
情報源符号化の目標:
- 平均符号語長が最小
- 語頭符号→クラフトの不等式を満足する
符号語長の集合がL={l1,12,⋯,ln}であるようなr元瞬時符号C={c1,c2,⋯,cn}が存在するための必要十分条件は,次式が成り立つことである.
i=1∑nr−li≤1
この不等式をクラフトの不等式という.
2元符号({0,1}の符号化)の場合のクラフトの不等式
i=1∑n2−li≤1
注意:
- 定理では,ある符号の符号語長がクラフトの不等式を満たすからといって,その符号が瞬時符号であることを保証している訳ではない
- 保証していることは,クラフトの不等式を満たす符号語長であれば,そこから瞬時符号が作れる
例
符号C3,C4,C5,C6についてクラフトの不等式が成立するか確認せよ.

平均符号語長の限界
平均符号語長の理論的な下限
情報源が与えられたとき,一意復号可能性を保証した上で,情報源符号化によってどこまで情報源記号の平均符号長を小さくできるか?ここではその下限を与える情報源符号化定理を紹介する. すなわち, 平均符号語長をエントロピーより小さくできないことを示す.
平均符号長の限界定理
定常分布を持つ情報源Sの各情報源記号を一意復号可能なr元符号に符号化したとき,その平均符号長Lは
log2rH1(S)≤L
を満たす.また,平均符号長Lが,
L<log2rH1(S)+1
となるr元瞬時符合を作ることができる.
- 1記号毎でなく,いくつかの記号をまとめて符号語を割り当てることで,効率よく符号化できないだろうか?
情報源符号化定理(シャノンの第一基本定理)
情報源Sは,任意の一意復号可能なr元符号で符号化する場合,その平均符号長Lは,
log2rH(S)≤L
を満たす.また,任意の正数ϵ>0について平均符号長Lが,
L<log2rH(S)+ϵ
となるr元瞬時符合を作ることができる.(2元符号の場合,log2r=1)
- どんなに工夫しても,平均符号長LはエントロピーH(S)までしか改善できない(でもがんばれば,そこまではできる)
シャノンの補助定理
q1,q2,⋯,qmを次式を満たす任意の数とする.
i=1∑mqi=q1+q2+⋯+qm≤1
qi≥0(i=1,2,⋯,m)かつP(ai)=0の時はqi=0としておく.この時,
−i=1∑mP(ai)log2qi≥−i=1∑mP(ai)log2P(ai)
が成り立つ.等号の成立は,全てのi=1,2,⋯,mについてP(ai)=qiの時,またその時に限る.
情報源符号化逆定理
情報源アルファベットAの値を確率分布Pに従ってとる確率をXとする.この時,任意の語頭符号Cの平均符号語長L(C)をエントロピーH(X)より小さくすることはできません.すなわち,
L(C)≥H(X)
が成り立つ.等号成立条件は,記号xの符号語長l(x)に対して,2−l(x)=P(X)が全ての記号x∈Aについて成り立つとき.
Shannon 符号, Shannon-Fano 符号
Shannon 符号
記号x(生起確率P(x))の符号語長を
l(x)=⌈−log2P(x)⌉,x∈A
を満足するように符号化する.ただし,⌈.⌉は天井関数である.天井関数は実数 x に対して x 以上の最小の整数と定義される(例:⌈1.5⌉=2)
- 各記号aiを出現確率P(ai)の高い順に並べ替える
- 各記号aiの符号語は以下のように割り当てる
- 第(i−1)記号までに出現確率の和∑j=1i−1P(aj)を計算し,それを2進数に変換する
- 得られた2進数において小数点以下l(ai)桁の数を符号語にする
最良な符号
情報源逆符号化定理よりL(C)=H(X)となるためには
2−l(x)=P(x)⇒l(x)=−log2P(x)
を満足すれば良い(このような符号語長を持つ符号は最良符号と呼ぶ).−log2P(x)を理想符号語長と呼ぶが,−log2P(x)が常に整数となるとは限らないため,天井関数「.」によって符号語長を定める.
Shannon-Fano符号
- 各記号aiを出現確率P(ai)の高い順に並べ替え(ソートする)表を作成する.
- 表を上下に分割する.ただし,確率の和がほぼ半分になるようにする.それぞれにシンボル“0”,“1”を割り当てる.
- 分割した表をさらに,確率の和がほぼ半分になるように上下に分割する.それぞれにシンボル“0”,“1”を割り当てる.
- すべての表に含まれる記号が1つになるまで3.を繰り返す
- 各記号に対して分割する際に割り当てられた“0”または“1”からなる系列をその記号の符号語とする.
情報源のエントロピーレート
情報源Xの出力列を表す確率変数をX1,⋯,Xnとする.n記号まとめて語頭符号化したときの平均符号語長の最小値Ln∗は
n1H(X1,⋯,Xn)≤n1Ln∗≤n1H(X1,⋯,Xn)+n1
を満足する.さらに情報源Xが定常情報源のときは
n→∞limn1Ln∗=H(X)
が成り立つ.ここでH(X)は情報源Xのエントロピーレートを表す.
例題
| 記号 |
情報源1 |
情報源2 |
| ai |
P(ai) |
P(ai) |
| a1 |
0.25 |
0.25 |
| a2 |
0.125 |
0.25 |
| a3 |
0.5 |
0.25 |
| a4 |
0.125 |
0.25 |
(1)次の二つの情報源の2元エントロピーをそれぞれ求め, Shannon符号, Shannon-Fano符号をそれぞれ適用しなさい.
情報源1
H(X)=−0.25log20.25−0.125log20.125−0.5log20.5−0.125log20.125=1.75
情報源2
H(X)=−0.25log20.25−0.25log20.25−0.25log20.25−0.25log20.25=2

先排序,计算∑j=1i−1P(aj)后转成二进制,小数点后l(ai)位即对应的符号语

先排序,然后按照概率50来上下做分割线,线以上是0,线以下是1,然后再分线,直到只有1个记号为止
(2)情報源1に対して, その記号をソートをせずに符号化したとする. このとき各符号語を求め, ソートする場合との違いを検討しなさい.
だめの例:

a1とa3の符号語は同じく0であるから.
ハフマン符号とLZ符号
本章では
- 最小の平均符号語長を与える語頭符号であるハフマン符号の構成法について説明する
- 情報源の確率分布を予め知られなくても、符号化する系列長が長くなるにつれて、1記号あたりの平均符号語長がエントロピーに収束するLempel-Ziv(LZ)符号について説明する
効率良い具体的な情報源符号化方法:ハフマン符号
ハフマン符号は1記号ずつ符号化する際,その平均符号長を最小とする効率のよい符号のことである.
拡大情報源とブロック符号化
もっと近似度を上げるために,拡大情報源という手法を導入する.Sの連続するn個の情報源記号列を情報源記号とするqn元情報源をq元情報源Sのn次の拡大情報源Snという.Sはいまのところ記憶のない情報源であるとしているので,Sの連続するn個の出力は互いに独立であり,その結合確率分布は
P(x0,⋯,xn−1)=P(x0)⋯P(xn−1)
となる.
情報源Sのn次拡大情報源Snの1次エントロピーH1(Sn)については,
H1(Sn)=nH1(S)
が成り立つ.つまり,
n次に拡大された情報源の1次エントロピー:拡大される前のもとの情報源の1次エントロピーのn倍である.
拡大情報源の導入に対応してブロック符号化,つまり,
情報源から発生する記号をまとめて符号化する方法が導入される.
ブロック符号化をすることによって,平均符号長を情報源エントロピーに近づけることができる.
記号{a1,a2}を発生する情報源を考える.それぞれの発生確率が 0.8, 0.2 であるとする.
| ai,aj |
P(ai,aj) |
Fano の符号化 |
| a1,a1 |
0.64 |
0 |
| a1,a2 |
0.16 |
10 |
| a2,a1 |
0.16 |
110 |
| a2,a2 |
0.04 |
111 |
- このとき2個分まとめて2元符号化することで効率化できる場合がある
- 平均符号語長は1.452(bits/2symbol) ⇒ 0.726(bits/symbol)
この例のように一定個数の記号毎にまとめて符号化する方法をブロック符号化(block coding)といい,それにより構成される符号をブロック符号という
特に,もとの情報源Sに対し,n次拡大情報源Snを考え,その上の記号に対してハフマン符号化を行う方法を,ブロックハフマン符号化(block Huffman coding)と呼ぶ
ハフマン符号の最良性
次の定理は,ハフマン符号が最良の語頭符号であることを示す
定理: ハフマン符号の平均符号語長は最小である.
ハフマン符号の構成法
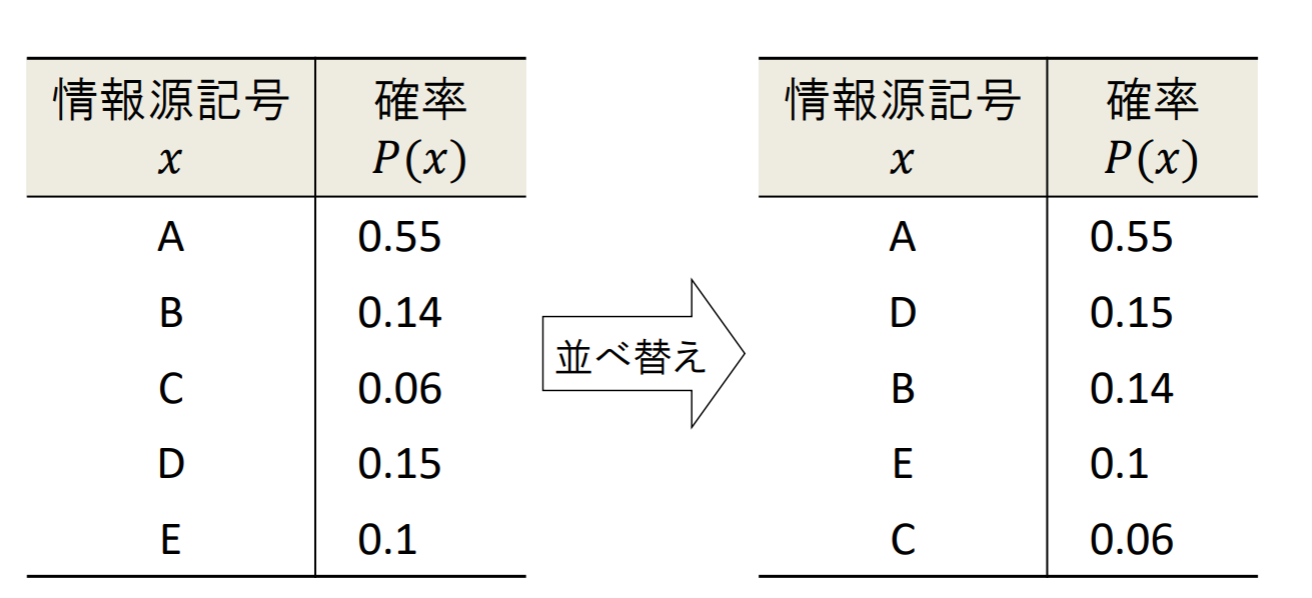
各記号が下の表で与えられる確率分布で出力されるような,記憶のない5元定常情報源を考える.
| 情報源記号x |
確率P(x) |
| A |
0.55 |
| B |
0.14 |
| C |
0.06 |
| D |
0.15 |
| E |
0.1 |
- まず初めに,確率の高い順に記号を並べ替える
- 各記号に対応する符号木の葉を作る葉には確率を添えて書いておく
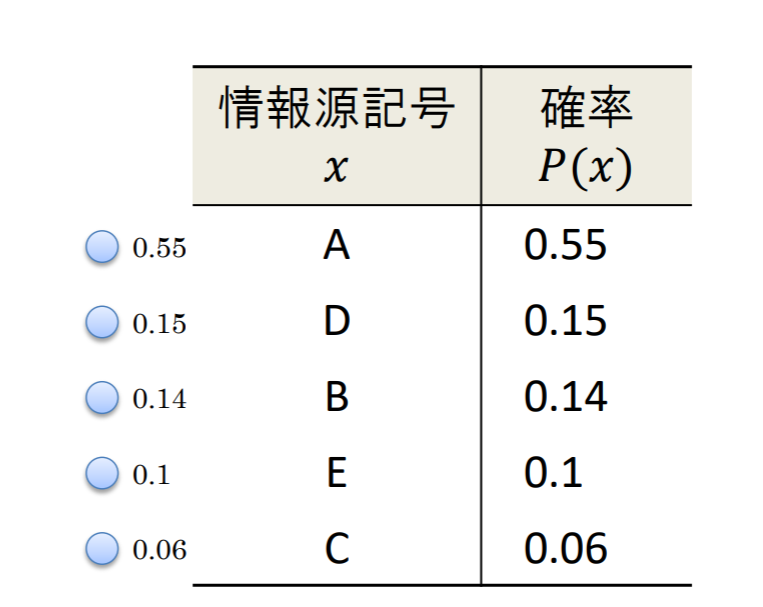
- 最も確率が小さい葉を二つ選び,それを集約するためのノードを新たに作って枝で結ぶ.そのノードを新しい葉として扱い,元の二つの葉の確率を足し合わせたものを添える
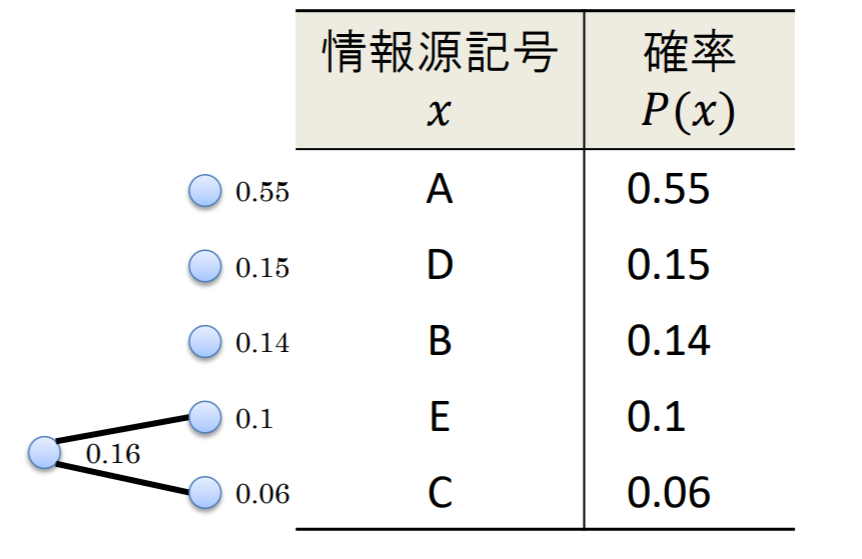
- STEP 2を,繰り返して符号木を作る.
- 各ノードから葉へ向かう方向の2本の枝に,0と1のラベルを割り当てる.
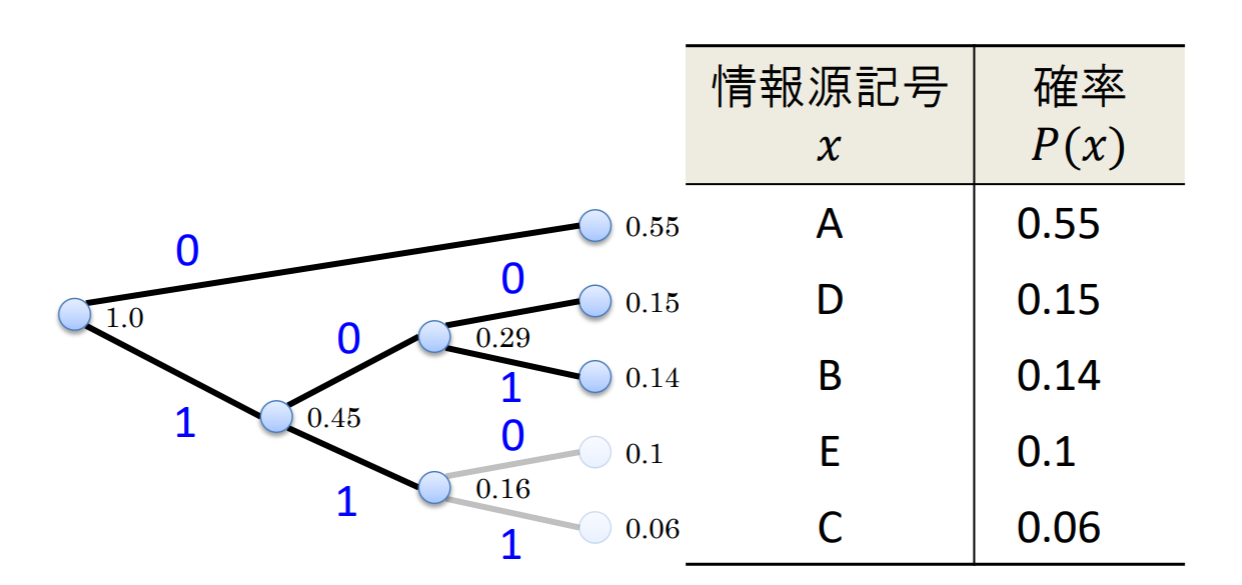
- 構築した符号木を用いて,根から各々の葉へ至るパスをなぞりながら,ラベルの列を符号語として記号に割り当てる
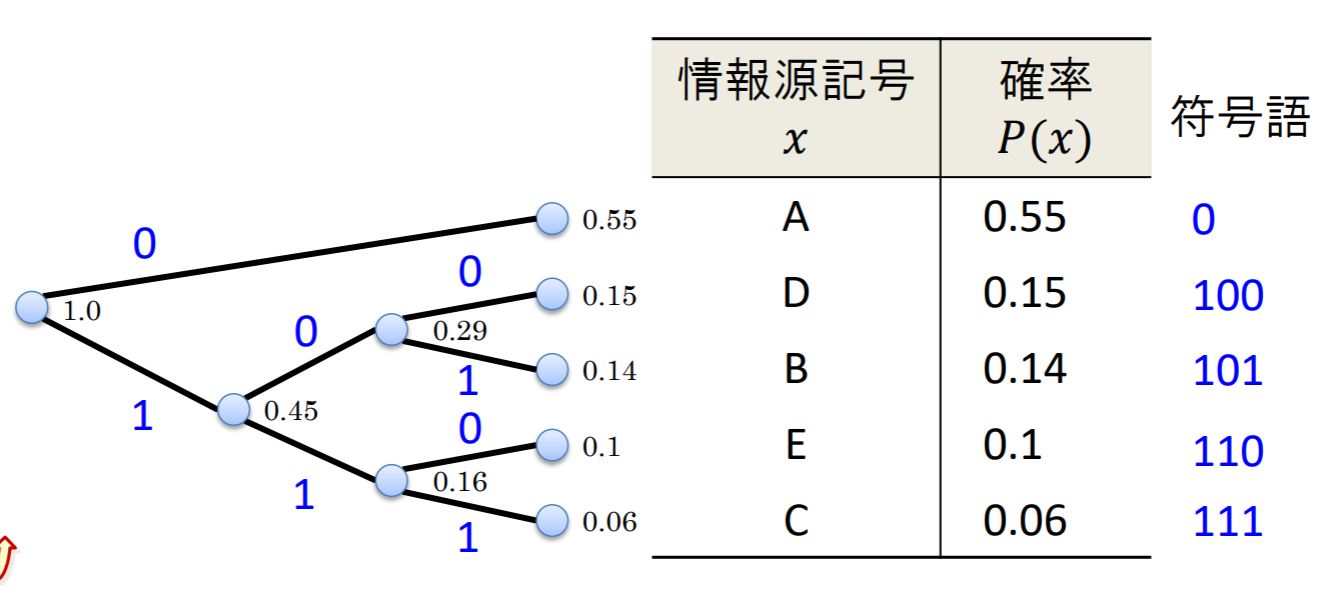
この処理過程において,符号語が符号の木の葉にだけ割り当てられているので,ハフマン符号は瞬時符号である.
例題(7.1)
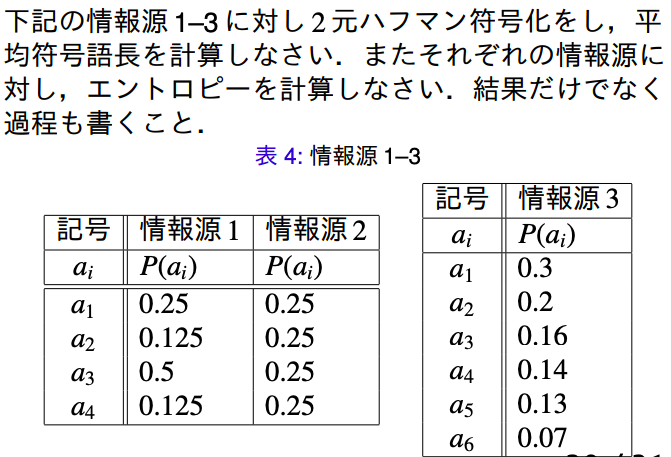
情報源1:
L(C1)H(X1)=0.5∗1+0.25∗2+0.125∗3+0.125∗3=1.75=−21log221−41log241−81log281−81log281=47
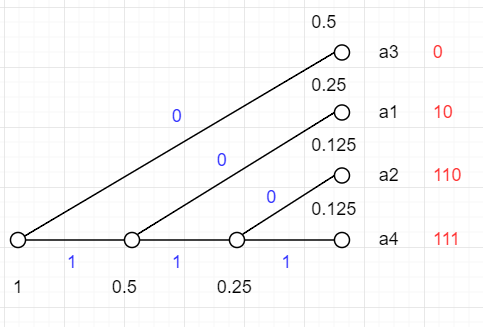
情報源2:
L(C2)H(X2)=0.5∗4=2=(−21log221)∗4=2
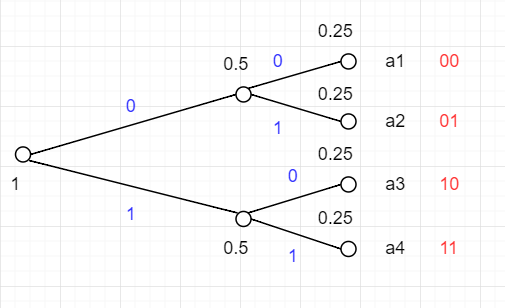
情報源3:
L(C3)H(X3)=0.3∗2+0.2∗2+0.16∗3+0.14∗3+0.13∗3+0.07∗3=2.5=−0.3log20.3−0.2log20.2−0.16log20.16−0.14log20.14−0.13log20.13−0.07log20.07≃2.4568
LZ符号
- ハフマン符号は最小の平均符号語長を与える
- しかし符号の構成には情報源の確率分布が必要
- 確率分布が未知でも符号を構成したい
- ユニバーサル符号としてLZ符号を扱う(正確にはLZ78 符号)
現実世界の通報系列は各通報の発生確率がわからないケースも多い
- 単純な解決法として,2スキャン方式がある
- 1回目のスキャンで各記号の発生確率を測定
- 2回目のスキャンで符号化
- ⇒ 符号化遅延の発生,対応表を添付する必要性が生じる
通報の発生確率が不明でも,効率よい符号化を実現する方式:
- LZ77法
- lha, gzip, zip, zoo 等の圧縮ツールで採用
- LZ78法
- compress, arc, stuffit等の圧縮ツールで採用
- LZW法
どのような情報源に対しても効率が良い ⇒ ユニバーサル符号化(universal coding)
LZ符号は増分分解と呼ばれる方法で系列を部分列に分解し,符号語を作る
増分分解
次の 2 つの性質を有するように系列を部分列に分解することを増分分解と呼ぶ.
- 最後の部分列を除いて,分解によって得られた部分列は全て異なっている
- 最後の部分列を除いて,分解によって得られた部分列は,その部分列より前に得られた部分列の後ろに 1 記号を付け加えたものになっている
必要なビット数
- k番目の部分列を表す順序対(i,x)
- 必要なビット数はLk=⌈log2k⌉+⌈log2∣A∣⌉
k番目の部分列を表す順序対(i,x)において,iの取りうる値は0からk−1までのk通り.また,xは⌈A⌉通りの値をとる.(eg.A={a,b,c})
従って,k番目の部分列を表すには,整数iを⌈log2k⌉ビットの2進数で表したものの後ろに,⌈log2∣A∣⌉ビットによる記号xの表示を続ければよい.これに必要なビット数Lkは
Lk=⌈log2k⌉+⌈log2∣A∣⌉
となり,Lkは符号化する系列にはよらず,情報源アルファベットが定まれば決まる.このようにして,全ての部分列を2進数で表したものを順に並べたものがLZ符号である.
LZ77方式
A. Lempel, J. Ziv により,1977年に提案された方式
通報の部分系列を,過去に出現したパターンとの最長一致により表現していく

アルゴリズム概要:
- 系列を先頭から動的にブロック化し、符号化する
- 一つのブロックを,(i,l,x)の3項組で表現
- 「 i 文字前から始まる長さ l の系列に x を追加したもの」
LZ77の符号化例
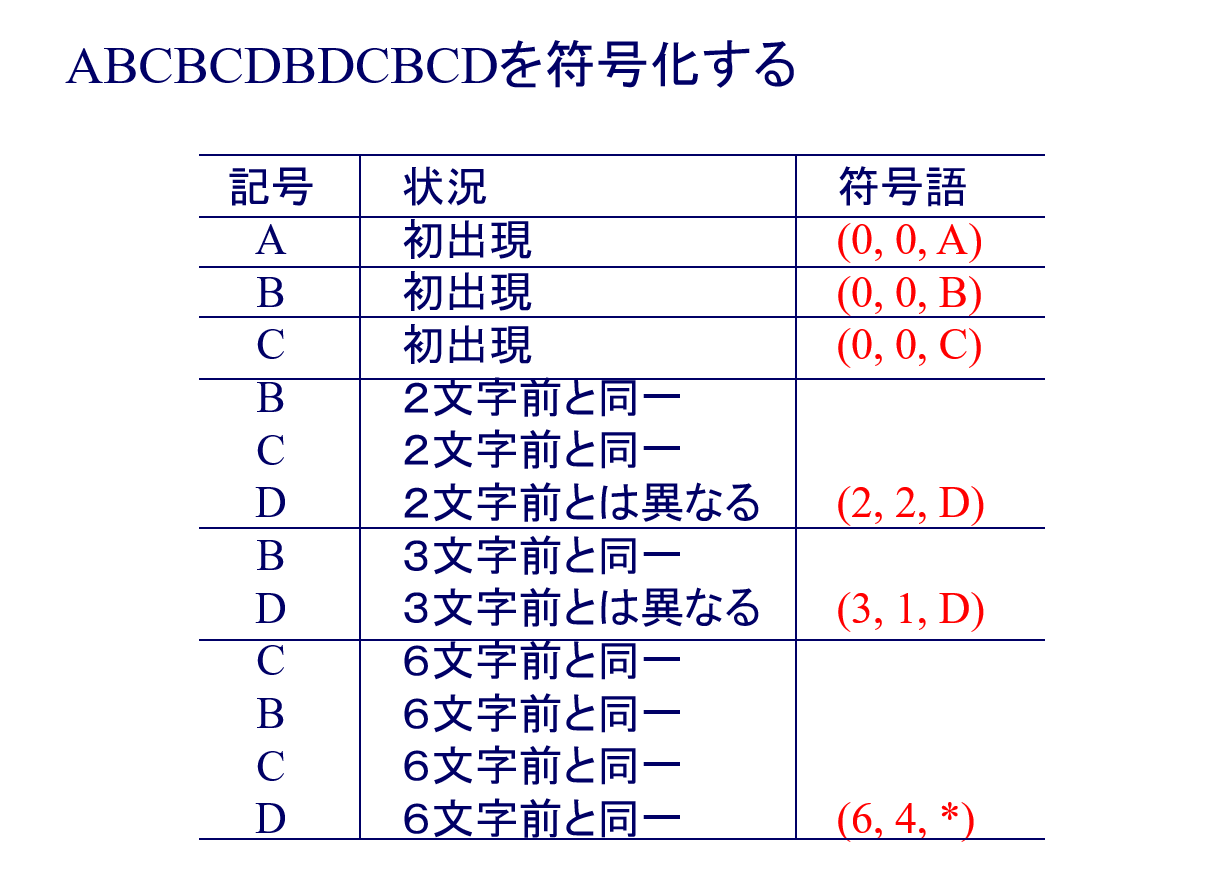
结合例题7.2一起看,分为Search Buffer和Look ahead buffer Buffer两部分,其根本就是不断的在匹配,然后不断往后继续匹配。(与前面第几个相同, 匹配几个字符, 新追加的字符)
例如图中例子,ABC进入Search Buffer后,再次出现BC发现是跟前面匹配的,再加一个D就不匹配了,于是标记为(2, 2, D),意思是2个字符前有2个字符(BC)是匹配的,再追加新字符D。
BCD进入Search Buffer后,再次出现B发现是跟前面匹配的,再加一个D就不匹配了,于是标记为(3, 1, D),意思是3个字符前有1个字符(B)是匹配的,再追加新字符D。
BCD进入Search Buffer后,再次出现CBCD发现是跟前面匹配的,于是标记为(6, 4, *),意思是6个字符前有4个字符(CBCD)是匹配的。
LZ77の復号例
(0, 0, A), (0, 0, B), (0, 0, C), (2, 2, D), (3, 1, D), (6, 4, *) を復号
- 得られた符号語から,もとの通報系列を逐次構成していく
LZ77解码就很简单了,结合例题7.2,将编码的括号一个一个按照顺序解码。在解码abr之后,轮到(3,1,c),根据3个字符前1个字符是匹配的基础上加上字符c可以得出(3,1,c)对应字符是ac,于是现在解码后的字符已经由abr增加为abr ac了。
继续看下一个编码(2,1,d),根据2个字符前1个字符是匹配的基础上加上字符d可以得出(2,1,d)对应字符是ad,于是现在解码后的字符已经由abrac增加为abrac ad了。
继续看下一个编码(7,4,r),根据7个字符前4个字符是匹配的基础上加上字符r可以得出(7,4,r)对应字符是abrar,于是现在解码后的字符已经由abracad增加为abracad abrar了。
继续看下一个编码(3,2,y),根据3个字符前2个字符是匹配的基础上加上字符y可以得出(3,2,y)对应字符是ray,于是现在解码后的字符已经由abracadabrar增加为abracadabrar ray了。
LZ77問題点: 整数値の表現をどうする?
- 大きな整数は,それなりに大きな表現長となってしまう
- 表現長を超えるようなブロックは,分割して表現する必要あり
LZ78方式
A. Lempel, J. Ziv により,1978年に提案された方式
- パターンを,(i,l,x) の3項組ではなく,(b,x) の2項組で表現
- 「 b 個前のブロックに,文字 x を追加したもの」
LZ78の符号化例
A={a,b,c}として,系列
aacabbcacababcabcbc
をLZ符号化しなさい.ただし,符号化の際,aは00,bは01,cは10という2進列で表すことにする.
| output |
index |
string |
| (0,a) |
1 |
a |
| (1,c) |
2 |
ac |
| (1,b) |
3 |
ab |
| (0,b) |
4 |
b |
| (0,c) |
5 |
c |
| (2,a) |
6 |
aca |
| (4,a) |
7 |
ba |
| (4,c) |
8 |
bc |
| (3,c) |
9 |
abc |
| (8,ϵ) |
10 |
bc |
The compressed message is (0,a),(1,c),(1,b),(0,b),(0,c),(2,a),(4,a),(4,c),(3,c),(8,ϵ)
L1=⌈log21⌉L2=⌈log22⌉L3=⌈log23⌉L9=⌈log29⌉L10=⌈log210⌉+⌈log2∣3∣⌉=2+⌈log2∣3∣⌉=3+⌈log2∣3∣⌉=4⋮+⌈log2∣3∣⌉=6+⌈log2∣0∣⌉=4
これらの組を2進数で表せば(k=1番目における順序対の変数iは必ず0になるため省略している)
00∣1,10∣01,01∣00,01∣000,10∣010,00∣100,00∣100,10∣0011,10∣1000
最終的な符号語は以下の通りである.
0011001010001000100100010000100100011101000
需要注意的是新出现的单个字符是(0,新字符),LZ78编码的括号只有两部分: (与前面第x个相同字符串部分,新追加的不同的字符)。编码时记得给每一个部分都标上顺序(index),以此记录该部分是第几个。
注意,得到序列对(i,x)后,需要转换为2进制,这个地方略麻烦。
竖线是分割线的意思,逗号左边是字符块的序号(index),右边是字符的记号.
特别注意:
- 逗号左右两边的index和记号全部转换成2进制表示,且左侧index的2进制需要的位数要根据Lk=⌈log2k⌉+⌈log2∣A∣⌉确定(k代表第几个序列对)
- 最左边只有00是因为index的2进制数因为等于0而省略了!(第一个序列对i必定是0)
LZ78の復号例
A={a,b,c,d}の系列をLZ符号化して次の符号語を得た.
001010011001000001011001011100110010100
この符号語を復号して符号化した系列を復元しなさい.ただし,aは00,bは01,cは10,dは11という2進列に符号化したとする.
区切りを入れて符号語を部分列に分割すると(从最左边由log2∣A∣一点一点向右划分即可)
00 ∣ 1,01 ∣ 00,11 ∣ 00,10 ∣ 000,01 ∣ 011,00 ∣ 101,11 ∣ 001,10 ∣ 0101,00
となる.ただし、 | は部分列の区切りを、 , は各部分列における部分列の番号と記号との区切りをそれぞれを表す.各区切りを部分列の番号と記号の組で表すと,
(0,a),(1,b),(0,d),(0,c),(0,b),(3,a),(5,d),(1,c),(5,a)
| output |
index |
string |
| a |
1 |
a |
| ab |
2 |
ab |
| d |
3 |
d |
| c |
4 |
c |
| b |
5 |
b |
| da |
6 |
da |
| bd |
7 |
bd |
| ac |
8 |
ac |
| ba |
9 |
ba |
従って,復号した結果は
a ab d c b da bd ac ba
LZ78方式
- LZ77法より,符号語がコンパクト
- 一符号語が表現するブロックサイズに,上限がない
例题(7.2)
LZ77符号について調べ符号化⋅復号の手順を述べよ.簡単な例に対し,符号化および復号を実行し途中経過および結果を示せ.
LZ77符号化: データを先頭から順番に符号化していく方式である.現在注目している位置から始まる記号列が,それ以前に出現していたかを探す.もし出現していたならば,記号列をその出現位置と長さのポインタに置き換える.記号列を探す範囲をスライド窓と呼ぶ.<滑动窗口中的偏移量(从头部到匹配开始的前一个字符), 匹配中的符号个数, 匹配结束后,前向缓冲区中的第一个符号>
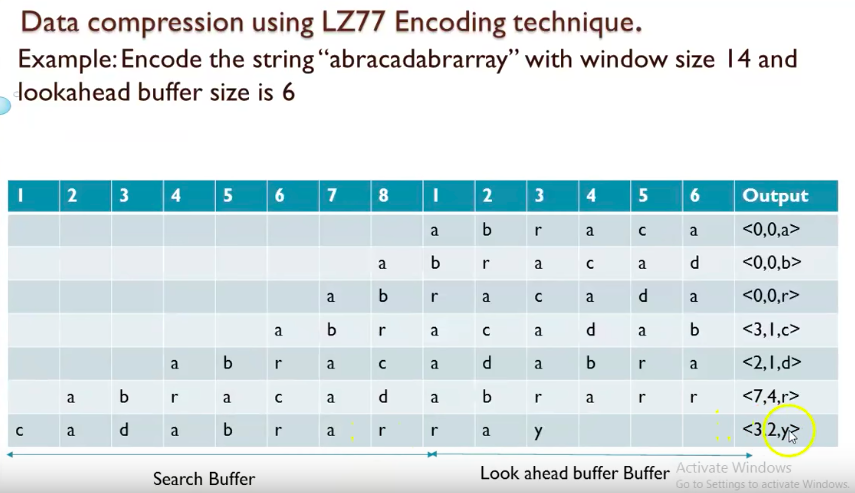
LZ77復号:Decoder keeps same dictionary window as encoder.For each message it looks it up in the dictionary and inserts a copy at the end of the string.

LZ符号の平均符号語長
LZ符号を用いて情報源アルファベットA上の確率分布Pを有する定常無記憶情報源からの出力列x1,x2,⋯,xnを符号化するとき,符号語長L(x1,x2,⋯,xn)は
n1×L(x1,x2,⋯,xn)≤−n1log2P(x1,x2,⋯,xn)+δn
を満足する.さらに平均符号語長は
n1E[L(x1,x2,⋯,xn)]≤H(X)+δn
を満足し,次式が成り立つ.
n→∞limn1E[L(x1,x2,⋯,xn)]=H(X)
これから,系列長を長くしたとき,LZ符号の1記号あたりの符号語長はエントロピーに収束することが分かる.
典型系列とその性質
本章では
- 確率論でよく知られている大数の法則について説明する
- 大数の法則に対応する情報理論の概念である漸近等分割性について説明する
- 漸近等分割性に基づいて,典型系列と呼ばれる系列を定義し,典型系列の性質を明らかにすると共に,典型系列が確率変数列の符号化においてどのような役割を果たすのかについて説明する
大数の法則
Aを実数の有限集合とし,(X1,X2,⋯,Xn)をA上の同一の確立分布Pに従う互いに独立なn個のの列とする.この時,任意に定めた小さな数ϵ>0に対し,
P(∣n1i=1∑nXi−E[X]∣>ϵ)≤nϵ2V[X]
が成り立つ.ただし,E[X]とV[X]は確立分布Pに従う確立変数Xの平均と分散を表し
E[X]=E[X1]=E[X2]=⋯=E[Xn]
並びに
V[X]=V[X1]=V[X2]=⋯=V[Xn]
が成り立つ.
チェビシェフの不等式(Chebyshev’s inequality)
P(∣X−E[X]∣≥k)≤k2V[X]
漸近等分割性(AEP)
(X1,X2,⋯,Xn)をA上の同一確率分布Pに従う,互いに独立なn個の確率変数列とする.この時,任意に定めた小さなϵ>0に対し
P(∣−n1logP(X1,X2,⋯,Xn)−H(X)∣>ϵ)→0(n→∞)
が成り立つ.ただし,H(X)は確率分布Pに従う確率変数Xのエントロピーを表す.
AEPは−n1logP(X1,X2,⋯,Xn)がn→∞に従いH(X)に収束することを意味している
典型系列
任意に定めた小さなϵ>0と,A上の同一確率分布Pに従う,互いに独立なn個の確率変数の列を考える.この時,系列(x1,x2,⋯,xn)の生起確率が
2−n(H(X)+ϵ)≤P(x1,x2,⋯,xn)≤2−n(H(X)−ϵ)
を満足するとき,典型系列と呼ぶ.ただし,
P(x1,x2,⋯,xn)=P(x1)P(x2)⋯P(xn)
であり,H(X)は確率分布Pに従う確率変数Xのエントロピーを表す.また,典型系列の集合をAϵnによって表す.
- 典型系列に属する系列はϵ-典型系列と呼ぶ
典型系列の性質
(x1,x2,⋯,xn)∈Aϵnならば,
H(X)−ϵ≤−n1logP(x1,x2,⋯,xn)≤H(X)+ϵ
が成り立つ.
十分大きなnについて
P(Aϵn)≥1−ϵ
が成り立つ.すなわち,Aϵnに属する系列はほぼ確率1で生じる
典型系列の総数は
∣Aϵn∣≤2n(H(X)+ϵ)
を満足する
十分大きなnに対し,典型系列の総数は
∣Aϵn∣≥(1−ϵ)2n(H(X)−ϵ)
を満足する
この性質から
- Aϵnに属する個々の典型系列の生起確率はP(x1,x2,⋯,xn)≃2−nH(X)である
- 典型系列の総数は∣Aϵn∣≃2nH(X)である
- 典型系列のいずれかが生じる確率はP(Aϵn)≃1を満足する
- 典型系列以外の系列が生じる確率がほぼゼロである
典型系列に関するまとめ
十分大きなnに対し
- 分布Pにしたがい i.i.d. な系列X1,⋯,Xnを発生したとき,得られる系列は非常に高い確率で典型である.その確率は 2−nH(X)に非常に近い値である
- 典型系列の要素数は2nH(X)に近い値である(確率の逆数)
典型系列の性質を用いて,以下が証明できる.
- 情報源符号化 (データ圧縮の限界)
- 通信路符号化 (誤り訂正符号の限界)
典型系列の応用(情報源符号化)
目標
- 情報源から発生した系列(分布Pにしたがい i.i.d. な系列)X1,⋯,Xnをデータ圧縮する
- 情報源として,例えば英語のテキストならばA={ab⋯z,.space;@#}∣A∣=32
- 情報源のエントロピーH(X)は既知とする
- H(X)は各記号の出現頻度から推定可能
表現
- 長さnで∣A∣n通りの系列パターンを用意する
- それらのリストに番号付けする{0,1,⋯,∣A∣n−1}(用意するビット数⌈log2∣A∣n⌉)
- 系列あたりのビット数はn⌈log2∣A∣⌉
典型系列を用いたデータ圧縮
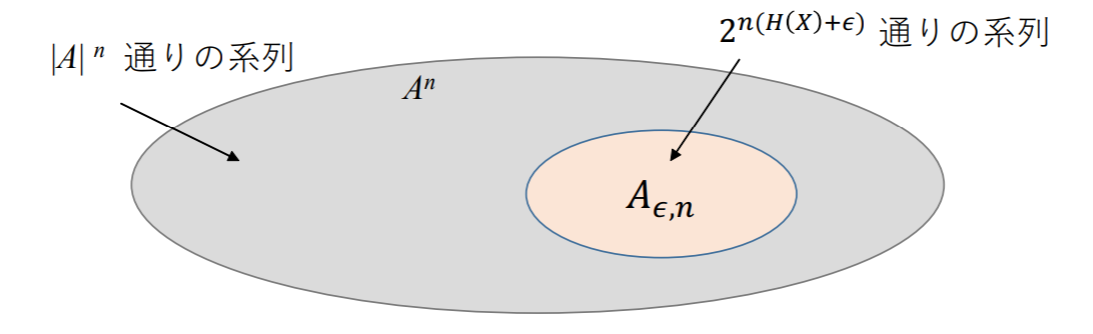
- 記号集合 A から記号が n 個発生
- 集合 An で全体の円を表す
- 集合 An の要素数 ∣An∣ は ∣An∣=∣A∣n
- 典型系列は Aϵ,n で表す
- 集合 Aϵ,n で An の部分集合である
- 集合 Aϵ,n の要素数 ∣Aϵ,n∣=2n(H(X)+ϵ)
集合の大きさで見れば Aϵ,n が全体に占める割合は小さいが,ほぼ確率 1 で Aϵ,n の要素いずれかが発生する.
圧縮方法
- 最大で 2n(H(X)+ϵ) 通りの ϵ-典型系列がある
- Aϵ,n に含まれるそれぞれの系列に対し番号付けをする (用意するビット数 ⌈log22n(H(X)+ϵ)⌉).これらの系列の先頭に 0 を付与
- 典型系列あたりのビット数は⌈n(H(X)+ϵ)⌉+1≤n(H(X)+ϵ)+2
- Aϵ,n に含まれないそれぞれの系列に対し番号付けをする (用意するビット数 ⌈log2∣A∣n⌉).これらの系列の先頭に 1 を付与
- 典型系列あたりのビット数は⌈nlog2∣A∣n⌉+1≤nlog2∣A∣+2
上記の方法によって An に含まれる系列に対しそれぞれ異なる符号語を割り当てることができる.
平均符号長の導出
l(Xn): 系列 Xn に割り当てられた符号語の長さ
E[l(Xn)]=xn∈An∑P(xn)l(xn)=xn∈Aϵ,n∑P(xn)l(xn)+xn∈/Aϵ,n∑P(xn)l(xn)≤xn∈Aϵ,n∑P(xn)(n(H(X)+ϵ)+2)+xn∈/Aϵ,n∑P(xn)(nlog2∣A∣+2)≤1×n(H(X)+ϵ)+ϵ×nlog2∣A∣+2=n(H(X)+ϵ′)
ここで,ϵ′=ϵ+ϵlog2∣A∣+n2である.ϵ′ を小さくするには ϵ を十分小さくすればよい.そして n を十分大きくすることで成り立つ.
従って.この符号化の平均符号語長の上限がnH(X)にいくらでも近づくことが分かる
圧縮の限界
典型系列を利用した符号化の定理
Xn=(X1,X2,⋯,Xn)をA上の同一確率分布Pに従う.互いに独立な確率変数列とする.任意に小さいϵ′>0を定めたとき,nを十分に大きくすることで,平均符号語長が
E(n1L(Xn))<H(X)+ϵ′
を満足するように,この確率変数列を符号化することができる.
この定理は,確率変数列Xnを平均nH(X)ビットを用いて表せること.すなわちXnの表示においては本質的に典型系列Aϵnのみを考慮すれば良い.
事実 H(X) より低い圧縮率で圧縮はできない (無歪圧縮の場合).すなわち圧縮した系列を一意に復号できる符号は次式を満足する.
E(n1L(Xn))≥H(X)
エントロピーは無歪圧縮の理論的な限界である
- このような方法は実用的ではない.なぜなら膨大な数の符号語 (系列) のパターンを記憶しないといけないため
- 実用的な方法としてハフマン符号化や LZ 符号化が挙げられる
例题(8.1)
χ={0,1}としてχ上の確率分布Pを
P(X=0)=31P(X=1)=32
とする.確率分布Pにしたがい i.i.d. で発生する.長さnの系列(X1,X2,⋯,Xn)によって定義される典型的系列Aϵ,nを考える.このときϵ=61,n=3として次の問題を解け.
(1)ϵ-典型系列を全て示せ.
H(X)=−31log231−32log232=log23−32
H(X)=log23−32なので,よって,
2−3(log23−32+61)≤P(x1,x2,x3)≤2−3(log23−32)−61
すなわち
0.1048≤P(x1,x2,x3)≤0.2095
を満たす系列(x1,x2,x3)∈{0,1}3が典型系列となる.X1,X2,X3は互いに独立なので,系列(x1,x2,x3)∈{0,1}3の同時確率P(x1,x2,x3)は次の4つの値のいずれかになる.
P(x1,x2,x3)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧(31)3,(31)2(32),(31)(32)2,(32)3,(x1,x2,x3)が全て0の場合(x1,x2,x3)のうち2つが0の場合(x1,x2,x3)のうち1つが0の場合(x1,x2,x3)が全て1の場合
この4つの値のうちで,典型系列の条件を満足するものは(31)(32)2=0.1481だけだ.従って,典型系列は(x1,x2,x3)のうち1つが0の系列となり,
Aϵn={(0,1,1),(1,0,1),(1,1,0)}
(2)∣Aϵ,n∣≤2n(H(X)+ϵ)
ϵ=61かつn=3の場合
2n(H(X)+ϵ)≃9.5459
であり,∣Aϵn∣=3なので,∣Aϵn∣≤2n(H(X)+ϵ)が成り立つ.
色々な情報量
相互情報量の考え方
情報量の応用
例题(7.2)
実数上で定義された次の実関数f(x)は凸関数であるか否か(狭義であるかも)答えなさい.凸関数であれば証明を,凸関数でなければそのような判例を示しなさい.
一変数の場合は,f′′(x)≥0がIの各店xで成立していると仮定する.この時fはI上の凸関数となる.
開区間I=(a0,b0)上の関数fが2階微分可能とする.この時f′′(x)>0が各点xにおいて成立するならばfはI上狭義凸関数である.
以上の2点で判断すれば,結果は以下の通りである.
(1)f(x)=x4
狭義凸関数である.
(2)f(x)=x3
x > 0において凸関数であり,x < 0において凹関数である.
(3)f(x)=2x
凸関数である.
(4)f(x)=log2x(ただしx > 0)
凹関数である.
(5)f(x)=xlog2x(ただしx > 0)
凸関数である.
賭けと情報理論
Kullback-Leibler(KL)情報量
同一の事象A上に値をとる二つの確率分布PとQを考える.これらの間のKL情報量を次で定義する.(logの底は2とする.)
KL情報量:D(P;Q)=x∈A∑P(x)logQ(x)P(x)
KL情報量は,相対エントロピー(relative entropy)あるいは, ダイバージェンス(divergence), KL-ダイバージェンスなどと呼ばれることもある.一般的には,確率分布の違いを表す量として知られている.
定理: KL情報量の非負性 D(P;Q)≥0
等号が成立するのは二つの分布が一致する場合すなわち,全てのx∈Aに対してP(x)=Q(x)のときのみである.
例題:以下の表のKL情報量D(P; Q),D(Q; P)を計算せよ.
| ai |
P(ai) |
Q(ai) |
| a1 |
41 |
21 |
| a2 |
41 |
41 |
| a3 |
41 |
81 |
| a4 |
41 |
81 |
競走馬のオッズ
通信路のモデル
前章までに述べた情報源符号化の目的は,効率的に情報を表現することにあった.
本章からは電気や光や無線などの媒体を用いて,送信者から受信者へ情報を送り届けるについて取り扱う.
- 情報理論における通信媒体のモデルとしての通信路について説明する
- 通信路には通信路容量と呼ばれる情報伝送の限界があることを説明する
通信路
入力アルファベット A 並びに出力アルファベット B を有する離散的通信路は,入力記号 x∈A が与えられた時の出力記号 y∈B の条件付き確率 P(y ∣ x) によって定まる.このように,通信路の出力の確率分布が,その時刻における入力のみ定まり,過去の入力列には依存しない時,この通信路を無記憶であるあるいは無記憶通信路と呼ぶ.
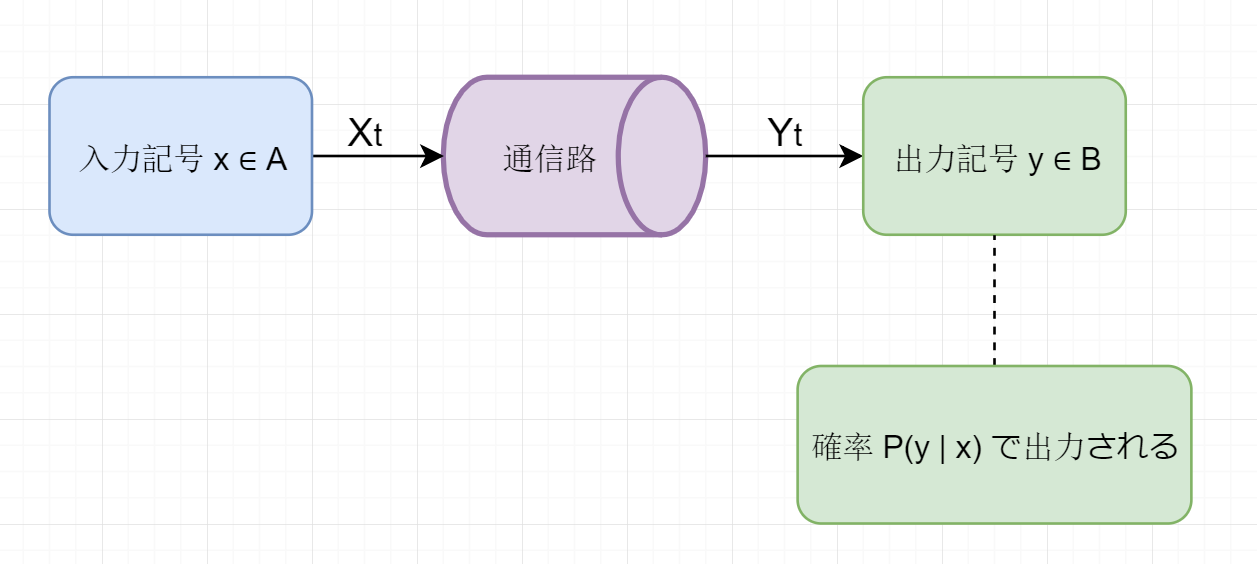
- ∣A∣=∣B∣=rのときは,r元通信路 (𝑟-ary channel) という
雑音のない通信路
雑音のない通信路: 入力記号によって出力記号が一意に定まる通信路である.
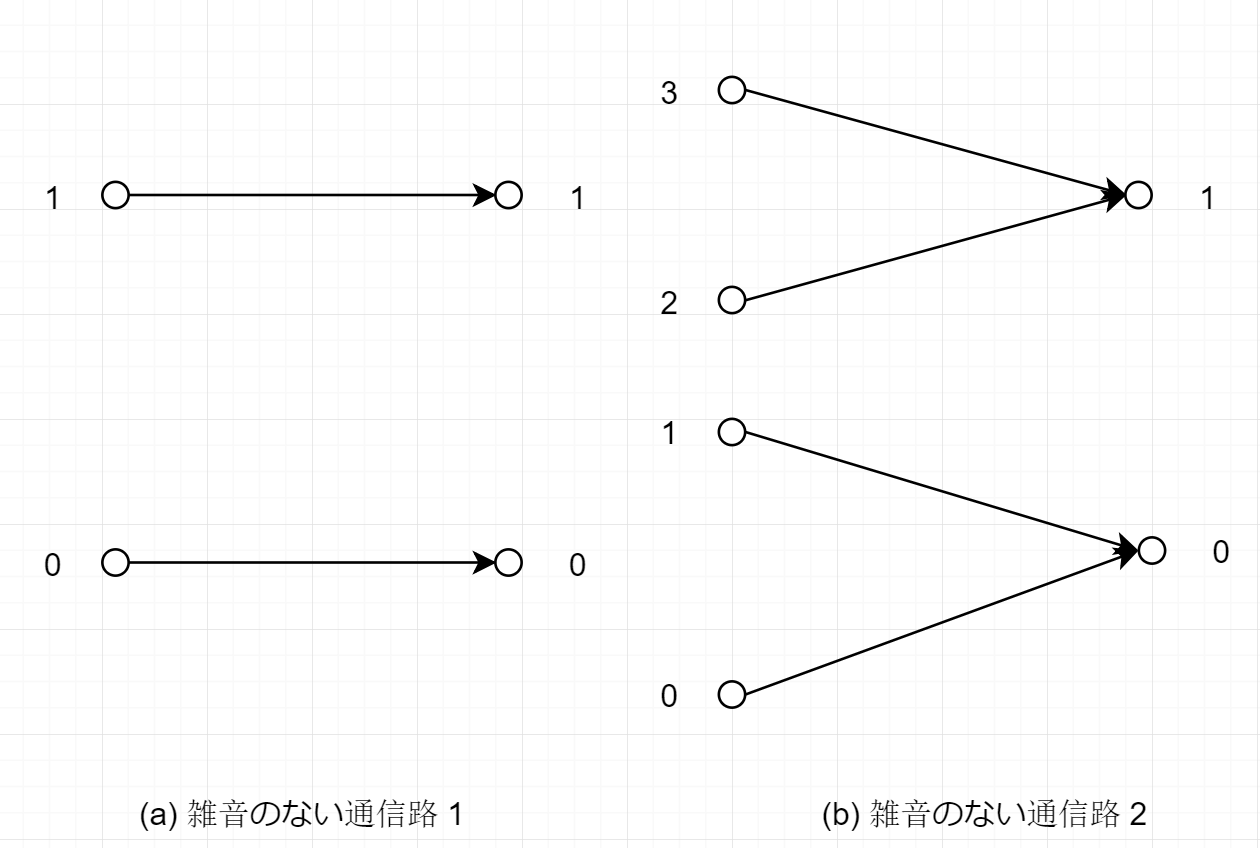
(a) A=B={0,1}で与えられる通信路
この時,入出力の間の条件付き確率は
P(0 ∣ 0)=1,P(1 ∣ 0)=0P(0 ∣ 1)=0,P(1 ∣ 1)=1
によって定まる.
雑音のある通信路
雑音のある通信路: 出力記号が入力記号によって確率的に変化する通信路である.
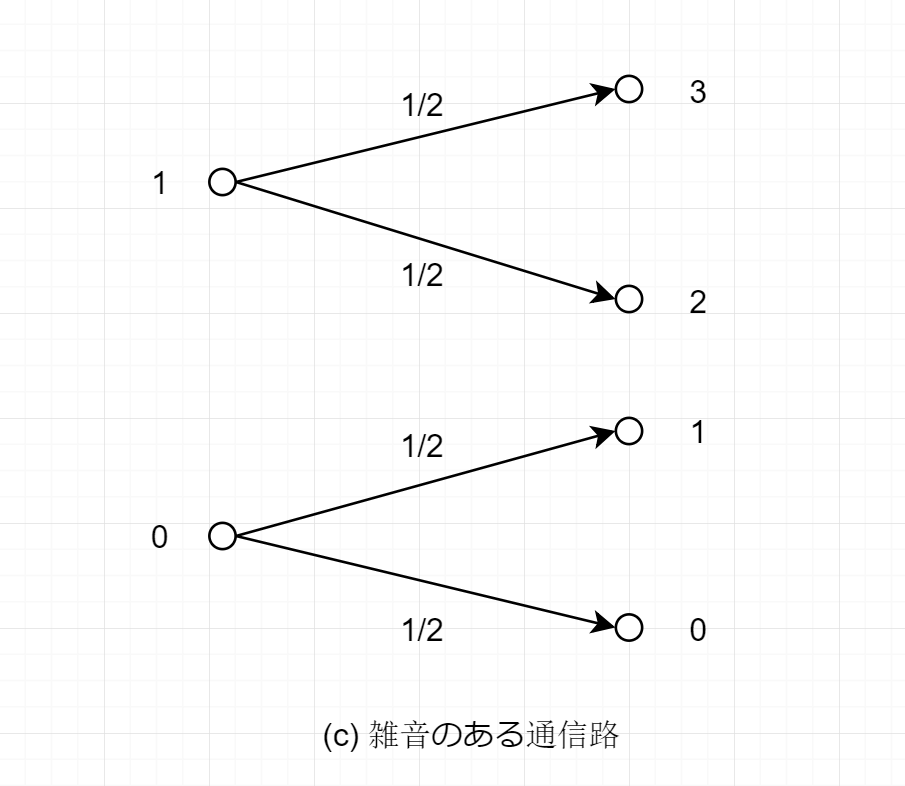
© 入力アルファベットA={0,1}, 出力アルファベットB={0,1,2,3}で与えられる通信路
この時,入出力の間の条件付き確率は
P(0 ∣ 0)=21,P(1 ∣ 0)=21,P(2 ∣ 0)=P(3 ∣ 0)=0P(0 ∣ 1)=P(1 ∣ 1)=0,P(2 ∣ 1)=21,P(3 ∣ 1)=21
によって定まる.
消失通信路
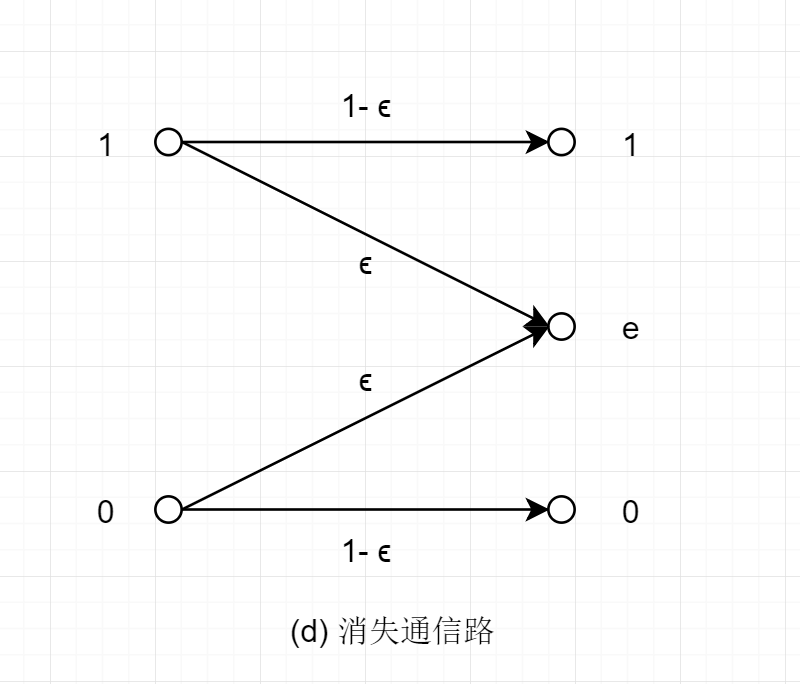
(d) 入力アルファベットA={0,1}, 出力アルファベットB={0,1,e}で与えられる通信路
この時,入出力の間の条件付き確率が,ある実数0≤ϵ≤1を用いて.
P(0 ∣ 0)=1−ϵ,P(1 ∣ 0)=0,P(e ∣ 0)=ϵP(0 ∣ 1)=0,P(1 ∣ 1)=1−ϵ,P(e ∣ 1)=ϵ
によって定まる.
通信路から記号 e が出力された場合,記号0か1のいずれかが送信されたかを,これだけからでは知ることはできない.
記号 e のことを消失(イレージャ)と呼ぶ.
これは,通信路に入力された記号が途中で失われて何も出力されなかったという状況を表している.
2元対称通信路(BSC)
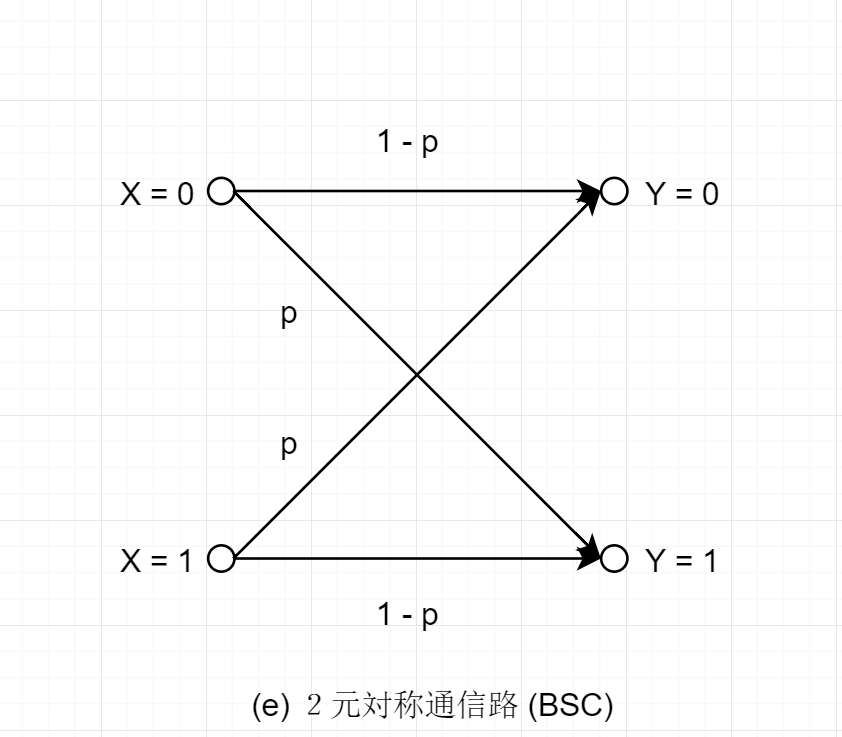
P(Y=0 ∣ X=0)=1−p,P(Y=1 ∣ X=1)=1−pP(Y=1 ∣ X=0)=p,P(Y=0 ∣ X=1)=p
- pは反転確率 (誤り確率): このような通信路を BSC(p) と呼ぶ
符号長 n を大きくするにしたがい
- 復号誤り確率は 0 に近づく (良)
- 符号化率 n1(bits/symbol) となり,0 に近づく (悪)
復号誤り確率は0に近づけ,かつ符号化率を定数にすることはできる.
BSC(0.1)に対しては, 符号化率を大きくとも0.53(bits/symbol)で復号誤り確率を任意に小さくすることができる.
対称通信路
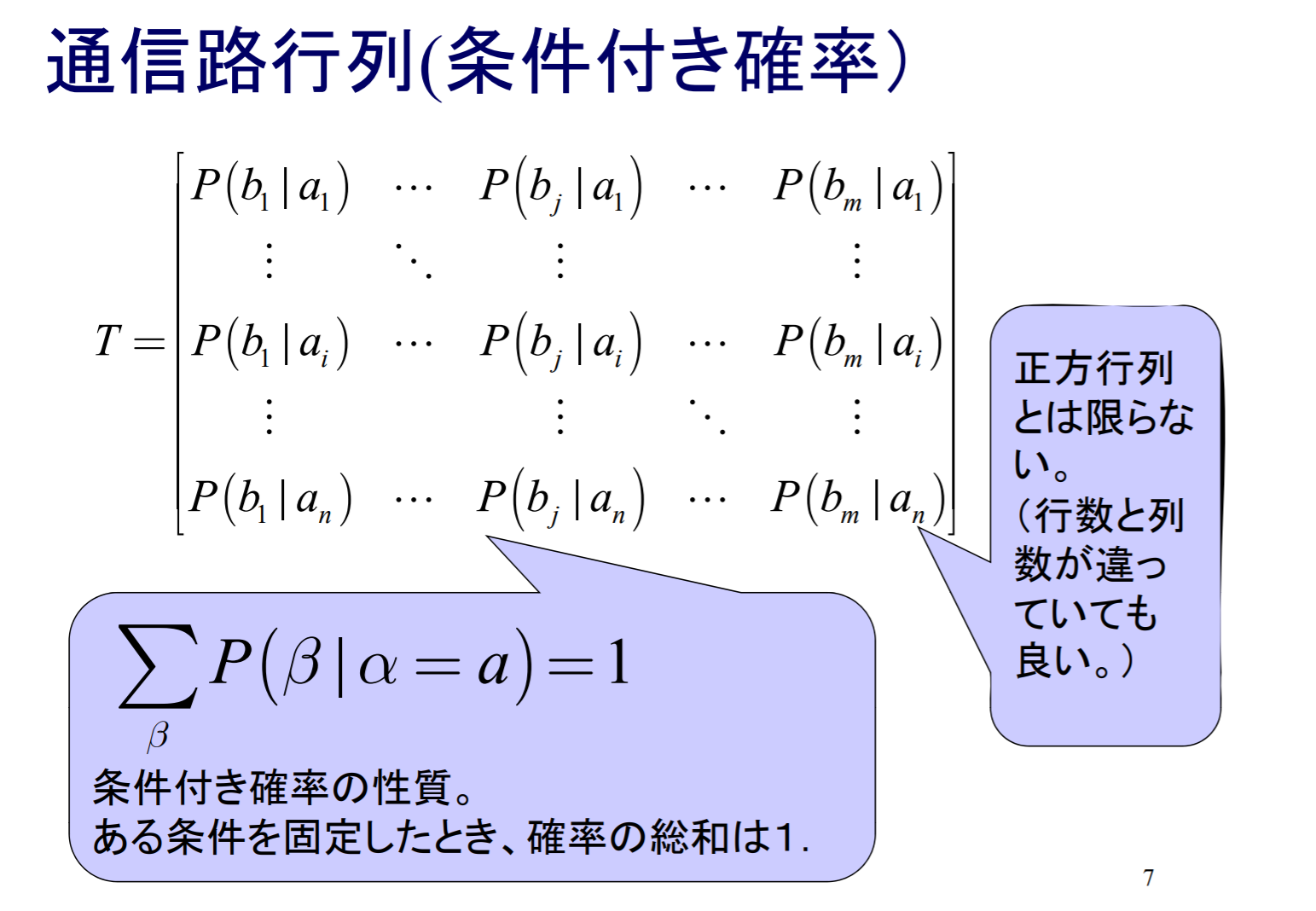
通信路行列において,
- 各行が最初の行の要素を並び替えたものになっているような通信路を入力対称通信路と呼ぶ
- 各列が最初の列の要素を並び替えたものになっているような通信路を出力対称通信路と呼ぶ
- 入力対称通信路であり,出力対称通信路である場合は,狭義の対称通信路と呼ぶ
入力対称通信路の例
∣∣∣∣∣acbbca∣∣∣∣∣
出力対称通信路の例
∣∣∣∣∣∣∣pqrqpr∣∣∣∣∣∣∣
狭義の対称通信路の例
∣∣∣∣∣∣∣acbbaccba∣∣∣∣∣∣∣
通信路容量(channel capacity)
入力アルファベット A 並びに出力アルファベット B を持つ無記憶通信路の入出力間の条件付き確率がP(y ∣ x)(x∈A,y∈B)で与えられるとする.この時,この通信路の通信路容量C0を
C0=P(x)max{I(X;Y)}
によって定義する.ただし, (X,Y)は同時確率 P(x,y)=P(x)P(y ∣ x)に従う確率変数とし,maxは入力アルファベット A 上の確率分布 P(x)(x∈A) を取り替えて得られる最大値を意味する.
誤りのない2元通信路容量
- I(X;Y)=H(X)−H(X ∣ Y)=H(X)
- H(X)を最大にするPX=(21,21)
- C0=maxPXI(X;Y)=maxPXH(X)=1(bit/symbol)
2元対称通信路(BSC)容量
BSC ではP(0 ∣ 0)=1−p,P(1 ∣ 0)=pである.また
H(Y ∣ X=0)=−y=0∑1P(y ∣ 0)log2P(y ∣ 0)=−P(0 ∣ 0)log2P(0 ∣ 0)−P(1 ∣ 0)log2P(1 ∣ 0)=h(p)
のため,次の式が成り立つ.
C0=PXmaxI(X;Y)=PXmax(H(Y)−H(X ∣ Y))=PXmax(H(Y)−h(p))
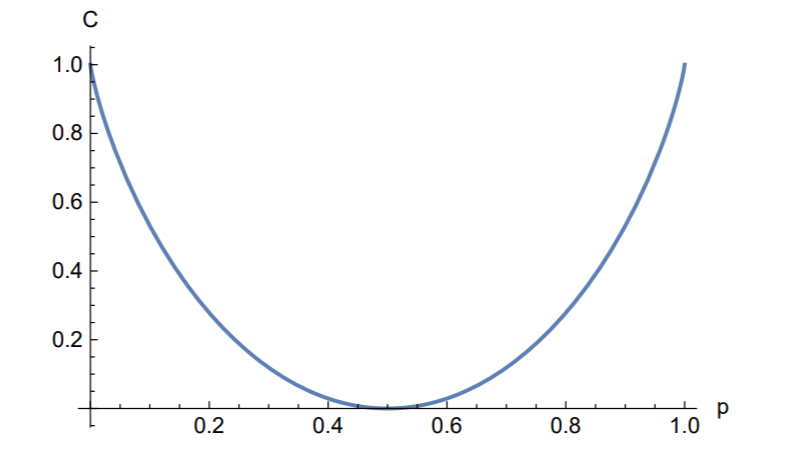
- 最大になるのはPX=(21,21)の時
- 従ってC0=1−h(p)となる
- p=0,p=1の時1で最大となる
- p=0.5の時0で最も小さい(1番訂正が難しい)
- p=0.1の時C=0.531(bits/symbol)
- BSCは狭義の対称通信路である
2元消失通信路(BEC)容量
入力分布をPX(0)=a,PX(1)=1−a(0≤a≤1)とし,C0=maxPXI(X;Y)=maxPX(H(Y)−H(Y∣X))を計算する.
H(Y)=(1−e)h(a)+h(e)H(Y∣X)=h(e)I(X;Y)=H(Y)−H(Y∣X)=(1−e)h(a)
- C0=maxPX(1−e)h(a)が最大となるのはa=21の時
- 従ってC0=1−eである
- e=0.1の時C=0.9(bits/symbol)
- BSCよりC0が大きい.すなわち,BSCより訂正しやすいと言える
- BECは入力対称通信路だが,狭義対称通信路ではない
対称通信路の通信路容量
前節述べたように,通信路容量は,入力記号の確率分布を変化させた時の相互情報量の最大値として定義された.
通信路行列
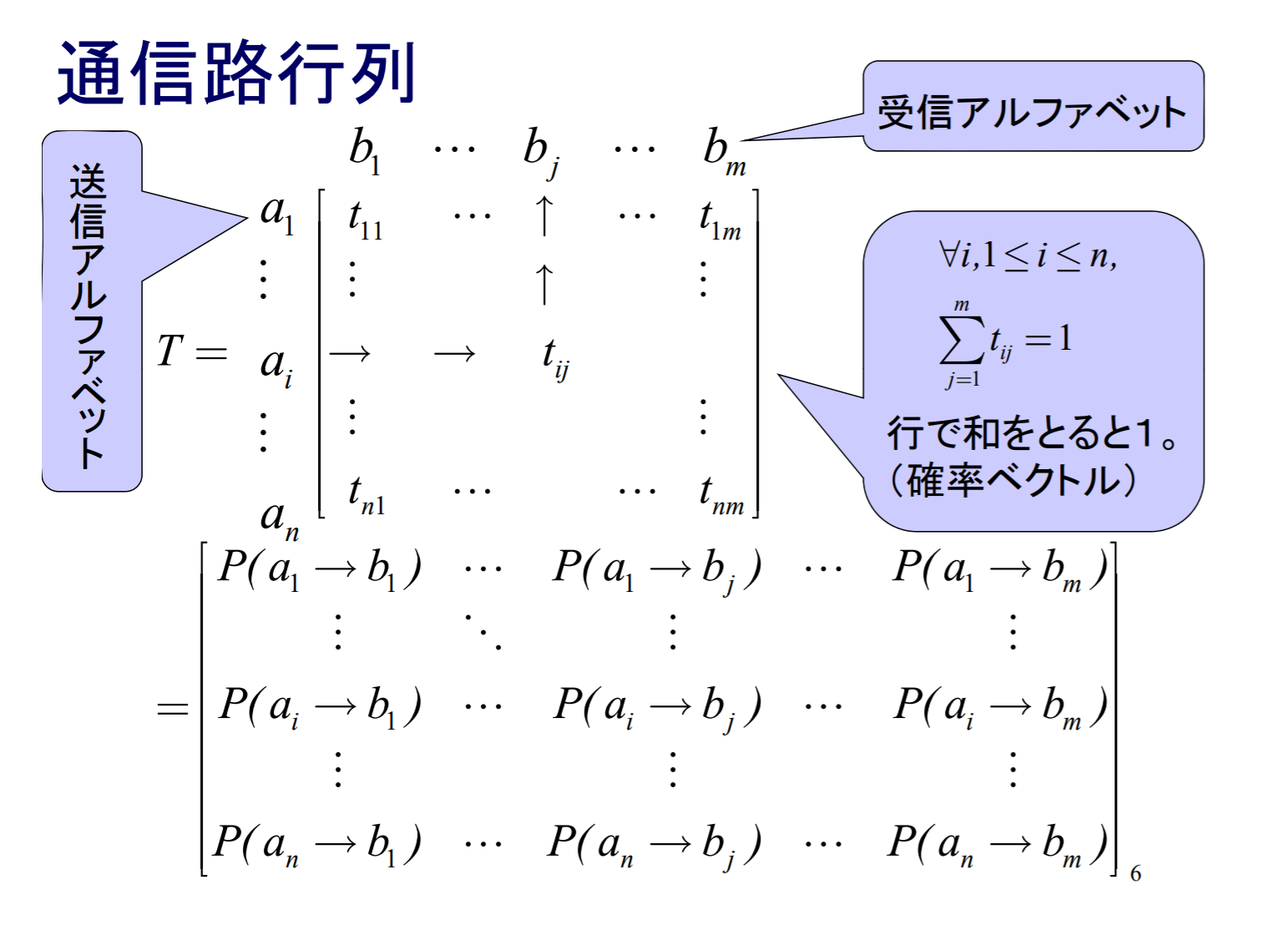
対称通信路では通信路容量の計算を簡単化できる場合がある.まず入力を表す確率変数をX, 出力を表す確率変数をYとする.
入力対称通信路の通信路容量
H(Y ∣ X=x)がx∈Aによらず一定の値を取るため,H(Y ∣ X)=H(Y ∣ X=x)が成り立つ.従って通信路容量は以下のように求められる
C0=PXmax(H(Y)−H(Y ∣ X=x))
狭義の対称通信路の通信路容量
相互情報量の最大化は X が一様分布のとき達成される.
X が一様分布のとき, Yの分布も一様分布になり, H(Y)は最大値log2∣B∣をとる.
C0=log2∣B∣−H(Y ∣ X=x)
例題:次の通信路行列が与えられた時,通信路容量を計算しなさい
∣∣∣∣∣∣∣∣∣4141420424104104241414104142∣∣∣∣∣∣∣∣∣
C0=log2∣B∣−H(Y ∣ X=x)∣B∣=4H(Y ∣ X=x)=−y∈Y∑P(y ∣ x)log2P(y ∣ x)
x = 0とする
H(Y ∣ X=0)=−41log241−42log242−0log20−41log241=23=H(Y ∣ X=1)=H(Y ∣ X=2)=H(Y ∣ X=3)
従って,
C0=log2∣B∣−H(Y ∣ X=x)=log2∣B∣−23=21
例題(9.1)
次の通信路行列によって表される条件付き確率P(y ∣ x)によって定まる通信路の通信路容量を求めなさい.
(1) x∈{0,1}とy∈{0,1,2,3}に対して
∣∣∣∣∣21041410214141∣∣∣∣∣
入力対称通信路なので,通信路容量C0は
C0=PXmax(H(Y)−H(Y ∣ X=0))=PXmax{H(Y)−(−2×41log41−21log21)}=PXmax{H(Y)−23}
となる.ここで,X=0となる確率を21として,Yの周辺確率を求めると{0,1,2,3}上の一様分布になるので,この時
H(Y)=−4×41log41=2
また,エントロピーの上界式によると,H(Y)≤log∣4∣なので,maxPX=2となる.
従って,通信路容量C0=2−23=0.5
(2) x,y∈{0,1,2}に対して
∣∣∣∣∣∣∣540515154005154∣∣∣∣∣∣∣
狭義の対称通信路なので,通信路容量C0=log2∣B∣−H(X ∣ Y=0)=log23−(−54log254−51log51)≃0.863034405833794
(3) x,y∈{0,1,2,3}に対して
∣∣∣∣∣∣∣∣∣a1−a001−aa0000a1−a001−aa∣∣∣∣∣∣∣∣∣
狭義の対称通信路なので,通信路容量C0=log2∣B∣−H(X ∣ Y=0)=log24−h(a)=2−h(a)となる.
例題(9.2)
次の通信路によって表される条件付き確率P(y ∣ x)によって定まる通信路をZ-通信路と呼びます.ただし,x,y∈{0,1}です.Z-通信路に対する通信路容量と通信路容量を達成する入力分布を求めなさい.入力分布を横軸に相互情報量I(X;Y)のグラフを描き,通信路容量との関係を述べなさい.
∣∣∣∣∣121021∣∣∣∣∣
ここで,まず与えられた通信路を一般の形に変わる(この問題ではp=21)
∣∣∣∣∣1p01−p∣∣∣∣∣
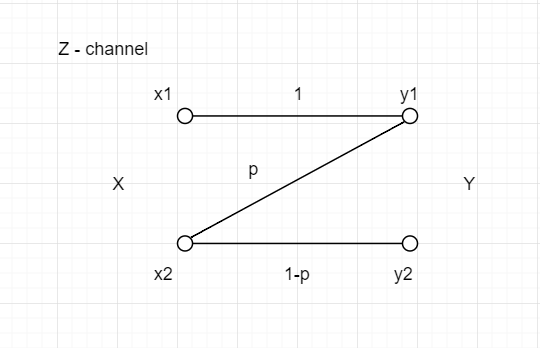
図に示したように,P(x1)の確率は1−α,P(x2)の確率はαと仮定する.
相互情報量は
I(X;Y)=H(Y)−H(Y ∣ X)
となる.
(1) Calculation of H(Y)
P(y1)P(y2)H(Y)=(1−α)+αp=α(1−p)=−(1−α+αp)log(1−α+αp)−α(1−p)logα(1−p)
(2) Calculation of H(Y ∣ X)
H(Y ∣ X)=−αplogp−α(1−p)log(1−p)
(3)
I(X;Y)∂α∂I(X;Y)=H(Y)−H(Y ∣ X)=−(1−α+αp)log(1−α+αp)−α(1−p)logα+αplogp=0⇒α0=1−p+p(p−1p)1
これを解くと,α0=52となり,従って,I(X;Y)の最大値は
C0=P(x)maxI(X;Y)=−(1−α0+α0p)log(1−α0+α0p)−α0(1−p)logα0+α0plogp=log(1−p+pp−1p)−p−1plogp=log5−2
となる.
グラフは以下のように示した
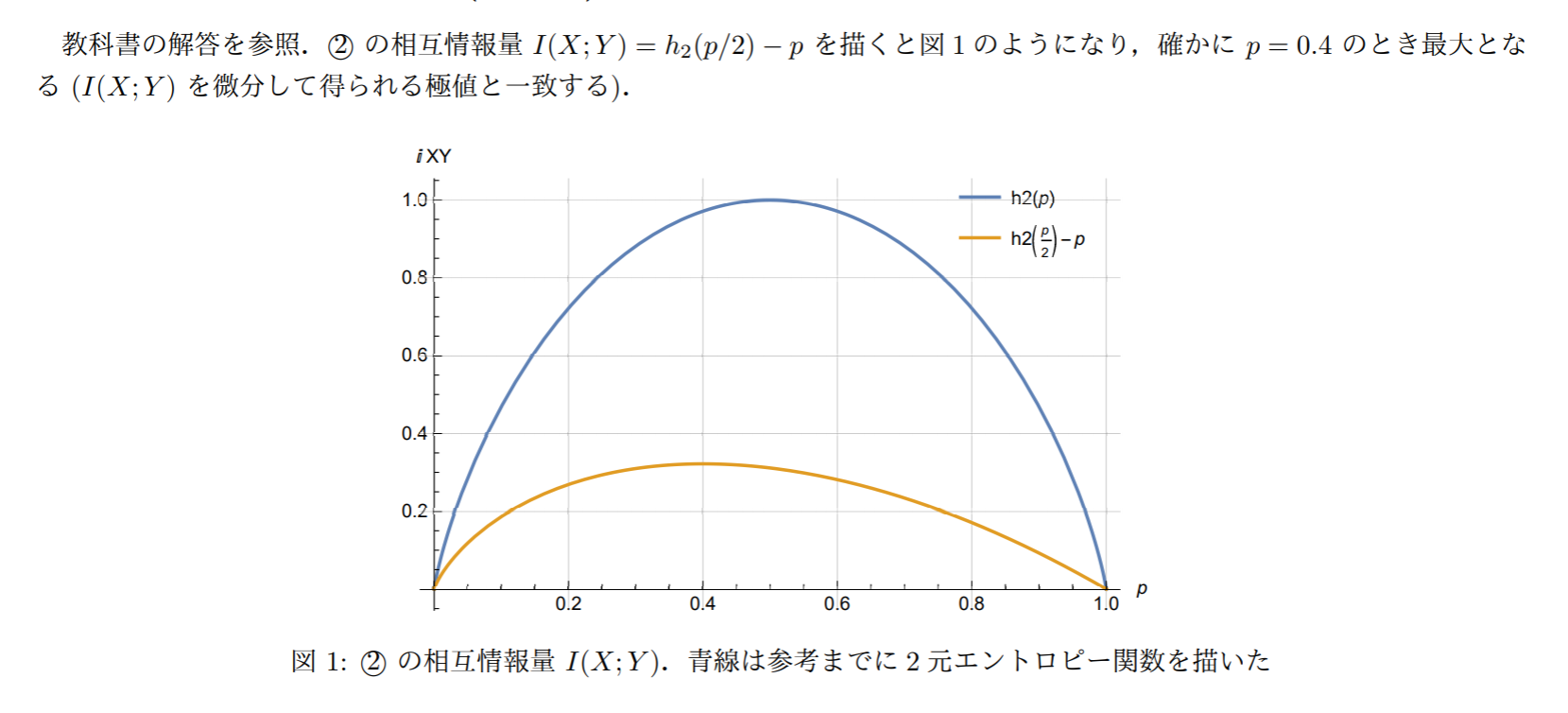
上のグラフにも明らかに,相互情報量I(X;Y)と通信路容量の関係は通信路容量は,通信路の入力と出力との間の相互情報量を,入力分布に関しては最大化した時の最大値によって与えられる. 相互情報量は通信路が情報を転送する能力を表す.
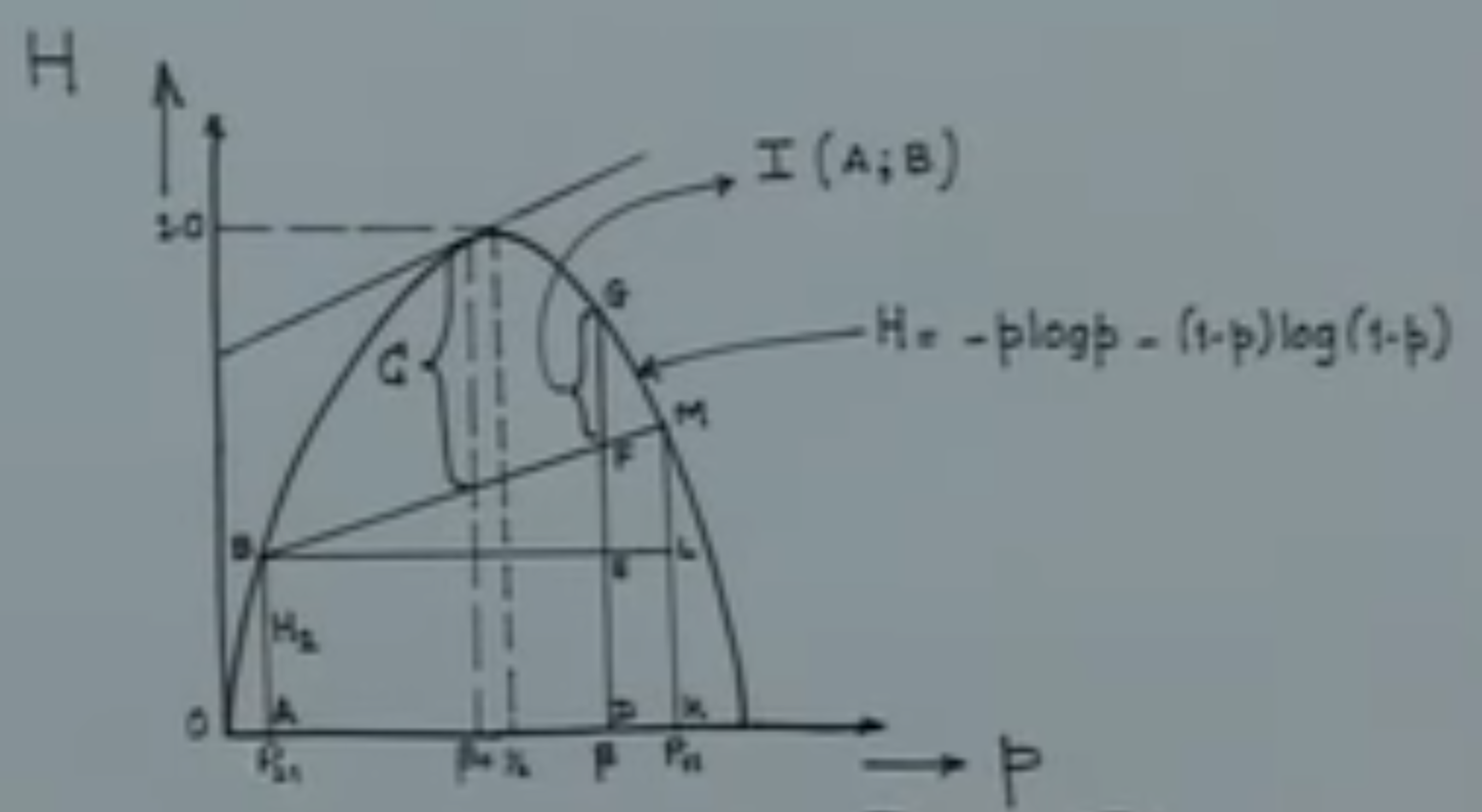
例題(9.3)
2値入力{0,1}に対して消失だけでなく誤りも起こりうる次の図で定まる通信路を考えます.
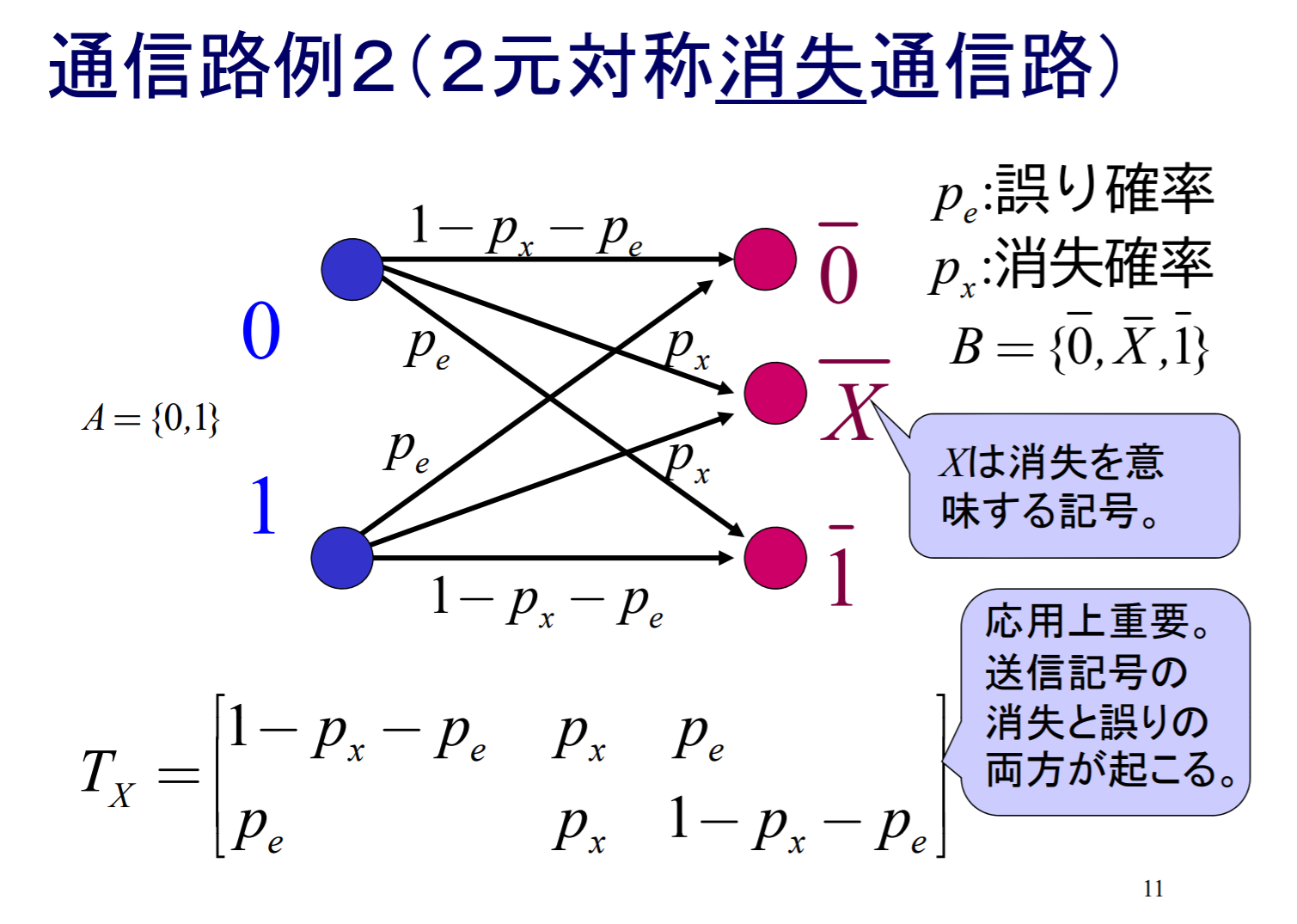
(a) この通信路の通信路容量を求めなさい.
この通信路の通信路行列は
∣∣∣∣∣1−ϵ−δδϵϵδ1−ϵ−δ∣∣∣∣∣
なので,この通信路は入力対称通信路である.従って,その通信路容量は
C0=P(x)maxH(Y)−H(Y∣X=x)=P(x)maxH(Y)+(1−ϵ−δ)log(1−ϵ−δ)+ϵlogϵ+δlogδ
となる.また,X=1となる確率をpをすると,
P(Y=0)=(1−p)(1−ϵ−δ)+pδ,P(Y=e)=ϵ,P(Y=1)=p(1−ϵ−δ)+(1−p)δ
なので,
H(Y)=−((1−p)(1−ϵ−δ)+pδ)log((1−p)(1−ϵ−δ)+pδ)−ϵlogϵ−(p(1−ϵ−δ)+(1−p)δ)log(p(1−ϵ−δ)+(1−p)δ)=(1−ϵ)h(1−ϵ(1−p)(1−ϵ−δ)+pδ)+h(ϵ)
となる.従って,H(Y)のpについての最大値を求めると,h(t)がt=21の時に最大値1を取ることから,
P(x)maxH(Y)=(1−ϵ)(pmaxh(1−ϵ(1−p)(1−ϵ−δ)+pδ))+h(ϵ)≤1−ϵ+h(ϵ)
となる.ただし,等号は1−ϵ1−ϵ(1−p)(1−ϵ−δ)+pδ=21の時,すなわちp=21において達成できる.以上から,
C0=P(x)maxH(Y)+(1−ϵ−δ)log(1−ϵ−δ)+ϵlogϵ+δlogδ=(1−ϵ+h(ϵ))+(1−ϵ−δ)log(1−ϵ−δ)+ϵlogϵ+δlogδ
(b) (a)で求めた通信路容量は, ϵ=0とすることで2元対称通信路の通信路容量と一致することを確かめなさい.
ϵ=0とすると,
C0=1+h(0)+(1−δ)log(1−δ)+δlogδ=1−h(δ)
となり,2元対称通信路の通信路容量となる.
© (a)で求めた通信路容量は, δ=0とすることで消失通信路の通信路容量と一致することを確かめなさい.
δ=0とすると,
C0=1−ϵ+h(ϵ)+(1−ϵ)log(1−ϵ)+ϵlogϵ=1−ϵ
となり,消失通信路の通信路容量となる.
通信路符号化定理
本章では、
- 通信路符号の伝送速度が通信路容量よりも小さい場合、符号長を長くするにつれて、いくらでも復号誤り率を小さくできる通信路符号が存在することを示す
通信路符号化定理(シャノンの第2基本定理)

通信路容量 C を持つ通信路に対して, R<C であれば,情報速度 R の符号で復号誤り率がいくらでも小さいものが存在する.しかし,R>C であれば,そのような符号は存在しない.
この定理は, 伝送速度 R が通信路容量 C より小さければnを大きくしていけば誤り確率が任意に小さい符号化復号化が構成可能であることを示している.
- 通信路容量を超えない情報速度でなら,いくらでも精度よく通信できるような符号法がある
通信路符号
入力アルファベット A の要素からなる長さ n の系列の集合 An の部分集合 C を通信路符号と呼ぶ.この時, n を符号長. C の要素を符号語, C の要素数符号語数をと呼ぶ.
符号の伝送速度
符号長 n の符号 C の伝送速度 R は
R=n1log2∣C∣
によって定義される.
通信路符号化
最尤復号法
ynを受信した際に,次式のように復号する方法
ψ(yn)=argimaxP(yn ∣ xn(i))
これはつまりynが与えられたもとで,尤度P(yn ∣ xn(i))を最大にする i へと復号する方式である.
尤度P(yn ∣ xn(i))が最大となる符号語が二つ以上あった場合どれに復号するか予め決定しておく.例えば「もっとも小さいiにする」等(これをタイブレークルール等という.)
このとき(M個の符号語が等確率で発生するという仮定の下で)平均誤り確率は
ϵn=M1i=1∑M(1−yn∈Yn∑imaxP(yn ∣ xn(i)))=1−M1i=1∑Myn∈Yn∑imaxP(yn ∣ xn(i))
となる.簡単な考察によりこれが平均誤り確率を最小にすることがわかる.またタイブレークルールは平均誤り確率に影響しない.つまり尤度が最大の符号語が複数ある場合,どれを選んでも平均誤り確率は等しいこともわかる.
例題
晴れ,雨をそれぞれ1,2に対応させ(M=2),その符号語をxn(1)=000,xn(2)=111とする.最尤復号法はynが与えられたときに,P(yn∣xn(i))を最大にする i へと復号する関数であるので,yn=010のときにP(010 ∣ 000),P(010 ∣ 111)を計算し,大小を比較する.
yn=010のときは
P(010 ∣ 000)=P(0 ∣ 0)×P(1 ∣ 0)×P(0 ∣ 0)=(1−p)×p×(1−p)=0.8×0.2×0.8=0.128
P(010 ∣ 000)=0.128>P(010 ∣ 111)=0.032
であるので,010は000を符号語として持つ符号語1(xn(1)=000)へと復号する.
yn=111のときは
P(111 ∣ 000)=0.008<P(111 ∣ 111)=0.512
であるのでxn(2)=111である符号語2へと復号する.
最尤復号法の問題点
- 最尤復号法は平均誤り確率を最小にするという意味で最適な復号法であるが,全ての符号語 i に対してP(yn ∣ xn(i))を計算し比較しなければならない.これは符号語の数 M が大きくなると現実的な計算量では困難となる.
- このため,最尤復号法は,非常に強力な復号法ではあるが限られた符号に対してしか用いられていない.計算量の観点からは次に説明する最小距離復号法の方がよい.
また各符号語 i の発生確率(事前確率)を一様(P(xn(i))=1/M)と仮定している.事前確率が非一様の場合は最尤復号法では不十分である
最小距離復号法
二つX上の長さ n の系列を
an=a1a2⋯an,bn=b1b2⋯bn
とする.このとき
dH(an,bn)=i=1∑nδ(ai,bi)
を系列 an と bn の間のハミング距離と呼ぶ.ただし,
δ(u,v)={0,u=v1,u=v
である.
ハミング距離とはつまり,二つの系列の対応した位置にある成分のうち互いに異なるものの数である.例えば,系列000と系列111のハミング距離はdH(000,111)=3である.またdH(101,111)=1である.なお,ハミング距離は距離の三公理を満たす.
ハミング距離に基づいて受信系列ynからそれに最も近い符号語xn(i)を持つ i へと復号する規則を最小距離復号法という.つまり
ψ(yn)=argimindH(yn,xn(i))
という復号化関数である.
例題:
先ほどの例:晴れ,雨をそれぞれ1,2に対応させる(M=2)とxn(1)=000,xn(2)=111.最小距離復号法ではynが与られた時に,各符号語とのハミング距離を比較する.yn=010の時に
yn=010の時は
dH(010,000)=1<dH(010,111)=2
であるので,010は000を符号語として持つ符号語1へ復号する.
yn=111の時は
dH(111,000)=3>dH(111,111)=0
であるのでxn(2)=111である符号語2へと復号する.
- 例から分かるように最小距離復号法を用いた復号は複雑な確率計算を必要としない.このことは,復号結果が通信路行列には依らないことを示している.
- 最小距離復号法を用いて高い誤り訂正能力,(低い誤り確率)を達成するには符号語間のハミング距離を大きくする必要がある.
符号の最小距離 d とは,符号に含まれる相異なる二つの符号語のハミング距離の最小値である.
d=min{dH(xn(i),xn(j)) ∣ i=j,1≤i,j≤M}
例題
符号語1∼4を2元符号C={00000,11100,00111,11011}を用いて送信する.つまりx5(1)=00000,x5(2)=11100,x5(3)=00111,x5(4)=11011である.このとき
(1) この符号の最小距離はいくらか
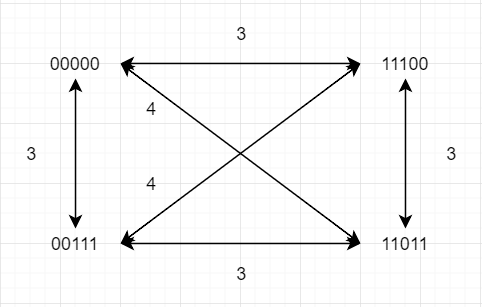
(2) 系列10111を最小距離復号法により復号した結果はどうなるか
yn=10111
| i |
dH(yn,xn(i)) |
| 1 |
4 |
| 2 |
3 |
| 3 |
1 |
| 4 |
2 |
符号語3
(3) 系列10011を最小距離復号法により復号した結果はどうなるか
yn=10011
| i |
dH(yn,xn(i)) |
| 1 |
3 |
| 2 |
4 |
| 3 |
2 |
| 4 |
1 |
符号語4
(4) 伝送速度はいくらか
伝送速度 R(n=5,M=4)
R=nlog2M=nlog22k=nk⇒R=52
BSCの場合における復号法
最小距離復号法と最尤復号法の復号結果は変わらない.これは偶然ではなく,誤り率p(ただしp < 0.5)のBSCにおいてはこれらの結果は常に一致する.
log21−pp<0
となるので,この符号はマイナスである.故に,
iargmaxP(yn ∣ xn(i))=iargmaxdH(yn,xn(i))log21−pp=iargmindH(yn,xn(i))
となる.これはハミング距離の最小になる符号語を復号していることにほかならない.
例題
次の通信路行列
W1=[0.90.20.10.8],W2=[0.60.70.40.3]
で定義される二つの通信路があるとしよう.この通信
路上で先ほどの例と同様,符号語1∼4を2元符号C={00000,11100,00111,11011}を用いて送信する.つまりx5(1)=00000,x5(2)=11100,x5(3)=00111,x5(4)=11011である.今受信系列 yn が10111であったとする.
(1) 通信路が W1 であった際に,最小距離復号法と最尤復号法の復号結果を比較せよ
[P(0 ∣ 0)P(0 ∣ 1)P(1 ∣ 0)p(1 ∣ 1)]
最尤復号法 yn=10111
| i |
P(yn∣xn(i)) |
| 1 |
P(1∣0)P(0∣0)P(1∣0)P(1∣0)P(1∣0) = 0.00009 |
| 2 |
P(1∣1)P(0∣1)P(1∣1)P(1∣0)P(1∣0) = 0.00128 |
| 3 |
P(1∣0)P(0∣0)P(1∣1)P(1∣1)P(1∣1) = 0.04608 |
| 4 |
P(1∣1)P(0∣1)P(1∣0)P(1∣1)P(1∣1) = 0.01024 |
よって,最尤復号法の復号結果は符号語3である.
(2) 通信路がW2であった際に,最小距離復号法と最尤復号法の復号結果を比較せよ
最大事後確率復号
最尤復号法は平均誤り確率を最小にするという意味で最適な復号法であるが,各符号語 i の発生確率(事前確率)を一様(P(xn(i))=M1)と仮定している.
事前確率が非一様の場合は復号誤り確率を最小にするためには最尤復号法では不十分であり,最大事後確率復号法を用いる必要がある.
ψ(yn)=iargmaxP(xn(i) ∣ yn)=iargmaxP(yn,xn(i))=iargmaxP(xn(i))⋅P(yn ∣ xn(i))
これはつまり yn が与えられたもとで,事後確率P(xn(i) ∣ yn)を最大にする i へと復号する方式である.
ベイズの定理
贝叶斯定理:贝叶斯定理是关于随机事件A和B的条件概率的一则定理。
P(A ∣ B)=P(B)P(B ∣ A)P(A)
其中A以及B为随机事件,且P(B)不为零。P(A ∣ B)是指在事件B发生的情况下事件A发生的概率。
在贝叶斯定理中,每个名词都有约定俗成的名称:
- P(A|B)是已知B发生后,A的条件概率。也由于得知B的取值而被称作A的后验概率
- P(A)是A的先验概率(或边缘概率)。之所以称为"先验"是因为它不考虑任何B方面的因素
- P(B|A)是已知A发生后,B的条件概率。也由于得知A的取值而被称作B的后验概率
- P(B)是B的先验概率
按照这些术语,贝叶斯定理可描述为:后验概率 = (似然性*先验概率)/标准化常量。也就是说,后验概率与先验概率和相似度的乘积成正比。
另外,比例P(B ∣ A)/P(B)也有时被称作标准似然度(standardised likelihood),贝叶斯定理可描述为:后验概率 = 标准似然度 * 先验概率
- 最大事後確率復号法はベイズの定理を利用
- 最尤復号法は最大事後確率復号法の一例(事前確率を一様とした場合が最尤復号法)と等価
P(x ∣ y)=P(y)P(x,y)P(y)=x∑P(x,y)(定数)∝P(x,y)=P(y ∣ x)⋅P(x)
例題(10.1)
下記のような通信路Wを介して符号語x4(1)=0000,x4(2)=0011,x4(3)=1100,x4(4)=0111を送信する.注意:復号の結果として2つ以上の符号語が候補として挙がった場合,全て解答すること.
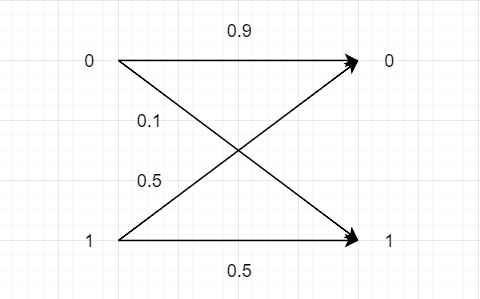
(1) この符号の最小距離dminと伝送速度Rを求めよ.
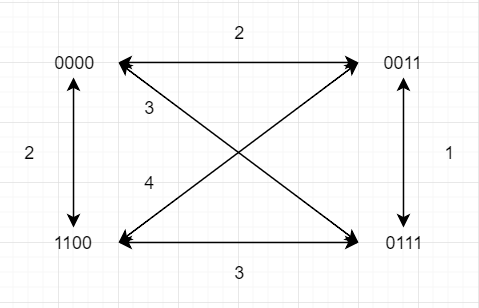
図に示したように,最小距離はdH(0011,0111)=1である.
伝送速度Rは
R=nlog2M=4log24=21
となる.(M = 4, n = 4)
(2) 受信系列0010を最小距離復号法,最尤復号法,それぞれで復号した結果を求めよ.根拠も述べること.
yn=0010
最小距離法より
| i |
dH(yn,xn(i)) |
| 1 |
1 |
| 2 |
1 |
| 3 |
3 |
| 4 |
2 |
符号語は1と2(argminidH(yn,xn(i))=1)
最尤復号法より
| i |
P(yn∣xn(i)) |
| 1 |
P(0∣0)P(0∣0)P(1∣0)P(0∣0) = 0.0729 |
| 2 |
P(0∣0)P(0∣0)P(1∣1)P(0∣1) = 0.2025 |
| 3 |
P(0∣1)P(0∣1)P(1∣0)P(0∣0) = 0.0225 |
| 4 |
P(0∣0)P(0∣1)P(1∣1)P(0∣1) = 0.1125 |
符号語2(argmaxiP(yn ∣ xn(i))=0.2025)
(3) 受信系列0010, 符号語の発生確率が非一様でP(x4(1))=P(x4(3))=81,P(x4(2))=P(x4(4))=83としたとき,最大事後確率復号法を実行したとき得られる符号語を答えよ.根拠も述べること.
ψ(yn)=iargmaxP(xn(i))⋅P(yn ∣ xn(i))
| i |
ψ(yn) |
| 1 |
81×0.0729 = 0.0091125 |
| 2 |
83×0.2025 = 0.0759375 |
| 3 |
81×0.0225 = 0.0028125 |
| 4 |
83×0.1125 = 0.0421875 |
符号語2(ψ(yn)=argmaxiP(xn(i))⋅P(yn ∣ xn(i))=0.0759375)
誤り訂正符号
これまでに最小距離復号法,最尤復号法,最大事後確率復号法の3つの復号法を説明したが,符号化法については説明していない.
またこれまでに説明した復号法も符号語の全探索を行う必要があるため,符号語数(情報記号数kに対し符号語数は2k個と膨大)が多くなるとその計算に莫大な時間がかかる.
従って,長い符号長でも復号誤り率の小さい通信路符号を効率的に構成するための方法が必要になる.
この問題に対する1つの解答が誤り訂正符号である.
「誤り訂正符号」とは,符号語の記号に生じた一定個数までの誤りを訂正できる通信路符号である.
本章では
- 誤り訂正符号の基本概念と誤り訂正の原理について説明する
- 符号語に生じた1個までの誤りを訂正できるハミング符号の構成法を示す
- ハミング符号による符号化を繰り返し行うことで,2元対称通信路において伝送速度を一定以上に保ったまま,符号長を長くすることで,いくらでも復号誤り率を小さくできる符号が作れることを明らかにし,通信路符号化定理を満足する符号の例を示す
2元ガロア体
2元のガロア体GF(2)上の要素F={0,1}の演算は表のように行なわれる.
| a |
b |
a+b |
a ⋅ b |
| 0 |
0 |
0 |
0 |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
表では,2元記号a,b間の演算を示す.例えば,演算でa=1,b=1のときa+b=2=0(mod2)として計算される.
誤り訂正符号の実用例
- 単一パリティ検査符号
- 水平垂直パリティ検査符号
- ハミング符号(RAID2, RAM)
- Reed-Solomon符号(衛星通信, DVD, BD, CD, QRコード)
- ターボ符号(3G, 4G)
- LDPC符号(DVB-S2, IEEE802.16c)
- Polar符号(5G)
誤り訂正符号の例
長さ1の情報ビット0もしくは1を送信したい.いまそれぞれの情報ビットに対し,同じ情報を2ビットをパリティ系列として付加した系列を通信路を介して送るとする.すなわち,0→000,1→111と符号化することである.
もし符号語x=(000)を送ってy=(010)を受信したとする.送られた符号語は000もしくは111のいれずれかであり,これらの系列が送られる確率は等確率であり,通信路は誤り確率が0≤ϵ<0.5のBSCの場合,000が送られたと推定する方が妥当である.
このように誤り訂正符号では,情報系列に対してパリティ系列を付加した符号語を送信する.
しかし,1ビットの情報に対して長い系列を送ることは効率が悪く,またできるだけ短い系列で多くの情報を送信したい.誤り訂正符号では訂正能力だけでなく,送信するビット数(符号語)に対する情報系列の長さの比率(符号化率)も重要な指標である.
(n, k, d)線形ブロック符号
2元(n,k,d)線形ブロック符号 C は長さ n の2元ベクトルxの集合であり,長さ k の2元ベクトルである情報系列wを符号化して得られる.ここで n は符号長(符号語xの長さ), k は情報記号数(情報系列wの長
さ), d は最小距離である.また符号 C の符号化率R=nkとする.
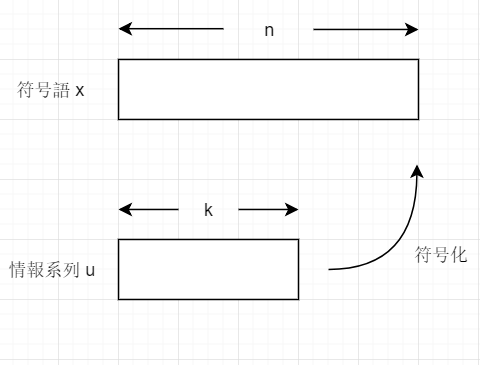
- 符号率R=nk
ハミング距離
2つのベクトルv=(v1,⋯,vn),v′=(v1′,⋯,vn′)をその成分毎に比較し,異なる個数の数をハミング距離DH(v1′,vn′)と定義する.
DH(v,v′)=i=1∑ndH(vi,vi′)dH(vi,vi′)={0,vi=vi′1,vi=vi′
例:n=8のハミング距離
長さがn=8である2つのベクトル(01001011),(01110010)のハミング距離は
DH(01001011,01110010)=4
である.
最小距離
最小距離はある符号Cの中で2つの異なる符号語x,x′間のハミング距離の最小値を表し,次式によって定義される.
d=x,x′∈C,x=x′minDH(x,x′)
符号語は2k個存在する.(22k)組み合わせ(C2k2)全てでの最小値.
- 符号Cの最小距離d(C)は,符号Cの符号語中に生じた何個までの誤りを訂正できるかを示す尺度になっている.
(n, n-1, 2)符号
符号語のハミング重みが偶数となるようにパリティビットを1ビット付加して符号化する.例えば,長さが4の情報系列w=(0111)を符号化すると長さが5の符号語x=(01111)を得る.この符号は偶重み符号とも呼ばれる.
例: (5,4,2)符号(n = 5)
w=(0111)→x=(01111)
- w八重 = 3, x八重 = 4
- x誤りが1個(11111): 符号語⇒検出できる
- x誤りが2個(10111): 符号語⇒検出できない
(n, 1, n)符号
1ビットの情報記号に対し同じパリティビットをn−1個付加して符号化される.例えば,w=(1)を符号化すると符号語x=(1111)を得る.この符号は繰り返し符号とも呼ばれる.
例: (4,1,4)符号(n = 4)
w=(1)→x=(1111)
最小距離と誤り検出⋅訂正能力
符号語の数は 2k 個存在するが,符号語の長さはnであるため, 2n 個の n 次元ベクトル空間のベクトル全てに符号語が割り当てられているわけではない.したがって,もし誤りが混入した受信語がどの符号語とも異なる系列であったとすると,受信側では誤りが混入したことが分かる.これを誤り検出と呼ぶ.
- 長さがkである{0,1}の情報系列の総数は 2k 個であるため
定理: (n,k,d)線形ブロック符号は d−1 個以下の誤りを必ず検出できる.
- (n,n−1,2)符号の場合,d−1=2−1=1個の誤りは必ず検出できる.
| d |
t |
| 2 |
0 |
| 3 |
1 |
| 4 |
1 |
| 5 |
2 |
| 6 |
2 |
定理: (n,k,d)線形ブロック符号はt個以下の誤りを必ず訂正できる.ただし,t=⌊2d−1⌋である.(床関数⌊a⌋はaを超えない整数の中で最大の値を表す)
- (n,1,n)符号でn=4の場合,t=⌊2d−1⌋=t=⌊24−1⌋=t=⌊1.5⌋=1個の誤りは必ず訂正できる.
生成行列とパリティ検査行列
符号器では長さ k の情報系列wを長さ n の符号語xにする.これは,情報系列wにk×nの行列Gを乗じることで得ることが出来る.すなわち,
x=wG
となる.生成行列Gは以下で定義される.
生成行列
(n,k,d)線形ブロック符号 C の生成行列Gはk×nの行列であり, C から全零の符号語を除く k 個のそれぞれ異なる符号語を取り出し,x1,x2,⋯,xkとし,それぞれをGの行ベクトルとする.
G=⎣⎢⎢⎢⎢⎡x1x2⋮xk⎦⎥⎥⎥⎥⎤
得られたGに対して,行列の基本操作を行なっても本質的に同じ符号が得られる.したがって行列の基本操作を行い以下の構造の生成行列G′を用いた方が扱いやすい.
G′=[Ik,P]
このような形式の生成行列を用いて符号化を行うと,符号語x=wG′の左からkビットx1,⋯,xkは情報系列w1,⋯,wkと一致するため,符号語から容易に情報ビットを取り出すことができる.
ここでIkはk×kの単位行列であり, Pはk×(n−k)のパリティビット付加行列と呼ばれる.
例: (5, 4, 2)符号の生成行列
G′=⎣⎢⎢⎢⎡10001010010010100011⎦⎥⎥⎥⎤
情報系列w=(0101)に対し,得られた生成行列G′を用いて符号化を行なうと
x=wG′=(01010)
が得られる.
パリティ検査行列
(n,k,d) 線形ブロック符号のパリティ検査行列Hは(n−k)×n行列であり,GHT=0を満足する.パリティ検査行列Hは生成行列がG′形であるとき
H′=[PT,In−k]
の形となる.
GHT=0を満足することより,xとHの関係は
wGHT=xHT=0
となることがわかる.
長さが n の通信路で雑音eと受信語y(=x+e)の関係を考える.GHT=0より,もし受信語yがyHT=(x+e)HT=0である場合は,受信語に誤りが混入していることが分かる.
またここで,誤り訂正を行なうための手がかりであるシンドロームと呼ばれる長さn−kのベクトルを計算する.
ハミング符号を用いた1個誤り訂正
ハミング符号は任意のm(≥2)に対して(n,k,d)=(2m−1,2m−1−m,3),m=n−kで与えられる線形ブロック符号である.
最小距離はd=3であるため,前の定理より最小距離復号法を行なうことでt=1ビットを必ず訂正することができる.
以下ではパリティ検査行列Hからハミング符号を構成する方法を説明する.
まずパリティ検査行列Hを以下のように表現する.
H=[h1,h2,⋯,hn]
ここでhi,i=1,2,⋯,nは全てが異なる長さがn−k(=m)の非ゼロの列ベクトルとすると,長さが m となる非ゼロベクトルは2m−1個あるので,n=2m−1であることがわかる.
(7, 4, 3)ハミング符号
次式でm=3となる(n,k,d)=(7,4,3)ハミング符号の
パリティ検査行列の一例を示す.
H=⎣⎢⎡000111101100111010101⎦⎥⎤
H′の形式に変換すると
H′=[PT,I7−4]=⎣⎢⎡011110010110101101001⎦⎥⎤
となる(各列の順番を入れ替えればよい).
またH′に対応する生成行列G′は
G′=[I4,P]=⎣⎢⎢⎢⎡1000011010010100101100001111⎦⎥⎥⎥⎤
である.ここで
P=⎣⎢⎢⎢⎡011101110111⎦⎥⎥⎥⎤
組織符号
G′,H′で与えられた生成行列やパリティ検査行列をもつ符号は 組織符号と呼ばれ,符号語に情報部系列がそのまま表れる(情報部と冗長部に分けられる)性質をもつ.組織符号に変換するためには,生成行列やパリティ検査行列に対し行列の基本変形を行って次式のように変形すればよい.
G′=[Ik,P]H′=[PT,In−k]
ハミング符号の復号
1ビット誤り訂正法
- シンドロームs=yHTを計算する
- s=hl,l=1,⋯,nとなるビット位置lの受信ビットylを反転させる.すなわち,l番目のビット位置が誤り位置であり,このビットを反転(0→1,1→0)させればよい
- 2より復号した符号語x^, 推定系列w^を得る
この復号法は最小距離復号を行なっており,ハミング符号を用いて最もハミング距離が近い符号語に訂正している.
例題(11.1)
(7,4,3)ハミング符号の生成行列とパリティ検査行列を用いて情報系列w=(0011)を送信したとする.このとき受信語 y が次の2つで受信したとき,最小距離復号を行って得られる推定系列および復号成功の可否を述べなさい.
パリティ検査行列の一例を示す.
H=⎣⎢⎡000111101100111010101⎦⎥⎤
H′の形式に変換すると
H′=[PT,I7−4]=⎣⎢⎡011110010110101101001⎦⎥⎤
またH′に対応する生成行列G′は
G′=[I4,P]=⎣⎢⎢⎢⎡1000011010010100101100001111⎦⎥⎥⎥⎤
である.ここで
P=⎣⎢⎢⎢⎡011101110111⎦⎥⎥⎥⎤
- y=(1111000)
符号語x=wG′=(0,0,1,1,0,0,1)である.
シンドロームs=yH′T=(1,1,1)より,(1,1,1)Tはパリティ検査行列H′の4番目と一致するので,4ビット目に誤りが生じたと考え,このビットの1と0を反転したy′=(1,1,1,0,0,0,0)が送信されたと見なす.
復号した推定系列w^=(1,1,1,0)より,ハミング符号において2個以上の誤りが生じた場合,正しく復号できない.
- y=(0111001)
上の手順と同様に,シンドロームs=yH′T=(1,0,1)である.(1,0,1)Tはパリティ検査行列H′の2番目と一致するので,2ビット目に誤りが生じたと考え,このビットの1と0を反転したy′=(0,0,1,1,0,0,1)が送信されたと見なす.
復号した推定系列w^=(0,0,1,1)より,正しく復号した.
例題(11.2)
ハミング符号のパラメータでm=4の場合の生成行列とパリティ検査行列の一例を示しなさい.ただし組織符号化が可能な形で答えなさい.
m=4となる(n,k,d)=(15,11,3)ハミング符号のパリティ検査行列の一例を示す.
組織符号化が可能な形にすると,
H′=[PT,I15−11]=⎣⎢⎢⎢⎡000000001111000000011110000100001100110010010010101010100001⎦⎥⎥⎥⎤
またH′に対応する生成行列G′は
G′=[I11,P]=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡100000000000000010000000000001001000000000010000100000000011000010000000100000001000000101000000100000110000000010000111000000001001000000000000101001000000000011010⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
である.ここで
P=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡00000001001000110100010101100111100010011010⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
暗号(Cryptography)
RSA暗号
- 受信者アリス(Alice)は鍵 n,e,dを作成し, n,eを公開し, dを秘密鍵として保持, p,q は廃棄
- 送信者ボブ(Bob)は公開された n,e を用いて, 平文 m を c≡memodn と暗号化して, 暗号文 c を送信する
- 暗号文 c を受信したアリスは秘密鍵 d を用いて, cdmodn を求めると,平文 m を得る
- cd≡(me)d=med=mkϕ+1≡mmodn
鍵 e,d の生成
- 2つの異なる大きな素数 p,q をランダムに選び,その積 n=pq を求める
- n=pq のオイラー関数 ϕ=(p−1)(q−1)に対し,これと互いに素となるような整数 e, (1<e<n) をランダムに選ぶ
- ed≡1modϕ となるような整数 d を求める. すなわち, ed=kϕ+1 なる d , 但し, k は適当な正整数, 0<d<ϕ. e と ϕ が素の時, このような d はただ一つのみ
例題: RSA 暗号について, 素数 p=3,q=5, 平文 m=3
- n=pq=15
- オイラー関数ϕ=(p−1)(q−1)=8, 整数 e(1<e<n)=7とする
- ed≡1modϕ となるような整数 d を求める.
| d |
ed |
modϕ |
| 1 |
7 |
7 |
| 2 |
14 |
6 |
| 3 |
21 |
5 |
| 4 |
28 |
4 |
| 5 |
35 |
3 |
| 6 |
42 |
2 |
| 7 |
49 |
1 |
| 8 |
56 |
0 |
よって,d=7
- 平文mを暗号化する
c≡memodn≡37mod15≡12
- 暗号文 c を復号する
cd≡(me)d=med=mkϕ+1≡mmodn349=36×8+1=3mod15
よって, 平文 m=3 が得た
フェルマーの定理
xp−1≡1(mod p)xp≡x(mod p)
オイラーの定理
xkϕ+1≡x
香农三大定理
香农第一定理
香农第一定理又称为无失真信源编码定理或变长码信源编码定理
香农第一定理的意义:将原始信源符号转化为新的码符号,使码符号尽量服从等概分布,从而每个码符号所携带的信息量达到最大,进而可以用尽量少的码符号传输信源信息。
对于第一定理的说明:
- 通过对扩展信源进行可变长编码,可以使平均码长无限趋近于极限熵值,但这是以编码复杂性为代价的
- 无失真信源编码实质:对离散信源进行适当的变换,使变换后新的符号序列信源尽可能为等概率分布,从而使新信源的每个码符号平均所含的信息量达到最大
- 香农第一定理仅是一个存在性定理,没有给出更有效的信源编码的实现方法
香农第二定理
香农第二定理又称为有噪信道编码定理
对于第二定理的说明:
- 第二定理纠正了人们传统固有的可靠性和有效性矛盾的观点,为信道编码理论和技术的研究指明了方向
- 第二定理仅指出编码的存在性,未给出编码的具体方法
- 第二定理指出:R<C是可靠传输的必要条件,但并未指出编码序列无限长是可靠传输的必要条件
- 香农进一步证明:R=C时,任意小的差错概率也是可以达到的
香农第三定理
香农第三定理又称为保失真度准则下的有失真信源编码定理