Operations Research

2020-09-11
作者 Qiang
~10.92K 字
次阅读
条评论

1. 简介
2. 线性规划与单纯形法
3. 对偶问题与灵敏度分析
4. 运输问题
5. 目标规划
6. 整数规划
7. 动态规划
8. 图与网络规划
9. 网络计划技术
10. 存储论
11. 排队论
12. 决策论
13. 层次分析法(AHP)
14. 数据包络分析法(DEA)
15. 博弈论(Game Theory)
16. 参考文献

运筹帷幄之中，决胜千里之外

简介

运筹学（Operations Research），是一门应用数学学科，利用统计学，数学模型和资料科学等方法，去寻找复杂问题中的最佳或近似最佳的解答。运筹学经常用于解决现实生活中的复杂问题，特别是改善或优化现有系统的效率。研究优化模型的规划论，研究排队(或服务)模型的排队论，及研究博弈模型的博弈论是运筹学最早的三个重要分支，通常称为运筹学早期的三大支柱。随着学科的发展和计算机的出现，现在分支更细，名目更多。

运筹学的工作步骤

提出问题：用自然语言描述问题
建立数学模型：用变量、函数、方程描述问题
求解：主要用数学方法求出模型的最优解、次优解、满意解，复杂模型求解要用计算机
解的检验：检查模型和求解步骤有无错误，检查解是否反映现实问题
解的实施：—决策者根据自己的经验和偏好，对方案进行选择和修改，作出实施的决定

运筹学的应用

制定生产计划：主要用于总体确定生产、存储和劳动力的配合等计划，以适应波动的需求计划，用线性规划和模拟方法等
运输问题：涉及空运、水运、公路运输、铁路运输、管道运输、厂内运输等。空运问题涉及飞行航班和飞行机组人员服务时间安排等。水运有船舶航运计划、港口装卸设备的配置和船到港后的运行安排。公路运输除了汽车调度计划外，还有公路网的设计和分析，市内公共汽车路线的选择和行车时刻表的安排，出租汽车的调度和停车场的设立等等
人事管理：人员的获得和需求估计；人才的开发，及进行教育和训练；人员的分配，主要是各种指派问题；各类人员的合理利用问题；人才的评价，例如如何测定一个人对组织、社会的贡献；工资和津贴的确定等
计算机和信息系统：用于计算机的内存分配，研究不同排队规则对磁盘工作性能的影响。利用整数规划寻找满足一组需求文件的寻找次序，利用图论、数学规划等方法研究计算机信息系统的自动设计等

运筹学的分支

数学规划（线性规划、整数规划、目标规划、非线性规划、动态规划、网络规划）：数学规划是研究在所给定的条件下，如何按某一衡量指标来寻求计划管理工作中的最优方案。必须满足的条件为约束条件，衡量指标为目标函数
图论与网络流：图论是数学的一个分支，它以图为研究对象。网络流是图论中的一种理论与方法，研究网络上的一类最优化问题，是一种类比水流的解决问题方法
决策分析：决策分析以假设一个具有完全信息的，可实现精度计算的，并且完全理性的理想决策者的方式达到最优的决策。其目标是帮助人们进行进一步良好决策的工具和方法论
排队论：排队论（随机服务系统理论）是通过对服务对象及服务时间的统计研究，得出这些数量指标（等待时间，排队长度，忙期长短等）的统计规律
可靠性数学理论：可靠性是指产品在一定条件下完成其预定功能的能力，丧失功能称为失效。可靠性理论以产品的寿命特征为研究对象，运用概率统计和运筹学的理论和方法对产品（单元或系统）的可靠性作定量研究
库存论
对策论
搜索论
计算机模拟

线性规划是运筹学的一个重要分支。线性规划在理论上比较成熟，在实用中的应用日益广泛与深入。特别是在电子计算机能处理成千上万个约束条件和决策变量的线性规划问题之后，线性规划的适用领域更为广泛了。从解决技术问题的最优化设计到工业、农业、商业、交通运输业、军事、经济计划和管理决策等领域都可以发挥作用。它已是现代科学管理的重要手段之一。

线性规划与单纯形法

线性规划问题及其数学模型

问题的提出

某工厂在计划期内要安排生产Ⅰ、Ⅱ两种产品，已知生产单位产品所需的设备台时及A、B两种原材料的消耗，如下表所示

产品	Ⅰ	Ⅱ
设备	1	2	8台时
原料A	4	0	16Kg
原料B	0	4	12Kg
利润	2元/件	3元/件

设 $x_1, x_2$ 分别表示计划生产I,II产品的数量，称它们为决策变量

生产 $x_1, x_2$ 的数量多少，受资源拥有量的限制，这是约束条件。生产的产品不能是负值，即 $x_1, x_2 \geq 0$ 也被称为变量的非负约束条件

x_1 + 2x_2 \leq 8, \quad 4x_1 \leq 16, \quad 4x_2 \leq 12, \quad x_1,x_2 \geq 0

如何安排生产，使利润最大，这是目标。因此我们可以得到数学模型：

\begin{aligned} &\text{目标函数} \quad \max \quad z = 2x_1 + 3x_2 \\ &\text{约束条件} \begin{cases} &x_1 + 2x_2 \leq 8 \\ &4x_1 \leq 16 \\ &4x_2 \leq 12 \\ &x_1, x_2 \geq 0 \end{cases} \end{aligned}

共同的特征：

每一个线性规划问题都用一组决策变量 $(x_1, \cdots, x_n)$ 表示某一方案，这组决策变量的值就代表一个具体方案。一般这些变量取值是非负且连续的
存在可以量化的约束条件，这些约束条件可以用一组线性等式或线性不等式来表示
都有一个达到目标的要求，它可用决策变量的线性函数(称为目标函数)来表示。按问题的不同，要求目标函数实现最大化或最小化

图解法

图解法顾名思义就是通过作图，在图形上直接求解线性规划问题，只适用于有2个决策变量或能够转化为2个决策变量的线性规划问题

从图解法中直观地见到，当线性规划问题的可行域非空时，它是有界或无界凸多边形。若线性规划问题存在最优解，它一定在有界可行域的某个顶点得到；若在两个顶点同时得到最优解，则它们连线上的任意一点都是最优解，即有无穷多最优解

线性规划问题的标准形式

线性规划问题有各种不同的形式，目标函数有的要求max，有的要求min；约束条件可以是 $\leq$ ，也可以是 $\geq$ 形式的不等式，还可以是等式。决策变量一般是非负约束，但也允许在 $(-\infty, \infty)$ 范围内取值，即无约束。

将这些多种形式的数学模型统一变换为标准型式

\begin{aligned} &\text{目标函数} \quad \max \quad z = c_1x_1 + c_2x_2 + \cdots + c_nx_n \\ &\text{约束条件} \begin{cases} &a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1 \\ &a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2 \\ &\cdots \\ &a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n = b_m \\ &x_1, \cdots, x_n \geq 0 \end{cases} \end{aligned}

特点：目标函数求极大；等式约束；变量非负

如何变换为标准型：

若要求目标函数实现最小化，即 $\min z = CX$ 这时只需将目标函数最小化变换求目标函数最大化，即令 $z' = -z$ ，于是得到 $\max z' = -CX$ 。这就同标准型的目标函数的形式一致了
约束方程为不等式
- 约束方程为 $\leq$ 不等式，则可在 $\leq$ 不等式的左端加入非负松弛变量，把原 $\leq$ 不等式变为等式
- 约束方程为 $\geq$ 不等式，则可在 $\geq$ 不等式的左端减去非负松弛变量，把不等式约束条件变为等式约束条件
若存在取值无约束的变量 $x_k$ ，可令 $x_k = x'_k - x''_k$ ，其中 $x'_k - x''_k \geq 0$

线性规划问题的解的概念

参考数理计划法-第三章用语定义部分

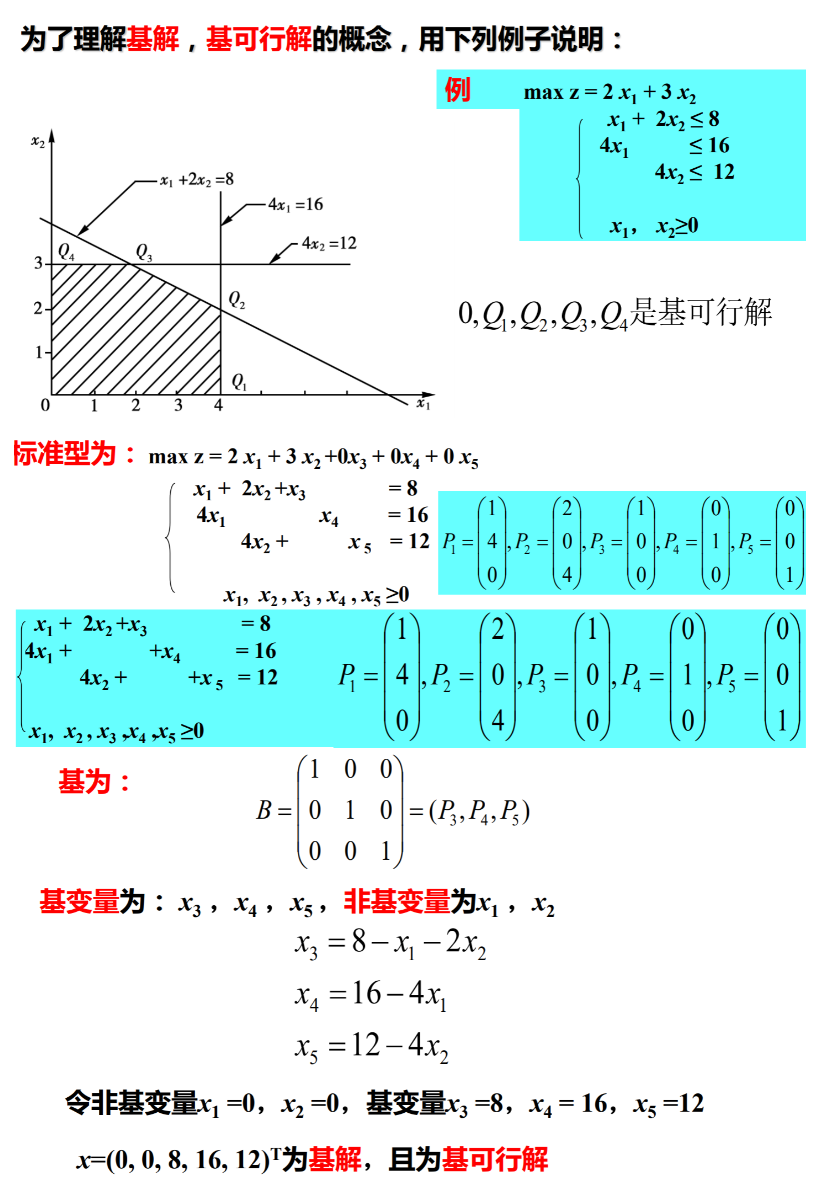
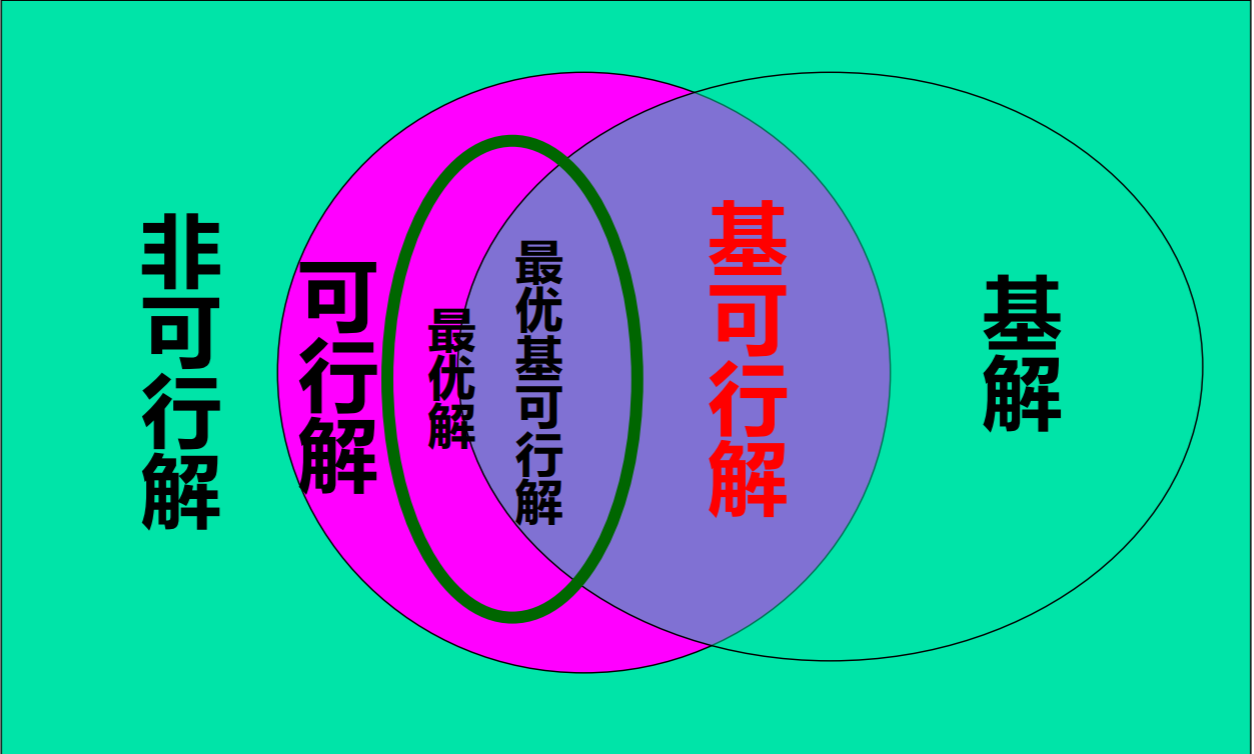
对应于基可行解的基，称为可行基
另外，基解中的非零分量的个数小于 $m$ 个时，该基解是退化解

线性规划问题的几何意义

基本概念

凸集

凸集（Convex set）：设 $D$ 是 $n$ 维欧氏空间的一个点集，若 $D$ 中的任意两点 $x^{(1)}, x^{(2)}$ 的连线上的一切点 $x$ 仍在 $D$ 中，则称 $D$ 为凸集。即：若 $D$ 中的任意两点 $x^{(1)}, x^{(2)} \in D$ ，存在 $0 < \alpha < 1$ 使得

x = \alpha x^{(1)} + (1 - \alpha)x^{(2)} \in D

则称 $D$ 为凸集

线性规划的可行域是凸集，任意两个凸集的交集也是凸集

凸组合

设 $X^{(1)}, X^{(2)}, \cdots, X^{(k)}$ 是 $n$ 维欧式空间 $E$ 中的 $k$ 个点。若存在 $\mu_1, \cdots, \mu_k$ ，且 $0 \leq \mu_i \leq 1, i = 1, \cdots, k$ ；

\sum_{i=1}^k \mu_i = 1

使得 $X = \mu_1 X^{(1)} + \cdots \mu_k X^{(k)}$ ，则称 $X$ 为 $X^{(1)}, X^{(2)}, \cdots, X^{(k)}$ 的凸组合。当 $0 < \mu_i < 1$ 时，称为严格凸组合

凸组合是一类特殊的线性组合，是若干个点在某种特定意义下的非负线性组合：

在R1维的空间 $a, b$ 两点的凸组合 $x$ ，就是以 $a, b$ 为端点的线段上的点
在R2维的空间里，两个向量的凸组合，就是连接这两个向量的顶点的线段上的点
三个向量的凸组合所表示的点的全体就是以这三个向量的端点为顶点的三角形的边界和内部的点

顶点

设 $K$ 是凸集， $X \in K$ ；若 $X$ 不能用不同的两点 $X^{(1)} \in K$ 和 $X^{(2)} \in K$ 的线性组合表示为

X = \alpha X^{(1)} + (1 - \alpha)X^{(2)}, \quad 0 < \alpha < 1

则称 $X$ 为 $K$ 的一个顶点(或极点)

凸集内点与其顶点之间的关系：若可行解集 $D$ 是有界的凸集，则 $D$ 中任意一点 $x$ ，都可表示成 $D$ 的顶点的凸组合

几个定理

定理1：若线性规划问题存在可行域，则其可行域 $D = \lbrace X \ |\ \sum_{j=1}^n P_jx_j = b, \quad x_j \geq 0 \rbrace$ 是凸集

引理1：线性规划问题的可行解 $x = (x_1, \cdots, x_n)^T$ 为基可行解的充要条件是 $X$ 的正分量所对应的系数列向量是线性独立的

定理2：线性规划问题的基可行解 $X$ 对应于可行域 $D$ 的顶点

定理3：若可行域有界，线性规划问题的目标函数一定可以在其可行域的顶点上达到最优

定理4：若线性规划有可行解，则必有基可行解

定理5：若线性规划有最优解，则必有最优基可行解

总结：

线性规划问题的所有可行解构成的集合（可行域）是凸集，也可能为无界域，它们有有限个顶点，线性规划问题的每个基可行解对应可行域的一个顶点

若线性规划问题有最优解，必在可行域的某个顶点达到最优解

虽然顶点数目是有限的(它不大于 $C_n^m$ 个)，若采用“枚举法”找所有基可行解，然后一一比较，最终可能找到最优解。但当 $n,m$ 的数较大时，这种办法是行不通的

单纯形法

单纯形法是求解线性规划问题的通用方法。是美国数学家G.B.丹捷格于1947年首先提出来的

详细参考以前日志数理计划法-第三章単体法

它的理论根据是：线性规划问题的可行域是 $n$ 维向量空间 $\mathbb{R}^n$ 中的多面凸集，其最优值如果存在必在该凸集的某顶点处达到。顶点所对应的可行解称为基可行解。

单纯形法的基本思想是：

先找出一个基可行解，对它进行鉴别，看是否是最优解
若不是，则按照一定法则转换到另一改进的基可行解,再鉴别
若仍不是，则再转换，按此重复进行
因基可行解的个数有限，故经有限次转换必能得出问题的最优解
如果问题无最优解也可用此法判别

对偶问题与灵敏度分析

详细参考以前日志数理计划法-第三章双对性

运输问题

运输问题的数学模型

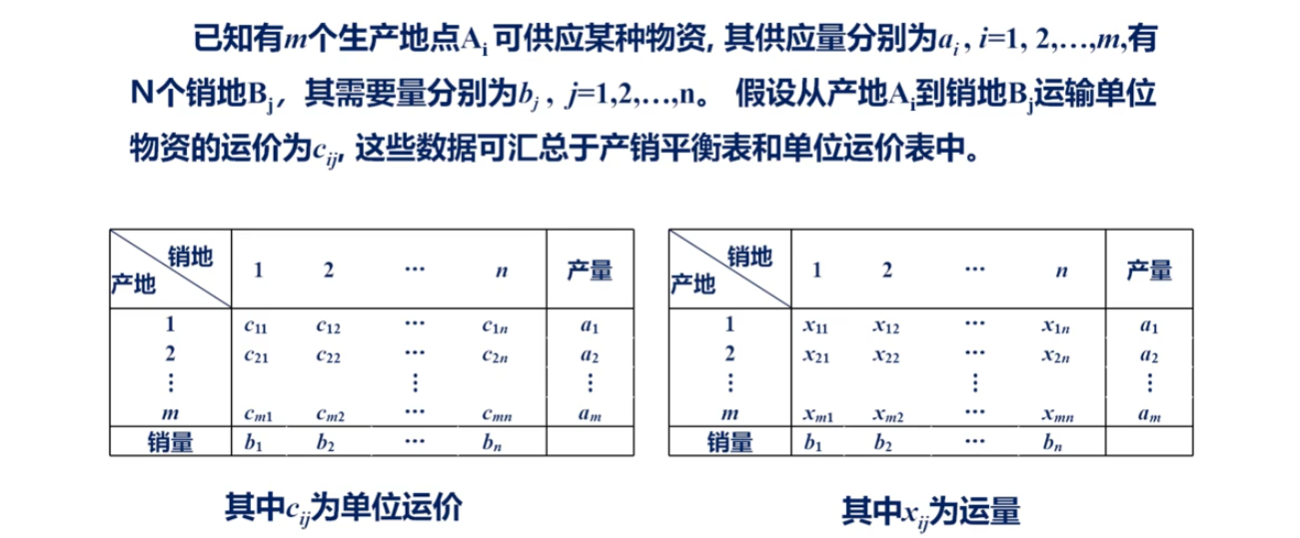
若用 $x_{ij}$ 表示从 $A_i$ 到 $B_j$ 的运量，那么在产销平衡( $\sum_{i=1}^m a_i = \sum_{j=1}^n b_j$ )的条件下，要求得总运费最小的调运方案，可求解以下数学模型

\begin{aligned} &\text{目标函数} \quad \min \quad z = \sum_{i=1}^m \sum_{j=1}^n b_j c_{ij}x_{ij} \\ &\text{约束条件} \begin{cases} &\sum_{i=1}^m x_{ij} = b_j, \quad j = 1, 2, \cdots, n \\ &\sum_{j=1}^n x_{ij} = a_i, \quad i = 1, 2, \cdots, m \\ &x_{ij} \geq 0 \end{cases} \end{aligned}

运输问题实际上是一个特殊的线性规划问题

产销平衡问题： $\sum_{i=1}^m a_i = \sum_{j=1}^n b_j$
产销不平衡问题： $\sum_{i=1}^m a_i \neq \sum_{j=1}^n b_j$

产销平衡的运输问题有最优解，有界闭区间内的连续函数一定有最大和最小值。由于有以上特征，所以求解运输问题时，可用比较简便的计算方法，习惯上称为表上作业法

表上作业法

表上作业法是单纯形法在求解运输问题时的一种简化方法，其实质是单纯形法。但具体计算和术语有所不同。可归纳为：

找出初始基可行解。即在 $(m \times n)$ 产销平衡表上用最小元素法或伏格尔(Vogel)法给出 $m + n - 1$ 个数字，称为数字格。它们就是初始基变量的取值
求各非基变量的检验数，即在表上计算空格的检验数，判别是否达到最优解。如已是最优解，则停止计算，否则转到下一步
确定换入变量和换出变量，找出新的基可行解。在表上用闭回路法调整
重复(2)、(3)直到得到最优解为止

产销不平衡的运输问题及其求解方法

前面所讲表上作业法，都是以产销平衡为前提条件的，但是实际问题中产销往往是不平衡的。就需要把产销不平衡的问题化成产销平衡的问题

目标规划

整数规划

动态规划

图与网络规划

网络计划技术

存储论

排队论

决策论

决策（Decision Making）是一种对已知目标和方案的选择过程，当人们已知确定需实现的目标是什么，根据一定的决策准则，在供选方案中做出决策的过程

决策分析的基本概念

决策：狭义决策认为决策就是做决定，单纯强调最终结果，广义决策认为将管理过程的行为都纳入决策范畴，决策贯穿于整个管理过程中

决策目标：决策者希望达到的状态，工作努力的目的。一般而言，在管理决策中决策者追求的当然是利益最大化

决策准则：决策判断标准，备选方案的有效性度量

决策属性：决策方案的性能，质量参数，特征和约束，如技术指标，重量，年龄，声誉等，用于评价它达到目标的程度和水平

科学决策过程：任何科学决策的形成都必须执行科学的决策程序。决策最忌讳的就是决策者拍脑袋决策，只有经历过预决策 $\rightarrow$ 决策 $\rightarrow$ 决策后三个阶段，才有可能产生科学的决策

决策问题的组成

决策者：决策的主体，一个人或团体
决策：两个以上可供选择的行动方案
状态（事件）：决策实施后可能遇到的自然状况
状态概率：对各状态发生可能性大小的主观估计
结局（损益）：当决策实施后遇到状态时所产生的效益（利润）或损失（成本）

决策分析基本分类

分类	内容
按影响范围	战略决策，策略决策，执行决策
按决策环境	确定型决策，不确定型决策，风险型决策
按决策结构	程序化决策，半程序化决策，非程序化决策
按描述方法	定性化决策，定量化决策
按目标数量	单目标决策，多目标决策
按连续性	单级决策，序贯决策
按决策者数量	个人决策，群决策
按问题大小	宏观决策，微观决策

不确定型决策

由于在不确定决策中，各种决策环境是不确定的，所以对于同一个决策问题，用不同的方法求值，将会得到不同的结论，在现实生活中，同一个决策问题，决策者的偏好不同，也会使得处理相同问题的原则方法不同

悲观主义准则maxmin

策略值为：

v = \max_i \lbrace \min_j a_{ij} \rbrace

	需求量大 $S_1$	需求量中 $S_2$	需求量小 $S_3$	$\min$	$\max$
生产产品1	800	320	-250	-250
生产产品2	600	300	-200	-200
生产产品3	300	150	50	50
生产产品4	400	250	100	100	100

乐观主义准则maxmax

策略值为：

v = \max_i \lbrace \max_j a_{ij} \rbrace

	需求量大 $S_1$	需求量中 $S_2$	需求量小 $S_3$	$\max$	$\max$
生产产品1	800	320	-250	800	800
生产产品2	600	300	-200	600
生产产品3	300	150	50	300
生产产品4	400	250	100	400

最小后悔值准则(Minmax regret criterion)

最小机会损失准则

编制机会损失表： $r_{ij} = \lbrace \max_j \lbrace a_{ij} \rbrace - a_{ij} \rbrace$
找出每个方案的最大机会损失 $Z_i$ ： $Z_i = \max_i \lbrace r_{ij} \rbrace$
选择最小的机会损失值： $Z_i^* = \min_i \lbrace Z_i \rbrace$
对应的方案记为所选决策方案

其含义是当某一事件发生后，由于决策者没有选用收益最大的策略，而形成的损失值

	需求量大 $S_1$	需求量中 $S_2$	需求量小 $S_3$
生产产品1	800	320	-250
生产产品2	600	300	-200
生产产品3	300	150	50
生产产品4	400	250	100

后悔矩阵

	需求量大 $S_1$	需求量中 $S_2$	需求量小 $S_3$	$\max$	决策结果
生产产品1	0	0	350	350
生产产品2	200	20	300	300	300
生产产品3	500	170	50	500
生产产品4	400	70	0	400

$Z_2^* = \min_i \lbrace Z_i \rbrace = 300$

等可能性原则

乐观系数法

层次分析法(AHP)

数据包络分析法(DEA)

DEA (数据包络分析)介绍及 python3 实现

博弈论(Game Theory)

何为博弈

所谓博弈是指在一定的游戏规则约束下，基于直接相互作用的环境条件，各参与人数依据所掌握的信息，选择各自的策略（行动），以实现利益最大化的过程

博弈就是你中有我，我中有你。由于直接相互作用（互动），每个博弈参与者的得益不仅取决于自己的策略（行动），还取决于其他参与者的策略（行动）。

博弈的核心在于整体思维基础上的理性换位思考，用他人的得益去推测他人的策略（行动），从而选择最有利于自己的策略（行动）

古诺模型：参加博弈的双方以各自在同一时间内相互独立的产量作为决策的变量，是一个产量竞争模型
伯川德模型：该模型与古诺模型的不同之处在于，企业把其产品的价格而不是产量作为竞争手段和决策变量，通过制定一个最优的销售价格来实现利润最大化
斯塔克尔伯格模型：该模型分析的是这么一种市场竞争：企业A先决定一个产量，然后企业B可以观察到这个产量，并根据所观察到的产量来决定它自己的产量

博弈论(Game Theory)：是一种研究人们怎么做策略（行动）选择及其最后的均衡结果会是什么的理论

博弈论的分类

博弈论的分类：合作博弈和非合作博弈

合作博弈：指参与者能够达成一种具有约束力的协议，在协议范围内选择有利于双方的策略
非合作博弈：指参与者无法达成这样一种协议

也可以分为：静态博弈和动态博弈

静态博弈：指在博弈中，参与者同时选择，或虽非同时选择，但是在逻辑时间上是同时的
动态博弈：指在博弈中，参与者的行动有先后顺序，且后行动者能够观察到先行动者的行动

还可分为：完全信息博弈与不完全信息博弈

完全信息博弈：指在博弈中，每个参与者对其他参与者的类型，策略空间及损益函数都有准确的信息
不完全信息博弈：总有一些信息不是所有参与者都知道的

	静态	动态
完全信息	完全信息静态博弈 $\quad$ 纳什均衡	完全信息动态博弈 $\quad$ 子博弈精炼纳什均衡
不完全信息	不完全信息静态博弈 $\quad$ 贝叶斯纳什均衡	不完全信息动态博弈 $\quad$ 精炼贝叶斯纳什均衡

还可分为：零和博弈与非零和博弈

零和博弈：指博弈前的损益总和与博弈后的损益总和相等
非零和博弈：指博弈后的损益大于（小于）博弈前的损益总和

Hi, Qiang

简介