在解决只有单个目标的复杂系统优化问题时,进化算法(EA)的优势得到了充分的体现。然而,现实世界中的优化问题通常是多属性的,一般是对多个目标的同时优化。多数情况下,被同时优化的多个目标之间是相互作用且相互冲突的,为了达到总目标的最优化,通常需要对相互冲突的子目标进行综合考虑,即对各子目标进行折衷(tradeoffs) 。由此,针对多个目标的优化问题,出现了多目标进化算法MOEA
按进化机制 的不同,MOEA可分为三类:
基于分解的MOEA(decomposition-based MOEA) :处理多目标优化问题时,最直接的方法,也是比较早期所使用的方法就是聚集函数 方法,这种方法将被优化的所有子目标组合(combine)或聚集(aggregate)为单个目标,从而将多目标优化问题转换为单目标优化问题基于支配关系的MOEA(domination-based MOEA) :这种方法的基本思路是基于Pareto的适应度分配策略,从当前进化群体中找出所有非支配个体 基于指标的MOEA(indicator-based MOEA) :基于指标的MOEA使用性能评价指标来引导搜索过程和对解的选择过程
按决策方式 不同,可以将MOEA分为三大类:
前决策技术(priori technique) :指在MOEA搜索之前就输入决策信息,然后通过MOEA运行产生一个解提供给决策者。主要优点是简单,易于实现,同时具有较高的效率;最大的不足是限制了搜索空间,从而不能找出所有的可能解后决策技术(posteriori technique) :通过运行MOEA产生一组解提供决策者选择,是最常用的方法,也是研究成果最多的方法交互决策技术(progressive technique) :决策与搜索或搜索与决策的交互过程,在此过程中既可能用到前决策技术,也可能用到后决策技术。不足之处是难以定义决策偏好,同时效率比较低
多目标优化问题的一般描述如下:
给定决策空间 X = ( x 1 , x 2 , ⋯ , x n ) \mathbf{X} = (x_1, x_2, \cdots, x_n) X = ( x 1 , x 2 , ⋯ , x n )
g i ( X ) ≥ 0 , i = 1 , 2 , ⋯ , k h i ( X ) = 0 , i = 1 , 2 , ⋯ , l \begin{aligned}
&g_i(\mathbf{X}) \geq 0, \quad i = 1, 2, \cdots, k
\\
&h_i(\mathbf{X}) = 0, \quad i = 1, 2, \cdots, l
\end{aligned}
g i ( X ) ≥ 0 , i = 1 , 2 , ⋯ , k h i ( X ) = 0 , i = 1 , 2 , ⋯ , l
设有 r r r r r r
f ( X ) = ( f 1 ( X ) , f 2 ( X ) , ⋯ , f r ( X ) ) \mathbf{f(X)} = (f_1(\mathbf{X}), f_2(\mathbf{X}), \cdots, f_r(\mathbf{X}))
f ( X ) = ( f 1 ( X ) , f 2 ( X ) , ⋯ , f r ( X ) )
寻求 f ( X ∗ ) = ( x 1 ∗ , x 2 ∗ , ⋯ , x n ∗ ) \mathbf{f(X^*)} = (x_1^*, x_2^*, \cdots, x_n^*) f ( X ∗ ) = ( x 1 ∗ , x 2 ∗ , ⋯ , x n ∗ ) f ( X ∗ ) \mathbf{f(X^*)} f ( X ∗ )
在多目标优化中,对于不同的子目标函数可能有不同的优化目标,有的可能是最大化目标函数,也有的可能是最小化目标函数:
最小化所有的目标函数
最大化所有的目标函数
最小化部分子目标函数,而最大化其他子目标函数
为了方便,可以把各子目标优化函数统一转化为最小化或最大化,例如,将最大化转为最小化可以表示为:
max f i ( X ) = − min ( − f i ( X ) ) \max f_i(\mathbf{X}) = -\min (-f_i(\mathbf{X}))
max f i ( X ) = − min ( − f i ( X ) )
为了统一,没有特别的说明,统一为求总目标的最小化,即
min f ( X ) = ( f 1 ( X ) , f 2 ( X ) , ⋯ , f r ( X ) ) \min \mathbf{f(X)} = (f_1(\mathbf{X}), f_2(\mathbf{X}), \cdots, f_r(\mathbf{X}))
min f ( X ) = ( f 1 ( X ) , f 2 ( X ) , ⋯ , f r ( X ) )
两个变量(个体)x x x y y y ( 2 , 6 ) (2, 6) ( 2 , 6 ) ( 3 , 5 ) (3, 5) ( 3 , 5 ) ( 2 , 6 ) (2, 6) ( 2 , 6 ) ( 3 , 8 ) (3, 8) ( 3 , 8 )
为此,讨论多目标个体之间非常重要的一种关系:支配关系
个体之间的支配关系
设 p p p q q q p p p 支配(dominate) q q q
对所有的子目标,p p p q q q f k ( p ) ≤ f k ( q ) ( k = 1 , 2 , ⋯ , r ) f_k(p) \leq f_k(q) \quad (k = 1, 2, \cdots, r) f k ( p ) ≤ f k ( q ) ( k = 1 , 2 , ⋯ , r )
至少存在一个子目标,使 p p p q q q ∃ l ∈ { 1 , 2 , ⋯ , r } ^\exist l \in \lbrace 1, 2, \cdots, r \rbrace ∃ l ∈ { 1 , 2 , ⋯ , r } f l ( p ) < f l ( q ) f_l(p) < f_l(q) f l ( p ) < f l ( q )
其中,r r r
此时,称 p p p 非支配的(non-dominated) ,或非劣的或占优的;q q q 被支配的(dominated) 。表示为 p ≻ q p \succ q p ≻ q ≻ \succ ≻
需要注意的是:这里定义的支配关系是"小"个体支配"大"个体,也可以按照完全相反的方式来定义支配关系,这取决于所求解的问题
上面所定义的支配关系是针对决策空间 的,类似的,可以在目标空间中 定义支配关系:
目标空间中的支配关系
设 U = ( u 1 , u 2 , ⋯ , u r ) \mathbf{U} = (u_1, u_2, \cdots, u_r) U = ( u 1 , u 2 , ⋯ , u r ) V = ( v 1 , v 2 , ⋯ , v r ) \mathbf{V} = (v_1, v_2, \cdots, v_r) V = ( v 1 , v 2 , ⋯ , v r ) U \mathbf{U} U V \mathbf{V} V U ≻ V \mathbf{U} \succ \mathbf{V} U ≻ V u k ≤ v k ( k = 1 , 2 , ⋯ , r ) u_k \leq v_k \quad (k = 1, 2, \cdots, r) u k ≤ v k ( k = 1 , 2 , ⋯ , r ) ∃ l ∈ { 1 , 2 , ⋯ , r } ^\exist l \in \lbrace 1, 2, \cdots, r \rbrace ∃ l ∈ { 1 , 2 , ⋯ , r } u l < v l u_l < v_l u l < v l
从上述定义可以看出:( 2 , 6 ) (2, 6) ( 2 , 6 ) ( 3 , 8 ) (3, 8) ( 3 , 8 ) ( 2 , 6 ) (2, 6) ( 2 , 6 ) ( 3 , 5 ) (3, 5) ( 3 , 5 )
值得注意的是:决策空间中的支配关系与目标空间中的支配关系是一致的 ,这一点由个体之间的支配关系的定义可以看出,因为决策空间中的支配关系实质上是由目标空间中的支配关系决定的
此外,个体之间的支配关系还有程度上的差异:
弱非支配(weak nondominance) :若不存在 X ∈ Ω \mathbf{X} \in \Omega X ∈ Ω f k ( X ) < f k ( X ∗ ) ( k = 1 , 2 , ⋯ , r ) f_k(\mathbf{X}) < f_k(\mathbf{X}^*) \quad (k = 1, 2, \cdots, r) f k ( X ) < f k ( X ∗ ) ( k = 1 , 2 , ⋯ , r ) X ∗ ∈ Ω \mathbf{X}^* \in \Omega X ∗ ∈ Ω 弱非支配解(a weakly nondominated solution)
强非支配(strong nondominance) :若不存在 X ∈ Ω \mathbf{X} \in \Omega X ∈ Ω f k ( X ) ≤ f k ( X ∗ ) ( k = 1 , 2 , ⋯ , r ) f_k(\mathbf{X}) \leq f_k(\mathbf{X}^*) \quad (k = 1, 2, \cdots, r) f k ( X ) ≤ f k ( X ∗ ) ( k = 1 , 2 , ⋯ , r ) i ∈ { 1 , 2 , ⋯ , r } i \in \lbrace 1, 2, \cdots, r \rbrace i ∈ { 1 , 2 , ⋯ , r } f i ( X ) < f i ( X ∗ ) f_i(\mathbf{X}) < f_i(\mathbf{X}^*) f i ( X ) < f i ( X ∗ ) X ∗ ∈ Ω \mathbf{X}^* \in \Omega X ∗ ∈ Ω 强非支配解(a strongly nondominated solution)
由上述定义可以看出:
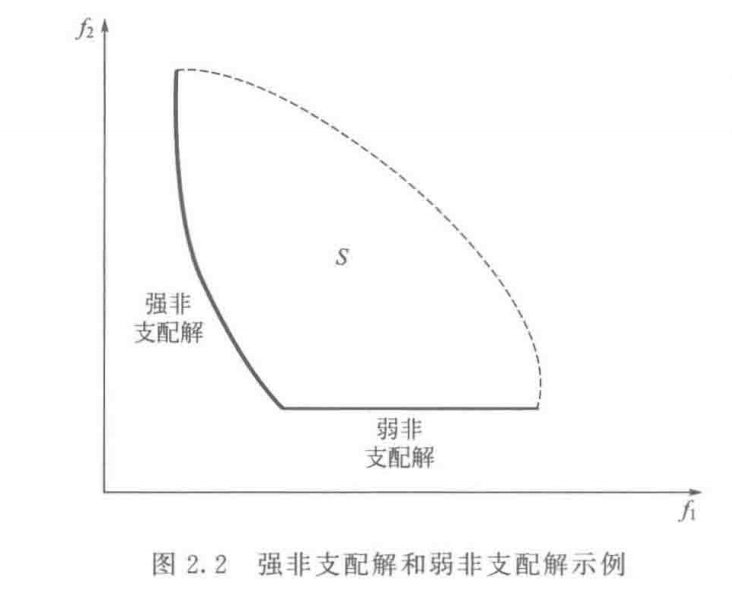
如果 X ∗ \mathbf{X}^* X ∗ X ∗ \mathbf{X}^* X ∗
如上图,在目标空间中强非支配解均落在粗曲线上,弱非支配解则落在细的直线上
在多目标优化中,由于是对多个子目标的同时优化,而这些被同时优化的子目标之间往往又是互相冲突的,照顾了一个子目标的"利益",同时必然导致其他至少一个子目标的"利益"收到损失。因此,针对一个多目标优化问题,没有绝对的或者说是唯一的最好解
多目标优化中的最优解通常称为Pareto最优解(Pareto optimum solution) ,一般地,可以描述如下:
给定一个多目标优化问题 f ( X ) \mathbf{f(X)} f ( X ) f ( X ∗ ) \mathbf{f(X^*)} f ( X ∗ )
f ( X ∗ ) = o p t X ∈ Ω f ( X ) \mathbf{f(X^*)} = \mathop{opt}\limits_{\mathbf{X} \in \Omega}\mathbf{f(X)}
f ( X ∗ ) = X ∈ Ω o pt f ( X )
其中 f : Ω → R r f:\Omega \rightarrow \mathbb{R}^r f : Ω → R r Ω \Omega Ω 可行解集 ,即
Ω = { X ∈ R n ∣ g i ( X ) ≥ 0 , h j ( X ) = 0 ( i = 1 , 2 , ⋯ , k ; j = 1 , 2 , ⋯ , l ) \Omega = \lbrace \mathbf{X} \in \mathbb{R}^n \ |\ g_i(\mathbf{X}) \geq 0, h_j(\mathbf{X}) = 0 \quad (i = 1, 2, \cdots, k; j = 1, 2, \cdots, l)
Ω = { X ∈ R n ∣ g i ( X ) ≥ 0 , h j ( X ) = 0 ( i = 1 , 2 , ⋯ , k ; j = 1 , 2 , ⋯ , l )
称 Ω \Omega Ω 决策变量空间(决策空间) ,向量函数 f ( X ) \mathbf{f(X)} f ( X ) Ω ⊆ R n \Omega \subseteq \mathbb{R}^n Ω ⊆ R n Π ⊆ R r \Pi \subseteq \mathbb{R}^r Π ⊆ R r Π \Pi Π 目标函数空间(目标空间)
多目标进化算法的优化过程是,针对每一代进化群体,寻找出其当前最优个体(即当前最优解),称一个进化群体的当前最优解为非支配解(non-dominated solution) 或着 非劣解(non-inferior solution) ;所有非支配解的集合称为当前进化群体的非支配集(non-dominated solution set, NDSet) 或着 非劣解集 ,并使非支配集不断逼近真正的最优解集,最终达到最优,即使 N D S e t ∗ ⊆ { X ∗ } NDSet^* \subseteq \lbrace \mathbf{X}^* \rbrace N D S e t ∗ ⊆ { X ∗ } N D S e t ∗ NDSet^* N D S e t ∗
为了更好地理解Pareto最优解,下面讨论它在目标函数空间中的表现形式。简单地说,一个多目标优化问题的Pareto最优解集在其目标函数空间中的表现形式就是它的Pareto最优边界 。Pareto最优边界 P F ∗ PF^* P F ∗ P F T r u e PF_{True} P F T r u e
给定一个多目标优化问题 min f ( X ) \min \mathbf{f(X)} min f ( X ) { X ∗ } \lbrace \mathbf{X}^* \rbrace { X ∗ }
P F ∗ = { f ( X ) = ( f 1 ( X ) , f 2 ( X ) , ⋯ , f r ( X ) ) ∣ X ∈ { X ∗ } } PF^* = \lbrace \mathbf{f(X)} = (f_1(\mathbf{X}), f_2(\mathbf{X}), \cdots, f_r(\mathbf{X})) \ |\ \mathbf{X} \in \lbrace \mathbf{X}^* \rbrace \rbrace
P F ∗ = { f ( X ) = ( f 1 ( X ) , f 2 ( X ) , ⋯ , f r ( X ) ) ∣ X ∈ { X ∗ } }
需要注意Pareto最优解集和Pareto最优边界之间的联系和区别 :
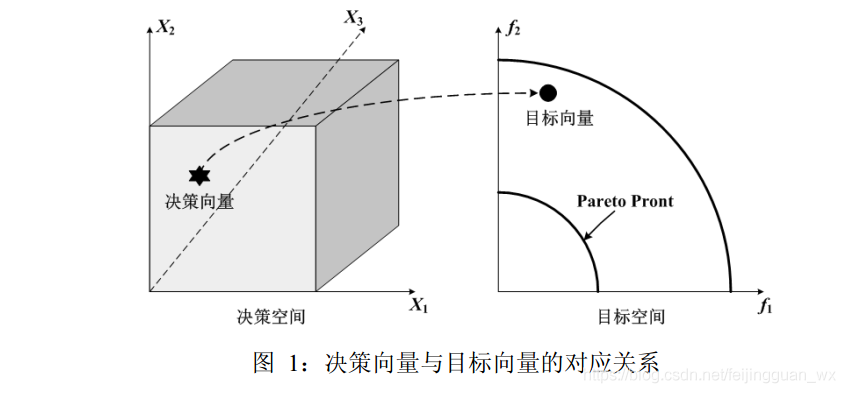
多目标优化是从决策空间 Ω ⊆ R n \Omega \subseteq \mathbb{R}^n Ω ⊆ R n Π ⊆ R r \Pi \subseteq \mathbb{R}^r Π ⊆ R r P ∗ P^* P ∗ 决策向量空间 的一个子集,即有 P ∗ ⊆ Ω ⊆ R n P^* \subseteq \Omega \subseteq \mathbb{R}^n P ∗ ⊆ Ω ⊆ R n 目标向量空间 的一个子集,即 P F ∗ ⊆ Π ⊆ R r PF^* \subseteq \Pi \subseteq \mathbb{R}^r P F ∗ ⊆ Π ⊆ R r
一个多目标问题的最优解 X ∗ ∈ P ∗ \mathbf{X}^* \in P^* X ∗ ∈ P ∗ Y ∗ = min f ( X ∗ ) ∈ P F ∗ \mathbf{Y}^* = \min \mathbf{f(X^*)} \in PF^* Y ∗ = min f ( X ∗ ) ∈ P F ∗
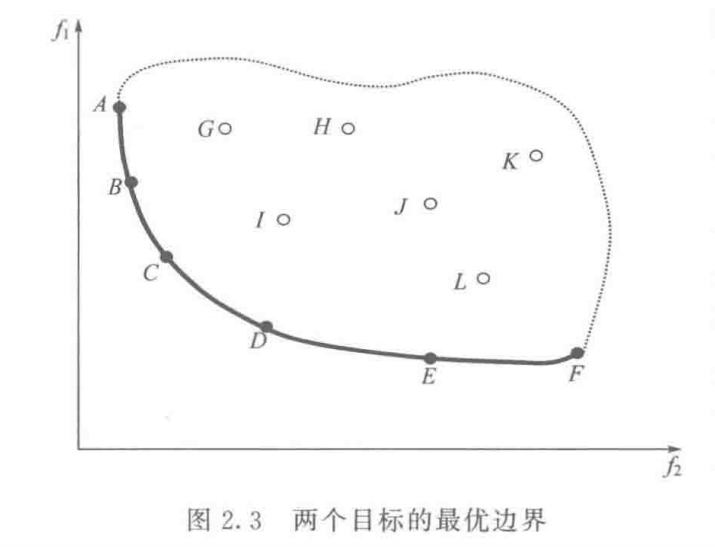
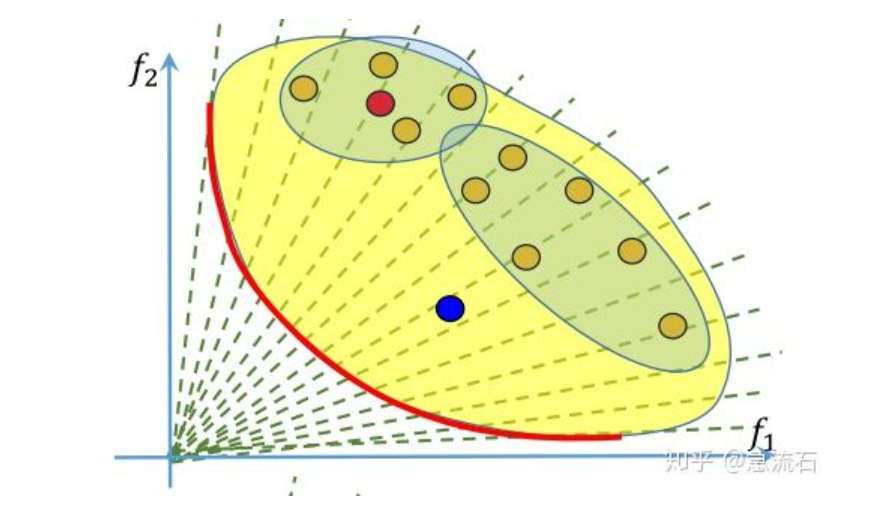
如图,最优边界上的点(或个体)A,B,C,D,E,F是Pareto最优解 ,它们属于目标空间
在目标空间中,最优解是目标函数的切点,它总是落在搜索区域的边界线(面)上。图中,粗线段表示两个优化目标的最优边界 ;三个优化目标的最优边界构成一个曲面 ;三个以上的最优边界则构成超曲面
图中,实心点A,B,C,D,E,F均处在最优边界上,它们都是最优解,是非支配的 ;空心点G,H,I,J,K,L落在搜索区域内,但不在最优边界上,不是最优解,是被支配的(dominated) ,它们直接或间接受最优边界上的最优解支配。
多目标遗传算法在优化过程中,初始时随机产生一个进化群体 Pop 0 p_0 p 0 p 0 p_0 p 0 N D S e t 0 NDSet_0 N D S e t 0 N D S e t 0 NDSet_0 N D S e t 0 { X ∗ } \lbrace \mathbf{X}^* \rbrace { X ∗ } N D S e t 0 NDSet_0 N D S e t 0 N D S e t 0 NDSet_0 N D S e t 0 N D S e t 1 NDSet_1 N D S e t 1 N D S e t 1 NDSet_1 N D S e t 1 N D S e t 1 NDSet_1 N D S e t 1 N D S e t 1 NDSet_1 N D S e t 1 N D S e t 0 NDSet_0 N D S e t 0 N D S e t 1 NDSet_1 N D S e t 1 N D S e t 0 NDSet_0 N D S e t 0 { X ∗ } \lbrace \mathbf{X}^* \rbrace { X ∗ } N D S e t i NDSet_i N D S e t i i → ∞ i \rightarrow \infty i → ∞ lim i → ∞ N D S e t i = N D S e t ∗ \lim_{i \rightarrow \infty} NDSet_i = NDSet^* lim i → ∞ N D S e t i = N D S e t ∗ N D S e t ∗ ⊆ { X ∗ } NDSet^* \subseteq \lbrace \mathbf{X}^* \rbrace N D S e t ∗ ⊆ { X ∗ }
分解策略是传统数学规划中解决多目标优化问题的基本思路。在给定权重偏好或者参考点信息的情况下,分解方法通过线性或者非线性方式将原多目标问题各个目标进行聚合,得到单目标优化问题,并利用单目标优化方法求得单个Pareto最优解。为得到整个Pareto前沿的逼近,张青富和李辉于2007年提出了基于分解的多目标进化算法(MOEA based on decomposition, MOEA/D)(Zhang Q et al, 2007)
下面先介绍分解策略中三类常用的聚合函数,然后再讨论MOEA/D
权重聚合方法(weighted sum approach) :是一种常用的线性多目标聚合方法(Hillermeier, 2001),其目标函数聚合形式定义为:
min g w s ( x ∣ λ ) = ∑ i = 1 m λ i f i ( x ) \min g^{ws}(\mathbf{x} \ |\ \bm{\lambda}) = \sum_{i = 1}^m \lambda_i f_i(x)
min g w s ( x ∣ λ ) = i = 1 ∑ m λ i f i ( x )
其中,x ∈ Ω x \in \Omega x ∈ Ω 决策向量 ,λ = ( λ 1 , λ 2 , ⋯ , λ m ) T \bm{\lambda} = (\lambda_1, \lambda_2, \cdots, \lambda_m)^T λ = ( λ 1 , λ 2 , ⋯ , λ m ) T 权重向量 ,满足 λ i ≥ 0 , i = 1 , ⋯ , m \lambda_i \geq 0, i = 1, \cdots, m λ i ≥ 0 , i = 1 , ⋯ , m ∑ i = 1 m λ i = 1 \sum_{i = 1}^m \lambda_i = 1 ∑ i = 1 m λ i = 1
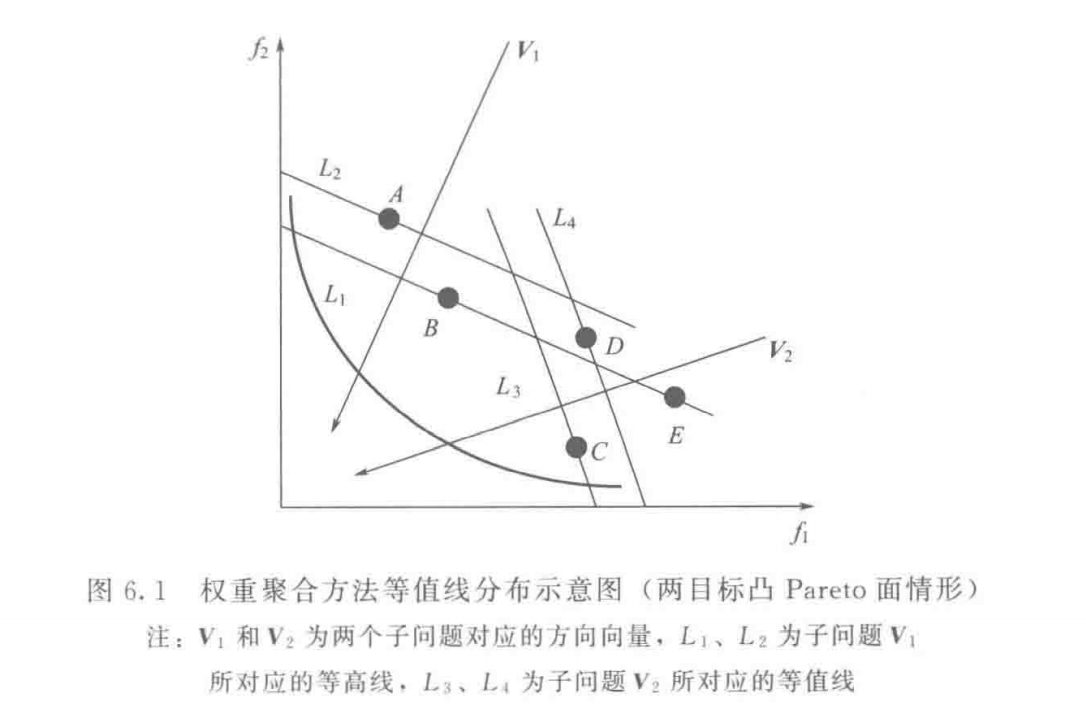
如图6.1,权重聚合方法的等值线为一族与方向向量垂直的平行直线 。由图可知,当最小化问题的真实Pareto前沿面为凸状 时,单个最优等值线与Pareto前沿面相交于一个切点 ,即上式描述问题的最优解
MOEA/D算法中同时考虑优化多权重聚合函数 ,所获得的最优解集能很好地逼近真实Pareto前沿面。在处理高维目标空间问题时,权重聚合方法被广泛运用
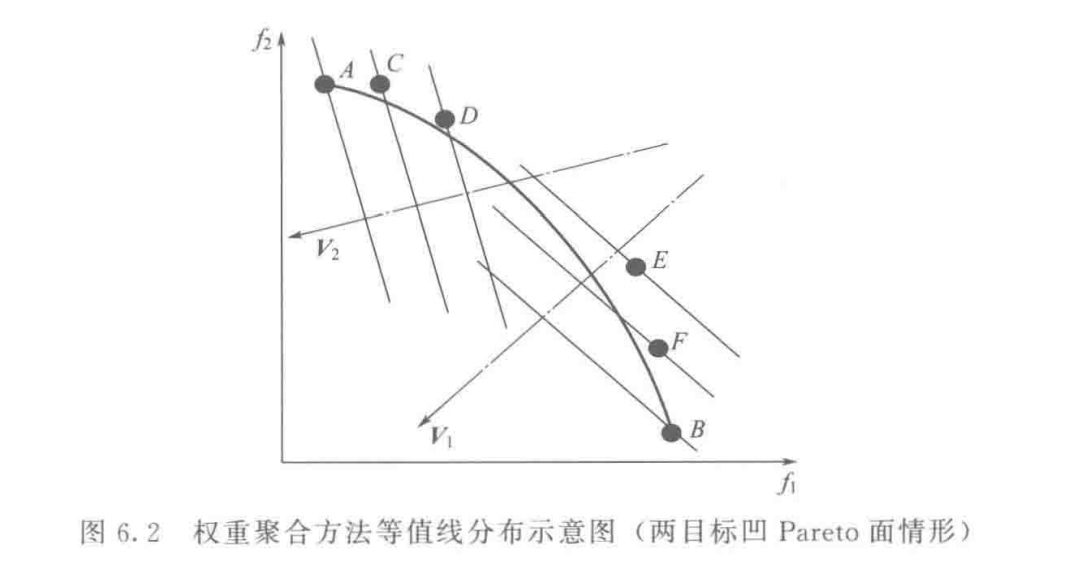
当最小化问题的真实Pareto前沿面为凹状 时,所有的权重聚合函数的最优解位于Pareto面的边缘区域 。这是因为位于Pareto面中间部分的解具有较差的适应度值,也就是说,相比Pareto面边缘的解具有更大的 g w s ( x ∣ λ ) g^{ws}(\mathbf{x} \ |\ \bm{\lambda}) g w s ( x ∣ λ )
如图6.2,个体E,F与B互不支配,但对应的方向向量在 V 1 \mathbf{V}_1 V 1 V 2 \mathbf{V}_2 V 2 权重聚合方法不能很好地处理真实Pareto面为凹状的问题
切比雪夫方法(Tchebycheff approach) :是一种非线性多目标聚合方法(Jaszkiewicz, 2002),其聚合函数定义如下:
min g t c h e ( x ∣ λ , z ∗ ) = max 1 ≤ i ≤ m { λ i ∣ f i ( x ) − z i ∗ ∣ } \min g^{tche}(\mathbf{x} \ |\ \bm{\lambda}, \mathbf{z}^*) = \max_{1 \leq i \leq m} \lbrace \lambda_i \ |\ f_i(\mathbf{x}) - \mathbf{z}_i^* \ |\ \rbrace
min g t c h e ( x ∣ λ , z ∗ ) = 1 ≤ i ≤ m max { λ i ∣ f i ( x ) − z i ∗ ∣ }
其中,z ∗ = min { f i ( x ) ∣ x ∈ Ω } , i ∈ { 1 , 2 , ⋯ , m } \mathbf{z}^* = \min \lbrace f_i(\mathbf{x}) \ |\ \mathbf{x} \in \Omega \rbrace, i \in \lbrace 1, 2, \cdots, m \rbrace z ∗ = min { f i ( x ) ∣ x ∈ Ω } , i ∈ { 1 , 2 , ⋯ , m } λ \bm{\lambda} λ
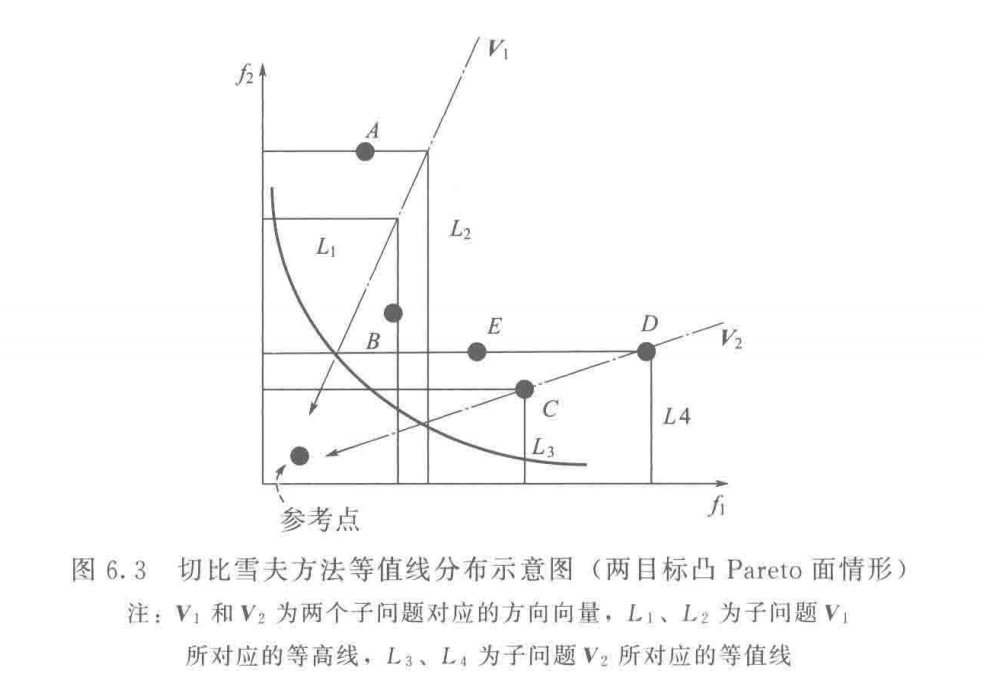
以其中一组权重向量 λ \lambda λ z z z 理想点 ,m m m 目标函数的个数 ,x x x 决策变量 。我们结合下面图说明,有两个目标函数 f 1 f_1 f 1 f 2 f_2 f 2 λ 1 ∗ ∣ f 1 ( x ) − z 1 ∣ \lambda_1 * | f_1(x) - z_1 | λ 1 ∗ ∣ f 1 ( x ) − z 1 ∣ λ 2 ∗ ∣ f 2 ( x ) − z 2 ∣ \lambda_2 * | f_2(x) - z_2 | λ 2 ∗ ∣ f 2 ( x ) − z 2 ∣ 这个数值越大说明什么呢?说明在这个目标函数上离理想点越远 。假设 λ 1 ∗ ∣ f 1 ( x ) − z 1 ∣ \lambda_1 * | f_1(x) - z_1 | λ 1 ∗ ∣ f 1 ( x ) − z 1 ∣ x x x z z z g ( x ) = λ 1 ∗ ∣ f 1 ( x ) − z 1 ∣ g(x) = \lambda_1 * | f_1(x) - z_1 | g ( x ) = λ 1 ∗ ∣ f 1 ( x ) − z 1 ∣ λ 1 ∗ ∣ f 1 ( x ) − z 1 ∣ \lambda_1 * | f_1(x) - z_1 | λ 1 ∗ ∣ f 1 ( x ) − z 1 ∣ λ 2 ∗ ∣ f 2 ( x ) − z 2 ∣ \lambda_2 * | f_2(x) - z_2 | λ 2 ∗ ∣ f 2 ( x ) − z 2 ∣
首先解释等高线为什么是这样的 。单看 f 1 f_1 f 1 λ i ∗ ∣ f i ( x ) − z i ∣ \lambda_i * | f_i(x) - z_i | λ i ∗ ∣ f i ( x ) − z i ∣ f 1 f_1 f 1 因为另外两个量是不变的 ),即纵坐标相等,所以 f 1 f_1 f 1 f 2 f_2 f 2
那么,图中的等高线是横竖相交且刚好交在权重向量的方向上的 ,这是巧合吗?可以稍微来证明一下,可知,对于任何一个可行的切比雪夫值 (自己叫的),我们从 f 1 f_1 f 1 f 1 f_1 f 1 y y y f 2 f_2 f 2 f 2 f_2 f 2 x x x ( x , y ) (x,y) ( x , y ) λ 1 ∗ ( y − z 1 ) = λ 2 ∗ ( x − z 2 ) \lambda_1 * (y - z_1) = \lambda_2 * (x - z_2) λ 1 ∗ ( y − z 1 ) = λ 2 ∗ ( x − z 2 ) ( y − z 1 ) / ( x − z 2 ) = λ 2 / λ 1 (y - z_1) / (x - z_2) = \lambda_2 / \lambda_1 ( y − z 1 ) / ( x − z 2 ) = λ 2 / λ 1
如图6.3,展示了两个切比雪夫聚合子问题 V 1 \mathbf{V}_1 V 1 V 2 \mathbf{V}_2 V 2 V 1 \mathbf{V}_1 V 1 λ 1 = ( 0.3 , 0.7 ) T \bm{\lambda}_1 = (0.3, 0.7)^T λ 1 = ( 0 . 3 , 0 . 7 ) T v = ( 0.7 , 0.3 ) T \mathbf{v} = (0.7, 0.3)^T v = ( 0 . 7 , 0 . 3 ) T V 2 \mathbf{V}_2 V 2 λ 2 = ( 0.7 , 0.3 ) T \bm{\lambda}_2 = (0.7, 0.3)^T λ 2 = ( 0 . 7 , 0 . 3 ) T v = ( 0.3 , 0.7 ) T \mathbf{v} = (0.3, 0.7)^T v = ( 0 . 3 , 0 . 7 ) T 切比雪夫聚合子问题权重向量与方向向量不一致
直观上看,在连续Pareto面情形下,切比雪夫子问题的最优解为方向向量与Pareto面的交点;在非连续Pareto面情形下,对应不同权重向量的子问题可能具有相同最优解 ,这是因为方向向量与Pareto面可能没有交点
不同于权重聚合子问题,切比雪夫子问题的等值线沿方向向量呈直角锯齿状 ,因此具有"更窄"的收敛接受区域。在处理高维问题时,切比雪夫方法限制收敛接受区域,因而能更好地保证种群地收敛性 。另外,切比雪夫方法既可以处理Pareto面为凸状地问题,也可以处理Pareto面为非凸形状的问题
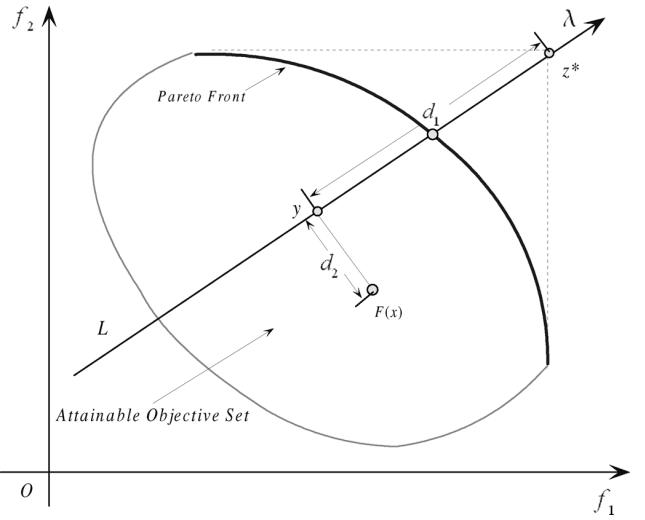
基于惩罚的边界交叉方法(penalty-based boundary intersection approach) :是由Zhang与Li与2007年提出的一种基于方向的分解方法,其具体定义如下:
{ min g p b i ( x ∣ λ , z ∗ ) = d 1 + θ d 2 d 1 = ∥ ( z ∗ − F ( x ) ) T λ ∥ ∥ λ ∥ d 2 = ∥ F ( x ) − ( z ∗ − d 1 λ ) ∥ \begin{aligned}
\begin{cases}
&\min g^{pbi}(\mathbf{x} \ |\ \bm{\lambda}, \mathbf{z}^*) = d_1 + \theta d_2
\\\\
&d_1 = \frac{\parallel (\mathbf{z}^* - F(\mathbf{x}))^T \bm{\lambda} \parallel}{\parallel \bm{\lambda} \parallel}
\\\\
&d_2 = \parallel F(\mathbf{x}) - (\mathbf{z}^* - d_1 \bm{\lambda}) \parallel
\end{cases}
\end{aligned}
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ min g p b i ( x ∣ λ , z ∗ ) = d 1 + θ d 2 d 1 = ∥ λ ∥ ∥ ( z ∗ − F ( x ) ) T λ ∥ d 2 = ∥ F ( x ) − ( z ∗ − d 1 λ ) ∥
其中,θ > 0 \theta > 0 θ > 0 预设参数(preset penalty parameter)
知算法放宽了对算法求出的解得要求,但加入了一个惩罚措施,说白了,就是你可以不把解生成在权重向量的方向上,但如果不在权重向量方向上,你就必须要接收惩罚,你距离权重向量越远,受的惩罚越厉害,以此来约束算法向权重向量的方向生成解
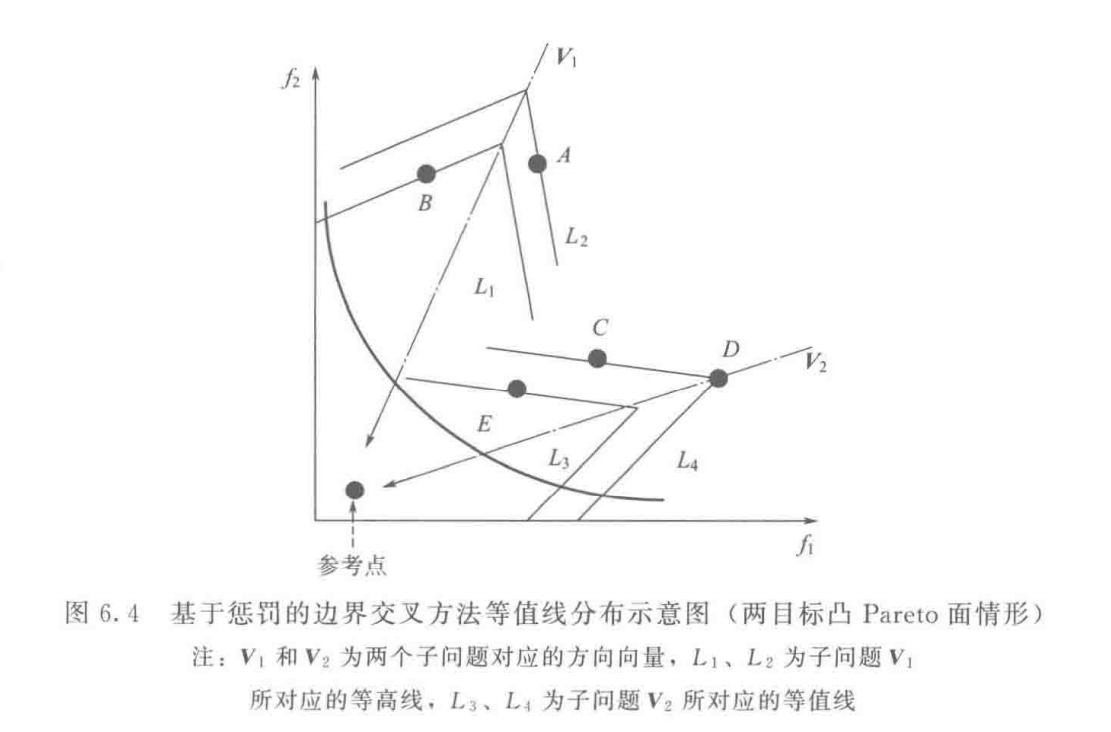
如图6.4中等值线分布情况,针对 V 1 \mathbf{V}_1 V 1 V 2 \mathbf{V}_2 V 2
基于惩罚的边界交叉方法需要计算两个距离,即 d 1 d_1 d 1 d 2 d_2 d 2 用于控制种群的分布性和收敛性 。需要注意的是,两者之间的平衡关系是通过调节参数 θ \theta θ θ \theta θ
MOEA/D算法的核心思想 :将多目标优化问题分解为一组单目标子问题或多个多目标子问题,利用子问题之间的邻域关系,通过协作的方式同时优化所有子问题,从而找到整个Pareto面的逼近。通常子问题的定义由权重向量 确定,子问题之间的邻域关系是通过计算权重向量之间的欧氏距离 来确定的
与其他MOEA算法不同,MOEA/D算法强调从邻域中选择父个体,通过交叉操作产生新个体,并在邻域中按照一定的规则进行种群更新 。因此,基于邻域的优化策略 是保证MOEA/D的搜索效率的重要特征。在进化过程中,针对某个子问题的高质量解一旦被搜索到,其好的基因信息就会迅速扩散至邻域内其他个体,从而加快种群的收敛速度
MOEA/D算法提供了一个基于分解策略的基本框架,其最大特点是分解与合作 。这里以基于切比雪夫方法最基本的MOEA/D算法,其基本数据结构如下:
用于定义切比雪夫子问题的权重向量集合 为 { λ 1 , ⋯ , λ N } \lbrace \bm{\lambda}^1, \cdots, \bm{\lambda}^N \rbrace { λ 1 , ⋯ , λ N } 参考点 z \mathbf{z} z
每个子问题分配一个个体,所有个体 { x 1 , ⋯ , x N } \lbrace x^1, \cdots, x^N \rbrace { x 1 , ⋯ , x N } 当前进化种群 P P P
用于保存Pareto解的精英种群 为 E P EP E P
子问题邻域 为 N S 1 , ⋯ , N S N NS_1, \cdots, NS_N N S 1 , ⋯ , N S N
MOEA/D算法框架:
上述算法中,初始化步骤2通过计算权重向量之间的欧几里得距离来计算子问题的邻域关系 。事实上,输入的权重向量均匀性对于输出种群EP的均匀性有着重要影响
更新操作中步骤1基因重组为交叉算子和变异算子 ,可以根据问题选择恰当的算子,如SBC(simulated binary crossover)或者DE(differential evolution)
更新操作中步骤4在领域中比较修正解与种群当前个体 ,注意,该步骤中的领域大小以及替换个体的次数将会影响的种群的收敛性与多样性
更新操作中步骤5在EP中保存搜索过程中所有可能的非占优解 ,为保存有限个解,一些已有的密度估计方法可用于控制外部EP的大小
MOEA/D特性:
引入分解的概念,简单但是有效;
由于算法将MOP问题分解成子问题(单维度)进行计算,适配度分配和多样性控制的难度都有所降低;
相较NSGA-II和MOGLS算法MOEA/D具有更低的计算复杂度,但在许多场景下解得表现上更为出色;
弥补传统不是基于分解的算法难以找到一个简单方法来利用标量(单维度)优化算法的缺点;
分解思想说完了,下面我们说说如何生成新解。这个算法假设相邻的权重上的解相似,每个权重都有邻居。下面图中红色的点,它的邻居就是附近的四个点,用这四个点去生成新解。生成新解之后,就要替换邻域中的解了。这里面策略很多,可以随机替换邻域中两个解如果这个新解比他们好的话。如此,种群可以更新,最终收敛至近似的Pareto front
Srinivas和Deb于1993年提出了NSGA(non-dominated sorting in genetic algorithm)(Srinivas et al, 1994)。NSGA主要有以下三个方面不足:
没有最优个体(elitist)保留机制 。最优个体保留机制一方面可以提高MOEA的性能,同时也能防止优秀解的丢失共享参数问题 :在进化过程中,主要采用共享参数 σ s h a r e \sigma_{share} σ s h a r e 构造Pareto最优解集(通常是构造进化群体的非支配集)的时间复杂度高 :O ( r N 3 ) O(rN^3) O ( r N 3 )
为此,Deb等于2000年在NSGA的基础上,提出了NSGA-II(Deb et al, 2000)
在NSGA-II中,将进化群体支配关系分为若干层,第一层为进化群体的非支配个体集合 ,第二层为在进化群体中去掉第一层个体后所求得的非支配个体集合 ,第三层为在进化群体中去掉第一层和第二层个体后所求得的非支配个体集合 ,依此类推
选择操作首先考虑第一层非支配集,按照某种策略从第一层中选取个体;然后再考虑在第二层非支配个体集合中选择个体,以此类推,直至满足新进化群体的大小要求
设群体 P o p Pop P o p N N N P o p Pop P o p m m m P 1 , P 2 , ⋯ , P m P_1, P_2, \cdots, P_m P 1 , P 2 , ⋯ , P m
∪ p ∈ { P 1 , ⋯ , P m } P = P o p \cup_{p_\in \lbrace P_1, \cdots, P_m \rbrace} P = Pop ∪ p ∈ { P 1 , ⋯ , P m } P = P o p ∀ i , j ∈ { 1 , ⋯ , m } \forall i, j \in \lbrace 1, \cdots, m \rbrace ∀ i , j ∈ { 1 , ⋯ , m } i ≠ j i \neq j i = j P i ∩ P j = ∅ P_i \cap P_j = \varnothing P i ∩ P j = ∅ P 1 ≺ P 2 ≺ ⋯ ≺ P m P_1 \prec P_2 \prec \cdots \prec P_m P 1 ≺ P 2 ≺ ⋯ ≺ P m P k + 1 P_{k+1} P k + 1 P k P_k P k ( k = 1 , 2 , ⋯ , m − 1 ) (k = 1, 2, \cdots, m-1) ( k = 1 , 2 , ⋯ , m − 1 )
对群体 P o p Pop P o p 为了将其划分成若干个满足上述三个性质的互不相交的子群体
设两个向量 { n p } \lbrace n_p \rbrace { n p } { s p } \lbrace s_p \rbrace { s p } p ∈ P o p p \in Pop p ∈ P o p n p n_p n p p p p s p s_p s p p p p
n p = ∣ { q ∣ q ≺ p p , q ∈ P o p } ∣ s p = { q ∣ p ≺ q p , q ∈ P o p } \begin{aligned}
n_p &= |\lbrace q \ |\ q \prec p \quad p, q \in Pop \rbrace|
\\
s_p &= \lbrace q \ |\ p \prec q \quad p, q \in Pop \rbrace
\end{aligned}
n p s p = ∣ { q ∣ q ≺ p p , q ∈ P o p } ∣ = { q ∣ p ≺ q p , q ∈ P o p }
首先通过一个二重循环计算每个个体的 n p n_p n p s p s_p s p P 1 = ∣ { q ∣ n q = 0 , q ∈ P o p } ∣ P_1 = |\lbrace q \ |\ n_q = 0, q \in Pop \rbrace| P 1 = ∣ { q ∣ n q = 0 , q ∈ P o p } ∣ P k = { 所有个体 q ∣ n q − k + 1 = 0 } P_k = \lbrace \text{所有个体} q \ |\ n_q - k + 1 = 0 \rbrace P k = { 所有个体 q ∣ n q − k + 1 = 0 } P 2 , P 3 , ⋯ P_2, P_3, \cdots P 2 , P 3 , ⋯
算法6.2中的 P 1 P_1 P 1
第一部分用于计算 n i n_i n i s i s_i s i P 1 P_1 P 1 ( r N 2 ) (rN^2) ( r N 2 ) r r r N N N
第二部分用于求 P 2 , P 3 , ⋯ , P m P_2, P_3, \cdots, P_m P 2 , P 3 , ⋯ , P m 最坏情况下,一个规模为 N N N N N N m = N m = N m = N ,此时其时间复杂度为 O ( N 2 ) O(N^2) O ( N 2 )
由此可得,算法6.2的总时间复杂度为 O ( r N 2 ) + O ( N 2 ) O(rN^2) + O(N^2) O ( r N 2 ) + O ( N 2 ) O ( r N 2 ) O(rN^2) O ( r N 2 )
为了保持解群体的分布性和多样性,Deb等在文献中,首先通过计算进化群体中每个个体的群集距离 ,然后依据个体所处的层次及其群集距离,定义一个偏序集(partial order set) ,构造新群体时依次在偏序集中选择个体
在产生新群体时,通常将优秀且聚集密度比较小 的个体保留并参与下一代进化。聚集密度小的个体其聚集距离反而大 ,一个个体的聚集距离可以通过计算与其相邻的两个个体在每个子目标上的距离差之和来求取
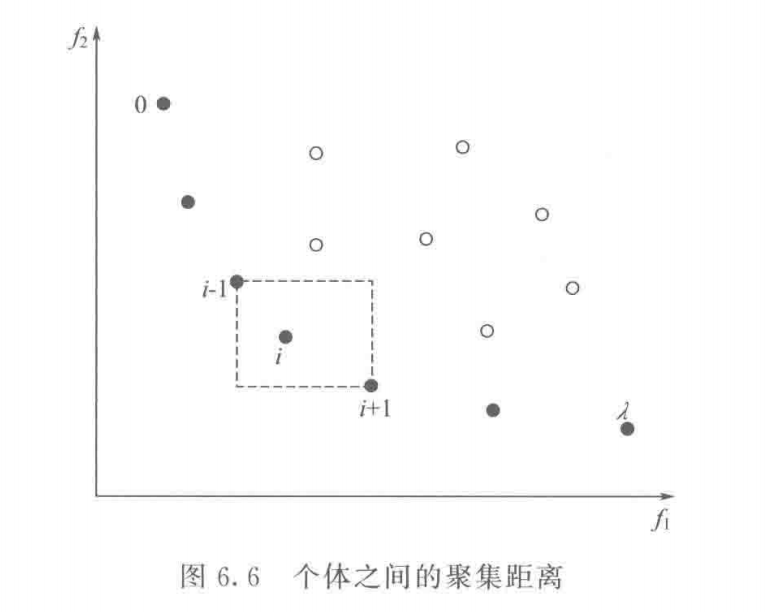
如上图,设有2个子目标 f 1 , f 2 f_1, f_2 f 1 , f 2 i i i 虚线四边形的长与宽之和 ,一般情况下,当有 r r r i i i
P [ i ] d i s t a n c e = ∑ k = 1 r ( P [ i + 1 ] . f k − P [ i − 1 ] . f k ) P[i]_{distance} = \sum_{k = 1}^r (P[i + 1].f_k - P[i - 1].f_k)
P [ i ] d i s t a n c e = k = 1 ∑ r ( P [ i + 1 ] . f k − P [ i − 1 ] . f k )
为了计算每个个体的聚集距离,需要对群体 P P P ,当采用最好的排序方法时(如快速排序,堆排序等),若群体规模为 N N N r r r O ( r N log N ) O(rN \log N) O ( r N log N )
在具体讨论NSGA-II之前,先讨论建立在进化群体上的一类偏序关系 ,因为NSGA-II在构造新群体时,将依据这种偏序关系进行选择操作 。定义进化群体的排序关系时,主要考虑以下2个因素:
个体 i i i i r a n k i_{rank} i r a n k i r a n k = k i_{rank} = k i r a n k = k i ∈ P k i \in P_k i ∈ P k
个体 i i i P [ i ] d i s t a n c e P[i]_{distance} P [ i ] d i s t a n c e
得到偏序关系的定义 如下:
定义6.1:设个体 i i i j j j ≺ n \prec_n ≺ n
i ≺ n j i f ( r r a n k < j r a n k ) o r ( i r a n k = = j r a n k ) a n d ( P [ i ] d i s t a n c e > P [ j ] d i s t a m c e ) i \prec_n j \quad if(r_{rank} < j_{rank}) or (i_{rank} == j_{rank}) and (P[i]_{distance} > P[j]_{distamce})
i ≺ n j i f ( r r a n k < j r a n k ) o r ( i r a n k = = j r a n k ) a n d ( P [ i ] d i s t a n c e > P [ j ] d i s t a m c e )
定义6.1表明:当两个个体属于不同的分类排序子集时,优先考虑序号 i r a n k i_{rank} i r a n k i r a n k i_{rank} i r a n k
在算法6.4中,通过 F = n o n d o m i n a t e d − s o r t ( R t ) F = nondominated-sort(R_t) F = n o n d o m i n a t e d − s o r t ( R t ) F = ( F 1 , F 2 , ⋯ ) F = (F_1, F_2, \cdots) F = ( F 1 , F 2 , ⋯ )
如上图所示,分类子集 F 1 F_1 F 1 F 2 F_2 F 2 P t + 1 P_{t + 1} P t + 1 F 3 F_3 F 3 P t + 1 P_{t + 1} P t + 1 ∣ F 1 ∣ + ∣ F 2 ∣ + ⋯ + ∣ F i − 1 ∣ ≤ N |F_1| + |F_2| + \cdots + |F_{i - 1}| \leq N ∣ F 1 ∣ + ∣ F 2 ∣ + ⋯ + ∣ F i − 1 ∣ ≤ N ∣ F 1 ∣ + ∣ F 2 ∣ + ⋯ + ∣ F i ∣ > N |F_1| + |F_2| + \cdots + |F_i| > N ∣ F 1 ∣ + ∣ F 2 ∣ + ⋯ + ∣ F i ∣ > N F i F_i F i 临界层分类子集 ,上图中的 F 3 F_3 F 3
算法6.4的时间开销主要由三部分组成(r r r
构造分类子集(non-dominated sort):O ( r ( 2 N ) 2 ) O(r(2N)^2) O ( r ( 2 N ) 2 )
计算聚集距离(crowding distance assignment):O ( r ( 2 N ) log ( 2 N ) ) O(r(2N)\log (2N)) O ( r ( 2 N ) log ( 2 N ) )
构造偏序集(sorting on ≺ n \prec_n ≺ n O ( 2 N log ( 2 N ) ) O(2N \log (2N)) O ( 2 N log ( 2 N ) )
由此可得,算法6.4的总时间复杂度为 O ( r N 2 ) O(rN^2) O ( r N 2 ) 主要的时间开销花费在构造边界集 上,因此一个快速的构造分类子集(或构造非支配集)的方法有利于提高MOEA的效率
在多目标优化研究中,随着目标维数的增高,优化的难度呈指数级增长,通常将4个及以上目标的优化问题称为高维多目标优化问题
随着目标维数的增加,如NSGA-II和SPEA2这些经典的基于Pareto支配关系的MOEA面临许多困难:
搜索能力的退化:随目标维数的增加,种群中非支配的个体数目呈指数级增加,从而降低了进化过程的选择压力
用来覆盖整个Pareto前沿的非支配解的数目呈指数级增加
最优解集的可视化困难
对解集分布性评价的计算开销增大
重组操作效率降低:在较大的高维空间中,两个相距较远的父个体重组产生的子个体离父个体可能较远,使得种群局部搜索的能力减弱
近年来提出的一些有效方法用于求解高维多目标优化问题:
一类是基于Pareto支配关系 的算法,通过扩展Pareto支配区域来减少非支配个体的数目,如:ϵ − M O E A \epsilon-MOEA ϵ − M O E A
第二类是基于聚合的算法 ,使用聚合函数将多个目标聚合成一个目标进行优化,如:MOEA/D,NSGA-III,MSOPS
第三类是基于指标的算法 ,将性能评价指标用于比较两个种群或者两个个体之间的优劣,如:IBEA,SMS-EMOA,HypE
还有基于多样性保持机制的角度 ,提出了基于移动的多样性评估方法(SDE),并将其整合到SPEA2中,取得了很好的效果;此外,一些学者通过尝试减少目标个数的方法 来处理高维多目标优化问题,处理方法主要有主成分分析(PCA) ,基于最小目标子集的冗余目标消除算法 等
减少冗余目标或不重要目标,也是高维MOEA研究的一个重要方向
NSGA-II只能处理低维优化问题(目标维数小于等于3),因为随着优化问题目标维数的增加,种群中的非支配个体呈指数增加,使得Pareto支配关系很难区分个体之间的好坏
为此,Deb等于2013年提出了NSGA-III(the reference-point based many-objective NSGA-II)
NSGA-III总体框架于NSGA-II相似,如算法7.1所示:随机产生大小为 N N N P t P_t P t Q t Q_t Q t R t = P t ∪ Q t R_t = P_t \cup Q_t R t = P t ∪ Q t 2 N 2N 2 N N N N R t R_t R t F 1 , F 2 , ⋯ F_1, F_2, \cdots F 1 , F 2 , ⋯ ∣ F 1 ∪ F 2 ∪ ⋯ F l − 1 ∣ < N |F_1 \cup F_2 \cup \cdots F_{l-1}| < N ∣ F 1 ∪ F 2 ∪ ⋯ F l − 1 ∣ < N ∣ F 1 ∪ F 2 ∪ ⋯ F l ∣ > N |F_1 \cup F_2 \cup \cdots F_{l}| > N ∣ F 1 ∪ F 2 ∪ ⋯ F l ∣ > N F l F_l F l N N N
与NSGA-II不同的是,NSGA-III的临界层选择方法采用参考点方法 选择个体,以使种群具有良好的分布性
以下为NSGA-III的临界层选择方法
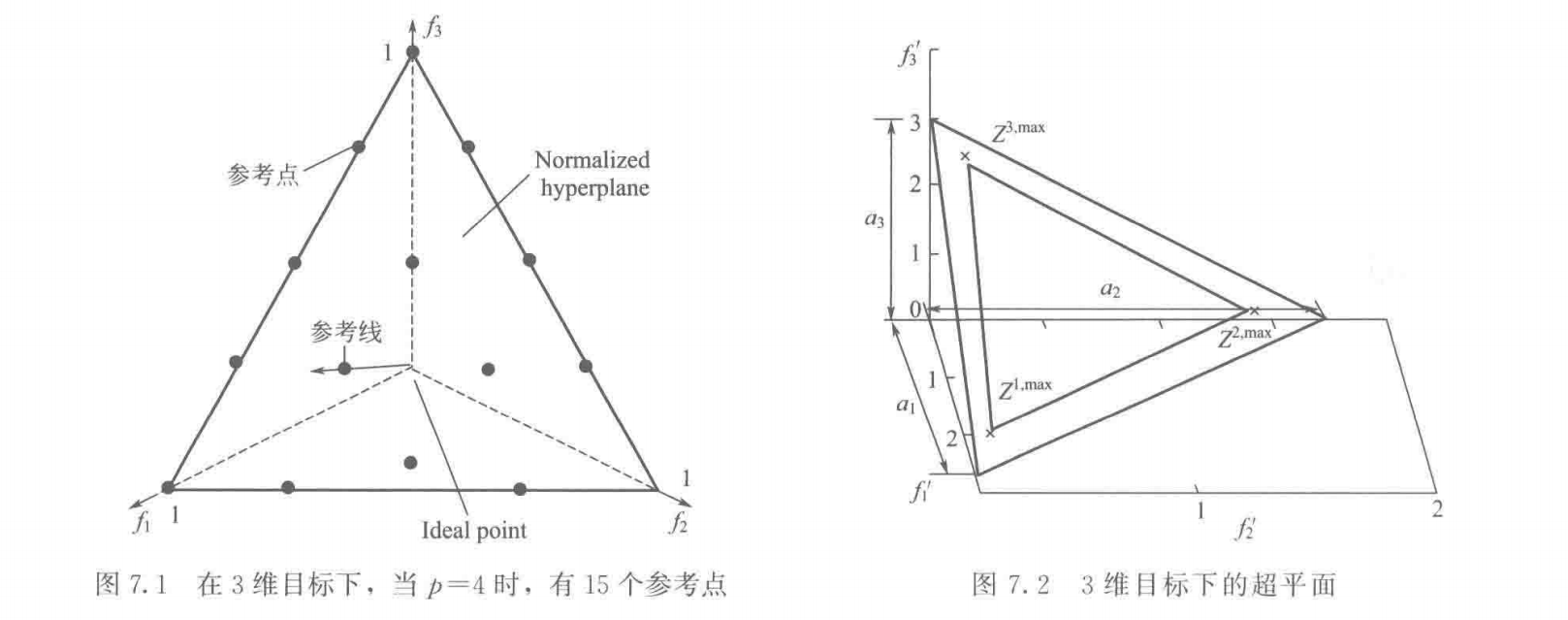
NSGA-III算法采用的是Das和Dennis于1998年提出的边界交叉构造权重的方法:在标准化超平面 上,根据
H = ( M + p − 1 p ) H = \binom{M + p - 1}{p}
H = ( p M + p − 1 )
均匀产生参考点,如果每一维目标被均匀分割成 p p p H H H
在环境选择过程中,NSGA-III除了强调支配关系外,还强调了各个参考点所关联的个体数目。当参考点均匀广泛的分布在整个标准化的超平面时,所选择的种群将会广泛地均匀分布在真实Pareto面上
首先,选取当前种群 S t S_t S t z i m i n ( i = 1 , 2 , ⋯ , M ) z_i^{min}(i = 1, 2, \cdots, M) z i m i n ( i = 1 , 2 , ⋯ , M ) z ‾ = z 1 m i n , z 2 m i n , ⋯ , z M m i n \overline{z} = z_1^{min}, z_2^{min}, \cdots, z_M^{min} z = z 1 m i n , z 2 m i n , ⋯ , z M m i n S t S_t S t f i ′ ( x ) = f i ( x ) − z i m i n f'_i(x) = f_i(x) - z_i^{min} f i ′ ( x ) = f i ( x ) − z i m i n z i , m a x z^{i, max} z i , m a x
A S F ( x , w ) = max i = 1 M f i ′ ( x ) / w i , x ∈ S t ASF(x, \mathbf{w}) = \max_{i = 1}^M f'_i(x) / \mathbf{w}_i, \quad x \in S_t
A S F ( x , w ) = i = 1 max M f i ′ ( x ) / w i , x ∈ S t
标量函数的最小值。其中 w \mathbf{w} w w i = 0 w_i = 0 w i = 0 1 0 − 6 10^{-6} 1 0 − 6
使用 M M M 截距 为 a i a_i a i
f i n ( x ) = f i ′ ( x ) a i − z i m i n = f i ( x ) − z i m i n a i − z i m i n i = 1 , ⋯ , M f_i^n(x) = \frac{f'_i(x)}{a_i - z_i^{min}} = \frac{f_i(x) - z_i^{min}}{a_i - z_i^{min}} \quad i = 1, \cdots, M
f i n ( x ) = a i − z i m i n f i ′ ( x ) = a i − z i m i n f i ( x ) − z i m i n i = 1 , ⋯ , M
其中 ∑ i = 1 M f i n = 1 \sum_{i = 1}^M f_i^n = 1 ∑ i = 1 M f i n = 1
最后,NSGA-III使用Das和Dennis提出的方法在上式所构造的超平面上设置参考点,其标准化过程如算法7.2:
参考点设置完成后,将进行关联操作,让种群中的个体分别关联到相应的参考点 :
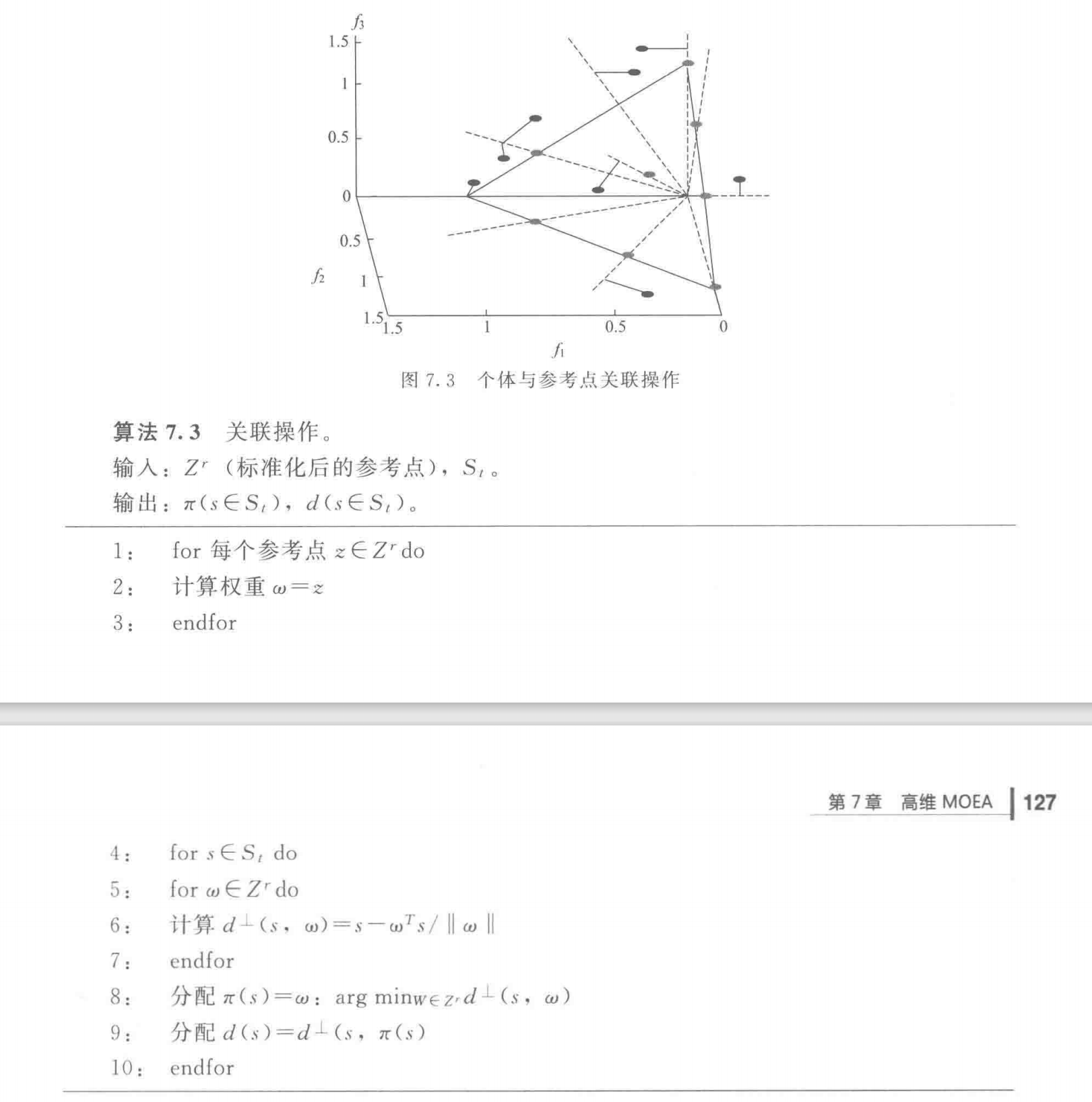
如算法7.3所示,首先需要将原点与参考点的连线作为该参考点在目标空间中的参考线(图7.3中虚线),然后计算 S t S_t S t
图7.3中灰色点代表参考点,黑色点代表目标空间中的个体,个体分别找到离它最近距离的参考线,然后将它与对应的参考点关联起来
通过关联操作后,可能出现以下情况:
NSGA-III记录了参考点 j j j P t + 1 = S t / F l P_{t + 1} = S_t / F_l P t + 1 = S t / F l ρ j \rho_j ρ j
在保留操作中,首先,NSGA-III选择关联数目最少的参考点 J m i n = { j : arg min j ρ j } J_{min} = \lbrace j: \argmin_j \rho_j \rbrace J m i n = { j : a r g m i n j ρ j } 随机 选择一个 j ‾ \overline{j} j
如果 ρ j = 0 \rho_j = 0 ρ j = 0 P t + 1 = S t / F l P_{t + 1} = S_t / F_l P t + 1 = S t / F l
在 F l F_l F l j ‾ \overline{j} j ρ j ‾ = ρ j ‾ + 1 \rho_{\overline{j}} = \rho_{\overline{j}} + 1 ρ j = ρ j + 1 P t + 1 P_{t + 1} P t + 1
在 F l F_l F l j ‾ \overline{j} j
当 ρ j ≥ 1 \rho_j \geq 1 ρ j ≥ 1 P t + 1 = S t / F l P_{t + 1} = S_t / F_l P t + 1 = S t / F l j ‾ \overline{j} j F l F_l F l j ‾ \overline{j} j ρ j ‾ = ρ j ‾ + 1 \rho_{\overline{j}} = \rho_{\overline{j}} + 1 ρ j = ρ j + 1 P t + 1 P_{t + 1} P t + 1
重复上述操作,直到 P t + 1 P_{t + 1} P t + 1 N N N
整个算法的最坏时间复杂度为 O ( N 2 log M − 2 N ) O(N^2 \log^{M - 2} N) O ( N 2 log M − 2 N ) O ( N 2 M ) O(N^2 M) O ( N 2 M )
这里记录一些从论文中学习到的算法知识点
MOEA/D-FRRMAB算法提出了一个新的自适应算子选择机制。该方法主要包括两部分:一是信用值积累,二是算子选择。其中,信用值积累主要由滑窗(sliding window)策略完成,滑窗大小为 W W W 适应值提升率 。滑窗由先进先出(First Input First Output, FIFO)队列组成,最近使用的算子的信用值被记录在滑窗尾部,已经记录过的从滑窗头部删除。滑窗中的每部分都包括算子的名称和其对应的使用值,该策略使用的主要目的是为了确保储存的使用值信息对应当前的搜索状态。**信用值(FIR)**的计算方式如下:
F I R i = p f i − c f i p f i FIR_i = \frac{pf_i - cf_i}{pf_i}
F I R i = p f i p f i − c f i
其中,p f i pf_i p f i c f i cf_i c f i i i i R e w a r d i Reward_i R e w a r d i 即每个算子在当前滑窗中的信用值之和 。然后对 R e w a r d i Reward_i R e w a r d i 降序排名 ,R a n k i Rank_i R a n k i i i i 排名较高的算子有更多机会被使用 。除此之外,算法引入了参数 D ∈ [ 0 , 1 ] D \in [0, 1] D ∈ [ 0 , 1 ] R e w a r d i Reward_i R e w a r d i D e c a y i Decay_i D e c a y i
D e c a y i = D R a n k i × R e w a r d i Decay_i = D^{Rank_i} \times Reward_i
D e c a y i = D R a n k i × R e w a r d i
之后,算法对算子 i i i
F R R i , t = D e c a y i ∑ j = 1 K D e c a y i FRR_{i, t} = \frac{Decay_i}{\sum_{j=1}^K Decay_i}
F R R i , t = ∑ j = 1 K D e c a y i D e c a y i
算子选择机制基于信用值来选择算子产生新的个体,该算法采用基于信用值的算子选择机制。在进化初期,每个算子具有相等的机会被算法选择,直到每个算子被使用后 FRRMAB 策略才会启用。算子具体的选择方式如下:
o p t = arg max i = { 1 , ⋯ , K } ( F R R i , t + C × 2 × ln ∑ j = 1 K n j , t n i , t ) op_t = \argmax_{i = \lbrace 1, \cdots, K \rbrace} (FRR_{i, t} + C \times \sqrt{\frac{2 \times \ln \sum_{j=1}^K n_{j, t}}{n_{i, t}}})
o p t = i = { 1 , ⋯ , K } a r g m a x ( F R R i , t + C × n i , t 2 × ln ∑ j = 1 K n j , t )