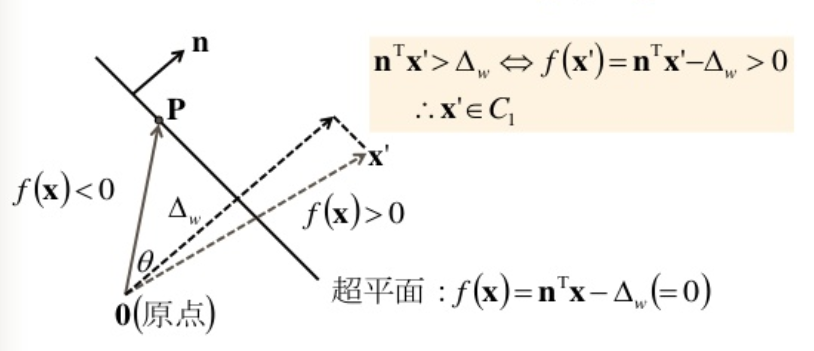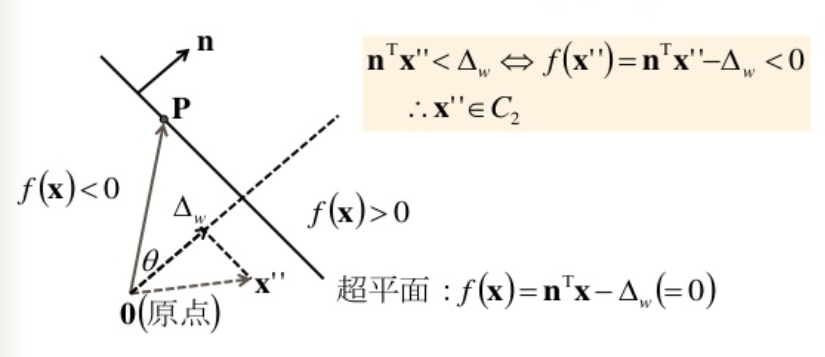Pattern Recognition

CS专业课学习笔记

Pattern recognition紹介

パターン認識は自然情報処理のひとつ。画像・音声などの雑多な情報を含むデータの中から、一定の規則や意味を持つ対象を選別して取り出す処理である

パターン認識が扱う問題

• 前立腺がんのリスク因子を特定する
• 録音された音声を分類する
• 個人属性情報(demographics)や、食習慣、検診記録から心臓発作になるかどうか予測する
• スパムメールを検出する
• 手書きの郵便番号を識別する
• 組織サンプルの遺伝子情報を使って癌のクラスわけを行う
• 衛星写真から、土地の利用目的分類を行う

機械学習・統計的学習とは

機械学習とは、人間が自然に行っている学習能力と同様に機能をコンピュータで実現しようとする技術や手法のこと。

統計的学習はモデリングに重点を置くのに対して、機械学習は、最適化理論からの学習のアプローチである場合は多い。

元々は、人工知能分野の一部として研究されていたが、機械学習は統計学と密接な関わりを持つようになり「統計的学習」と言われるようになった

応用分野:

• パターン認識
• データマイニング
• 自然言語処理
• 音声処理、画像処理
• バイオインフォマティクス(Bioinformatics)
• 脳科学
• 農業
• 経済・金融

パターン認識はICT(information and Computer Technology)の要素技術

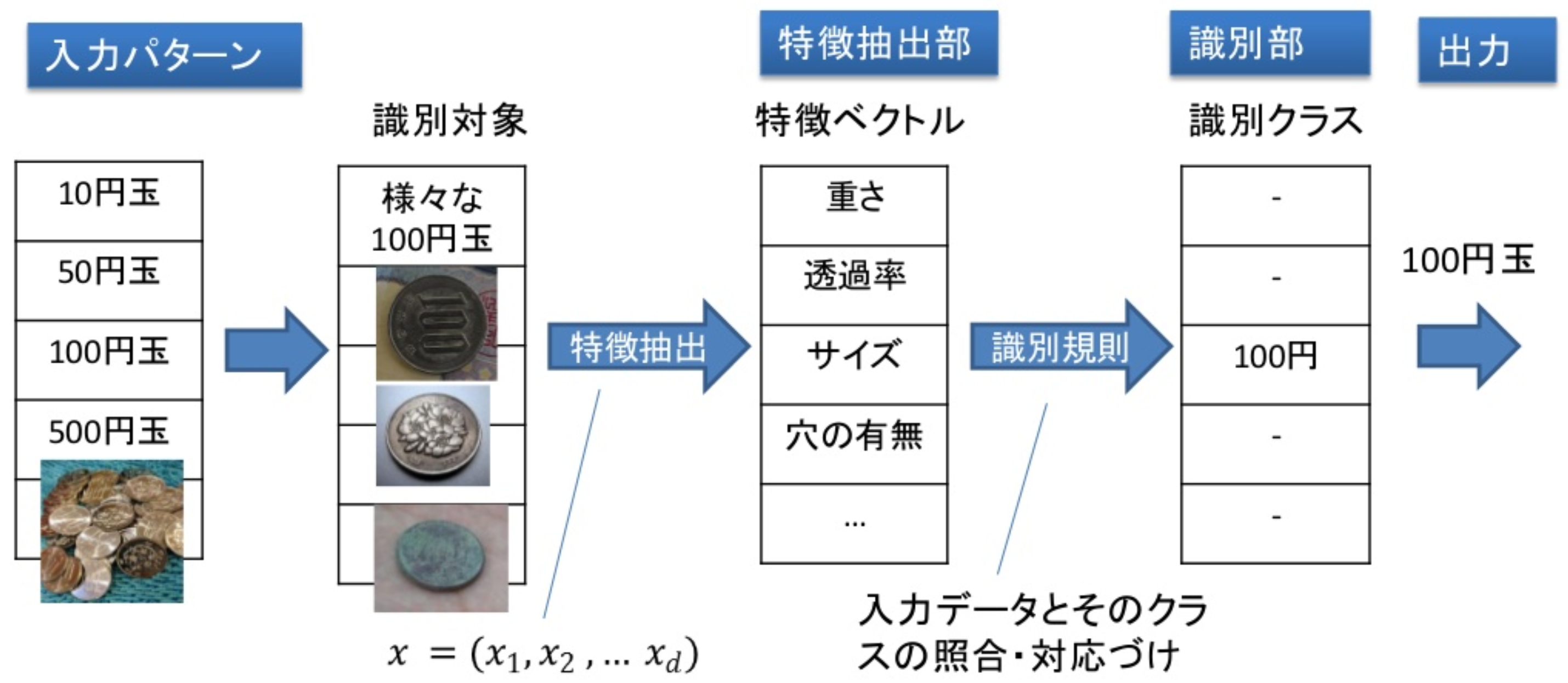
特徴抽出

入力データから抽出されるたくさんの特徴をまとめること

例: 硬貨の識別問題なら、硬貨の重さ、サイズ、穴の有無など

特徴ベクトル

特徴量をベクトルの形に並べたもの

このような特徴量のベクトルを入力として、予め用意しておいた「型・類型」に当てはめること

例: 硬貨の識別問題なら、1, 5, 10, 50, 100, 500円,(それ以外)のどれかの「パターン(型)」に対応させる

この識別(分類分け)するためにの規則のことを識別規則という

識別規則を作るためには、入力データとそのクラスを対にした、たくさんのデータ(学習データ)を学習する必要がある

学習データを用いて設計したシステムが、未知の入力データに対しても正しいクラスを識別できるかが問題で、そのような能力を汎化能力という。汎化性能の高い識別器を作ることが目的

特徴の型

抽出された特徴量は、定性的特徴(非数値データ)と定量的特徴(数値データ)に大別される

• 非数値データはさらに、名義尺度、順序尺度に分類される
  • 性別と血液型は順序関係がないから、名義尺度である
  • 一方、S, A, Bの成績評価や癌の進行を表すステージは順序関係があるので、順序尺度である
• 数値データもさらに、比例尺度、間隔尺度に分類される
  • 比例尺度は長さや重さなどゼロを基準に倍数の意味がある尺度である
  • 感覚尺度はテストの点や気温など、数値の間隔が意味を持つ尺度である

定性的な特徴を表現するために、符号を用いる。例えば、二つのクラスラベル([勝・敗])([合格・不合格])を表すのに、「1と-1」や「-1と1」で符号化する

パターン認識で扱う、型や類型などのクラスは定性的特徴である

識別規則と学習法

代表的な識別規則の構成法

• 事後確率による方法: ベイズの最大事後確率法(線形判別分析)
• 距離による方法: 最近傍法
• 関数値による方法: パーセプトロン型学習回路(ニューラルネットワーク、ロジスティック回帰)、サポートベクターマシン
• 決定木による方法

識別規則の構成法

入力データ$\mathbf{x}$からクラス$C_i \in \omega = \lbrace C_1, \cdots, C_k \rbrace$への写像を識別規則という

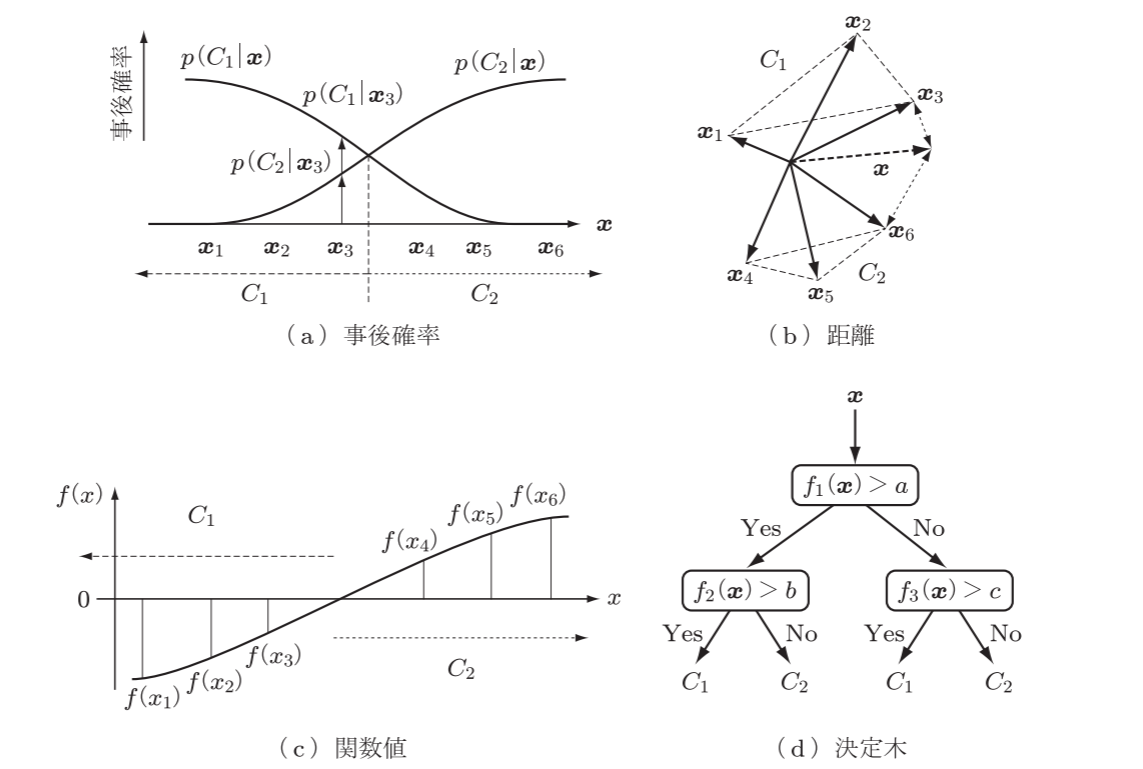
代表的な識別規則には、事後確率による方法、距離による方法、関数値による方法、決定木による方法がある

• 事後確率による方法: 特徴ベクトルの空間に確率分布を仮定し、事後確率が最大のクラスに分類する
  • ベイズ識別規則が代表例で、線形判別分析もこのクラスに該当する
• 距離による方法: 入力ベクトル$\mathbf{x}$の各クラスの代表ベクトルとの距離を最小にするクラスに分類する
  • 最近傍法が代表例
• 関数値による方法: 関数の正負、あるいは最大値(他クラスの場合)でクラスを決める
  • パーセプトロン型学習回路(ニューラルネットワーク、ロジスティック回帰)、サポートベクターマシンが代表例
• 決定木による方法: 識別規則の真偽に応じて次の識別規則を順序適用し、決定木でクラスを決める

教師付き学習(Supervised learning)

識別規則が関数値による方法としよう: $\mathbf{y} = f(\mathbf{x})$

2クラス問題の線形識別関数の場合、識別規則は

$$\begin{aligned} \mathbf{y} = f(\mathbf{x};\mathbf{w}) = w_1x_1 + \cdots + w_dx_d = \mathbf{w}^T\mathbf{x} \end{aligned}$$

ここで、$\mathbf{x}$は入力ベクトル(特徴量のベクトル)、$\mathbf{w}$はパラメータで、識別クラスは$y$の正負によって決まるとする。

学習の目的は、パラメータ$\mathbf{w}$を調整すること

学習データは入力データ(特徴ベクトル)$\mathbf{x}$とクラスデータ$y$(教師データ)のペア$(\mathbf{x}, y)$である

2クラスの識別問題を正負の値で識別する場合, クラスデータを$t \in \lbrace -1, 1 \rbrace$で表すとする.

他クラスの場合は, ダミー変数表現を用いて$\mathbf{t} = (0, 1, 0, 0, 0, 0, 0, 0, 0, 0)^T$のように表すと, この表現は, 10クラスある中の2番目のクラスに属していることを表している.

学習データが$N$個あるとき, 入力データと教師データの対を次のように表す.

$$(\mathbf{x}_i, \mathbf{t}_i), \quad i = 1, \cdots, N$$

教師なし学習(unsupervised learning)

入力データのクラスを自動的に生成する場合がある。クラスタリング(Cluster analysis)など。この時、クラスデータ$y$は存在しないので、教師なし学習という。自己組織型学習ともいう

一部のデータに教師を付き、他は教師なしで学習を行うことを半教師付き学習(形質導入学習)という

汎化能力

学習とは、学習データに対する識別関数の出力値と教師データとの誤差が最小になるように、識別関数のパラメータを調整することである。

しかし、学習で得られた識別関数が学習データに含まれていない未知データに対して上手く働くという保証はない。

そこで、学習データから取り除いておいたテストデータを用いて性能評価を行い、未知データに対する動作をテストデータに対する誤り率という形で予測することが行われている。

未知のデータに対する識別能力を汎化能力という

未知のデータに対する識別誤差を汎化誤差という

学習データとテストデータの作り方

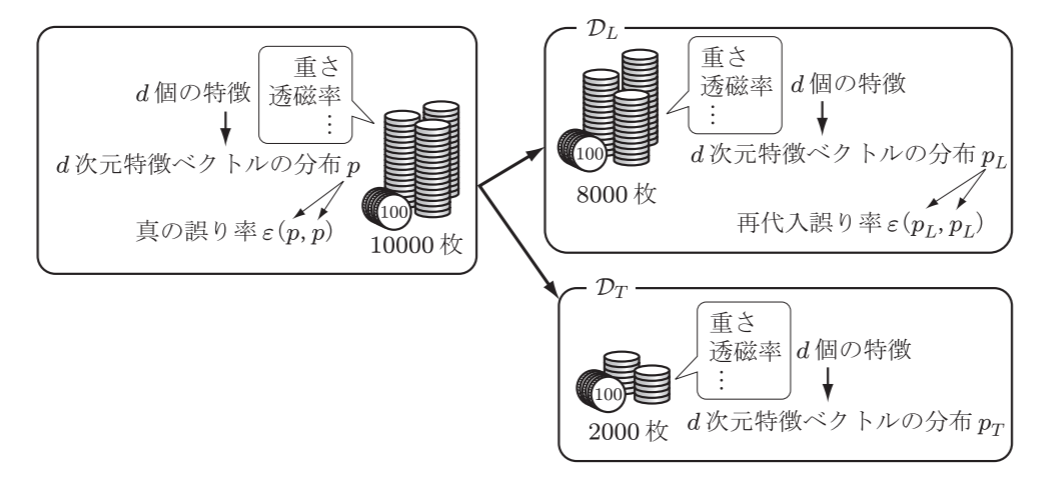
• 手元にあるデータを分割して学習データセット: $\mathcal{D}_L$とテストデータセット: $\mathcal{D}_T$を作る
• 特徴量ベクトルは$d$次元とし, その確率分布を$p_L, p_T$と表す
• 学習データセット$\mathcal{D}_L$を使って, $\mathcal{D}_T$をテストしたときの誤り率を$\epsilon(p_L, p_T)$と表す.
• 母集団の特徴ベクトルの確率分布を$p$とし, 真の分布とする.
• $p_L$と$p_T$はランダムなサンプルから推定された確率分布なので, 真の分布$p$の各特徴と同じにならない. このずれを偏り(バイアス))という
• 真の誤り率$\epsilon(p,p)$は真の分布$p$に従う学習データを用いて識別規則を作成し, 真の分布$p$に従うテストデータを用いてテストした場合の誤り率を表す
• 再代入誤り率とは, $p_L$からサンプリングしたデータを用いて識別規則を作成し, 同じデータでテストしたときの誤り率である

手元にあるデータを学習用とテスト用に分割する代表的な方法には、次のようなものがある。

ホールドアウト法(Holdout法)

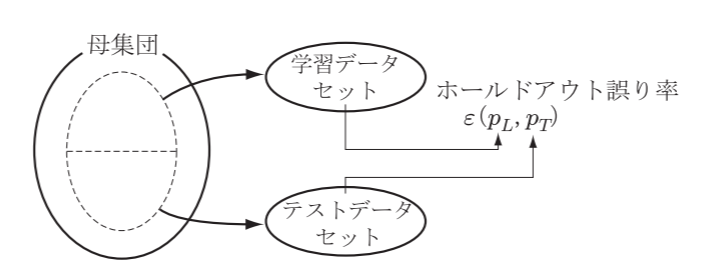
手元のデータを2分割し, 一方を学習データ$(p_L)$, もう一方をテスト$(p_T)$のために取り置いて誤り率を推定するために使用する

• ホールドアウト誤り率といい, $\epsilon(p_L,p_T)$で表す.

真の誤り率と再代入誤り率, ホールドアウト誤り率の関係は次の通り

$$\color{blue}{E_{\mathcal{D}_L} \lbrace \epsilon(p_L, p_L) \rbrace \leq \epsilon(p, p) \leq E_{\mathcal{D}_T } \lbrace \epsilon(p_L, p_L) \rbrace}$$

手元のデータが大量にある場合を除いて, 良い性能評価を与えない欠点がある

非線形回帰

次の関数からデータが生成されているとする

$$f(x) = 0.5 + 0.4 \times \sin(2 \pi x) + \epsilon = h(x) + \epsilon$$

関数$h(x)$を次の$p$次多項式で近似する

$$y(x;\mathbf{a}) = a_0 + a_1x + \cdots + a_px^p, \quad \mathbf{a} = (a_0, \cdots, a_p)^T$$

近似の良さは平均二乗誤差(MSE; mean square error)で評価する

$$\color{blue}{MSE = \int (y(x;\mathcal{D}) - h(x))^2 p(x)dx = E \lbrace (y(x;\mathcal{D}) - h(x))^2 \rbrace}$$

交差確認法(Cross Validation:CV)

手元の各クラスのデータを$m$個のグループに分割し, $m - 1$個のグループのデータを使って識別器を学習し, 残りの一つのグループでテストを行う.

これを$m$回繰り返し, それらの誤り率の平均を性能予測値とする.

$i$番目のグループを除いて学習し, $i$番目のグループでテストしたときの誤り率を$\epsilon_{-i}$とすると, 識別規則の誤り率は

$$\epsilon = \frac{1}{m} \sum^m_{i=1} \epsilon_{-i}$$

となる.

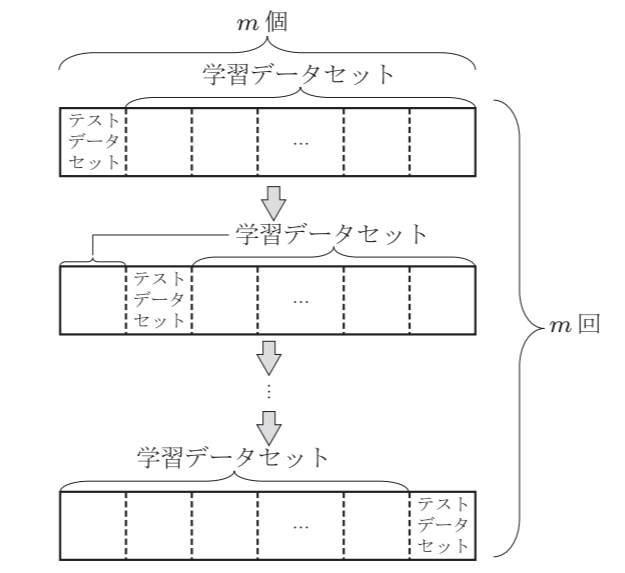
K-分割交差検証法(K-fold cross validation)

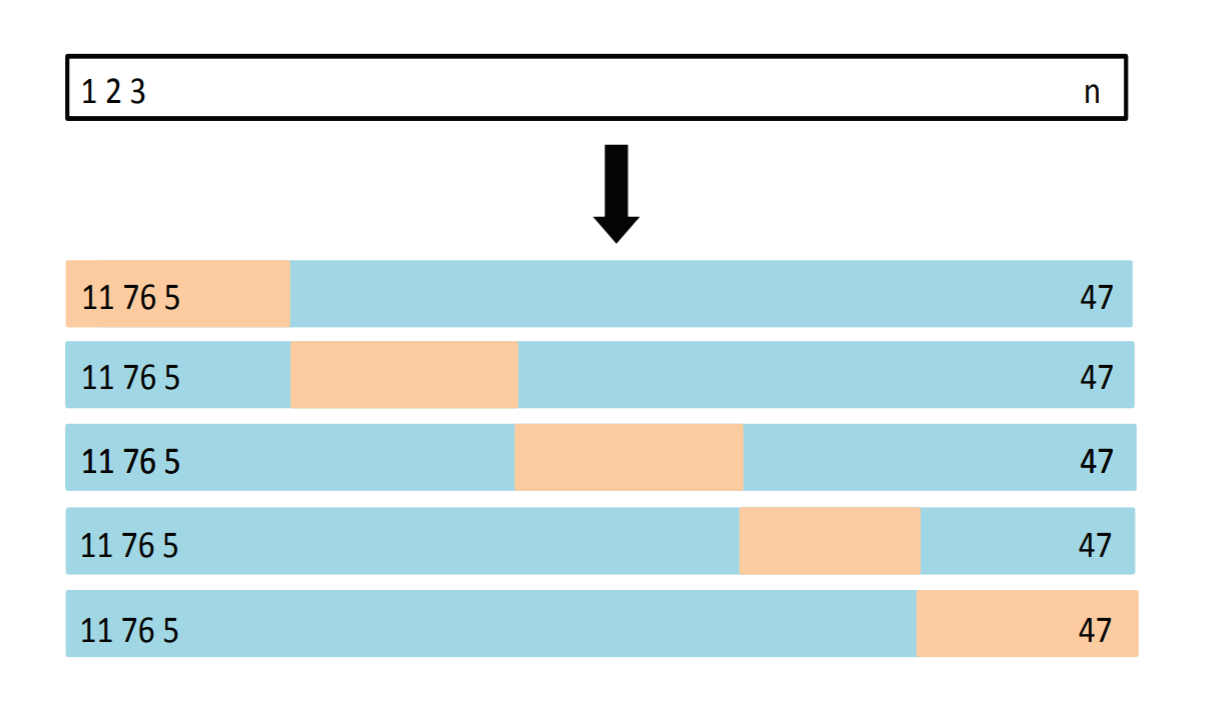
データを均等に$K$分割する$(K = 5)$

一つ抜き法(LOOCV)

交差検証法において, データの数とグループの数を等しくした場合. ジャックナイフ法ともいう

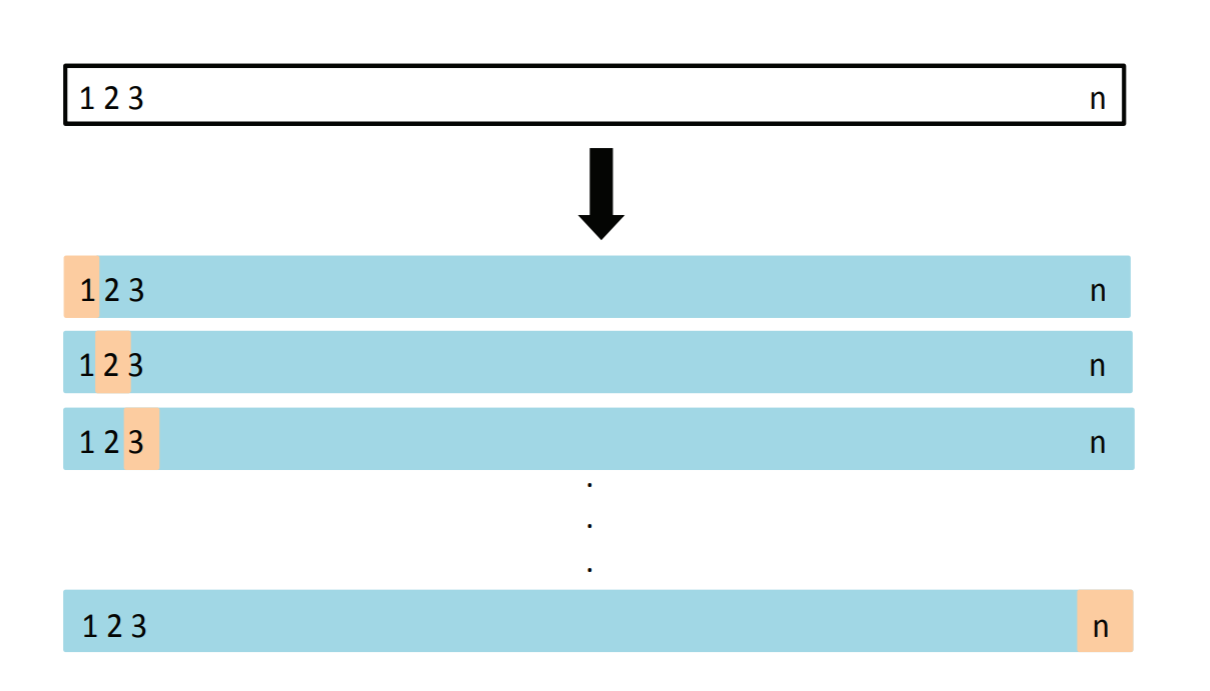
一つ抜き交差確認法 (LOOCV), 学習データ（青いところ）を使ってテストデータ（ベージュ）を予測する. 全部のパターンで計測した予測誤差の平均が CV.

ブートストラップ法(bootstrap)

再代入誤り率のバイアス補正に使用する. $N$個のデータで学習したデータで再代入誤り率を計算し,$\epsilon(N, N)$と表す

$N$個のデータから$N$回復元抽出して, 学習データを作成し, 再代入誤り率を計算し, $\epsilon(N^*, N^*)$とする

バイアスは, 元のデータ集合 N をテストデータとして得られる誤識別率$\epsilon(N^*, N)$との差

$$bias = \epsilon(N^*, N^*) - \epsilon(N^*, N)$$

で推定する. ブートストラップサンプルをいくつも作って, 誤識別率の平均値を計算しそれを$\overline{bias}$とすれば, 誤識別率の予測値$\epsilon$は

$$\epsilon = \epsilon(N, N) - \overline{bias}$$

で与えられる

汎化能力の評価法とモデル選択

学習データによってパラメータ調整を行い、誤り率を評価しても、目標以上の精度が出ない場合は識別関数を変える必要がある。誤り率が最も小さくなるパラメータを選択する方法をモデル選択という

バイアス・分散トレードオフ

近似した関数は目標関数$h(x)$との誤差の項(バイアス)と訓練データから生まれる誤差の項(分散)に整理できる

• バイアス
  • $h(x)$との誤差
  • モデル精度の悪さ
• 分散
  • 訓練データから生まれる誤差
  • モデル作成の不安定さ(再現性の悪さ)
• モデルが単純
  • 性能は良くないが、教師データに対して安定
  • 高バイアス・低バリアンス
• モデルが複雑
  • 性能は良いが、教師データに対して不安定（過学習など）
  • 低バイアス・高バリアンス
• 過学習
  • 訓練誤差は小さくなっているが汎化誤差(テスト誤差)が大きく乖離した状態を過適合/過剰適合/過学習と呼ぶ

ベイズ識別規則

医者の診断では, いろんな検査項目をもとに, 健康かそうでないかを判断する. 検査項目の値が高くても健康な人もいるし, 正常の範囲内でも健康でないかもしれない. このように, 検査項目の値の影響は確率的である.

ベイズ識別規則では, 入力データ$\mathbf{x}$とクラス$\mathbf{y}$に確率分布を仮定する.

病気の診断では, 検査対象を調べると健康な人と病気の人の割合が大きく異なることが一般的である. このときクラスの学習データのサンプル数に偏りが生じる (不均衡データ; Umbalanced data という).

ROC曲線とは, このようなデータに対して有効な性能評価法である.

ベイズの定理

ベイズ識別規則は, 次の事後確率が最大になるクラスにデータを分類する.

観測データを$\mathbf{x}$, 識別クラスを$C_i (i - 1, \cdots, K)$とする

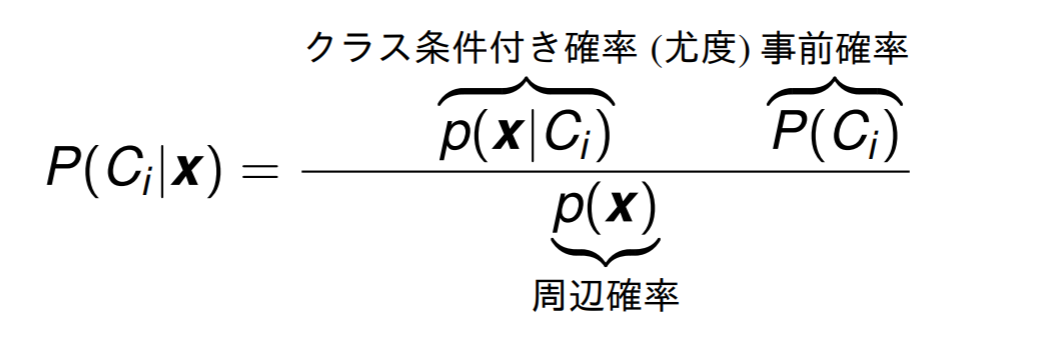
これはベイズの定理と呼ばれる. 同時分布は

$$p(C_i, \mathbf{x}) = p(C_i \ |\ \mathbf{x}) p(\mathbf{x}) = p(\mathbf{x} \ |\ C_i) P(C_i)$$

となる.

クラス識別は, 事後確率が最大になるクラスにデータ $\mathbf{x}$ を割り付ければ良い, すなわち, 入力データ $\mathbf{x}$ に対して, 2クラス $C_i, C_j$ の事後確率を計算し, $P(C_i \ |\ \mathbf{x}) > P(C_j \ |\ \mathbf{x})$ ならば, $\mathbf{x}$ は $C_i$ に属すると識別する

多クラスの識別は, 識別クラス = $\argmax_i p(\mathbf{x} \ |\ C_i) P(C_i)$ とすれば良い.

事後確率

事後確率 $P(C_i \ |\ \mathbf{x})$ は観測データ $\mathbf{x}$ が与えられたもとで, そのデータがクラス $C_i$ に属する条件付き確率である

事前確率

事前確率 $P(C_i)$ はデータ分析者は, 各クラス $C_i$ の生起確率を予め用意しないといけない.

尤度

クラス条件付き確率 (尤度) $p(\mathbf{x} \ |\ C_i)$ はクラスが与えられたもとで,観測データの確率分布を表している.

周辺確率

周辺確率 $p(\mathbf{x})$ は, 観測データ $\mathbf{x}$ の生起確率である. 周辺分布は, 同時分布から, 興味のない変数を積分や総和を取ることで消去することで得られた. このような操作を周辺化という.

$$p(\mathbf{x}) = \sum_{i=1}^K p(C_i, \mathbf{x})$$

例題1

以下の手順で健康か否かの事後確率を求める.

1. クラス条件付き確率を求める. 周辺分布$P(S \ |\ G), P(T \ |\ G)$と同時分布$P(S,T \ |\ G)$の両方で
2. 同時確率を求める. $P(S, T, G)$
3. 周辺確率を求める. $P(S, T)$
4. 事後確率を求める. $P(G \ |\ S, T)$

• $S$ と $T$ の間には条件付き独立性を仮定する
• クラス事前確率は表から明らかなので, 次のようにして計算する

$$\begin{aligned} P(G = 1) = \frac{800}{1000} = \frac{4}{5}, \quad P(G = 0) = \frac{200}{1000} = \frac{1}{5} \end{aligned}$$

---

クラス条件付き確率を求める

$S$ に関するクラス条件付き確率は次の通り

$$\begin{aligned} &P(S = 1 \ |\ G = 1) = \frac{320}{800} = \frac{2}{5}, \quad P(S = 0 \ |\ G = 1) = \frac{480}{800} = \frac{3}{5} \\\\ &P(S = 1 \ |\ G = 0) = \frac{160}{200} = \frac{4}{5}, \quad P(S = 0 \ |\ G = 0) = \frac{40}{200} = \frac{1}{5} \end{aligned}$$

$T$ に関するクラス条件付き確率は次の通り

$$\begin{aligned} &P(T = 1 \ |\ G = 1) = \frac{640}{800} = \frac{4}{5}, \quad P(T = 0 \ |\ G = 1) = \frac{160}{800} = \frac{1}{5} \\\\ &P(T = 1 \ |\ G = 0) = \frac{40}{200} = \frac{1}{5}, \quad P(T = 0 \ |\ G = 0) = \frac{160}{200} = \frac{4}{5} \end{aligned}$$

次に、$G$を与えた時に、$S$と$T$の条件付き同時確率を求める。$P(S,T \ |\ G)$は$G$が1あるいは0の場合に、$S$と$T$の両方の変数の関係性を表している。

ここで、条件付き独立性を仮定しているので、同時確率が周辺確率の積で得られる

$$\begin{aligned} &\color{blue}{P(S = 1, T = 1 \ |\ G = 1) = P(S = 1 \ |\ G = 1) \cdot P(T = 1 \ |\ G = 1) = \frac{8}{25}} \\\\ &P(S = 0, T = 1 \ |\ G = 1) = \frac{12}{25} \\\\ &P(S = 1, T = 0 \ |\ G = 1) = \frac{2}{25} \\\\ &P(S = 0, T = 0 \ |\ G = 1) = \frac{3}{25} \\\\ &P(S = 1, T = 1 \ |\ G = 0) = \frac{4}{25} \\\\ &P(S = 0, T = 1 \ |\ G = 0) = \frac{1}{25} \\\\ &P(S = 1, T = 0 \ |\ G = 0) = \frac{16}{25} \\\\ &P(S = 0, T = 0 \ |\ G = 0) = \frac{4}{25} \end{aligned}$$

同時確率を求める

$G$を与えた時の$S$と$T$の条件付き確率を求めたので、その確率に周辺確率を乗じることで得ることができる。

$$\begin{aligned} &\color{blue}{P(S = 1, T = 1, G = 1) = P(S = 1, T = 1 \ |\ G = 1) \cdot P(G = 1) = \frac{32}{125}} \\\\ &P(S = 0, T = 1, G = 1) = \frac{48}{125} \\\\ &P(S = 1, T = 0, G = 1) = \frac{8}{125} \\\\ &P(S = 0, T = 0, G = 1) = \frac{12}{125} \\\\ &P(S = 1, T = 1, G = 0) = \frac{4}{125} \\\\ &P(S = 0, T = 1, G = 0) = \frac{1}{125} \\\\ &P(S = 1, T = 0, G = 0) = \frac{16}{125} \\\\ &P(S = 0, T = 0, G = 0) = \frac{4}{125} \end{aligned}$$

周辺分布を求める

先程求めた$S$と$T$と$G$の3変数の同時確率から、変数$G$を消去してあげれば、$S$と$T$の周辺分布が得られる

$G$の消去方法は、$G$は離散なので$G$の台で総和を取れば良い

$$\begin{aligned} \color{blue}{P(S = 1, T = 1) = P(S = 1, T = 1, G = 1) + P(S = 1, T = 1, G = 0) = \frac{36}{125}} \\\\ P(S = 0, T = 1) = P(S = 0, T = 1, G = 1) + P(S = 0, T = 1, G = 0) = \frac{49}{125} \\\\ P(S = 1, T = 0) = P(S = 1, T = 0, G = 1) + P(S = 1, T = 0, G = 0) = \frac{24}{125} \\\\ P(S = 0, T = 0) = P(S = 0, T = 0, G = 1) + P(S = 0, T = 0, G = 0) = \frac{16}{125} \end{aligned}$$

事後確率を求める

$S, T, G$の同時確率を$S$と$T$の周辺確率で除せば良い

$$\begin{aligned} &P(G = 1 \ |\ S = 1, T = 1) = \frac{P(S = 1, T = 1, G = 1)}{P(S = 1, T = 1)} = \frac{8}{9} \\\\ &P(G = 1 \ |\ S = 0, T = 1) = \frac{P(S = 0, T = 1, G = 1)}{P(S = 0, T = 1)} = \frac{48}{49} \\\\ &P(G = 1 \ |\ S = 1, T = 0) = \frac{P(S = 1, T = 0, G = 1)}{P(S = 1, T = 0)} = \frac{1}{3} \\\\ &P(G = 1 \ |\ S = 0, T = 0) = \frac{P(S = 0, T = 0, G = 1)}{P(S = 0, T = 0)} = \frac{3}{4} \\\\ &P(G = 0 \ |\ S = 1, T = 1) = \frac{P(S = 1, T = 1, G = 0)}{P(S = 1, T = 1)} = \frac{1}{9} \\\\ &P(G = 0 \ |\ S = 0, T = 1) = \frac{P(S = 0, T = 1, G = 0)}{P(S = 0, T = 1)} = \frac{1}{49} \\\\ &P(G = 0 \ |\ S = 1, T = 0) = \frac{P(S = 1, T = 0, G = 0)}{P(S = 1, T = 0)} = \frac{2}{3} \\\\ &P(G = 0 \ |\ S = 0, T = 0) = \frac{P(S = 0, T = 0, G = 0)}{P(S = 0, T = 0)} = \frac{1}{4} \end{aligned}$$

これで、入力データ$S, T$の情報から$G$の事後確率を得ることができた。後は、各条件の時に事後確率の大小を比較して識別すれば良い

• 事後確率を次の表にまとめると(赤字が健康と識別された確率)

$(S, T)$	(1, 1)	(0, 1)	(1, 0)	(0, 0)
$P(G = 1 \vert S, T)$	$\color{red}{\frac{8}{9}}$	$\color{red}{\frac{48}{49}}$	$\frac{1}{3}$	$\color{red}{\frac{3}{4}}$
$P(G = 0 \vert S, T)$	$\frac{1}{9}$	$\frac{1}{49}$	$\color{red}{\frac{2}{3}}$	$\frac{1}{4}$

• 条件付きベイズ誤り率は次の通り

$$\begin{aligned} \epsilon^* &= \sum_{s, t \in \lbrace 0, 1 \rbrace} \min \lbrace P(G = 1 \ |\ S, T), P(G = 0 \ |\ S, T) \rbrace \cdot p_{S, T}(S, T) \\\\ &= \frac{1}{9} \times \frac{36}{125} + \frac{1}{49} \times \frac{49}{125} + \frac{1}{3} \times \frac{24}{125} + \frac{1}{4} \times \frac{16}{125} \\\\ &= \frac{17}{125} \end{aligned}$$

• $S, T = 1$の場合、事後確率の高い健康のクラスに識別される
• 喫煙の習慣があって、お酒を飲まない人は事後確率の高い不健康のクラスに識別される
• 喫煙も飲酒の習慣のある人の方が、喫煙も飲酒もしない人よりも健康である確率が高い

喫煙も飲酒の習慣もある人の場合、健康のクラスに識別されるので、$\frac{1}{9}$の不健康の人も健康に識別されてしまう。これが$S, T = 1$の場合の誤り率

以下、$S$と$T$の全ての場合について誤り率を求めて、その条件の同時確率で重み付けをすれば良い。求めた誤り率は$\frac{17}{125} \simeq 13.6 \%$

尤度比(事前確率の比率)

クラス条件付き確率と事前確率の積で識別している

$$\begin{aligned} \begin{cases} p(\mathbf{x} \ |\ C_i) \cdot P(C_i) > p(\mathbf{x} \ |\ C_j) \cdot P(C_j) \Rightarrow C_i \\\\ p(\mathbf{x} \ |\ C_i) \cdot P(C_i) < p(\mathbf{x} \ |\ C_j) \cdot P(C_j) \Rightarrow C_j \end{cases} \end{aligned}$$

この式より, 尤度比で識別規則を構成してもよい

$$\begin{aligned} \begin{cases} \frac{p(\mathbf{x} \ |\ C_i)}{p(\mathbf{x} \ |\ C_j)} > \frac{P(C_j)}{P(C_i)} \Rightarrow C_i \\\\ \frac{p(\mathbf{x} \ |\ C_i)}{p(\mathbf{x} \ |\ C_j)} < \frac{P(C_j)}{P(C_i)} \Rightarrow C_j \end{cases} \end{aligned}$$

尤度比が事前確率の比 $P(C_j / C_i) = h_{ij}$ よりも大きければクラス $i$ に識別する.

誤り率最小化

ベイズ識別規則の誤り率 $\epsilon(\mathbf{x})$ は事後確率の小さい方なので

$$\epsilon(\mathbf{x}) = \min \lbrace P(C_1 \ |\ \mathbf{x}), P(C_2 \ |\ \mathbf{x}) \rbrace$$

これを条件付きベイズ誤り率という. ベイズ誤り率は条件付きベイズ誤り率の期待値

$$\epsilon^* = E\lbrace \epsilon(\mathbf{x}) \rbrace = \int_{R_2} p(\mathbf{x} \ |\ C_1) P(C_1)dx + \int_{R_1} p(\mathbf{x} \ |\ C_2) P(C_2)dx$$

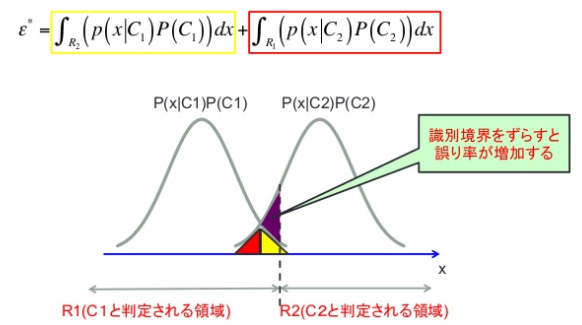
ベイズの識別規則によって識別境界が定められているとすると,

• $R_2$の領域では$P(\mathbf{x} \ |\ C_1) P(C_1) < P(\mathbf{x} \ |\ C_2) P(C_2)$
• $R_1$の領域では$P(\mathbf{x} \ |\ C_2) P(C_2) < P(\mathbf{x} \ |\ C_1) P(C_1)$

最小損失基準

誤りを犯すことによる危険性 (リスク) を考える. 誤りによって発生する危険性はクラス間で対称ではないから.

$L_{ij}$は真のクラスが$C_j$のとき$C_i$と判断することによる損失を表す

データ $\mathbf{x}$ をクラス $C_i$ と判断したときの損失は

$$r(C_i \ |\ \mathbf{x}) = \sum_{k = 1}^K L_{ik} P(C_k \ |\ \mathbf{x})$$

• $P(C_k \ |\ \mathbf{x})$は観測データ$\mathbf{x}$を$C_k$と判断する確率

識別規則は, 損失がもっとも小さいクラスに識別する

$$\text{識別クラス} = \argmin_i r(C_i \ |\ \mathbf{x})$$

このとき損失の期待値は

$$r = E\lbrace r(\mathbf{x}) \rbrace = \int_{R_1 + R_2} \min \lbrace r(C_1 \ |\ \mathbf{x}), r(C_2 \ |\ \mathbf{x}) \rbrace p(\mathbf{x})d\mathbf{x}$$

最小損失基準に基づく識別の例

期待損失最小化

期待損失は次のようにして計算された

$$r = E\lbrace r(\mathbf{x}) \rbrace = \int_{R_1} (L_{11} p(\mathbf{x} \ |\ C_1) P(C_1) + L_{12} p(\mathbf{x} \ |\ C_2) P(C_2))d\mathbf{x} + \int_{R_2} (L_{21} p(\mathbf{x} \ |\ C_1) P(C_1) + L_{22} p(\mathbf{x} \ |\ C_2) P(C_2))d\mathbf{x}$$

期待損失が最小になるクラスに識別すればよいので, 識別規則は次のようになった

$$L_{11} p(\mathbf{x} \ |\ C_1) P(C_1) + L_{12} p(\mathbf{x} \ |\ C_2) P(C_2) < L_{21} p(\mathbf{x} \ |\ C_1) P(C_1) + L_{22} p(\mathbf{x} \ |\ C_2) P(C_2) \Rightarrow C_1$$

$$L_{11} p(\mathbf{x} \ |\ C_1) P(C_1) + L_{12} p(\mathbf{x} \ |\ C_2) P(C_2) > L_{21} p(\mathbf{x} \ |\ C_1) P(C_1) + L_{22} p(\mathbf{x} \ |\ C_2) P(C_2) \Rightarrow C_2$$

$L_{11}, L_{22}$ は正しく識別できているので, 損失を考える必要はない, そこで $L_{11} < L_{12}, L_{22} < L_{21}$ を仮定しよう. すると次の識別規則が得られる.

$$(L_{21} - L_{11}) p(\mathbf{x} \ |\ C_1) P(C_1) > (L_{12} - L_{21}) p(\mathbf{x} \ |\ C_2) P(C_2) \Rightarrow C_1$$

ROC曲線

識別性能の指標に受信者動作特性曲線 (ROC 曲線) がある

ROC曲線は, 偽陽性率と真陽性率の関係をグラフに表したもの

偽陽性率も真陽性率も, 本来偽 (真) であるものの中から計算されるので, 真のクラスと偽のクラスのデータ数に大きな差があってもROC は大きく影響を受けない.

ベイズ識別規則のように識別境界を移動することで識別クラスを制御できるものがある.

混同行列(Confusion Matrix)

２クラス問題では, 対象 $\mathbf{x}$ が１つに属していると判断する場合を p(positive), 属していないと判断する場合を, n (negative) と表記する.

• $p^*, n^*$は$\mathbf{x}$の真のクラスを表すとする
• この識別の様子を混同行列としてまとめることができる

	識別クラスp	識別クラスn	行和
$p^*$	TP(True Positive): 真陽性	FN(False Negative): 偽陰性	$P = TP + FN$
$n^*$	FP(False Positive): 偽陽性	TN(True Negative): 真陰性	$N = FP + TN$

• Positive：陽性と判断
• Negative：陰性と判断
• True：判断が正しい
• False：判断が誤り

偽陽性率：健康な人の中で陽性が出てしまった割合

$$False-Positive-rate = \frac{FP}{FP + TN} = \frac{FP}{N}$$

真陽性率：病気の人の中で陽性を正しく出せた割合

$$True-Positive-rate = \frac{TP}{TP + FN} = \frac{TP}{P}$$

正確度：正しく当てられた割合

$$Accuracy = \frac{TP + TN}{TP + FP + FN + TN}$$

適合率：陽性を出した中でそれが合っていた割合。モデルの正確性を表す

$$Precision = \frac{TP}{TP + FP}$$

再現率：適合している全文書からどれだけ検索できているかを示す網羅性の指標。真の陽性に対してどれだけ真と答えられたか

$$Recall = \frac{TP}{TP + FN} = \frac{TP}{P}$$

F-値：PrecisionとTrue-Pisitive rateの調和平均。(適合率と再現率はトレードオフの関係にあるから)

$$F_{value} = \frac{2 \times Precision \times TP-rate}{Precision + TP-rate} = \frac{2}{\frac{1}{Precision} + \frac{1}{Recall}}$$

ROCによる性能評価

ROC曲線の下側の面積を ROC曲線下面積（AUC）(area under anROC curve) といい, 識別器の性能評価尺度

• 完全な識別器の ROC 曲線は, 原点, (0,1), (1,1) を通る直線で, AUCは 1 になる.
• 原点と (1,1) を結んだ 45 度線は, ランダムな識別器の ROC 曲線で, AUC は 0.5 となる.

どの識別器も AUC は (0.5, 1) の間の値となり, 大きいほど性能が良い.

動作点の選択

動作点 (真陽性率と偽陽性率の組み合わせ) をどこに選択すべきか？

最小損失識別規則は, $L_{11} = L_{22} = 0$ とすれば,

$$\begin{aligned} \frac{p(\mathbf{x} \ |\ p^*)}{p(\mathbf{x} \ |\ n^*)} > \frac{L_{12}P(n^*)}{L_{21}P(p^*)} \Rightarrow p \\\\ \frac{p(\mathbf{x} \ |\ p^*)}{p(\mathbf{x} \ |\ n^*)} < \frac{L_{12}P(n^*)}{L_{21}P(p^*)} \Rightarrow n \end{aligned}$$

損失の期待値 $r$ は

$$\begin{aligned} r &= \int_{R_1} (L_{12}p(\mathbf{x} \ |\ n^*) P(n^*))dx + \int_{R_2} (L_{21}p(\mathbf{x} \ |\ p^*) P(p^*))dx \\\\ &= L_{12}P(n^*) \epsilon_2 + L_{21}P(p^*) \epsilon_1 \end{aligned}$$

となる

ROC空間の定義で書けば,

$$\begin{aligned} 1 - \epsilon_1 &= \frac{L_{12}P(n^*)}{L_{21}P(p^*)} \epsilon_2 + (1 - \frac{r}{L_{21}P(p^*)}) \\\\ &= \alpha \epsilon_2 + h(r) \end{aligned}$$

となる.

課題3.1

次のデータはある疾病に関して, 病気の人($G = 1$で表す)100人と, 健康な人($G = 0$)900人の検査値が一定数以上の場合を $S = 1$, 一定値以下を $S = 0$, 男性を $T = 1$, 女性を $T = 0$ とした 1000 人の仮想的なデータである. 検査値と性別から, 病気であるかどうかを識別したい. $S$ と $T$ の間には条件付き独立性 $P(S, T \ |\ G) = P(S \ |\ G)P(T \ |\ G)$ が成り立つと仮定する. このとき, 以下の問に答えなさい.

	サンプル数	検査値 $x$ がある値以上($S = 1$)	性別$(T = 1$)
病気の人(G = 1)	100	80	70
健康な人(G = 0)	900	300	180

(1) 検査値に関するクラス条件付き確率を $P(S \ |\ G)$ を求めよ

$S$ に関するクラス条件付き確率は次の通り

$$\begin{aligned} &P(S = 1 \ |\ G = 1) = \frac{80}{100} = \frac{4}{5}, \quad P(S = 0 \ |\ G = 1) = \frac{20}{100} = \frac{1}{5} \\\\ &P(S = 1 \ |\ G = 0) = \frac{300}{900} = \frac{1}{3}, \quad P(S = 0 \ |\ G = 0) = \frac{600}{900} = \frac{2}{3} \end{aligned}$$

(2) 事後確率 $P(G = 1 \ |\ S = 1, T = 1)$ を計算せよ

$T$ に関するクラス条件付き確率

$$P(T = 1 \ |\ G = 1) = \frac{70}{100} = \frac{7}{10}$$

$P(S, T \ |\ G)$のクラス条件付き確率

$$P(S = 1, T = 1 \ |\ G = 1) = \frac{4}{5} \times \frac{7}{10} = \frac{14}{25}$$

同時確率$P(S, T, G)$

$$P(S = 1, T = 1, G = 1) = P(S = 1, T = 1 \ |\ G = 1) \times P(G = 1) = \frac{14}{25} \times \frac{100}{1000} = \frac{7}{125}$$

周辺確率$P(S, T)$

$$P(S = 1, T = 1) = P(S = 1, T = 1, G = 1) + P(S = 1, T = 1, G = 0) = \frac{7}{125} + \frac{3}{50} = \frac{29}{250}$$

事後確率$P(G = 1 \ |\ S = 1, T = 1)$

$$P(G = 1 \ |\ S = 1, T = 1) = \frac{P(S = 1, T = 1, G = 1)}{P(S = 1, T = 1)} = \frac{14}{29}$$

(3) ベイズ誤り率を求めよ.

• 事後確率を次の表にまとめると(赤字が健康と識別された確率)

$(S, T)$	(1, 1)	(0, 1)	(1, 0)	(0, 0)
$P(G = 1 \vert S, T)$	$\frac{14}{29}$	$\frac{7}{67}$	$\frac{1}{11}$	$\frac{1}{81}$
$P(G = 0 \vert S, T)$	$\color{red}{\frac{15}{29}}$	$\color{red}{\frac{60}{67}}$	$\color{red}{\frac{10}{11}}$	$\color{red}{\frac{80}{81}}$

• 条件付きベイズ誤り率は次の通り

$$\begin{aligned} \epsilon^* &= \sum_{s, t \in \lbrace 0, 1 \rbrace} \min \lbrace P(G = 1 \ |\ S, T), P(G = 0 \ |\ S, T) \rbrace \cdot p_{S, T}(S, T) \\\\ &= \frac{14}{29} \times \frac{29}{250} + \frac{7}{67} \times \frac{67}{500} + \frac{1}{11} \times \frac{33}{125} + \frac{1}{81} \times \frac{243}{500} \\\\ &= \frac{1}{10} \end{aligned}$$

(4) 損失を $L_{11} = L_{22} = 0, L_{12} = 5, L_{21} = 10$ とした場合の識別結果を求めよ

損失行列は

$$\begin{aligned} \begin{bmatrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{bmatrix} = \begin{bmatrix} 0 & 5 \\ 10 & 0 \end{bmatrix} \end{aligned}$$

$L_{11}$ は真のクラスが $G = 0$ のとき $G = 0$ と判断するときの損失, $L_{21}$ は真のクラスが $G = 0$ のとき $G = 1$ と判断するときの損失, $L_{12}$ は真のクラスが $G = 1$ のとき $G = 0$ と判断するときの損失であるから、識別クラスは事後確率に損失をかけて大きい値のクラスになる.

	$(1, 1)$	$(0, 1)$	$(1, 0)$	$(0, 0)$
$L_{21}P(G = 1 \mid S,T)$	$\color{red}{\frac{140}{29}}$	$\frac{70}{67}$	$\frac{10}{11}$	$\frac{10}{81}$
$L_{12}P(G = 0 \mid S,T)$	$\frac{75}{29}$	$\color{red}{\frac{300}{67}}$	$\color{red}{\frac{50}{11}}$	$\color{red}{\frac{400}{81}}$
識別クラス	1	0	0	0

最小損失基準に基づく、以下の識別結果になる

• $S = 1, T = 1$: 病気の人
• $S = 0, T = 1$: 健康な人
• $S = 1, T = 0$: 健康な人
• $S = 0, T = 0$: 健康な人

課題3.2

次の混同行列から, 偽陽性率, 真陽性率, 適合率, 正確度, F 値を求めよ.

	識別クラス$p$	識別クラス$n$
$p^*$	TP: 20	FN: 80
$n^*$	FP: 150	TN: 750

• 偽陽性率: $\frac{FP}{N} = \frac{150}{150 + 750} = \frac{1}{6}$
• 真陽性率: $\frac{TP}{P} = \frac{20}{20 + 80} = \frac{1}{5}$
• 適合率: $\frac{TP}{TP + FP} = \frac{20}{20 + 150} = \frac{2}{17}$
• 正確度: $\frac{TP + TN}{P + N} = \frac{20 + 750}{20 + 80 + 150 + 750} = \frac{77}{100}$
• F値: $\frac{2}{1/\text{適合率} + 1/\text{再現率}} = \frac{2}{\frac{1}{\frac{2}{17}} + \frac{1}{\frac{1}{5}}} = \frac{4}{27}$
  • 再現率 = 真陽性率

確率モデルと識別関数

学習データ $\mathbf{x}_i$ は, 母集団からのランダムサンプルであるから, 誤差を伴う観測が一般的である. また, 特徴ベクトルは単位や変数変換の仕方によりばらつきが変わったり, 分布の形状が変化する.

そこで, 単位変換や相関係数に依存しない変数変換の方法を学ぶ.

母集団分布を記述する確率モデルを定義し, 確率モデルを使ったベイズ識別規則を紹介する.

観測データの線形変換

平均ベクトル

観測データは, d次元の特徴ベクトル $\mathbf{x} = (x_1, \cdots, x_d)^T$とする. $\mathbf{x}$の確率分布 (密度関数) を $p(\mathbf{x})$ とするとき, 平均ベクトルを次のように表す.

$$\mu = (\mu_1, \cdots, \mu_d)^T = (E \lbrace x_1 \rbrace, \cdots, E \lbrace x_d \rbrace)^T$$

ここで $E \lbrace x_i \rbrace$ は $i$ 番目の特徴ベクトルの期待値演算で, $\mathbf{x}$が連続型の場合

$$\mu_i = E \lbrace x_i \rbrace = \int_{\mathcal{R}^d} x_i p(\mathbf{x}) \, d\mathbf{x} = \int_{-\infty}^{\infty} x_i p(x_i) \,dx$$

となる.

$p(x_i)$ は d次元密度関数$p(\mathbf{x})$の周辺分布であった.

$$p(x_i) = \int_{-\infty}^{\infty} \cdots \int_{-\infty}^{\infty} p(x_1, \cdots, x_d) \,dx_1 \cdots \,dx_{i-1} \,dx_{i+1} \cdots \,dx_d$$

共分散行列

観測データの平均ベクトル周りのばらつきの尺度を分散共分散行列で表す

$$\begin{aligned} \Sigma &= Var[\mathbf{x}] = E\lbrace (\mathbf{x} - \mu) (\mathbf{x} - \mu)^T \rbrace \\ &= [\sigma_{ij}]_{i.j = 1, \cdots, d} \end{aligned}$$

• $\sigma_{ij}$は$x_i$と$x_j$の平均周りの2次モーメントして以下のようにして計算した

$$\sigma_{ij} = E\lbrace (x_i - \mu_i) (x_j - \mu_j) \rbrace = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} (x_i - \mu_i) (x_j - \mu_j) p(x_i, x_j) \,dx_i \,dx_j$$

標本平均ベクトルと標本共分散行列

データ分析者は, データの母集団分布$p(\mathbf{x})$を特定する術がありませんから, 観測データを使って, 母平均ベクトル$(\mathbf{\mu})$や母分散共分散行列$(\mathbf{\Sigma})$を推定する必要がある

$N$個の観測データを$\mathbf{x}_1, \cdots, \mathbf{x}_N$と表したとき, 標本平均ベクトルは次の様にして計算した

$$\overline{\mathbf{x}} = \frac{1}{N} \sum_{i=1}^N \mathbf{x}_i$$

また, 標本分散共分散行列$\mathbf{S}$の第$i, j$要素は次のようにして計算する

$$S_{ij} = \frac{1}{N}\sum_{n=1}^N (x_{ni} - \overline{x_i}) (x_{nj} - \overline{x_j})$$

$x_i$と$x_j$の関連性の指標を相関係数といい, 母相関係数と標本相関係数は次の様にして定義された

$$\begin{aligned} \rho_{ij} = \frac{\sigma_{ij}}{\sigma_i \sigma_j}, \quad r_{ij} = \frac{S_{ij}}{S_i S_j} \end{aligned}$$

ただし, $\sigma_i^2 = \sigma_{ij}^2$また$S_i^2 = S_{ii}$である.

観測データの標準化

観測データの個々の特徴量の分布は, 測定単位のとり方でばらつきが大きくもなるし小さくもなる. そこで, 単位変換の影響を取り除いたデータを用いた方が望ましい分析結果が得られる.

• 個々の特徴量を平均0, 分散1に変換することを標準化という.

平均$\mu$, 分散$\sigma^2$をもつ$X$の線形変換$Y = aX + b$の期待値と分散の性質を思い出すと

$$E(Y) = E(aX+b) = aE(X) + b, \quad Var(Y) = Var(aX+b) = a^2 Var(X)$$

変換$z = \frac{x - \mu}{\sigma}$の期待値と分散は, それぞれ0と1になる.

$$\begin{aligned} &E(Z) = E(\frac{X - \mu}{\sigma}) = \frac{E(X) - \mu}{\sigma} = \frac{\mu - \mu}{\sigma} = 0 \\\\ &Var(Z) = Var(\frac{X - \mu}{\sigma}) = \frac{Var(Z)}{\sigma^2} = \frac{\sigma^2}{\sigma} = 1 \end{aligned}$$

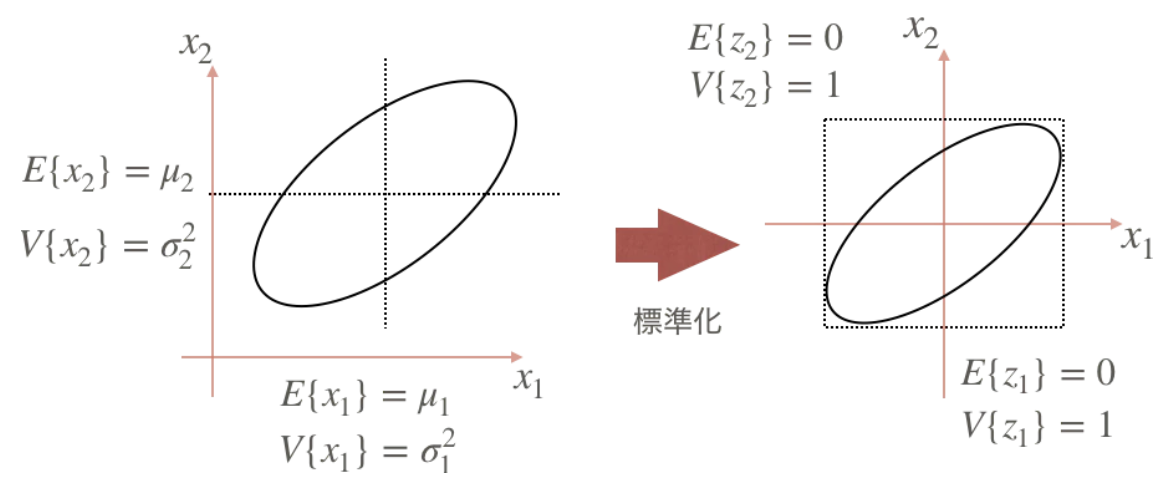
観測データの無相関化

データ間の相関を取り除く処理のことを無相関化という

分散共分散行列$\mathbf{\Sigma}$の固有値を$\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_d$とし, その固有値に対応する固有ベクトルを$\mathbf{s}_1, \mathbf{s}_2, \cdots, \mathbf{s}_d$とすると, 対称行列である分散共分散行列$\mathbf{\Sigma}$は次のように対角化された

$$\mathbf{\Sigma} = \mathbf{S} \mathbf{\Sigma} \mathbf{S}^T, \quad \mathbf{\Lambda} = \mathbf{S}^T \mathbf{\Sigma} \mathbf{S}$$

そこで, データ$\mathbf{X}$の線形変換$\mathbf{Y} = \mathbf{S}^T(\mathbf{X})$を考えると, $\mathbf{Y}$の平均は

$$E(\mathbf{Y}) = E(\mathbf{S}^T(\mathbf{X})) = \mathbf{S}^T \mathbf{\mu}$$

であり, 分散共分散行列は

$$\begin{aligned} Var(\mathbf{Y}) &= Var(\mathbf{S}^T \mathbf{X}) = E\lbrace [\mathbf{S}^T (\mathbf{X} - \mathbf{\mu})][\mathbf{S}^T (\mathbf{X} - \mathbf{\mu})]^T \rbrace \\\\ &= \mathbf{S}^T E \lbrace (\mathbf{X}- \mu) (\mathbf{X} - \mu)^T \rbrace \mathbf{S} \\\\ &= \mathbf{S}^T \mathbf{\Sigma} \mathbf{S} = \mathbf{\Lambda} \end{aligned}$$

• $\mathbf{\Lambda}$は, 固有値が対角に並んだ対角行列であったので, その非対角要素は0であった.

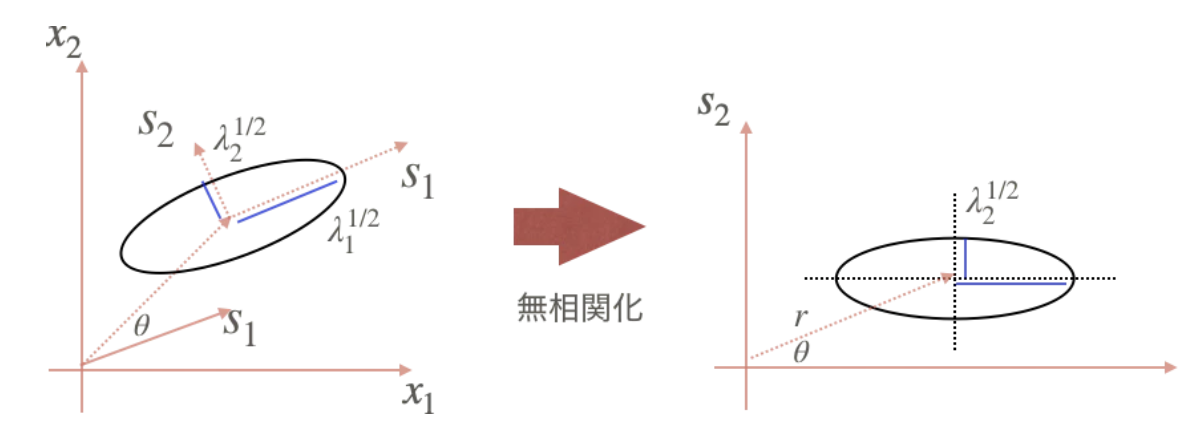
観測データの白色化

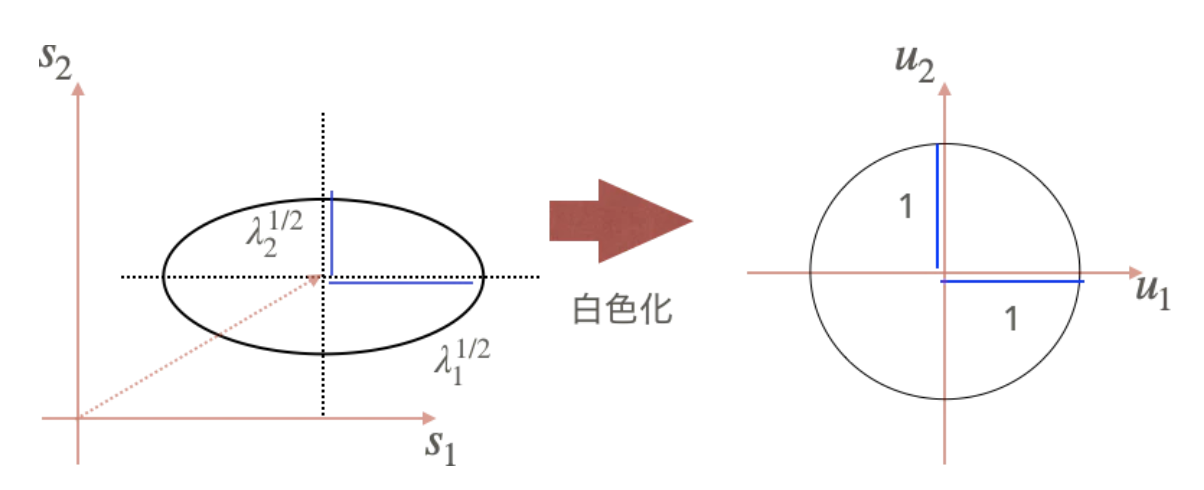
全ての特徴量を無相関化かつ標準偏差を1に正規化し, 平均ベクトルを0に中心化する操作を白色化という

白色化の変換公式は以下のように定義すればよい.

$$\mathbf{u} = \mathbf{\Lambda}^{-\frac{1}{2}} \mathbf{S}^T (\mathbf{X} - \mu)$$

$\mathbf{u}$の平均ベクトルは

$$E(\mathbf{u}) = E(\mathbf{\Lambda}^{-\frac{1}{2}} \mathbf{S}^T (\mathbf{X} - \mu)) = \mathbf{\Lambda}^{-\frac{1}{2}} \mathbf{S}^T \lbrace E(\mathbf{X} - \mu) = \mathbf{0}$$

となり, 分散共分散行列は

$$\begin{aligned} Var(\mathbf{u}) &= Var(\mathbf{\Lambda}^{-\frac{1}{2}} \mathbf{S}^T (\mathbf{X} - \mu)) \\\\ &= E \lbrace \mathbf{\Lambda}^{-\frac{1}{2}} \mathbf{S}^T (\mathbf{X} - \mu) (\mathbf{X} - \mu)^T \mathbf{S} \mathbf{\Lambda}^{-\frac{1}{2}} \rbrace \\\\ &= \mathbf{\Lambda}^{-\frac{1}{2}} \mathbf{S}^T \mathbf{\Sigma} \mathbf{S} \mathbf{\Lambda}^{-\frac{1}{2}} \\\\ &= \mathbf{\Lambda}^{-\frac{1}{2}} \mathbf{\Lambda} \mathbf{\Lambda}^{-\frac{1}{2}} \\\\ &= \mathbf{\Lambda}^{-\frac{1}{2}} \mathbf{\Lambda}^{\frac{1}{2}} \mathbf{\Lambda}^{\frac{1}{2}} \mathbf{\Lambda}^{-\frac{1}{2}} \\\\ &= \mathbf{I_d} \end{aligned}$$

確率モデル

パラメトリックモデル: 確率モデルを仮定し, 学習データからその確率モデルのパラメータを推定して識別規則を構成する手法

• ベイズ識別規則, 判別分析, ロジスティック回帰

ノンパラメトリックモデル: 確率モデルを用いずに, 識別規則を構成する手法

• k最近傍法, サポートベクターマシン(SVM), 分類木, ヒストグラム法

1次元正規分布の密度関数は

$$\mathcal{N}(x \ |\ \mu, \sigma^2) = \frac{1}{\sqrt{2\pi} \sigma} \exp(-\frac{(x - \mu)^2}{\sigma^2})$$

となり, 平均$\mu$, と標準偏差$\sigma$(分散$\sigma^2$)が形を決める

d次元正規分布関数

d次元正規分布の密度関数は

$$\mathcal{N}(\mathbf{x} \ |\ \mathbf{\mu}, \mathbf{\Sigma}) = \frac{1}{(2\pi)^{d/2} |\mathbf{\Sigma}|^{1/2}} \exp(-\frac{1}{2} (\mathbf{x} - \mathbf{\mu})^T \mathbf{\Sigma}^{-1} (\mathbf{x} - \mathbf{\mu}))$$

任意の点$\mathbf{x}$と$\mathbf{\mu}$の間の距離をマハラノビス距離といい, 次のように表す

$$d(\mathbf{x}, \mathbf{\mu}) = \sqrt{(\mathbf{x} - \mathbf{\mu})^T \mathbf{\Sigma}^{-1} (\mathbf{x} - \mathbf{\mu})}$$

ユークリッド距離を共分散で割っているので, 各変数のバラつき方を考慮した距離になっている

正規分布から導かれる識別関数

$i$番目のクラスのクラス条件付き確率が$d$次元正規分布だと仮定し,ベイズの誤り率最小識別規則を満たす識別関数を求めよう. クラス事前確率を$P(C_i)$とすると, 事後確率は

$$P(C_i \ |\ \mathbf{x}) \propto \frac{P(C_i)}{(2\pi)^{d/2} |\mathbf{\Sigma}|^{1/2}} \exp(-\frac{1}{2} (\mathbf{x} - \mathbf{\mu})^T \mathbf{\Sigma}^{-1} (\mathbf{x} - \mathbf{\mu}))$$

各クラスに表れる共通項を省略して整理して, 評価値を表せば,

$$g(x_i) = (\mathbf{x} - \mu_i)^T \mathbf{\Sigma}_i^{-1} (\mathbf{x} - \mu_i) + \ln |\mathbf{\Sigma}_i| - 2\ln P(C_i)$$

となるので, 識別クラスとしてこの値の最も小さなクラスを選択すれば良い.

識別クラスは 識別規則 = $\argmin_i[g_i(\mathbf{x})]$となるので, クラス$i, j$の識別境界は, 次のような2次曲面になる

$$f_{ij}(\mathbf{x}) = g_i(\mathbf{x}) - g_j(\mathbf{x}) = \mathbf{x}^T \mathbf{S} \mathbf{x} + 2\mathbf{c}^T \mathbf{x} + F = 0$$

ここで

$$\begin{aligned} &\mathbf{S} = \mathbf{\Sigma}_i^{-1} - \mathbf{\Sigma}_j^{-1}, \quad \mathbf{c}^T = \mathbf{\mu}_j^T \mathbf{\Sigma}_j^{-1} - \mathbf{\mu}_i^T \mathbf{\Sigma}_i^{-1} \\\\ &F = \mathbf{\mu}_i^T \mathbf{\Sigma}_i^{-1} \mathbf{\mu}_i - \mathbf{\mu}_j^T \mathbf{\Sigma}_j^{-1} \mathbf{\mu}_j + \ln \frac{|\mathbf{\Sigma}_i|}{|\mathbf{\Sigma}_j|} - 2\ln \frac{P(C_i)}{P(C_j)} \end{aligned}$$

• $\mathbf{\Sigma}_i^{-1} = \mathbf{\Sigma}_j^{-1}$を仮定すれば, 線形識別関数$f_{ij}(\mathbf{x}) = 2\mathbf{c}^T \mathbf{x} + F = 0$になる

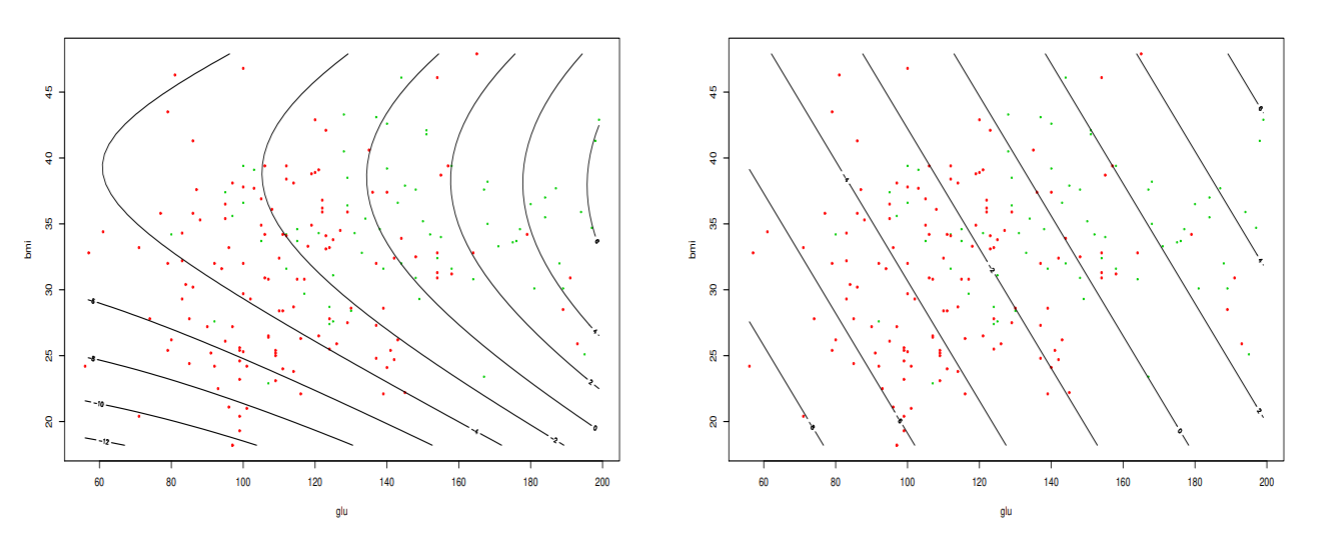
確率モデルパラメータの最尤推定

最尤法: 確率分布の未知母数の推定する方法

学習データ$\mathbf{x}_i$はパラメータ$\theta$をもつ真の分布$f(\mathbf{x} \ |\ \theta)$から独立に得られた標本とする. 確率モデルの母数$\theta$は未知であるから, 学習データから推定しないといけない.

$N$個の学習データの同時分布を考えると, サンプルの独立性から

$$f(\mathbf{x}_1, \cdots, \mathbf{x}_N \ |\ \theta) = \prod_{i = 1}^N f(\mathbf{x}_i \ |\ \theta)$$

が成り立つ.

同時分布関数は$\mathbf{x}_i$の関数だが, 学習データは既に得られた標本を使えばいいので, 上の関数を$\theta$の関数と考えると, 尤度関数が定義できる

$$L(\theta) = f(\mathbf{x}_1, \cdots, \mathbf{x}_N \ |\ \theta)$$

この尤度関数を最大にする$\theta$を求めることを最尤法といい, 最尤推定量は次のように定義される

$$\hat{\theta} = \argmax_{\theta} L(\theta) = \argmax_{\theta} \mathcal{L}(\theta)$$

ここで$\mathcal{L}(\theta) = \ln L(\theta)$を対数尤度関数という.

正規分布の最尤推定

最尤推定量は, 対数尤度関数の最大化で求まるので, 最大化の1階の条件$\frac{\partial \mathcal{L}(\mathbf{\theta})}{\partial \theta_i} = \mathbf{0}$を解けば良い

1変量正規分布の母数, $\mathbf{\theta} = (\mu, \sigma^2)^T$の最尤推定を考えよう.

尤度関数は次のとおり

$$L(\mu, \sigma^2) = \prod_{i=1}^N \frac{1}{\sqrt{2\pi} \sigma} \exp(-\frac{(x_i - \mu)^2}{2\sigma^2}) = (2\pi \sigma^2)^{-N/2} \exp(-\frac{1}{2\sigma^2} \sum_{i=1}^N (x_i - \mu)^2)$$

対数尤度関数は次のとおり

$$\mathcal{L}(\mu, \sigma^2) = -\frac{N}{2} \ln (2\pi) - \frac{N}{2} \ln \sigma^2 - \frac{1}{2\sigma^2} - \frac{1}{2\sigma^2} \sum_{i=1}^N (x_i - \mu)^2$$

最大化の1階の条件より, 正規分布のパラメータの最尤推定量は

$$\begin{aligned} &\frac{\partial \mathcal{L}(\mu, \sigma^2)}{\partial \mu} = \frac{1}{\sigma^2} \sum_{i=1}^N (x_i - \mu) = 0 \Rightarrow \hat{\mu} = \frac{1}{N}\sum_{i=1}^N x_i \\\\ &\frac{\partial \mathcal{L}(\mu, \sigma^2)}{\partial \sigma^2} = -\frac{N}{2} \frac{1}{\sigma^2} + \frac{2}{(2\sigma^2)^2} \sum_{i=1}^N (x_i - \mu)^2 = 0 \Rightarrow \hat{\sigma^2} = \frac{1}{N} \sum_{i = 1}^N (x_i - \hat{\mu})^2 \end{aligned}$$

• 標本平均と標本分散 (不偏分散 (N − 1 で割る方) ではない) になる.

k最近傍法(KNN)

最近傍法: 入力データと全ての学習データ (鋳型; template) との距離を計算し,最も近い鋳型が所属するクラスに識別する方法

k最近傍法KNN: 最も近い鋳型のクラスに識別する代わりに, 最も近い$k$個の鋳型の所属するクラスの数が最も多いクラスに識別する方法

kNN法は計算量が多いのが欠点だが, その緩和策と近似最近傍探索を勉強する.

最近傍法とボロノイ境界

$K$個のクラスを$\Omega = \lbrace C_1, \cdots, C_k \rbrace$とする. $i$番目のクラスの学習データ数$N(i)$とし, その集合を$S_i = \lbrace \mathbf{x}_1^{(i)}, \cdots, \mathbf{x}_{N(i)}^{(i)} \rbrace$と表す.

最近傍法では, 入力データ$\mathbf{x}$と各学習データ$\mathbf{x}_j^{(i)}$の類似度をユークリッド距離$d(\mathbf{x}, \mathbf{x}_j^{(i)}) = \parallel \mathbf{x} - \mathbf{x}_j^{(i)} \parallel$で計算する.

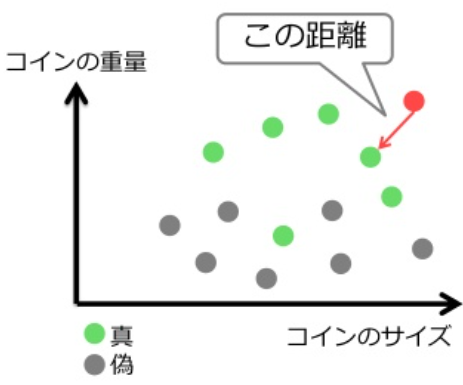
学習データのことを鋳型ともいう. $t$は学習データとの距離が大きいときにリジェクトするための値である.

リジェクトは誤り率が大きいときに判断を保留することである.

最近傍法の識別規則:

$$\begin{aligned} \text{識別クラス} = \begin{cases} \argmin_i \lbrace \min_j d(\mathbf{x}, \mathbf{x}_j^{(i)}) \rbrace, \quad &\min_{i, j} d(\mathbf{x}, \mathbf{x}_j^{(i)}) < t \\ \text{リジェクト}, \quad \min_j d(\mathbf{x}, \mathbf{x}_j^{(i)}) \rbrace, \quad &\min_{i, j} d(\mathbf{x}, \mathbf{x}_j^{(i)}) \geq t \end{cases} \end{aligned}$$

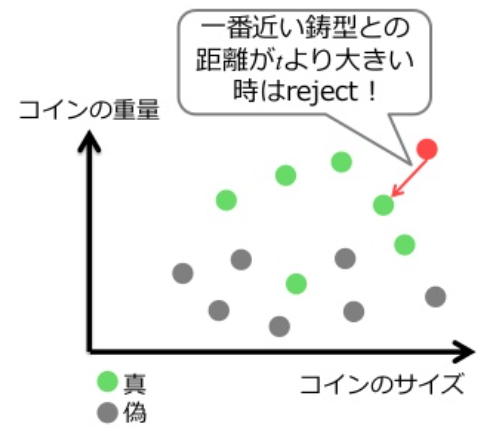
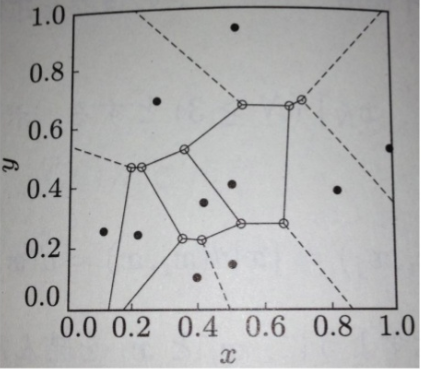
ボロノイ図

最近傍法は入力データに最も近い鋳型を見つけること

各鋳型は隣接する鋳型と等距離にある境界 (ボロノイ境界) で囲まれた支配領域 (ボロノイ領域) をもつ. 入力データが支配領域に入った鋳型が最も近い鋳型になる.

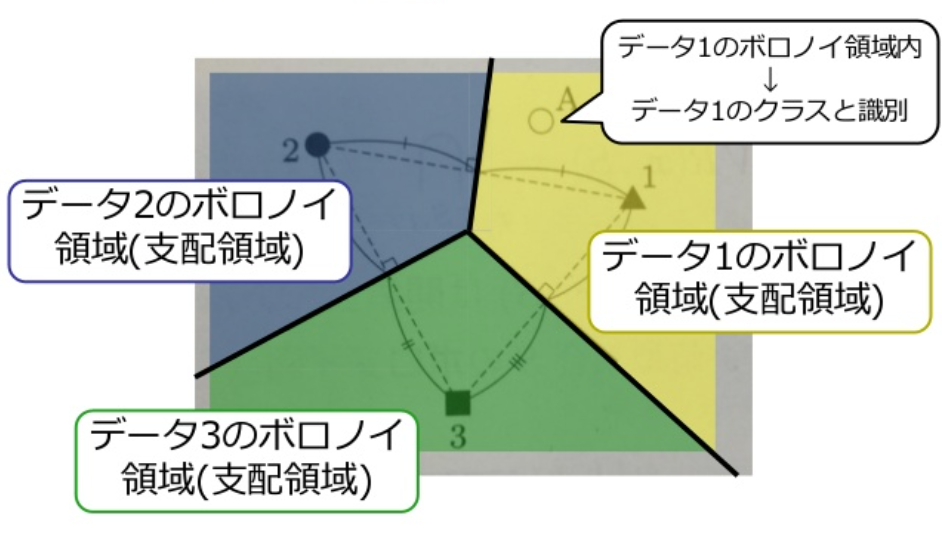
鋳型の集合を$\mathbf{S} = \lbrace \mathbf{x}_1, \cdots, \mathbf{x}_N \rbrace$とする. ボロノイ境界は$\mathbf{x}_i, \mathbf{x}_j \in \mathbf{S}$から等距離の点の集合である.

$$B(\mathbf{x_i}, \mathbf{x}_j) = \lbrace \mathbf{x} \ |\ d(\mathbf{x}_i, \mathbf{x}) = d(\mathbf{x}_j, \mathbf{x}) \rbrace$$

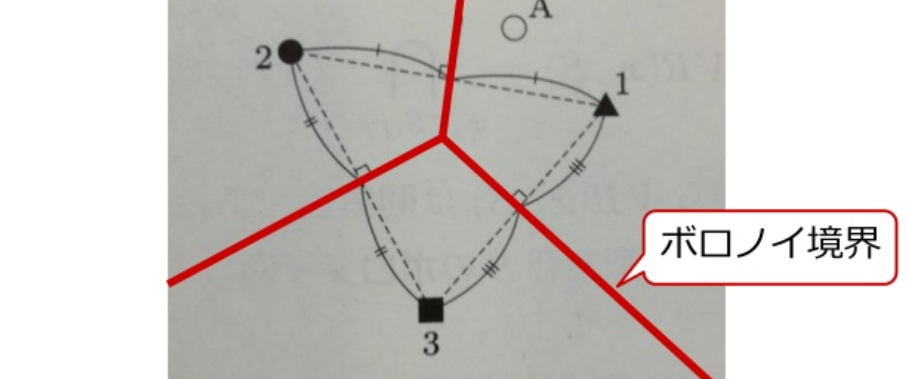
$\mathbf{x}_i$と$\mathbf{x}_j$を結んだ直線 (法線ベクトル$\mathbf{n}$) の中心$\overline{\mathbf{x}}$を通り, 直交する超平面になる.

$$(\mathbf{\overline{x}} - \mathbf{x})^T \mathbf{n} = 0, \quad \mathbf{\overline{x}} = (\mathbf{x_i} + \mathbf{x}_j) / 2, \quad \mathbf{n} = \mathbf{x}_i - \mathbf{x}_j$$

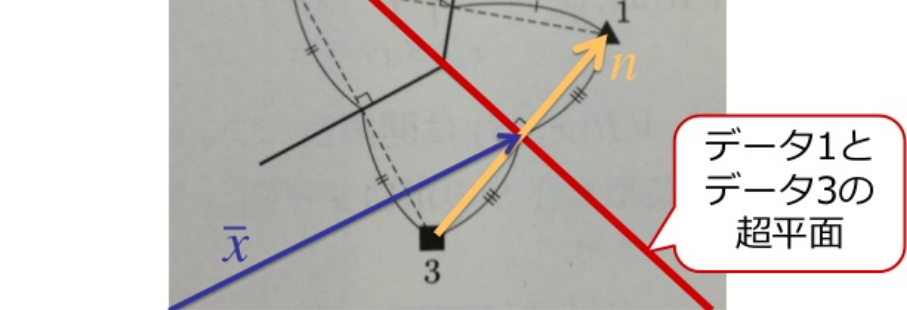
この超平面は,$\mathbf{x}_i$を含む半空間と$\mathbf{x}_j$を含む半空間に2分割する.

$$\begin{aligned} D(\mathbf{x}_i, \mathbf{x}_j) = \lbrace \mathbf{x} \ |\ d(\mathbf{x}_i, \mathbf{x}) < d(\mathbf{x}_j, \mathbf{x}) \rbrace \\ D(\mathbf{x}_j, \mathbf{x}_i) = \lbrace \mathbf{x} \ |\ d(\mathbf{x}_j, \mathbf{x}) < d(\mathbf{x}_i, \mathbf{x}) \rbrace \end{aligned}$$

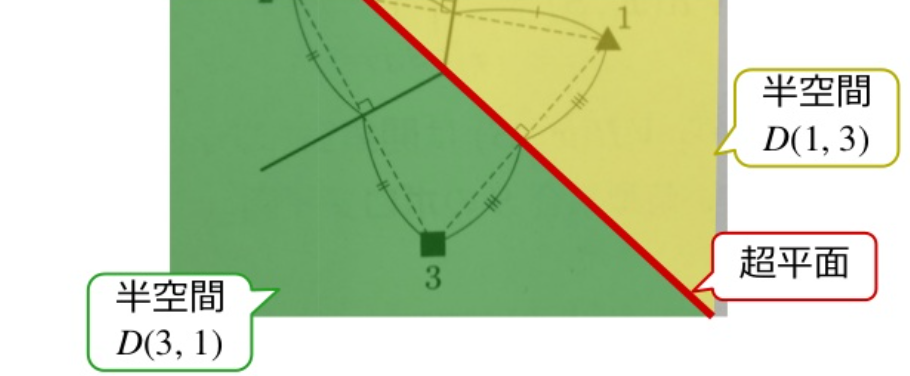
$\mathbf{x}_i$のボロノイ領域の定義は次のとおり

$$\begin{aligned} VR(\mathbf{x}_i, \mathbf{S}) = \bigcap_{x_j \in S, j \neq i} D(\mathbf{x}_i, \mathbf{x}_j) \end{aligned}$$

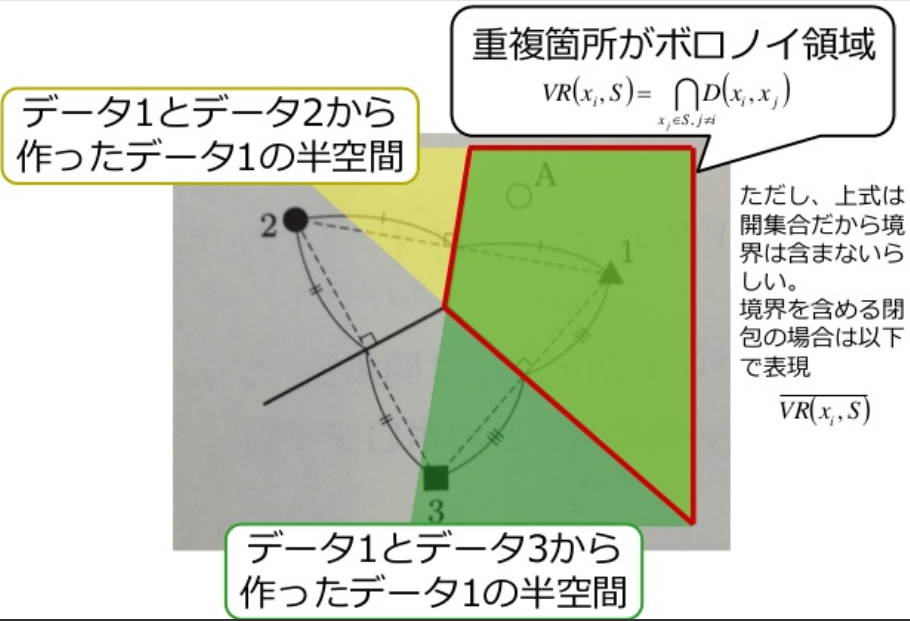
$VR(\mathbf{x}_i, \mathbf{S})$は開集合なので, 境界も含めて閉包を$\overline{VR(\mathbf{x}_i, \mathbf{S})}$と表すとボロノイ図は次のように定義される.

$$V(\mathbf{S}) = \bigcup_{x_i, x_j \in \mathbf{S}, i \neq j} = \overline{VR(\mathbf{x_i}, \mathbf{S})} \cap \overline{VR(\mathbf{x_j}, \mathbf{S})}$$

例題:

$\mathbf{x}_i = (1, 0)^T, \mathbf{x}_2 = (0, 1)^T$の場合のボロノイ境界を求めよ.

$x_1, x_2$の中点:

$$\overline{\mathbf{x}} = (\frac{1}{2}, \frac{1}{2})^T$$

2点$x_1$と$x_2$を結ぶ法線ベクトル:

$$\mathbf{n} = \mathbf{x}_1 - \mathbf{x}_2 = \binom{1}{0} - \binom{0}{1} = \binom{1}{-1}$$

従って、法線ベクトル$\mathbf{n} = \binom{1}{-1}$と直交する直線の方程式:

$$x - y + c = 0 \Rightarrow \frac{1}{2} - \frac{1}{2} + c = 0 \Rightarrow c = 0$$

$$x - y = 0$$

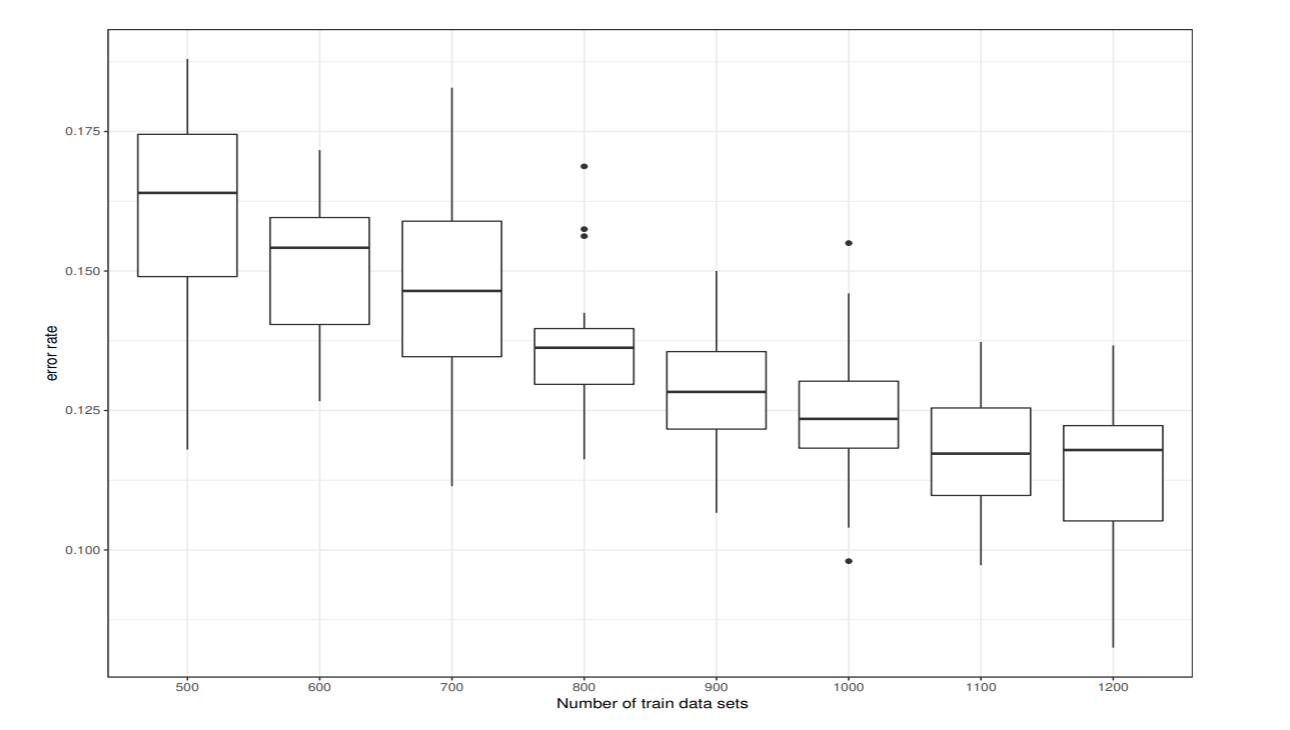
鋳型の数と識別性能

各クラスから$M$個のデータをランダムに選び, $10 \times M$ 個のデータから 1つ抜き法で汎化誤差を推定した. これを20回繰り返したときの鋳型の数と汎化誤差の関係を図示した.

kNN法

最近傍の鋳型を$k$個取ってきて, それらが最も多く所属するクラスに識別する方法を$k$最近傍法という

鋳型の集合を$T_N = \lbrace \mathbf{x}_1, \cdots, \mathbf{x}_N \rbrace$,それらが属するクラスの集合を$\Omega = \lbrace C_1, \cdots, C_K$とする.

入力$\mathbf{x}$にもっとも近い$k$個の鋳型の集合を$k(\mathbf{x}) = \lbrace \mathbf{x}_{i_1}, \cdots, \mathbf{x}_{i_k} \rbrace$とし, これらの鋳型のうちクラス$j$に属する鋳型の数を$k_j$とする.$k = k_1 + \cdots + k_K$が成り立つ.

$k$最近傍法の識別規則:

$$\begin{aligned} \text{識別クラス} = \begin{cases} j, \quad &\lbrace k_j \rbrace = \max \lbrace k_1, \cdots, k_K \rbrace \\ \text{リジェクト}, \quad &\lbrace k_1, \cdots k_K \rbrace = \max \lbrace k_1, \cdots, k_K \rbrace \end{cases} \end{aligned}$$

• 近傍$k$個の鋳型の内、数が最も多いクラス$j$と識別する
• 近傍$k$個の鋳型の内、数が最も多いクラスが複数存在する場合はrejectする

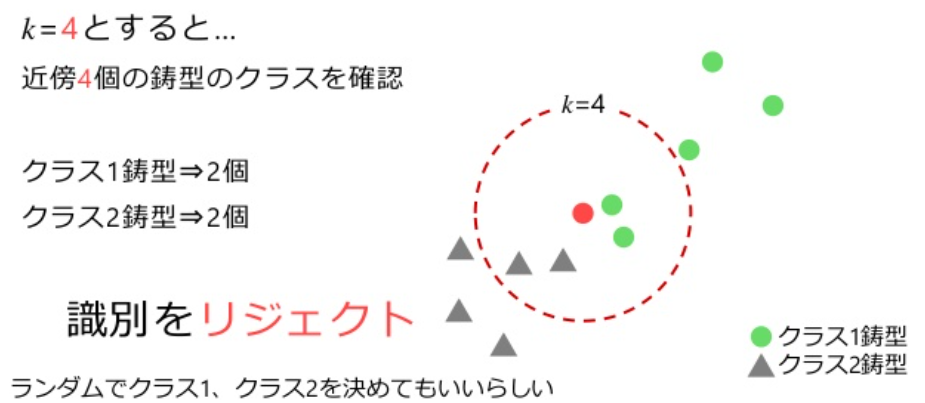
ピマインディアンデータの$k$最近傍法による識別境界

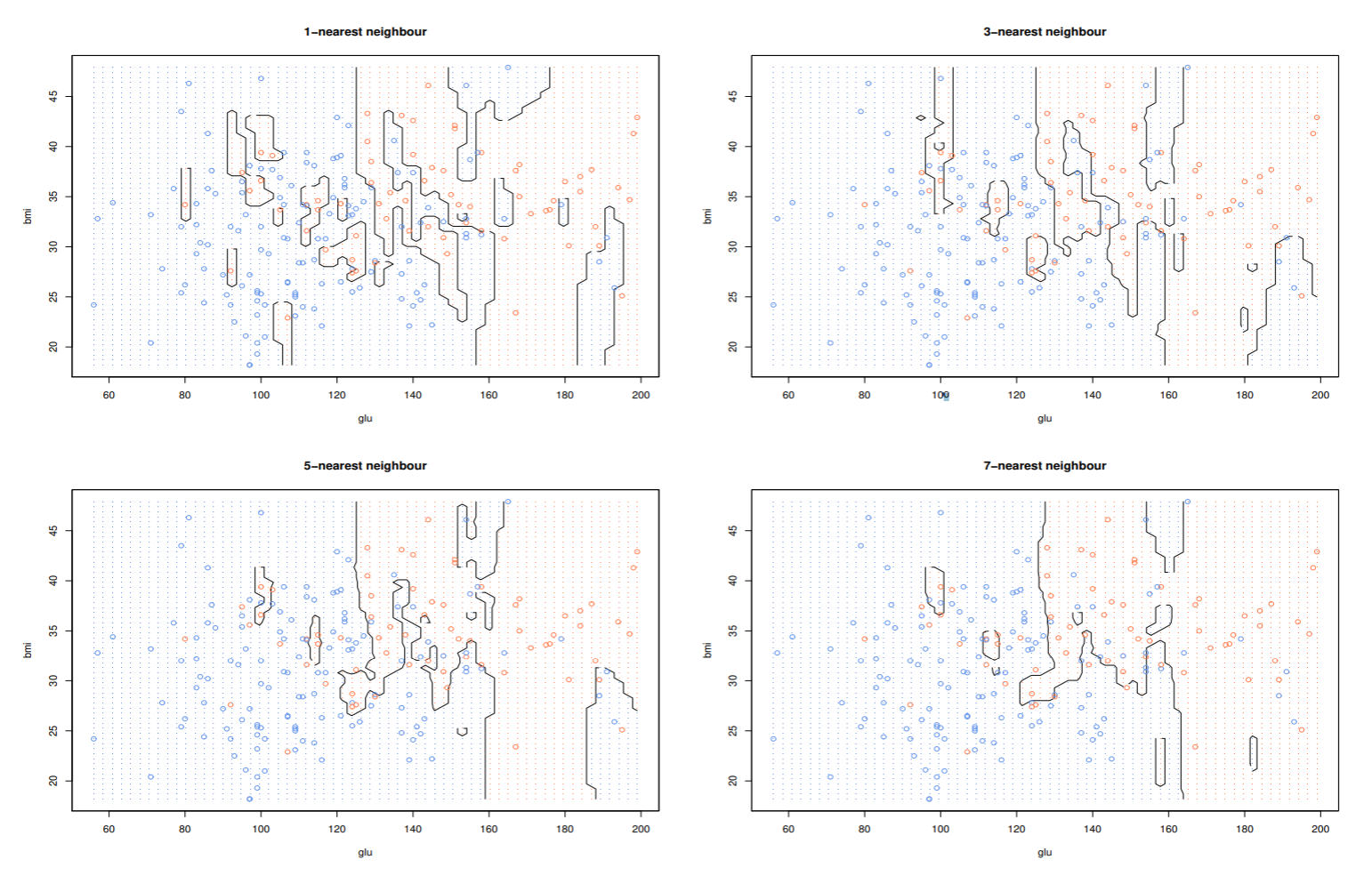
最適な最近傍数kを求める

kNN 法では, 最近傍法と同様に, 学習データ数が多くなれば誤り率は減少する. ピマ・インディアンデータでは, 学習データを大きくすることはできない. 1つ抜き法では, 全ての学習データが利用できるので , $k$が60以上になるところで安定した誤り率を示す.

漸近仮定とkNN誤り率の期待値

条件付きベイズ誤り率は, 事後確率の小さい方であった.

$$\epsilon(\mathbf{x}) = \min \lbrace P(C_1 \ |\ \mathbf{x}), P(C_2 \ |\ \mathbf{x}) \rbrace$$

ベイズ誤り率は, その期待値

$$\epsilon^* = \int \epsilon(\mathbf{x}) p(\mathbf{x}) \, d\mathbf{x}$$

入力$\mathbf{x}$の最近傍鋳型を$\mathbf{x}_{1NN}$とする. $N$個の鋳型の集合を$\mathcal{T}_N$とする.

漸近仮定が成り立つとき, kNN誤り率とベイズ誤り率の間には次の関係が成り立つ.

$\lim_{N \rightarrow \infty} \mathcal{T}_N \Rightarrow d(\mathbf{x}, \mathbf{x}_{1NN}) \rightarrow 0$であれば,

• $N$: 鋳型の数
• $\mathcal{T}_N$: $N$個の鋳型の集合
• $d(x, x_{1NN})$: 入力$x$と、最近傍鋳型$x_{1NN}$の距離

$$\frac{1}{2}\epsilon^* \leq \epsilon_{2NN} \leq \epsilon_{4NN} \leq \cdots \leq \epsilon^* \leq \cdots \leq \epsilon_{3NN} \leq \epsilon_{1NN} \leq 2\epsilon^*$$

• $k$は偶数の時、誤り率が低い
• $k$は奇数の時、誤り率が高い

kNN法の改善

誤り削除型KNN法(Edited kNN)

kNNで識別境界を作成した時に、不正解の識別領域に含まれる鋳型を削除する

• 削除すると識別境界が変わるので、最適的に削除を行う

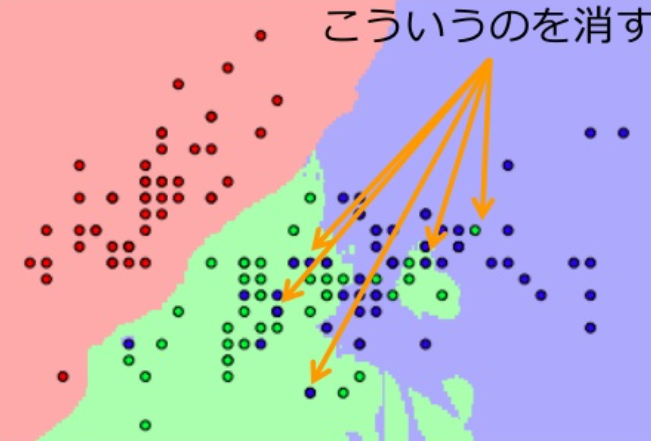
圧縮型kNN(Condensed kNN)

識別に関係ない鋳型を削除する

• 削除前と後で、誤り率が同じになるように選ぶ

分枝限定法

分枝法と限定法を用いて、近傍の探索を効率化させる

• 分枝法: クラスタリングによって木構造のように組織化する
• 限定法: 分枝法で作成した木構造をもとに近傍の探索を行う

近似最近傍探索

次元が大きくなると, 制約された時間の中で正確な解を求めるのが困難なため, 近似最近傍探索を行う.

学習データの集合を$P = \lbrace \mathbf{x}_i \rbrace (i = 1, \cdots, N)$とし, 入力データ$\mathbf{q}$の最近傍解$\mathbf{x}^*$の$\epsilon$-近似解$\mathbf{x}$を次を満たす$\mathbf{x}$とする.

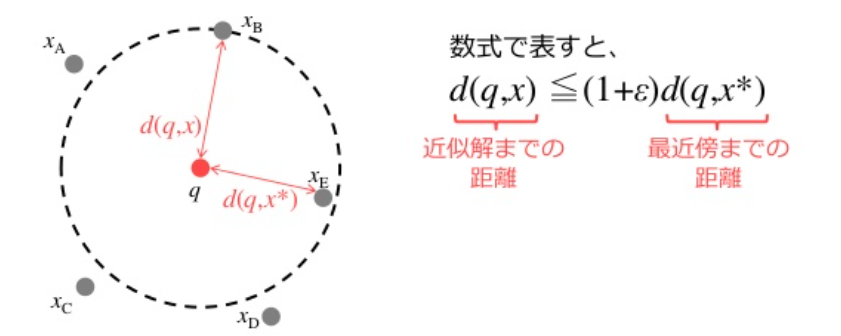
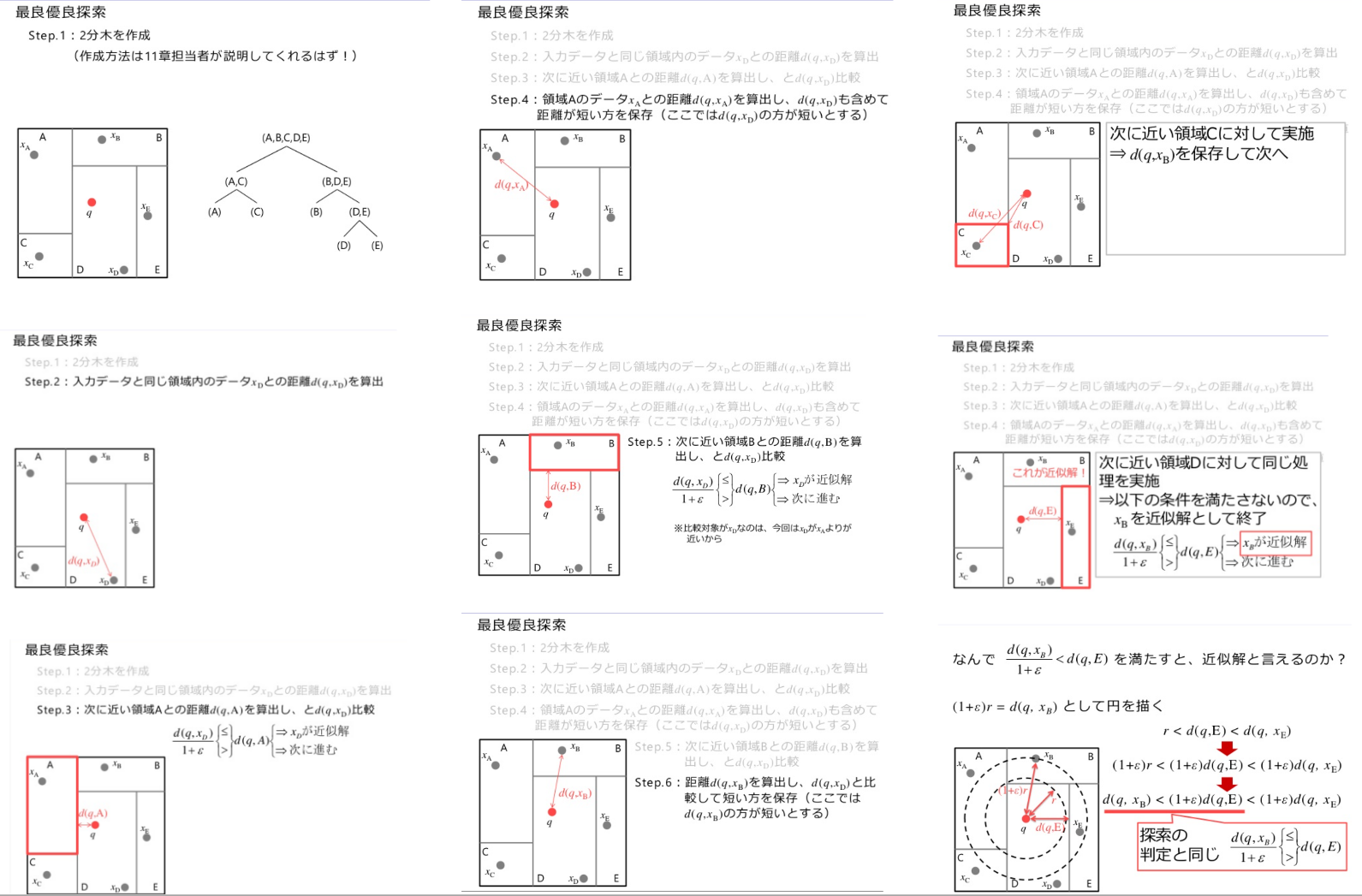
$d(\mathbf{q}, \mathbf{x}^*)$の値は, 2分木等の最良優先探索を使って求める.

線形識別関数

線形識別関数は$f(\mathbf{x}) = \mathbf{w}^T \mathbf{x} + w_0$と表すことができる. $\mathbf{w}$を線形識別関数の係数ベクトル, $w_0$をバイアスという.

入力データの次元を$d$とすれば, 識別境界は$d - 1$次元の超平面となる.

線形識別関数の定義の目的:

• 線形識別関数が2つのクラスを超平面で区別
• 多クラス問題への拡張

ここでは, 2乗誤差最小化基準とフィッシャーの判別関数を紹介する.

超平面の方程式

$d$次元の入力ベクトルを$\mathbf{x} = (x_1, \cdots, x_d)^T$, 係数ベクトルを$\mathbf{w} = (w_1, \cdots, w_d)^T$,バイアス項を$w_0$とすれば, 2 クラス問題の識別関数は, 次のように表される.

$$f(\mathbf{x}) = \mathbf{w}^T\mathbf{x} + w_0$$

識別境界を$f(\mathbf{x}) = 0$とすれば, 識別規則は,

$$\begin{aligned} \text{識別クラス} = \begin{cases} C_1, \quad (f(\mathbf{x}) \geq 0) \\ C_2, \quad (f(\mathbf{x}) < 0) \end{cases} \end{aligned}$$

識別境界では, $\mathbf{w}^T\mathbf{x} = -w_0$が成り立つので, 両辺を係数ベクトルのノルム$\parallel \mathbf{w} \parallel$で正規化して

$$\begin{aligned} \frac{\mathbf{w}^T}{\parallel \mathbf{w} \parallel} \mathbf{x} = -\frac{w_0}{\parallel \mathbf{w} \parallel} \end{aligned}$$

となる.

$\mathbf{n} = \frac{\mathbf{w}}{\parallel \mathbf{w} \parallel}, \Delta_w = -\frac{w_0}{\parallel \mathbf{w} \parallel}$とおけば,

$$\mathbf{n}^T\mathbf{x} = \Delta_w$$

となるので, 識別境界は, $f(\mathbf{x}) = \mathbf{n}^T\mathbf{x} - \Delta_w = 0$と表される.

識別境界上の任意の点のベクトル$\mathbf{P}$を考えると,

$$f(\mathbf{P}) = \mathbf{n}^T\mathbf{P} - \Delta_w = 0$$

が成り立つので

$$f(\mathbf{x}) = \mathbf{n}^T\mathbf{x} - \Delta_w = \mathbf{n}^T(\mathbf{x} - \mathbf{P}) = 0$$

となる.

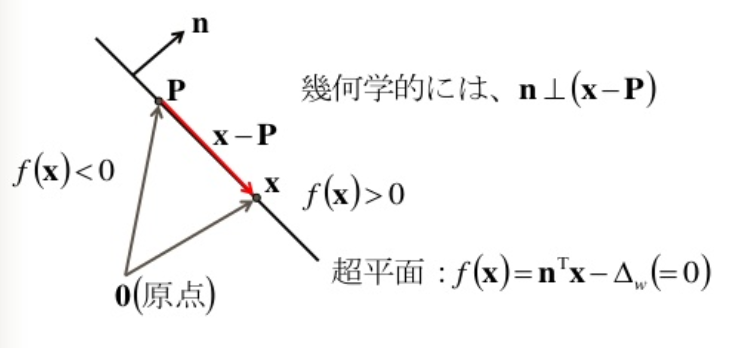
識別境界は単位法線ベクトル$n$をもつ超平面となる.

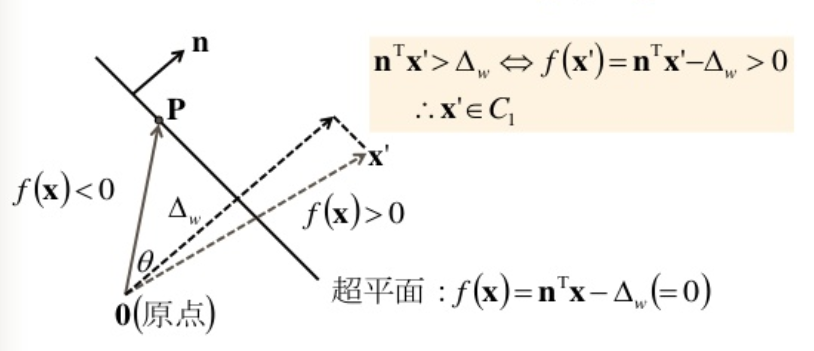
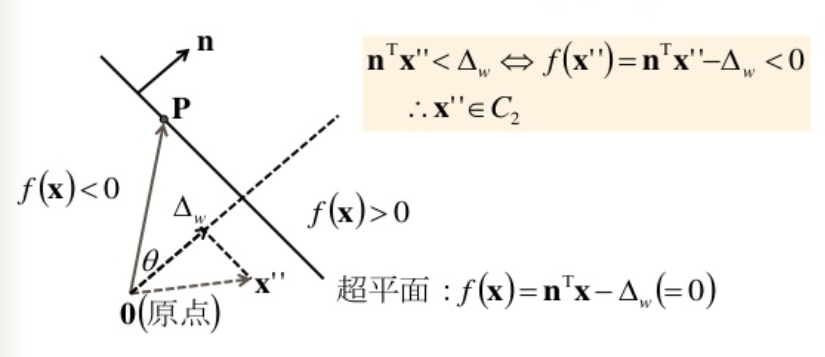
例題:

最小2乗誤差基準によるパラメータの推定

目的:

• 最小2乗誤差基準による線形識別関数のパラメータが正規方程式により得られること
• 多クラス問題への拡張

正規方程式

最小2乗誤差基準は, 識別関数の出力値と教師入力との差を最小にするパラメータを求める手法.

$$f(\mathbf{x}) = w_0 + w_1x_1 + \cdots + w_dx_d = \mathbf{w}^T\mathbf{x}$$

入力ベクトル$\mathbf{x}_i$が所属するクラスは, 教師入力$t_i$により, 次のように与える.

$$\begin{aligned} t_i = \begin{cases} +1, \quad \mathbf{x}_1 \in C_1 \\ -1, \quad \mathbf{x}_1 \in C_2 \end{cases} \end{aligned}$$

学習データ数を$N$, 学習用の入力ベクトルを並べた行列を$\mathbf{X}$, 教師入力を並べたベクトルを$\mathbf{t}$とすれば, 出力値の教師入力の差を2乗誤差で評価した評価関数$E(\mathbf{w})$は次のようになる.

$$\begin{aligned} E(\mathbf{w}) &= \sum_{i=1}^N (t_i - f(\mathbf{x}_i))^2 \\\\ &= (\mathbf{t} - \mathbf{X}\mathbf{w})^T (\mathbf{t} - \mathbf{X}\mathbf{w}) \\\\ &= \mathbf{t}^T\mathbf{t} - 2\mathbf{t}^T \mathbf{X}\mathbf{w} + \mathbf{w}^T \mathbf{X}^T \mathbf{X}\mathbf{w} \end{aligned}$$

評価関数$E(\mathbf{w}) = \mathbf{t}^T\mathbf{t} - 2\mathbf{t}^T \mathbf{X}\mathbf{w} + \mathbf{w}^T \mathbf{X}^T \mathbf{X}\mathbf{w}$は下に凸な関数, 故に, $\mathbf{w}$での微分が0になるパラメータが$E(\mathbf{w})$の最小を与える.

評価関数を最小にする$\mathbf{w}$は, 次のようにして求める.

$$\frac{\partial E(\mathbf{w})}{\partial \mathbf{w}} = -2\mathbf{X}^T \mathbf{t} + 2\mathbf{X}^T \mathbf{X}\mathbf{w} = 0$$

これを解いて,

$$\hat{\mathbf{w}} = (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T \mathbf{t}$$

学習データに対する予測値$\hat{t}$は

$$\hat{\mathbf{t}} = \mathbf{X}\hat{\mathbf{w}} = \mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T \mathbf{t}$$

行列$\mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T$は, 教師データ$\mathbf{t}$予測値$\hat{\mathbf{t}}$に変換する行列であり, 射影行列(ハット行列)と呼ばれる.

例題:

多クラス問題への拡張

K(> 2)クラスの識別関数の作り方:

• 一対多
  • 識別不能領域(空白クラス)発生
• 一対一
  • 識別不能領域(空白クラス)発生
• 最大識別関数法
  • 識別不能領域解消

一対多

一対多では, 1 つのクラスと他のすべてのクラスを識別する$K - 1$個の2クラス識別関数$f_j(\mathbf{x}), j = 1, \cdots, K - 1$を用意する.

一対一

一対一では, クラス$i, j$を識別する$K(K - 1) / 2$個の 2クラス識別関数$f_{ij}(\mathbf{x}), 1 \leq i < j \leq K$を用意して, 多数決で識別クラスを決める.

この方法でも識別クラスの矛盾が生じる空白領域のクラスが決定できなかったり, 関係しない識別関数が出るため多数決がとれなくなることもある.

最大識別関数法

最大識別関数法では, $K$個の識別関数を用意して,

$$\text{識別クラス} = \argmax_j f_j(\mathbf{x}) = \argmax_j \mathbf{w}_j^T \mathbf{x} + w_{j0}$$

となるよう, 識別関数値が最大になるクラスに識別すれば良い.

このとき, 識別境界は$f_i(\mathbf{x}) = f_j(\mathbf{x})$となるので,

$$f_{ij} = (\mathbf{w}_i - \mathbf{w}_j)^T \mathbf{x} + (w_{i0} - w_{j0}) = 0$$

を満たす$K - 1$個の識別境界ができる.

最大識別関数法では, $K$個の識別関数$f_K(\mathbf{x}) = \mathbf{w}_K^T \mathbf{x}$を用意して, 2乗誤差を最小にするパラメータ$\mathbf{w}_K$を2クラス問題と同様に求めれば良い.

2乗誤差を最小にするパラメータ$\hat{\mathbf{W}}$は

$$\hat{\mathbf{W}} = (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T \mathbf{T}$$

となる.

識別関数は

$$f(\mathbf{x}) = \hat{\mathbf{W}} \mathbf{x} = (\mathbf{w}_1, \cdots, \mathbf{w}_K)^T \mathbf{x} = (f_1(\mathbf{x}), \cdots, f_K(\mathbf{x}))^T$$

となるので, 識別クラス = $\argmax_j f_j(\mathbf{x})$となる.

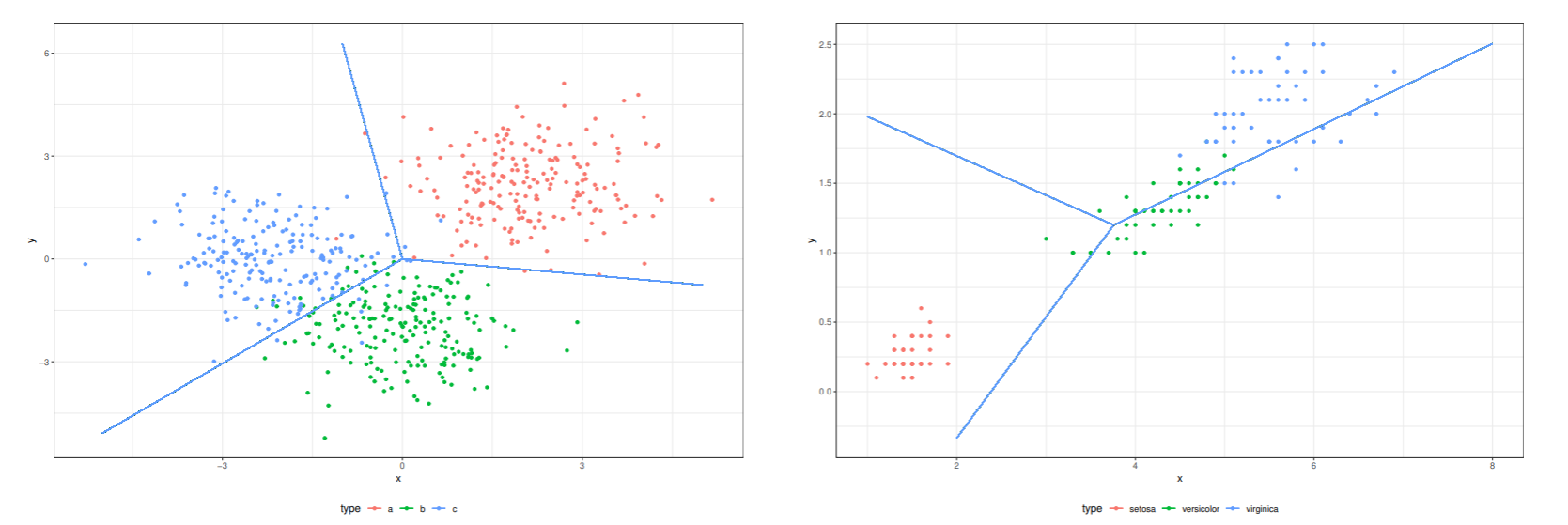
• 線形識別関数を最大識別関数法で求めた場合の識別境界
• うまく構成できる場合 (左) と複数のクラスが一直線上に並んでいる場合はうまく識別できない.

線形判別分析

線形識別関数は, $d$次元ベクトル$\mathbf{x}$を, ベクトル$\mathbf{w}$上のスカラ関数に写像する.

最小2乗誤差基準では, 教師データに忠実になるように, 線形識別関数を求めた.

線形判別分析では, 1次元に写像されたとき, クラス間ができるだけ重ならないような写像方向を見つける.

重なりの少ない写像を実現するベクトル$\mathbf{w}$を見つけることが大事

フィッシャーの線形判別関数

線形識別関数は, クラス間変動とクラス内変動の比を最大にする軸へ射影する.

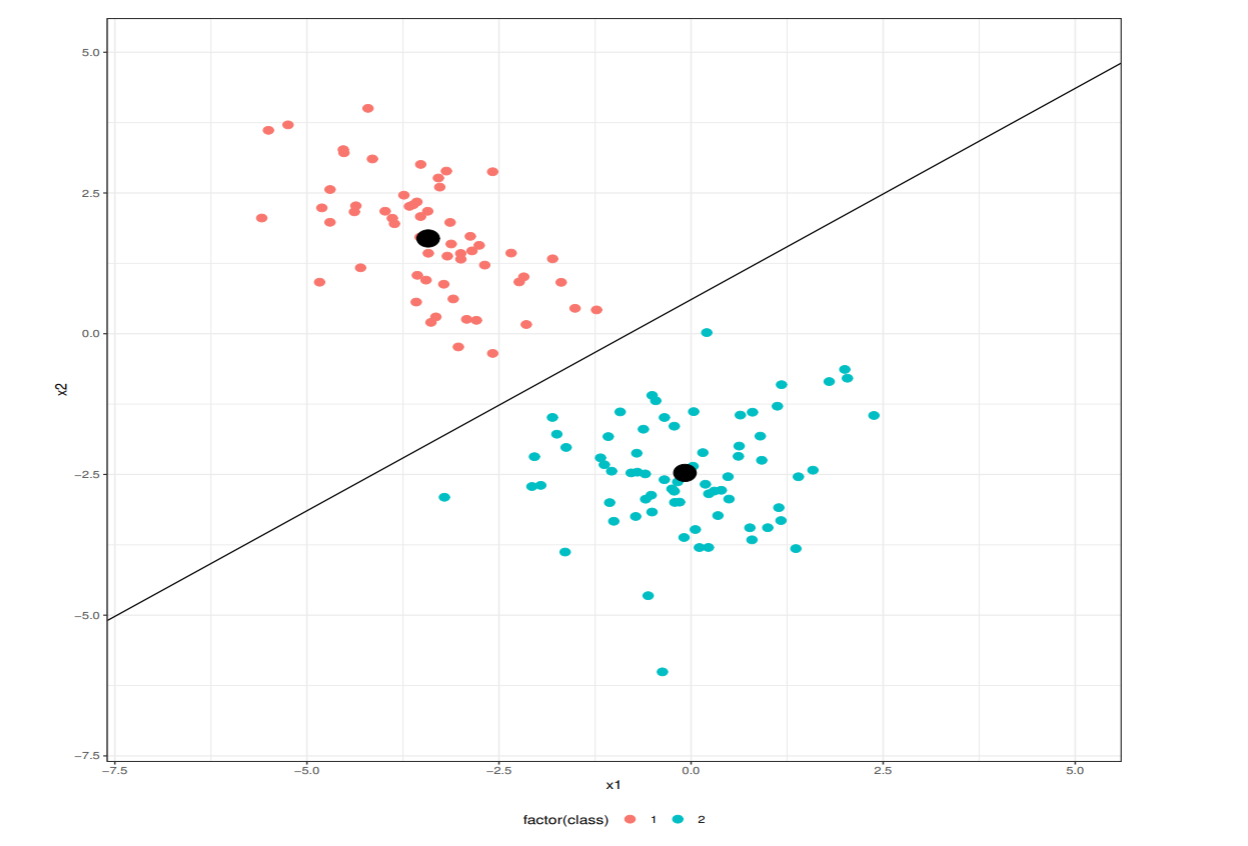
学習データ数が各クラス$N_1, N_2$で全データ数が$N = N_1 + N_2$の2クラス問題を考える.

線形識別関数$y = \mathbf{w}^T \mathbf{x}$は平均ベクトル

$$\mathbf{\mu}_k = \frac{1}{N_k} = \sum_{i \in C_k} \mathbf{x}_i, \quad k = 1, 2$$

を$m_K = \mathbf{w}^T \mu_k$に写像する. この時, 写像した平均の差が大きいほどクラス分離が良くなる

$$m_1 - m_2 = \mathbf{w}^T (\mu_1 - \mu_2)$$

平均差の2乗をクラス間変動(between)という.

また, クラス内の変動は小さい方が重なりも小さくなる.

$$S_k^2 = \sum_{i \in C_k}(y_i - m_k)^2$$

これをクラス内変動という. 全クラス内変動は$S_1^2 + S_2^2$である.

フィッシャー基準とは, クラス間変動とクラス間変動の比

$$J(\mathbf{w}) = \frac{(m_1 - m_2)^2}{S_1^2 + S_2^2}$$

これを最大にする$\mathbf{w}$を求める.

フィッシャー基準は, 次のように表すことができる.

$$J(\mathbf{w}) = \frac{\mathbf{w}^T \mathbf{S}_B \mathbf{w}}{\mathbf{w}^T \mathbf{S}_W \mathbf{w}}$$

ここで,

$$\begin{aligned} &\mathbf{w}^T \mathbf{S}_B \mathbf{w} = \mathbf{w}^T (\mu_1 - \mu_2)(\mu_1 - \mu_2)^T \mathbf{w} \\\\ &\mathbf{w}^T \mathbf{S}_W \mathbf{w} = (\sum_{i \in C_k} (\mathbf{x}_i - \mu_k) (\mathbf{x}_i - \mu_k)^T) \mathbf{w} \end{aligned}$$

である.

これを最大にする解$\mathbf{w}$は, 次の一般化固有値問題の解

$$\mathbf{S}_B \mathbf{w} = \lambda \mathbf{S}_W \mathbf{w}$$

判別分析法

フィッシャー基準はクラス間変動を用いているため, 線形変換$y = \mathbf{w}^T\mathbf{x}$の$w_0$を明示的に扱うことが出来ない.そこで, クラス識別のためのバイアス項$w_0$を明示的に扱うような定式化をする.

線形変換後の$y$の平均と分散は, 各クラス$k = 1, 2$について次のようになる.

$$m_k = \mathbf{w}_T \mu_K + w_0, \quad \sigma_k^2 = \mathbf{w}^T \mathbf{\Sigma}_k \mathbf{w}$$

ここで,

$$\begin{aligned} &\mu_k = \frac{1}{N_k} \sum_{i \in C_k}x_i \\\\ &\mathbf{\Sigma}_k = \frac{1}{N_k} \sum_{i \in C_k} (x_i - \mu_k)(x_i - \mu_k)^T \end{aligned}$$

である.

クラス分離度の評価関数を$h(m_1, \sigma_1^2, m_2, \sigma_2^2)$とすると, この評価関数の最大化にする$\mathbf{w}$と$w_0$求める

$$\begin{aligned} &\frac{\partial h}{\partial \mathbf{w}} = \frac{\partial h}{\partial \sigma_1^2} \frac{\partial \sigma_1^2}{\partial \mathbf{w}} + \frac{\partial h}{\partial \sigma_2^2} \frac{\partial \sigma_2^2}{\partial \mathbf{w}} + \frac{\partial h}{\partial m_1^2} \frac{\partial m_1^2}{\partial \mathbf{w}} + \frac{\partial h}{\partial m_2^2} \frac{\partial m_2^2}{\partial \mathbf{w}} = 0 \\\\ &\frac{\partial h}{\partial w_0} = \frac{\partial h}{\partial \sigma_1^2} \frac{\partial \sigma_1^2}{\partial w_0} + \frac{\partial h}{\partial \sigma_2^2} \frac{\partial \sigma_2^2}{\partial w_0} + \frac{\partial h}{\partial m_1^2} \frac{\partial m_1^2}{\partial w_0} + \frac{\partial h}{\partial m_2^2} \frac{\partial m_2^2}{\partial w_0} = 0 \end{aligned}$$

ここで

$$\begin{aligned} \frac{\partial \sigma_k^2}{\partial \mathbf{w}} = 2\mathbf{\Sigma}_k \mathbf{w}, \quad \frac{\partial \sigma_k^2}{\partial w_0} = 0, \quad \frac{\partial m_k^2}{\partial \mathbf{w}} = \mu_k, \quad \frac{\partial m_k^2}{\partial w_0} = 1 \end{aligned}$$

を先程の式に代入して整理すれば, 最適な$\mathbf{w}$を求めることができる.

$$2(\frac{\partial h}{\partial \sigma_1^2} + \frac{\partial h}{\partial \sigma_2^2}) (s\mathbf{\Sigma}_1 + (1 - s)\mathbf{\Sigma}_w) \mathbf{w} = \frac{\partial h}{\partial m_1} (\mu_2 - \mu_1)$$

ベクトルの向きが問題なので, スカラー項は無視して良い. よって, 最適な$\mathbf{w}$は次式となる.

$$\begin{aligned} \mathbf{w} = (s \mathbf{\Sigma}_1 + (1 - s) \mathbf{\Sigma}_2)^{-1} (\mu_1 - \mu_2) \end{aligned}$$

評価関数をクラス間分散とクラス内分散の比

$$\begin{aligned} h = \frac{P(C_1) (m_1 - \overline{m}^2) + P(C_2) (m_2 - \overline{m})^2}{P(C_1)\sigma_1^2 + P(C_2)\sigma_2^2} \end{aligned}$$

で定義した判別関数を判別分析法という. $\overline{m}$は全データの平均.

$s = P(C_1)$が得られることから, 最適な$\mathbf{w}$は

$$\begin{aligned} \mathbf{w} = (P(C_1) \mathbf{\Sigma}_1 + P(C_2) \mathbf{\Sigma}_2)^{-1} (\mu_1 - \mu_2) \end{aligned}$$

最適なバイアス項は次の通り.

$$w_0 = \overline{m} - \mathbf{w}^T (P(C_1)\mu_1 + P(C_2)\mu_2)$$

判別分析2値化法

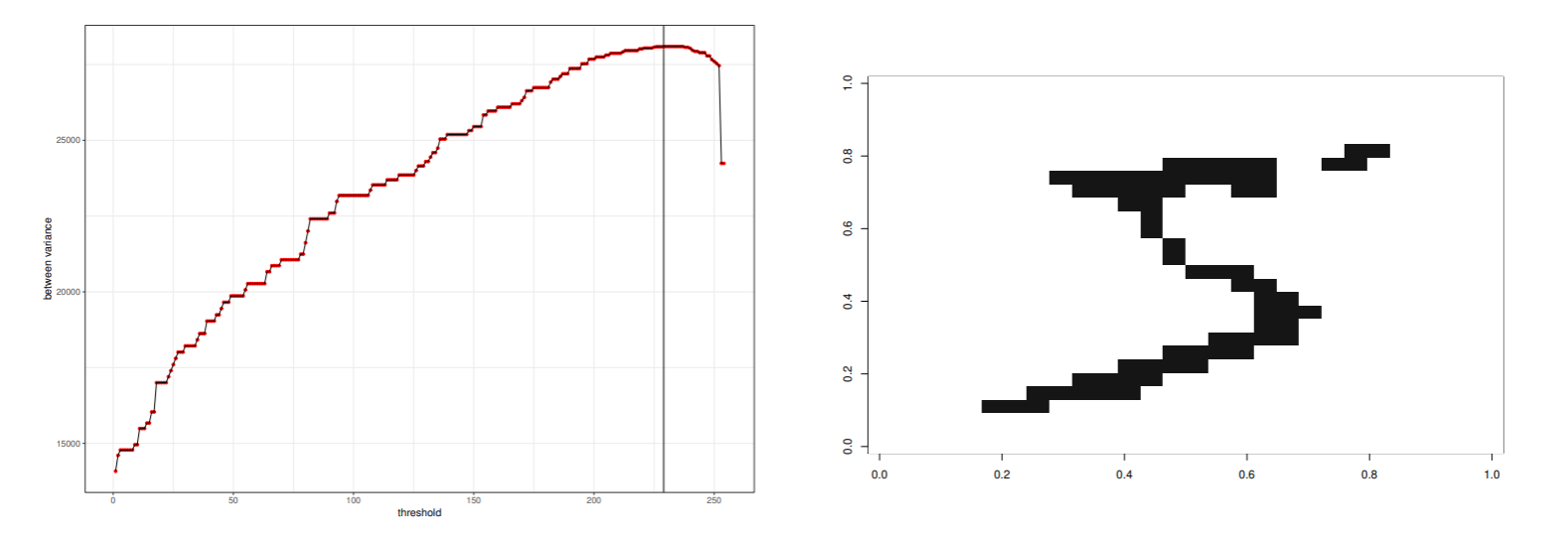
画像の判別分析2値化法を紹介する.

左の図は, 1文字の原画で, 右の図が画像の濃度ヒストグラム.

図 (数字) と地の分布の境界を決定するために判別分析法を用いる.

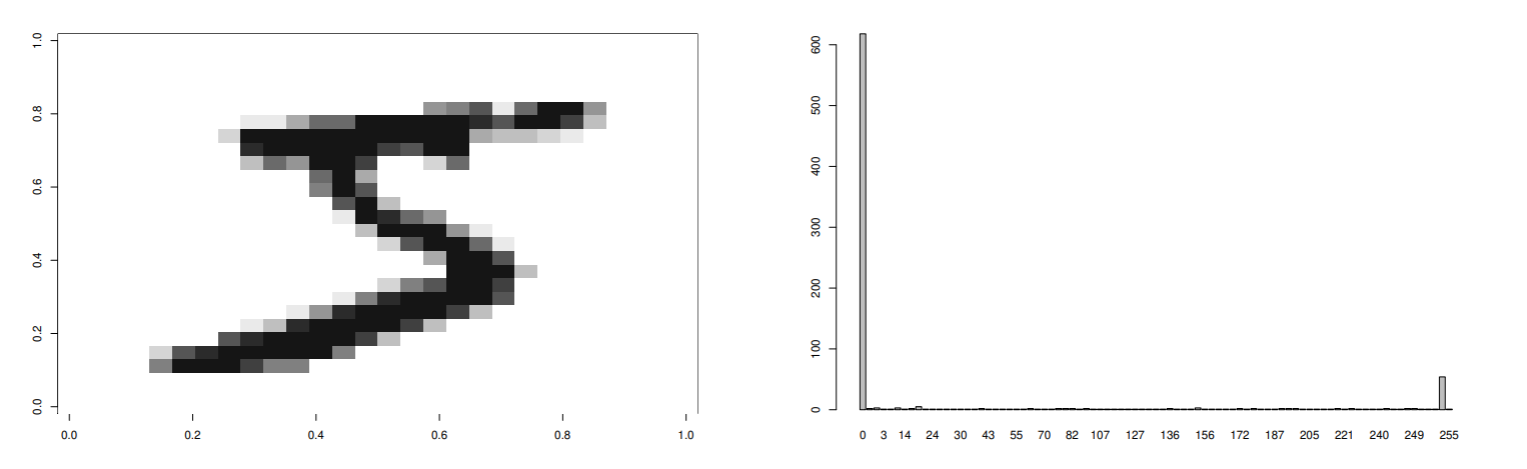
クラス間分散を$\sigma_B^2$, クラス内分散を$\sigma_W^2$と全分散$\sigma_T^2$の関係は以下の様になるから,

$$\sigma_T^2 = \sigma_W^2 + \sigma_B^2, \quad h = \frac{\sigma_B^2}{\sigma_W^2} = \frac{1}{\sigma_T^2 / \sigma_B^2 - 1}$$

• $\sigma_B^2 / \sigma_T^2$を最大にすれば, 分散比$h$も最大になる.

多クラス問題への拡張

フィッシャー基準を$K > 2$の場合に拡張する. 各クラスのデータ数を$N_k, k = 1, \cdots, K$とする.

2クラスの場合に識別境界を計算できたが, 多クラスの場合は, $d(> K)$次元のデータを高々$K - 1$次元の特徴空間に写像する線形変換行列を見つける問題になるので, 識別境界は計算できない.

各クラスのクラス内変動を次のように定義する.

$$\mathbf{S}_k = \sum_{i \in C_k} (\mathbf{x}_i - \mu_k) (\mathbf{x}_i - \mu_k)^T, \quad \mu_k = \frac{1}{N_k} \sum_{i \in C_k} \mathbf{x}_i$$

全クラスのクラス内変動の和を$\mathbf{S}_W = \sum_{i = 1}^K \mathbf{S}_K$とする.

全データの変動の和を, 次のように定義する. (全変動という.)

$$\mathbf{S}_T = \sum_{i=1}^N (\mathbf{x}_i - \mu)(\mathbf{x}_i - \mu)^T$$

全変動$\mathbf{S}_T$は次のようにクラス内分散$\mathbf{S}_W$を含むように分解できる.

$d > K$であれば, $d$次元空間から$K - 1$次元への線形写像

$$y_k = \mathbf{w}_k^T \mathbf{x}, k = 1, \cdots, K-1$$

を考える. ($d$: バイアス項を除いたデータの次元)

$$\begin{aligned} \mathbf{y} &= (y_1, \cdots, y_{K-1})^T \\ \mathbf{W} &= (\mathbf{w}_1, \cdots, \mathbf{w}_{K-1}) \end{aligned}$$

とすれば, $K - 1$個の線形変換は

$$\mathbf{y} = \mathbf{W}^T \mathbf{x}$$

と書ける.

2クラス問題と同様, 最適な写像行列$\mathbf{W}$を求める基準は, クラス間変動行列$\tilde{\mathbf{S}_B}$とクラス内変動行列$\tilde{\mathbf{S}_W}$の比を最大にすること.

しかし,行列の比なので何らかのスカラー量に変換しないと, 最大値を求めることができない.

例えば, 次のような基準がある.

$$J(\mathbf{W}) = Tr(\tilde{\mathbf{S}_W}^{-1} \tilde{\mathbf{S}_B}) = Tr((\mathbf{W}^T \mathbf{S}_W \mathbf{W})^{-1} \mathbf{W}^T \mathbf{S}_B \mathbf{W})$$

ここで

$$\begin{aligned} &\tilde{\mathbf{S}_W} = \sum_{i=1}^K \sum_{i \in C_k} (\mathbf{y}_i - \mathbf{m}_k) (\mathbf{y}_i - \mathbf{m}_k)^T = \mathbf{W}^T \mathbf{S}_W \mathbf{W} \\\\ &\tilde{\mathbf{S}_B} = \sum_{k=1}^K N_k (\mathbf{m}_k - \mathbf{m}) (\mathbf{m}_k - \mathbf{m})^T = \mathbf{W}^T \mathbf{S}_B \mathbf{W} \\\\ &\tilde{\mathbf{S}_T} = \tilde{\mathbf{S}_W} + \tilde{\mathbf{S}_B} \end{aligned}$$

あやめデータの判別空間の構成

あやめデータは3クラス, 4次元データなので, 線型判別関数により4次元特徴空間から2次元判別空間への写像を得ることができる.

図は正規分布を仮定した線形判別関数による識別境界を示した.

課題6.1

識別境界が直線$y = -2x + 3$で表されたとする. この直線の法線ベクトルを求め, 識別境界上の適当な位置ベクトル$\mathbf{P}$を用いて,$f(x) = \mathbf{n}^T\mathbf{x} - \Delta_w = \mathbf{n}^T(\mathbf{x} - \mathbf{P})$)と表現できることを確かめよ.

$-2x - y + 3 = 0 \Leftrightarrow \binom{-2}{-1}^T \binom{x}{y} + 3 = 0$より, $\mathbf{x} = (x, y)^T$と$\mathbf{w} = (-2, -1)^T$は直交である

$\parallel \mathbf{w} \parallel = \sqrt{(-2)^2 + (-1)^2} = \sqrt{5}$より, 法線ベクトル$\mathbf{n} = \frac{\mathbf{w}}{\parallel \mathbf{w} \parallel} = (\frac{-2}{\sqrt{5}}, \frac{-1}{\sqrt{5}})^T$

$\mathbf{P} = (a, b)^T$を直線上の任意の点とすると, $-2a - b + 3 = 0$を満たす

$$\begin{aligned} \mathbf{n}^T (\mathbf{x} - \mathbf{P}) = (\frac{-2}{\sqrt{5}}, \frac{-1}{\sqrt{5}})\binom{x - a}{y - b} = \frac{1}{\sqrt{5}} \lbrace -2(x - a) - (y - b) \rbrace = \frac{1}{\sqrt{5}} (-2x - y + 3) \end{aligned}$$

即ち, $y = -2x + 3$を$\mathbf{n}^T (\mathbf{x} - \mathbf{P}) = 0$として表現できた.

課題6.2

識別関数を$f(x_0 = 1, x_1) = w_0 + w_1x_1$とする. 学習データ対を$(t_1, x_{11}) = (+1, -2), (t_2, x_{21}) = (-1, 1)$としたとき, 下記の問に答えよ.

(1) $\hat{\mathbf{w}}$を求めよ.

データ行列は

$$\begin{aligned} \mathbf{X} = \begin{pmatrix} x_0 & x_{11} \\ x_0 & x_{21} \end{pmatrix} = \begin{pmatrix} 1 & -2 \\ 1 & 1 \end{pmatrix} \end{aligned}$$

であり, 教師ベクトル$\mathbf{t} = \binom{t_1}{t_2} = \binom{1}{-1}$である.

$$\begin{aligned} \mathbf{X}^T = \begin{pmatrix} 1 & 1 \\ -2 & 1 \end{pmatrix}, \mathbf{X}^T \mathbf{X} = \begin{pmatrix} 2 & -1 \\ -1 & 5 \end{pmatrix}, (\mathbf{X}^T \mathbf{X})^{-1} = \begin{pmatrix} \frac{5}{9} & \frac{1}{9} \\ \frac{1}{9} & \frac{2}{9} \end{pmatrix} \end{aligned}$$

$$\begin{aligned} \hat{\mathbf{w}} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{t} = \begin{pmatrix} \frac{5}{9} & \frac{1}{9} \\ \frac{1}{9} & \frac{2}{9} \end{pmatrix} \begin{pmatrix} 1 & 1 \\ -2 & 1 \end{pmatrix} \binom{1}{-1} = \binom{-\frac{1}{3}}{-\frac{2}{3}} \end{aligned}$$

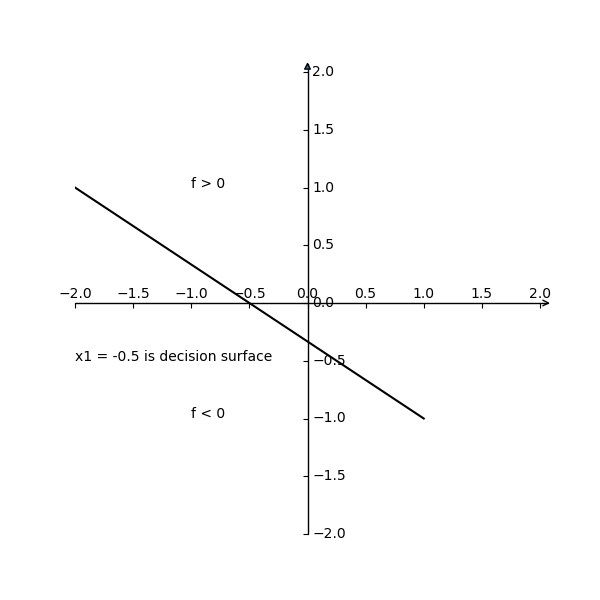
(2) 識別関数を平面に図示せよ.

識別関数$f(\mathbf{x}) = \hat{\mathbf{w}}^T \mathbf{x}, \mathbf{x} = (1, x_1)^T, \hat{\mathbf{w}}^T = (-\frac{1}{3}, -\frac{2}{3})$より

$$y = f(\mathbf{x}) = (-\frac{1}{3}, -\frac{2}{3})\binom{1}{x_1} = -\frac{1}{3} - \frac{2}{3}x_1$$

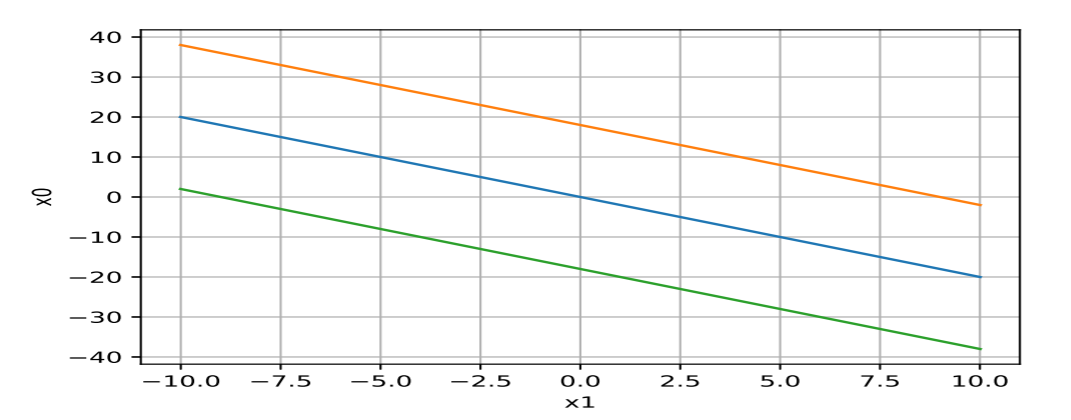
(3) バイアス項への入力を1に固定せず, $x_0$も変数と考え, $(x_0, x_1)$平面内に識別関数値が$-6, 0, 6$となる等高線を描け.

識別関数$f(\mathbf{x}) = \hat{\mathbf{w}}^T \mathbf{x}, \mathbf{x} = (x_0, x_1)^T, \hat{\mathbf{w}}^T = (-\frac{1}{3}, -\frac{2}{3})$より

$$y = f(\mathbf{x}) = (-\frac{1}{3}, -\frac{2}{3})\binom{x_0}{x_1} = -\frac{1}{3}x_0 - \frac{2}{3}x_1$$

識別間数値が−6, 0, 6から順:

課題6.3

ロジスティック回帰

線形識別関数$\mathbf{y} = \mathbf{w}^T \mathbf{x}$の関数の大きさは、識別境界から離れるに従って線形に上昇し続ける

識別関数値を(0, 1)に制限し, 確率的な解釈を可能にするロジスティック回帰を説明する.

2クラス問題を考える. クラス$C_1$の事後確率$P(C_1 \ |\ \mathbf{x})$は

$$\begin{aligned} P(C_1 \ |\ \mathbf{x}) = \frac{P(\mathbf{x} \ |\ C_1) P(C_1)}{P(\mathbf{x} \ |\ C_1) P(C_1) + P(\mathbf{x} \ |\ C_2) P(C_2)} \end{aligned}$$

であるが,

$$a = \ln \frac{P(\mathbf{x} \ |\ C_1) P(C_1)}{P(\mathbf{x} \ |\ C_2) P(C_2)}$$

と置けば,

$$P(C_1 \ |\ \mathbf{x}) = \frac{1}{1 + \exp(-a)} = \sigma (a)$$

と表すことができる. 関数$\sigma (a)$をロジスティック関数(Sigmoid function)と呼ぶ.

ロジスティック関数の逆関数をロジット関数という

$$a = \ln (\frac{\sigma (a)}{1 - \sigma (a)}) = \ln \frac{P(C_1 \ |\ \mathbf{x})}{P(C_2 \ |\ \mathbf{x})}$$

事後確率の比をオッズ, その対数を対数オッズ (ログオッズ) という.

ロジスティック回帰モデル

ロジスティック回帰モデルは, 2値データ(0, 1)の生起確率をロジスティック関数で表した手法.

喫煙量と肺がんの発症の有無を示す仮想的な例を考える. 喫煙量$x$の人が肺がんになる確率を

$$P(1 \ |\ x) = f(x) = \frac{1}{1 + \exp(-(w_0 + w_1x))}$$

とする. パラメータを$\mathbf{w} = (w_0, w_1)^T$とし, 入力データは$\mathbf{x} = (1, x)^T$とする. $a = \mathbf{w}^T\mathbf{x}$とすれば,

$$f(x) = \sigma (a) = \frac{1}{1 + \exp(-a)} = \frac{\exp(a)}{1 + \exp(a)}$$

となる. このモデルは一般化線形モデルといわれる.

ロジスティック関数の逆関数であるロジット関数とオッズは次のようになる

$$\begin{aligned} &a = \ln \frac{P(1 \ |\ x)}{1 - P(1 \ |\ x)} = \mathbf{w}^T\mathbf{x} \\\\ &\frac{P(1 \ |\ x)}{1 - P(1 \ |\ x)} = \frac{P(1 \ |\ x)}{P(0 \ |\ x)} = \exp(\mathbf{w}^T\mathbf{x}) \end{aligned}$$

喫煙量$x$と肺がん発生の有無$y$を示す仮想的な例を下の図に示した

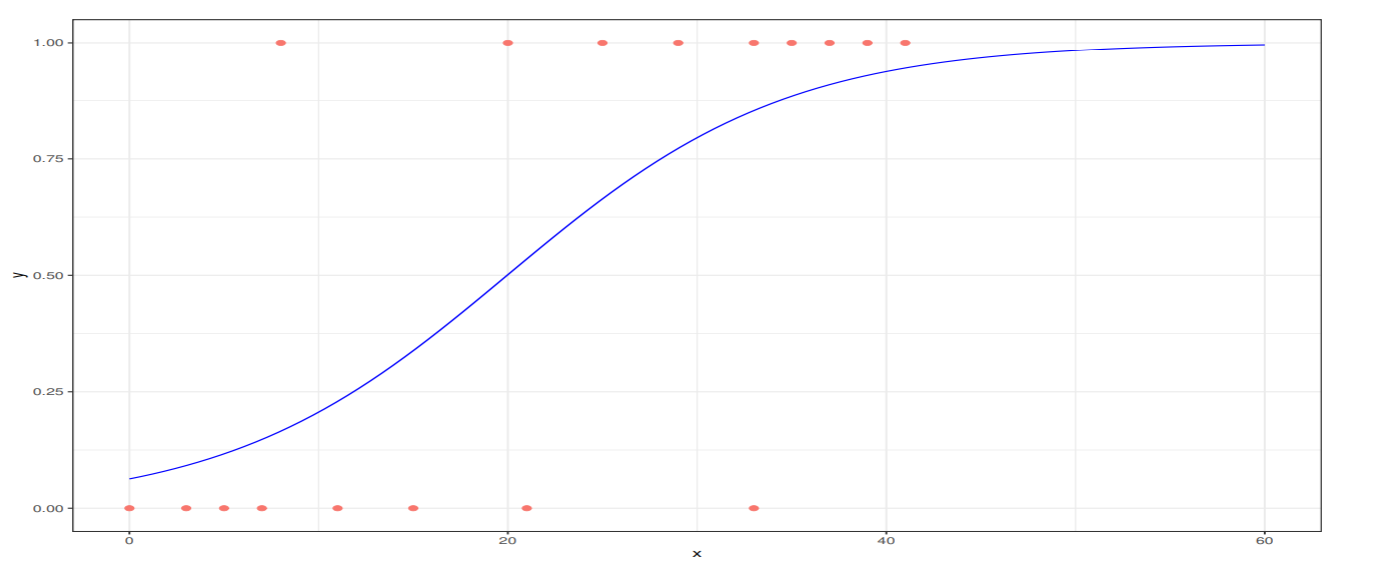
赤い丸が個別事象で, 肺がんの有無を$\lbrace 0, 1 \rbrace$の2値で示している.

ロジスティック回帰モデルの係数の最尤推定値は,$w_0 = -2.7, w_1 = 0.135$であった.

2クラス識別は, 予測確率が0.5を超えるときに$y = 1$と予測する.

$x$が1増えた状態を考える. $\tilde{\mathbf{x}} = (1, (x + 1))^T$. このとき$\mathbf{x}$と$\tilde{\mathbf{x}}$のオッズ比は,

$$\begin{aligned} \frac{\exp(\mathbf{w}^T\tilde{\mathbf{x}})}{\exp(\mathbf{w}^T \mathbf{x})} = \frac{\exp(w_0 + w_1(x + 1))}{\exp(w_0 + w_1x)} = \exp(w_1) \end{aligned}$$

$x$の1単位の増加はオッズ比が$\exp(w_1)$増加する.

オッズ比について

オッズ比の解釈について仮想的な実験を考えよう.

２つの異なる環境で条件を変えて実験を行なった結果を次の図にまとめた.

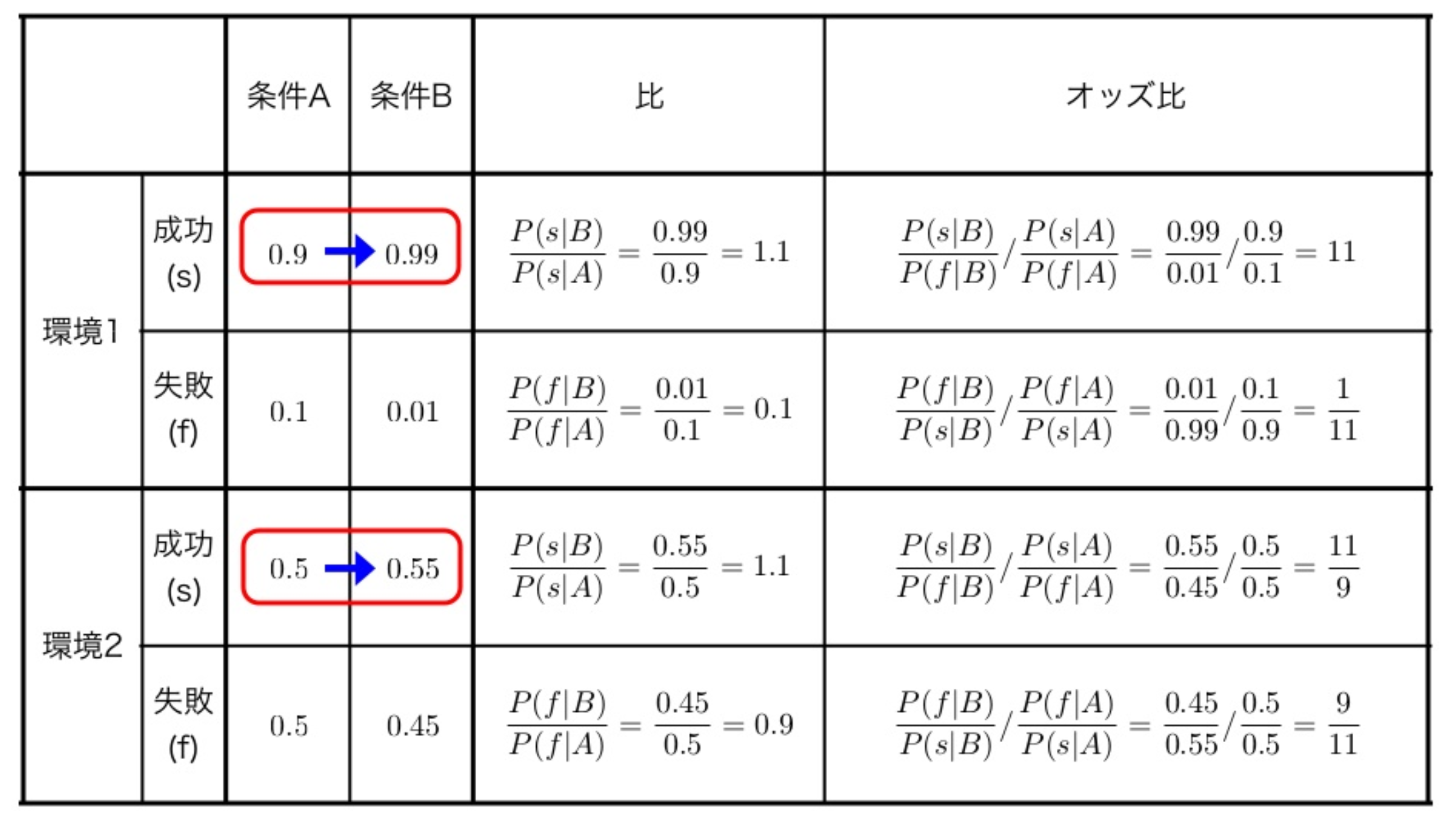
• 環境1と環境2で、条件を変えた時の成功の増加割合は1.1で同じである
• 環境1では成功の割合が殆ど100%に上昇したのに対して、環境2では50%から1割上昇に過ぎない

オッズ比を比べてみると、成功割合の増加についての質的な違いが現れている

パラメータの最尤推定

2クラスロジスティック回帰モデルのパラメータの最尤推定を考える

確率変数$t$はモデルの出力

• $t$が1となる確率: $P(t = 1) = \pi$
• $t$が0となる確率: $P(t = 0) = 1 - \pi$

確率変数$t$はパラメータ$\alpha$を持つベルヌーイ試行

$$f(f \ |\ \pi) = \pi^t (1 - \pi)^{1 - t}, \quad t = 0, 1$$

に従う.

よって、$N$回の試行に基づく尤度関数は、

$$L(\pi_1, \cdots, \pi_N) = \prod_{i=1}^N f(t_i \ |\ \pi_i) = \prod_{i=1}^N \pi_i^{t_i} (1 - \pi_i)^{1 - t_i}$$

となる. これを最大化したい.

負の対数尤度関数は、

$$\mathcal{L}(\pi_1, \cdots, \pi_N) = \ln L(\pi_1, \cdots, \pi_N) - \sum_{i=1}^N (t_i \ln \pi_i + (1 - t_i) \ln(1 - \pi_i))$$

となる. これを最小化したい.

この評価関数は、交差エントロピー型評価関数という

ここで，

$$\pi_i = \sigma (\mathbf{x}_i) = \frac{\exp(\mathbf{w}_T\mathbf{x_i})}{1 + \exp(\mathbf{w}^T\mathbf{x}_i)}$$

を代入し整理して,

$$\mathcal{L}(\mathbf{w}) = -\sum_{i=1}^N \lbrace t_i \mathbf{w}^T\mathbf{x}_i - \ln(1 + \exp(\mathbf{w}^T\mathbf{x}_i)) \rbrace$$

負の対数尤度関数を最小にするパラメータ$\mathbf{w}$を得るために、$\mathbf{w}$で微分することを考える。

$$\frac{\partial \mathcal{L}(\mathbf{w})}{\partial \mathbf{w}} = -\sum_{i=1}^N (t_i\mathbf{x}_i - \frac{\mathbf{x}_i \exp(\mathbf{w}^T\mathbf{x}_i)}{1 + \exp(\mathbf{w}^T\mathbf{x}_i)}) = \sum_{i=1}^N \mathbf{x}_i (\pi_i - t_i)$$

$\sum_{i=1}^N \mathbf{x}_i (\pi_i - t_i) = 0$となる$\mathbf{w}$が解であるが、解析的に解くことは不可能なので、最急降下法やニュートン・ラフソン法で数値的に求める。

多クラス問題への拡張と非線形変換

多クラス$K > 2$への拡張は, 各クラスごとに線形変換$a_k = \mathbf{w}^T_k \mathbf{x}$を求め, 事後確率を最大にするクラスに分類すればよい.

$$P(C_k \ |\ \mathbf{x}) = \pi_k(\mathbf{x}) = \frac{\exp(a_k)}{\sum_{j=1}^K \exp(a_j)}$$

この関数はソフトマックス関数という.

線形関数でうまく分離できない場合, 非線形関数$\varphi ()$

$$\varphi (\mathbf{x}) = (\varphi_0 = 1, \varphi_1(\mathbf{x}), \cdots, \varphi_M(\mathbf{x}))^T$$

とし, 変換した$M + 1$次元空間でロジスティック回帰を行う.

変換された$M + 1$次元空間でロジスティック回帰を$a_k = \mathbf{w}_k^T \varphi(\mathbf{x})$と行なっても, その空間内での識別境界は超平面になる. このような非線形関数を非線形基底関数という.

クラス数を$K$, 学習データを$\mathbf{X} = (\mathbf{x}_1, \cdots, \mathbf{x}_N)^T$, 教師データを$\mathbf{T} = (\mathbf{t}_1, \cdots, \mathbf{t}_N)^T$とする.

$i$番目のデータ$\mathbf{x}_i$に対応する教師データ$\mathbf{t}_i$はダミー変数表現のベクトルで,$\mathbf{x}_i$が所属するクラスが$k$なら$t_{ik}$のみが1でそれ以外の要素は0である.

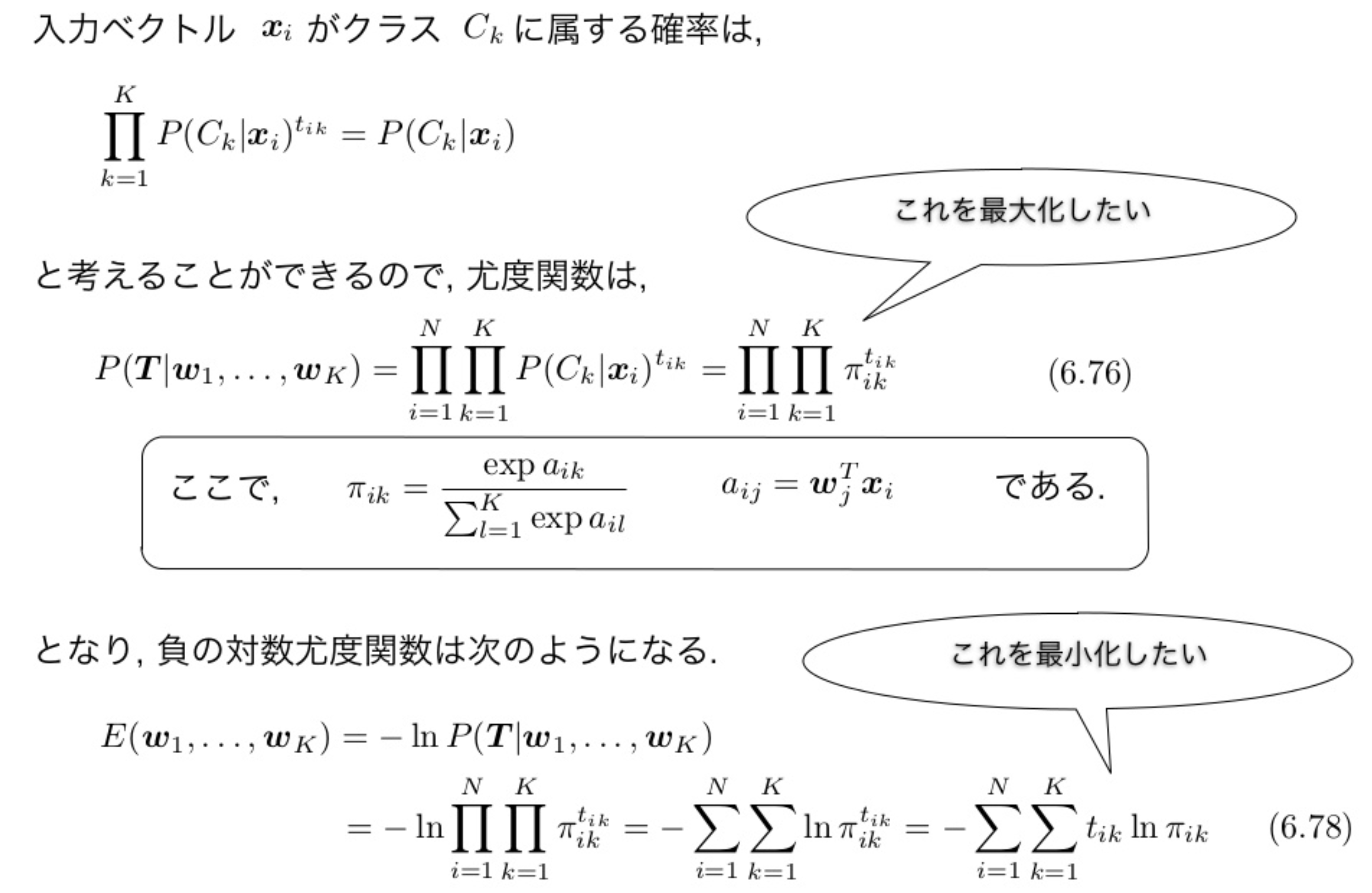
各$\mathbf{w}_j$の最尤推定は、評価変数を$\mathbf{w}_j$で微分して0とおけば求められる。

ここで、

$$\pi_{ik} = \frac{\exp(a_{ik})}{\sum_{i=1}^K \exp(a_{ij})}, \quad a_{ij} = \mathbf{w}_j^T \mathbf{x}_i$$

よって、

$$\frac{\partial E}{\partial \mathbf{w}_j} = -\sum_{i=1}^N \sum_{k=1}^K t_{ik} \frac{1}{\pi_{ik}}\pi_{ij} (\delta_{jk} - \pi_{ik}) \mathbf{x}_i = \sum_{i=1}^N (\pi_{ij} - t_{ij}) \mathbf{x}_i = 0$$

同じく解析的に解けないので、2クラスの場合と同様、ニュートン・ラフソン法などを用いて解くことになる。

非線形基底関数による変換とロジスティック回帰

非線形基底関数を使った2クラスロジスティック回帰の分析例を紹介する.

2次元あやめデータの setosa と virginica を1クラスにまとめて, 線形分離不可能な2クラス問題のデータを用意した.

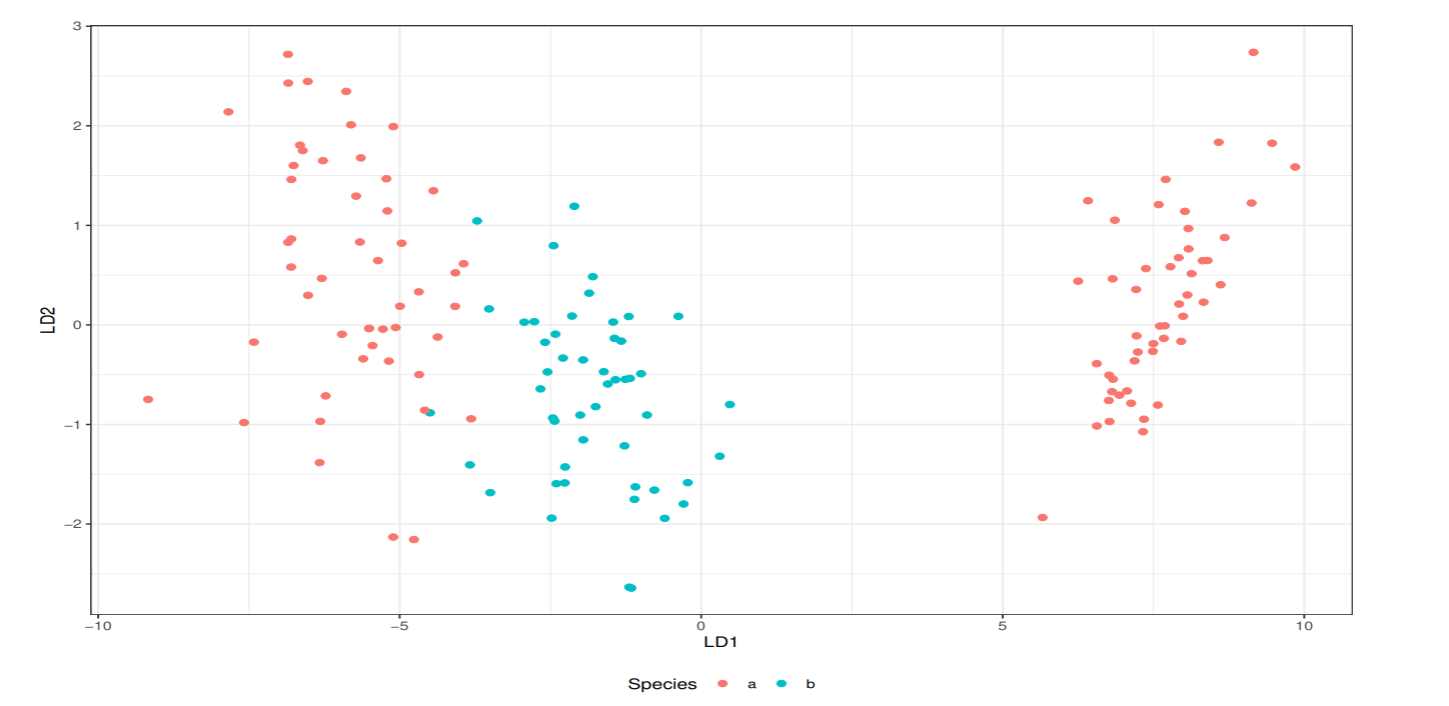
ここでは, ガウス核関数を用いる.

$$f(\mathbf{x}) = \exp(-\alpha(\mathbf{x} - \mu)^T \mathbf{\Sigma}^{-1} (\mathbf{x} - \mu))$$

ここで$\alpha$は核関数の広がりを, $\mu$は中心を,$\mathbf{\Sigma}$は広がりの形を制御するパラメータ.

Setosaの分布から$\alpha_s = 0.005$,

$$\begin{aligned} \mu_s = \begin{pmatrix} -7.61 \\ 0.22 \end{pmatrix}^T, \quad \mathbf{\Sigma}_s = \begin{pmatrix} 0.72 & -0.53 \\ -0.53 & 0.84 \end{pmatrix} \end{aligned}$$

とし, Versicolor の分布から$\alpha_c = 0.1$,

$$\begin{aligned} \mu_s = \begin{pmatrix} 1.83 \\ -0.73 \end{pmatrix}^T, \quad \mathbf{\Sigma}_c = \begin{pmatrix} 1.07 & 0.24 \\ 0.24 & 0.76 \end{pmatrix} \end{aligned}$$

以下の図は，ガウス核関数の等高線を示したもの. setosa は$f_s$が大きく, $f_c$が小さな値の領域に, versicolor は $f_s$が小さく$f_c$が大きな領域に, verginica は両方とも小さな値の領域に写像される.

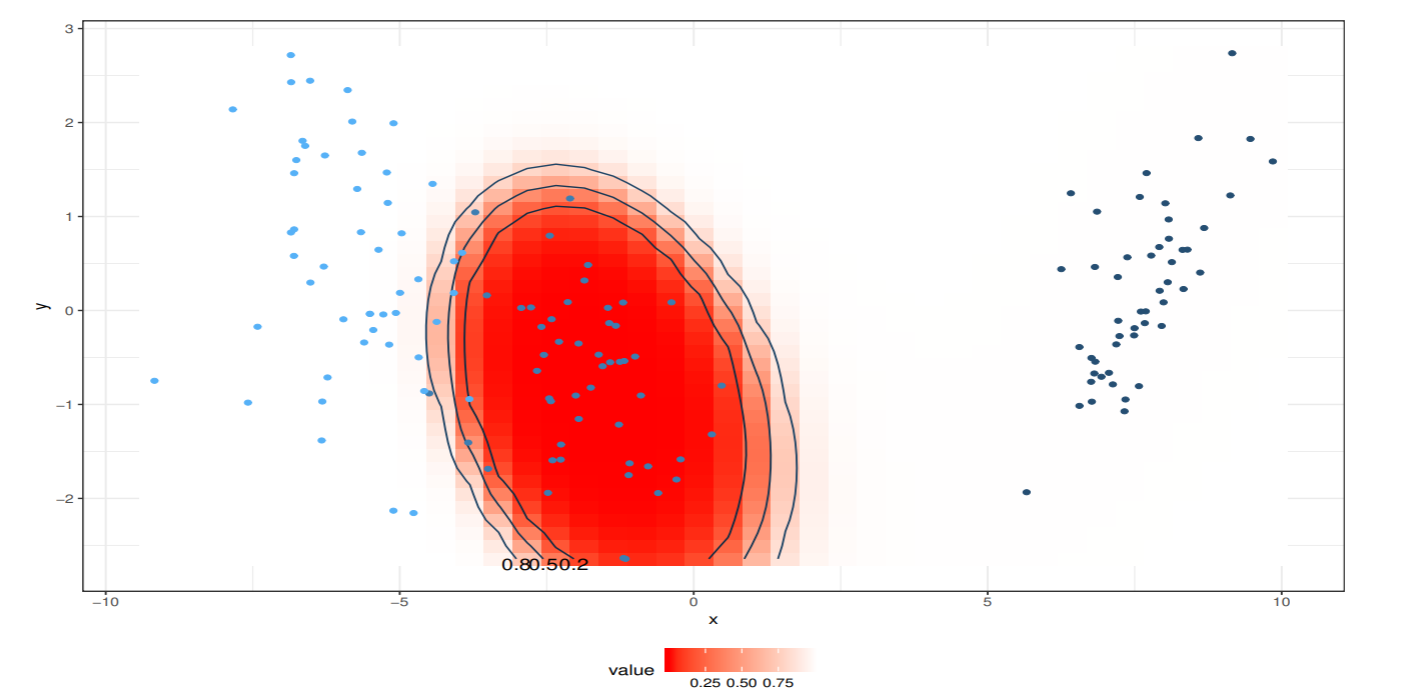
以下の図では, 非線形特徴空間での分布と, 線形ロジスティック回帰モデルによる事後確率が0.2, 0.5, 0.8の等高線を示した.

事後確率が0.5のところが識別境界である.

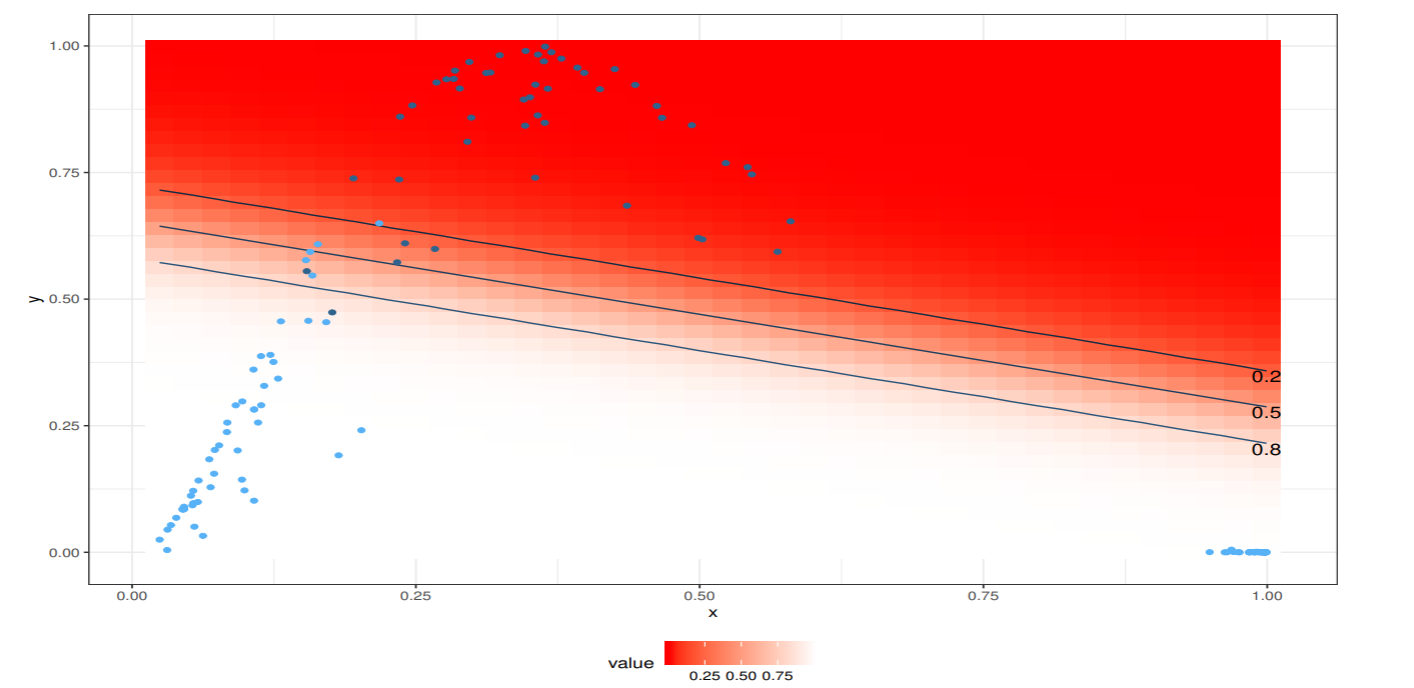
ピマインディアンデータのロジスティック回帰

ピマインディアンデータの7変数の特徴量を用いたロジスティック回帰を行う.

入力ベクトルは, 妊娠回数 (npreg), 血漿グルコース濃度 (glu), 血圧(bp), 脂肪厚 (skin), 肥満度 (bmi), 糖尿病家系関数 (ped), 年齢 (age)であった.

係数の推定結果は以下である

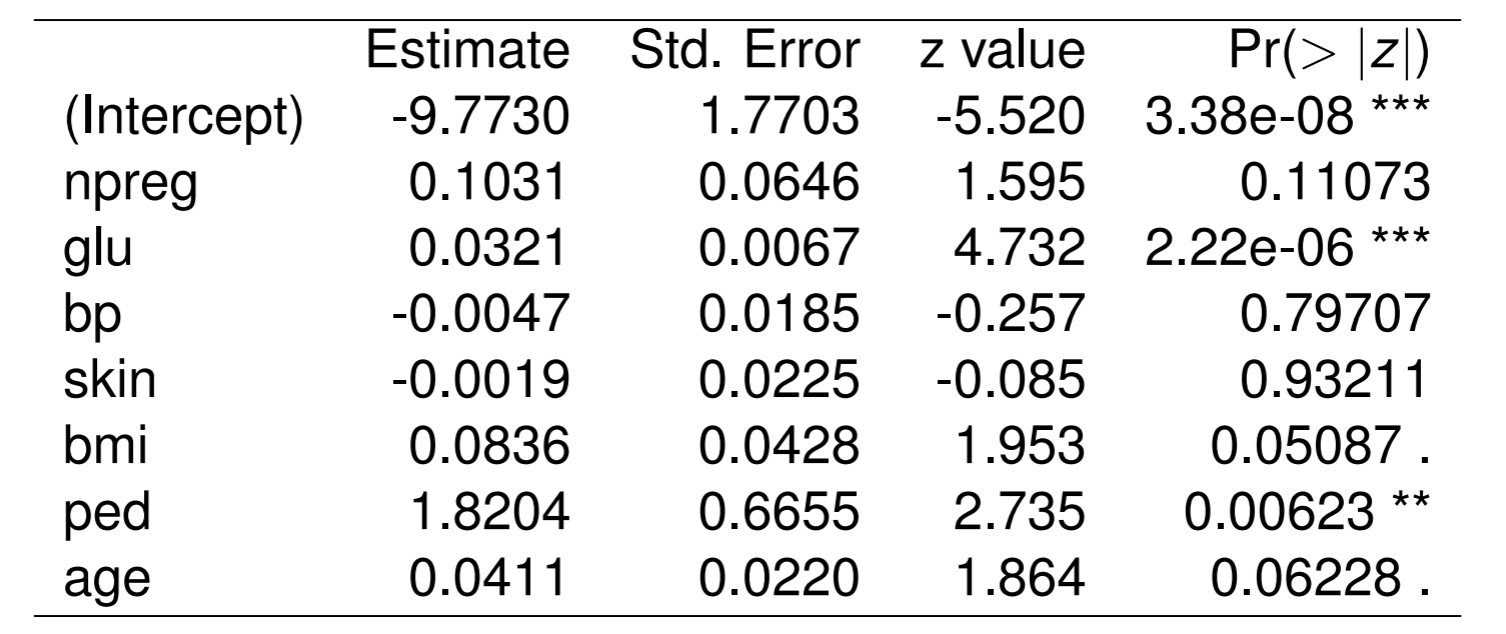
ロジスティック回帰では、事後確率の値を0.5から上下に変更することで識別境界を変えることができる.

このとき, 識別境界を様々な事後確率の値で取ることで, 真陽性率, 偽陽性率が得られる.

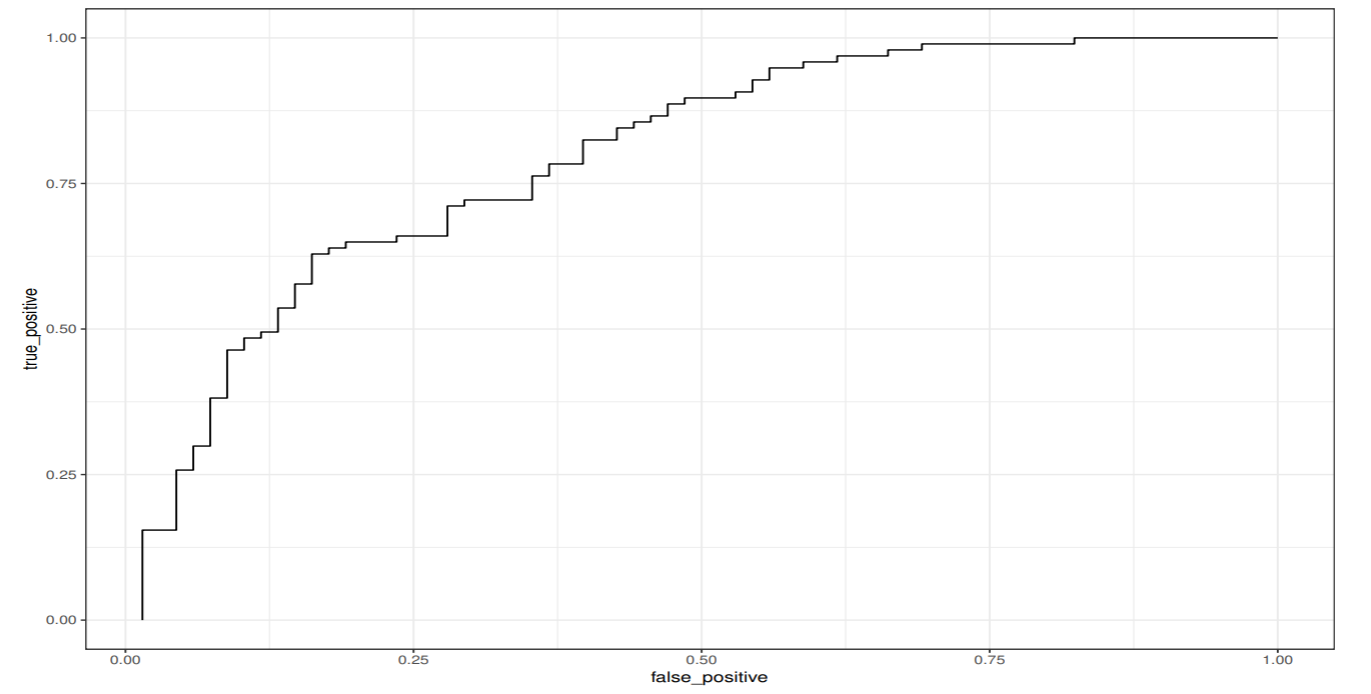
パーセプトロン型学習規則(Perceptron)

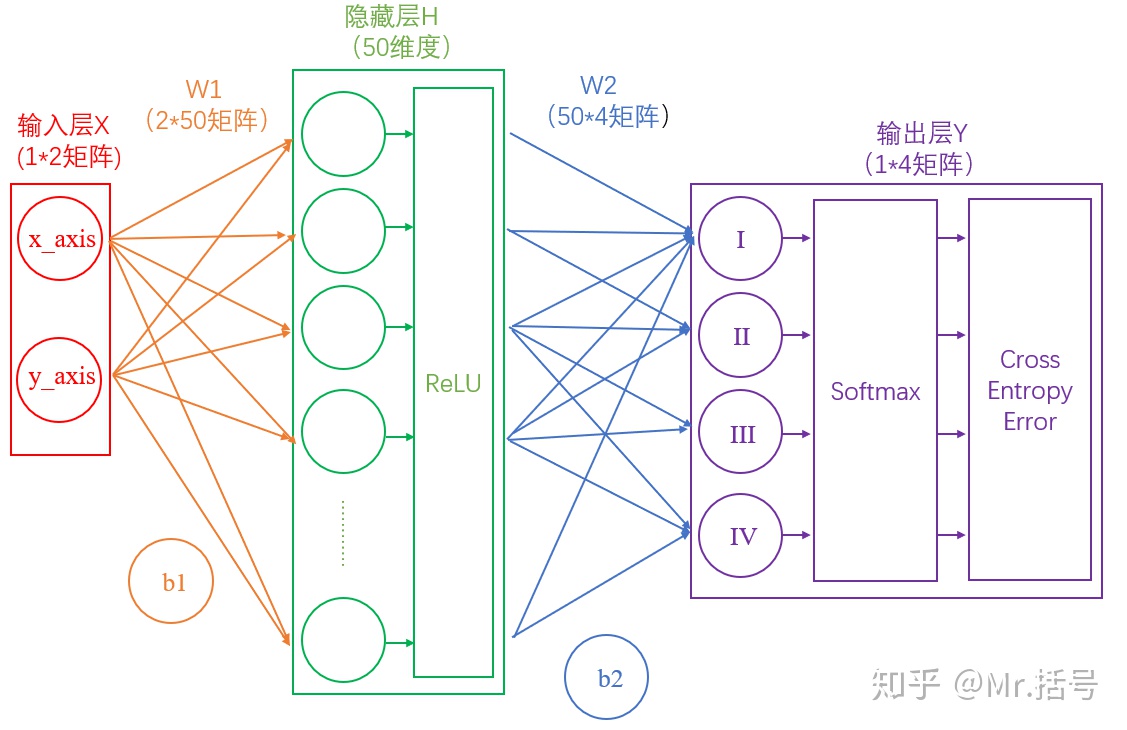
パーセプトロンの学習規則は2クラスの線形識別関数を求める古典的な方法

パーセプトロンの収束定理: 2クラスが線形分離可能であれば, パーセプトロン学習規則のアルゴリズムは収束する.

パーセプトロンを多層化し, 非線形識別関数を使った, 誤差逆伝搬法(BP)は線形分離可能性の制約を外した手法

局所最適解がたくさんあること, 解の解釈が困難であることがデメリットだが, ディープラーニングへ発展する重要なモデルである.

パーセプトロン

線形識別関数 $f(\mathbf{x}) = \mathbf{w}^T \mathbf{x}$ を用いて, $f(\mathbf{x}) \geq 0$ のとき $\mathbf{x} \in C_1, f(\mathbf{x}) < 0$ のとき $\mathbf{x} \in C_2$ とする 2 クラス問題を考える. 同時座標系を用いて $\mathbf{w} = (w_0, \cdots, w_d)^T$ とする.

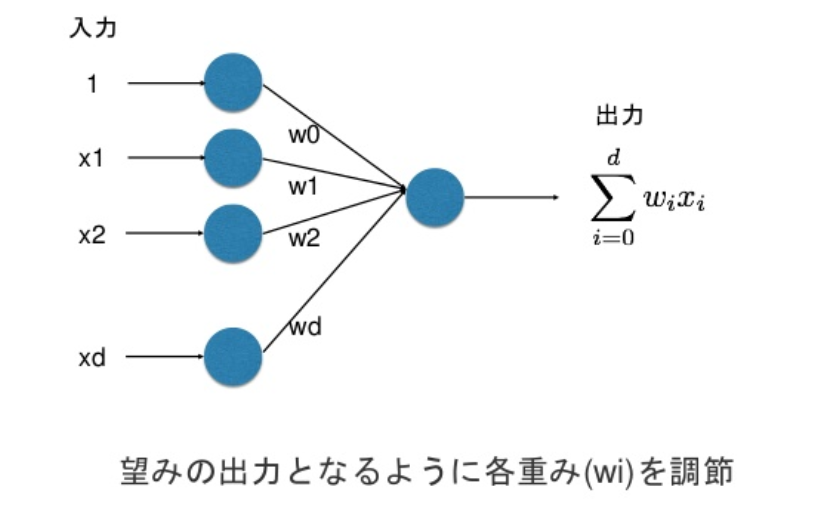
各入力に重みをつけて総和を出力とするネットワークモデルをパーセプトロンと呼ぶ

データが線形分離可能であるとき, 片方のクラスに属するデータの符号を反転させると, どちらのクラスも超平面の同じ側にできる. 分類が正しければ $f(\mathbf{x}) \geq 0$ となり, 誤っていれば $f(\mathbf{x}) < 0$ となる.

学習データの系列を $\mathbf{x}_1, \cdots, \mathbf{x}_i, \cdots$ とする. パーセプトロンの学習規則は $i + 1$ 番目の係数ベクトルを $\mathbf{w}_{i+1}$ を, $i$ 番目の学習データ $\mathbf{x}_i$ を入力したときの出力 $f(\mathbf{x}_i)$ に応じて,

$$\begin{aligned} \begin{cases} f(\mathbf{x}_i) \geq 0, \quad \mathbf{w}_{i+1} = \mathbf{w}_i \\ f(\mathbf{x}_i) < 0, \quad \mathbf{w}_{i+1} = \mathbf{w}_i + \eta \mathbf{x}_i \end{cases} \end{aligned}$$

とする.

• $\eta$ は学習の収束速度を決めるパラメータで, $\eta = 1$ の場合を固定増分誤り訂正法と呼ぶ.

学習の難しさの尺度

学習データが識別超平面からある値 $h > 0$ (マージンとよぶ) より近い距離であれば誤りとして $\mathbf{w}$ を更新するようにすれば, $h$ より小さなノイズに対して正しく識別できるようになる.

ステップ関数

$$\begin{aligned} f(a) = \begin{cases} 1, \quad a > 0 \\ 0, \quad a \leq 0 \end{cases} \end{aligned}$$

を用いれば $\mathbf{w}_i$ の更新量 $\Delta \mathbf{w}_i$ は, 符号反転を行った学習データについて

$$\begin{aligned} \Delta \mathbf{w}_i = \eta f(h - \mathbf{w}_i^T \mathbf{x}_i / \parallel \mathbf{w}_i \parallel) \mathbf{x}_i = \begin{cases} \eta \mathbf{x}_i, \quad &h > \mathbf{w}_i^T \mathbf{x}_i / \parallel \mathbf{w}_i \parallel \\ 0, \quad &h \leq \mathbf{w}_i^T \mathbf{x}_i / \parallel \mathbf{w}_i \parallel \end{cases} \end{aligned}$$

と書くことができる.

マージンの大きさ

マージンの大きさ $D(\mathbf{w})$ は, $C_2$ の学習データを識別関数の法線ベクトル上に射影した長さの最小値の半分である.

$$\rho(\mathbf{w}) = \min_{x \in C_1} \frac{\mathbf{w}^T\mathbf{x}}{\parallel \mathbf{w} \parallel} - \max_{x \in C_2} \frac{\mathbf{w}^T\mathbf{x}}{\parallel \mathbf{w} \parallel}$$

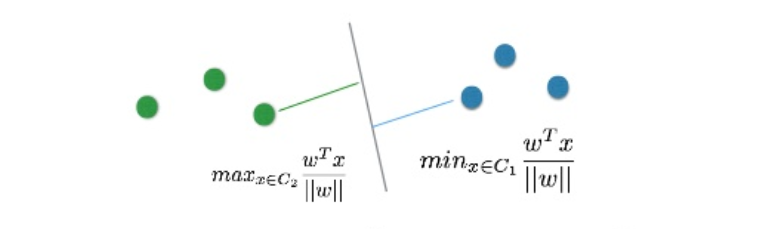
$\rho(\mathbf{w})$ をクラス間マージンとよび, 最大マージンは最大クラス間マージンの半分である.

$$D_{max} = \frac{1}{2} \rho_{max}(\mathbf{w})$$

符号反転を行った場合, すべての学習データを超平面の法線ベクトル上に射影した最小値

$$D(\mathbf{w}) = \min_{x \in C_1,C_2} \frac{\mathbf{w}^T\mathbf{x}}{\parallel \mathbf{w} \parallel}$$

パーセプトロンの収束定理

パーセプトロンの収束定理とは, パーセプトロンの学習規則が有限の学習回数で収束すること.

マージン $h$ は, 次元ごとに $\alpha$ の大きさを取り, $h = \alpha d$ とする. 同次座標系で表現されたデータ $\mathbf{x}_i$ が学習で使用された回数を $M_i$ とすると, 学習の総数は $M = \sum_i M_i$ となる.

$M$ 回の学習で獲得された係数ベクトル $\mathbf{w}$ は, 初期値を 0 として,

$$\mathbf{w} = \eta \sum_{x_i \in C_1, C_2} M_i \mathbf{x}_i$$

学習が収束したときの係数ベクトルを $\mathbf{w}^*$ とし, $\mathbf{w}$ との内積を計算すると, 内積は $M$ に比例して増加し, 係数ベクトルは解ベクトルに近づく.

$$\begin{aligned} \mathbf{w}^T \mathbf{w}^* &= \eta \sum_{x_i \in C_1, C_2} M_i \mathbf{x}_i^T \mathbf{w}^* \geq \eta M \min_{x_i \in C_1, C_2} \mathbf{x}_i^T \mathbf{w}^* \\\\ &= \eta MD(\mathbf{\mathbf{w}^*}) \parallel \mathbf{w}^* \parallel \end{aligned}$$

$\parallel \mathbf{w} \parallel$ の上限を求める. 学習データの長さが $\parallel \mathbf{x}_i \parallel^2$ を満たしていると仮定し, $\mathbf{x}_i$ による係数ベクトルの変化量を求めると,

$$\begin{aligned} \Delta \parallel \mathbf{w} \parallel^2 &= \parallel \mathbf{w} + \eta \mathbf{x}_i \parallel^2 - \parallel \mathbf{w} \parallel^2 = \eta^2 \parallel \mathbf{x}_i \parallel^2 + 2\eta \mathbf{w}^T \mathbf{x}_i \\\\ &\leq \eta^2d + 2\eta \alpha d = d \eta (\eta + 2\alpha) \end{aligned}$$

$\mathbf{w}$ と $\mathbf{w}^*$ の方向余弦の 2 乗は, $\phi = (\mathbf{w}^T \mathbf{w}^*)^2 / (\parallel \mathbf{w} \parallel^2 \parallel \mathbf{w}^* \parallel^2)$ となるので, 次が得られる.

$$\begin{aligned} M \frac{D^2 (\mathbf{w}^* \eta)}{d(\eta + 2\alpha)} \leq \phi \leq 1 \Rightarrow M \leq d\frac{1 + 2\alpha/\eta}{D^2_{max}} \end{aligned}$$

学習回数には上限があるので, 学習は収束する. データの次元 $d$ とマージン $\alpha$ が大きくなると, 上限が大きくなるので, 時間がかかる.

$D^2_{max}$ に反比例するので, 2 クラス間の距離が大きくなると学習が少なくて済む.

サポートベクトルマシンは, マージンが最大となる線形識別規則を見つける方法.

誤差伝搬法(BP)

多層パーセプトロン

排他的論理和のような線形識別関数では識別出来ないような場合, 別の入力を用意すれば識別できる.

$x_1$	$x_2$	出力	教師データ
0	0	0	-1
0	1	1	+1
0	1	1	+1
1	1	0	-1

第3の素子は, 隠れ素子と呼ばれ, 隠れ素子で構成されるグループを隠れ層という.

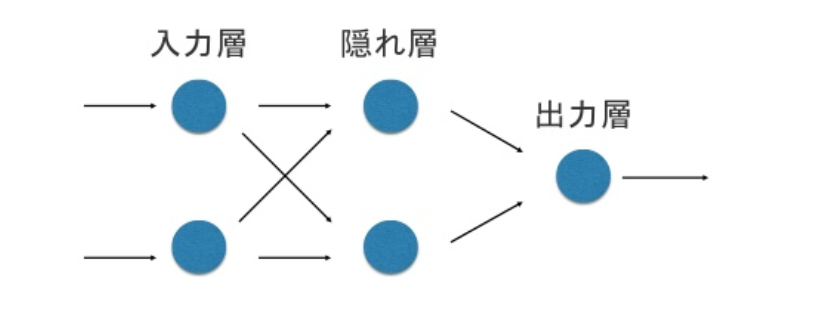
多層回路とは, 隠れ層のみから出力層に入力を与えるような隣り合った層間ネットワークのこと.

多層パーセプトロンの誤差逆伝搬法と呼ばれるパーセプトロン型の学習アルゴリズムを考える.

入力層に学習データ $\mathbf{x}^n(n = 1,\cdots, N)$ が与えられている. 学習データの次元を $d$ とする.

バイアス項も含めて $n$ 番目の学習データは $\mathbf{x}^n = (1, x_1^n, \cdots, x_d^n)^T$ で表す.

$n$ 番目の学習データが入力されると, 隠れ層の素子 $V_j = (j = 1, \cdots, M)$ には次の入力が入る.

$$h_j^n = \sum_{i=0}^d w_{ji}x_i^n = \mathbf{w}_j^T \mathbf{x}^n$$

出力関数 $g(u)$ を介して, $V_j^n = g(h_j^n)$ が出力される. $g(u)$ は非線形でなければならない.

$g(u)$ は非線形出力関数とよばれ, $u$ に対して微分可能で, シグモイド関数がよく使用される.

$$g(u) = \frac{1}{1 + \exp(-\beta u)}$$

出力素子 $o_k(k = 1 ,\cdots, K)$ への入力は, 次のように与えられる.

$$h_k^n = \sum_{j = 0}^M w_{kj}V_j^n = \sum_{j = 0}^M w_{kj}g(\sum_{i = 0}^d w_{ji}x_i^n)$$

その出力は, 次のように与えられる.

$$o_k^n = \tilde{g}(h_k^n) = \tilde{g}(\sum_{j = 0}^M w_{kj}V_j^n) = \tilde{g}(\sum_{j = 0}^M w_{kj}g(\sum_{j = 0}^M w_{kj}V_j^n))$$

$\tilde{g}(\cdot)$ をソフトマックス関数で表現すると

$$\tilde{g}(o_k^n) = \frac{\exp o_k^n}{\sum_{\mathcal{l}}^K \exp o_\mathcal{l}^n} (= p(t_k^n = 1 \ |\ \mathbf{x}^n))$$

確率的な解釈ができる

誤差逆伝搬法の学習規則

隠れ素子から出力素子への結合係数の学習は, 2 乗誤差最小化を最急降下法に従って行う.

$n$ 番目の学習データの評価関数は

$$E_n(\mathbf{w}) = \frac{1}{2} \sum_{k = 1}^K (t_k^n - o_k^n)^2 = \frac{1}{2} \sum_{k = 1}^K (t_k^n - \tilde{g}(\sum_{j = 0}^M w_{kj}g(\sum_{j = 0}^M w_{kj}V_j^n)))^2$$

学習データ全体で $E(\mathbf{w}) = \sum_{i = 1}^N E_n(\mathbf{w})$ となる.

バッチアルゴリズムでは, 結合係数の修正量を計算し更新することを1エポックという. $\tau$ エポックの更新量は,

$$\begin{aligned} \Delta w_{kj}(\tau) &= \sum_{n=1}^N (-\eta \frac{\partial E_n(\mathbf{w})}{\partial w_{kj}}) = -\eta \sum_{n=1}^N (\frac{\partial E_n(\mathbf{w})}{\partial o_k^n} \cdot \frac{\partial o_k^n}{\partial w_{kj}}) \\\\ &= \eta \sum_{n=1}^N (t_k^n - o_k^n)\tilde{g}'(h_k^n)V_j^n = \eta \sum_{n=1}^N \delta_k^n V_j^n \end{aligned}$$

• $\delta_k^n$ は誤差信号で, 出力が 0, 1 に近いときに 0 となり, 学習が進まなくなる.

確率降下法とは $n$ 番目の学習データによる $w_{kj}$ の修正量を次のように与える方法

$$\Delta w_{kj}^n(\tau) = \eta \delta_k^n(\tau)V_j^n(\tau)$$

入力素子 $x_i$ から隠れ素子 $V_j$ への結合係数 $w_{ji}$ の学習のための評価関数は $w_{kj}$ の場合と同じだが, 修正量は次のようになる.

$$\begin{aligned} \Delta w_{ji}(\tau) = \sum_{n=1}^N (-\eta \frac{\partial E_n(\mathbf{w})}{\partial w_{ji}}) = \eta \sum_{n=1}^N \sum_{k=1}^K \delta_k^n w_{kj} g'(h_j^n) x_i^n \end{aligned}$$

隠れ素子 $j$ の誤差信号を $\delta_j^n$ と定義すると, 次の表現を得る.

$$\delta_j^n = g'(h_j^n)\sum_{k=1}^N \delta_k^n w_{kj}, \quad \Delta w_{jk}(\tau) = \eta \sum_{n=1}^N \delta_j^n x_k^n$$

各出力素子で発生した誤差 $\delta_k^n$ を結合係数 $w_{kj}$ を介して, 出力素子 $k$ から隠れ素子 $j$ に戻しているので, 誤差逆伝搬法, BP 法 error back probagation 法という.

実行例-手書き数字の学習

MNIST データを使って誤差逆伝搬法による認識実験を行なった. データ数は 1000 とした.

入力層はバイアス項を含めて $14 \times 14 + 1$, 隠れ層の素子数は $10 + 1$ 個、出力層はクラス数 10 である.

元のデータは $28 \times 28$ の画像だが、縦横 $\frac{1}{2}$ に圧縮したものを入力とした.

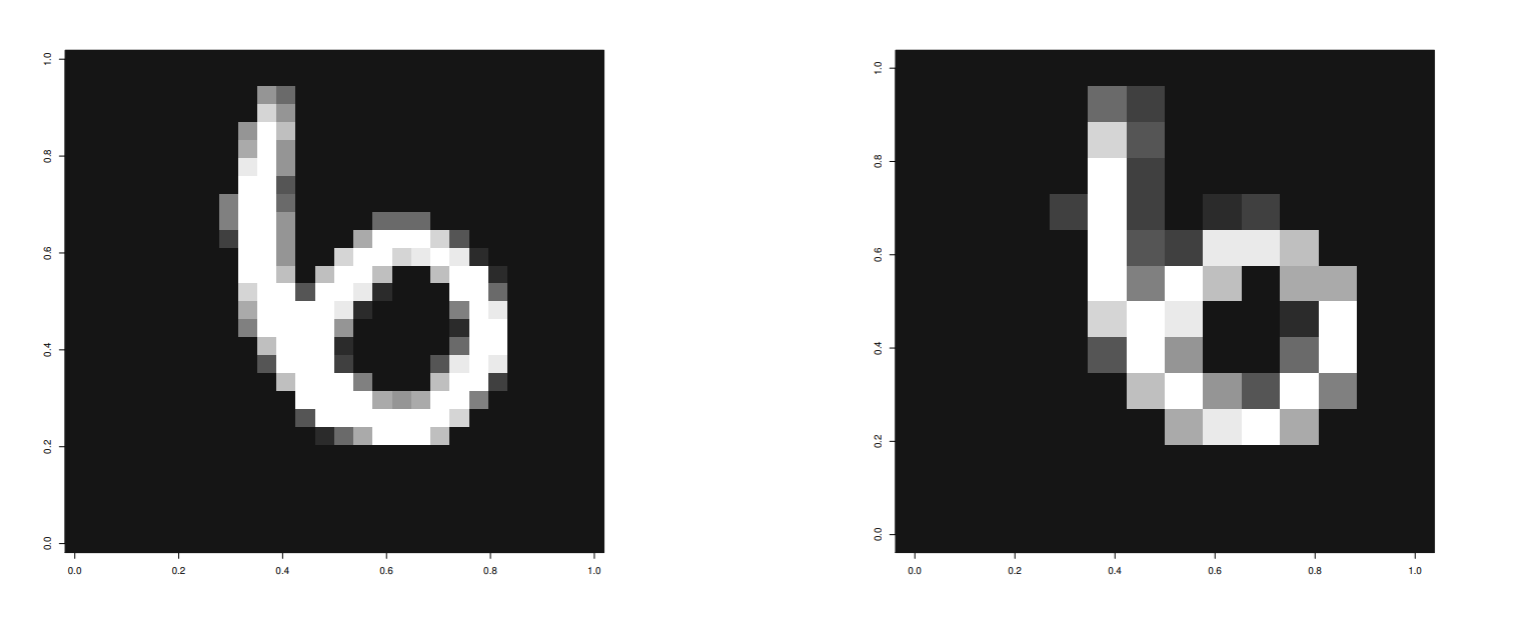
10 個の隠れ素子の画像

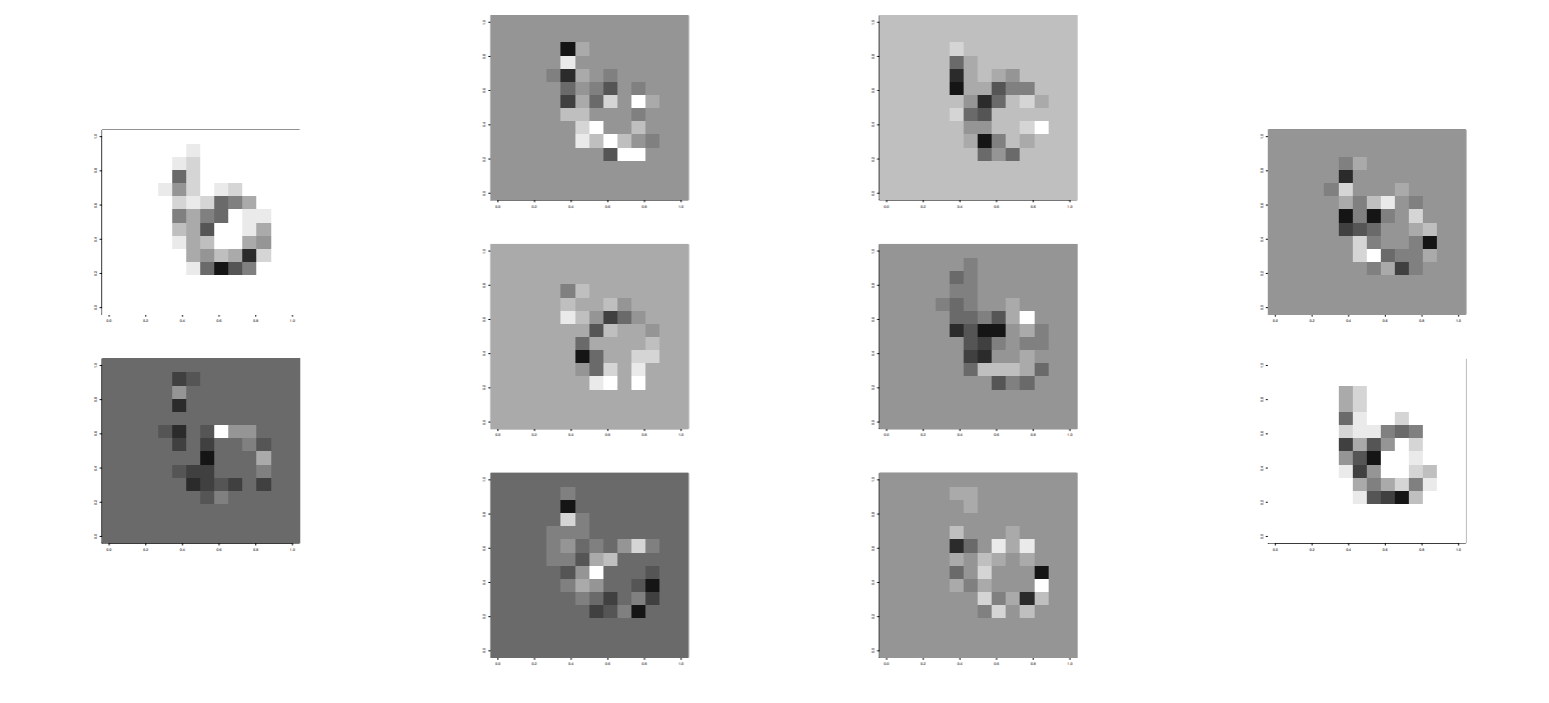
出力は 6 の確率が 0.9999988, 8 の確率が 0.0000012, あとの確率は 0 より, 6 と識別された.

隠れ素子数を 10 とした場合、再代入誤り率は 0 で、テストデータの誤り率が 20% 程度であった.

隠れ素子数を 1 から 20 まで変えながら誤り率を計算してプロットした, 汎化誤差を最小にする K は 20 であった. そのときの誤り率は13%であった.

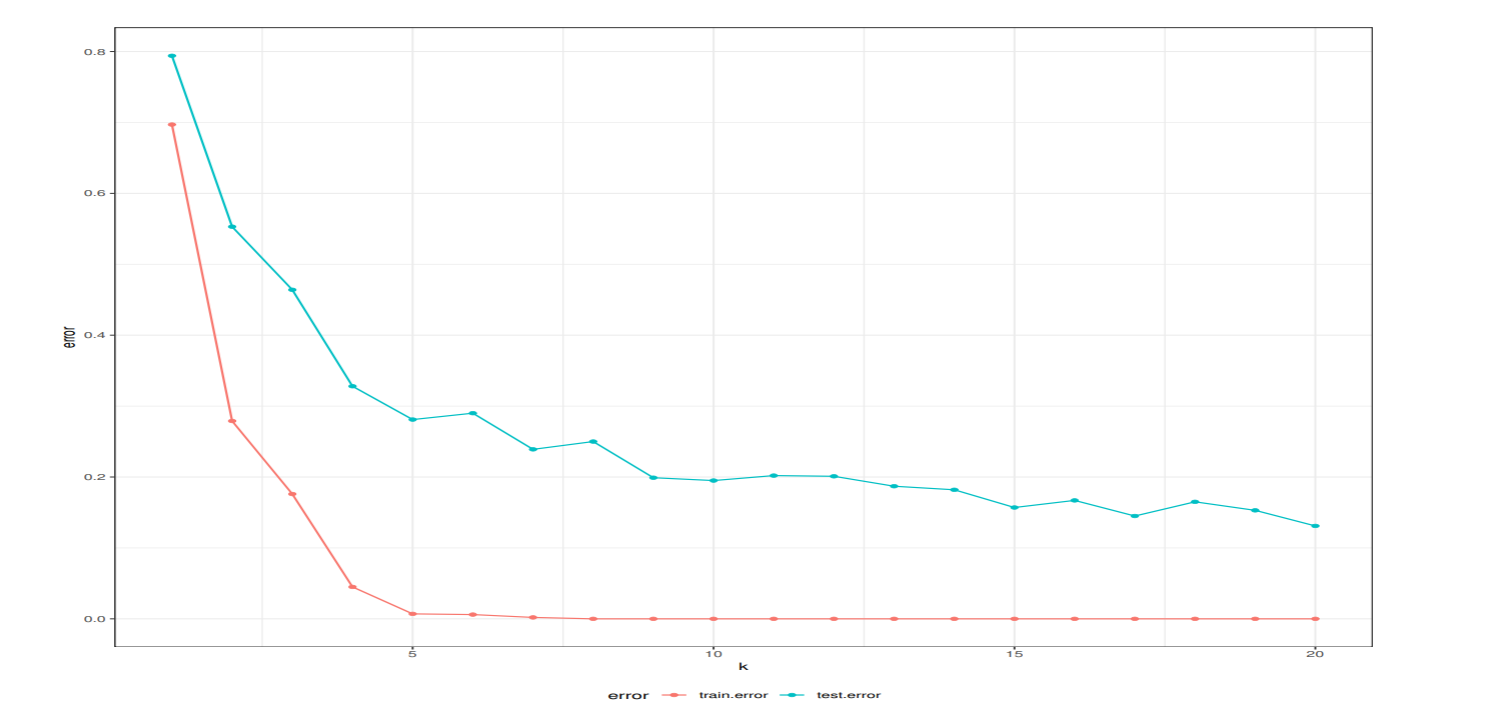
誤差逆伝搬法の学習特性

初期値依存性

初期値依存性: 非線形最適化問題を解く際, 最急降下法や共役勾配法を使う. そのとき, 大域的な最適解を得ることは難しく, 初期値に依存した局所解を学習することがある.

隠れ素子の数

隠れ素子の数は多ければ多いほど良いのであろうか？

実行例-初期値依存性と隠れ素子の数による誤り率の変化

ピマ・インディアンデータを用いて初期値依存性と隠れ素子の数が誤り率にどのように影響を与えるか検証した.

標準化した 7 つの特徴すべてを用いて学習した. 初期値を変えて 20 回学習したときの誤り率をプロットした.

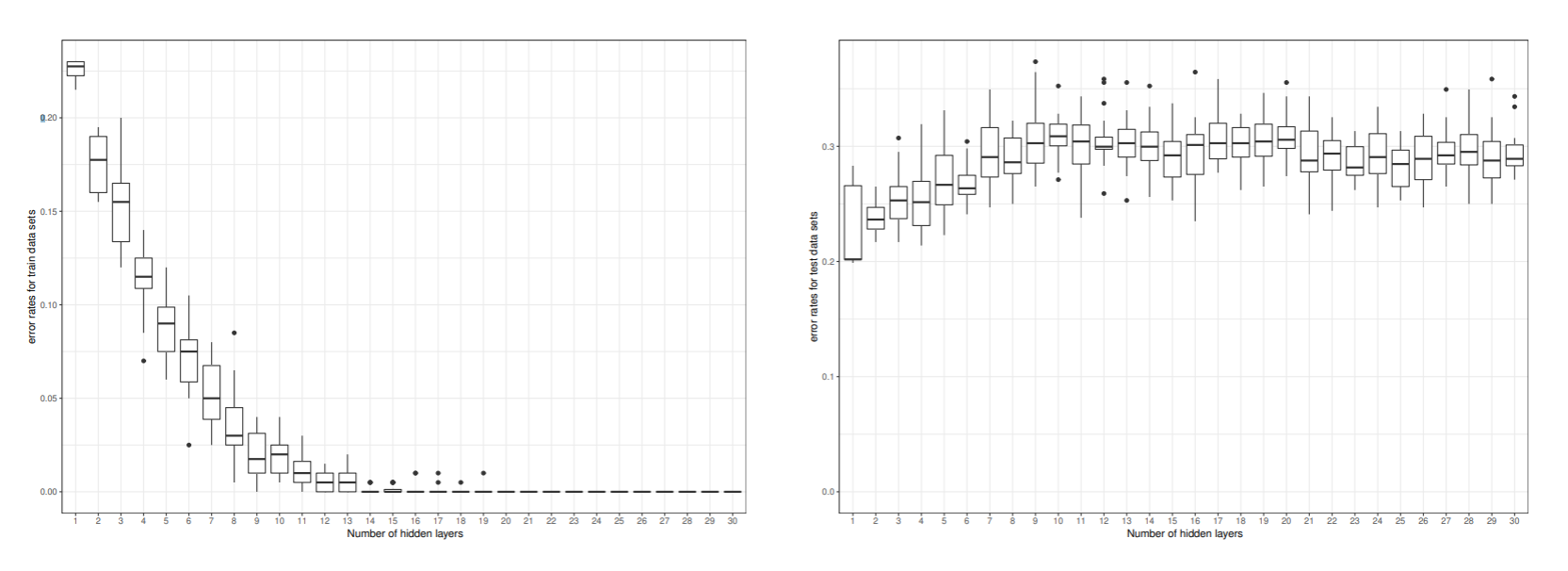
再代入誤りは隠れ素子数が20以上で殆ど0になっているが, 汎化誤差は隠れ素子数が3のところで最も低い値を取っている. 隠れ素子数を更に増やすと, 汎化誤差が次第に増加する. このような現象は, 過学習と言われる.

最適な隠れ素子数はホールドアウト法や交差確認法などで求める必要がある

過学習と正則化

隠れ素子の数が多くなると過学習が起きやすい. また非線形性が強くなっても過学習が起きやすい. 結合係数が大きくならないような正則化法が提案されている.

正則化は, 誤差の評価関数にペナルティ項を加えた次の式で実現される.

$$\begin{aligned} \tilde{E}(\mathbf{w}) &= E(\mathbf{w}) + \lambda R(\mathbf{w}) \\ &= \frac{1}{2} \sum_{n=1}^N \sum_{k=1}^K (t_k^n - o_k^n)^2 + \lambda (\sum_{i=0}^d \sum_{j=1}^M w_{ji}^2 + \sum_{j=0}^M \sum_{k=1}^K w_{kj}^2) \end{aligned}$$

• この正則化を荷重減衰ペナルティ(weight decay penalty)という
• $\lambda$ を正則化パラメータという.

実行例-あやめデータにおける正則化項の効果

setosaとvirginicaを一つのクラスにまとめたあやめデータに対して, 隠れ素子数は10にして学習した

左が正則化項を用いない場合の識別境界で, 右が $\lambda = 0.01$ としたときの識別境界

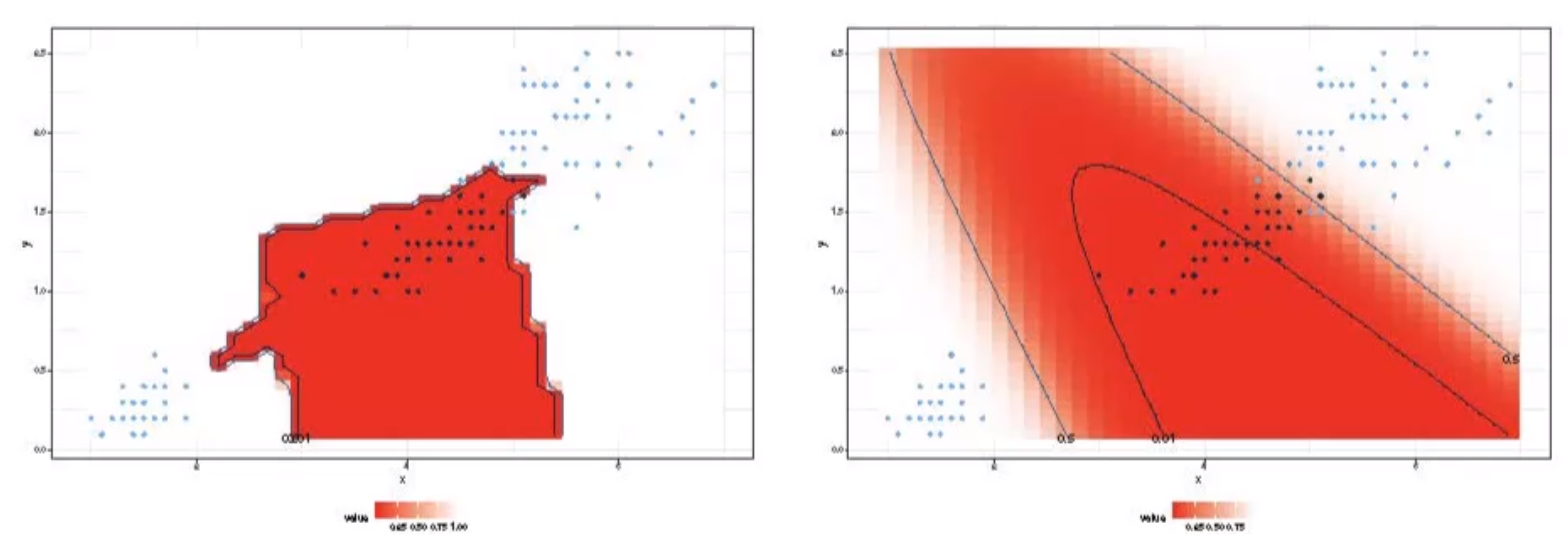
結合係数の個数は, 入力層から隠れ層に対して $2 \times 10 + 10$, 隠れそうから出力層に対して $10 \times 2 + 2$ で, 合計 52 個のパラメータ.

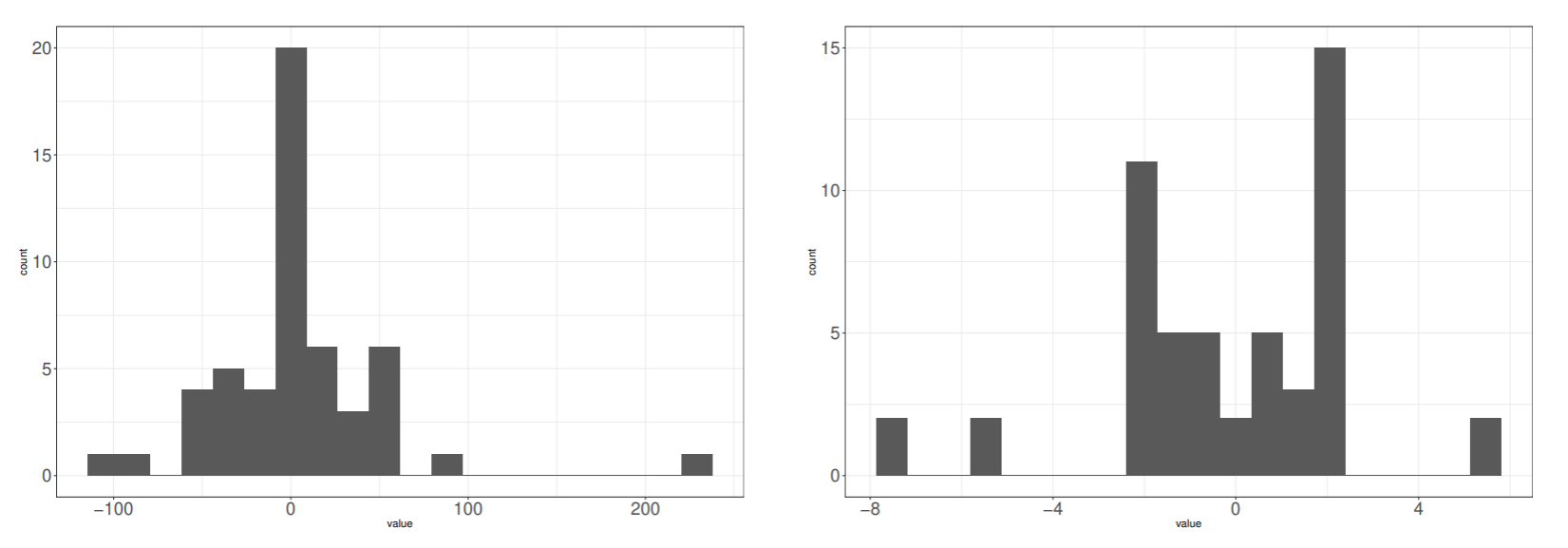
結合係数の大きさのヒストグラムより, 正則化項を用いない場合の結合係数は, 用いた場合よりも一桁大きな値になっている.

隠れ層の数と識別能力

隠れ層はいくあってもよい.

• 1層は直線状の識別境界
• 2層なら凸領域
• 3層なら飛び地や穴の空いた領域が表現できる.

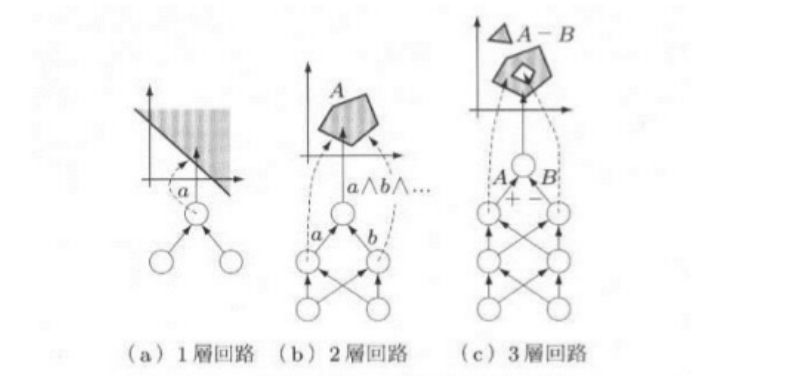
層の数が増えると, 表現できる識別関数は複雑になる

学習回路の尤度

尤度関数を誤差関数として使用すると良い

出力の活性化関数と誤差関数 $\Rightarrow$ 解くべき問題の型で選択

	活性化関数(出力関数)g()	誤差関数E()
回帰問題	線形出力関数	二乗和誤差
2クラス分類問題(多数の独立な)	ロジスティックシグモイド関数 ソフトマックス関数(2クラス)	二乗和誤差 交差エントロピー誤差関数
多クラス分類問題	ソフトマックス関数	多クラス交差エントロピー誤差関数

クラス分類問題では, 交差エントロピー誤差関数を使う方が訓練が早く, 同時に汎化能力が高まる

サポートベクトルマシン(SVM)

サポートベクトルマシンは, もっとも広く利用されているパターン認識学習アルゴリズムの一つで, 最大マージンを実現する2クラス問題の線形識別関数構成法.

マージン最大化は, 学習データによって与えられた不等式制約条件下で最適化問題を解くことで得られる. 線形分離不可能な場合もスラック変数の導入により誤り最小の線形識別関数を得ることができる.

線形分離不可能な場合のさらに良い対処法は, 非線形特徴写像により高次元非線形特徴空間に写像し, 線形分離可能にすることである. 高次元空間の内積計算にはカーネルトリックを用いる.

サポートベクトルマシンには様々な変種があるが, $\upsilon$-サポートベクトルマシンと1クラスサポートベクトルマシンを紹介する.

サポートベクトルマシンの導出

サポートベクトルマシンSVMは最大マージン $D_{max}$ を実現する2クラス線形識別関数の学習法である

最適識別超平面

標準座標系を考え, クラスラベル付き学習データの集合を $\mathcal{D}_L = \lbrace (t_i, \mathbf{x}_i) \rbrace (i = 1, \cdots, N)$ とする. $t_i = \lbrace -1, +1 \rbrace$ は教師データであり, 学習データ $\mathbf{x}_i \in \mathbb{R}^d$ がどちらのクラスに属するかを指定する.

線形識別関数のマージンを $\kappa$ とすれば, すべての学習データに対して, $|\mathbf{w}^T \mathbf{x} + b| \geq \kappa$ が成り立つ. $\kappa$ で正規化すると線形識別関数は

$$\begin{aligned} t_i = +1, \quad \mathbf{w}^T \mathbf{x}_i + b \geq +1 \\ t_i = -1, \quad \mathbf{w}^T \mathbf{x}_i + b \leq -1 \end{aligned}$$

となる. この場合分けは $t_i(\mathbf{w}^T \mathbf{x} + b) \geq 1$ とまとめることができる.

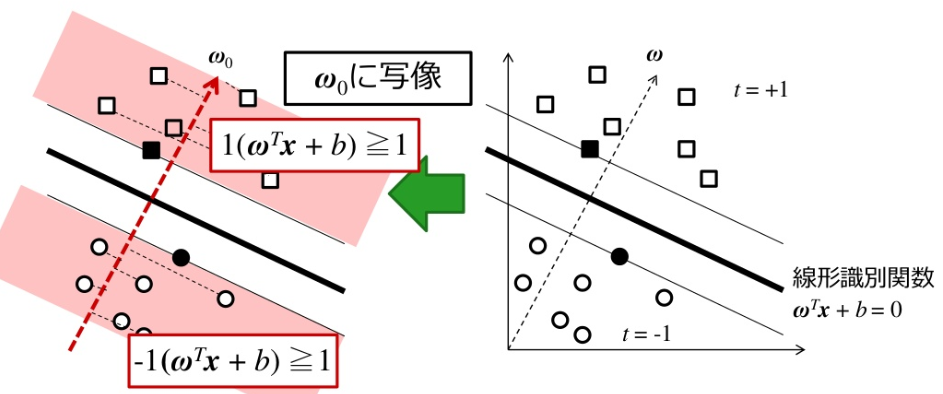
クラス間マージンは, 各クラスのデータを $\mathbf{w}$ の方向へ射影した長さの差の最小値で与えられる.

$$\begin{aligned} \rho(\mathbf{w}, b) &= \min_{x \in C_y=+1} \frac{\mathbf{w}^T \mathbf{x}}{\parallel w \parallel} - \max_{x \in C_y=-1} \frac{\mathbf{w}^T \mathbf{x}}{\parallel w \parallel} \\\\ &= \frac{1 - b}{\parallel \mathbf{w} \parallel} - \frac{-1 - b}{\parallel \mathbf{w} \parallel} \\\\ &= \frac{2}{\parallel \mathbf{w} \parallel} \end{aligned}$$

最適な超平面の式を $\mathbf{w}_0^T \mathbf{x} + b_0 = 0$ とすれば, この超平面は最大クラス間マージンを与える.

$$\rho(\mathbf{w}_0, b_0) = \max_w \rho(\mathbf{w}, b)$$

最適識別超平面は $t_i (\mathbf{w}^T \mathbf{x} + b) \geq 1$ の制約下で, $\mathbf{w}$ のノルムを最小にする解

$$\mathbf{w}_0 = \min \parallel \mathbf{w} \parallel$$

として求めることができる.

KKT条件

KKT条件

マージン最大の最適識別超平面は, 次の不等式制約条件の主問題を解くことで得られる.

主問題 1:

$$\begin{aligned} &\text{評価関数(最小化)} \quad L_p(\mathbf{w}) = \frac{1}{2} \mathbf{w}^T\mathbf{w} \\ &\text{不等式制約条件} \quad t_i(\mathbf{w}^T\mathbf{x}_i + b) \geq 1 \end{aligned}$$

この問題は, 次のラグランジュ関数として定式化される.

$$\tilde{L}_p(\mathbf{w}, b, \alpha) = \frac{1}{2}\mathbf{w}^T\mathbf{w} - \sum_{i=1}^N \alpha_i (t_i(\mathbf{w}^T\mathbf{x}_i + b) - 1)$$

ここで $\mathbf{\alpha} = (\alpha_1, \cdots, \alpha_N)^T (\alpha_i \geq 0)$ はラグランジュ未定乗数である.

この最適化問題の解 $\mathbf{w}_0$ と $b_0$ は次のKKT条件を満たす解として得られる.

KKT条件(1)より, 最適解は

$$\mathbf{w}_0 = \sum_{i=1}^N \alpha_it_i\mathbf{x}_i$$

となるので, 最適解は有効な不等式制約条件をもつ学習データの線形結合となる. この解とKKT条件(2)をラグランジュ関数に代入すれば

$$\begin{aligned} L_d(\mathbf{\alpha}) &= \frac{1}{2}\mathbf{w}_0^T\mathbf{w}_0 - \sum_{i=1}^N \alpha_it_i\mathbf{w}_0^T\mathbf{x}_i - b\sum_{i=1}^N \alpha_i t_i + \sum_{i=1}^N \alpha_i \\ &= \sum_{i=1}^N \alpha_i - \frac{1}{2}\mathbf{w}_0^T\mathbf{w}_0 = \sum_{i=1}^N \alpha_i - \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j t_i t_j \mathbf{x}_i^T \mathbf{x}_j \end{aligned}$$

が得られる. 最適解が学習データの線形結合で表現されることから係数 $\alpha_i$ を求める問題に置き換えることができる.

最適な $\alpha_i$ は $L_d(\alpha)$ を最大にする $\alpha$ により得られる. これを主問題に対する双対問題という.

$N$ 個の1を並べたベクトルを $\mathbf{1} = (1, \cdots, 1)^T$, 学習データから作られる行列を $\mathbf{H} = \lbrace H_{ij} = t_i t_j \mathbf{x}_i^T \mathbf{x}_j \rbrace$, 教師データベクトルを $\mathbf{t} = (t_1, \cdots, t_N)^T$ とする

双対問題1

$$\begin{aligned} &\text{評価関数(最大化)} \quad L_d(\mathbf{\alpha}) = \mathbf{\alpha}^T\mathbf{1} - \frac{1}{2} \mathbf{\alpha}^T \mathbf{H} \mathbf{\alpha} \\ &\text{制約条件} \quad \mathbf{\alpha}^T\mathbf{t} = 0 \end{aligned}$$

と表現できる. 従って, 双対問題のラグランジュ関数 $\tilde{L}_d(\mathbf{\alpha})$ は, ラグランジュ未定乗数を $\beta$ とすれば

$$\tilde{L}_d(\mathbf{\alpha}, \beta) = \frac{1}{2}\mathbf{\alpha}^T \mathbf{H} \mathbf{\alpha} - \beta \mathbf{\alpha}^T \mathbf{t}$$

となる.

サポートベクトル

KKT条件(5)より, $\alpha_i (t_i(\mathbf{w}^T \mathbf{x}_i + b) - 1) = 0$ がすべての $i = 1, \cdots, N$ で成り立てばよいので

$$\begin{aligned} t_i(\mathbf{w}^T\mathbf{x}_i + b) - 1) = 0, \quad \alpha_i > 0 \\ t_i(\mathbf{w}^T\mathbf{x}_i + b) - 1) \neq 0, \quad \alpha_i = 0 \end{aligned}$$

となる. $\alpha_i > 0$ となる $\mathbf{x}_i$ をサポートベクトルといい, 最適識別超平面を構成する要素となる.

ラグランジュ乗数法による最適解を $\tilde{\alpha} = (\tilde{\alpha}_1, \cdots, \tilde{\alpha}_N)^T$ とすれば

$$\mathbf{w}_0^T \mathbf{w}_0 = \sum_{i=1}^N \tilde{\alpha}_i t_i \mathbf{x}_i^T \mathbf{w}_0 = \sum_{i=1}^N \tilde{\alpha} (1 - t_ib_0) = \sum_{i=1}^N \tilde{\alpha}_i$$

となるので, 最大マージンは

$$D_{max} = \frac{1}{\parallel \mathbf{w}_0 \parallel} = \frac{1}{\sqrt{\mathbf{w}_0^T \mathbf{w}_0}} = \frac{1}{\sqrt{\sum_{i=1}^N \tilde{\alpha}_i}}$$

線形分離可能な場合

ワインデータから2クラスを選択し, 線形判別分析を使い2次元に射影したデータを使う.

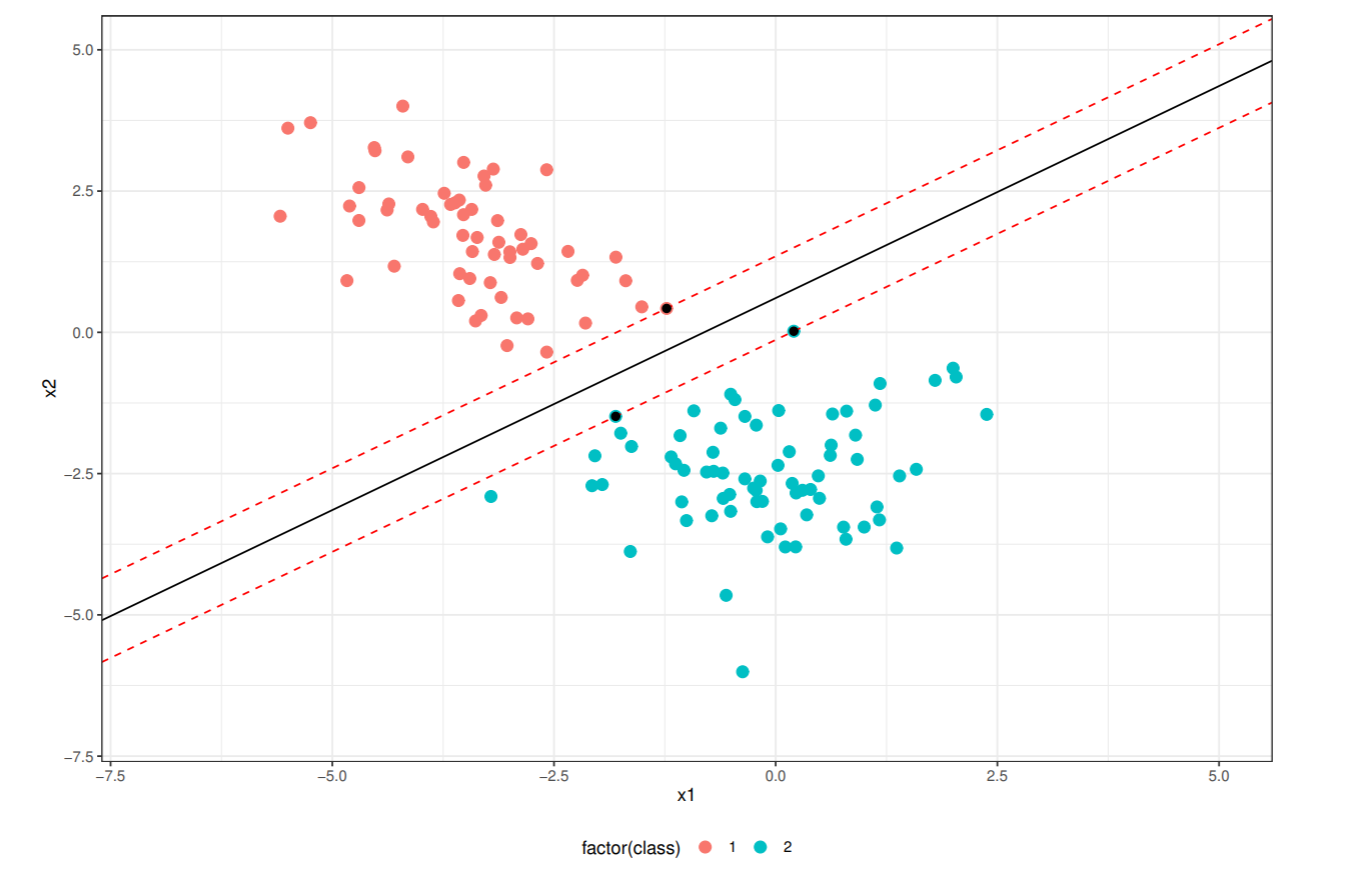
線形分離可能でない場合への拡張

線形分離可能でない場合, 制約条件をすべて満たす解は求まらない. 次のような変数 $\xi_i$ を導入し, $t_i(\mathbf{x}_i^T \mathbf{w}_0 + b) - 1 + \xi_i \geq 0$

$$\begin{aligned} &\xi_i = 0, \quad \text{マージン内で正しく識別できる場合} \\ &0 < \xi_i < 1, \quad \text{マージン境界を超えるが正しく識別できる場合} \\ &\xi_i > 1, \quad \text{識別境界を超えて誤識別される場合} \end{aligned}$$

とすると, 制約条件を満たすことができる. 変数 $\xi_i$ をスラック変数といい, このような手法をソフトマージン識別器という.

$\xi_i$ は

$$\xi_i = \max [0, 1 - t_i(\mathbf{w}^T\mathbf{x}_i + b)] = f_+(1 - t_i(\mathbf{w}^T\mathbf{x}_i + b))$$

のように表現することもできる. 識別器の損失を表現しているので損失関数と呼ばれる. $f_+$ は

$$\begin{aligned} f_+(x) = \begin{cases} x, \quad x > 0 \\ 0, \quad x \leq 0 \end{cases} \end{aligned}$$

で定義される.

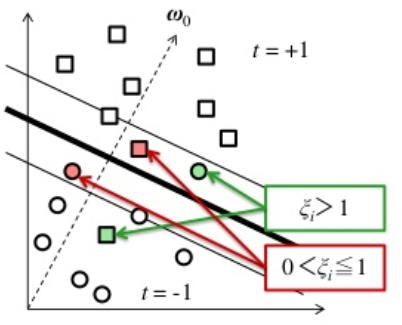
すべての学習データのスラック変数の和 $\sum_{i=1}^N \xi_i(\xi_i \geq 0)$ は, 誤識別の上限を数える.

ソフトマージン識別器の主問題2

$$\begin{aligned} &\text{評価関数(最小化)} \quad L_p(\mathbf{w}) = \frac{1}{2} \mathbf{w}^T\mathbf{w} + C\sum_{i=1}^N \xi_i \\ &\text{不等式制約条件} \quad t_i(\mathbf{w}^T\mathbf{x}_i + b) - 1 + \xi_i \geq 0, \quad \xi_i \geq 0 \end{aligned}$$

パラメータ $C$ は誤識別数に対するペナルティの強さを表す. 適切な $C$ は交差確認法などで実験的に選ぶ.

パラメータ $C$ を使うので, C-SVM(C-support vector machine) と略称されている.

KKT条件

$\xi_i \geq 0$ を強制するラグランジュ未定乗数を $\mu_i \geq 0$, 誤識別数の上限を抑えるペナルティ定数を $C$ とする.

ソフトマージン最大化

KKT条件(3)から, $\alpha_i = C$ となる. このようなサポートベクトルを上限サポートベクトル(bounded SV)という.

$\xi_i = 0$ で, $0 < \alpha_i < C$ となっているサポートベクトルを自由サポートベクトル(free SV)という.

ソフトマージン識別器の双対問題2

$$\begin{aligned} &\text{評価関数(最大化)} \quad L_d(\mathbf{\alpha}) = \mathbf{\alpha}^T\mathbf{1} - \frac{1}{2} \mathbf{\alpha}^T \mathbf{H} \mathbf{\alpha} \\ &\text{制約条件} \quad 0 \leq \alpha_i \leq C, \mathbf{\alpha}^T\mathbf{t} = 0 \end{aligned}$$

解ベクトルは, $\mathbf{w}_0 = \sum_{i=1}^N \alpha_i t_i \mathbf{x}_i$ で得られ, $\alpha_i \neq 0$ の要素がサポートベクトルである.

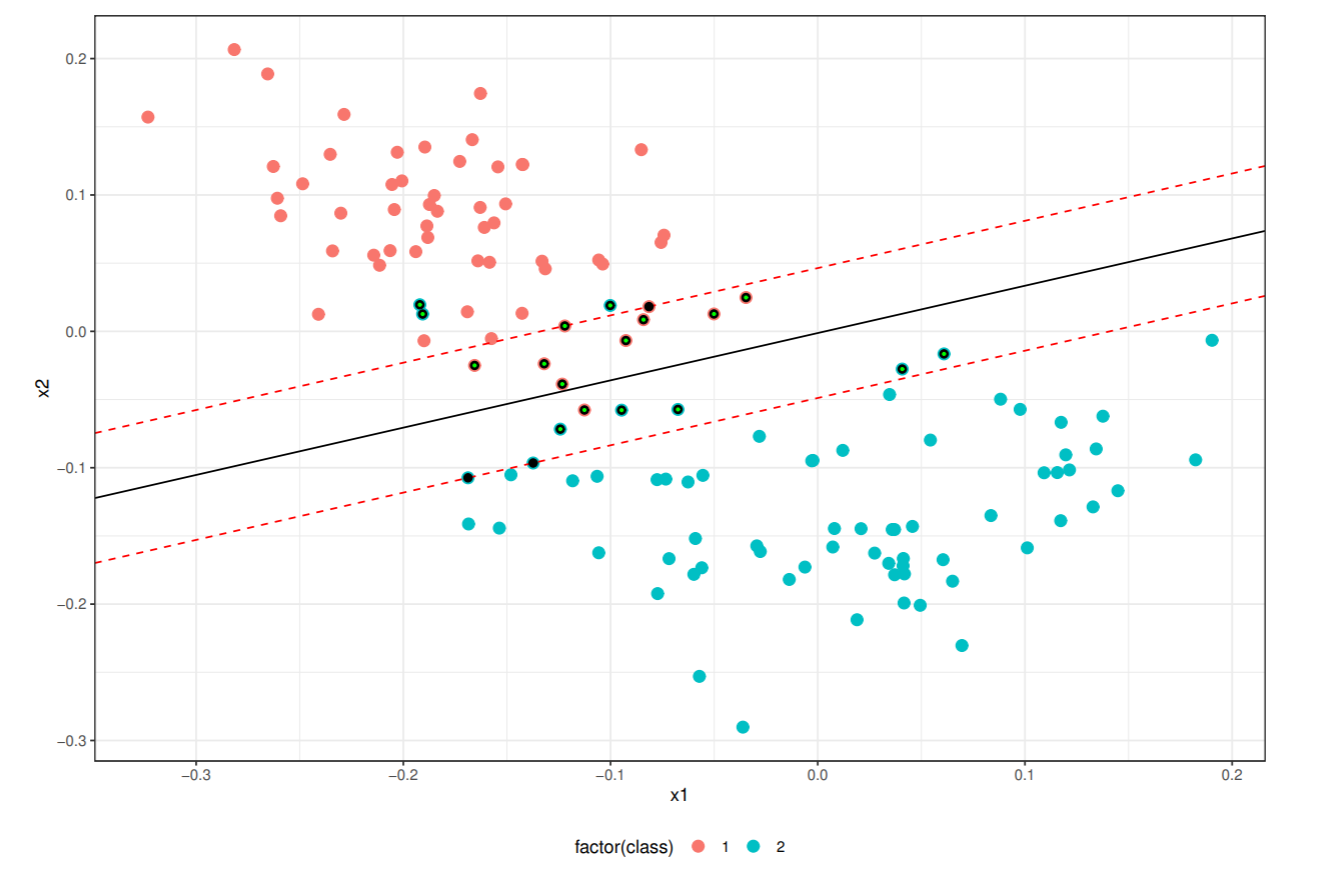
線形分離可能でない場合

ワインデータから2クラスを選択し, 特異値分解により2次元に射影したデータを使う.

非線形特徴写像

SVMは解が学習データの線形結合で表される識別超平面となる. 識別境界が学習データの線形関数では表せないような場合には, 誤差逆伝搬法のような非線形識別関数を直接構成することも一つの方法である.

ここでは, 非線形特徴写像を用いて非線形特徴空間に写像し, その空間内で線形識別関数を用いる方法を紹介する.

$d$ 次元の学習データ $\mathbf{x} \in \mathbb{R}^d$ と, その非線形写像の集合 $\lbrace \varphi_j(\mathbf{x}) \rbrace_{j=1,\cdots,M}$ を考える.

非線形写像空間のベクトルを, 次のように表す. $\varphi_0(\mathbf{x}) = 1$ はバイアス項である.

$$\varphi(\mathbf{x}) = (\varphi_0(\mathbf{x}) = 1, \varphi_1(\mathbf{x}), \cdots, \varphi_M(\mathbf{x}))^T$$

非線形特徴空間での線形識別関数を次のように表す.

$$h(\varphi(\mathbf{x})) = \sum_{j=0}^M w_j\varphi_j(\mathbf{x}) = \mathbf{w}^T \varphi(\mathbf{x})$$

この非線形空間内でSVMを考えれば, 最適識別超平面は次のようになる.

$$\mathbf{w}_0 = \sum_{i=1}^N \alpha_it_i\varphi(\mathbf{x}_i)$$

識別関数が

$$h(\varphi(\mathbf{x})) = \mathbf{w}_0^T \varphi(\mathbf{x}) = \sum_{i=1}^N \alpha_i t_i \varphi^T(\mathbf{x}_i) \varphi(\mathbf{x}_i) = \sum_{i=1}^N \alpha_i t_i K(\mathbf{x}_i, \mathbf{x})$$

のように, 元の空間のベクトル関数 $K(\mathbf{x}_i, \mathbf{x})$ を用いて表せれば都合が良い.

このような関数 $K(\mathbf{x}_i, \mathbf{x})$ を核関数, カーネル関数という.

ソフトマージン識別器のラグランジュ未定乗数 $\alpha_i$ は, 次の双対問題を解くことによって得られる.

$K(\mathbf{x}_i, \mathbf{x}) = \varphi^T(\mathbf{x}_i^T) \varphi(\mathbf{x}_j)$ を $(i, j)$ 要素とする $N \times N$ 対称行列 $\mathbf{K}(\mathbf{X}, \mathbf{X})$ をグラム行列という. $\mathbf{X} = (\mathbf{x}_1, \cdots, \mathbf{x}_N)^T$ はデータ行列である.

双対問題3

$$\begin{aligned} \text{評価関数(最大化)} \quad L_d(\mathbf{\alpha}) &= \sum_{i=1}^N \alpha_i - \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j t_i t_j \varphi^T(\mathbf{x}_i^T) \varphi(\mathbf{x}_j) \\ &= \sum_{i=1}^N \alpha_i - \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j t_i t_j K(\mathbf{x}_i, \mathbf{x}) \end{aligned}$$

$$\text{制約条件} \quad 0 \leq \alpha_i \leq C, \mathbf{\alpha}^T\mathbf{t} = 0$$

多項式カーネル

実定数 $\alpha \geq 0$ に対して, $p$ 次の多項式カーネルを次のように定義する.

$$K_p(\mathbf{u}, \mathbf{v}) = (\alpha + \mathbf{u}^T\mathbf{v})^p$$

$\mathbf{u} = (u_1, u_2)^T, \mathbf{v} = (v_1, v_2)^T$ とする. $\alpha = 1$ とし, 2次の多項式カーネルを次のように定義する.

$$\begin{aligned} K_2(\mathbf{u}, \mathbf{v}) &= (1 + \mathbf{u}^T \mathbf{v})^2 = (1 + u_1v_1 + u_2v_2)^2 \\\\ &= 1 + 2u_1v_1 + 2u_2v_2 + 2u_1u_2v_1v_2 + u_1^2v_1^2 + u_2^2v_2^2 \end{aligned}$$

$\mathbf{u}$ と $\mathbf{v}$ に由来する項に分離する

$$\begin{aligned} \varphi(\mathbf{u}) = (1, u_1^2, \sqrt{2}u_1u_2, u_2^2, \sqrt{2}u_1, \sqrt{2}u_2)^T \\\\ \varphi(\mathbf{v}) = (1, v_1^2, \sqrt{2}v_1v_2, v_2^2, \sqrt{2}v_1, \sqrt{2}v_2)^T \end{aligned}$$

すると, $K_2(\mathbf{u}, \mathbf{v}) = \varphi(\mathbf{u})^T \varphi(\mathbf{v})$ と表現できる.

動径基底関数カーネル

動径基底関数カーネル, RBFカーネルは次式で定義される.

$$K_{\sigma}(\mathbf{u}, \mathbf{v}) = \exp(-\frac{1}{2\sigma^2} \parallel \mathbf{u} - \mathbf{v} \parallel^2)$$

$\sigma$ はカーネル関数の広がりを制御するパラメータである.

動径基底関数カーネルの非線形特徴ベクトルは無限次元となる.

$$K_{\sigma}(\mathbf{u}, \mathbf{v}) = \exp(-\frac{1}{2\sigma^2} \parallel \mathbf{u} - \mathbf{v} \parallel^2) = \exp(-\frac{\parallel \mathbf{u} \parallel^2}{2\sigma^2}) \exp(-\frac{\parallel \mathbf{v} \parallel^2}{2\sigma^2}) \exp(\frac{\mathbf{u}^T \mathbf{v}}{\sigma^2}) = g(\mathbf{u})g(\mathbf{v})\exp(\frac{K_1(\mathbf{u}, \mathbf{v})}{\sigma^2})$$

$g(\mathbf{u})$ と $g(\mathbf{v})$ は最初の二つの指数関数である.

$$\begin{aligned} &\exp(\frac{K_1(\mathbf{u}, \mathbf{v})}{\sigma^2}) = \prod_{i=1}^d \exp(\frac{u_i}{\sigma}\frac{v_i}{\sigma}) \\\\ &\exp(\frac{u_i}{\sigma}\frac{v_i}{\sigma}) = \sum_{n=0}^{\infty}\frac{1}{n!}(\frac{u_i}{\sigma}\frac{v_i}{\sigma})^n = \mathbf{u}_i^T\mathbf{v}_i \end{aligned}$$

ピマインディアンデータのSVMによる識別

Pima.trデータからgluとbmiを使いSVMによる識別を考えよう.

動径基底関数(RBF)カーネルを使い, $\sigma = 0.2, 0.4, 0.8, 4, 8$ とし, $\alpha_i$ の上限を決定するためのパラメータは $C = 10^i, i = 0, 1, 2, 3, 4$ とした.

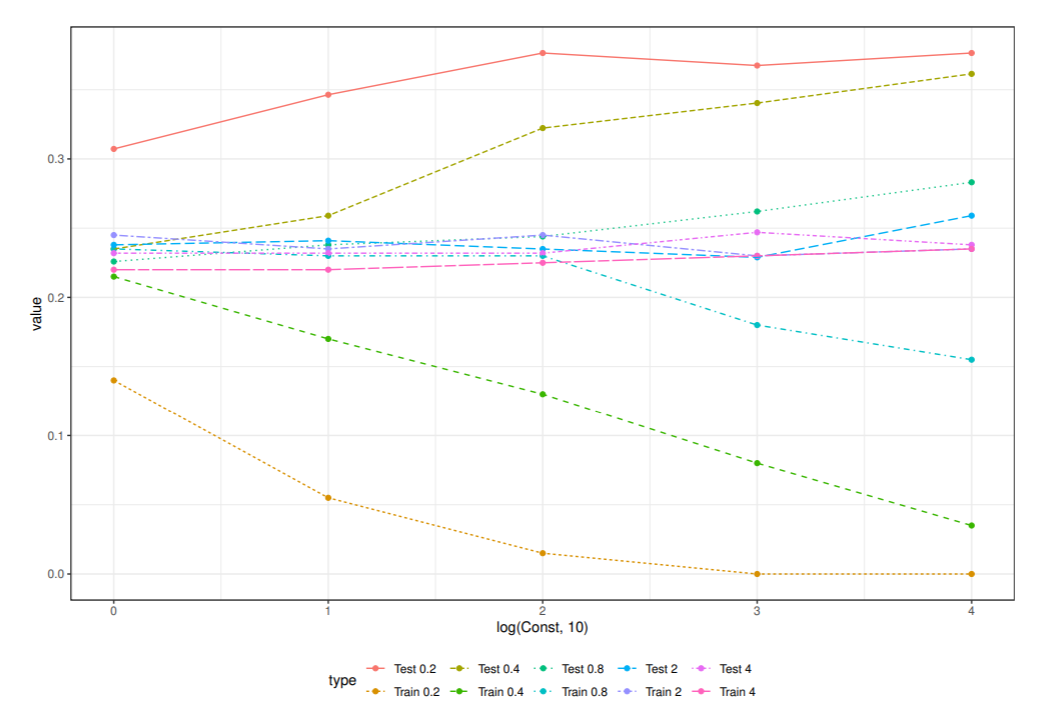
識別関数が学習パラメータによってどのように変わるか見るために,汎化誤差が最小になった場合と訓練誤差が最小になった場合の識別関数とサポートベクトルの分布をプロットした.

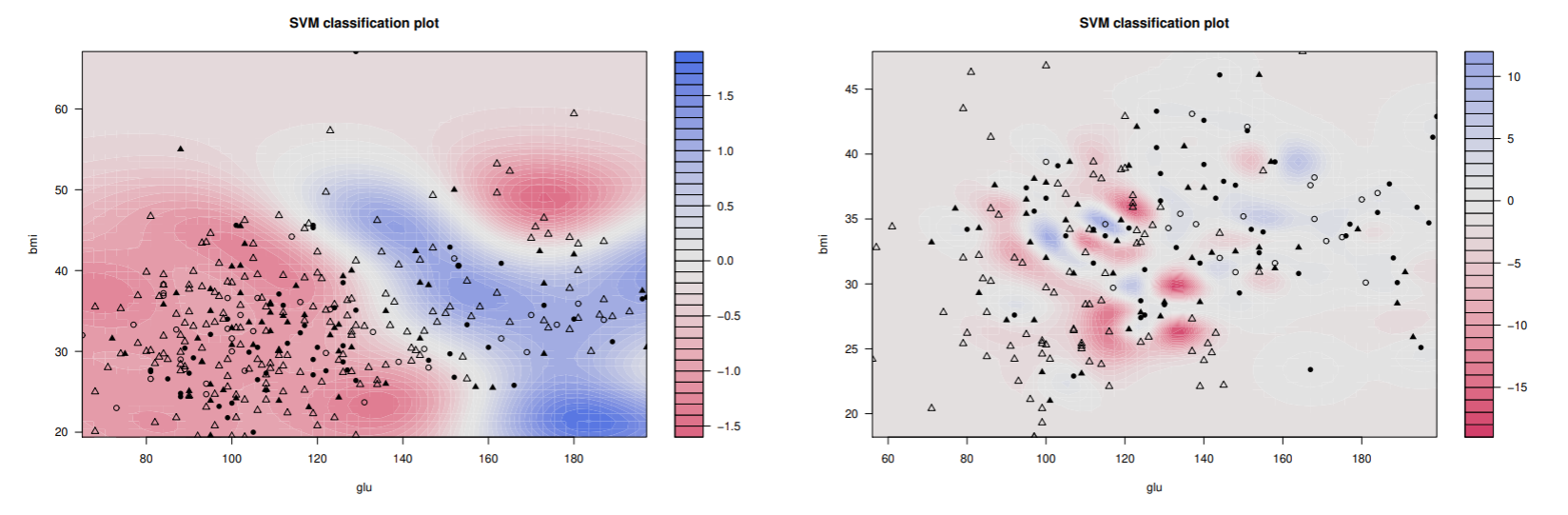
汎化誤差が最小になった場合と訓練誤差が最小になった場合のサポートベクトルの係数 $t_i \alpha_i$ のヒストグラムを示した.

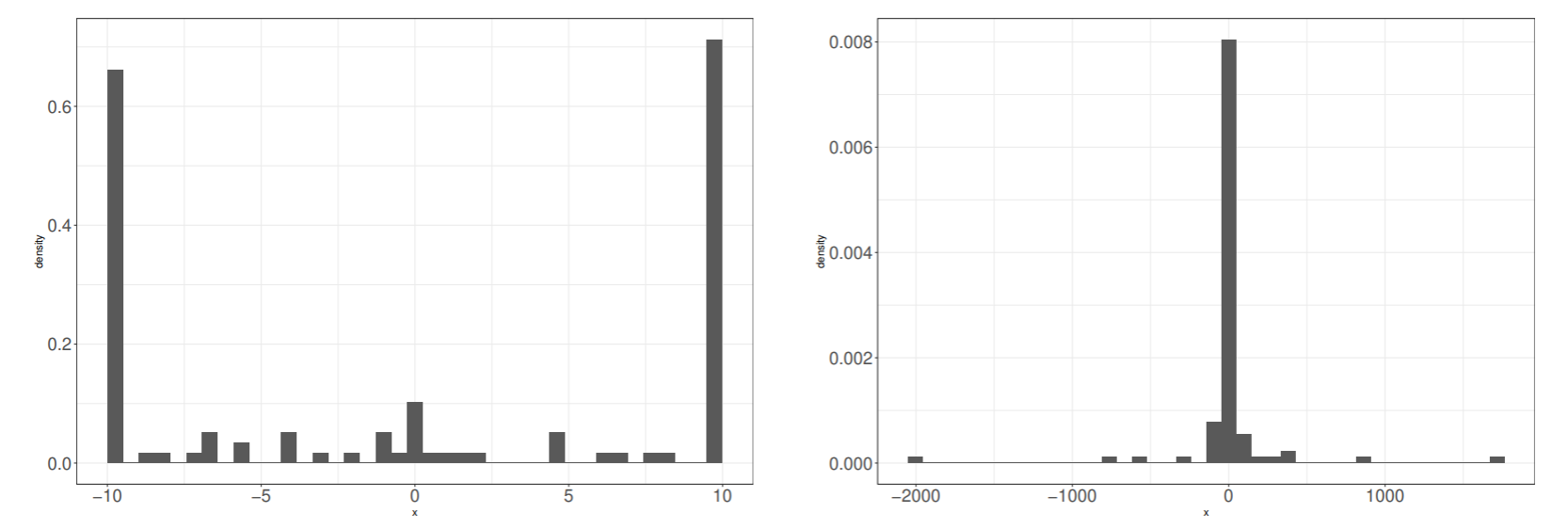
ν-サポートベクトルマシン

ソフトマージン識別器では, $C$ が誤識別数に対するペナルティ係数として導入され, $C$ が $\alpha_i$ の上限を決めた. 誤識別数を学習データで割った誤識別率にした方が, 学習データが変わった場合にも対応でき便利.

そこで, 学習器の複雑さと誤り率のトレードオフを $ν$ を介して取り入れたものが, ν-サポートベクトルマシンである.

サポートベクトルマシンの損失関数は

$$\xi_i = f_+(1 - t_i(\mathbf{w}^T\mathbf{x}_i + b))$$

であり, 非線形特徴写像を用いた場合, $f(\mathbf{x}_i) = \mathbf{w}_T \varphi(\mathbf{x}_i) + b$ とすれば,

$$\xi_i = f_+(1 - t_if(\mathbf{x}_i))$$

となる. ここで損失を

$$\xi_i = f_+(\rho - t_if(\mathbf{x}_i))$$

と変更し, $\rho$ の値も最適化することを考える.

最適化問題は, 損失が小さくなるように学習するので, 損失関数から見れば, $\rho$ は小さい方が良い.

一方, マージン $\rho$ が小さいと最適化問題が難しくなり, 結合係数 $\mathbf{w}$ のノルムが大きくなる.

そこで, マージンが小さくなりすぎないように評価関数に $-\rho$ に比例した項を加えて最適化問題にする.

主問題4

$$\begin{aligned} &\text{評価関数(最小化)} \quad L_p(\mathbf{w}, \rho, \xi) = \frac{1}{2} \mathbf{w}^T\mathbf{w} - v\rho + \frac{1}{N}\sum_{i=1}^N \xi_i \\ &\text{不等式制約条件} \quad t_i(\mathbf{w}^T \varphi(\mathbf{x}_i) + b) - \rho + \xi_i \geq 0, \quad \xi_i \geq 0 \end{aligned}$$

$v = \sum_{i=1}^N \alpha_i \leq \frac{1}{N} \times$ サポートベクトルであるから, vはサポートベクトルの割合の下限と上限サポートベクトルの割合の上限を与えている.

ピマインディアンデータへのν-SVMの適用

ピマインディアンデータの場合 $N^+ = 68, N^1 = 132$ なので, $v_{max} = 0.68$ である.

ν を0.1から0.6まで変化させ, 上限サポートベクトルの割合をRBFカーネルのパラメータ $\sigma$ を変えてプロットした.

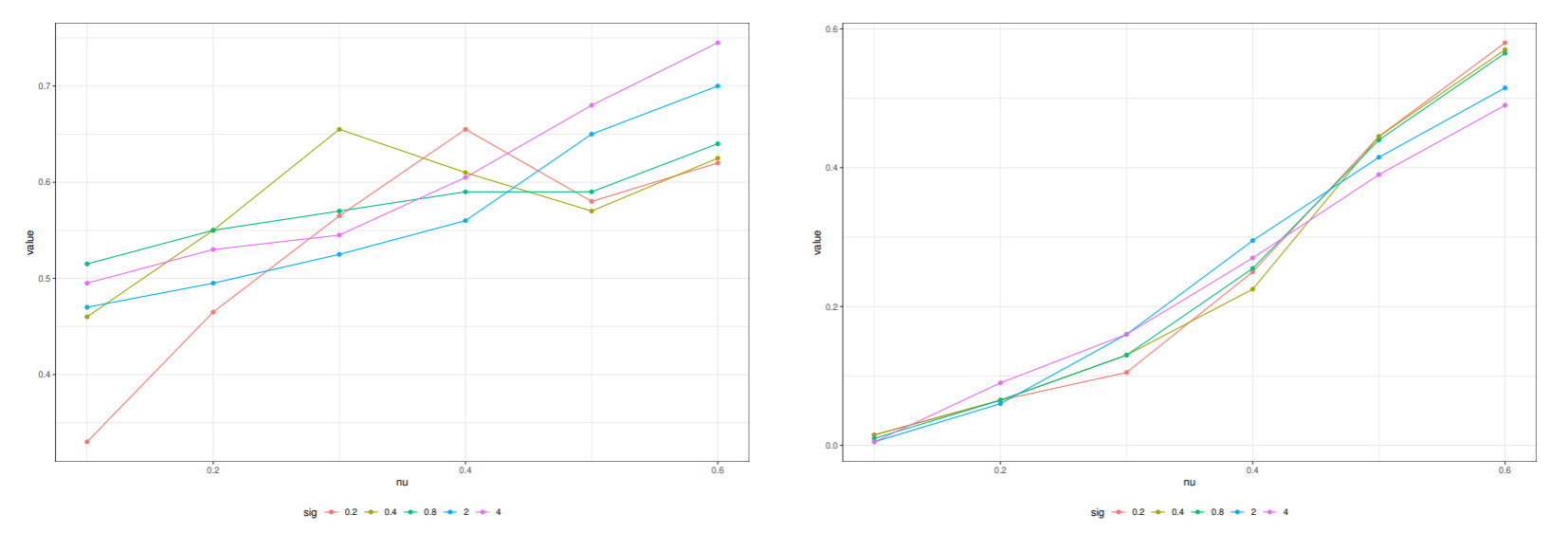
1クラスサポートベクトルマシン

サポートベクトルマシンは, 2クラスの識別関数を構成するためのものであったが, 1クラスのみの学習に用い, 入力データがそのクラスに入るか入らないかのみを判断する方法が提案されている. 新規性判断や例外検出, 外れ値検出に利用できる.

主問題5

$$\begin{aligned} &\text{評価関数(最小化)} \quad L_p(\mathbf{w}, \mathbf{\xi}) = \frac{1}{2} \mathbf{w}^T\mathbf{w} - \rho + \frac{1}{vN}\sum_{i=1}^N \xi_i \\ &\text{不等式制約条件} \quad \mathbf{w}^T \varphi(\mathbf{x}_i) - \rho + \xi_i \geq 0, \quad \xi_i \geq 0 \end{aligned}$$

正例か外れ値かの識別関数は, 次のように与えられ, $f(\mathbf{x}) = 1$ のとき正例, $f(\mathbf{x}) = -1$ のとき外れ値である.

$$\begin{aligned} f(\mathbf{x}) = sgn(\sum_{i=1}^N \alpha_i K(\mathbf{x}_i, \mathbf{x}) - \rho), \quad sgn(a) = \begin{cases} +1, \quad &a > 0 \\ 0, \quad &a = 0 \\ -1, \quad &a < 0 \end{cases} \end{aligned}$$

ピマインディアンの外れ値検出

Pima.trを用いて学習したときの外れ値検出率と Pima.te を用いたときの外れ値検出率を図に示した.

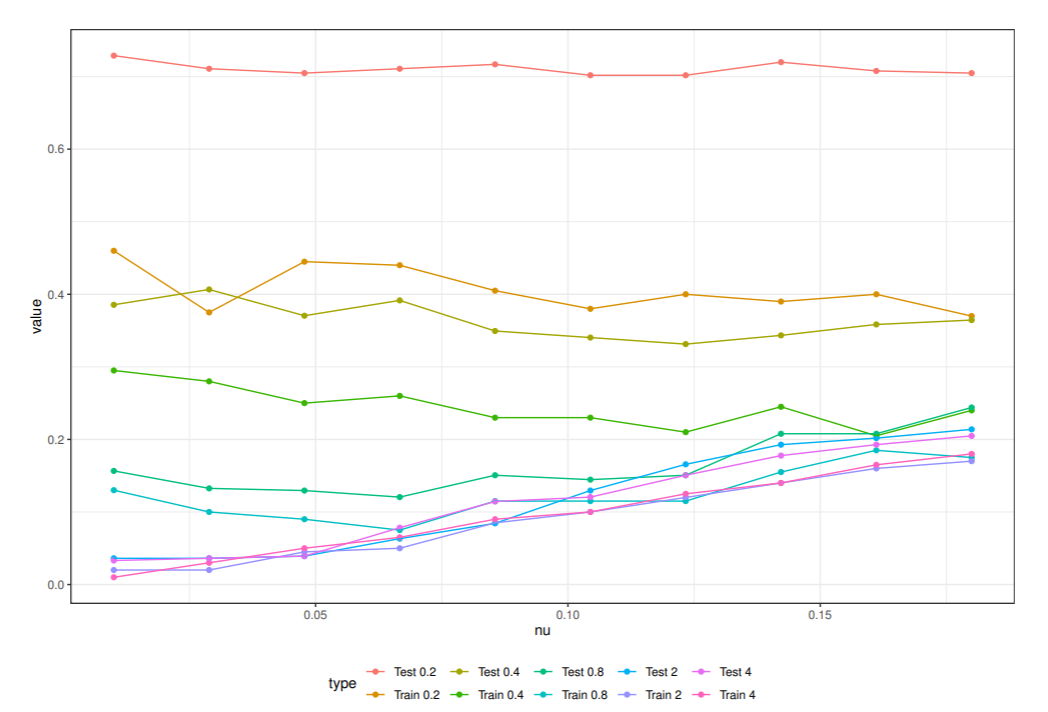
外れ値検出率が最も小さかったパラメータを用いて学習したときのサポートベクトルの位置と, テストデータで外れ値と判断されたデータを図に示した.

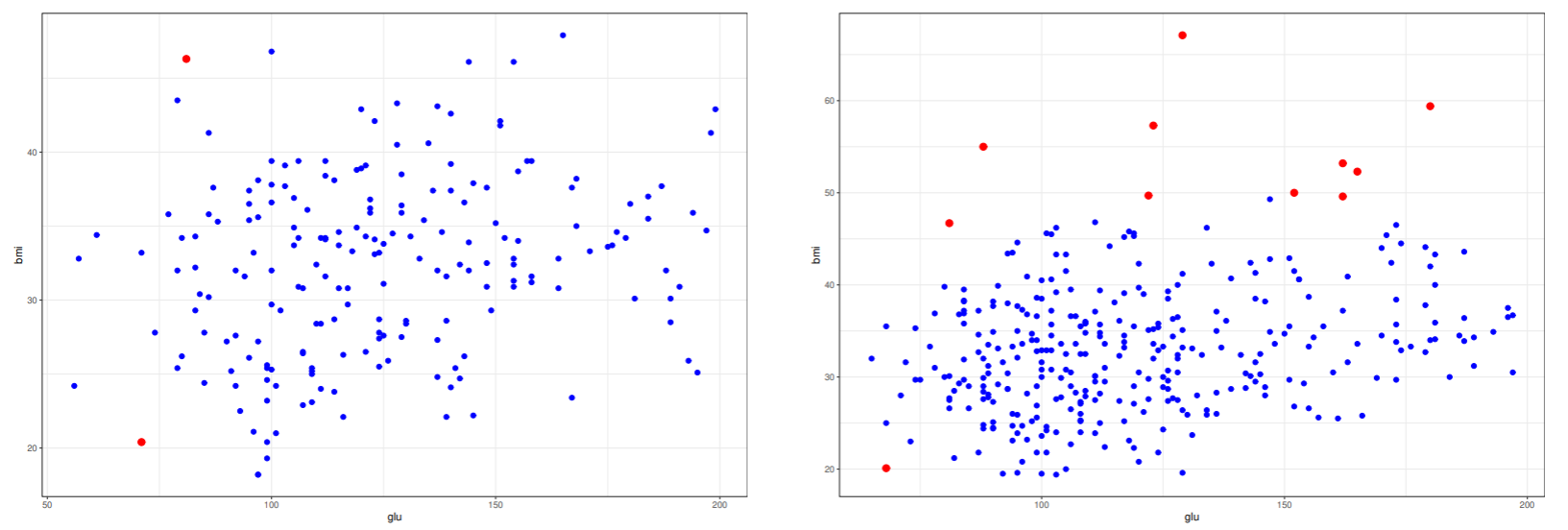
部分空間法

計算コストを抑える目的のためにも, 解釈可能な識別器を構成するためにも, データの次元数は少ないほうが良い. ここでは, $d$ 次元特徴ベクトル空間を重要な情報をもつ $r(\leq d)$ 次元空間に縮約する方法を紹介する.

主成分分析では, 共分散行列の固有値問題を解き, 大きな固有値に対応する固有ベクトルで部分空間を構成し, 元の情報の低次元で近似する.

クラスごとに主成分分析を行い, それそれのクラスのデータで部分空間を構成して識別器を構成する方法を部分空間法という. 部分空間法は, 多クラス問題への拡張が容易なこと, 識別能力が高いことから, 広く利用されている. カーネル法を取り入れた, カーネル主成分分析やカーネル部分空間法を紹介する.

部分空間

$d$ 次元ベクトル空間 $V$ の部分空間は次のように定義された.

$\mathbf{x}_1, \cdots, \mathbf{x}_r, (r \leq d)$ を $V$ のベクトルとすると

$$W = \lbrace a_1\mathbf{x}_1 + \cdots + a_r\mathbf{x}_r \ |\ a_i \in \mathcal{R}, i = 1, \cdots, r \rbrace$$

は $V$ の部分空間となる.

$W$ が $\mathbf{x}_1, \cdots, \mathbf{x}_r$ で張られる $r$ 次元の部分空間であるとは, $\mathbf{x}_1, \cdots, \mathbf{x}_r$ が一次独立であることであった.

$W$ が $V$ の部分空間であるための必要十分条件は以下が成り立つことである.

1. $W \neq 0$
2. $\mathbf{x}, \mathbf{y} \in W \Rightarrow \mathbf{x} + \mathbf{y} \in W$
3. $\mathbf{x} \in W, \lambda \in \mathcal{R} \Rightarrow \lambda \mathbf{x} \in W$

MNIST 手書き数字を用いて, $28 \times 28$ 次元ベクトル空間の 10 次元の部分空間を作ってプロットした

ベクトル空間 $V$ は, 部分空間 $\mathbf{S}$ とそれと直交する部分空間 $\mathbf{S}^{\bot}$ に分解できた. $V = \mathbf{S} \cup \mathbf{S}^{\bot}, \mathbf{S} \cap \mathbf{S}^{\bot} = \empty$ が成り立つので, 任意のベクトル $\mathbf{x}$ は, $\mathbf{x} = \mathbf{x}_S + \mathbf{x}_{S^{\bot}}$ と分解できた.

直交座標系に変換するには, グラムーシュミットの正規直交化を使う.

10 次元部分空間からQR分解によりグラムーシュミットの正規直交基底を作成した.

主成分分析(Principal Component Analysis PCA)

主成分分析方法，是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

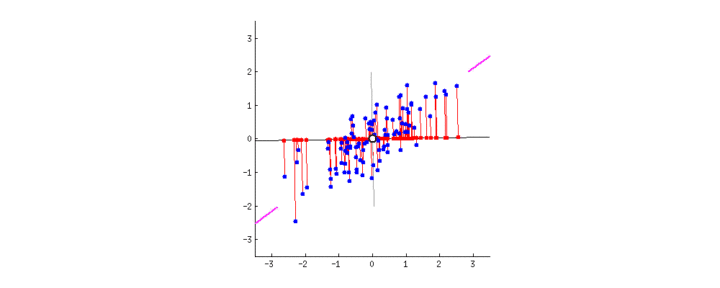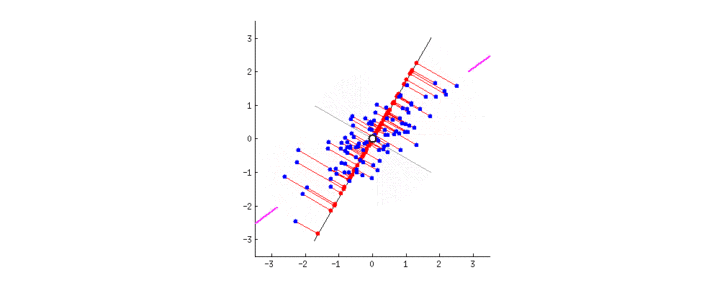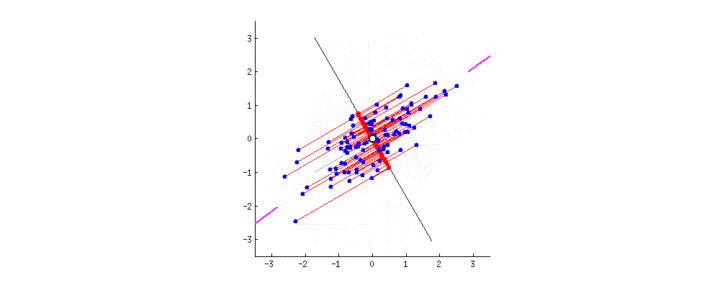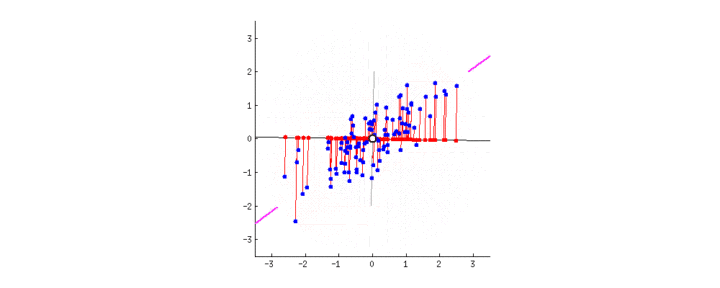
主成分分析は, 学習データ $\mathbf{x}_i = (x_{i1}, \cdots, x_{id})^T (i = 1, \cdots, N)$ の分散が最大になる方向への線形変換を求める手法である

$N$ 個のデータからデータ行列 $\mathbf{X} = (\mathbf{x}_1, \cdots, \mathbf{x}_N)^T$ の平均ベクトル $\overline{\mathbf{x}} = (\overline{\mathbf{x}_1}, \cdots, \overline{\mathbf{x}_N})^T$ を求める. $\overline{\mathbf{x}}$ を引いたデータ行列を $\overline{\mathbf{X}} = (\mathbf{x}_1 - \overline{\mathbf{x}}, \cdots, \mathbf{x}_N - \overline{\mathbf{x}})^T$ とし, データの分散共分散行列を次のようにして定義する.

$$\mathbf{\Sigma} = \text{Var}(X) = \frac{1}{N} \overline{\mathbf{X}}^T \overline{\mathbf{X}}$$

$N$ 個のデータ $\mathbf{x}_i - \overline{\mathbf{x}}$ を係数ベクトル $\mathbf{a}_j = (a_{j1}, \cdots, a_{jd})^T, (j = 1, \cdots, d)$ を用いて線形変換すれば,

$$\mathbf{s}_j = (s_{1j}, \cdots, s_{Nj})^T = \overline{\mathbf{X}} \mathbf{a}_j$$

が得られる. このとき, $\mathbf{s}_j$ の分散は

$$\text{Var}(\mathbf{s}_j) = \frac{1}{N} \mathbf{s}^T \mathbf{s}_j = \frac{1}{N} (\overline{\mathbf{X}} \mathbf{a}_j)^T (\overline{\mathbf{X}} \mathbf{a}_j) = \frac{1}{N} \mathbf{a}_j^T \overline{\mathbf{X}}^T \overline{\mathbf{X}} \mathbf{a}_j = \mathbf{a}_j^T \text{Var}(\overline{\mathbf{X}}) \mathbf{a}_j$$

線形変換 $\mathbf{s}_j$ の分散が最大になる射影ベクトル $\mathbf{a}_j$ は, ラグランジュ関数

$$E(\mathbf{a}_j) = \mathbf{a}_j^T \text{Var}(\overline{\mathbf{X}}) \mathbf{a}_j - \lambda(\mathbf{a}_j^T \mathbf{a}_j - 1)$$

を最大にする $\mathbf{a}_j$ を見つければ良い.

$\mathbf{a}_j$ で微分して 0 とおけば

$$\frac{\partial E(\mathbf{a}_j)}{\partial \mathbf{a}_j} = 2\text{Var}(\overline{\mathbf{X}}) \mathbf{a}_j - 2\lambda \mathbf{a}_j = 0 \Leftrightarrow \text{Var}(\overline{\mathbf{X}}) \mathbf{a}_j = \lambda \mathbf{a}_j$$

$\mathbf{a}_j$ はデータの分散共分散行列の固有値問題を解けば良い

分散共分散行列が実対称行列なので, 非ゼロの固有値は分散共分散行列のランクで, 最大 $d$ である. 固有ベクトルは直交する.

$$\begin{aligned} \mathbf{a}_i^T \mathbf{a}_j = \delta_{ij} = \begin{cases} 1, \quad i = j \\ 0, \quad i \neq j \end{cases} \end{aligned}$$

最大固有値が線形変換したデータの分散になる.

$$\text{Var}(\mathbf{s}_j) = \mathbf{a}_1^T \text{Var}(\overline{\mathbf{X}}) \mathbf{a}_1 = \lambda_1 \mathbf{a}_1^T \mathbf{a}_1 = \lambda_1$$

最大固有値に対応する固有ベクトル $\mathbf{a}_1$ を第1主成分という. データの分散は, 固有値の合計になる.

$$V_{total} = \sum_{i=1}^d \lambda_i$$

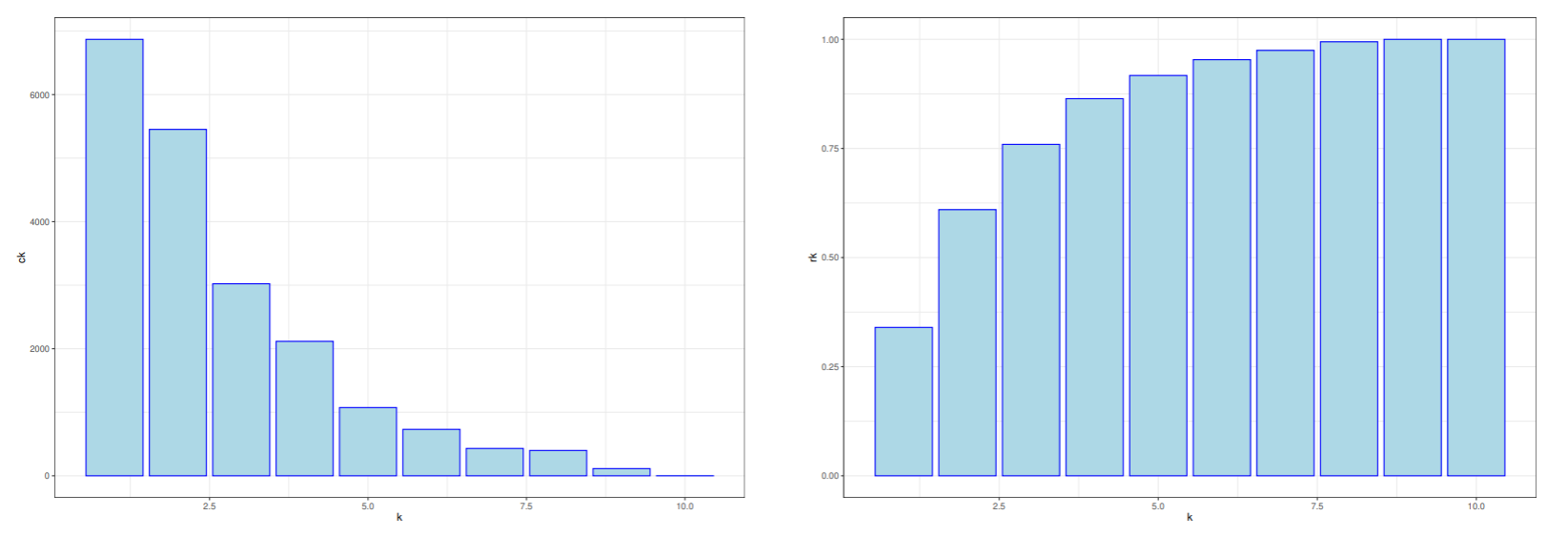
第 $k$ 主成分の全分散に対する割合 $(c_j = \lambda_k / V_{total})$ を第 $k$ 主成分の寄与率といい, 第 $k$ 主成分までの累積寄与率は $r_k = \sum_{i=1}^k c_k$ で表す.

画像データの主成分分析

10枚の画像の主成分分析を行う. 中心化を行うため, $\overline{x}_i$ が一次独立でなくなるため, 最大ランクが9になる. 主成分も9個. 第1主成分から第9主成分までの固有ベクトルを下の図に示した.

寄与率と累積寄与率をプロットした.

特異値分解

行列を複数の行列の積に分析する方法として, グラム-シュミットの正規直交基底を得るためのQR分解がある. 一方, 主成分分析に密接に関連した行列の分解法に, 特異値分解(SVD)がある.

特異値分解とは, 任意の $n \times p$ 行列 $\mathbf{X}$ を

$$\begin{aligned} \mathbf{X} &= \mathbf{U}\mathbf{\Lambda}\mathbf{V}^T \\ &= (\mathbf{u}_1, \cdots, \mathbf{u}_p) \begin{pmatrix} \sqrt{\lambda_1} & 0 & \cdots & 0 \\ 0 & \sqrt{\lambda_2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sqrt{\lambda_p} \end{pmatrix} \begin{pmatrix} \mathbf{v}_1^T \\ \mathbf{v}_2^T \\ \vdots \\ \mathbf{v}_p^T \end{pmatrix} \end{aligned}$$

のように分解することができる.

• $\mathbf{U}$ は $\mathbf{X}\mathbf{X}^T$ の非ゼロ固有値に対応する固有ベクトルで, $n \times p$ の正規直交行列.
• $\mathbf{V}$ は $\mathbf{X}^T\mathbf{X}$ の非ゼロ固有値に対応する固有ベクトルで, $p \times p$ の正規直交行列.
• $\Lambda$ は, $\mathbf{X}\mathbf{X}^T$ または, $\mathbf{X}^T\mathbf{X}$ の非ゼロ固有値の平方根(特異値)である.

特異値分解と主成分分析の関係は $\mathbf{X} = \mathbf{U}\mathbf{\Lambda}\mathbf{V}^T$ から $\mathbf{X}\mathbf{V} = \mathbf{U}\mathbf{\Lambda}$ が成り立つので

$$(\mathbf{X}\mathbf{v}_1 \ \mathbf{X}\mathbf{v}_2 \ \cdots \ \mathbf{X}\mathbf{v}_p) = (\sqrt{\lambda_1}\mathbf{u}_1 \ \sqrt{\lambda_2}\mathbf{u}_2 \ \cdots \ \sqrt{\lambda_p}\mathbf{u}_p)$$

データ行列 $\mathbf{X}$ を $\mathbf{v}_1$ で線形変換したベクトルが $\sqrt{\lambda_1}\mathbf{u}_1$ になるので,
分散をとれば

$$\text{Var}(\mathbf{X}\mathbf{v}_1) = \lambda_1$$

となるので, $\mathbf{X}\mathbf{v}_j$ が第1主成分になっている.

第1主成分から第 $q$ 主成分までの $\mathbf{v}_i$ で構成された部分空間 $\tilde{\mathbf{V}}$ と射影 $\mathbf{X}\tilde{\mathbf{V}}$ を考えると,

$$\tilde{\mathbf{V}} = (\mathbf{v}_1 \ \cdots \ \mathbf{v}_q)$$

共分散行列が $\text{Var}(\mathbf{X}\tilde{\mathbf{V}}) = \Lambda_q^2$ となるから, 行列分解 $\tilde{\mathbf{X}} = \mathbf{U}\Lambda_q \mathbf{V}^T = \sum_{i=1}^q \sqrt{\lambda_i} \mathbf{u}_i \mathbf{v}_i^T$ はランク $q$ の誤差最小の意味での最良近似になっている.

部分空間法

部分空間法とは, クラスごとに部分空間を構成する正規直交基底を求め, 入力データを各クラスの部分空間に射影して識別する手法のこと.

クラスごとに独立に部分空間を構成できるから, 多クラスの識別器が容易に構成できる.

部分空間法には, 相関行列を使う方法と共分散行列を使う方法があり, 相関行列を使う方法にはCLAFIC法がある.

CLAFIC法

データ $\mathbf{x} \in \mathcal{R}^d$ は $K$ 個のクラスのどれかに属しているとする. クラスごとの部分空間を $\mathbf{S}_1, \cdots, \mathbf{S}_K$ とし, クラス $i$ の部分空間を張る基底ベクトルを次のように表す.

$$\lbrace \mathbf{u}_{i1}, \cdots, \mathbf{u}_{id_i} \rbrace$$

部分空間 $\mathbf{S}_i$ へ正射影した長さの期待値を $\mathbf{u}_{ij} = 1$ の制約の下で最大にするようにする.

$$E\lbrace \mathbf{x}^T \mathbf{P}_i \mathbf{x} \ |\ \mathbf{x} \in C_i \rbrace = E\lbrace \mathbf{x}^T (\sum_{j=1}^{d_i} \mathbf{u}_{ij} \mathbf{u}_{ij}^T) \mathbf{x} \rbrace$$

行列 $\mathbf{P}_i$ は射影行列という.

識別規則は全ての $j \neq i$ について, $\mathbf{x}^T \mathbf{P}_j \mathbf{x} < \mathbf{x}^T \mathbf{P}_i \mathbf{x}$ ならば $\mathbf{x} \in C_i$

手書き数字の部分空間法による認識

$28 \times 28$ の数字画像のベクトルの長さを1にそろえた各クラス1000個の学習データを用いる. クラスごとの部分空間の次元数 $d_i(i = 1, \cdots, 10)$ は忠実度 $\kappa$ が0.75となる次元を採用した.

$$a(d_i - 1) \leq \kappa \leq a(d_i), \quad a(d_i) = \sum_{j=1}^{d_i} \lambda_{ij}$$

学習データの誤識別率は 4.98%, テストデータの誤識別率は 8.89%であった. 次のようになった.

カーネル主成分分析

カーネル法を用いて非線形特徴空間で主成分分析を考える. $\mathbf{x}_i \in \mathcal{R}^d (i = 1, \cdots, N)$ を学習データ, 非線形特徴変換を $\varphi(\mathbf{X}_i):\mathbf{x}_i \in \mathcal{R}^d \rightarrow \varphi(\mathbf{x}_i) \in \mathcal{R}^M (M > d)$ とする.

$\sum_{i=1}^N \varphi(\mathbf{x}_i) = \mathbf{0}$ なら, $M \times M$ 分散共分散行列

$$\mathbf{C} = \frac{1}{N} \sum_{i=1}^N \varphi(\mathbf{x}_i) \varphi(\mathbf{x}_i)^T$$

の固有値問題 $\mathbf{C}\mathbf{\nu}_m = \lambda_m \mathbf{\nu}_m$ を解いて, 主成分 $\lambda_m$ と固有ベクトル $\mathbf{\nu}_m$ を得ることができる.

非線形変換の平均を0にするためには, 次のようにする.

$$\tilde{\varphi}(\mathbf{x}_i) = \varphi(\mathbf{x}_i) - \frac{1}{N} \sum_{j=1}^N \varphi(\mathbf{x}_j)$$

平均を0にしたグラム行列 $\tilde{\mathbf{K}}$ のは, 全要素が $\frac{1}{N}$ とする $N \times N$ 行列を$\mathbf{1}_{NN}$とすれば

$$\tilde{\mathbf{K}} = \mathbf{K} - \mathbf{1}_{NN}\mathbf{K} - \mathbf{K}\mathbf{1}_{NN} + \mathbf{1}_{NN}\mathbf{K}\mathbf{1}_{NN}$$

と計算すれば平均を0にすることができる.

元のデータの次元 $d$ での計算は次のように考えれば良い. 非線形変換の学習データを次のようにする.

$$\mathbf{X}_{\tilde{\varphi}} = (\tilde{\varphi}(\mathbf{x}_1), \cdots, \tilde{\varphi}(\mathbf{x}_N)) \in \mathcal{R}^{M \times N}$$

$\mathbf{X}_{\tilde{\varphi}}$ の共分散行列 $\tilde{\mathbf{C}} = \frac{1}{N} \mathbf{X}_{\tilde{\varphi}} \mathbf{X}_{\tilde{\varphi}}^T \in \mathcal{R}^{M \times M}$ なので, $\mathbf{X}_{\tilde{\varphi}} \mathbf{X}_{\tilde{\varphi}}^T$ の固有値を $\lambda_1 \geq \cdots \geq \lambda_N$ とし,$\Lambda$ は $r$ 個の固有値の平方根を対角要素に並べた行列とすると, $\mathbf{X}_{\tilde{\varphi}} = \mathbf{U} \mathbf{\Lambda} \mathbf{V}^T$ と分解できる.

$\mathbf{U} = \mathbf{X}_{\tilde{\varphi}} \mathbf{V} \mathbf{\Lambda}^{-1}$ より

$$\mathbf{u}_i = \frac{1}{\sqrt{\lambda_i}} \mathbf{X}_{\tilde{\varphi}} \mathbf{v}_i$$

が成り立つので, 入力ベクトル $\mathbf{X}_{\tilde{\varphi}}$ の $\mathbf{u}_i$ 方向への射影は

$$\mathbf{u}_i \tilde{\varphi}(\mathbf{x}) = (\frac{1}{\sqrt{\lambda_i}} \mathbf{X}_{\tilde{\varphi}} \mathbf{v}_i)^T \tilde{\varphi}(\mathbf{x}) = \frac{1}{\sqrt{\lambda_i}} \mathbf{v}_i \tilde{\mathbf{K}}(\mathbf{X}, \mathbf{x})$$

となるので, $d$ 次元空間での内積カーネルの計算と $r$ 回の $N$ 次元ベクトルの内積計算で求めることができる.

カーネル部分空間法

CLAFIC 法の内積カーネルを使った非線形特徴空間内の部分空間法を考える.

クラス $i$ の学習データを $\mathbf{X}_i = (\mathbf{x}_{i1}, \cdots, \mathbf{x}_{iN_i})$ とし, その非線形特徴写像による変換を $\mathbf{X}_{i\varphi} = (\varphi(\mathbf{x}_{i1}), \cdots, \varphi(\mathbf{x}_{iN_i}))$ とする.

$\mathbf{X}_{i\varphi}$ の特異値分解を $\mathbf{X}_{i\varphi} = \mathbf{U}_i \mathbf{\Lambda}_i \mathbf{V}_i^T$ とする. クラス忠実度を満たす $d_i$ 個の固有値を $\lambda_{i1}, \cdots, \lambda_{id_i}$ とすれば, $d_i$ 次元の比線型部分空間を構成できる.

$\varphi(\mathbf{X})$ を $\hat{\mathbf{U}}_i$ に射影したときのベクトルの長さは, 次のようになる.

$$l_i^2 (\mathbf{x}) = \sum_{j=1}^{d_i} (\mathbf{u}_{ij}^T \varphi(\mathbf{x}))^2 = \parallel \hat{\mathbf{\Lambda}_i}^{-1} \hat{\mathbf{V}}^T \mathbf{K}(\mathbf{X}, \mathbf{x}) \parallel^2$$

識別規則は 識別クラス = $\argmax_i l_i^2(\mathbf{x}), \quad i = 1, \cdots, K$ である

クラスタリング(Cluster analysis)

前章までの学習データには, 入力データの教師ラベルが付与されていた.

本章では教師なしデータに対しては, 類似度や非類似度を手がかりに, データのグループ分けを行う. このような, 教師なしデータのグループ分けをクラスタリング(Cluster analysis)という

クラスタリングには, 非階層的な手法と階層的な手法がある. いずれもデータやクラスタ間の距離や類似度に基づく方法で, 各データはどれか一つのクラスタのみに属する.

一方, データが確率分布に従い, 全体をそれらの混合分布で表現するクラスタリングがある. 異なるクラスのデータが混在したことを確率分布の混合分布で表す場合もある. 混合分布モデルの推定には, EMアルゴリズムという画期的な手法を使う.

教師なし学習の応用例：

• 遺伝子表現データから乳がん患者のグループ分け
• ユーザのウェブページの閲覧履歴と購入履歴からグループ分け
• 映画視聴者のレーティングによる映画のグループ分け
• コメントや感想からその人の感情を自動的に評価する取り組み
• 計算機実験などから得られるラベルなしデータは, 人手が介入する必要があるラベルありデータに比べて入手しやすい

類似度と非類似度

距離の公理

クラスタリングでは, データやクラス間の類似度あるいは非類似度を使って, 似たようなデータを集めてクラスタを作る.

データやクラスタ間の類似度を測るに距離を導入する. 2つのベクトル $\mathbf{x}$ と $\mathbf{y}$ の距離 $d(\mathbf{x}, \mathbf{y})$ を定義するためには, 距離の公理を満たさないといけない.

距離の公理

1. 非負性: $d(\mathbf{x}, \mathbf{y}) \geq 0$
2. 反射率: $d(\mathbf{x}, \mathbf{y}) = 0$ となるのは, $\mathbf{x} = \mathbf{y}$ のときのみ
3. 対称性: $d(\mathbf{x}, \mathbf{y}) = d(\mathbf{y}, \mathbf{x})$
4. 三角不等式: $d(\mathbf{x}, \mathbf{z}) \leq d(\mathbf{x}, \mathbf{y}) + d(\mathbf{y}, \mathbf{z})$

ミンコフスキー距離(Minkowski distance)

$N$ 個の $d$ 次元データの $i$ 番目のデータを $\mathbf{x}_i = (x_{i1}, \cdots, x_{id})^T$ とする. 2つのベクトル $\mathbf{x}_i$ と $\mathbf{x}_j$ のミンコフスキー距離は,

$$\begin{aligned} d(\mathbf{x}_i, \mathbf{x}_j) = \begin{pmatrix} \sum_{k=1}^d |x_{ik} - x_{jk}|^a \end{pmatrix}^{1/b} \end{aligned}$$

で定義する. $a$ は特徴間の差の重みを調整するパラメータで, $b$ は特徴間の差の $a$ 乗の重みを調整するパラメータ.

$a = b = 1$ のときは市街地距離(マンハッタン距離)で, 四角いマス目状の道路で移動する距離

$$d(\mathbf{x}_i, \mathbf{x}_j) = \sum_{k=1}^d |x_{ik} - x_{jk}|$$

$a = b = 2$ の場合はユークリッド距離

$$\begin{aligned} d(\mathbf{x}_i, \mathbf{x}_j) = \begin{pmatrix} \sum_{k=1}^d |x_{ik} - x_{jk}|^2 \end{pmatrix}^{1/2} \end{aligned}$$

$a = 2, b = 1$ の場合, ユークリッド距離の2乗

$$d(\mathbf{x}_i, \mathbf{x}_j) = \sum_{k=1}^d |x_{ik} - x_{jk}|^2$$

$a = b = \infin$ の場合, チェビシェフ距離

$$\begin{aligned} d(\mathbf{x}_i, \mathbf{x}_j) = \begin{pmatrix} \sum_{k=1}^d |x_{ik} - x_{jk}|^a \end{pmatrix}^{1/a} \quad \lim_{a \rightarrow \infty} = \max_k |x_{ik} - x_{jk}| \end{aligned}$$

データ間の類似度を測るその他の代表的な尺度には, 次のものがある

キャンベラ尺度: データの正規化する仕組みを入れた尺度

$$d(\mathbf{x}_i, \mathbf{x}_j) = \sum_{k=1}^d \frac{|x_{ik} - x_{jk}|}{|x_{ik}| + |x_{jk}||}$$

方向余弦ベクトル間の角度を用いた距離

$$d(\mathbf{x}_i, \mathbf{x}_j) = \frac{\sum_{k=1}^d x_{ik} x_{jk}}{\sqrt{(\sum_{k=1}^d x_{ik}^2) (\sum_{k=1}^d x_{jk}^2)}}$$

非階層型クラスタリング(K-平均法)

k-平均聚类的目的是：把n个点（可以是样本的一次观察或一个实例）划分到k个聚类中，使得每个点都属于离他最近的均值（此即聚类中心）对应的聚类，以之作为聚类的标准

这个问题在计算上是NP困难的，不过存在高效的启发式算法。一般情况下，都使用效率比较高的启发式算法，它们能够快速收敛于一个局部最优解。这些算法通常类似于通过迭代优化方法处理高斯混合分布的最大期望算法（EM算法）

$d$ 次元データ $\mathcal{D} = \lbrace \mathbf{x}_1, \cdots, \mathbf{x}_N \rbrace$ をあらかじめ定めた $K$ 個のクラスタに割り当てる手法.

各クラスの代表ベクトルの集合を $\mathcal{M} = \lbrace \mu_1, \cdots, \mu_K \rbrace$ とし, 代表ベクトルが支配する領域を $M(\mu_k)$ とする. $i$ 番目のデータがクラス $k$ に帰属するかどうかを表す変数を $q_{ik}$ とする.

$$\begin{aligned} q_{ik} = \begin{cases} 1, \quad \mathbf{x}_i \in M(u_k) \\ 0, \quad \mathbf{x}_i \notin M(u_k) \end{cases} \end{aligned}$$

$K$ 平均法の評価関数を次のように定義する. 各クラスの代表ベクトルはそのクラスの平均ベクトルになる.

$$J(q_{ik}, \mu_k) = \sum_{i=1}^N \sum_{j=1}^K q_{ik} \parallel \mathbf{x}_i - \mu_k \parallel^2$$

アルゴリズムK-平均法

初期化: $N$ 個のデータをランダムに $K$ 個のクラスタに分け, そのクラスタの平均ベクトルを求める.

1. $q_{ik}$ に関する最適化: $\mu_k$ を固定したもとで, $q_{ik}$ を次のように求める.

$$\begin{aligned} q_{ik} = \begin{cases} 1, \quad k = \argmin_j \parallel \mathbf{x}_i - \mu_j \parallel^2 \\ 0, \quad k \neq \argmin_j \parallel \mathbf{x}_i - \mu_j \parallel^2 \end{cases} \end{aligned}$$

2. $\mu_k$ の最適化: $q_{ik}$ を固定し, セントロイド $\mu_k$ を求める
3. 繰り返し: クラスタが変化しなくなるまで (1), (2) を繰り返す

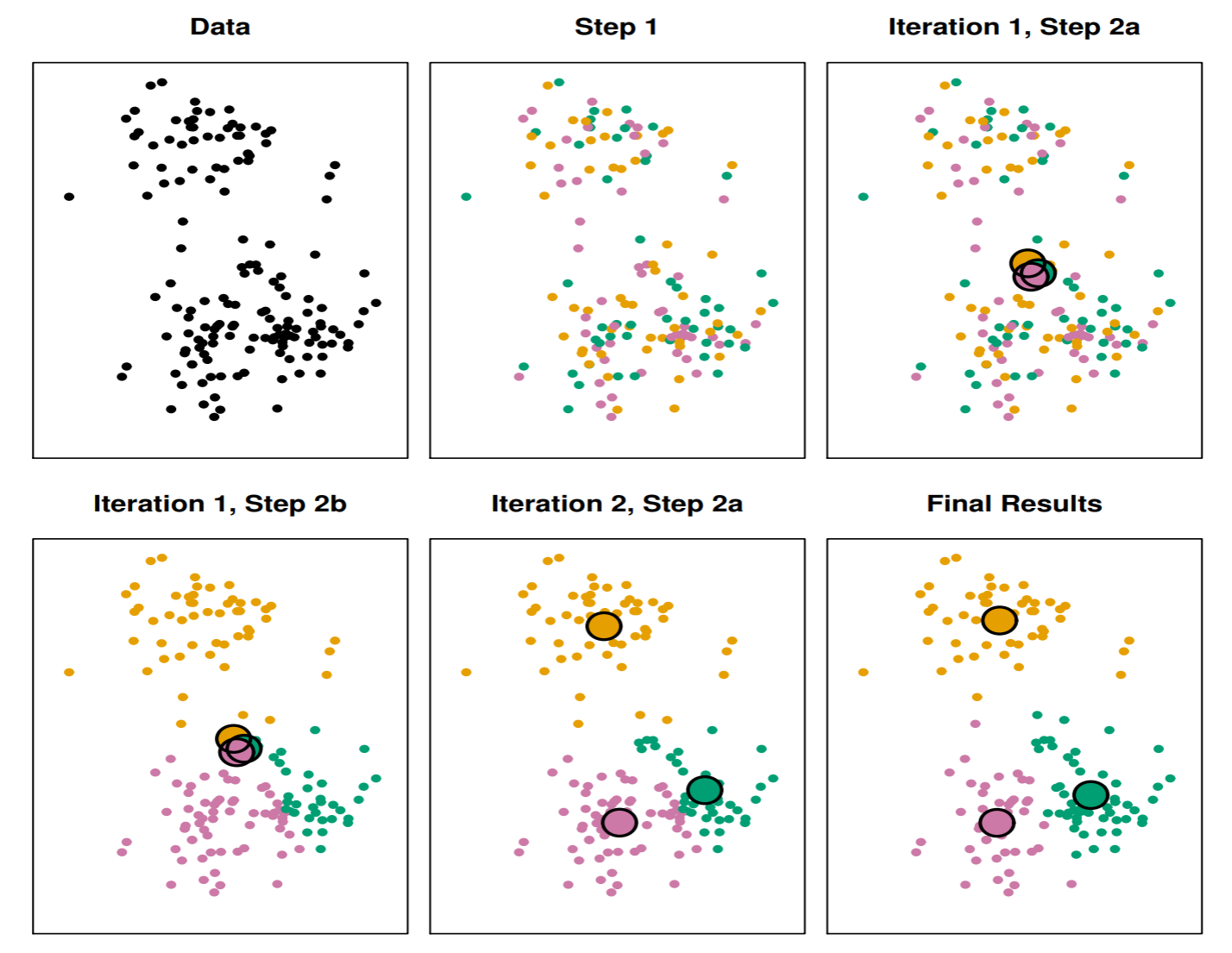
$K$ 平均法のアルゴリズムは初期値に依存するので, 最適解を得るためには何回か初期値を変えて実行する必要がある.

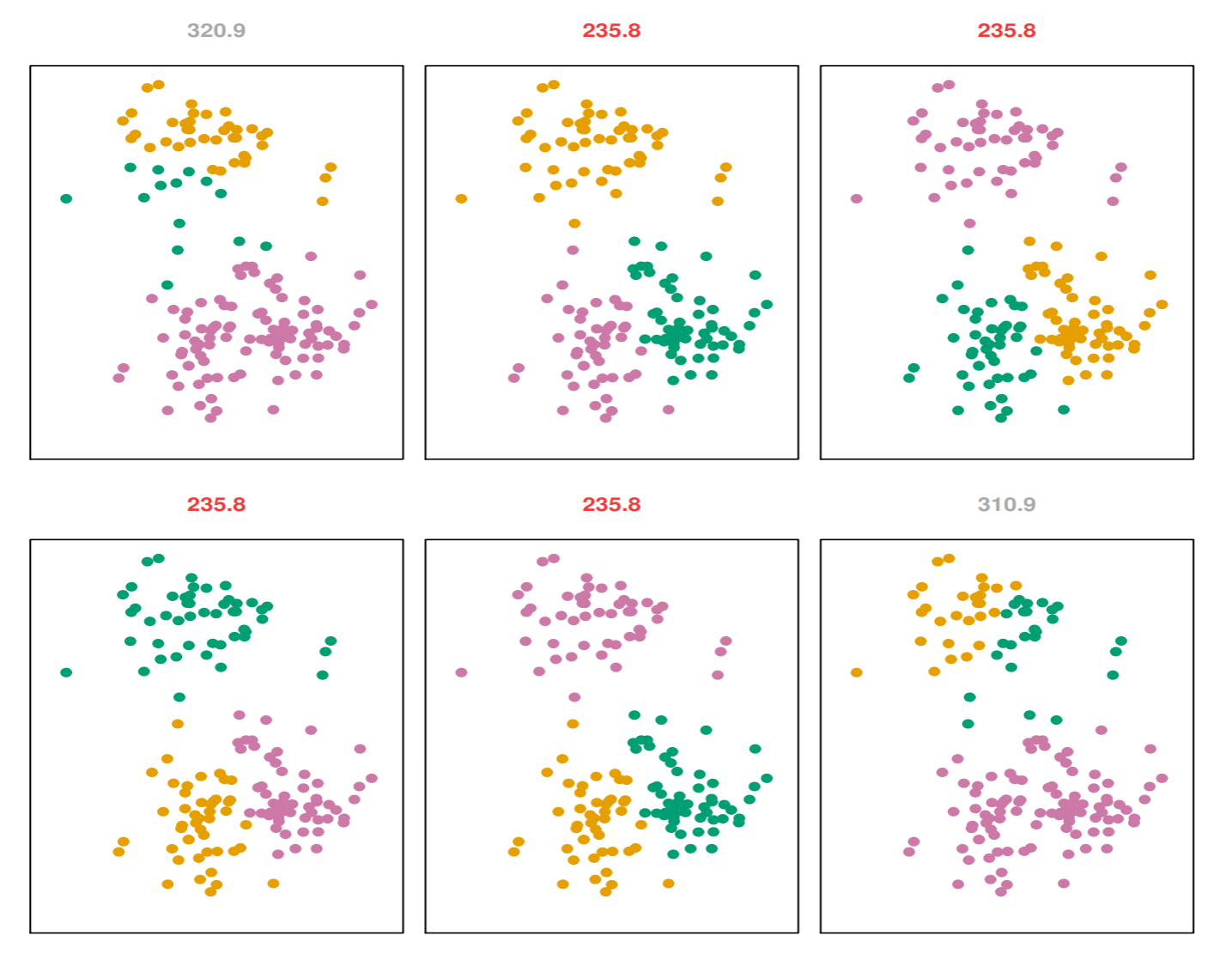
この図は初期値を変えながら6回K平均法を実行した時の結果である. 図の上にある数字は評価関数値で, 小さい値の方が良くクラス分けができていることを示している. 6回中3回は同じ結果で評価関数値が235.8となり, この結果を採用する.

階層型クラスタリング(融合法)

$K$ 平均法では, 事前に決定したクラスタ数 $K$ に応じた分割を行った. 階層的クラスタリングでは, クラスタ数は決定する必要はない.

階層的クラスタリングのボトムアップ法, 融合法を説明する. 葉を結合して幹にする. この図を樹状図, デンドログラムという.

アルゴリズム融合法

1. $n = N$ とする
2. $n \times n$ の距離行列を作る
3. 最も距離が近い二つのデータやクラスタをまとめて, 一つのクラスタにする
4. $n = n - 1$ にする
5. $n > 1$ であれば, (2) へ, $n = 1$ であれば終了する

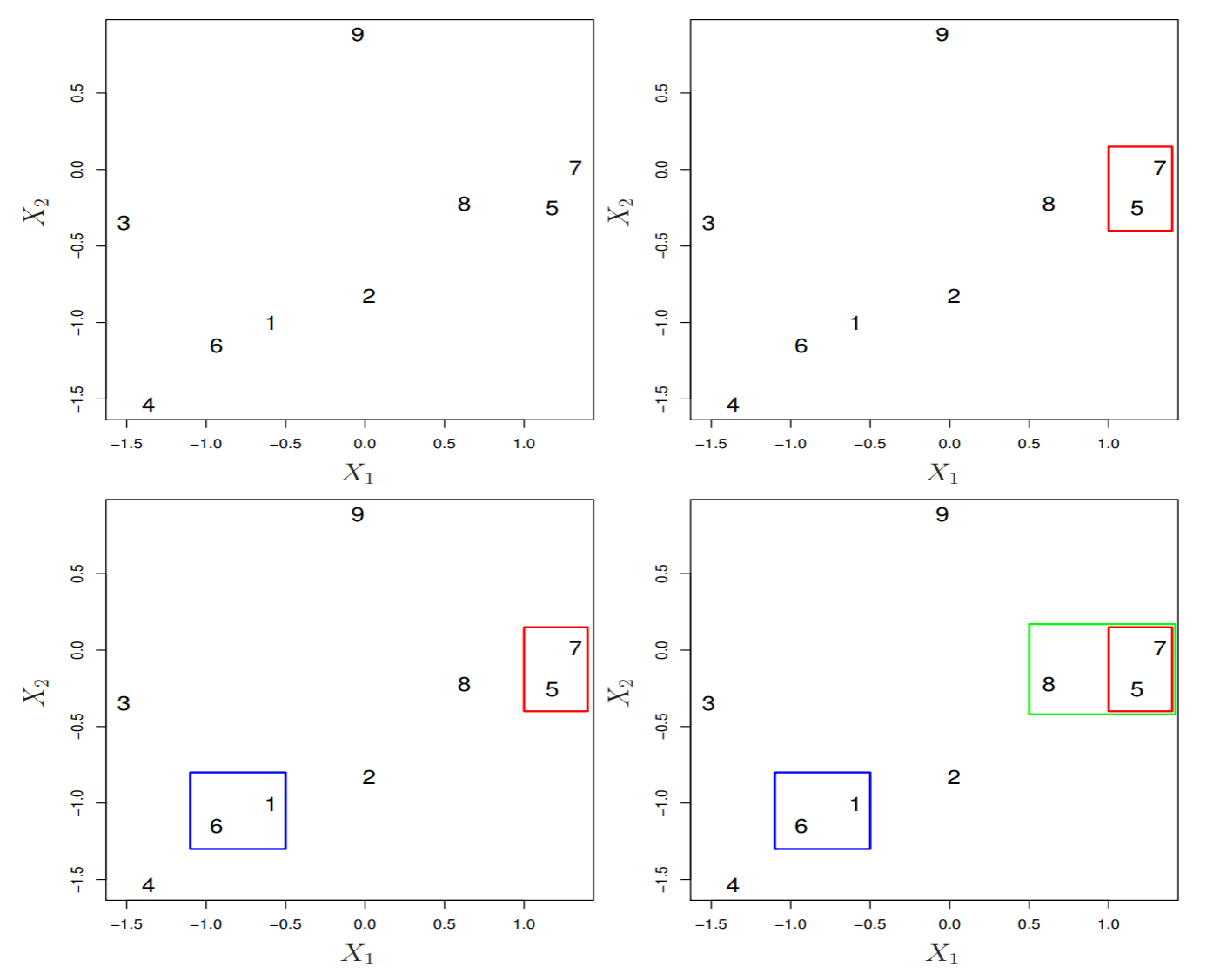
この5と7が結合された距離を記録し, デンドログラムの縦軸に高さで示す.

データの連結方法

完全連結法（最長距離法）: クラスター内の非類似性が最大になるような方法. クラスタ $A$ と $B$ の観測値の非類似性を全てのペアで計算し非類似性が最大になるものを記録していく.

単連結法（最短距離法）: クラスタ内の非類似性が最小になるような方法. クラスタ $A$ と $B$ の観測値の非類似性を全てのペアで計算し非類似性が最小になるものを記録していく.

群平均法: クラスタ内の非類似性の平均で距離を計算する方法. クラスタ $A$ と $B$ の観測値の非類似性を全てのペアで計算し非類似性の平均を記録していく.

重心法: クラスタ内の非類似性の重心で距離を計算する方法. クラスタ $A$ と $B$ の観測値の非類似性を全てのペアで計算し非類似性の平均を記録していく.

ウォード法: クラスタ $A$ と $B$ を融合したときに, クラスタ内変動の増分が小さくなるようにクラスタを融合する方法.

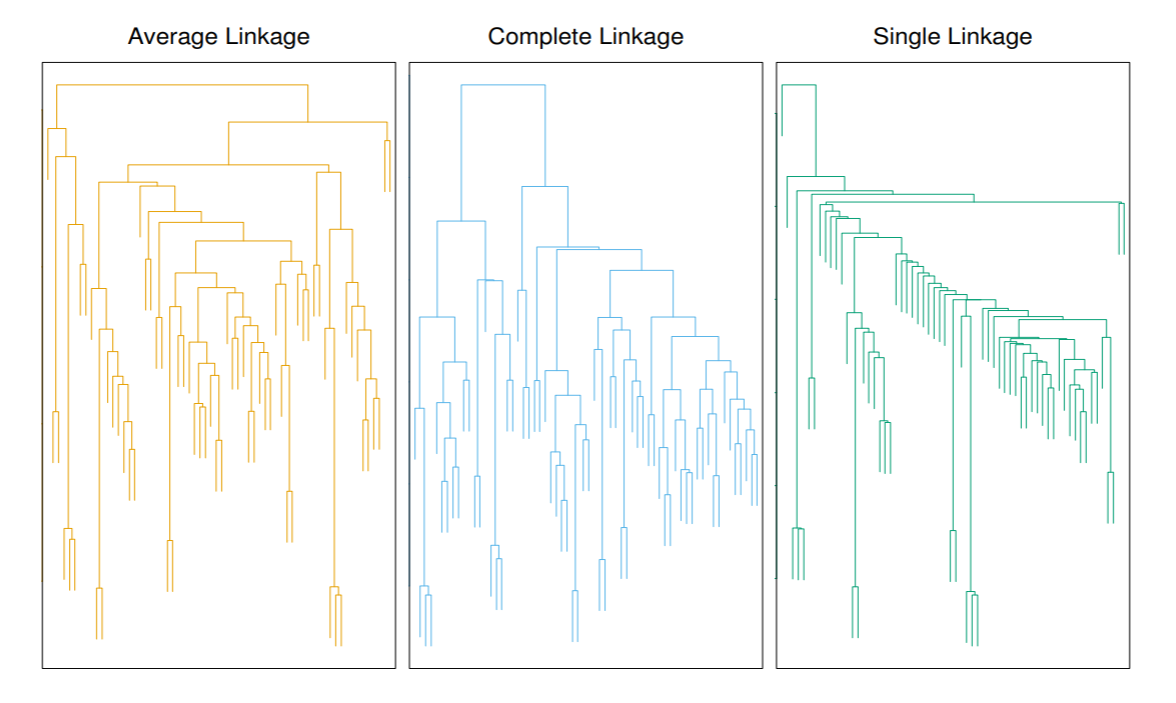
左から右にかけて, 群平均法, 完全連結法, 単連結法である.

単連結法では, 連結されたクラスタが新たなデータを取り込んでクラスタを形成するため, クラスタ形成の様子が鎖効果となって表れるため, 距離によってクラスを分割する時に, 特徴のあるデータのまとまりとしてクラスを形成することが困難になることがある.

階層的クラスタリングの分析例

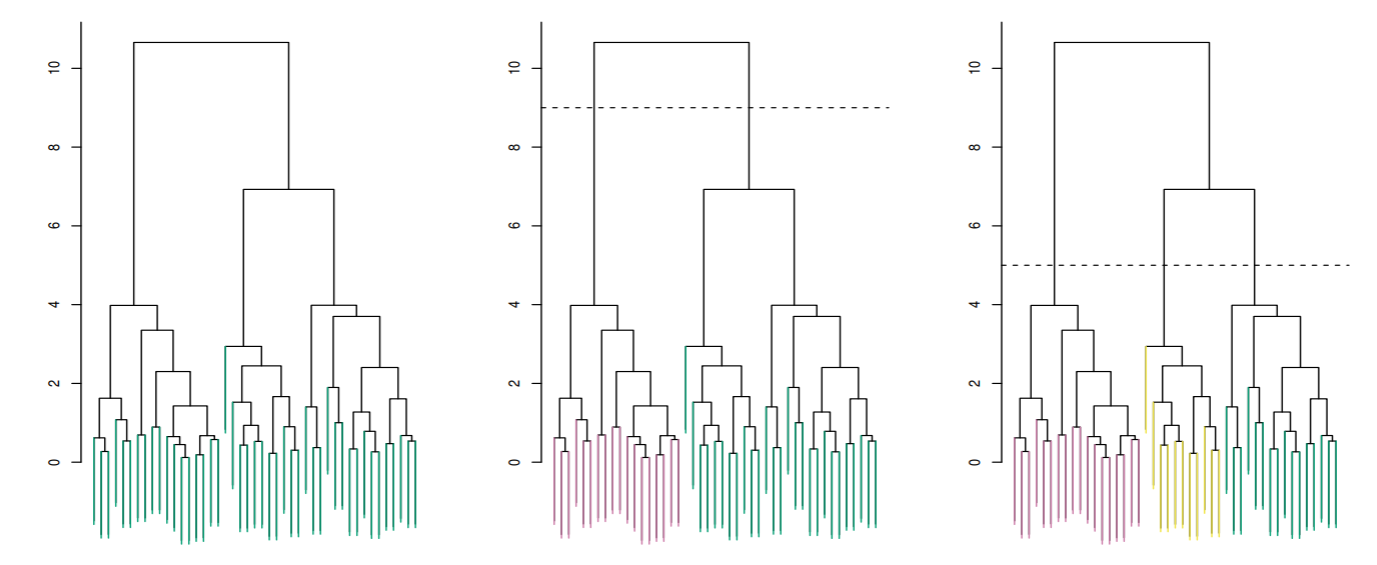
左: 階層的クラスタリングのデンドログラム: ユークリッド距離と完全連結法(complete linkage).

中: 左のデンドロクラムをクラスタ数が2になるように分類した結果. 点線は距離9を指している.

右: のデンドロクラムをクラスタ数が3になるように分類した結果. 点線は距離5を指している.

確率モデルによるクラスタリング

K-平均法や融合法によるクラスタリングでは, 一つのデータは一つのクラスタにのみ分類されるので, ハードクラスタリングとも呼ばれる. 階層的クラスタリングやK平均法では, データに基づいた簡便法なので確率モデルの推論ができない.

主にクラスタリングが, 探索的データ解析に用いられるなら問題ではない.

確率的クラスタリングやモデルに基づいたクラスタリングは, 確率的にデータをグルーピングする手法. データ構造を解釈しやすい.

混合分布モデル

有限な潜在クラスの異質性を扱うモデル. 有限混合分布モデルは, 潜在クラスモデル, 教師なし学習モデルと考えて良い. 有限混合分布モデルは, 分類問題, クラスタリング, 分類学に応用される.

クラスが異なるから効果(応答)も異なると考える.

• 異なるブドウ品種のワインの特性
• 健康な人か病気の人
• 株式市場, “bull”, "bear"マーケット

K-コンポーネントの確率分布 $f_1, f_2, \cdots, f_K$ の混合モデルを次のように定義する.

$$f(x) = \sum_{k=1}^K \lambda_k f_k(x)$$

ここで $\lambda_k$ を混合比率といい, $\lambda_k > 0, \sum_k \lambda_k = 1$ を満たす.

データの生成は次のように考える.

$$Z \sim \text{Mult}(\lambda_1, \cdots, \lambda_k) \quad X|Z \sim f_Z$$

確率分布 $f$ は任意の分布を考えても良いが, 正規分布がよく用いられる.

k-コンポーネントのパラメータベクトルを $\theta_k$ とすると

$$f(x) = \sum_{k=1}^K \lambda_k f_k(x;\theta_k)$$

となり, 混合分布モデルのすべてのパラメータベクトルは, $\theta = (\lambda_1, \cdots, \lambda_k, \theta_1^T, \cdots, \theta_K^T)^T$ となる.

識別可能性

各コンポーネントのパラメータベクトル $\theta$ の次元を $d$ とする $(\theta \in \mathbb{R}^d)$.

このとき混合分布モデルのパラメータの次元は, $\theta \in \mathbb{R}^D, D = dK + K$ であるが, 実際は, $\sum_{i=1}^K \lambda_i = 1$ の制約から, ラムダの自由度が１つ減るため, $D = dK + K - 1$ になる.

確率モデルがパラメータ $\theta$ に対して一意に定まることを識別可能という.

$$\theta_1 \neq \theta_2 \Leftrightarrow f(x;\theta_1) \neq f(x;\theta_2)$$

例えば, ラベルスイッチングがあり, $K = 2. \lambda_1 = 0.3, \lambda_2 = 0.7, \theta_1 = (\mu_1, \sigma_1)^T, \theta_2 = (\mu_2, \sigma_2)^T$ と $\lambda_1 = 0.7, \lambda_2 = 0.3, \theta_1 = (\mu_2, \sigma_2)^T, \theta_2 = (\mu_1, \sigma_1)^T$ 混合比率と確率モデルを入れ替えて表現した確率モデルが同じモデルになるため, 識別可能ではない。

黒線: $N(0, 1^2)$, 赤線: $N(5, 2^2)$

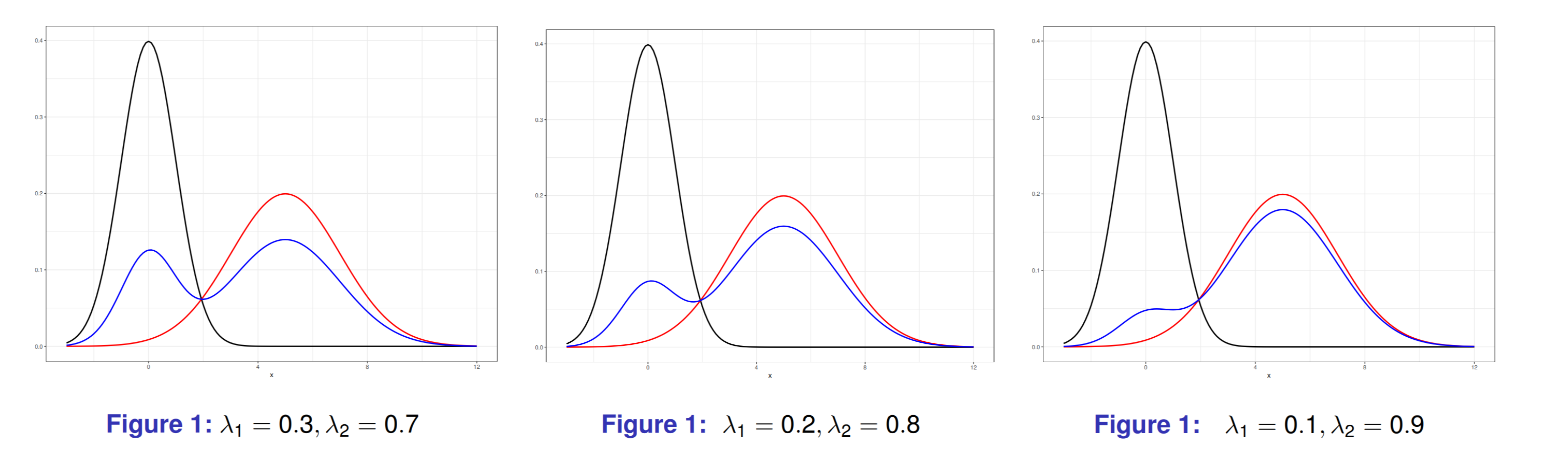
混合比率 $\lambda$ を変えることで, 様々な形状の2峰分布を得ることができる. 図はそれぞれ第1コンポーネントの割合を0.3, 0.2, 0.1とした場合.

第1コンポーネントの割合を0.1とした場合は, このような2峰性ではなく, 非対称性を表している.

色彩強度の混合モデルによる推定

ワインデータは3個のクラスで構成されたデータ. 色彩強度(color intensity)のみを特徴量とした.

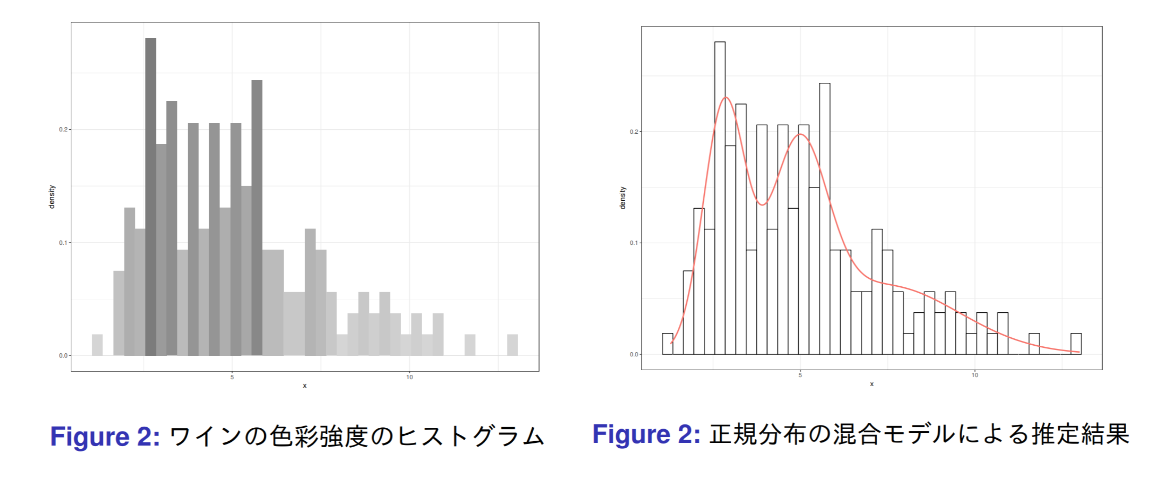
色彩強度の分布を三つの正規分布の混合モデルで表現できたことが分かった.

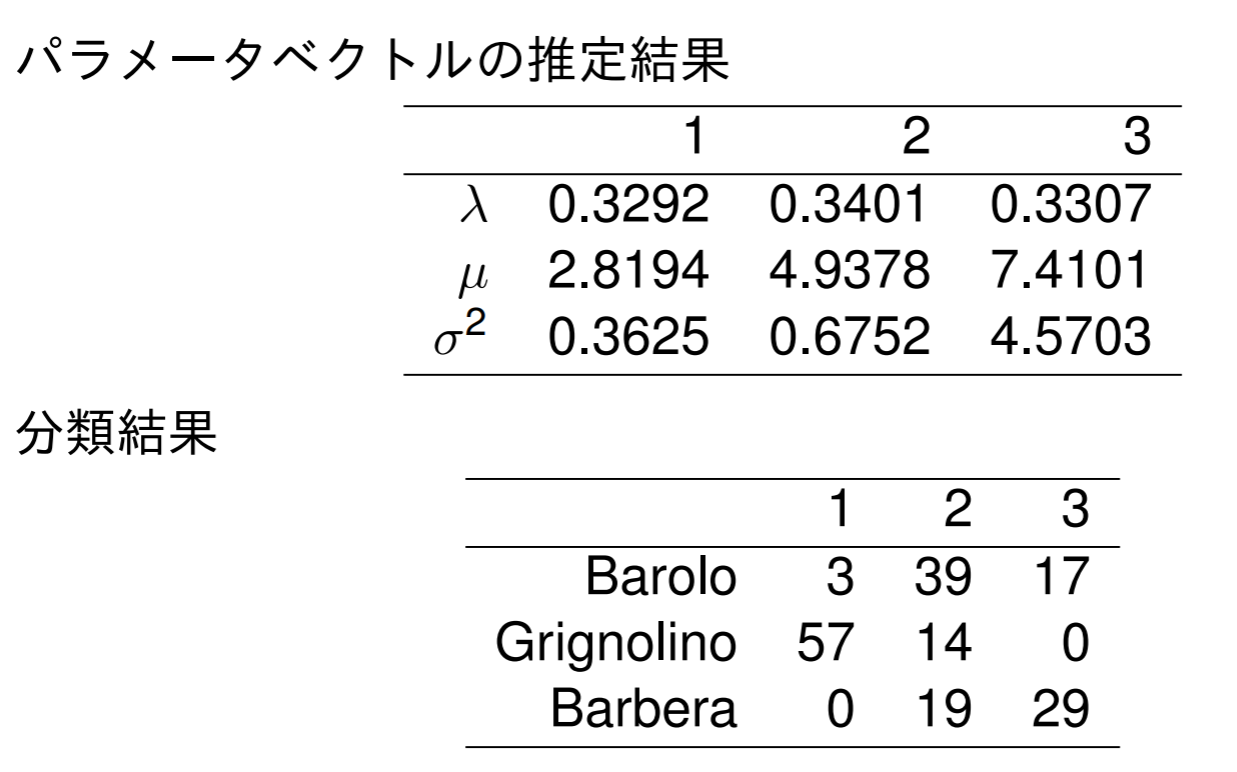
完全データの対数尤度

観測値のベクトルを $\mathbf{X} = (X_1, \cdots, X_n)$ とし, 潜在変数のベクトルを $\mathbf{Z} = (Z_1, \cdots, Z_n)$ とする.

$h(\mathbf{x}, \mathbf{z}|\theta)$ を $\mathbf{Z}$ と $\mathbf{Z}$ の同時密度とし, $k(\mathbf{z}|\theta, \mathbf{x})$ を観測値が与えられたときの潜在変数の条件付き密度とする. $g(\mathbf{x})$ を $\mathbf{X}$ の同時密度とすれば, 条件付き密度関数の定義から $k(\mathbf{z}|\theta, \mathbf{x})$ は次のように与えられる.

$$k(\mathbf{z}|\theta, \mathbf{x}) = \frac{h(\mathbf{x}, \mathbf{z}|\theta)}{g(\mathbf{x})}$$

観測値に基づく尤度関数を $L(\theta | \mathbf{x}) = g(\mathbf{x} | \theta)$ とし, 完全尤度を次のように定義する.

$$L^c(\theta|\mathbf{x}, \mathbf{z}) = h(\mathbf{x}, \mathbf{z}|\theta)$$

完全尤度の情報を使って, 尤度関数を最大化するパラメータ $\theta$ を求めたい

EMアルゴリズム(Expectation-Maximum)

$\theta_0 \in \Omega$ に対して,

$$\log L(\theta|\mathbf{x}) = E_{\theta_0}[\log L^c (\theta|\mathbf{x}, \mathbf{Z})|\theta_0, \mathbf{x}] - E_{\theta_0}[\log k (\mathbf{Z}|\theta, \mathbf{x})|\theta_0, \mathbf{x}]$$

最後の期待値は条件付き密度 $k(\mathbf{z}|\theta_0, \mathbf{x})d\mathbf{z}$ の下で計算している.

上式の第1項を

$$Q(\theta | \theta_0, \mathbf{x}) = E_{\theta_0}[\log L^c (\theta|\mathbf{x}, \mathbf{Z})|\theta_0, \mathbf{x}]$$

と定義すれば, これはEMアルゴリズムにおけるE-ステップに相当する.

問題は, 尤度 $L(\theta|\mathbf{x})$ の最大化だった. このことは, E-ステップを最大化することで到達可能. これをEMアルゴリズムにおけるM-ステップという.

初期値ベクトル $\theta^{(0)}$ から始めて, $Q(\theta | \theta^{(0)}, \mathbf{x})$ を最大にする $\theta$ を $\hat{\theta}^{(1)}$ とし, 収束するまで繰り返すアルゴリズムをEMアルゴリズムという.

EMアルゴリズム: $m$ 番目の推定値を $\hat{\theta}^{(m)}$ とする. $(m + 1)$ 番目の推定値は次のようにして計算する.

Eステップ: 次を計算する.

$$Q(\theta | \hat{\theta}^{(m)}, \mathbf{x}) = E_{\hat{\theta}^{(m)}}[\log L^c (\theta|\mathbf{x}, \mathbf{Z})|\hat{\theta}^{(m)}, \mathbf{x}]$$

Mステップ:

$$\hat{\theta}^{(m+1)} = \argmax Q(\theta | \hat{\theta}^{(m)}, \mathbf{x})$$

次の定理は, ステップを繰り返すことに尤度は必ず増加することを述べたもの.

EMアルゴリズムによって得られる推定値の系列 $\hat{\theta}^{(m)}$ は必ず $L(\hat{\theta}^{(m+1)} | \mathbf{x}) \geq L(\hat{\theta}^{(m)} | \mathbf{x})$ を満たす

2コンポーネントの正規混合モデルの推定

確率変数 $Y_1$ は $N(\mu_1, \sigma_1^2)$ に従い, $Y_2$ は $N(\mu_2, \sigma_2^2)$ に従うとする. $Z$ は $Y_1, Y_2$ と独立はベルヌーイ試行を表す確率変数とし, その成功確率を $\pi = P(Z = 1)$ とする. 観測値は, 2コンポーネントの混合正規分布モデルで $X = (1 - Z)Y_1 + ZY_2$ とする.

推定すべきパラメータベクトルは $\theta = (\mu_1, \mu_2, \sigma_1^2, \sigma_2^2, \pi)$ である.

標準正規分布の密度関数を $\phi(z)$ とすると, $X$ の密度関数は次のとおり

$$f(x) = (1 - \pi)f_1(x) + \pi f_2(x), \quad f_j = \frac{1}{\sigma_j} \phi (\frac{x - \mu_j}{\sigma_j})$$

標本データ $\mathbf{X} = (X_1, \cdots, X_n)$ を得たき対数尤度関数は次のとおり

$$\mathcal{l}(\theta | \mathbf{x}) = \sum_{i=1}^n \log [(1 - \pi)f_1(x_i) + \pi f_2(x_i)]$$

$i$ 番目の観測値に対応する潜在変数を次のように定義する.

$$\begin{aligned} Z_i = \begin{cases} 0, \quad X_i \text{が密度関数} f_1(x) \text{を持つ時} \\ 1, \quad X_i \text{が密度関数} f_2(x) \text{を持つ時} \end{cases} \end{aligned}$$

完全尤度は次のようになる.

$$L^c(\theta | \mathbf{x}, \mathbf{z}) = \prod_{Z_i=0} f_1(x_i) \prod_{Z_i=1} f_2(x_i)$$

これより, 対数完全尤度関数は次のとおり

$$\begin{aligned} l^c(\theta | \mathbf{x}, \mathbf{z}) &= \sum_{Z_i=0} \log f_1(x_i) + \sum_{Z_i=1} \log f_2(x_i) \\ &= \sum_{i=1}^n [(1 - z_i) \log f_1(x_1) + z_i \log f_2(x_i)] \end{aligned}$$

Eステップでは, $\theta^{(0)}$ の下で, $\mathbf{x}$ を与えたときに, $Z_i$ の条件付き期待値を計算しないといけない.

$$E_{\theta_0} [Z_i | \theta^{(0)}, \mathbf{x}] = P(Z_i = 1 | \theta^{(0)}, \mathbf{x})$$

この期待値の推定量には次のものを用いる.

$$\gamma_i = \frac{\hat{\pi} f_2(x_i|\theta^{(0)})}{(1 - \hat{\pi}) f_1(x_i | \theta^{(0)}) + \hat{\pi} f_2 (x_i | \theta^{(0)})}$$

$z_i$ の代わりに $\gamma_i$ を使えば, Mステップの目的関数は次のようになる.

$$Q(\theta | \theta^{(0)}, \mathbf{x}) = \sum_{i=1}^n [(1 - \gamma_i) \log f_1(x_i) + \gamma_i \log f_2 (x_i)]$$

この最大化は, $\mu_1$ に関して偏微分係数を計算し, それが0となる $\mu_1$ について解けば陽に解が得られる.

$$\frac{\partial Q}{\partial \mu_1} = \sum_{i=1}^n (1 - \gamma_i)(-\frac{1}{2\sigma_1^2})(-2)(x_i - \mu_1)$$

これより, Mステップで得られる解は,

$$\hat{\mu_1} = \frac{\sum_{i=1}^n (1 - \gamma_i)x_i}{\sum_{i=1}^n (1 - \gamma_i)}, \qquad \hat{\mu_2} = \frac{\sum_{i=1}^n \gamma_i x_i}{\sum_{i=1}^n \gamma_i}$$

$$\hat{\sigma_1^2} = \frac{\sum_{i=1}^n (1 - \gamma_i) (x_i - \hat{\mu_1})^2}{\sum_{i=1}^n (1 - \gamma_i)}, \qquad \hat{\sigma_2^2} = \frac{\sum_{i=1}^n \gamma_i (x_i - \hat{\mu_2})^2}{\sum_{i=1}^n \gamma_i}$$

$\gamma_i$ は $P(Z_i = 1 | \theta^{(0)}, \mathbf{x})$ の推定値なので, その平均 $\hat{\pi} = n^{-1} \sum_{i=1}^n \gamma_i$ は $\pi = P(Z_i = 1)$ の推定値である.

識別器の組み合わせによる性能評価

最近, 複数の識別器を組み合わせる方法が提案されていて, 本章では, 決定木を組み合わせた方法を紹介する.

組み合わせ方法には, 学習データのブートストラップを用いて複数の識別器を構成し, それらの多数決で識別するバギングという手法がある. もう一つは, 誤った学習データを次の識別器で重点的に学習させ, これを逐次行うアダブーストという手法を紹介する.

ランダムフォレストは決定木のノードをランダムに選択する手法でバギングを改良する.

ノーフリーランチ定理

ノーフリーランチ定理: すべての識別問題に対して, ほかの識別機より識別性能が良い識別器は存在しない

決定木

階層(stratifying)や区分(segment)を使って特徴ベクトルの空間を簡単な領域に分割する. 領域に分割する法則が木構造になるので, 決定木(desicion-tree)による方法という.

木を構成する要素はノードとノードを結ぶリンク. 木の一番上にあるノードを, 木の始まりという意味で根ノードという. 終端ノードあるいは葉ノードは, 分岐の最終ノードのこと.

学習方法は, ボトムアップ的な手法とトップダウン的な手法がある.

決定木と線形モデル

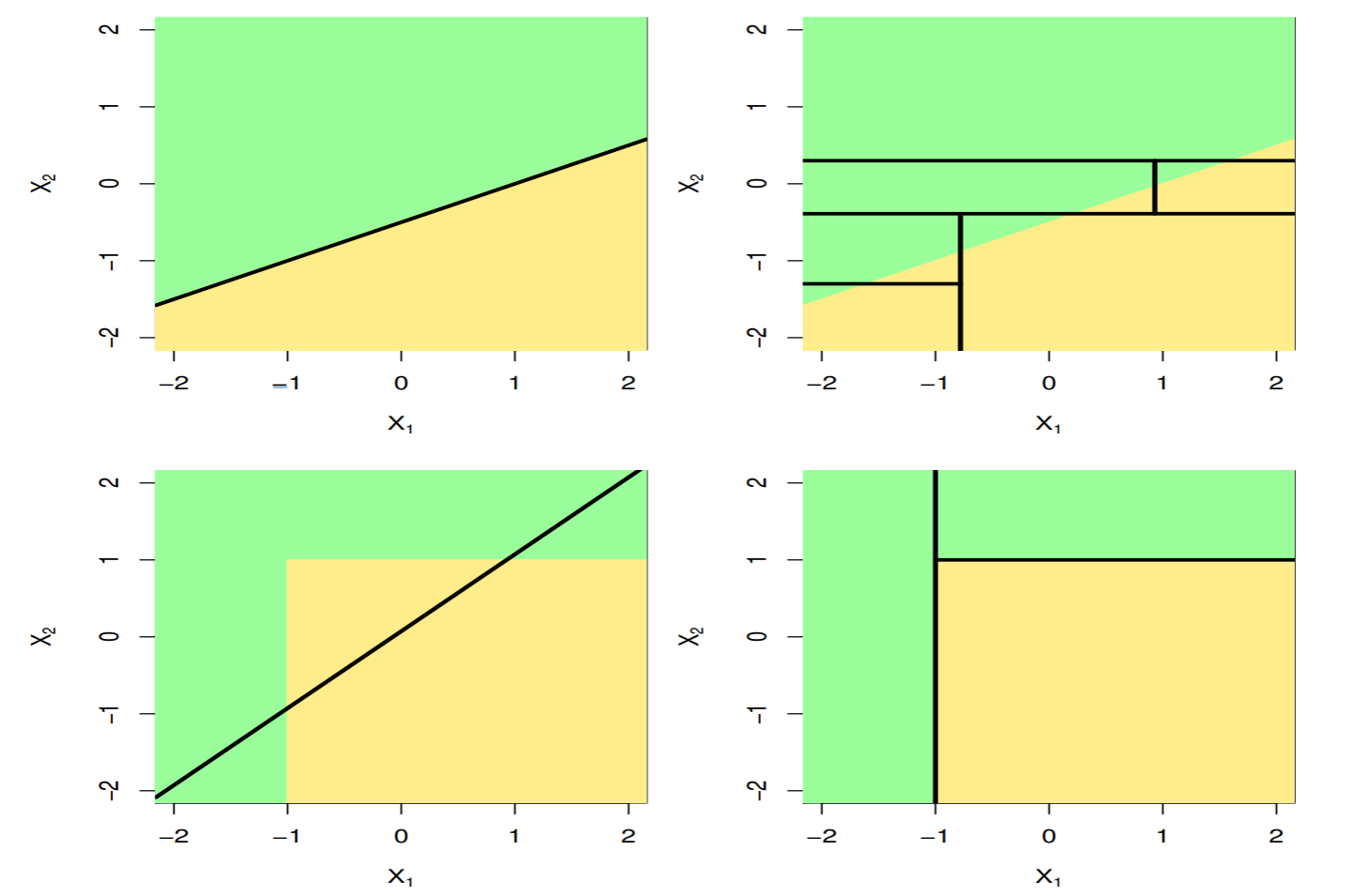
心臓病データ

胸痛(chest pain)を訴える303患者のHDの2値データ. Yesは血管造影(angiographic)テストによる心臓疾患の持ち主で, Noは心臓疾患ではない患者. 心臓や肺機能に関するデータや, Age, Sex, Chol 等の13個の予測子がある. 交差確認法より6個の最終節を持つ木が選択された.

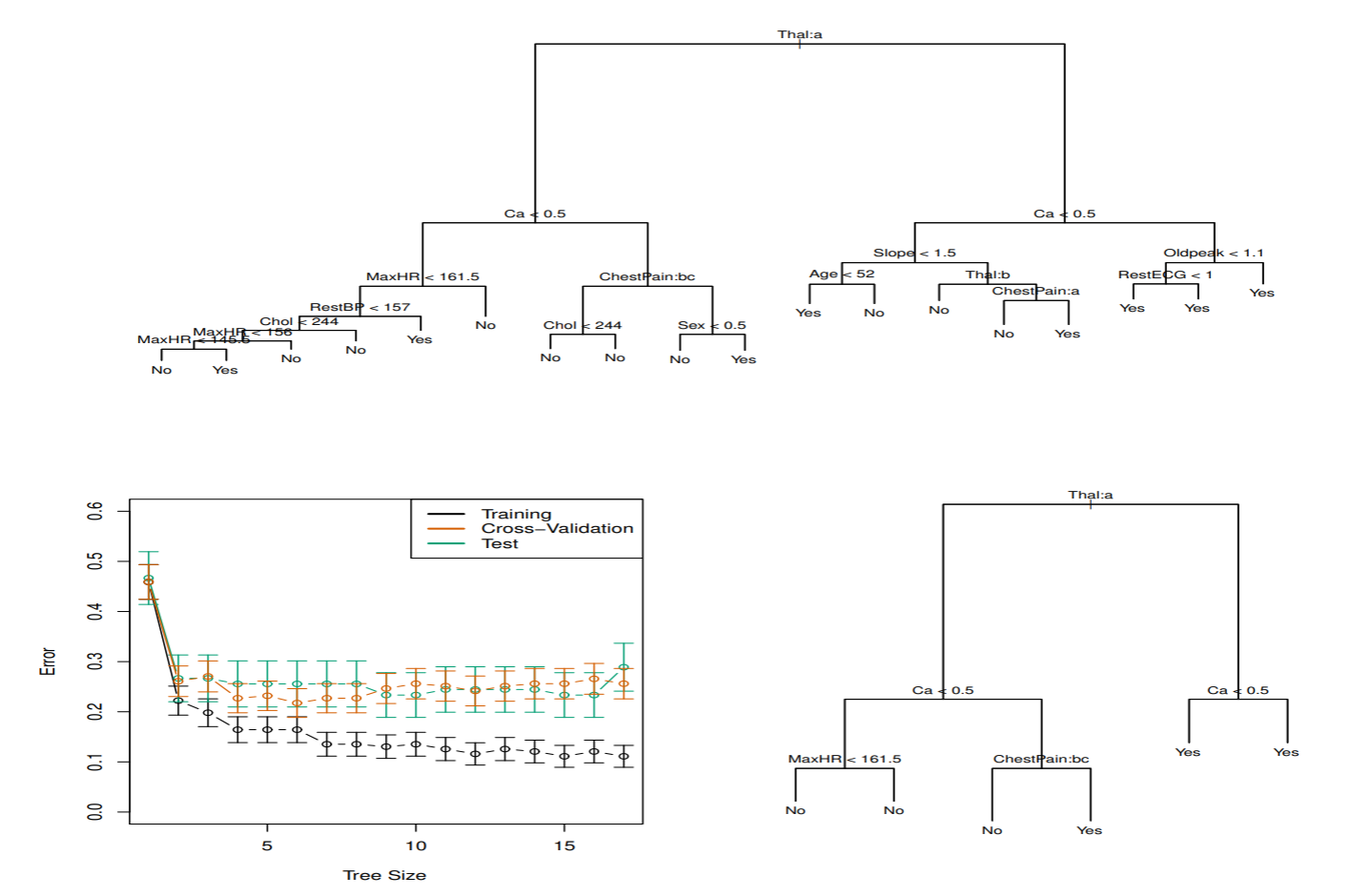
トップダウン的な手法

トップダウン的な手法は, まず根ノードですべての学習データをできるだけ誤りの少ないようにクラス分けできる特徴軸を探して特徴空間を 2分割する規則を求める. さらに分割された空間を2分割する規則を求めることを繰り返す手法. 分割統治法と呼ばれる.

トップダウン的な手法で決定木を学習データから構成するためには, 次の要素について考える必要がある.

1. トップダウン法に必要な要素
2. 各ノードにおいて特徴空間分割規則構成するための特徴軸としきい値の選択
3. 終端ノードの決定. 大きくなった木の剪定をどこまで行うか？
4. 終端ノードに対する多数決によるクラスの割当

決定木の学習方法には, CART, ID3, C4.5と呼ばれるものがある. ここではCARTを中心に説明する.

決定木に関する諸定義

木は, 0でない有限個の正の整数からなる有限の集合 $T$ と, $t \in T$ から $T \cup \lbrace 0 \rbrace$ への2つの関数left() と right() で構成される. lerft() と right() は左側, 右側の次ノード番号を与える関数.

木が満たす性質:

1. 各 $t \in T$ について, left(t) = right(t) = 0 (最終ノード) か, left(t) > t かつ right(t) > t(非最終ノード) のいずれかが成り立つ.
2. 各 $t \in T$ について, T 内の最小数 (根ノード) を除いて, t = left(s) または t = right(s) のどちらかを満たすただ一つの $s \in T$ が存在する. s を親ノード, t を子ノードといい, s = parent(t) で表す.

ノード分割規則

各ノードにおける $d$ 次元特徴空間の最適な分割は, 特徴軸ごとに可能な考えうる分割を不純度とよばれる評価関数で評価して選択する.

ノード $t$ の不純度を

$$\mathcal{I} = \phi(P(C_1 \ |\ t), \cdots, P(C_k \ |\ t))$$

で定義する. ここで関数 $\phi(z_1, \cdots, z_K)$ は, $z_i \geq 0, \sum_{i=1}^K z_i = 1$ で, 次の3つを満たす.

1. $\phi()$ はすべての $i = 1, \cdots, K$ に対して, $z_i = 1/K$ のときに最大になる.
2. $\phi()$ は, ある $i$ について $z_i = 1$ となり, $j \neq i$ のときはすべて $z_j = 0$, ただ一つのクラスに定まるとき最小になる.
3. $\phi()$ は $z_1, \cdots, z_K$ に関して対称な関数である.

ノード $t$ で分割を作るとき, 不純度の減り方が一番大きな分割を選べば良い

木の剪定

不純度が最小, あるいは十分小さくなるまで木を成長させ, 次に誤り率と木の複雑さできまる許容範囲まで木を剪定する.

終端ノード $t \in \tilde{T}$ における誤り数 $M(t)$ は終端ノードに属する学習データのうち事後確率を最大にしない学習データ数なので, このノードの誤り率は $R(t) = \frac{M(t)}{N}$ である. $N$ は総学習データ数.

木全体での誤り率は次のようになる

$$R(T) = \sum_{t \in \tilde{T}} R(t)$$

木の複雑さを終端ノードの数で評価する: 木 $T$ のノード数を $|T|$ とすると, 終端ノード数は $|\tilde{T}|$ となる.

複雑さのコストを $\alpha$ とすれば, 一つの終端ノードにおける誤り率と複雑さのコストの和で木全体のコストを評価できる.

$$R_{\alpha}(T) = \sum_{t \in \tilde{T}} R_{\alpha}(t) = R(T) + \alpha |\tilde{T}|$$

木のコスト $R_{\alpha}(T)$ を最小にすれば良い.

バギング(bagging)

Bagging：用的是随机有放回的选择训练数据然后构造分类器，最后组合

バギングは, 学習データのブートストラップサンプルを用いて複数の学習器を学習させ, それらの識別器の多数決で入力データのクラスを予測する.

個々の識別器の性能はランダム識別器よりも少し良ければいいので, 弱識別器と呼ばれる.

複数の決定木から多数決をとることで, 決定木よりも安定した精度の良い識別器が構成できる.

決定木は, 学習データの少しの変化で識別器の性能が大きく変化してしまう不安定な識別器だった.

識別器のバラツキはブートストラップサンプルのバラツキが反映されるので, 決定木間の相関が高くなり, 性能が似る.

アダブースト(AdaBoost)

AdaBoost是英文"Adaptive Boosting"（自适应增强）的缩写，它的自适应在于：前一个基本分类器被错误分类的样本的权值会增大，而正确分类的样本的权值会减小，并再次用来训练下一个基本分类器。同时，在每一轮迭代中，加入一个新的弱分类器，直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数才确定最终的强分类器。

ブースティングは, 複数の弱識別器を用意して, 学習を直列的にし,前の弱識別器の学習結果を参考にしながら, 一つずつ弱識別器を学習する方法.

各弱識別器は, 学習データに対する誤り率が $\epsilon \leq \frac{1}{2} - \gamma(\gamma > 0)$ を満たすように学習が行われる. 代表的なブースティングアルゴリズムにアダブーストがある.

アダブーストでは, 弱識別器の学習結果に従って学習データに重みが付く. 誤った学習データに対して重みを大きくし, 正しく識別された学習データに対する重みを小さくすることで, 集中的に誤りの多い学習データを学習する.

• $E_m$ は誤った学習データの正規化された重みの和なので, 誤差が小さいほど大きな値になる
• (3)の $Y_M (\mathbf{x})$ の計算では, 誤りの小さな $y_m(\mathbf{x})$ に大きな重みを与えている
• 重みの更新では, 正しく識別された学習データの重みは更新されないが, 誤った学習データの重みが $\exp \alpha_m > 1$ 倍になる.
• 評価関数 $E_m$ を変えることで, 勾配ブースティングなどに発展していく.

AdaBoost的优点:

1. Adaboost提供一种框架，在框架内可以使用各种方法构建子分类器。可以使用简单的弱分类器，不用对特征进行筛选，也不存在过拟合的现象
2. Adaboost算法不需要弱分类器的先验知识，最后得到的强分类器的分类精度依赖于所有弱分类器。无论是应用于人造数据还是真实数据，Adaboost都能显著的提高学习精度
3. Adaboost算法不需要预先知道弱分类器的错误率上限，且最后得到的强分类器的分类精度依赖于所有弱分类器的分类精度，可以深挖分类器的能力。Adaboost可以根据弱分类器的反馈，自适应地调整假定的错误率，执行的效率高
4. Adaboost对同一个训练样本集训练不同的弱分类器，按照一定的方法把这些弱分类器集合起来，构造一个分类能力很强的强分类器，即“三个臭皮匠赛过一个诸葛亮”

AdaBoost的缺点:

1. 在Adaboost训练过程中，Adaboost会使得难于分类样本的权值呈指数增长，训练将会过于偏向这类困难的样本，导致Adaboost算法易受噪声干扰。此外，Adaboost依赖于弱分类器，而弱分类器的训练时间往往很长

ランダムフォレスト(random forests)

随机森林在bagging基础上做了修改。基本思路是：

1. 从样本集中用Bootstrap采样（有放回的采样）选出n个样本（重采样）
2. 从所有属性中随机选择k个属性，选择最佳分割属性作为节点建立CART决策树
3. 重复以上两步m次，即建立了m棵CART决策树
4. 这m个CART形成随机森林，通过投票表决结果，决定数据属于哪一类

随机性在于n个样本的随机，及其k个特征属性的选择，这两个随机

バギングの問題点として, ブートストラップサンプルによる生成のため決定木間の相関が高くなる.

$M$ 個の確率変数の任意の2つの確率変数間に正の相関 $\rho$ がある場合, 標本平均の分散は

$$\text{Var}(\overline{X}) = \frac{1 - \rho}{M}\sigma_2 + \rho \sigma_2$$

となる. ブートストラップサンプル数の $M$ を増やせば, 第1項は減少するが第2項は減少しない.

ランダムフォレストは $\rho$ を減らす仕組みを入れてバギングを強化した手法.

ランダムフォレストの学習アルゴリズムは, 決定木の各非最終ノードにおいて, 識別に用いる特徴をあらかじめ決められた数だけランダムに選択すること.

ランダムフォレストを用いると, 森のサイズによる誤り率の変化や, 特徴の重要さに関する情報, 学習データ間の近さに関する情報を得ることができる.

ランダムフォレストによるデータ解析

Out-of-Bag(OOB)誤り率とは, 学習に使われなかった決定木を集めて部分木を構成して, その学習データをテストデータにして誤り率を評価したものである.

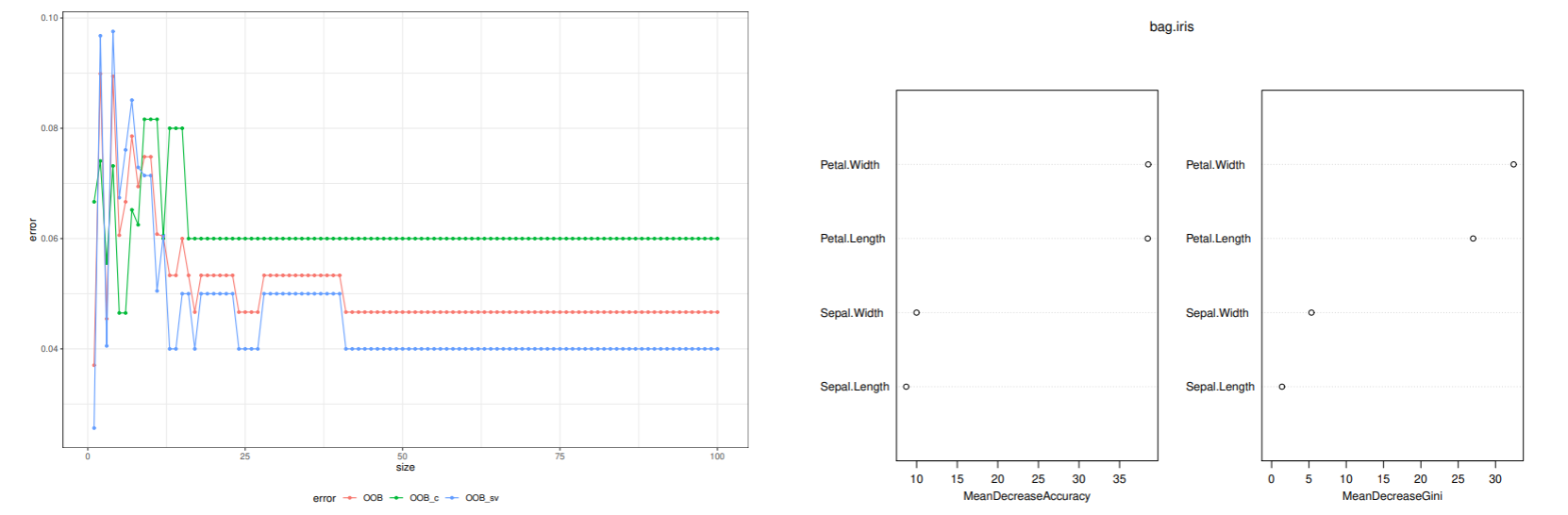
特徴量 $x$ が識別にどのように寄与しているかを調べるのに部分依存グラフを使う.

$i$ 番目の学習データの分析対象の変数を $x$ と置き換えて, 以下を計算する.

$$f_k(x) = \sum_{i=1}^N (\ln p_k(\mathbf{x}_i^{(x)}) - \frac{1}{K} \sum_{j=1}^N \ln p_j(\mathbf{x}_i^{(x)}))$$

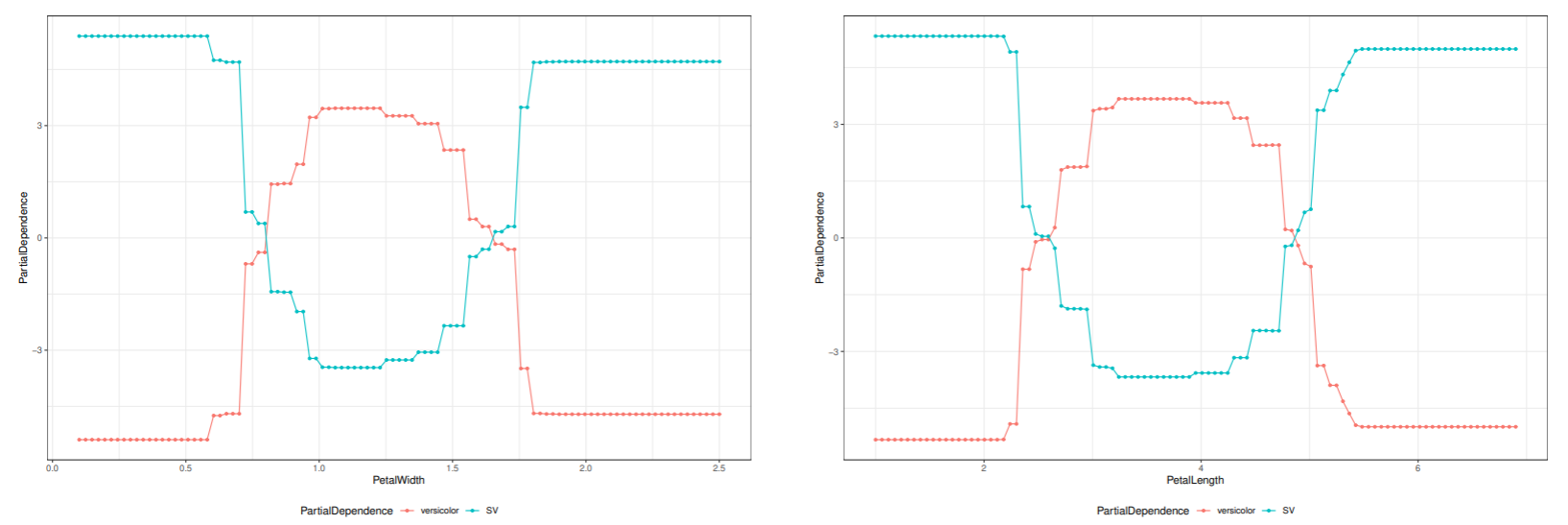
$i$ 番目と $j$ 番目の学習データが, OOB で同じ終端ノードに分類される木であれば, $N ×\times N$ の近接行列の $(i, j), (j, i)$ 要素に1を加える.

この近接行列を多次元尺度構成法により2次元に射影する. アヤメデータについて学習データ間の近さを表す近接グラフをプロットした

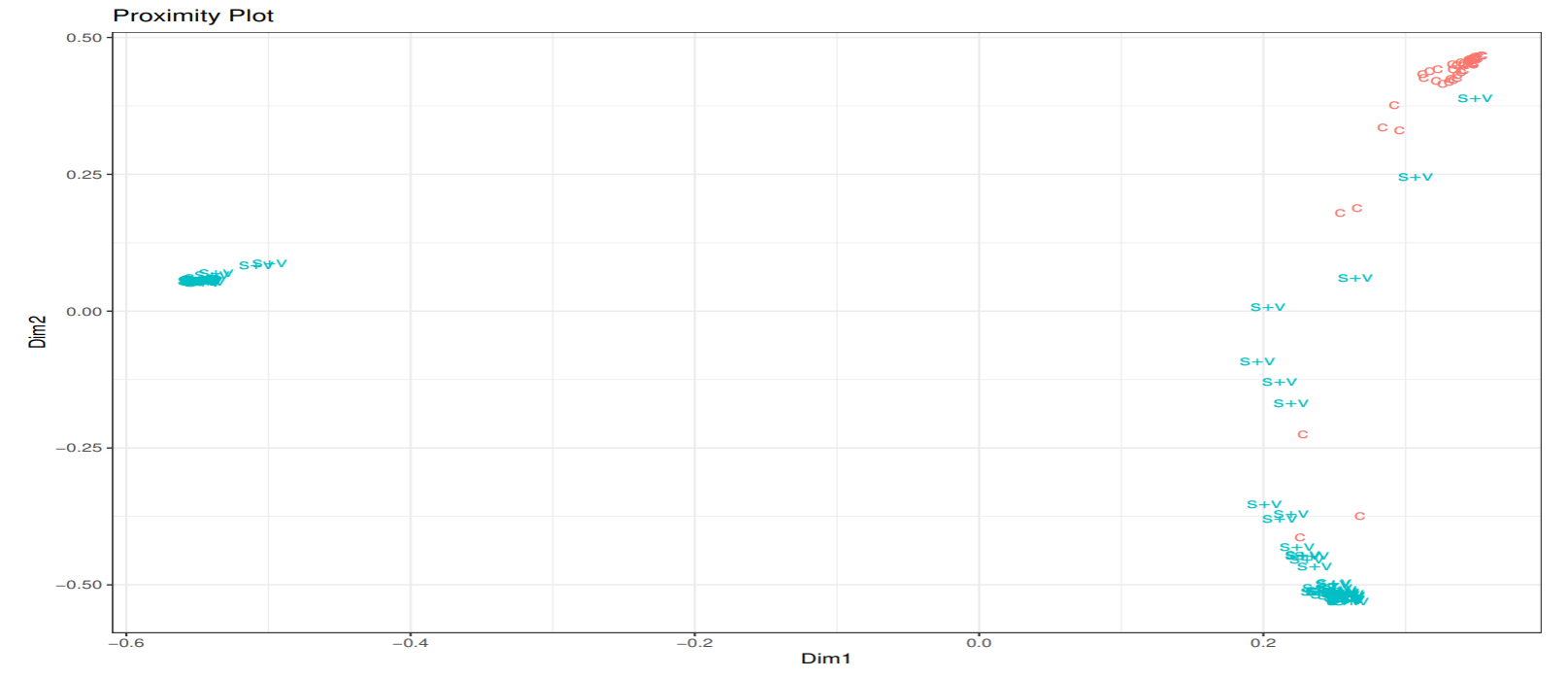
あやめデータによる性能評価

setosa と virginica を1つのクラスに, versicolor をもう1つのクラスにした2クラスの識別問題を考える. 特徴量は, 4変数すべて使い, 10分割交差検証法による汎化誤差を推定した.

	決定木	バギング	アダブースト	ランダムフォレスト
誤り率	0.16	0.053	0.04	0.04

どの手法でも木は最大に成長させ, 剪定はしていない. アダブーストとランダムフォレストが最も良い結果となっている.

总结-机器学习与数据挖掘

问题

• 分类
• 聚类
• 回归
• 异常检测
• 自动机器学习
• 关联规则
• 强化学习
• 结构预测
• 特征学习
• 线上机器学习
• 无监督学习
• 半监督学习
• 排序学习
• 语法归纳

监督式学习(分类・回归)

• 决策树
• 集成（装袋，提升，随机森林）
• k-NN
• 线性回归
• 朴素贝叶斯
• 神经网络
• 逻辑回归
• 感知器
• 支持向量机（SVM）
• 相关向量机（RVM）

聚类

• BIRCH
• 层次
• k-平均
• 期望最大化（EM）
• DBSCAN
• OPTICS
• 均值飘移

降维

• 因子分析
• CCA
• ICA
• LDA
• NMF
• PCA
• LASSO
• t-SNE

结构预测

• 概率图模型（贝叶斯网络，CRF, HMM）

异常检测

• k-NN
• 局部离群因子

神经网络

• 自编码
• 深度学习
• 多层感知机
• RNN
• 受限玻尔兹曼机
• SOM
• CNN

强化学习

• Q学习
• SARSA
• 时序差分学习
• 深度强化学习

理论

• 偏差/方差困境
• 计算学习理论
• 经验风险最小化
• PAC学习
• 统计学习
• VC理论

参考文献

• はじめてのパターン認識 - 平井有三
• [机器学习] 非监督学习初探—聚类
• EM算法详解
• 神经网络15分钟入门！足够通俗易懂了吧
• 集成学习中Adaboost, 提升树，bagging和随机森林有什么区别？