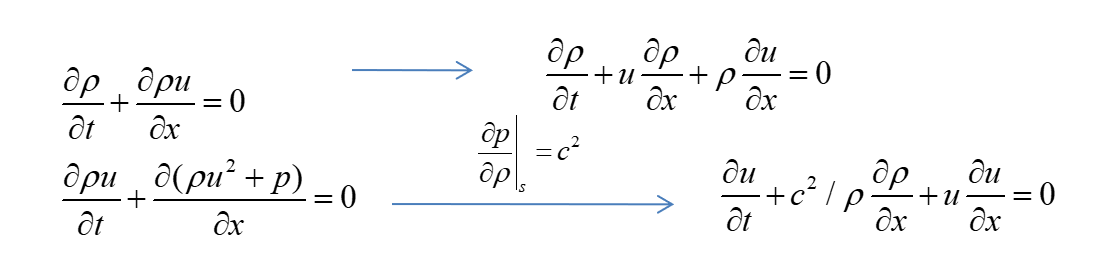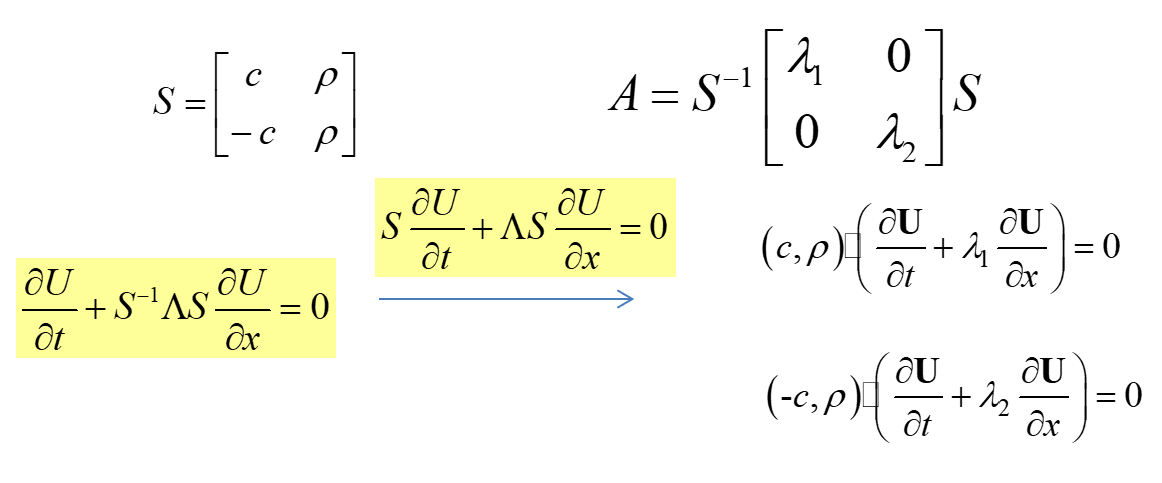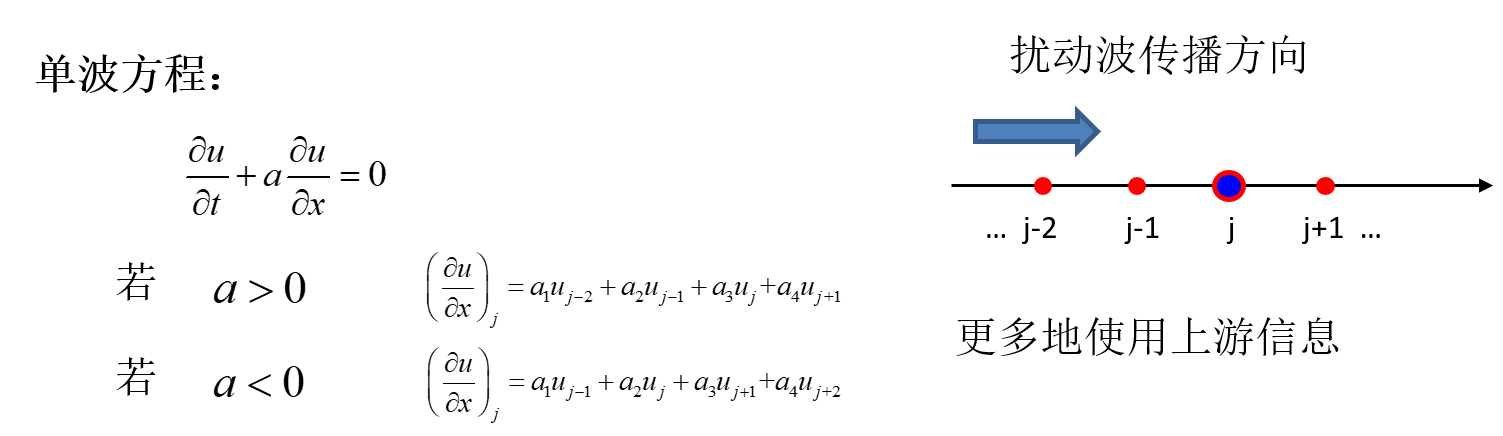计算流体力学:Computational Fluid Dynamics 简称CFD,是通过数值方法求解流体力学控制方程,得到流场的离散的定量描述,并以此预测流体运动规律的学科
序言
CFD简介

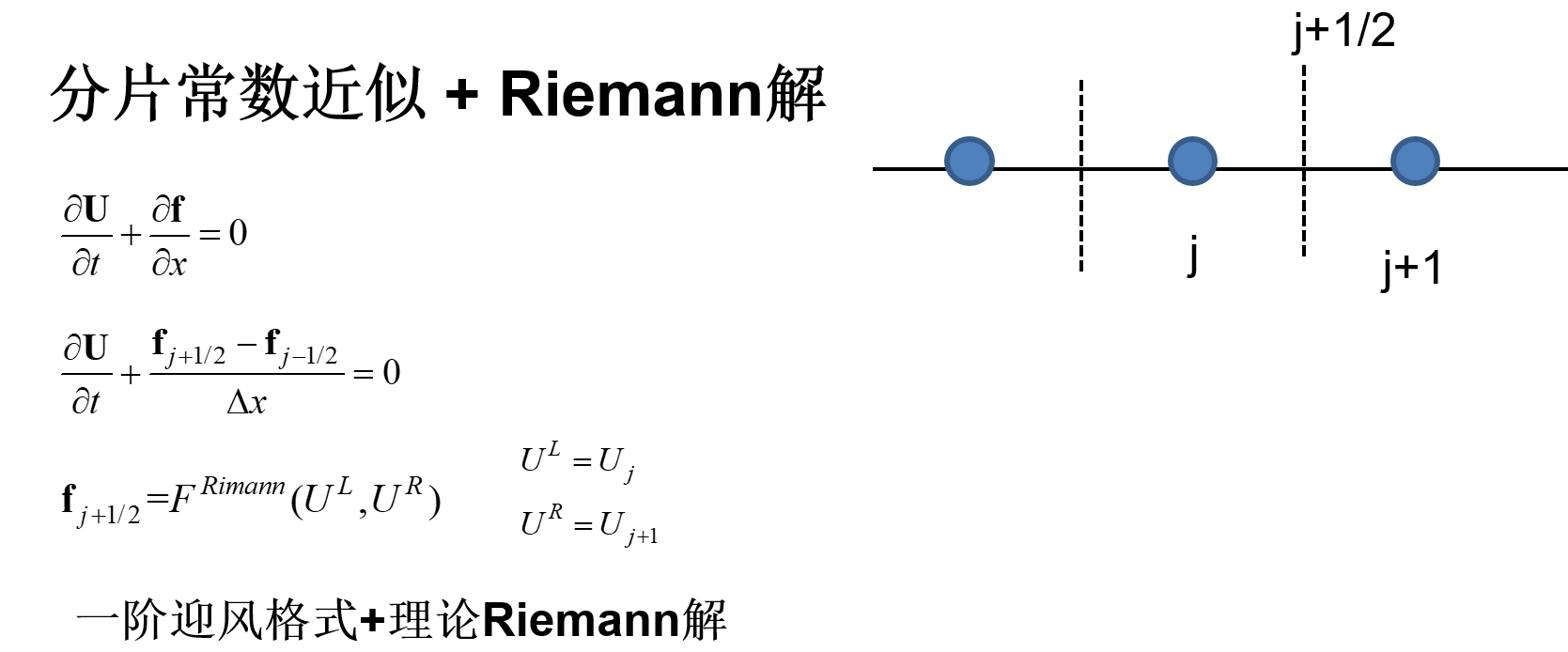
有了流动控制方程,有2种方法可以求它的解:理论解(解析解)和数值解。
- 理论解
- 精确解:Poiseuille解,Blasius解,Plantdl端流边界层解
- 渐进解,近似解:Stokes解
- 数值解
- 差分法,有限体积法,边界元法,谱(元)方法,粒子方法等等
但是由于方程复杂(非线性偏微分方程组),解析解很难获得,所以需要借助计算机来实现数值求解。
CFD面临的挑战及主要任务
- 复杂流动的数学模型
- 湍流的计算模型
- 转捩的预测模型
- 燃烧及化学反应模型
- 噪声模型
- 高精度高效算法
- 高精度激波捕捉法
- 间断有限元法
- 大规模代数方程组高效解法
- 复杂外形、复杂网格处理方法
- 自适应网格
- 直角网格,浸入边界法
- 无网格法:粒子算法
CFD的计算方法
传统计算方法:有限差分法,有限体积法,有限元法,谱方法(谱元法)等;最近发展的方法:基于粒子的算法(格子-Boltzmann, BGK),无网格
| CFD计算方法 |
优点 |
缺点 |
适用范围 |
| 有限差分法 |
简单成熟,可构造高精度格式 |
处理复杂网格不够灵活 |
相对简单外形的高精度计算 |
| 有限体积法 |
守恒性好,可处理复杂网格 |
不易提高精度(二阶以上方法复杂) |
复杂外形的工程计算 |
| 有限元法 |
基于变分原理,守恒性好 |
对于复杂方程处理困难 |
多用于固体力学等 |
| 间断有限元法(DG) |
精度高、守恒性好、易于处理复杂网格 |
计算量大;捕捉激波(限制器)难度大 |
复杂外形的高精度计算 |
| 谱方法 |
精度高 |
外形、边界条件简单 |
简单外形的高精度计算 |
| 粒子类方法 |
算法简单,可处理复杂外形 |
精度不易提高 |
复杂外形的工程计算 |
流体力学基本方程组
基本概念
控制方程非常复杂,为了研究基于连续介质假设:假设流体连续地充满整个空间,用连续函数描述。
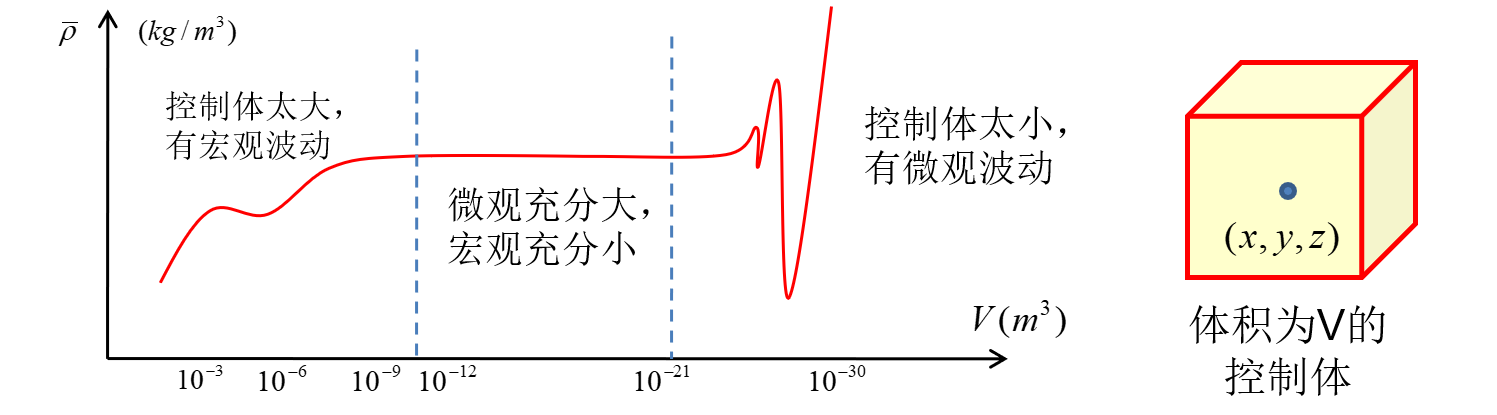
对于流体质点的定义:微观充分大,宏观充分小。
流体密度定义:平均密度:控制体内流动的总质量 / 控制体体积
ρ(x,y,z)=V→0limρ(x,y,z)
有了流体质点的定义,那么怎么描述流体的流动呢?描述流体信息:密度,速度,压力,温度等
流动描述方法:Euler描述和Lagrange描述
- Euler描述:给出每个时刻每个空间点上的物理量
- Lagrange描述:跟踪每个流体质点,记录物理量随时间的变化
连接这两个描述有一个基本概念叫:物质(随体)导数
dtdx=∂t∂f+V⋅∇f
物质导数dtdx的物理意义为:它是运动的流体微团的物理量随时间的变化率,它等于该物理量由当地时间变化所引起的变化率与由流体对流引起的变化率的和。
- ∂t∂f:时间影响
- V⋅∇f:空间影响
- 例:乘火车从北京到上海,一路上记录车厢外的温度随时间变化
CFD方法:
计算网格不动,求解NS方程:Euler描述
计算网格跟踪流体质点:Lagrange描述
计算网格运动,但不完全跟踪流体质点:ALE(动网格)
基本方程-基于Euler描述
目的:给出物理量(密度,速度、压力、温度)满足的方程:
ρ(x,y,z,t),V(x,y,z,t),p(x,y,z,t),T(x,y,z,t)
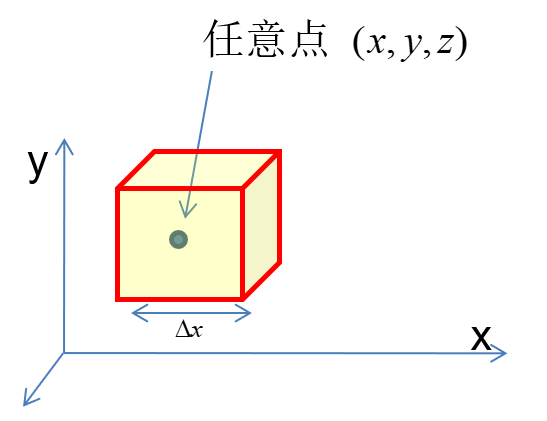
- 围绕(x,y,z)点取一控制体
- 根据基本定律(质量、动量、能量守恒),给出控制体内总量(积分量)的变化规律;(总质量、总动量、总能量的变化规律:积分型方程)
- 令控制体尺度趋近于0, 得到(x,y,z)点物理量的微分型方程
特点:控制体不动(Euler描述)
控制方程-三大守恒定律
- ρ:质量密度,单位体积内的质量
- θ:动量密度,单位体积内的动量
- 它等于质量密度ρ乘当地流体质点运动的速度v:θ=ρv
- E:能量密度,单位体积内的总能量
- 能量包括动能和内能,即E=21ρV2+CvρT
- E=CvρT+21ρ(u2+v2+w2)=γ−1p+21ρ(u2+v2+w2)
- Cv为定容比热,参考空气动力学:CvρT=RCvp=γ−1p
控制体内的总质量,总动量,总能量为:
∫ΩρdV,∫ΩρvdV,∫ΩEdV
控制体质量(动量、能量)增加 = 穿过控制面流入的净质量(动量、能量)
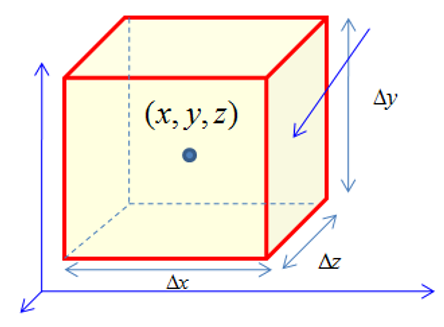
对于这个小控制体来说,它里面要发生变化的原因是什么?假设这里不考虑元项,这里面没有质量元,动量元,能量元,它的原因显然是穿过这个控制体边界流入了净质量,净动量,净能量,那么到底流入了多少呢?这里以质量为例:
(ρ(t+Δt)−ρ(t))ΔxΔyΔz=−[(Fxpright−Fxpleft)ΔyΔz+(Fxptop−Fxpbottom)ΔxΔz+(Fxpfront−Fxpback)ΔxΔz]Δt
这个方程的物理含义是:小体积内质量的变化等于Δt这段时刻内穿过控制体表面流进的净质量
- 这里Fxp是穿过垂直x方向单位面积面元的质量通量
Δtρ(t+Δt)−ρ(t)=−ΔxFxpright−Fxpleft−ΔyFxptop−Fxpbottom−ΔzFxpfront−Fxpback
当Δx,Δy,Δz,Δt→0的时候,原先积分形的方程变为以下微分形的方程
∂t∂ρ=−[∂x∂Fxp+∂y∂Fyp+∂z∂Fzp]
这里对x,y,z求导数的原因是:流通量本身不会带来物理量的变化,单位时间内流过这个小面元多少质量,动量,能量本身不会带来小体积内质量的变化,因为如果是均匀的,从左端流入多少从右端流出多少,小体积内质量不会发生变化。但是,是不均匀的,x方向有梯度,流入多,流出的少,里面的质量才会增加,里面存在梯度。
通样对动量密度,能量密度有如下式子:
∂t∂θ=−[∂x∂Fxθ+∂y∂Fyθ+∂z∂Fzθ]
∂t∂E=−[∂x∂FxE+∂y∂FyE+∂z∂FzE]
物理含义是:流通量的变化(散度)导致净通量
计算流通量
到这里得到了核心方程,质量密度,动量密度,能量密度的控制方程,关键是怎么计算这个流通量。
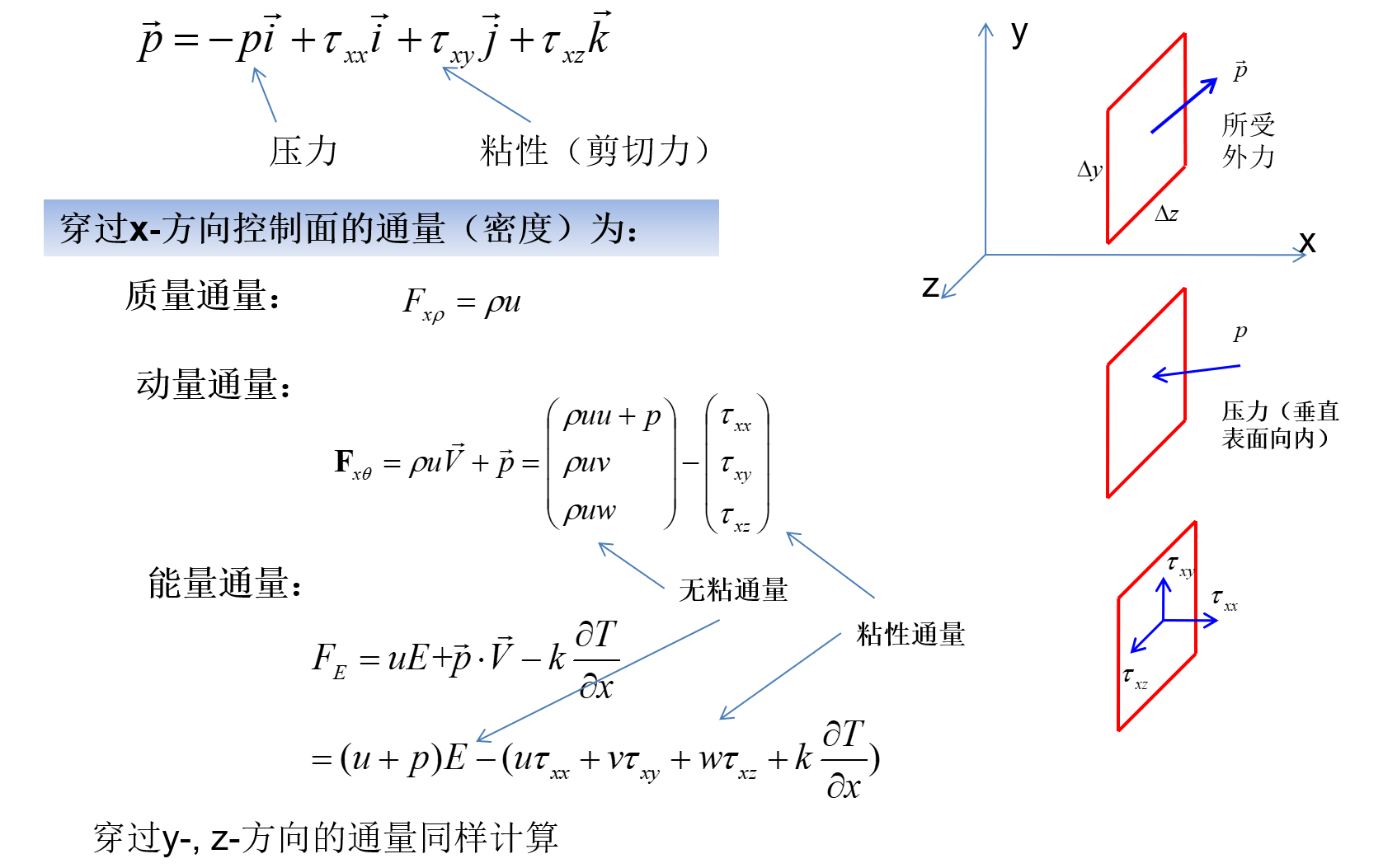
问题:如图,试计算单位时间内流过右侧单位面积面元的质量、动量和总能量。注:外力冲量等同于流过的动量;外力做功等同于流过的能量
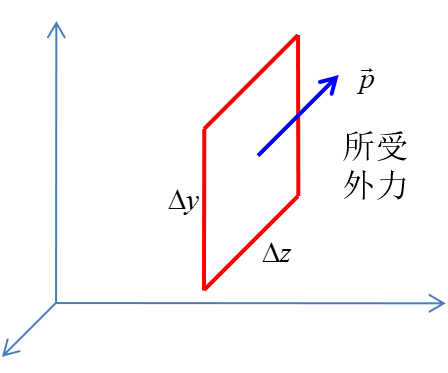
- 质量通量:Fxp=ρu(向右为正)
- u:流过的体积,它是沿着x方向的速度乘单位时间,就是这个流体穿过这个小面元流过多少长度乘上小面元的单位面积,这就是流过的体积
- 这么多的体积乘以密度,就是流过的质量,即质量密度
- 动量通量:流过质量附带的动量 + 表面上外力的冲量
- Fxθ=ρuV+p
- ρuV:质量附带动量
- p:表面上(单位面积)所受外力
- 能量通量:流过质量附带的能量 + 表面上外力做功 + 热传递
- FxE=uE+p⋅V−k∂x∂T
- E:能量密度,单位体积的能量
- k∂x∂T:Fourier热传导定律:热流与温度梯度呈正比
应力(张量)
到这里,这个方程还有一个问题没解决,即p:表面上(单位面积)所受外力,这个力是怎么描述的呢?流体的力有压强会成为压力,还有剪切力,由于粘性产生的粘性力等等,怎么来描述这些力,这里涉及到怎么描述连续体内部的力
描述连续体内部的力通常引入一个叫应力的概念。把物体切开,其内部的力就暴露出来,但是切的方向不同,表面上的力也不同。
实际上,切3次就够了:垂直x轴, 垂直y轴,垂直z轴各切一次
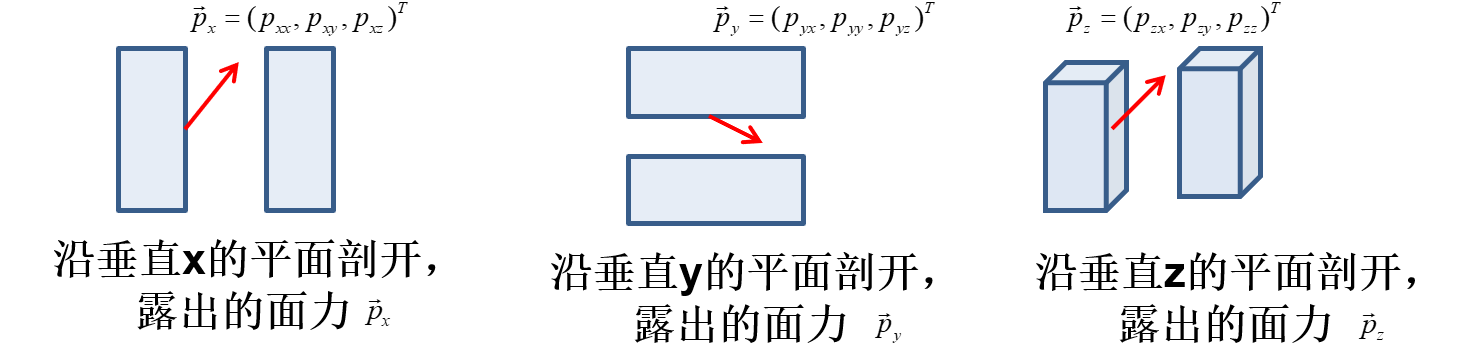
沿任意方向切割,暴露出的力如下计算:
pn=P⋅n,P=⎣⎢⎡pxxpyxpzxpxypyypzypxzpyzpzz⎦⎥⎤
这个矩阵P是一个张量,称为应力张量,有了应力张量以后,沿着x,y,z方向各切一刀,搞清楚这3个力即可。例如沿着n方向切一刀,它表面上暴露出来的力pn=P⋅n
力与变形的关系(本构方程,应力-应变关系)
对于水和空气这样的流体,它的应力是什么样的状态呢?它们的应力状态可以写为以下形式,流体内部的力可以写成两部分,静止部分 + 运动部分
Pij=−pδij+τij
- 静止流体Pij=−pδij,即帕斯卡定律
流体特性:静止状态不能承受剪切力
这是传统流体的基本定义,与弹性体不同,弹性体静止了也能承受剪切,剪切完还能变形回来,但是静止的流体不能承受剪切,剪切完了它就不变了。
流体特性:粘性力与变形速率呈正比(牛顿粘性定律)
广义牛顿粘性定律如下:
τij=λVk,kδij+μ(Vi,j+Vj,i)
通常情况下,λ=−32μ
这样通过利用这个应变关系,流体的力与变形之间建立了关系。这样刚才的p就可以计算了:
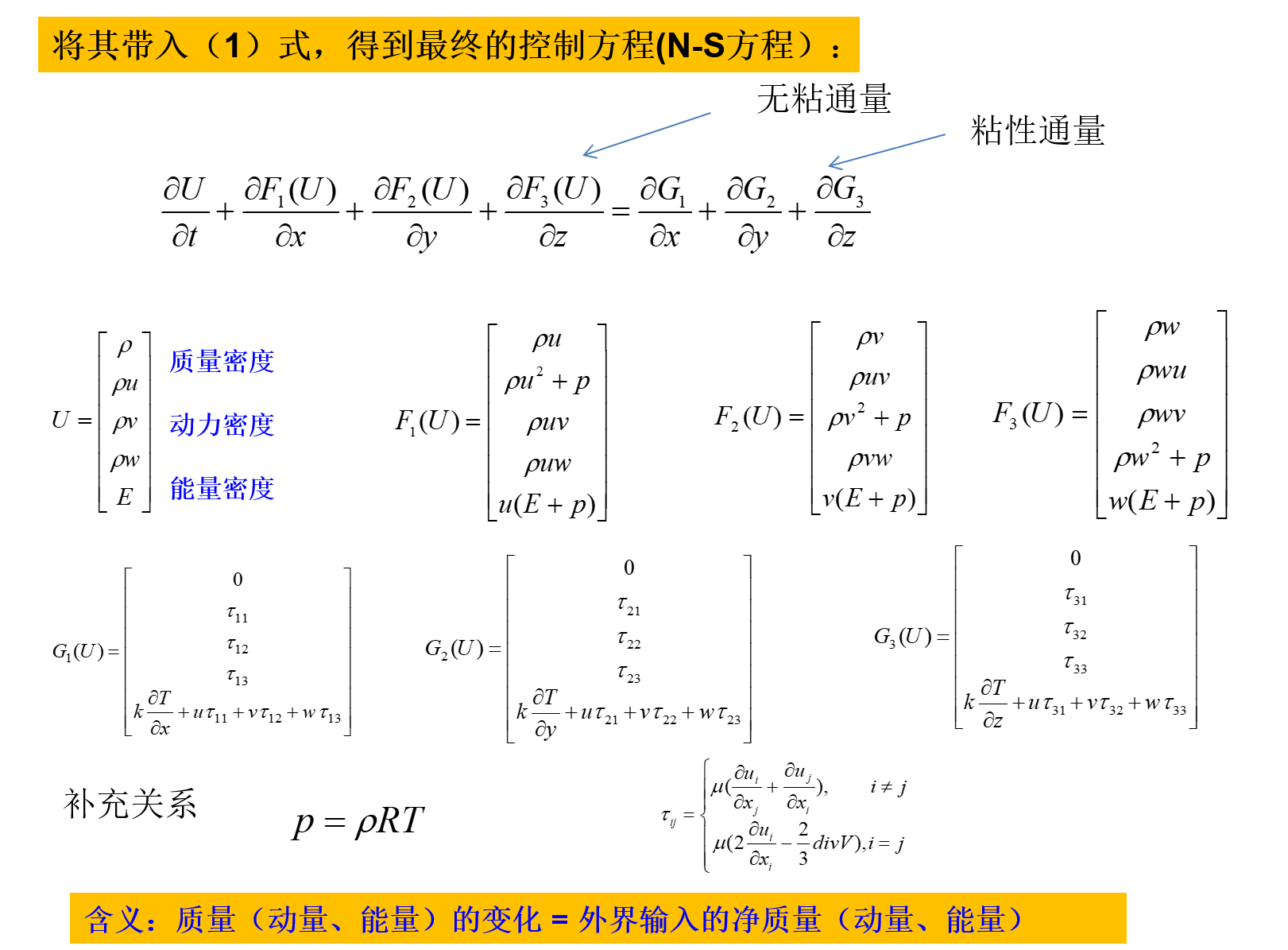
N-S方程各项物理含义剖析

N-S方程的无量纲化
求解CFD时常涉及将方程无量纲化。
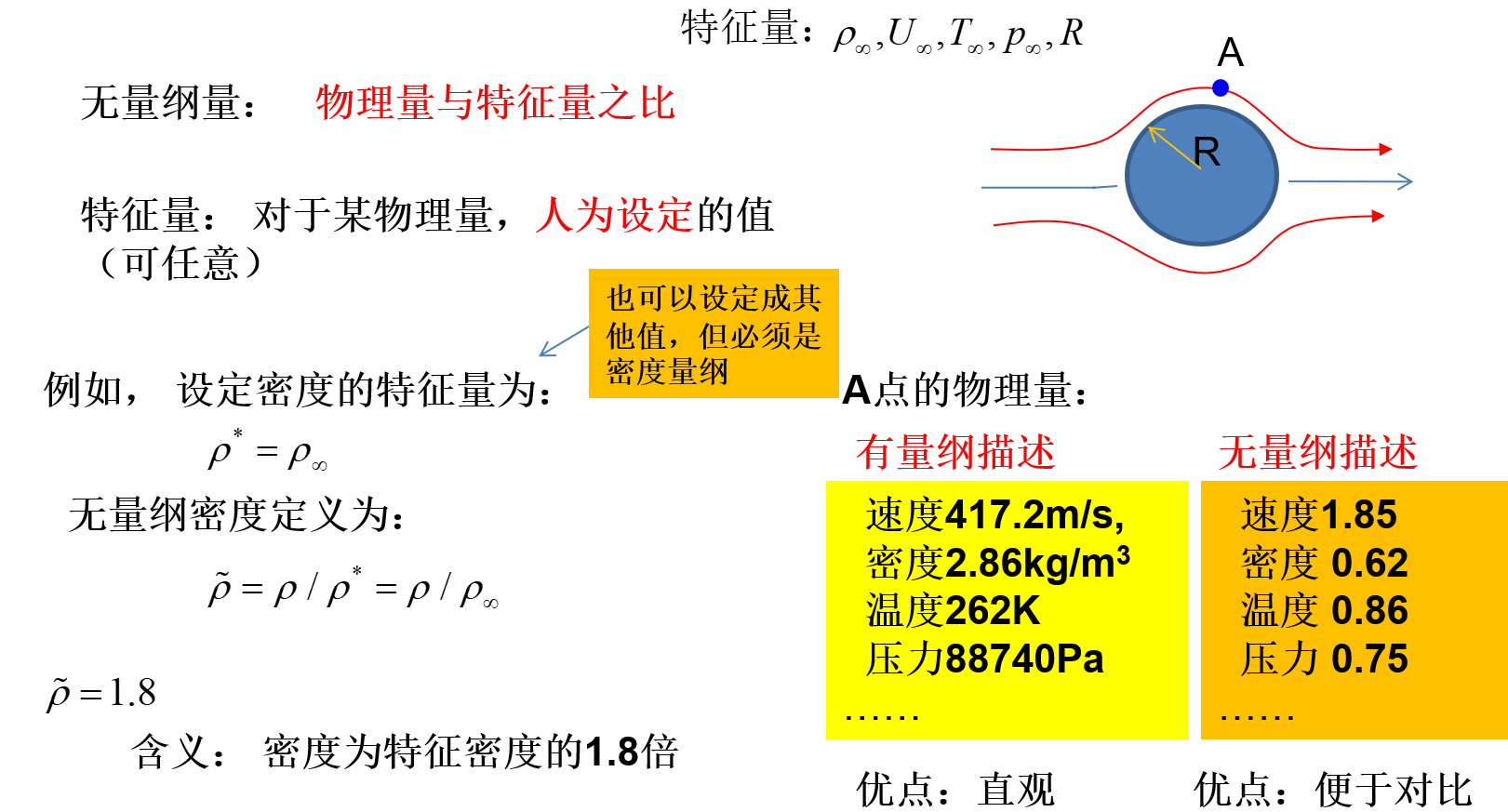
- 无量纲形式的优点:数值更加简洁、便于对比;通用性更强
- 无量纲形式的缺点:数值的物理直观性差
N-S方程的简化

CFD经常研究的方程以Euler方程为代表,相对下,粘性情况容易计算,粘性项离散相对简单,通常用中心差分就可以离散了。
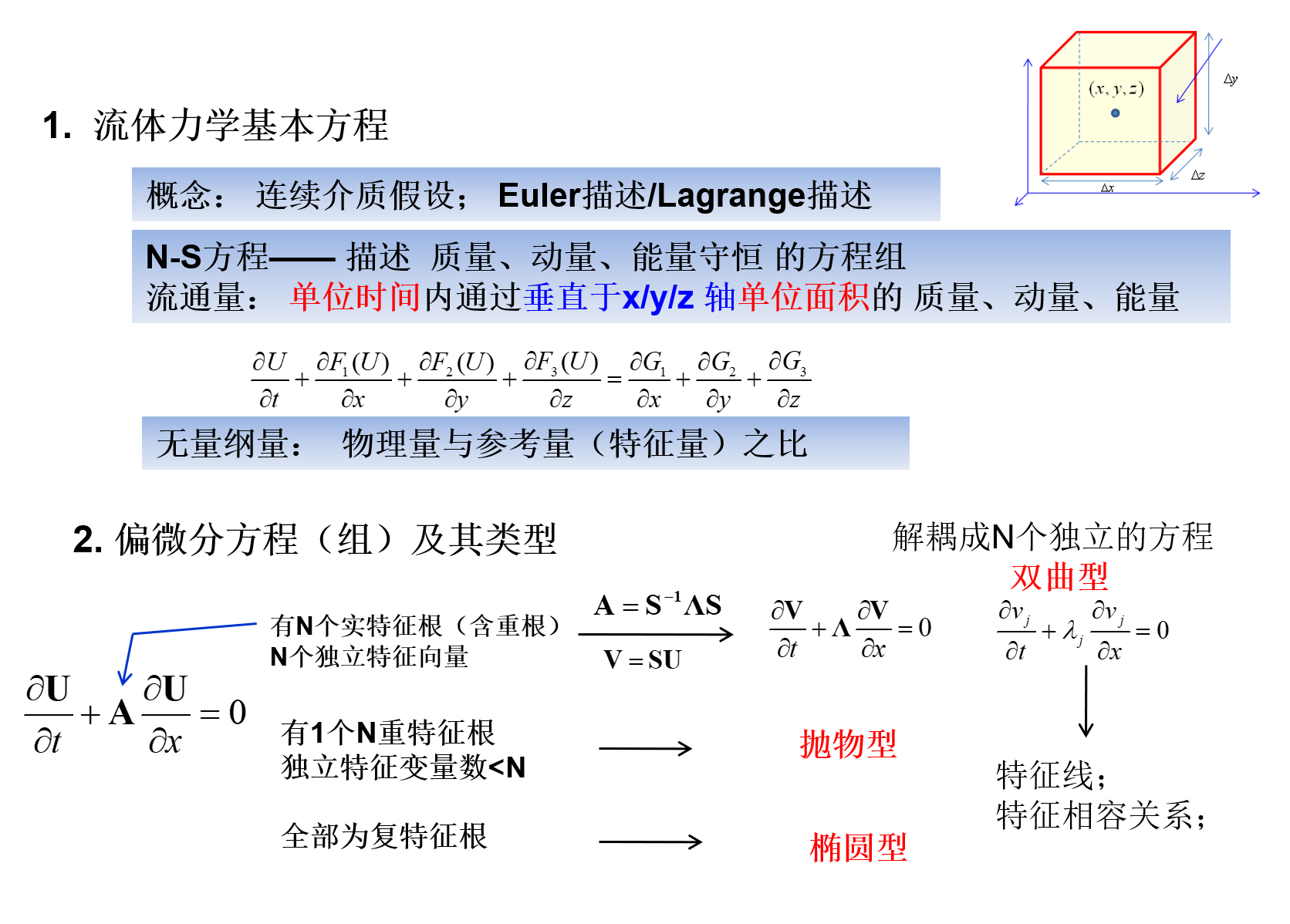
偏微分方程的分类及特征
一阶偏微分方程
常系数线性单波方程
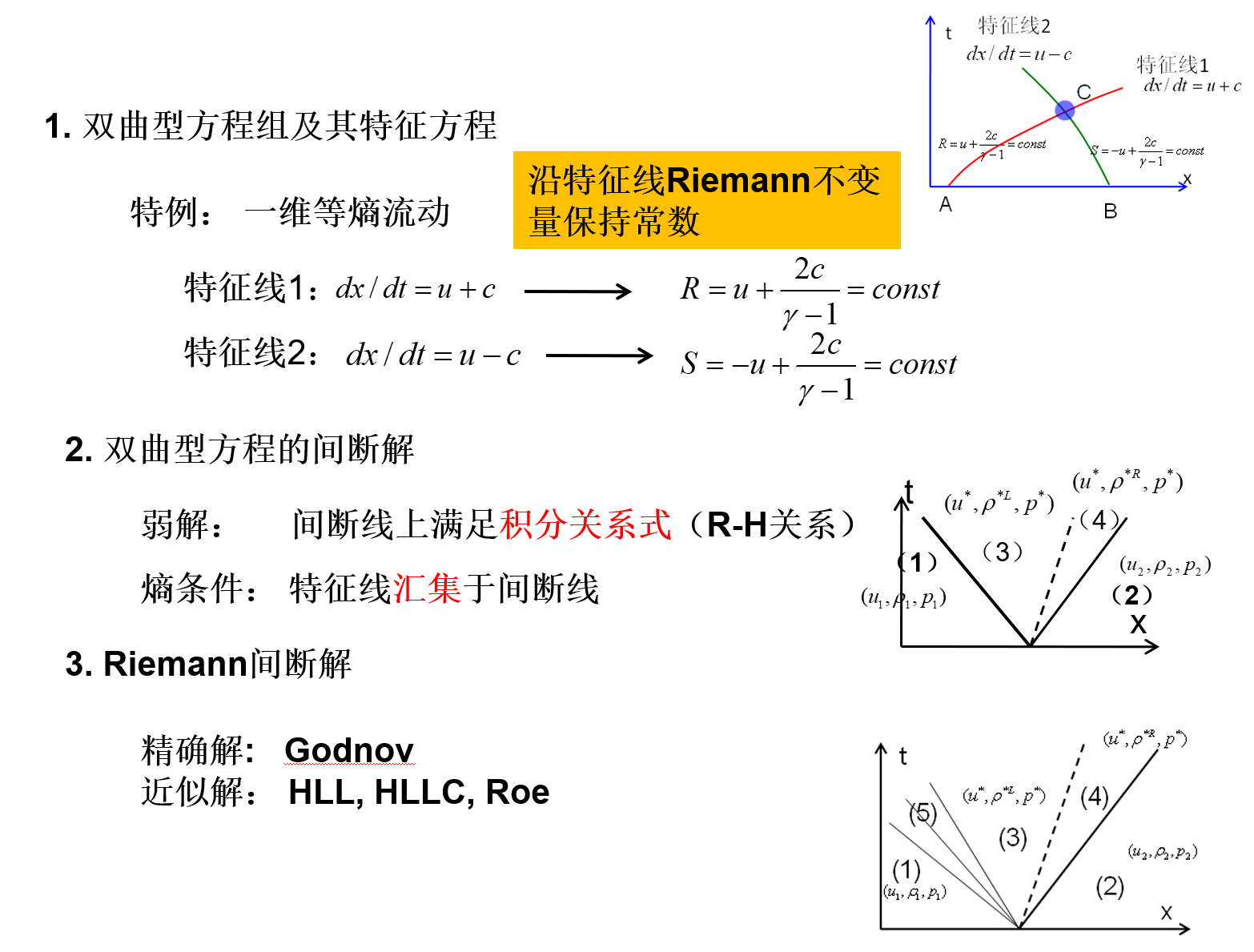
从数学上讲,偏微方程可以分为椭圆型,双曲线型,抛物线方程。首先看双曲型方程的分类:
(常用)特例:常系数线性单波方程
∂t∂u+c∂x∂u=0,x∈(−∞,∞)
- 这个一阶偏微分方程称为1维单波方程,它有时间导数和空间导数还有c
- 初值:u(x,0)=φ(x)
- 方程的精确解:u(x,t)=φ(x−ct)
- 含义:以常速度c向右传播。 波形,振幅保持不变
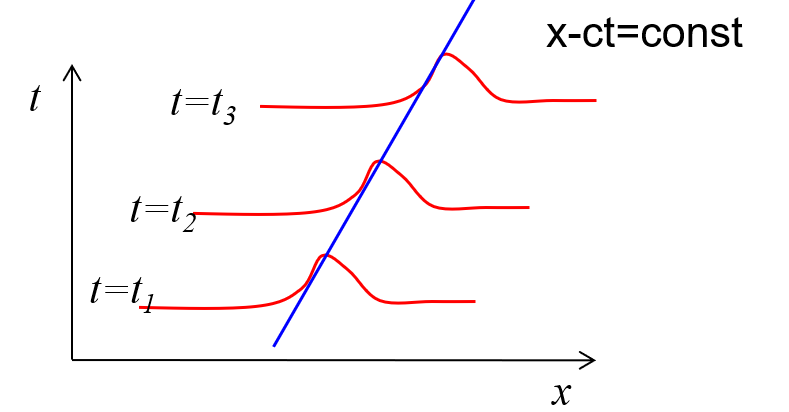
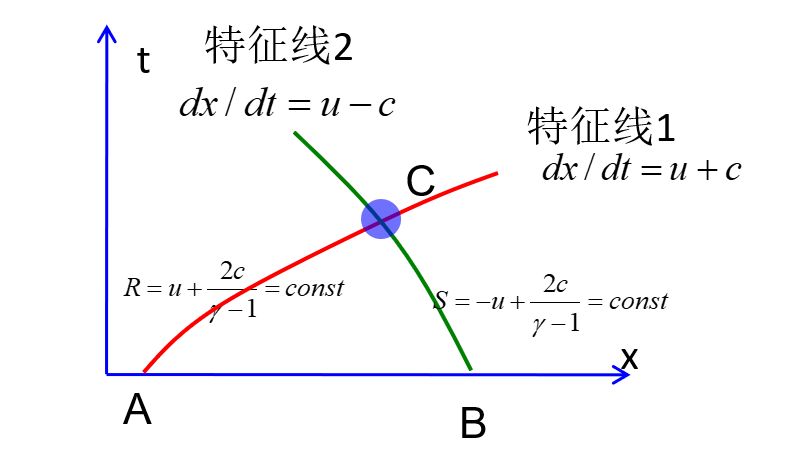
如图,在x-t空间上,物理量沿着蓝色线x−ct=const保持不变,这样的线称为特征线。在特征线上,物理量的值,变化规律称为特征相容关系,这个图中的特征相容关系就是在这条特征线上,物理量u本身保持常数。
线性单波方程的边界条件

∂t∂u+c∂x∂u=0,x∈[a,b]
- 初值:u(x,0)=φ(x)
- 问题:如何给定边界条件?
c>0时,扰动波向右传播:左端(A)需要给定边界条件;右端(B)只能被动接受,无法给定边界条件(即使给定,对计算域也无任何影响, 且造成B端的非适定性)。
c<0时,扰动波向左传播:右端(B)需要给定边界条件;左端(A)无需给定
对于初值问题,如果微分方程解的定解域中存在、唯一、且连续依赖于初始值,则称数学问题的提法是适定的。
(一般形式)一阶线性偏微方程
a(x,y)∂x∂u+b(x,y)∂y∂u=c(x,y)
采用特征线法,可转化为常微分方程。假设在x−y空间内,有曲线Γ:x=x(s);y=y(s),显然,沿着该曲线Γ有如下关系:
∂s∂u=∂x∂udsdx+∂y∂udsdy
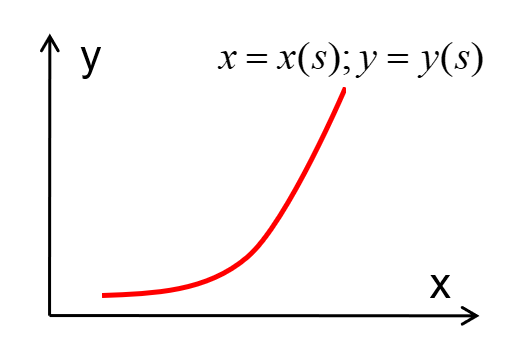
如果该曲线Γ满足特征线:
⎩⎪⎪⎨⎪⎪⎧dsdx=adsdy=b
则有特征相容关系(特性线上物理量的简化方程):
dsdu=a∂x∂u+b∂y∂u=c
偏微分方程在特征线上变成了常微分方程
那么如何利用特征线计算物理量?
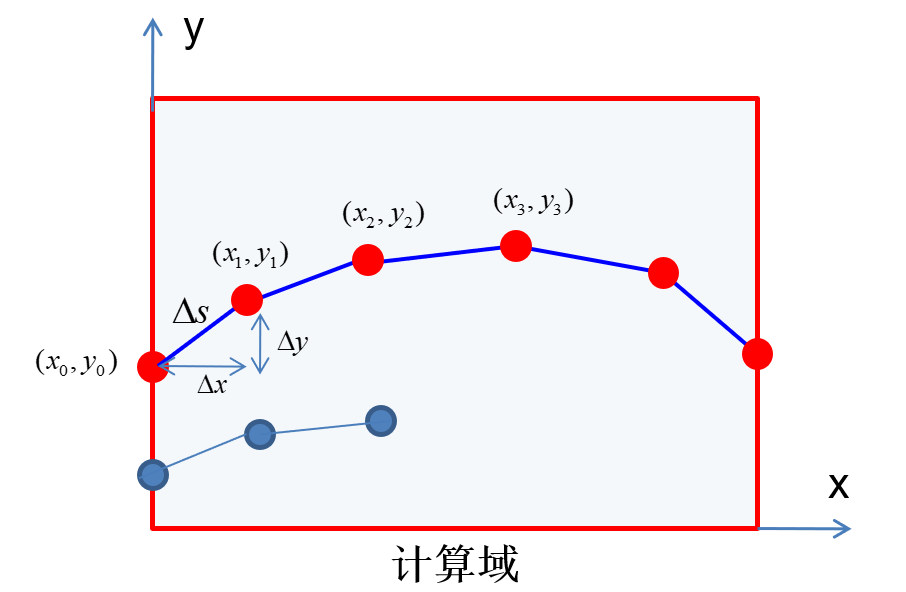
- 设定积分步长Δs(根据精度需求设定,例如0.1)
- 在边界上选取初始点(x0,y0),在边界上选取初始点物理量值u0
- 根据特征线及特征相容关系数值积分,求出特征线下一个点的坐标(x1,y1)和函数值u1。递推下去,计算出整条特征线的(离散)坐标及物理量的(离散)值。
- 在边界上选取新的点,重复步骤3,计算出整个计算域物理量的分布
边界条件:在特征线"流入"的区域设定;特征线"流出"的区域不能设定。
一阶常系数偏微方程组
∂t∂U+A∂x∂U=0,U=(u1,⋯,um)T
如果矩阵A可以被对角化:A=S−1ΛS,Λ=diag(λ1,⋯,λm):
∂t∂U+S−1ΛS∂x∂U=0⇒S∂t∂U+ΛS∂x∂U=0
令V=SU,有∂t∂V+Λ∂x∂V=0,即:
∂t∂vj+λj∂x∂vj=0
- m个方程完全解耦,可独立求解
- m个特征相容关系式:vj∣Γ=const
如果矩阵A能够(相似变换)对角化,则原方程是双曲型的
如果矩阵A具有m个实特征值,这些特征值共具有m个线性无关的特征向量,则称为双曲型方程
如果矩阵A的特征值为m重根,而且对应的独立特征向量数小于m,则称为抛物型方程
如果矩阵A的特征值均为复数,则称为椭圆型方程
二阶偏微方程

讨论Euler方程组
以一维欧拉方程为例讨论。
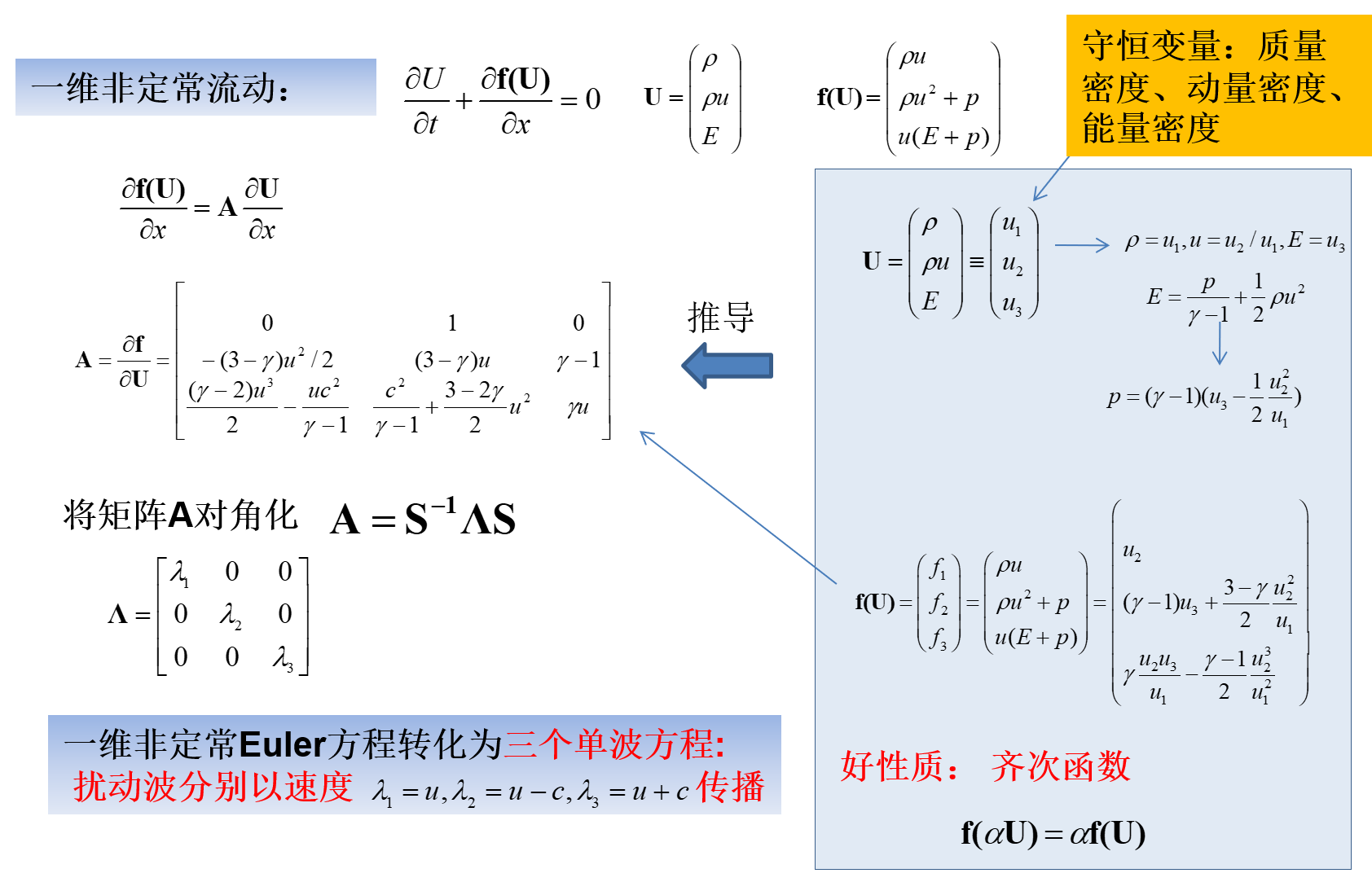
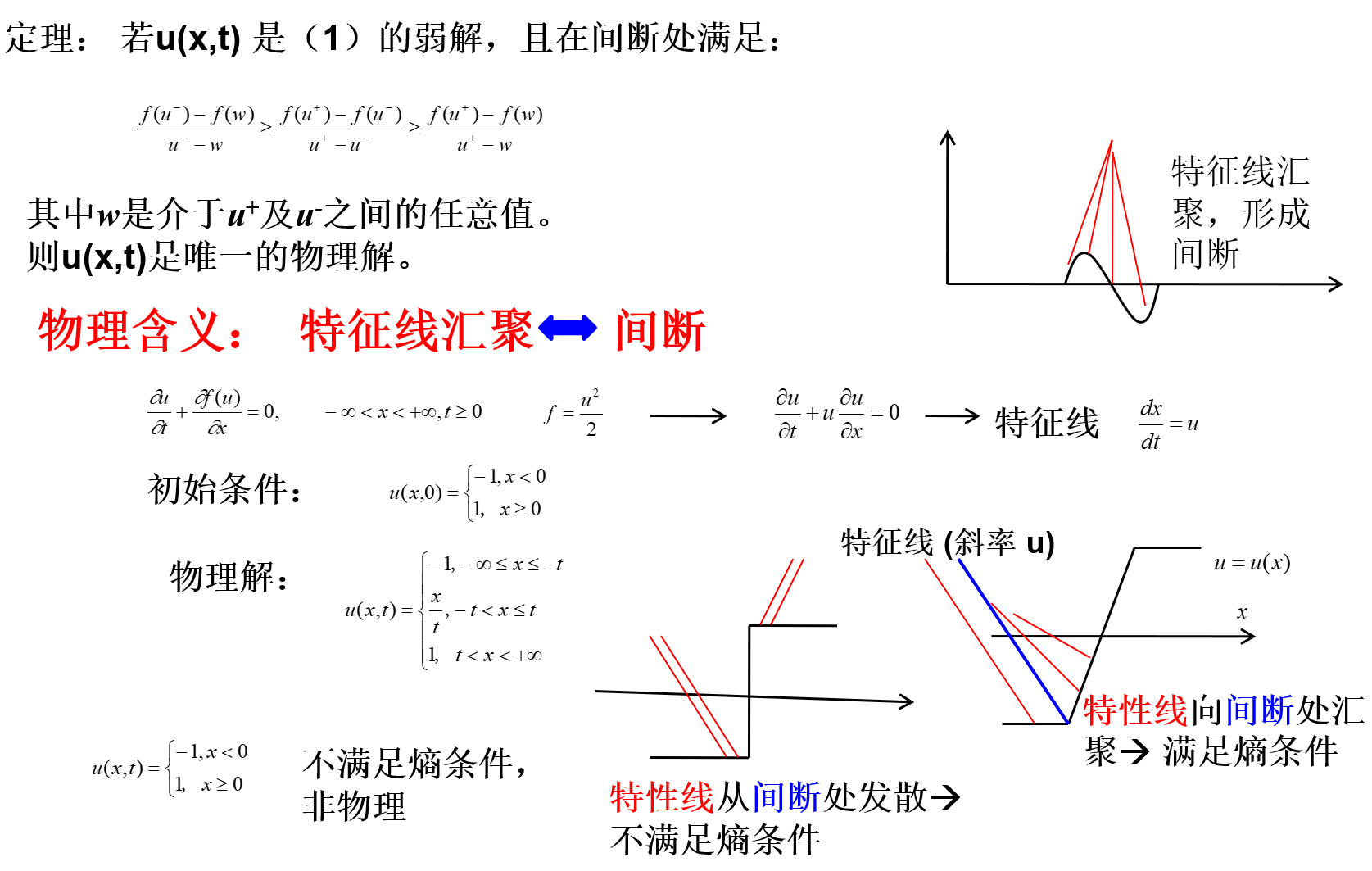
这个方程的物理含义可看出:Euler方程是双曲的,因为它的雅可比矩阵可以通过相似变换对角化。
这个双曲的3个特征值有着物理含义:Euler方程中蕴含着3道波,假设控制方程是个1维的Euler方程,那么实际上就是一个1维的管道里流动。
这个1维管道内充满着无粘的可压缩的流体,初始时刻给一个扰动,这个扰动瞬间转化为3道波在传播,有一道波是速度为u在传播,就是和流体微团相同的速度传播。跟踪这个波会发现有一个物理量保持不变:熵,因为这是无粘的流体,不考虑粘性,那么就没有热传导,所以流体微团自己的熵保持不变
另外还有2道波,一道波是相对于当地流体的速度以声速向右传播,另一道波是相对于当地流体的速度以声速向左传播。
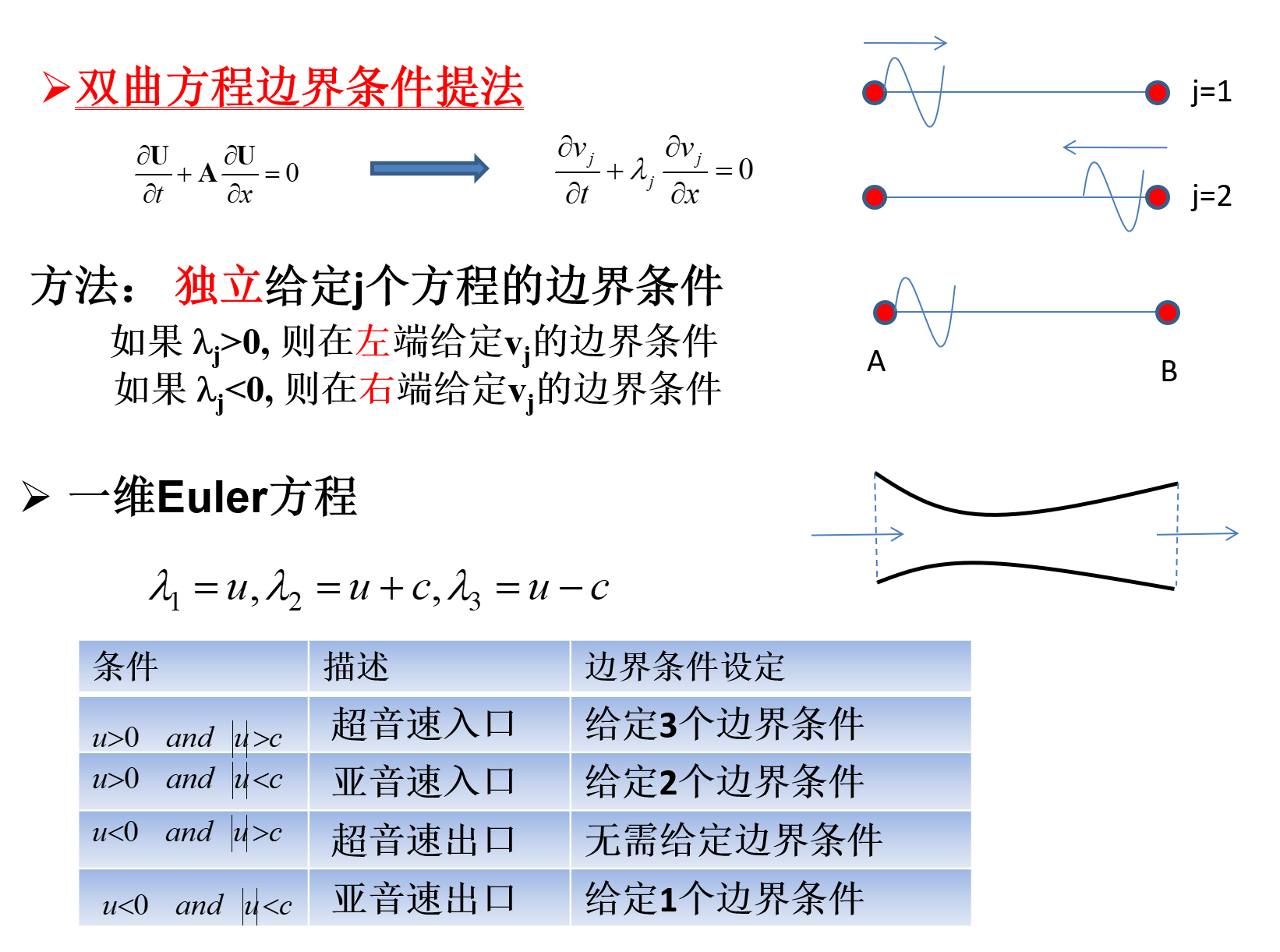
双曲型方程组边界条件提法

特点:左、右边界总共给定n个边界条件,各自的个数视特征值的符号确定
可推广到一般的双曲型方程组。
下面看一个例子,一维Euler方程
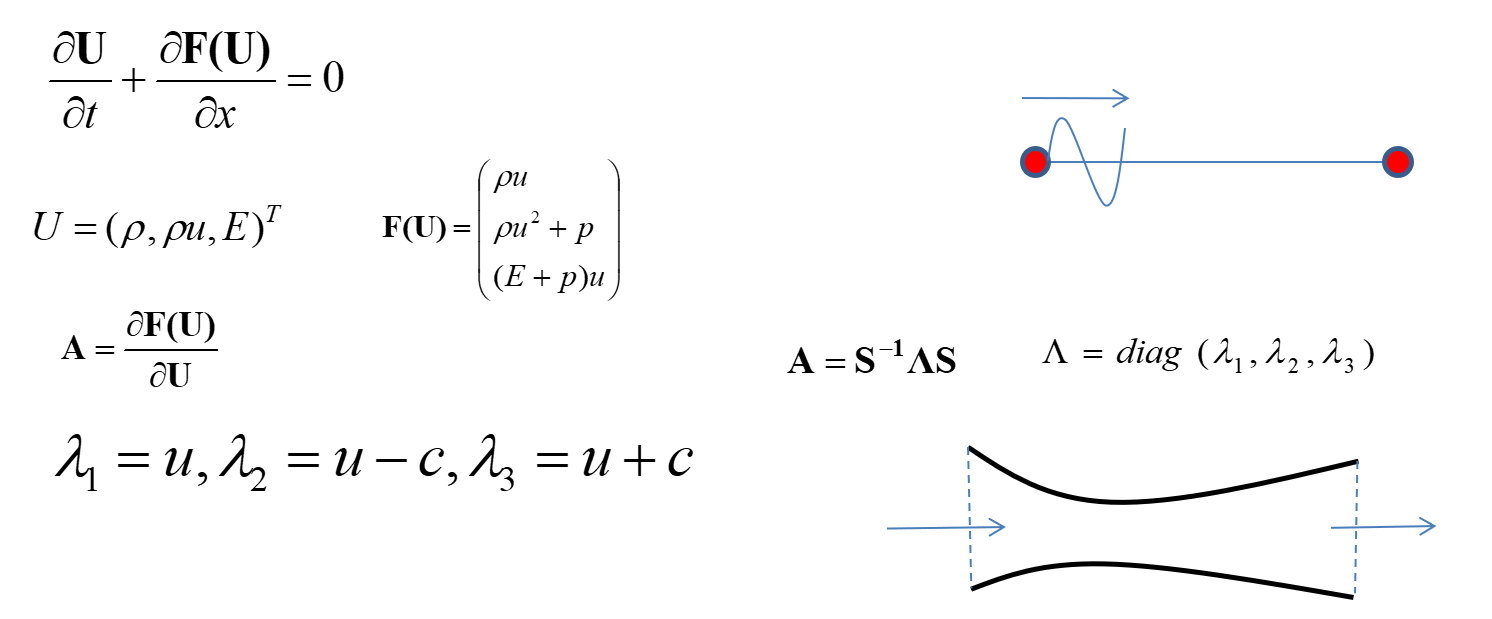
对于左边界:
| 边界 |
描述 |
边界条件设定 |
| u>0并且∣u∣>c |
超音速入口 |
给定3个边界条件 |
| u>0并且∣u∣<c |
亚音速入口 |
给定2个边界条件 |
| u<0并且∣u∣>c |
超音速出口 |
无需给定边界条件 |
| u<0并且∣u∣<c |
亚音速出口 |
给定1个边界条件 |
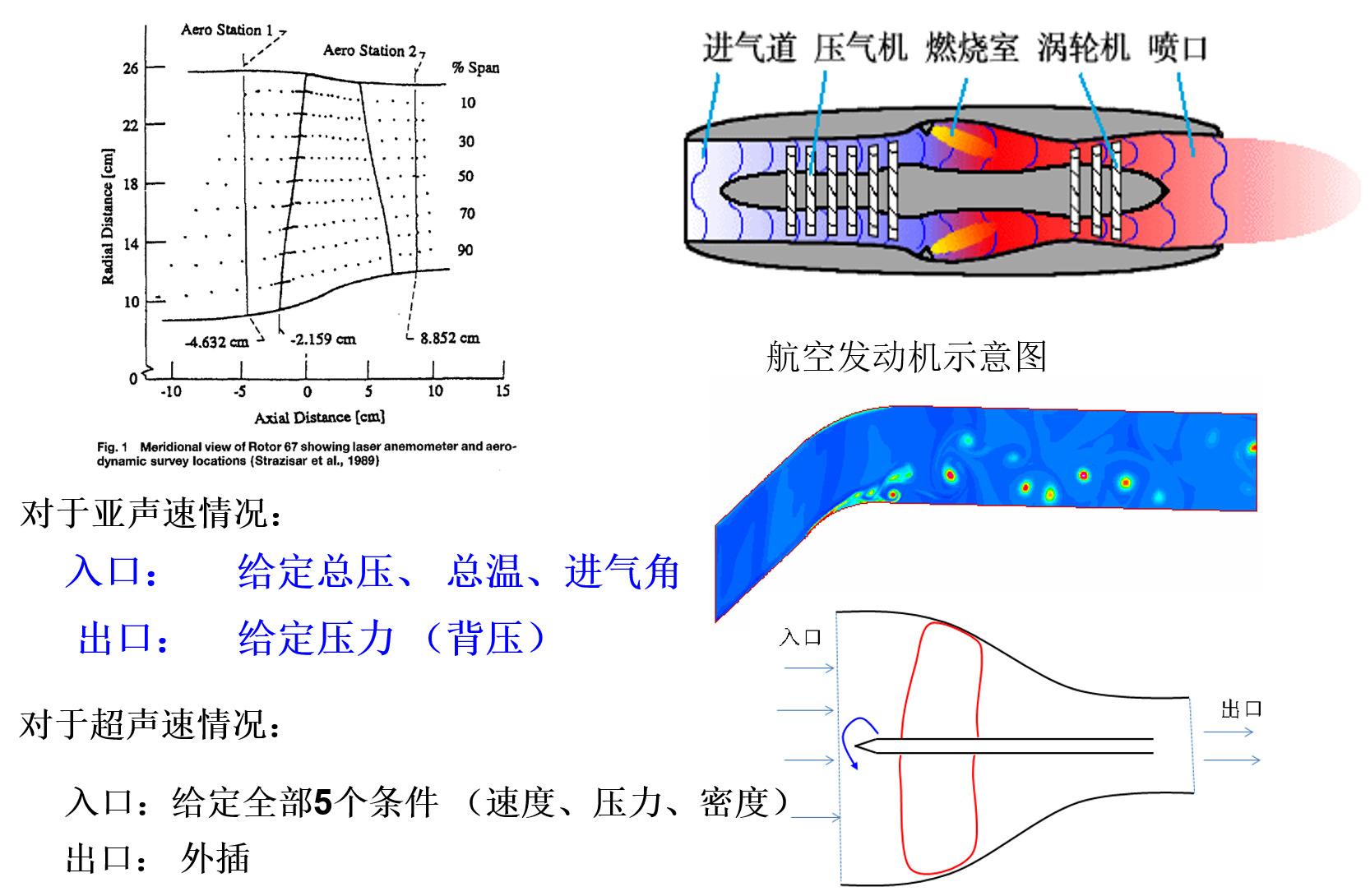
椭圆型方程:Laplace方程
∂x2∂2Φ+∂y2∂2Φ=0
降阶:
u=∂x∂Φ,v=∂y∂Φ⇒⎩⎪⎪⎨⎪⎪⎧∂x∂u+∂y∂v=0∂x∂v+∂y∂u=0
一阶拟线性方程:
∂x∂U+A∂y∂U=0,U=(vu),A=(0−110)
- 特征值:λ1=i,λ2=−i
- 类型:椭圆型方程
椭圆型方程边界条件的提法
知识总结1
双曲型方程及其间断解
双曲型方程组的特征方程
前面提到过,双曲型方程 ∂t∂U+A(U)∂x∂U=0 中的矩阵 A 如果可以通过相似变换对角化,可以得到很大的化简,特别是如过A是一个常系数矩阵,也就是这个矩阵跟 x−t 无关的话,这个可以解耦成 m 个独立的单波方程
⇒∂t∂U+S−1ΛS∂x∂U=0∂t∂V+Λ∂x∂V=0,V=SU
这样就解耦为 m 个独立方程求解,但是这是特殊情况,即矩阵 A 是常系数矩阵。那么如果 A 不是常系数矩阵呢?例如像欧拉方程都不是常系数矩阵,这样的情况虽然不能解耦,但仍然可以转换为常微方程组。
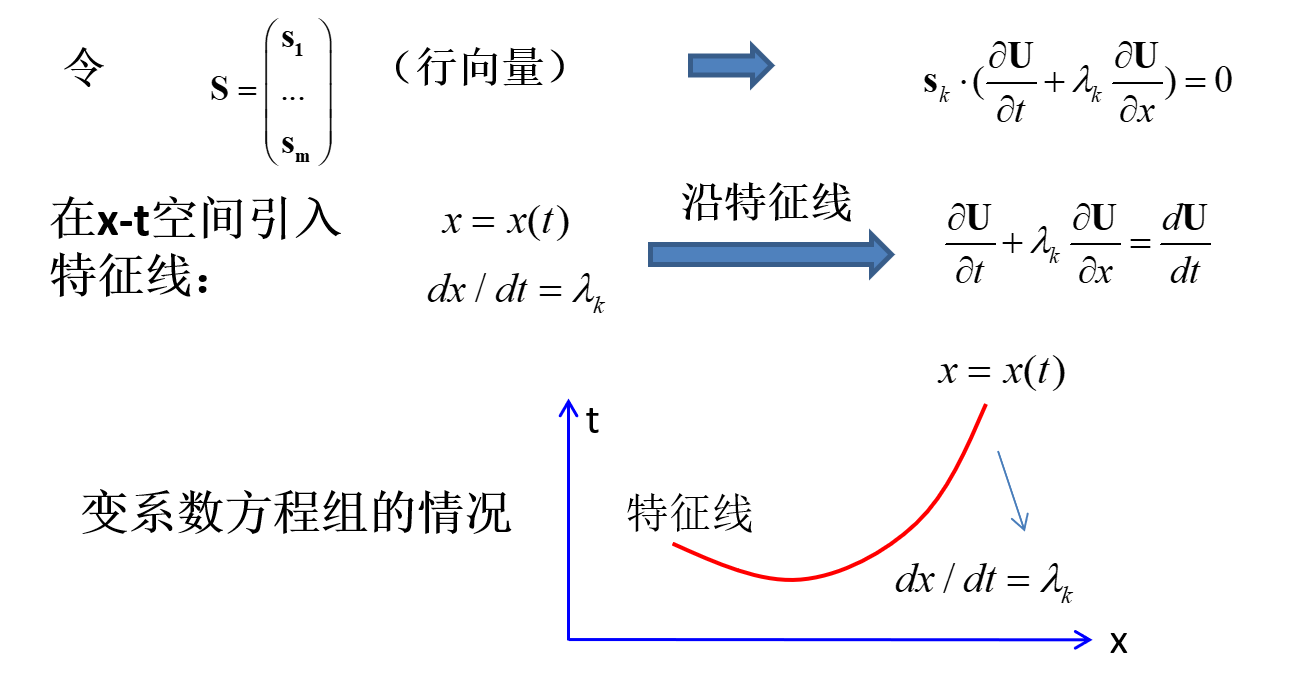
也就是说,这个探测点在 x−t 空间上以 λk 这个速度移动,这个测点上的导数 dtdU 满足的方程如下
sk⋅dtdU=0
这个方程就变成了常微分方程了,也就是说,它在这个空间上,有 m 条特征线,在特征线上化成了 m 个常微分方程组,仍然可以得到简化。
一维均熵流动控制方程
下面看一个求解双曲型方程的例子:一维等(均)熵运动
对于Euler方程来说,整个流域是无黏的,无黏就意味着没有热传导,没有热传导意味着熵没有变化。如果来流是均熵的,那么在该流域中流体的流动就会保持熵不变。
流体里的热力学量包括: ρ,p,T,s,H,U,c (密度,压力,温度,熵,焓,内能,声速),给定任意两个,其余的都可以由这两个推导出来。
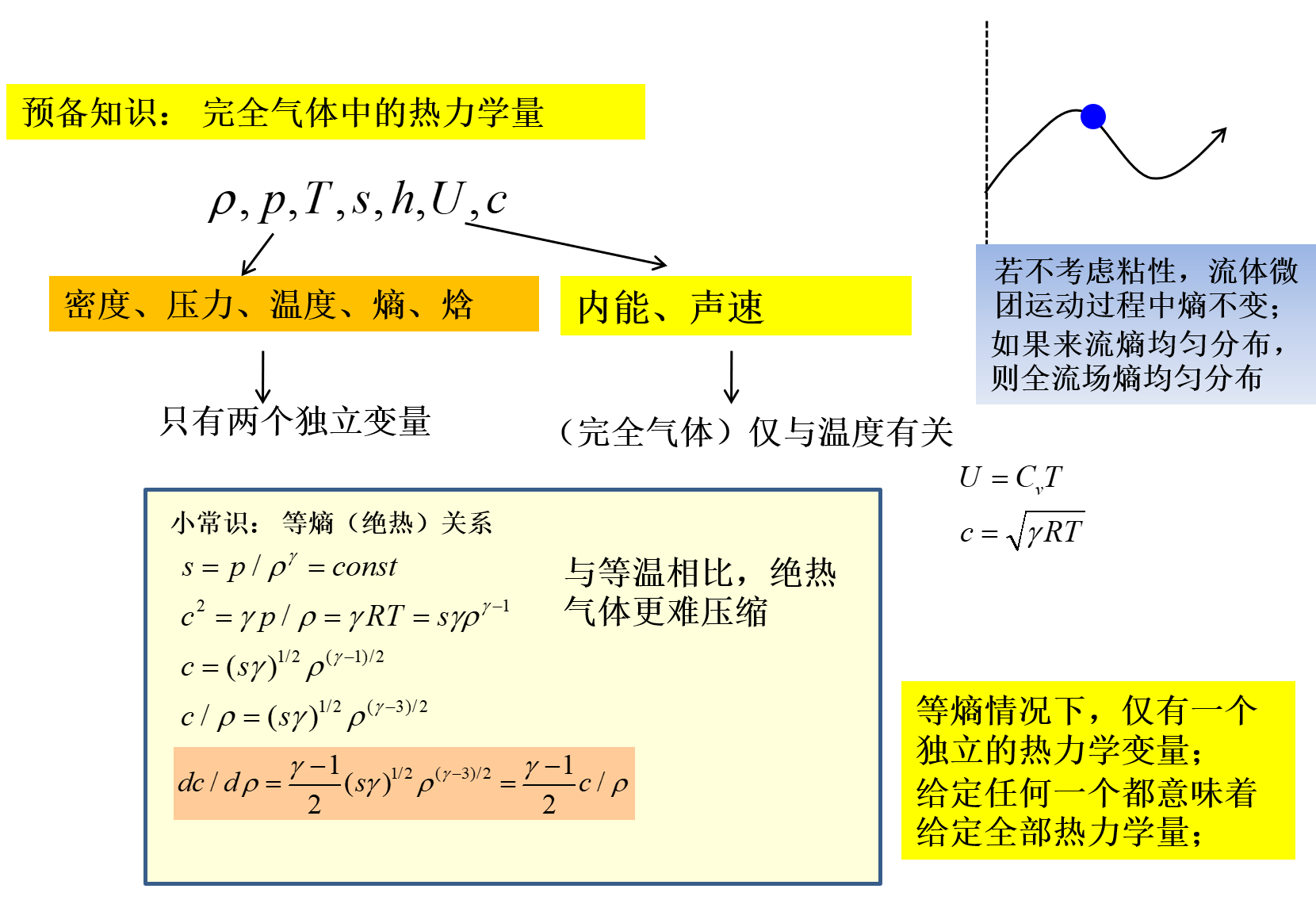
均熵运动情况下,能量方程可用熵为常数替代
这样的话,未知变量就只有2个了(1个热力学量+速度),那么只需要两个方程就可以求解。我们选择形式比较简单的质量方程和动量方程进行求解,即:
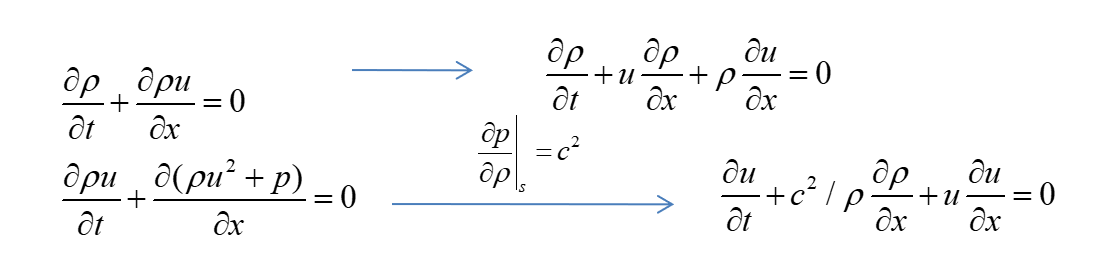
然后可以得到一维均熵流动控制方程(Euler方程简化版):
∂t∂U+A∂x∂U=0U=[ρu]A=[uρc2ρu]
矩阵 A 的特征值:λ1,2=u±c。它的物理含义就是:一维均熵方程中蕴含着2道声波,一道声波相对于当地流体微团以声速向右传播,另一道以声速向左传播。
然名继续求特征向量,矩阵 A 就变成:
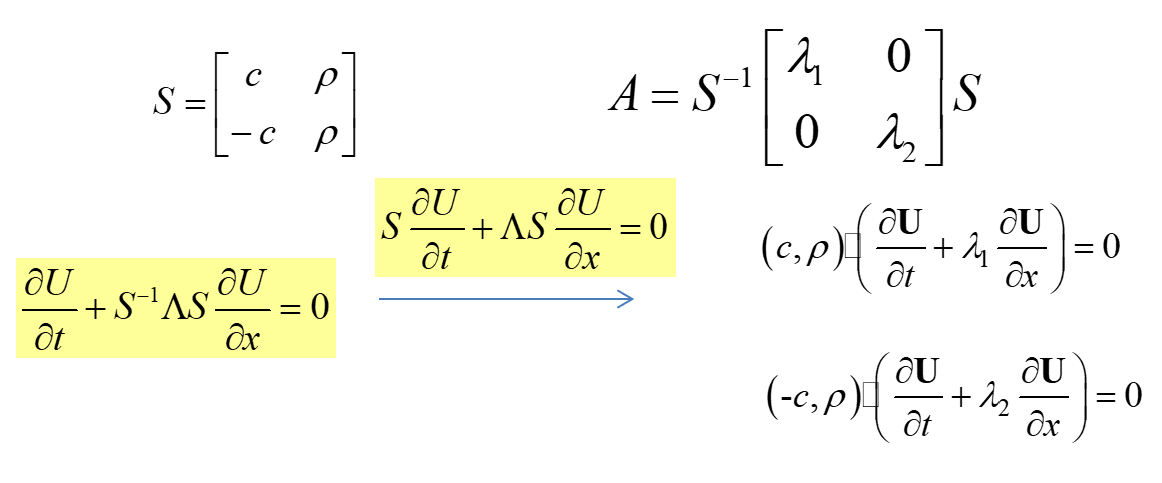
接下来分别看得到的两个方程:
(c,ρ)⋅(∂t∂U+λ1∂x∂U)=0
沿特征线1:dtdx=λ1=u+c 方程1可转化为:
(c,ρ)⋅dtdU=0
将这个方程式写开后可得:
dtdu+ρcdtdρ=0
方程变成这个形式,物理量虽然还是2个:ρ,u,但是方程自变量减少了,只有时间 t。原先的偏微方程变成了在这条特征线上的常微方程了。这里的 dtdu,dtdρ 变成随体导数,随着当地的探测点,以 c 的速度运动。
这里使用积分因子的方法可将方程进一步化简,定义 R=u+γ−12c,有如下关系
dtdR=dtdu+γ−12dρdcdtdρ=dtdu+ρcdtdρ=0
可以得到特征相容关系:
R=u+γ−12c=const
沿着特征线1,右传Riemann不变量保持常数不变
同理推到,沿特征线2:dtdx=λ2=u−c 也有特征相容关系:
S=−u+γ−12c=const
沿着特征线2,左传Riemann不变量保持常数不变
- 利用这两个代数方程,就可以把S这一点处的物理量 ρ,u 给计算出来,在一维均熵情况下,所有热力学量是独立的,用其他的量都可以表示出来
- 根据 c 可以把密度,温度,压强等等计算出来
一维均熵流动沿特征线Riemann不变量保持不变
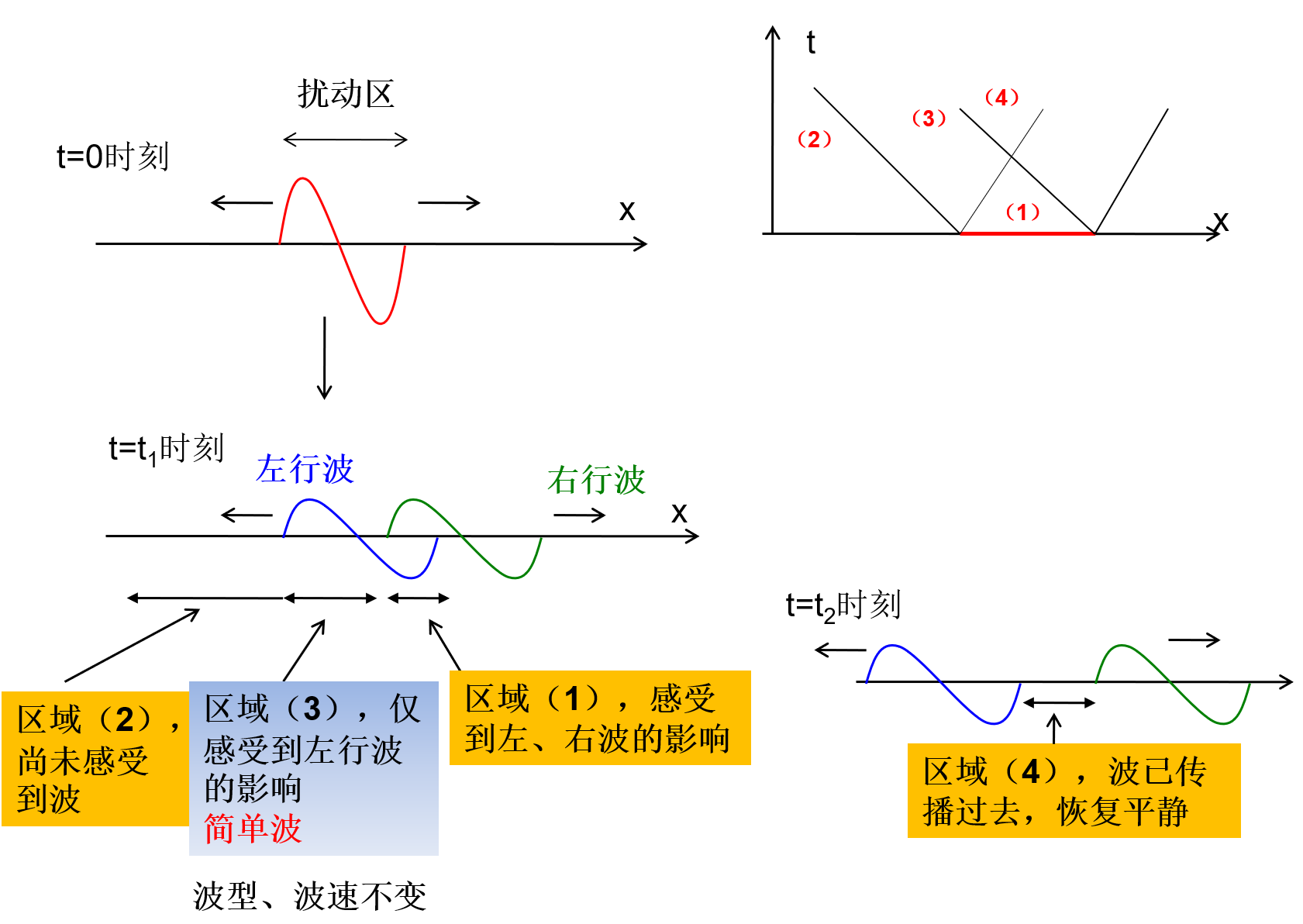
有限区域扰动波传播问题
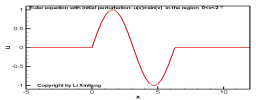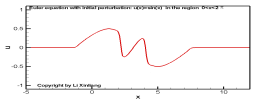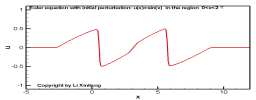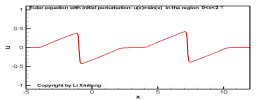
目的:学会如何运用Riemann不变量解题
考虑一维无粘流动(Euler方程),初始时刻(t=0)流动状态如下:
u,ρ={u′(x),ρ′(x),xa≤x≤xb0,ρ0(=const),others
试分析 t=t0 时刻的流动状态(假设流场不出现间断)
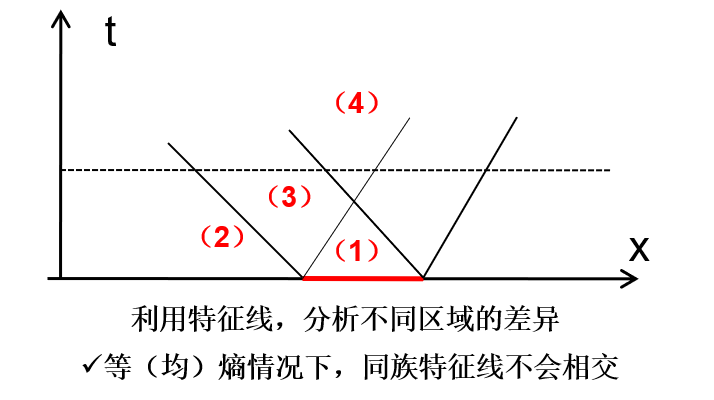
区域(2),(4)未扰动,区域(1)内的流动实验基本方法计算,区域(3)内的计算可简化:区域(3)内的波传播速度为常数,且在传播过程中物理量保持不变——简单波,因此特征线为直线
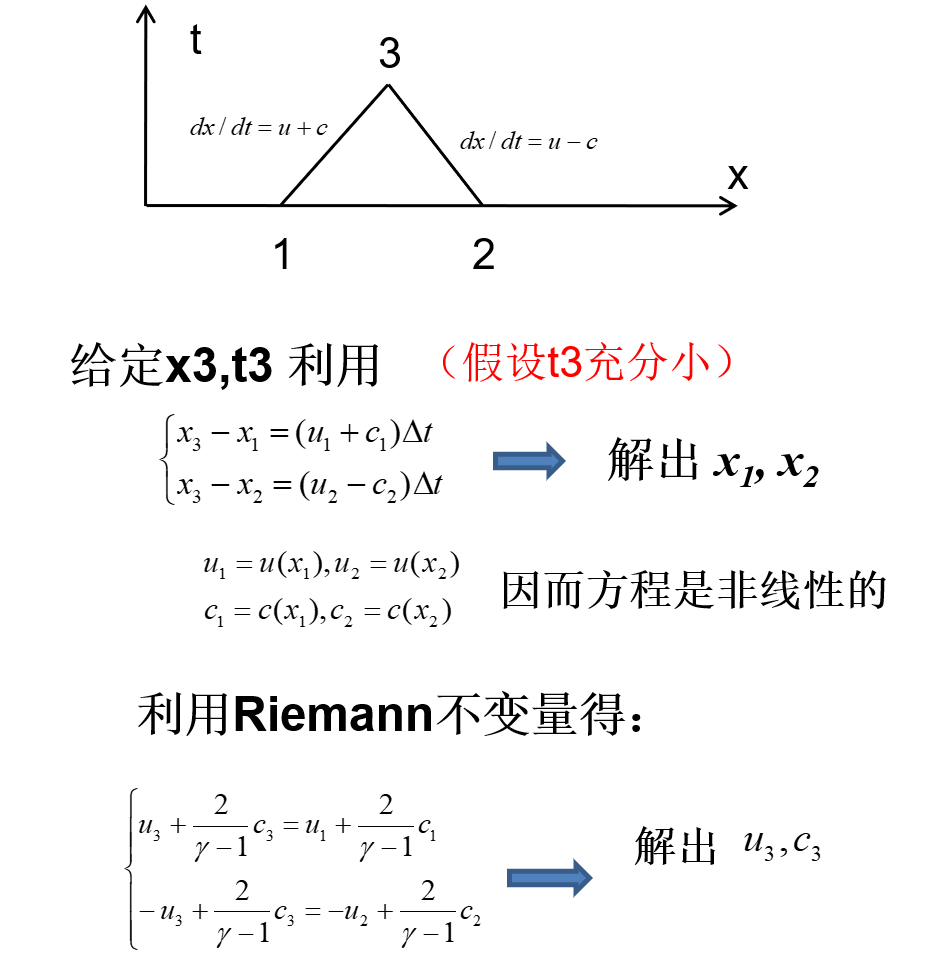
解出 t3 时刻的流场,继续推进下个时刻
区域(3)内扰动波的传播特点: 考虑(3)区内的, 同属一条特征线M上的任意两个点4和5:
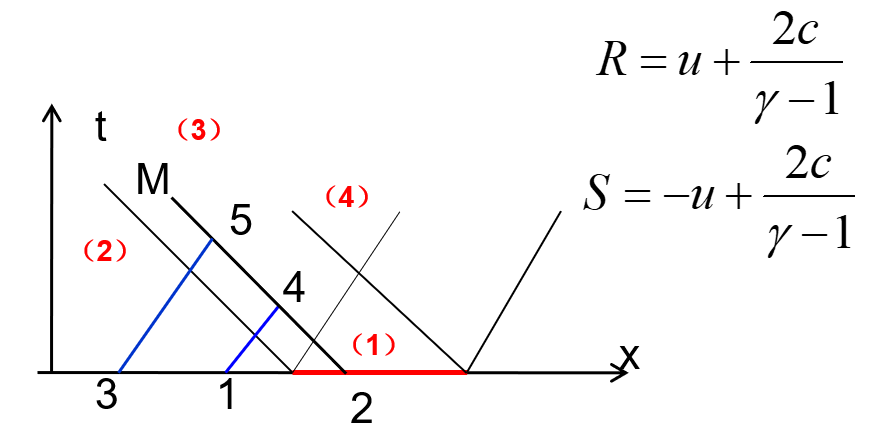
- S5=S4=S2
- R5=R3,R1=R4
- 由于点1和点3均在未扰动区: R3=R1
由此可得 R3=R1:
{S5=S4R5=R4→{u4=u5c4=c5
在(3)内,所有物理量(u,c)沿特征线M不变特征保持直线,特征波传播速度不变 → 简单波
双曲型方程的间断解(弱解)
前面叙述了双曲型方程可以怎么化简:可以利用特征线,在特性线上满足特征相容关系,在特殊情况下(一维均熵Euler方程)可简化,两条特征线上满足守恒的代数方程:一个是R,即右传Riemann不变量,一个是S,即左传Riemann不变量保持常数。
接下来看一下双曲型方程的间断解。
双曲型方程的特点:由于扰动波传播速度有限,不同扰动波传播可能会汇聚起来,从而产生一道间断。即使初始时刻解是光滑的,但是在发展过程中流场会自发的产生间断
- 弱间断:函数连续,但导数间断(如稀疏波的波头,波尾)
- 强间断:函数本身间断(如激波,接触间断)
- 流体力学控制方程:积分型(假设函数连续,光滑) → 微分型
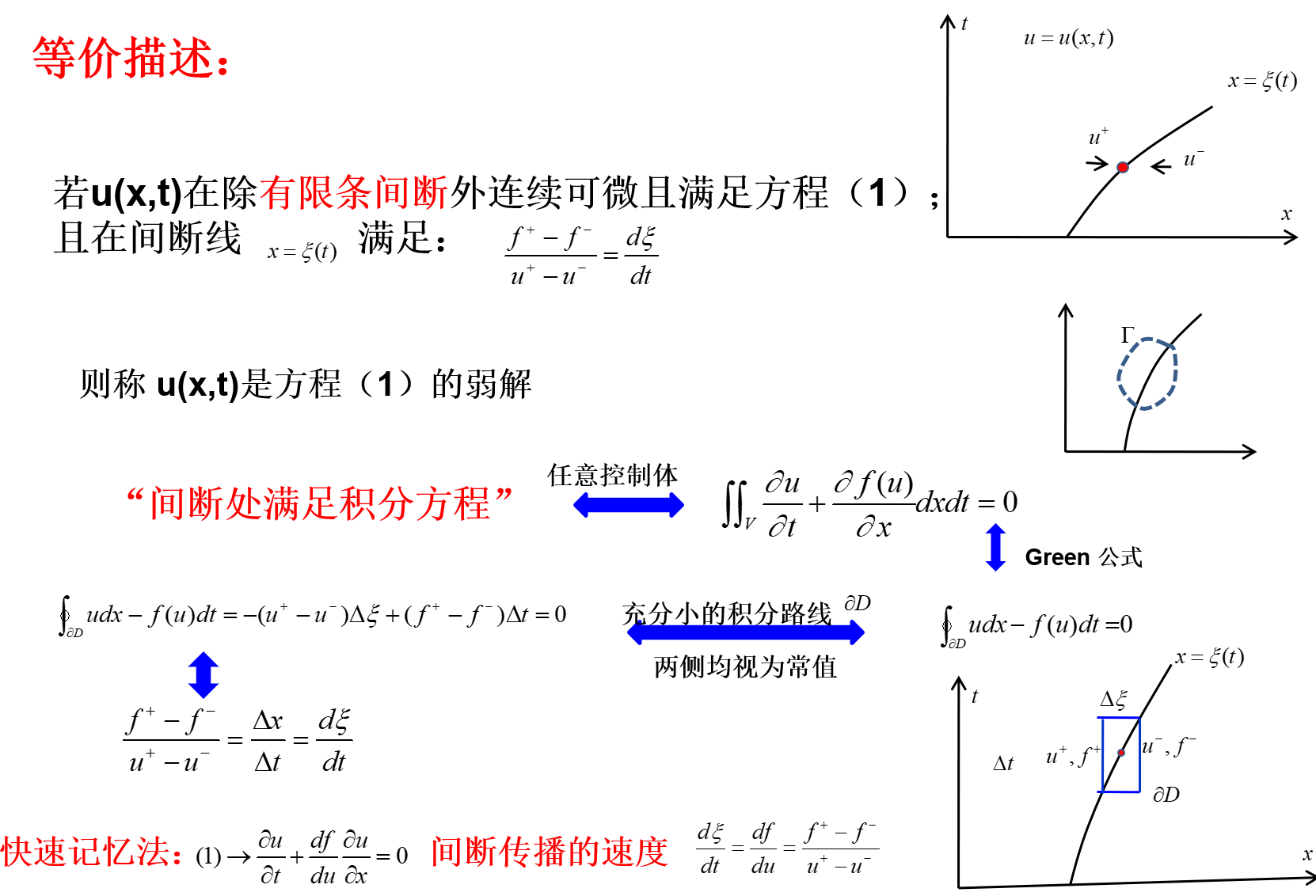
弱解
遇到间断情况下,定义这样的解是弱解:
在连续处满足微分方程:
∂t∂u+∂x∂f(u)=0,−∞<x<+∞,t≥0u(x,0)=φ(x)
在非连续处满足积分方程:
∬V∂t∂u+∂x∂f(u)dxdt=0
熵条件
概念:当 ϵ→0 时收敛得到的解为双曲型方程的物理解, ϵ 为粘性系数
∂t∂u+∂x∂f(u)=ϵ∂x2∂2u(ϵ>0)
利用弱解求解间断问题
例:一维Euler方程对应的积分条件(间断两侧关系式)
间断处虽然无法满足微分型方程,但积分型方程(三大守恒律)仍然满足
例如:激波两侧关系
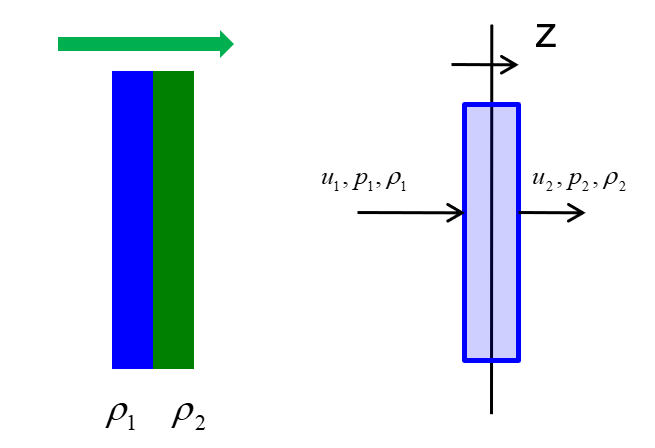
⎩⎪⎪⎨⎪⎪⎧ρ1(u1−Z)=ρ2(u2−Z)ρ1u1(u1−Z)+p1=ρ2u2(u2−Z)+p2E1(u1−Z)+u1p1=E2(u2−Z)+u2p2
原则:连续区需满足微分方程(Euler方程),间断两侧必须满足上述积分关系
特殊间断:接触间断(密度间断)
- u1=u2=Z
- p1=p2
- ρ1=ρ2
Riemann间断解
Riemann问题:一维无粘流动初始间断的演化问题
例:激波管问题
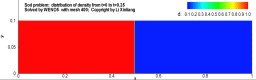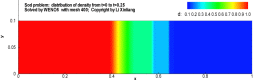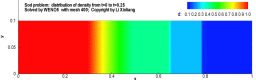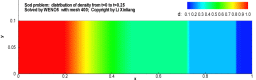
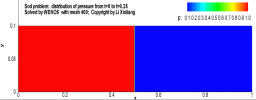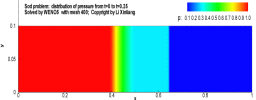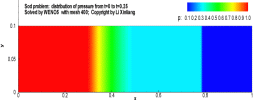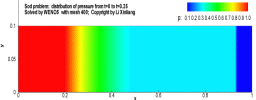
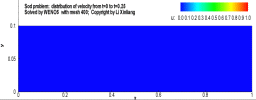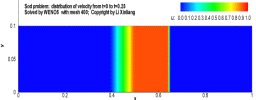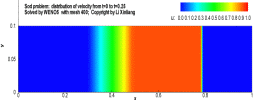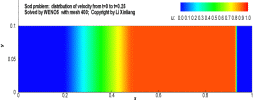
有一个一维的管道,管道内充满着无粘的可压缩流体,初始时刻在管道内有一个隔膜,定义右侧的密度较低,左侧高压高密度,将满足如下关系

Riemann问题对CFD的意义
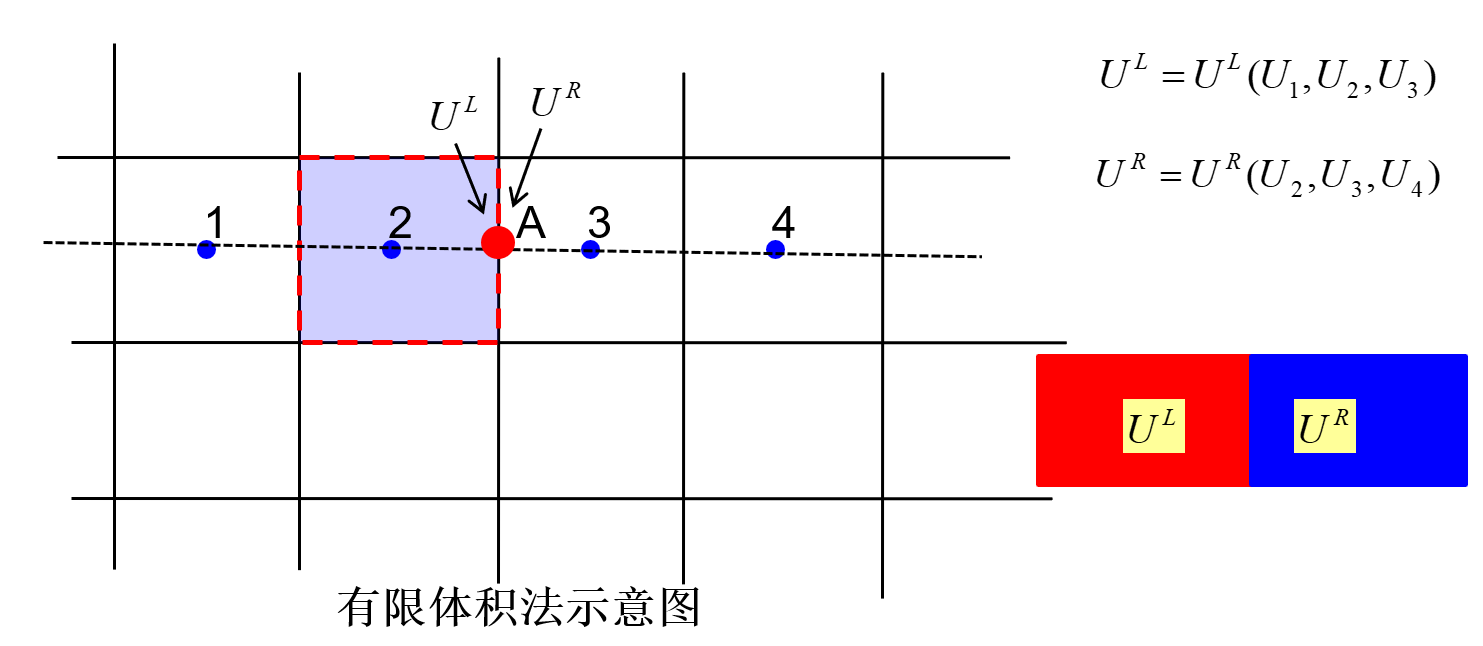
目的:计算A点所在界面的通量(以便获知控制体内物理量的变化)
- 利用数值方法(“插值”),用(偏)左侧点的值计算出 UL,用(偏)右侧点的值计算出 UR
- 求解Riemann问题(界面左侧为 UL 右侧为 UR)获得穿过界面的通量
Riemann问题求解思路

膨胀波(稀疏波)
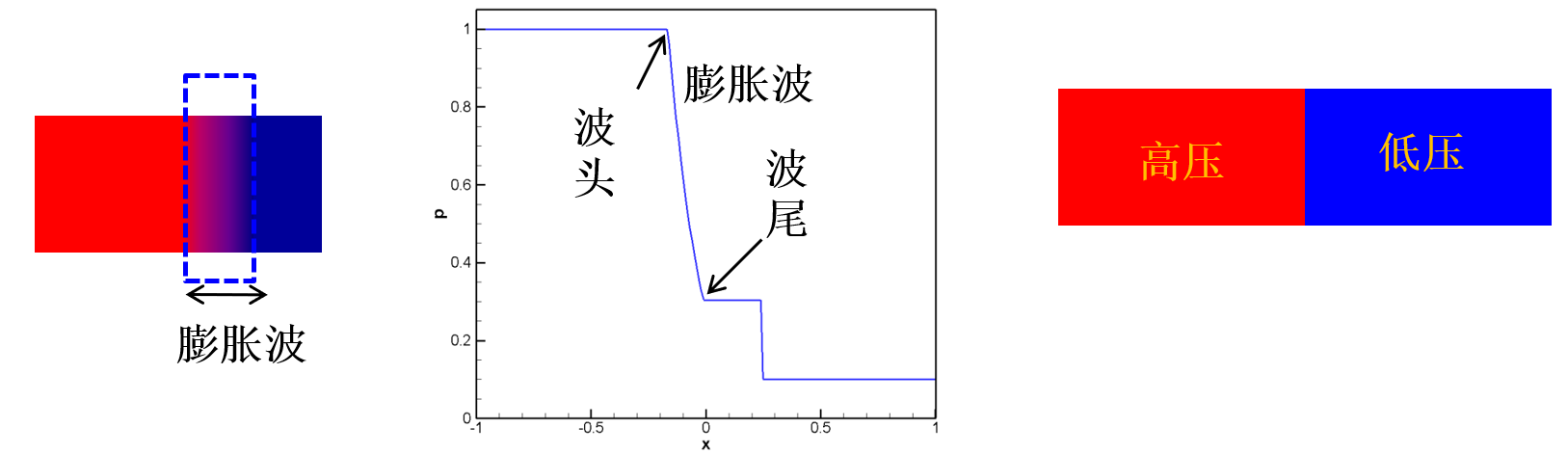
膨胀波:内部物理量连续、光滑头、尾物理量连续,但导数不连续(弱间断)
膨胀波两侧物理量的关系式:
- 熵不变:p∗/(ρ∗L)γ=p1/(ρ1)γ
- Riemann不变量不变:u1+γ−12c1=u∗+γ−12cL
Riemann解的5种情况
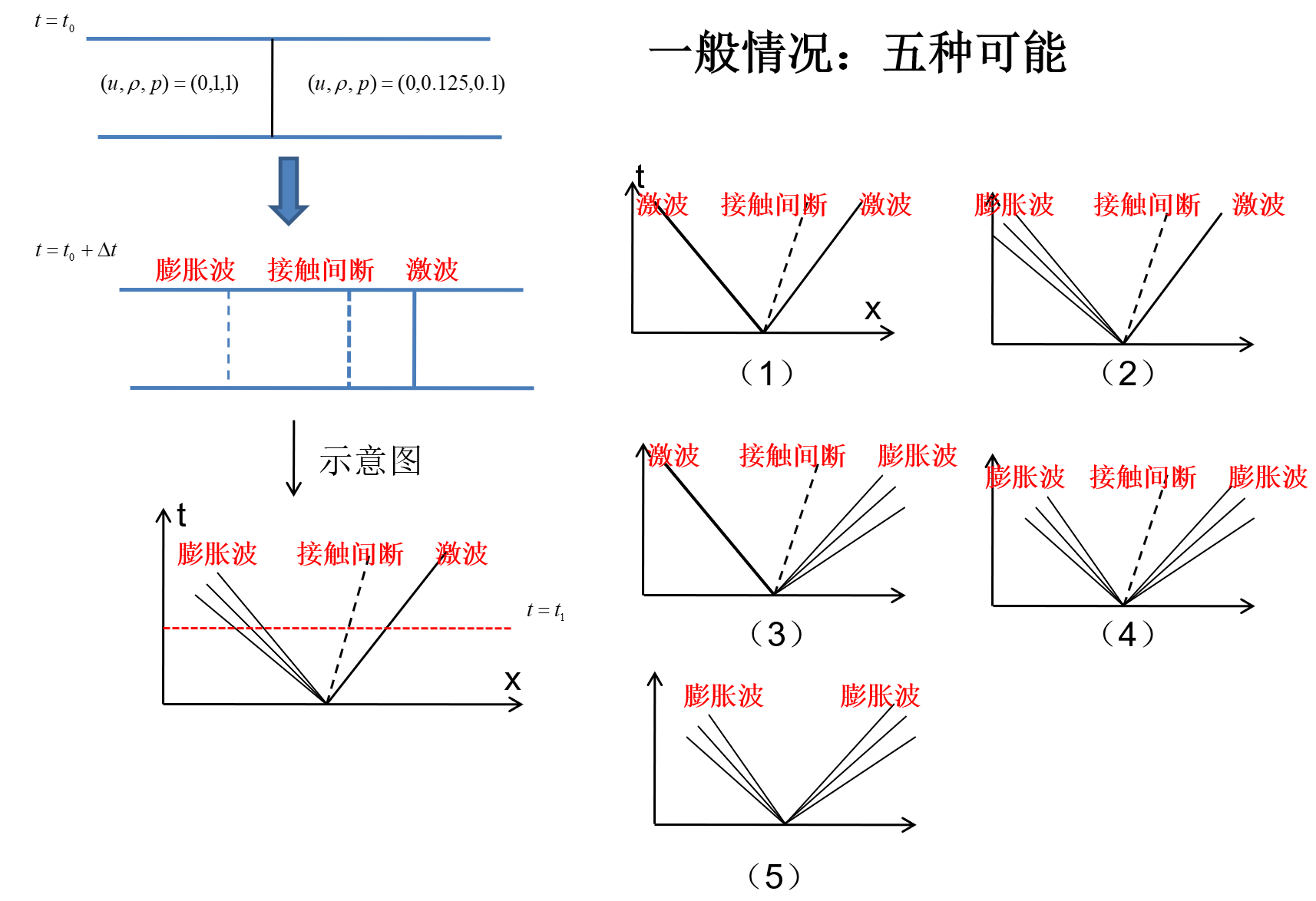
求解方法:针对每种情况分别考虑,利用积分关系,将微分方程化成代数方程计算
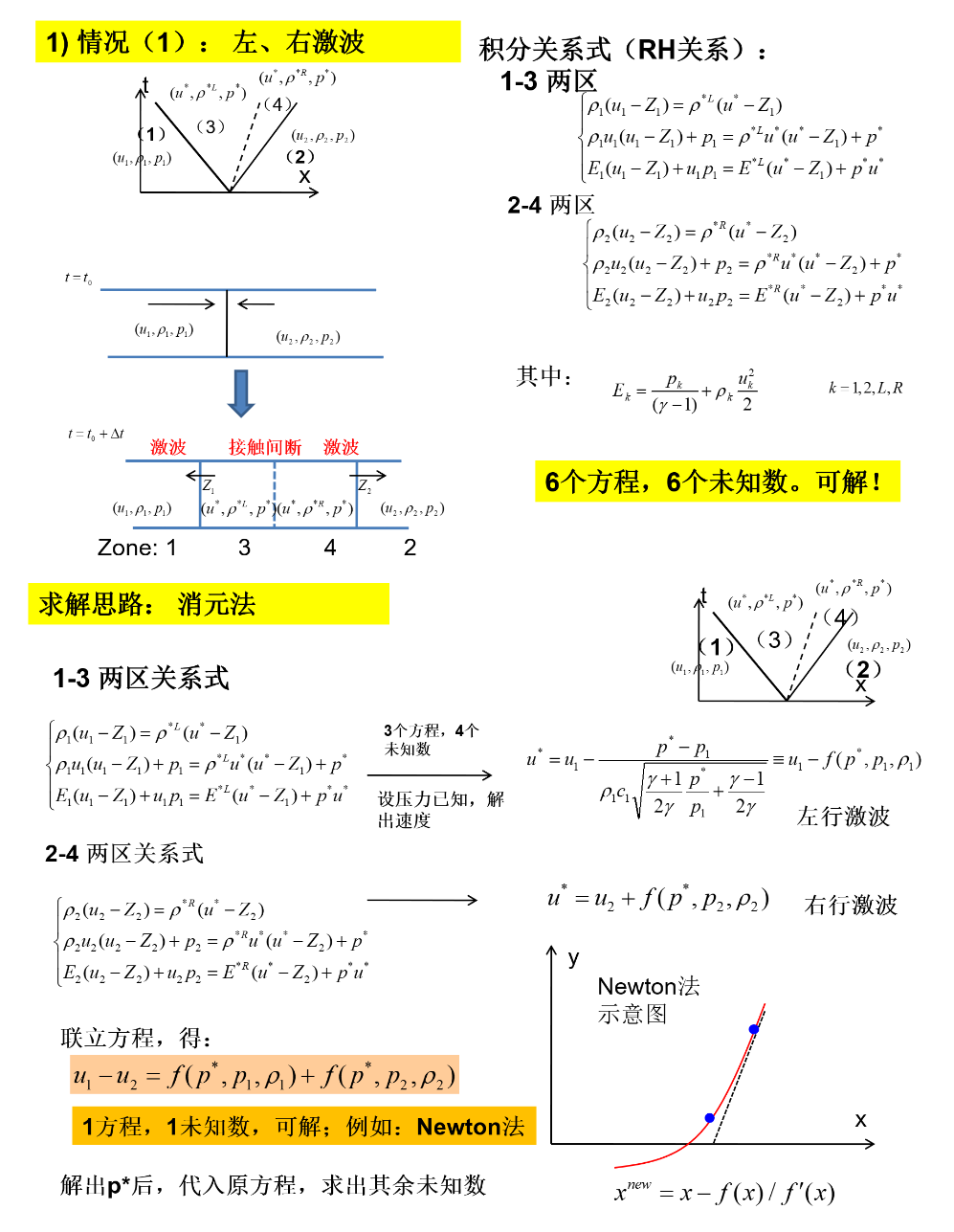
情况(2):右激波,左膨胀波
Sod激波管问题属于该情况!方法:先计算(3),(4)两区的值;再计算膨胀波内部(5)区的值
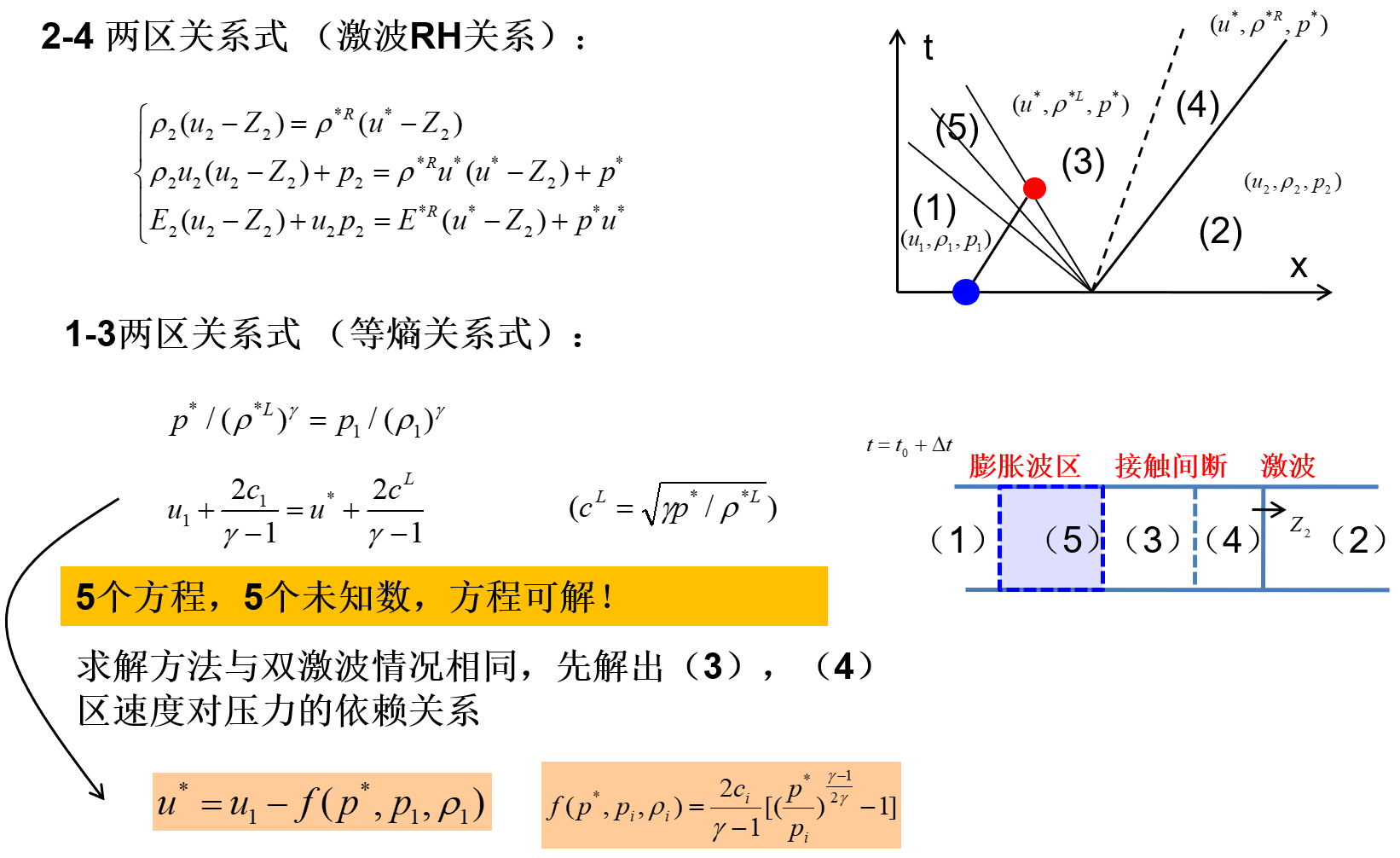
也可以不用区分到底是激波还是膨胀波,Riemann问题中间间断一打开,肯定会向左右两侧辐射出2道波(激波或膨胀波),所以激波、膨胀波前后速度-压力的依赖关系可写成统一的形式:
求解得到(3),(4)两区的压力 p∗ 然后解出速度和密度:
u∗=u1−f(p∗,p1,ρ1)
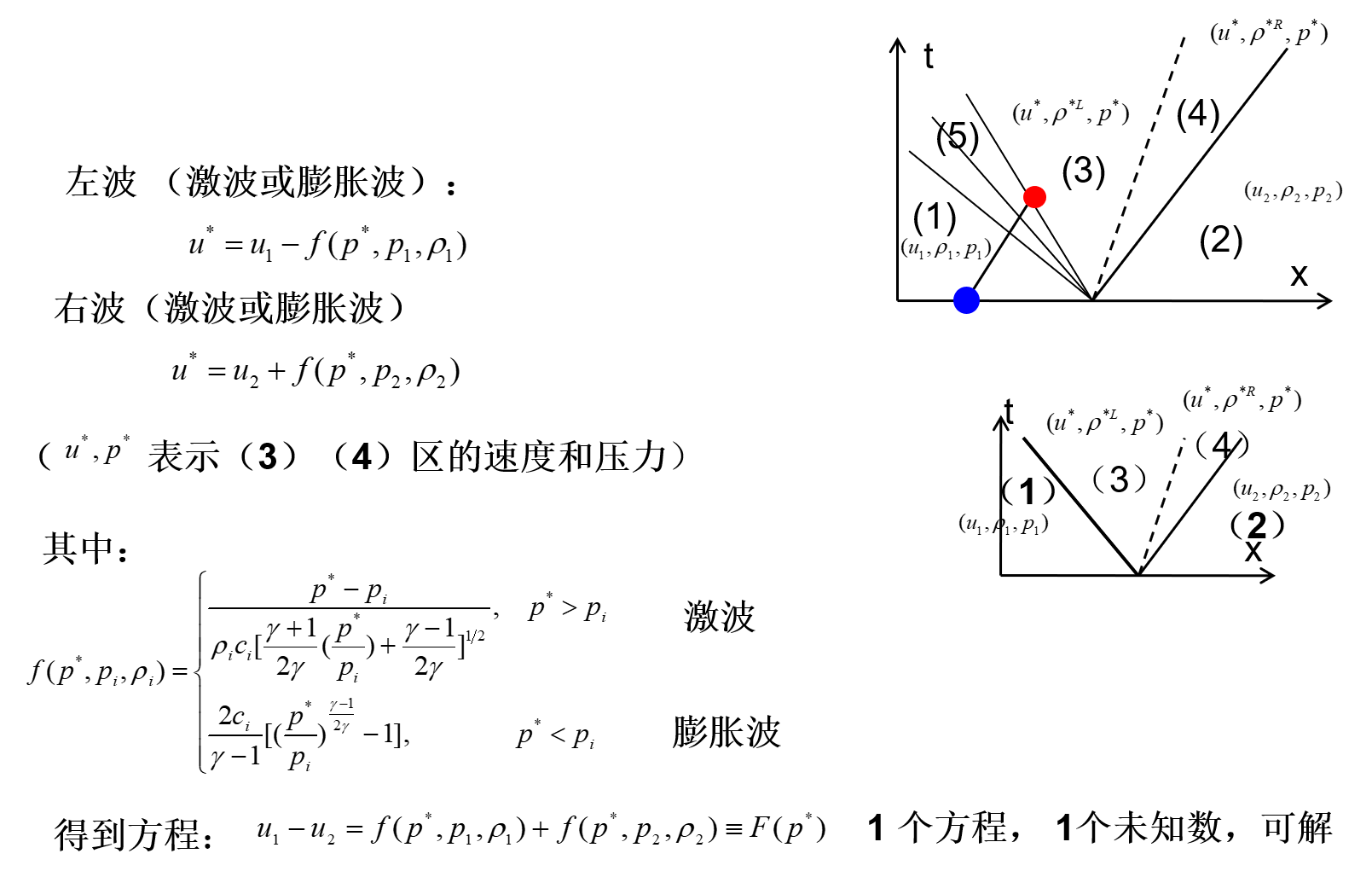
5种情况的区分
如何区分左、右行波时激波还是膨胀波?
判断原理:激波后压力升高,膨胀波后压力降低
设 p1≥p2 求解 F(p∗)=u1−u2 计算出中间区域压力 p∗
- p∗>p1:两侧均为激波(中间区域压力比两侧高)
- p1>p∗>p2:左膨胀波,右激波(中间压力比左侧低,比右侧高)
- p2>p∗:两侧均为膨胀波(中间压力低于两侧)
- p∗≤0:中间为真空区(真实压力不能小于0,只能是真空)
如仅判断左、右侧波的性质,无需求解 F(p∗)=u1−u2 计算出 p∗ 利用 F(p∗) 函数的单调递增特性即可
近似Riemann解初步
由于精确Riemann解(Godnov)计算量较大,且对精度要求也不高,所以大多数情况下采用近似Riemann解
近似Riemann解: 积分型(HLL, HLLC)、微分型(Roe)
HLL近似Riemann解(Harten, Lax & van Leer)
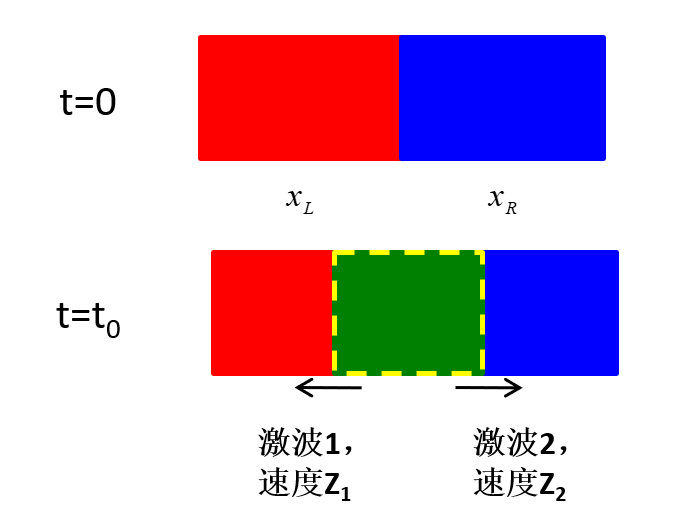
基本原理:双激波近似
假设间断面产生两道激波,速度分别为 Z1,Z2 根据质量、动量、能量守恒,容易计算出图中控制体积内的总质量、总动量、总能量。t0 时刻激波才传到控制体边界,因此0到 t0 时刻,控制体边界处物理量保持0时刻的值。利用总量,求出图中控制体内的平均值,作为该区域物理量的近似值
HLLC近似Riemann解(Toro)
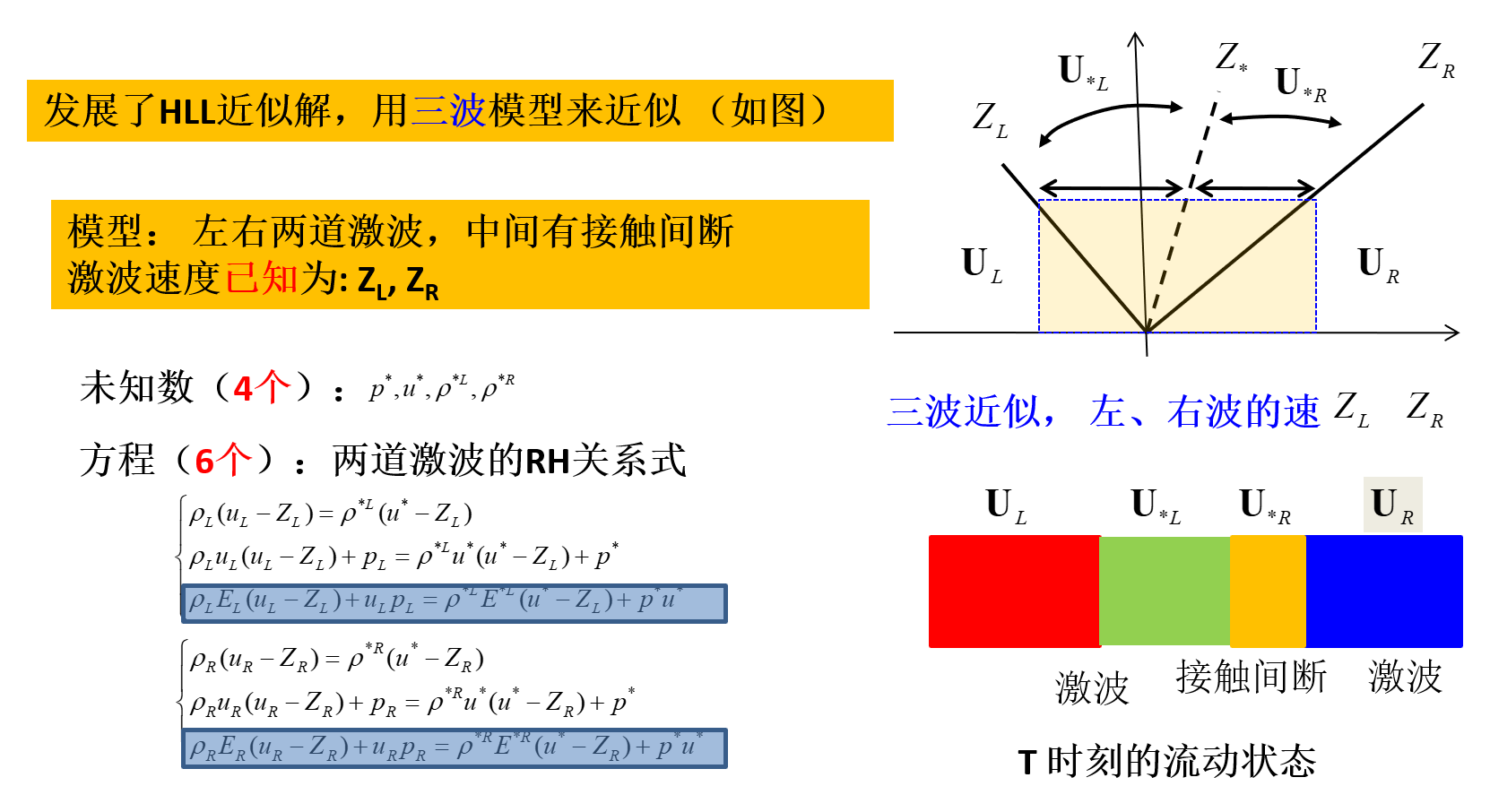
因为假设激波速度已知,常用方法:去掉两个方程,去掉两个能量方程,4个未知数,4个方程,求解求解过程简单,轻易可给出表达式
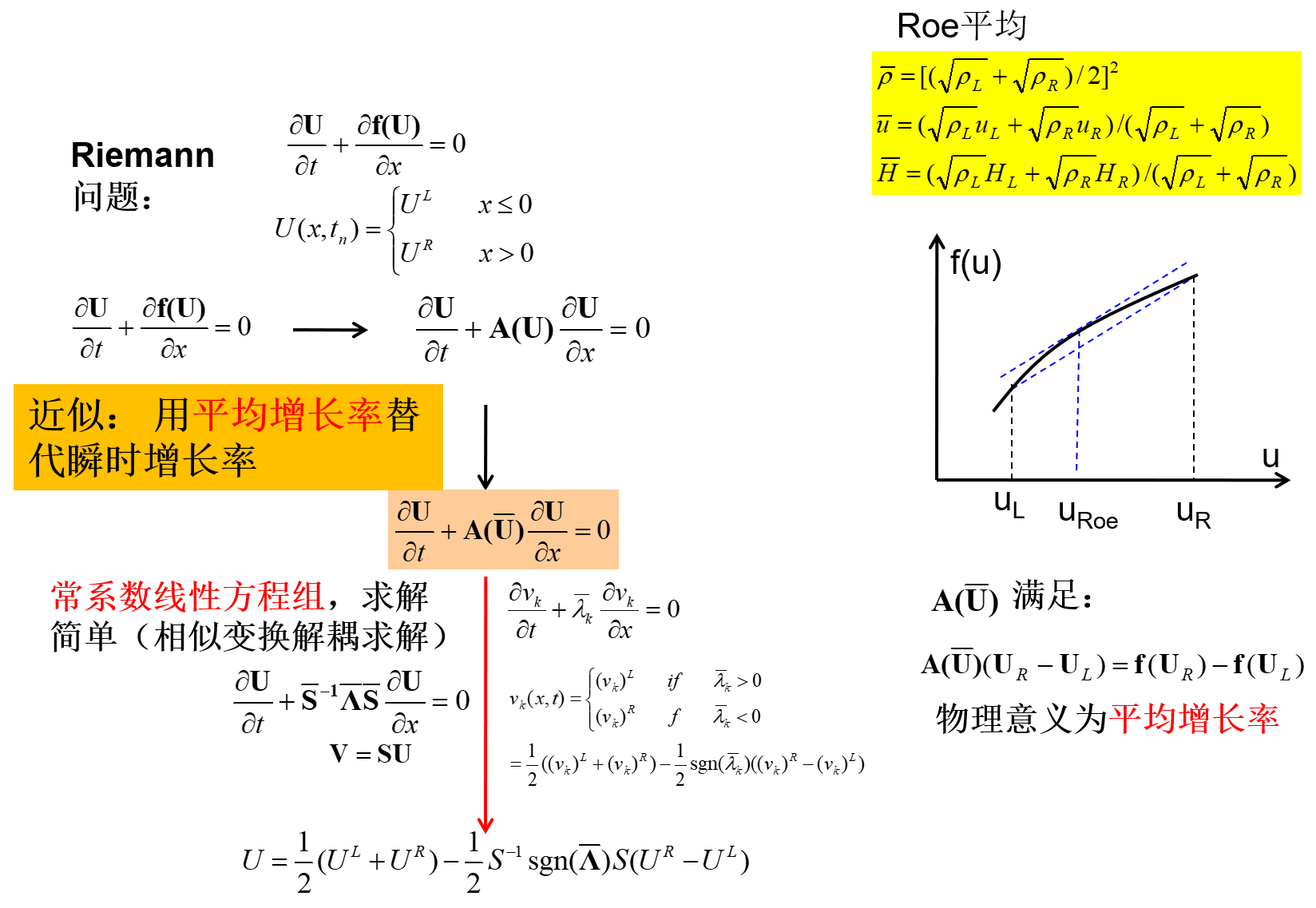
Roe近似Riemann解
这是目前应用最广泛的近似Riemann解,是微分型的Riemann解,它的核心是微分方程里面把非线性变系数矩阵 A 线性化,利用在这个区间内 f−u 的平均增长率来代替瞬时增长率,那么这个 A 就变成了常系数线性矩阵,从而方程大幅简化继而求解
知识总结2
有限差分法
- 传统计算方法:有限差分法,有限体积法,有限元法,谱方法(谱元法)等
- 最近发展的方法:基于粒子的算法(格子-Boltzmann, BGK),无网格
| CFD计算方法 |
优点 |
缺点 |
适用范围 |
| 有限差分法 |
简单成熟,可构造高精度格式 |
处理复杂网格不够灵活 |
相对简单外形的高精度计算 |
| 有限体积法 |
守恒性好,可处理复杂网格 |
不易提高精度(二阶以上方法复杂) |
复杂外形的工程计算 |
| 有限元法 |
基于变分原理,守恒性好 |
对于复杂方程处理困难 |
多用于固体力学等 |
| 间断有限元法(DG) |
精度高、守恒性好、易于处理复杂网格 |
计算量大;捕捉激波(限制器)难度大 |
复杂外形的高精度计算 |
| 谱方法 |
精度高 |
外形、边界条件简单 |
简单外形的高精度计算 |
| 粒子类方法 |
算法简单,可处理复杂外形 |
精度不易提高 |
复杂外形的工程计算 |
知识点1:
- 差分方法的理论基础(相容、收敛、稳定性;Lax等价定理;精度、修正方程; 守恒性)
- 差分格式的构造
- 差分格式的分辨率分析及优化
知识点2:
- 激波捕捉格式——人工粘性、TVD、MUSCL、NND、GVC、WENO
知识点3:
- 通量技术简介——Steger-Warming,Roe
- 常用的隐式处理方法——LU-SGS
知识点4:
- WENO格式及其发展
- 混合格式
- 高精度粘性项离散方法
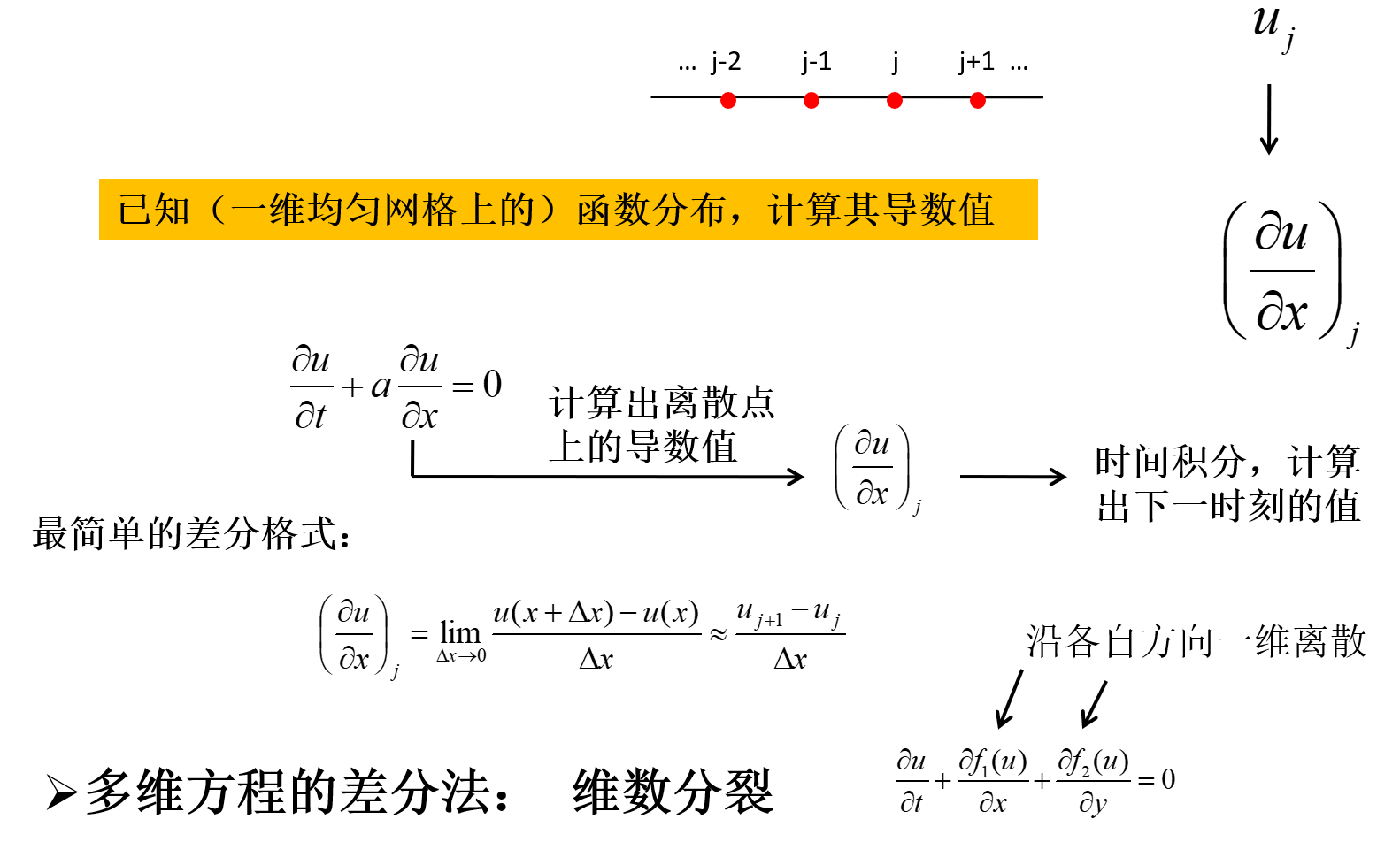
差分法基本概念
差分的基本功能:计算导数
构建差分格式
已知均匀网格点上物理量的分布为 {uj},试给出导数在 j 点值 (∂x∂u)j 的表达式。
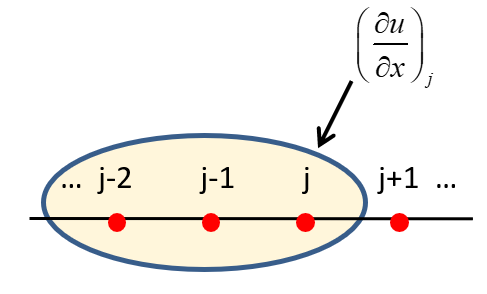
- 例:使用 j−2,j−1,j 3个点上信息计算 (∂x∂u)j
方法一:Taylor展开法(待定系数法)
- 确定网格基架点(Stencil):差分基架点:计算 j 点导数需要使用的点根据计算量、精度需求等要求而定
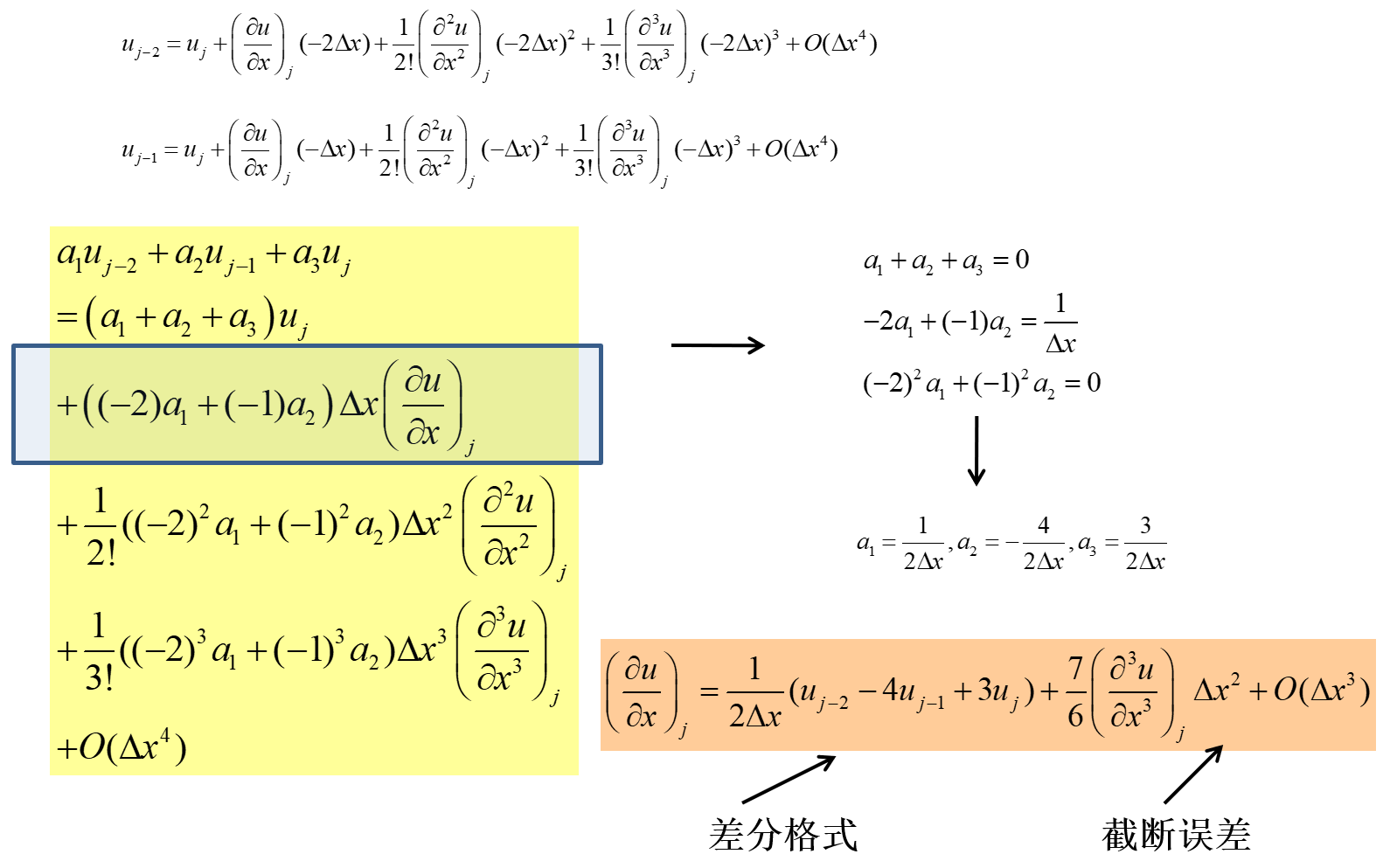
- 写成待定系数形式:(∂x∂u)j=a1uj−2+a2uj−1+a3uj+O(Δxn)
- 利用Taylor展开,确定系数
方法二:多项式逼近法
如图,已知函数 u(x) 在 j−2,j−1,j,j+1 四个点上的值分别为:uj−2,uj−1,uj,uj+1,试计算 (∂x∂u)j 的近似值。
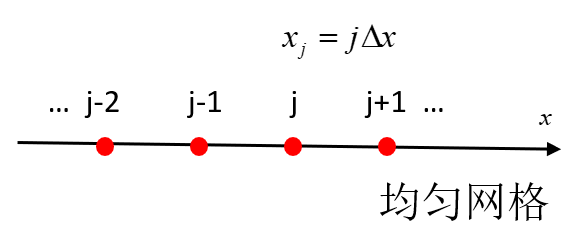
- 假设 u(x) 在该区间呈多项式函数分布:u(x)=ax3+bx2+cx+d
- 利用已知条件(已知点上的值),定出上式系数
- 计算导数:∂x∂u=3ax2+2bx+c
(∂x∂u)j=2Δx1(uj−2−4uj−1+3uj)
该方法也适合于非均匀网格,甚至非结构网格
差分格式的精度
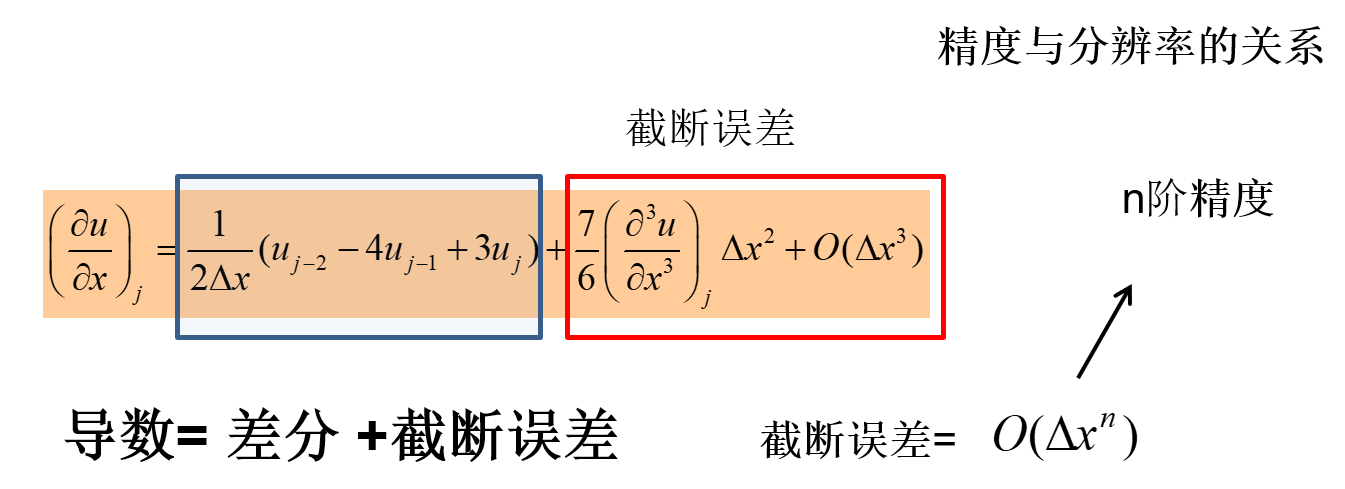
那么给定一个差分格式,如何判断精度?
- 方法1:理论推导: Taylor展开,计算截断误差项(非线性格式推导困难)
- 方法2:数值实验,即给定一测试函数(可精确求导),计算误差对网格尺度的依赖关系
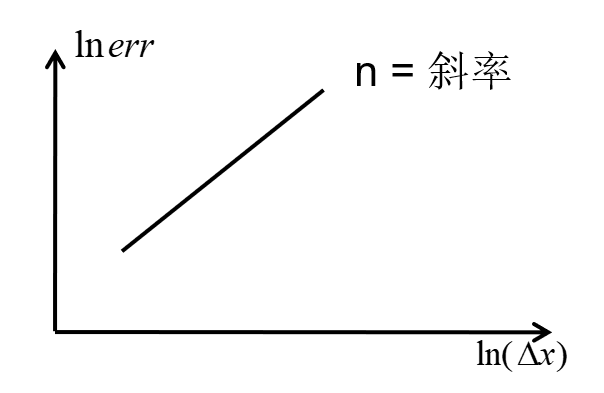
err=AΔxn→lnerr=lnA+nlnΔx
差分方程的修正方程
修正方程:逼近于差分方程的微分方程
- 差分方程:把原先微分方程差分化,所有的导数差分化,得到一种代数方程
- 修正方程:差分方程准确逼近(无误差逼近)的方程
- 微分方程 = 差分方程 + 截断误差
差分方程 = 微分方程 - 截断误差 = 修正方程
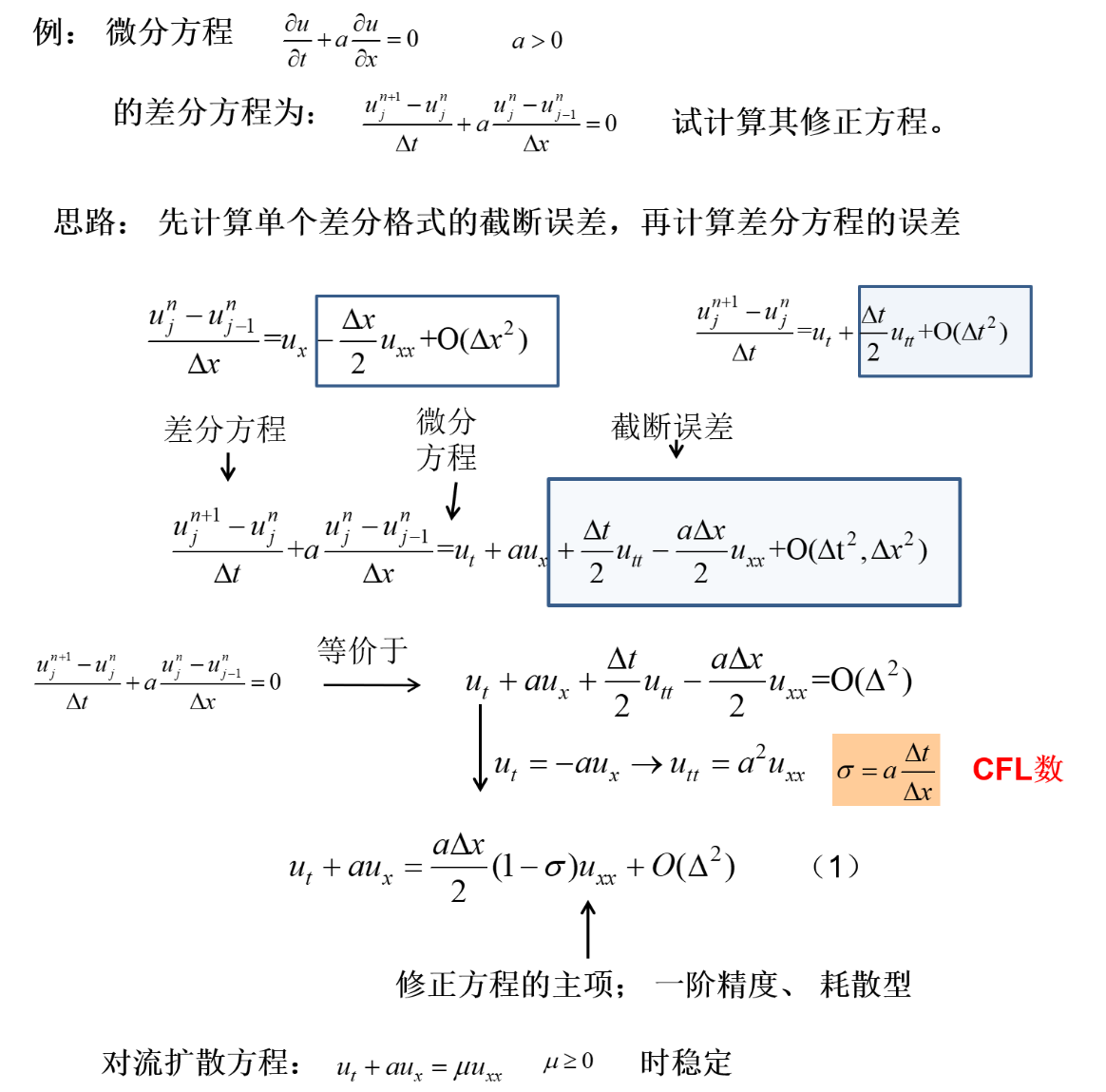
通常,修正方程不出现时间高阶导数项(便于进行空间分析)
一些记号的约定:

迎风型差分格式
对于双曲型方程有特征波,波是有传播方向的,点上增加一个扰动,就沿着特征波的方向传播,因此构建差分格式时,要尽量利用这个特征波传播方向,利用(偏)上游信息构造差分格式
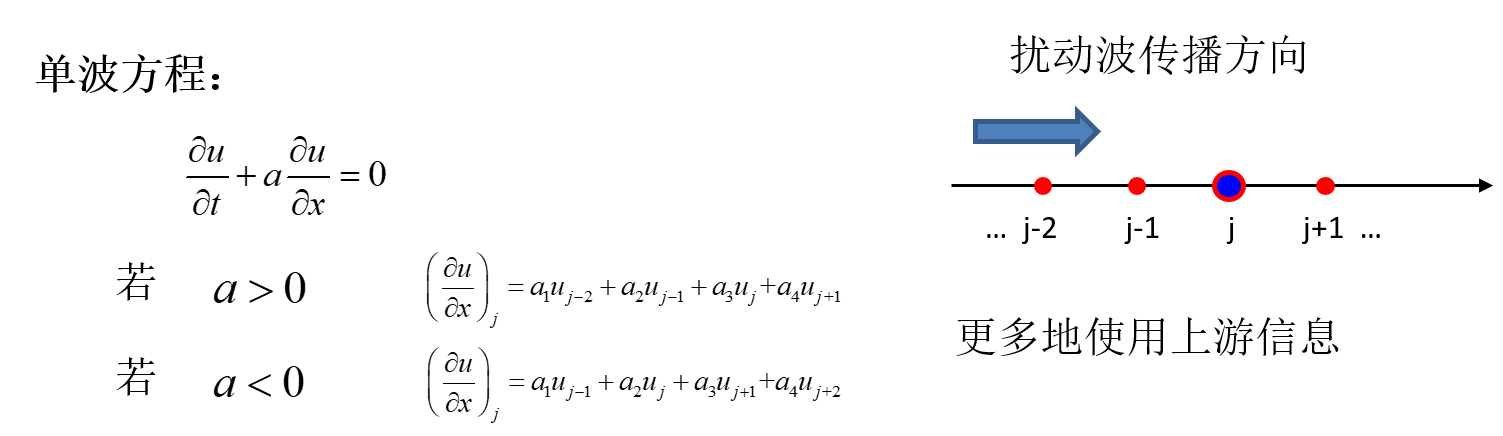
对于一般双曲型方程(例如Euler方程)看不出扰动波是从左侧还是从右侧传播过来的,这时可以用其他方法做:

复杂网格的处理方法
一维情况(非均匀网格)
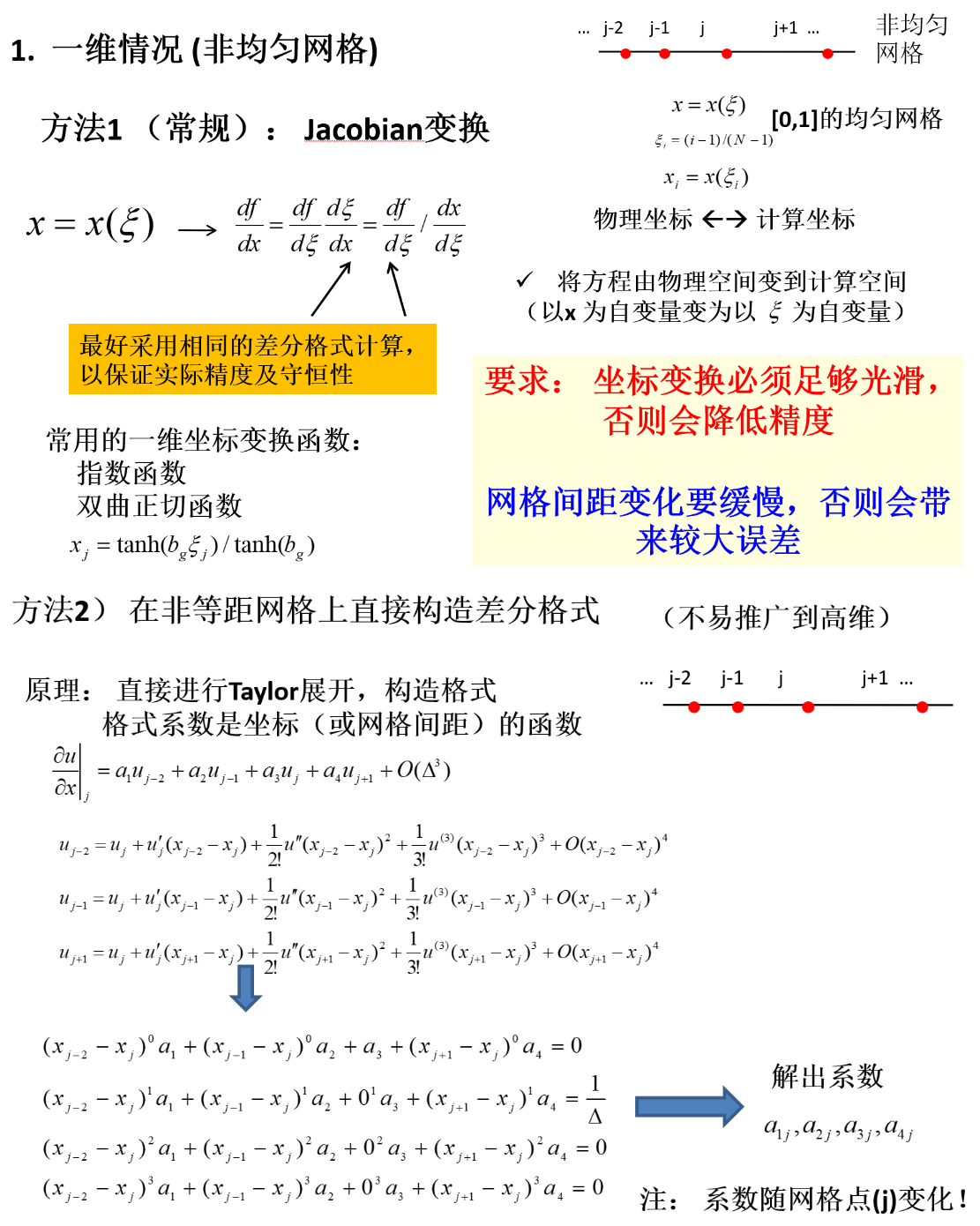
- 对于方法2:网格非光滑、间距剧烈变化不会降低精度;随机网格也可保证精度;不易推广到高维
二维情况
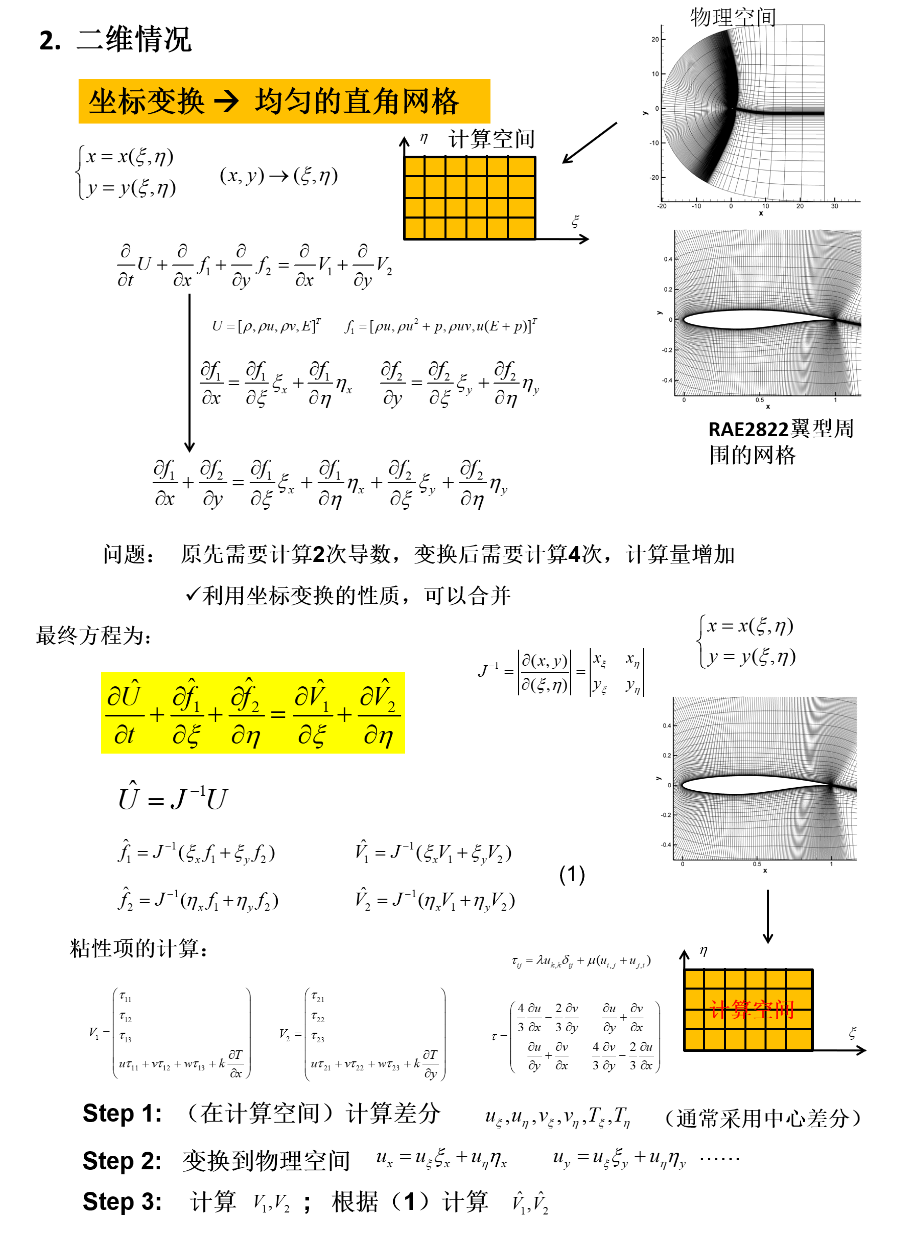
具体合并方法:
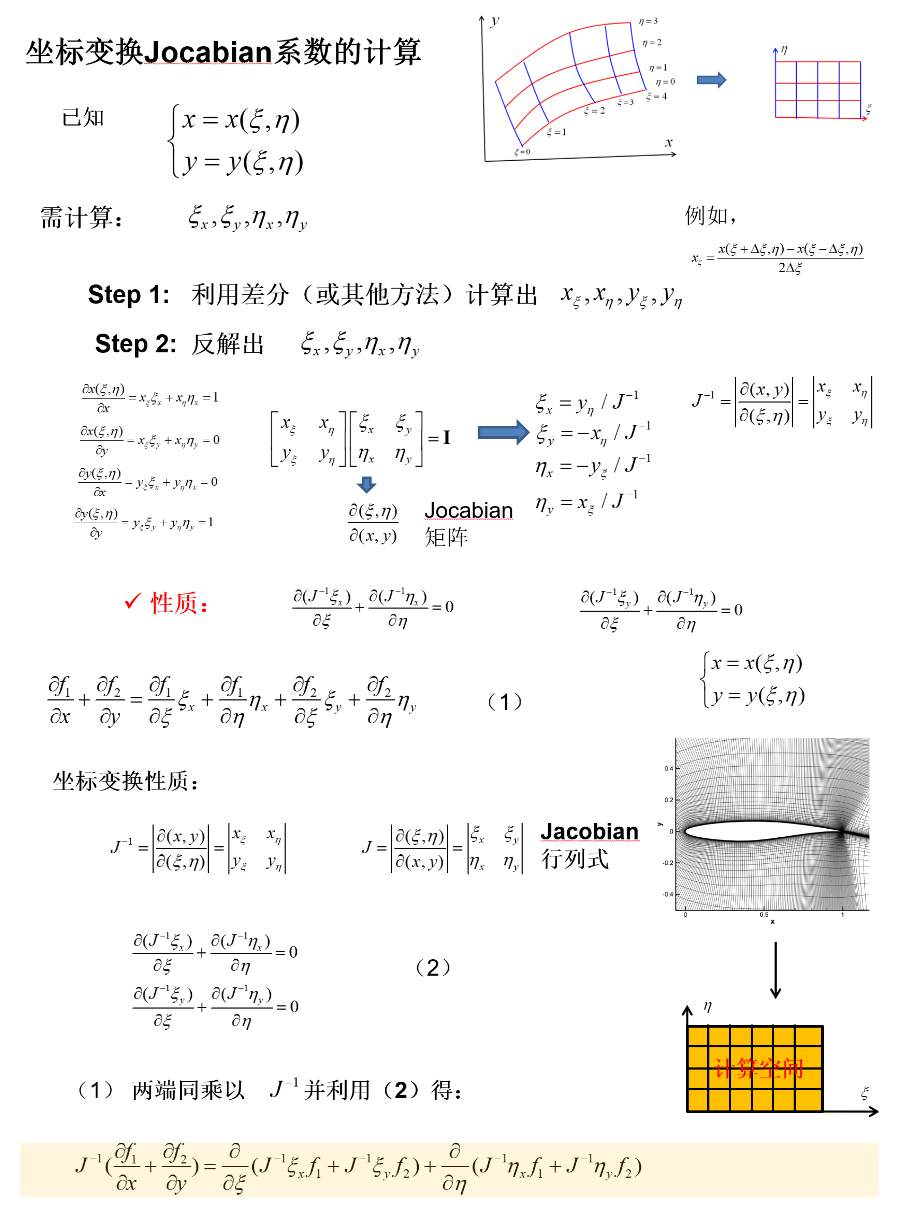
坐标变换系数的几何含义
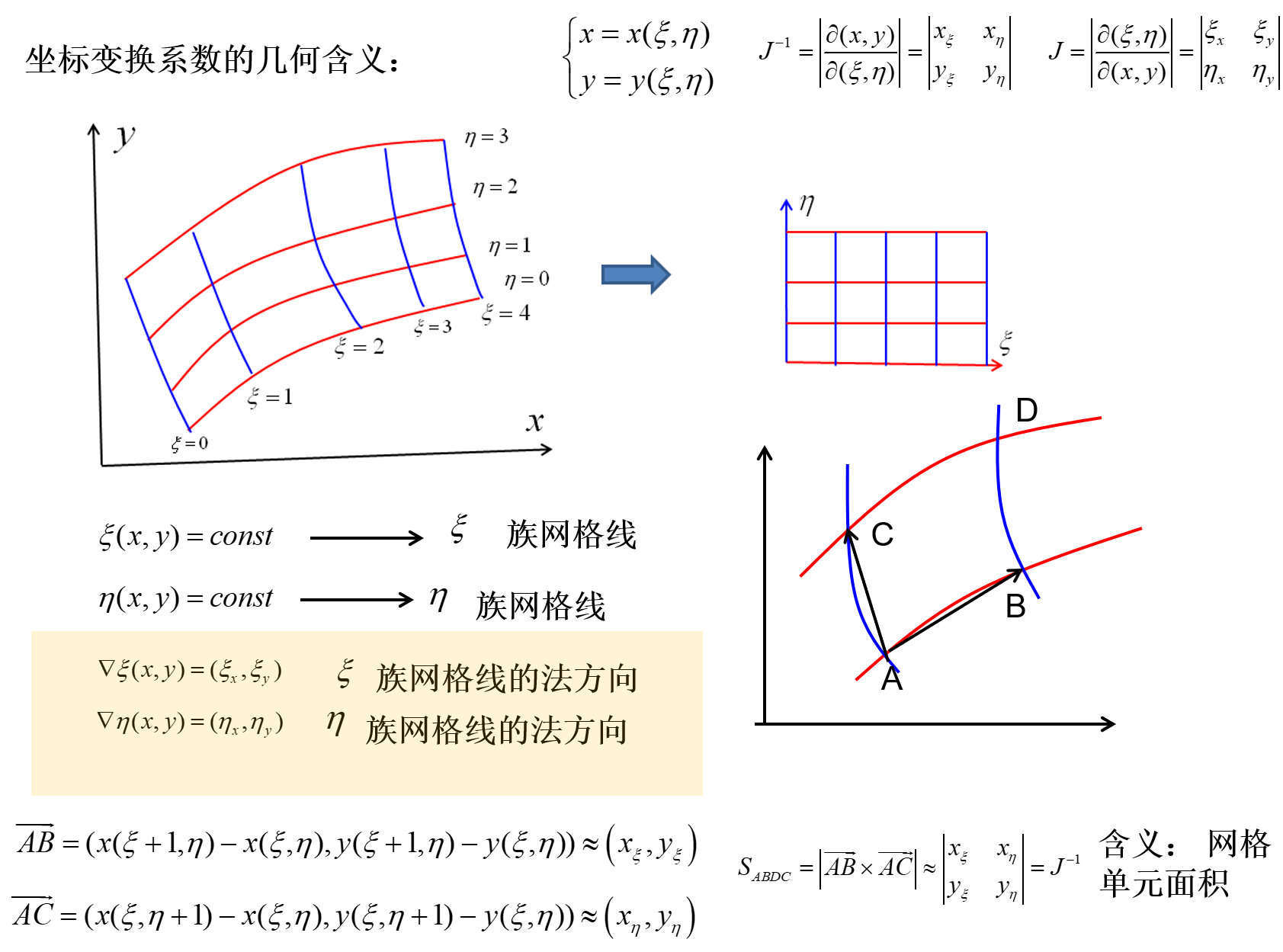
三维情况
守恒型差分格式
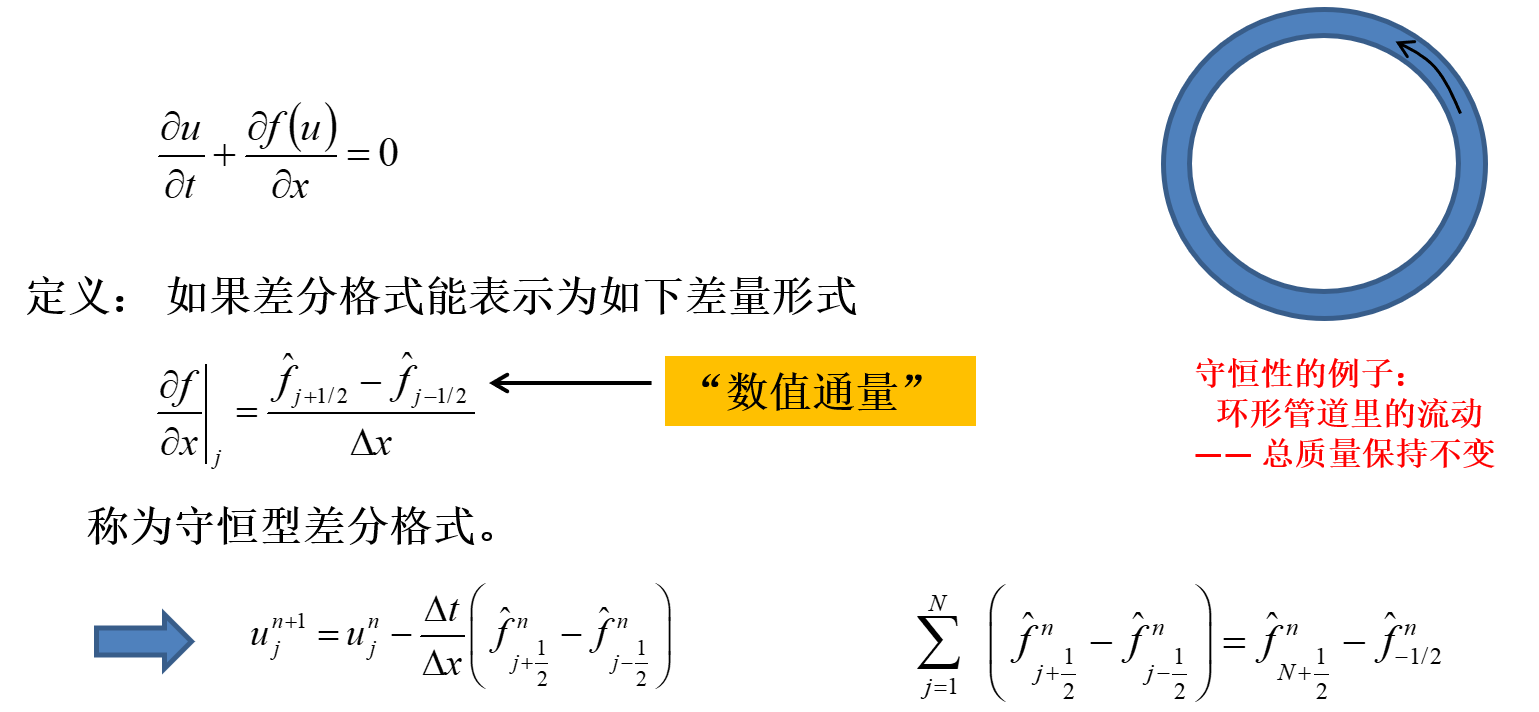
- 基本思想:保证(整个区域)积分守恒率严格满足
- 特点:消去了中间点上的值,只保留两端
- 守恒方程 + 守恒格式 = 守恒解
物理含义:只要边界上没有误差,总积分不会有任何误差
关于守恒性格式的一些注解

数值通量(numerical flux)
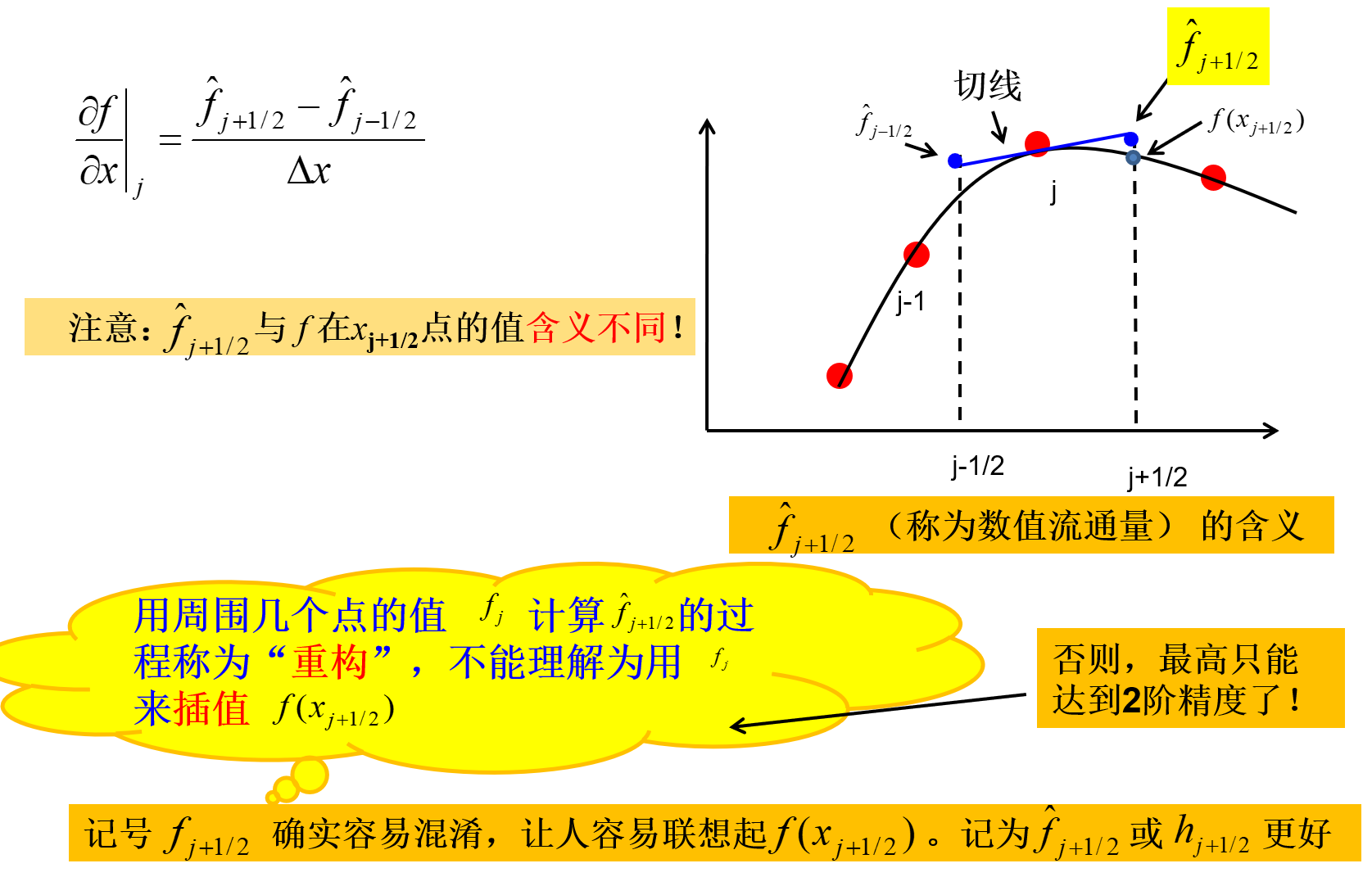
数值通量的数学含义如下:
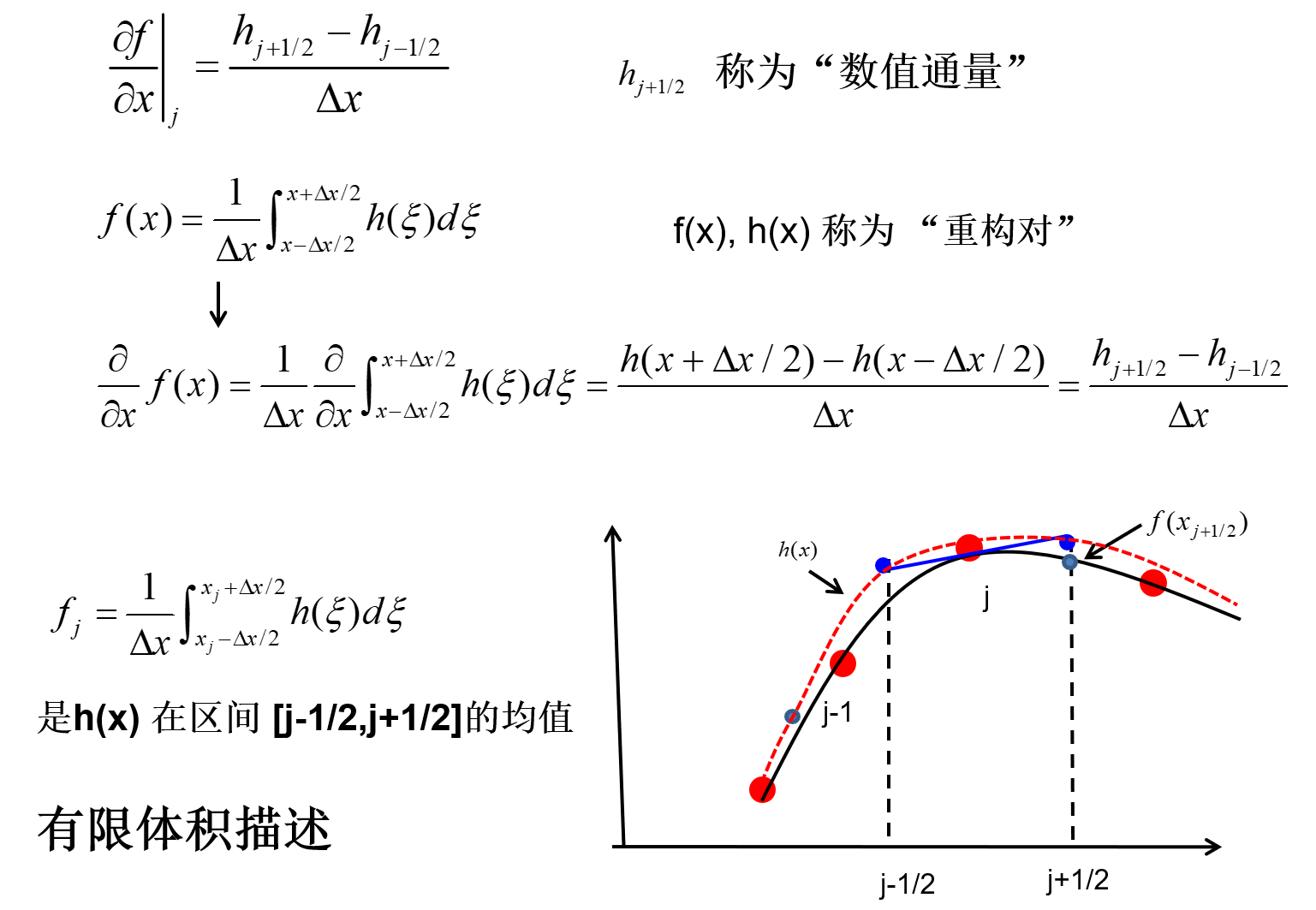
已知物理量的积分平均值,来计算物理量在 j+21 半点处值的一个过程
此外,常系数线性格式是守恒的
例如:差分格式
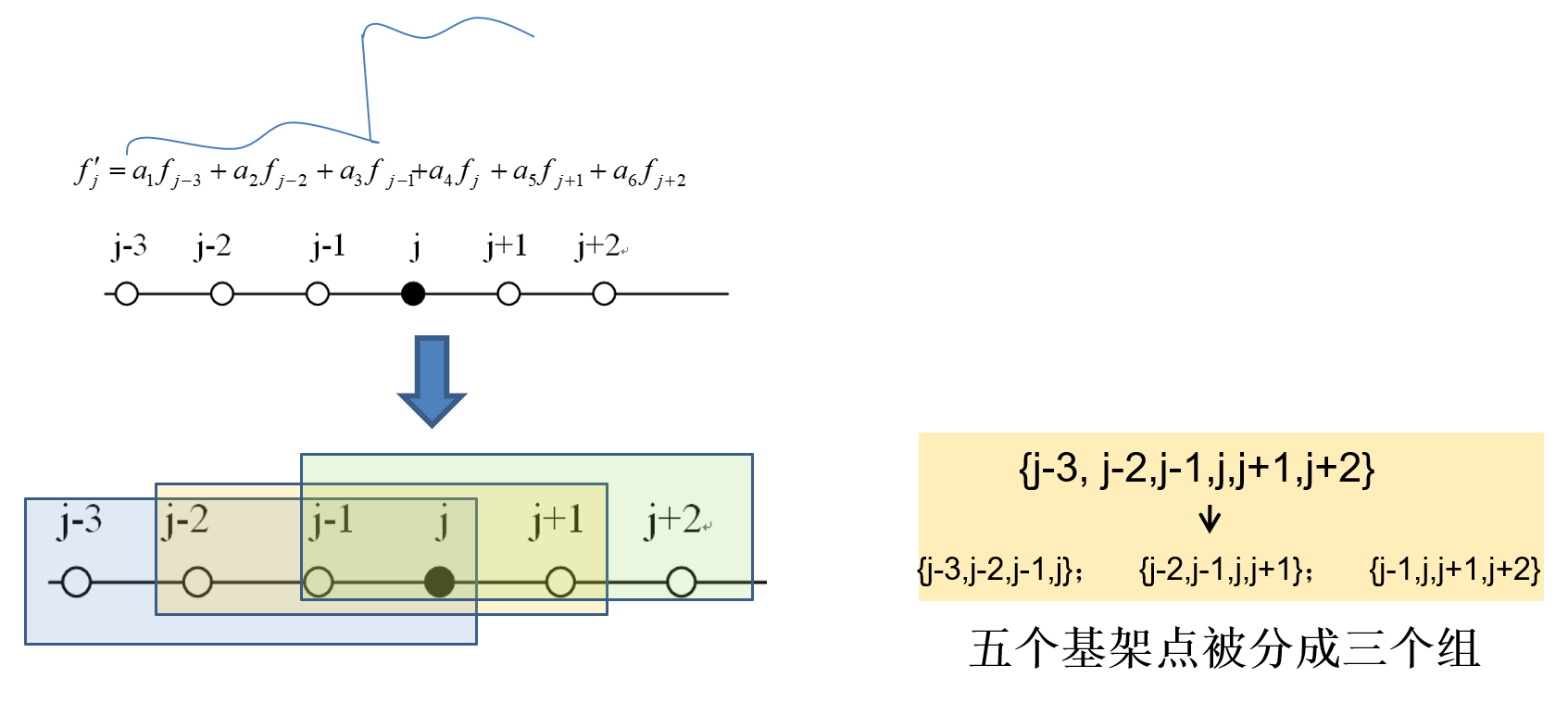
(∂x∂fj)=Δx1(a1fj−3+a2fj−2+a3fj−1+a4fj+a5fj+1+a6fj+2)
等价于
(∂x∂fj)fj+1/2=Δxfj+1/2−fj−1/2=b1fj−2+b2fj−1+b3fj+b4fj+1+b5fj+2
其中,b1=−a1,bk=bk−1−ak
时间离散
刚刚叙述了守恒性的格式,空间上的离散,下面叙述时间上的离散
显格式及隐格式
显格式:在计算时都利用了已知物理量的值,无需解方程就可以直接计算 n+1 层的值
Δtujn+1−ujn+aΔxujn−uj−1n=0
隐格式:物理量写在未知层上,必须求解方程组才能计算 n+1 层的值
Δtujn+1−ujn+aΔxujn+1−uj−1n+1=0
常用的显格式:

时空独立离散及耦合离散
Lax-Wendroff格式
下面举一个例子:Lax-Wendroff格式
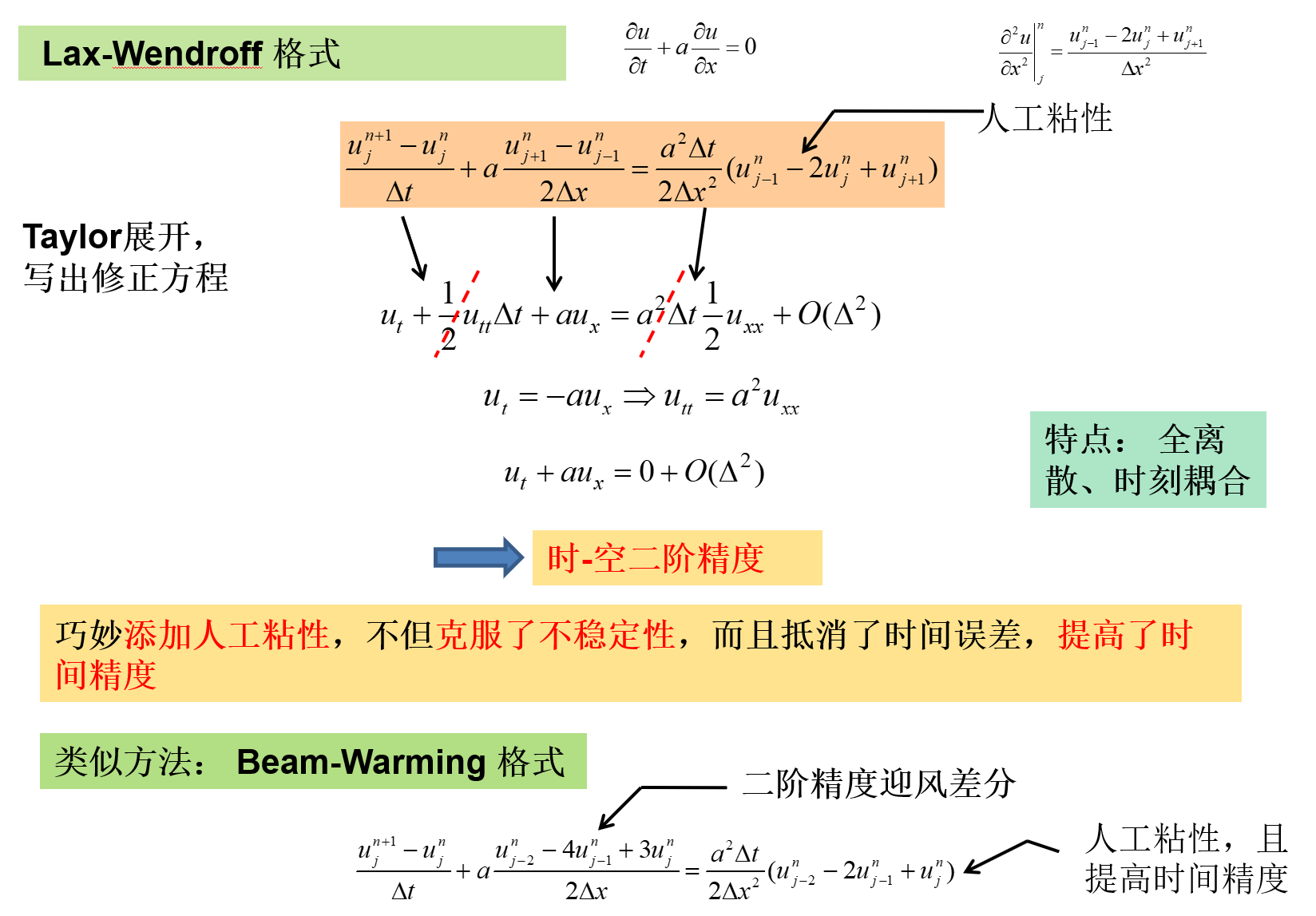
增加的人工粘性项有误差,这个误差刚好于时间导数的2阶项误差抵消掉了,精度还提高了。这就是Lax-Wendroff格式的巧妙之处
Lax-Wendroff格式巧妙添加了人工粘性,不但克服了流动方程的不稳定型,而且还抵消了时间误差,提高了时间的精度
现在很多构造格式的时候,为了抵消时空之间的误差,通常添加空间导数,添加空间格式精度,利用它抵消时间误差,从而提高它的时间精度等等这类格式叫做Lax-Wendroff类的格式
差分方程的稳定性
相容、收敛、稳定性与Lax等价定理
相容性
相容性:含义:方程趋近。当差分方程中,时间与空间步长均趋近于0时,差分方程的截断误差也趋近于0,则称差分方程与原微分方程是相容的
收敛性
收敛性:含义:解趋近(更强)。当时间与空间步长均趋近于0时,差分方程的解趋近于微分方程的解,则称差分方程的解收敛于原微分方程的解

稳定性
定义:称差分方程的初值问题是稳定的,如果当 Δt 和 Δx 做够小时,存在于 Δt 和 Δx 无关的常数C1和C2使得:
∥uh(x,tn)∥≤c1exp(c2(tn−t0))∥uh(x,t0)∥
含义:在差分方程的求解过程中,如果引入的误差随时间的增长有界,则称差分方程是稳定的
Lax等价定理
Lax等价定理:如果微分方程的初边问题是适定的,差分方程是相容的,则差分方程解的收敛性与稳定性是等价的
含义:如果微分方程不出问题(适定),差分方程性质好(稳定),则方程逼近就可保证解逼近。如果方程逼近就可以导致解逼近,则差分方程的性质肯定好(稳定)
差分格式稳定性分析方法
Fourier分析法(针对线性系统):基本思想:初始时刻引入单波扰动,考虑其随时间的变化。原理:任何扰动都可认为是单波扰动的叠加;线性情况下不同波之间独立发展。引入单波扰动,带入差分方程,如果其振幅放大,则不稳定;否则稳定
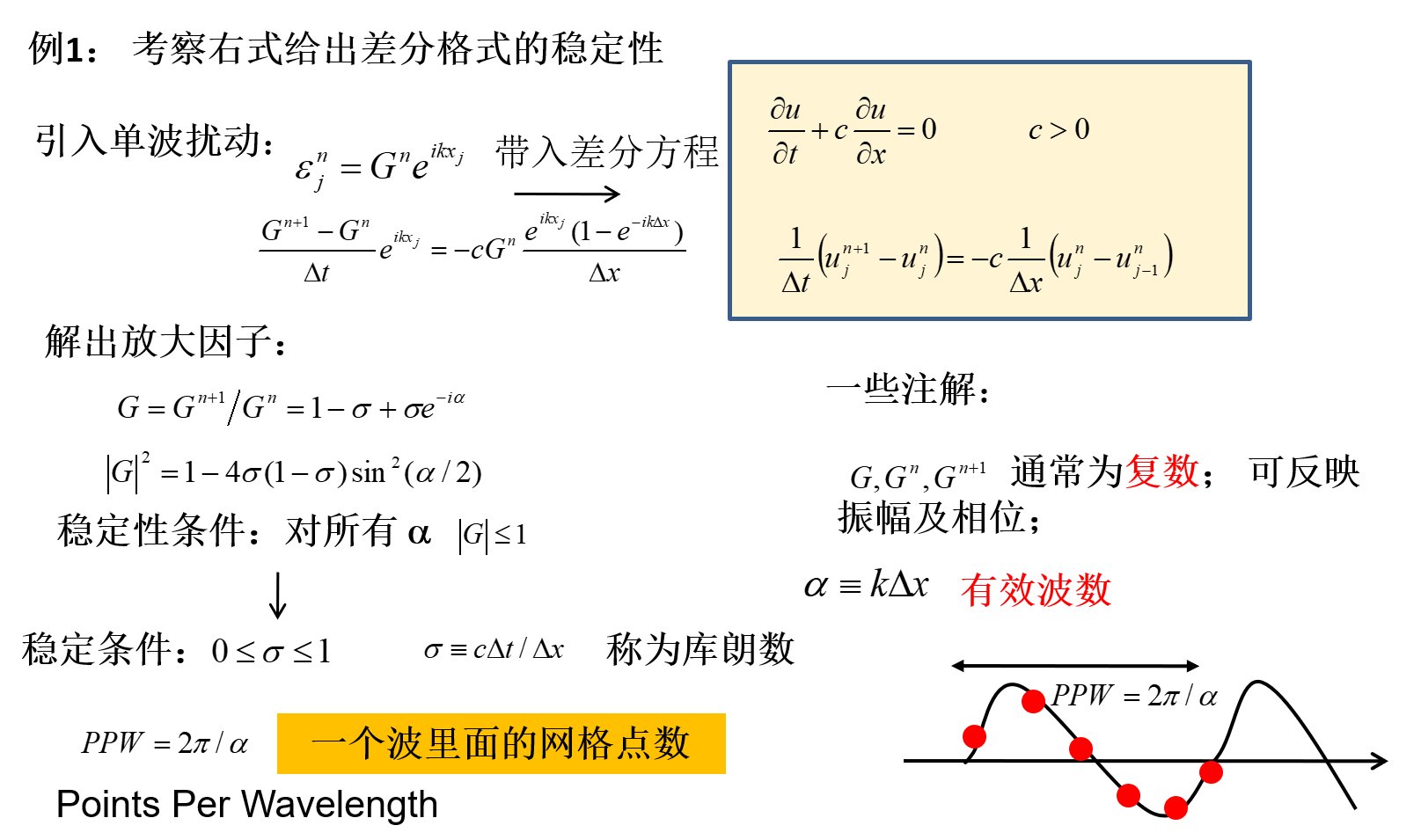
库朗数(CFL)的含义:推进的时间步长除以特征时间步长,这里特征时间步长指的是扰动波跑过一个网格所需时间
差分格式的分辨率及色散/耗散误差
分辨率相关概念
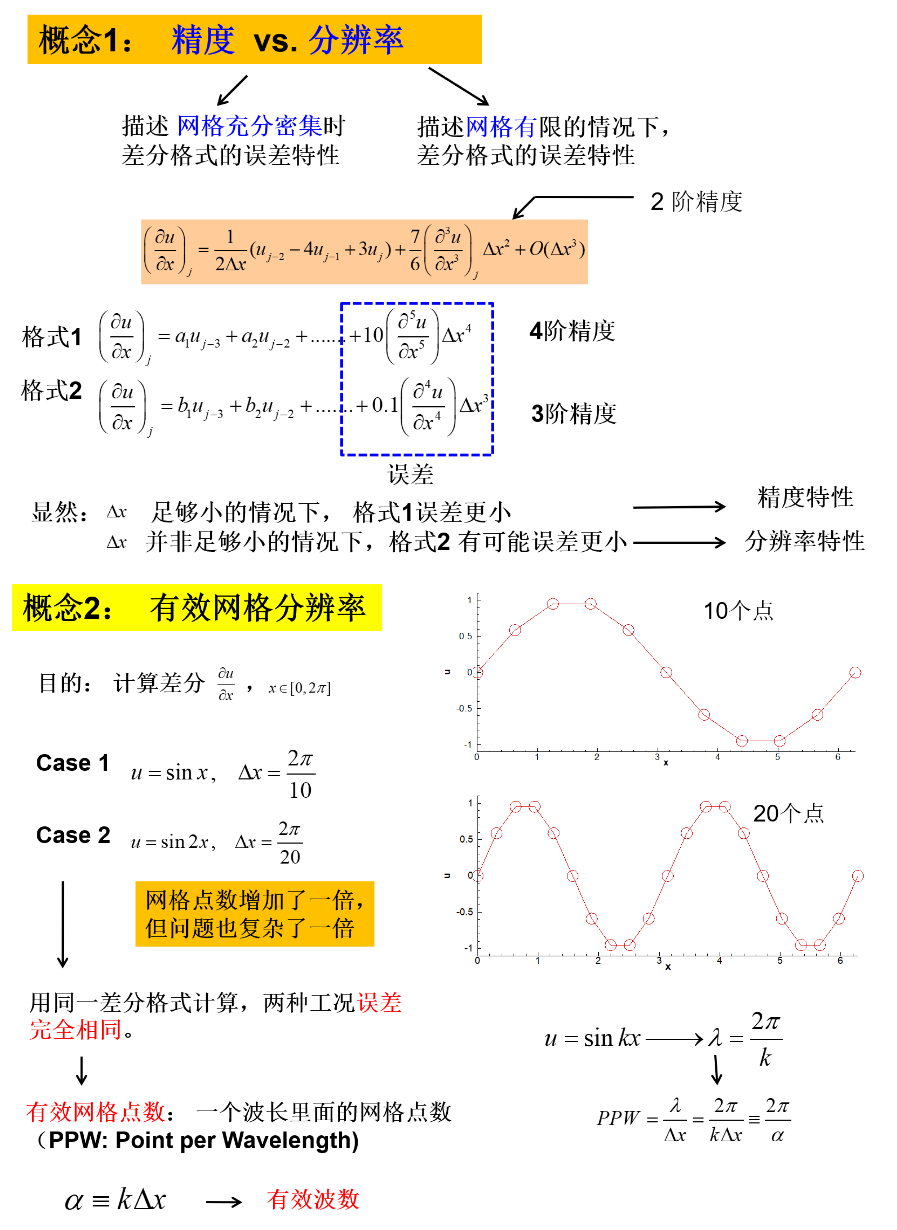
耗散与色散误差
以下面一个数值实验为例:
∂t∂u+∂x∂u=0u(x,0)=sin(x)x∈[0,2π]

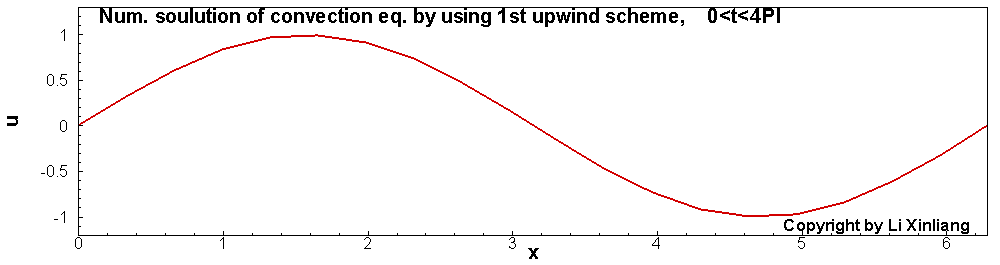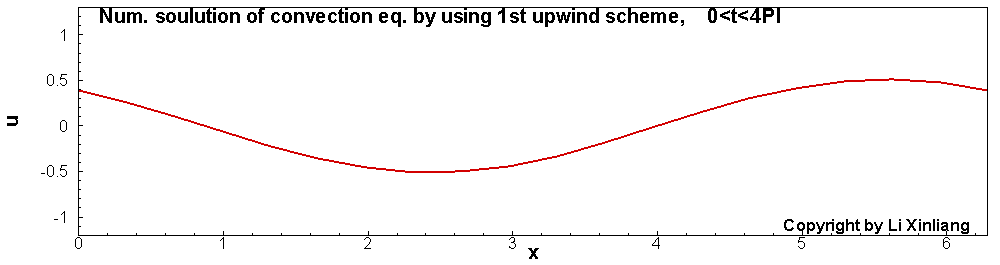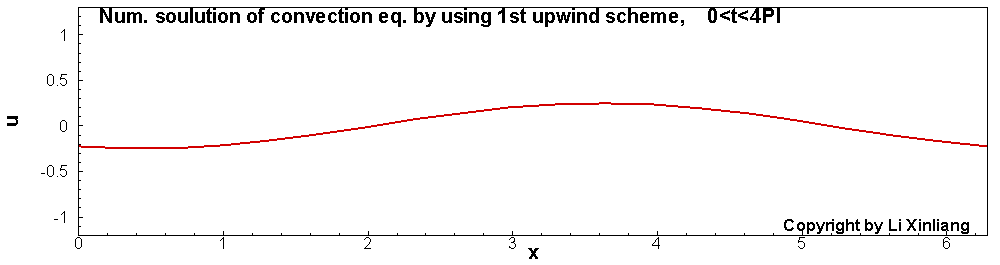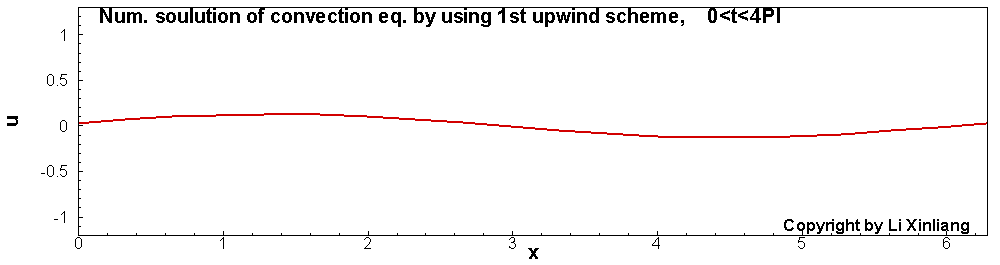
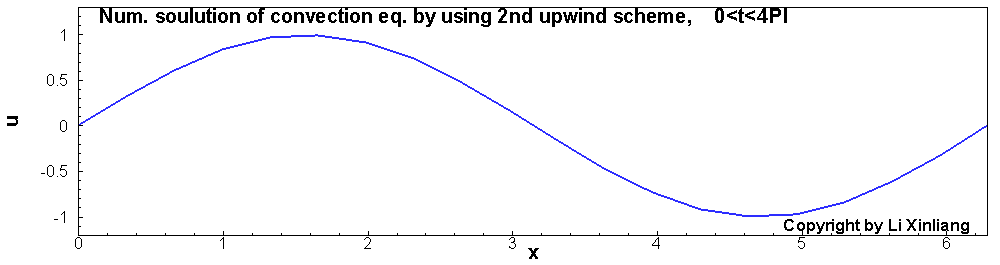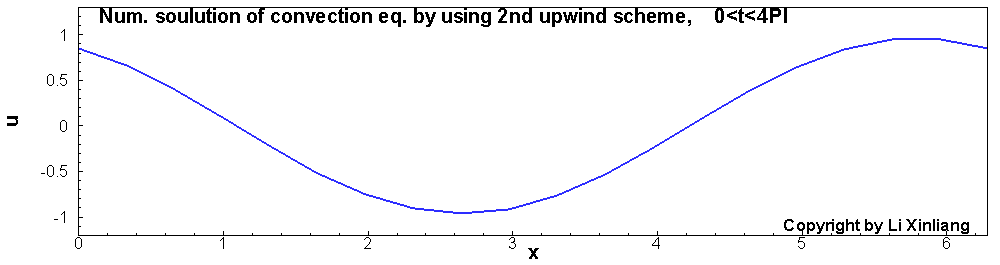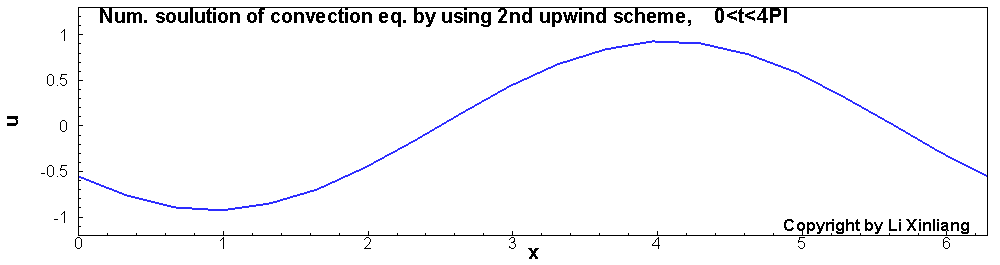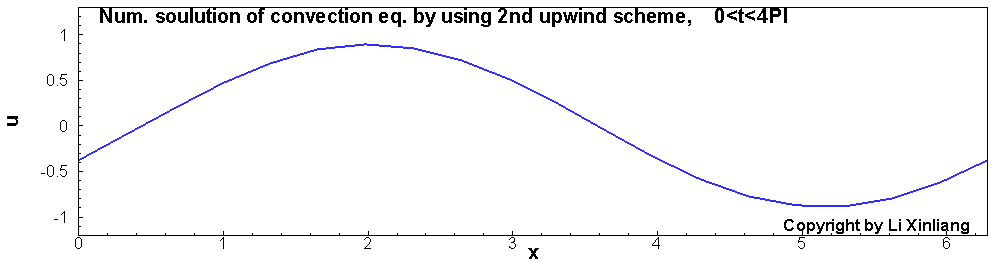
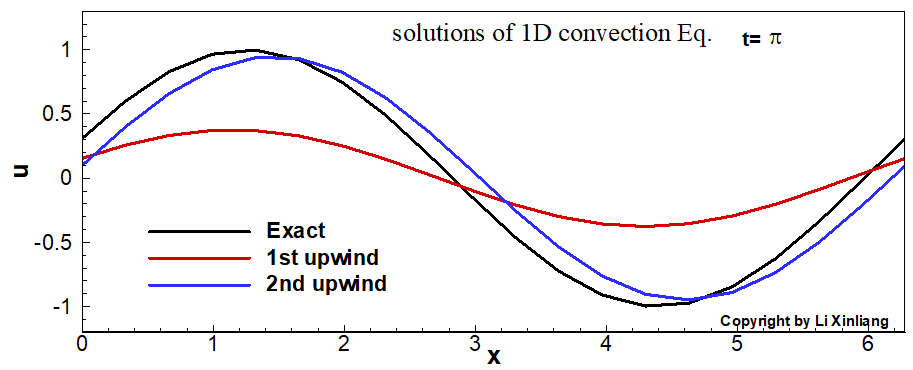
- 时间推进:3步TVD型Runge-Kutta, 且时间步长足够小(误差忽略)
- 空间离散:1阶及2阶迎风格式(20个网格点)
如上图,1阶差分格式的解,波在传播的过程中振幅越来越低,最终振幅趋近于0。这种误差称为耗散误差(振幅越来越小)。另外一个采用2阶迎风差分格式对它进行离散,结果与精确解对比发现波传播的速度产生了误差(相位误差),这种误差称为色散误差
修正波数及Fourier分析
激波捕捉格式
计算流体力学主要是关于可压缩的计算流体力学,当马赫数(Ma)比较高的时候,流场中可能会出现间断,计算流体力学中相当大的一部分工作就是怎么处理这个间断。比如说怎么构造含有间断的差分格式,让它既可以锐利的捕捉这道激波,而且又不产生非物理振荡
激波捕捉格式:
- 迎风格式(Godunov格式)
- TVD格式(Harten,1983)
- TV(un+1)≤TV(un)
- 限制器
- 极值点一阶精度
- ENO格式(Harten et al., 1987)→ (1997)
- TV(un+1)≤TV(un)+O(Δxp)
- 一致高精度
- WENO格式(Liu et al., 1994; Jiang & Shu 1996)
- ENO: 光滑区信息浪费、逻辑判断等
- 光滑区高精度,捕捉激波具有ENO性质
首先看一个例子:普通差分格式遇到间断会怎么样
∂t∂u+a∂x∂u=0a=1u(x,0)={0,x<0.51,x≥0.5
- 时间推进:3阶Runge-Kutta
- 空间离散1:δxuj=(uj+1−uj−1)/(2Δx) 二阶中心格式
- 空间离散2:δxuj=(3uj+1−4uj−1+uj−2)/(2Δx) 二阶迎风格式
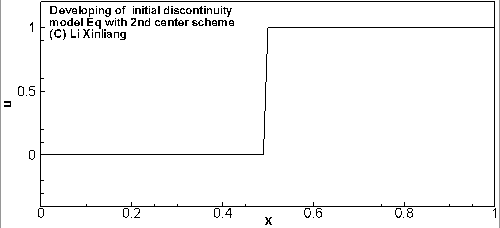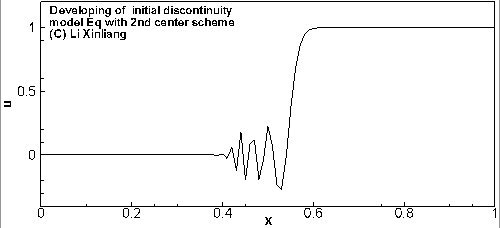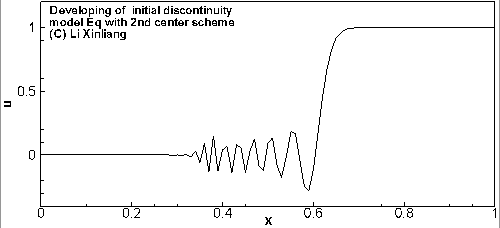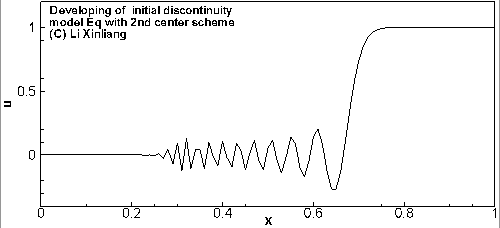
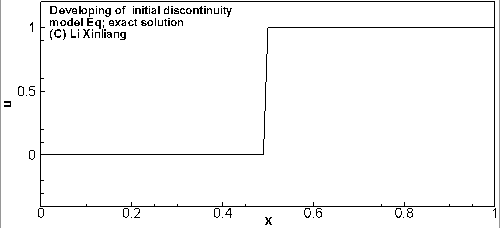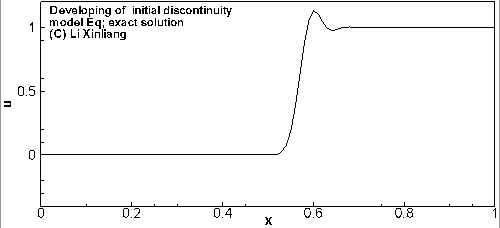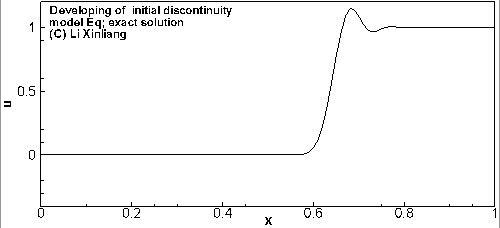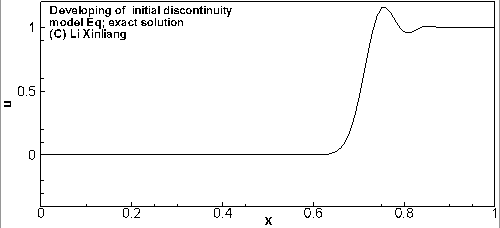
初始时刻在 x=0.5 时有一个间断,用两个不同差分格式对方程进行离散求解,2阶中心格式出现振荡,2阶迎风格式虽然好一点,但也有振荡
现象:间断附近产生非物理振荡
那么,这些非物理振荡产生的根源是什么呢?怎么来处理它呢,间断 → 非物理振荡 → 激波捕捉格式
非物理振荡根源:
- 理论1:粘性不足,无法压制 → 人工粘性法
- 理论2:格式失去(保)单调性 → TVD, 保单调限制器
- 理论3:色散误差导致间断色散 → 群速度控制格式
人工粘性法
首先从一个数值实验开始,构造一个对流方程,右端加了一个粘性项,然后对方程离散。时间推进是一阶精度向前差分格式,中心格式离散是2阶中心差分格式
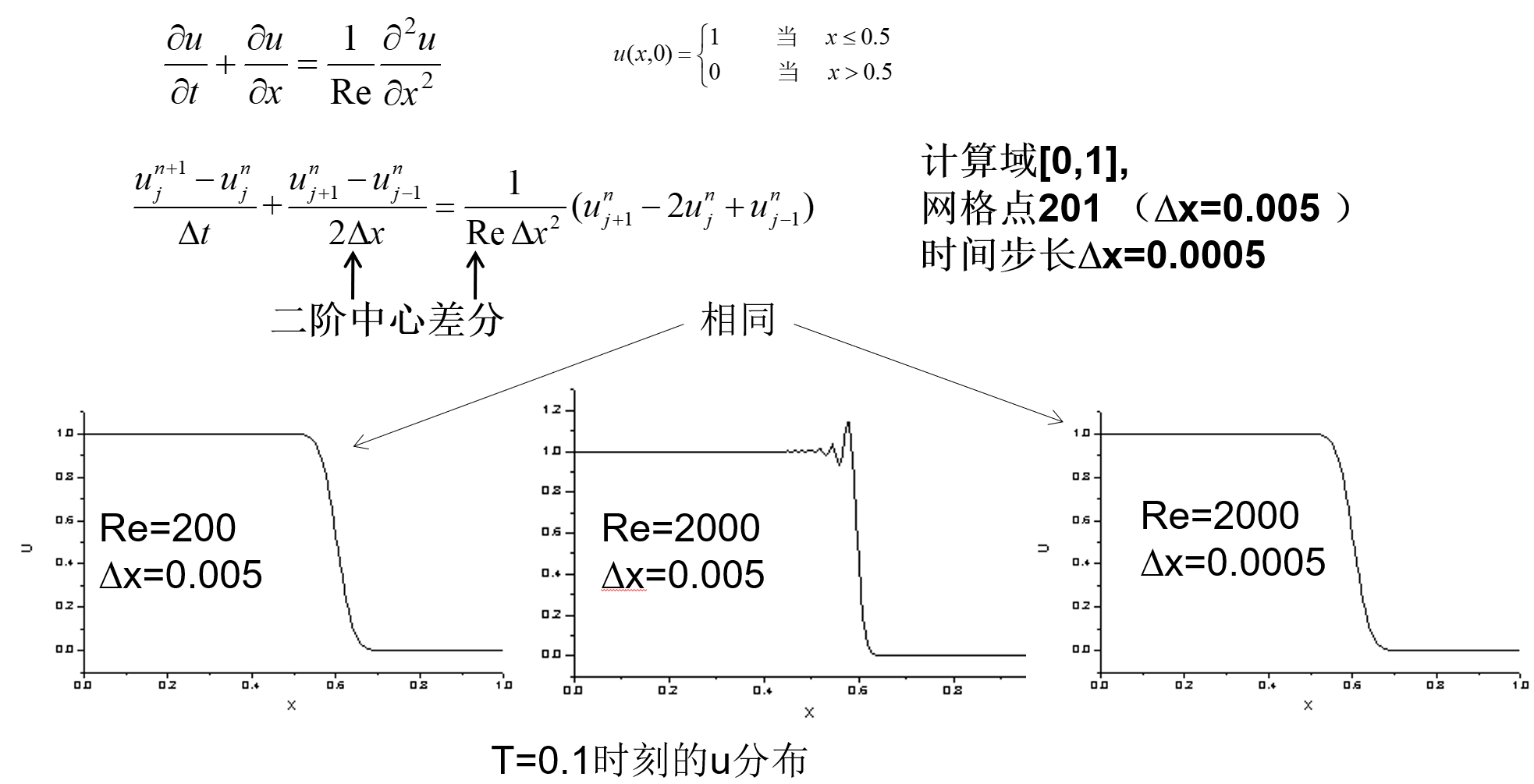
- 第一种情况:雷诺数200,发现没有振荡,振荡被上式等号右边的物理粘性抑制了
- 第二种情况:雷诺数2000,网格不变的情况下物理粘性变小,发现振荡出现
- 第三种情况:雷诺数2000,将网格加密10倍,2000个网格区间,2001个网格点,发现振荡又消失了
现象:Δx 一定时,减小Reynolds数可抑制振荡,Reynolds数一定时,减小 Δx 可抑制振荡
- 这一现象暗示 Re⋅Δx 是某一特征量
对流-扩散方程的特性:
∂t∂u+a∂x∂u=Re1∂x2∂2u
(线性)差分方程:
ujn+1=k∑akuj+kn
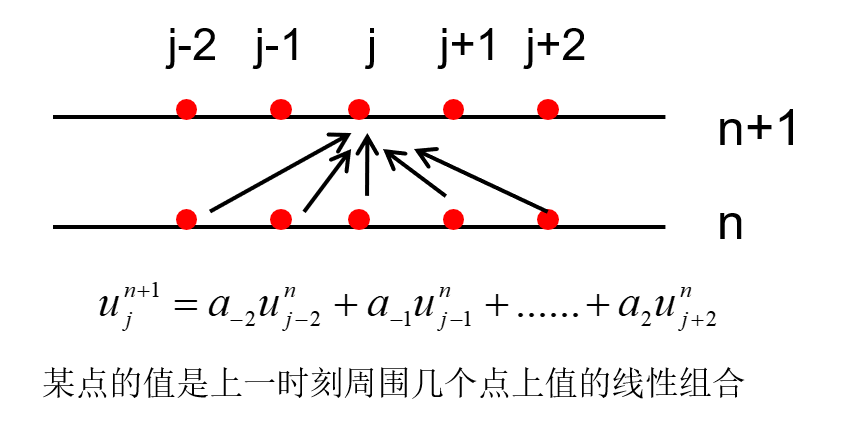
- 物理上要求系数 ak 均非负
- 含义:某处浓度的增加对下一时刻周围浓度的影响为正,类比河流中投入一块污染物
差分方程单调性(无振荡)条件: 差分方程 ujn+1=∑kakuj+kn 中的系数非负
网格Reynolds数
网格Reynolds数(Re⋅Δx=ReΔx):以网格尺度度量的Reynolds数
网格Reynolds数的含义:
- 数值振荡 —— 流动尺度为网格尺度
- 网格Reynolds数小,该尺度的能量被耗散掉 —— 不发生振荡
网格足够小:不会发生振荡;网格小于激波的实际厚度,则不会振荡
- Re⋅Δx=ReΔx≤2:过于苛刻的条件
- Re=2×106:单方向网格点数 106,三维 1018
网格Reynolds数足够小时,物理粘性发挥作用,抑制振荡,单纯靠物理粘性抑制振荡,网格间距必须足够小,通常难以实现
工程上一般是大的雷诺数的问题,例如飞机,航空航天,汽车一类问题通常难以实现,那么这些问题怎么办呢?
人工粘性
由于物理粘性 Re⋅Δx=ReΔx 足够小才发挥作用,Reynolds数很高时很难做到,可以采取补充人工粘性的方法
由于粘性可以抑制振荡,受计算资源所限网格不够,无法密集到一定程度时,在网格粗的时候在后面补上一个人工粘性项,原先的N-S方程,Euler方程在原先物理粘性后面再加一个人工粘性项
但是加了人工粘性项相当于改变了原先的雷诺数,这样也不可以,所以需要有技巧的加入人工粘性项:有间断的地方,出现振荡不好计算时,在这个地方加人工粘性。原本流场光滑的地方没必要加人工粘性项,否则会改变雷诺数,整个流场特征会发生变化
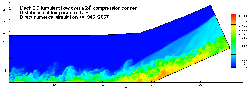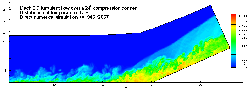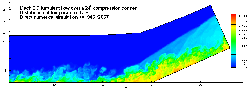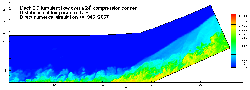
Jameson人工粘性法

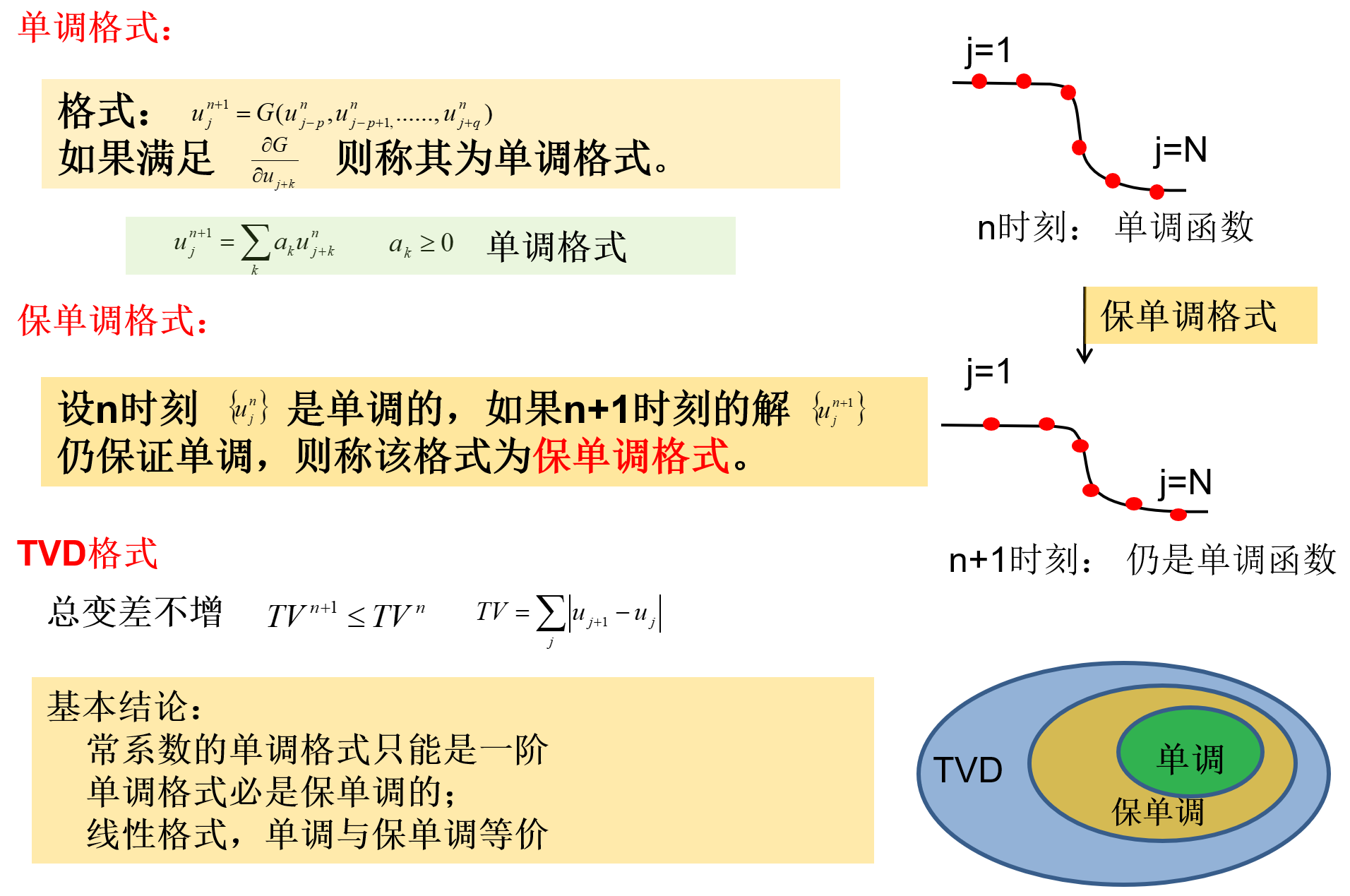
TVD格式(Total Variation Diminishing:TVD)
总变差(Total Variation)
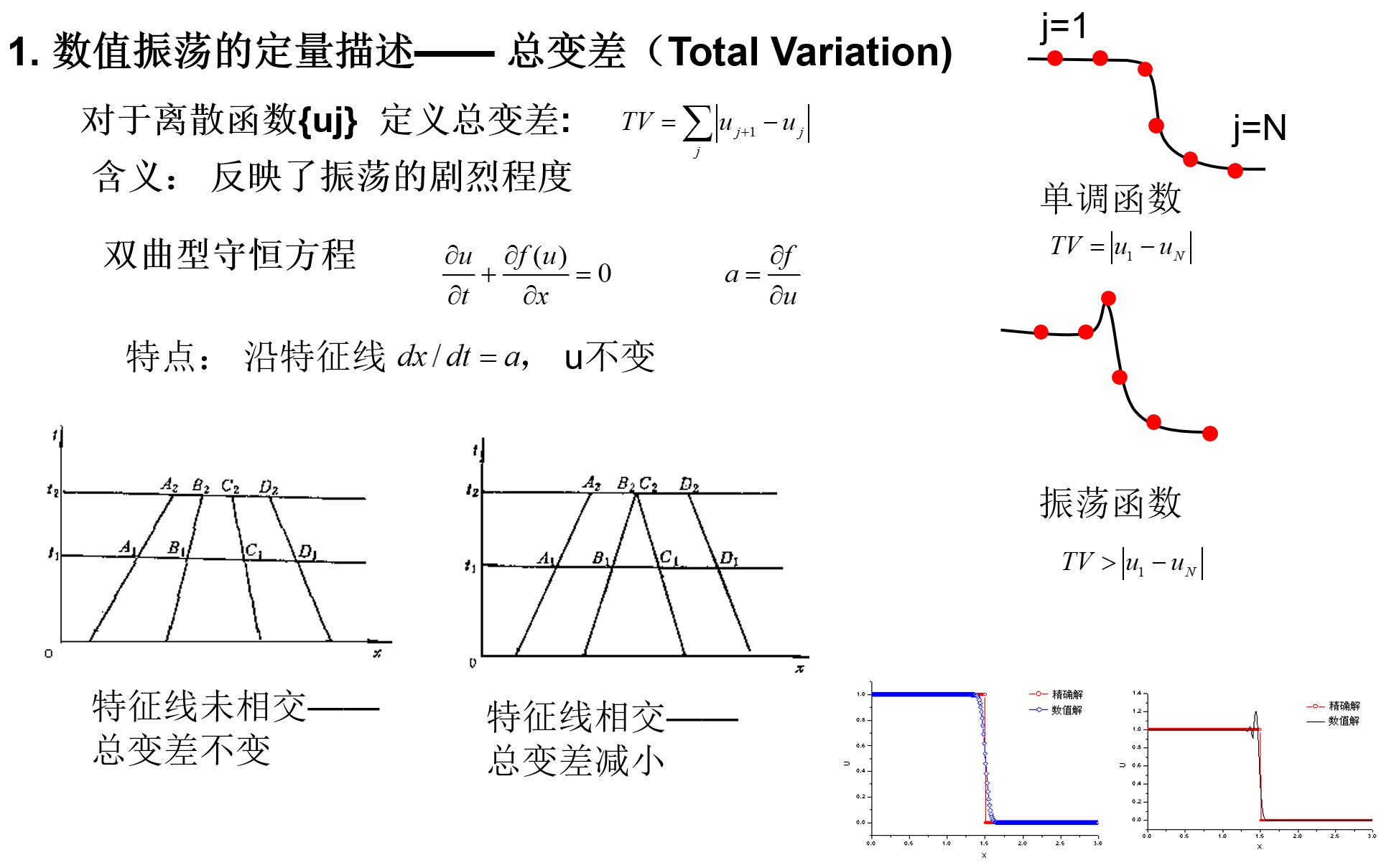
单个双曲型方程总变差不增(Total Variation Diminishing:TVD)
相关概念
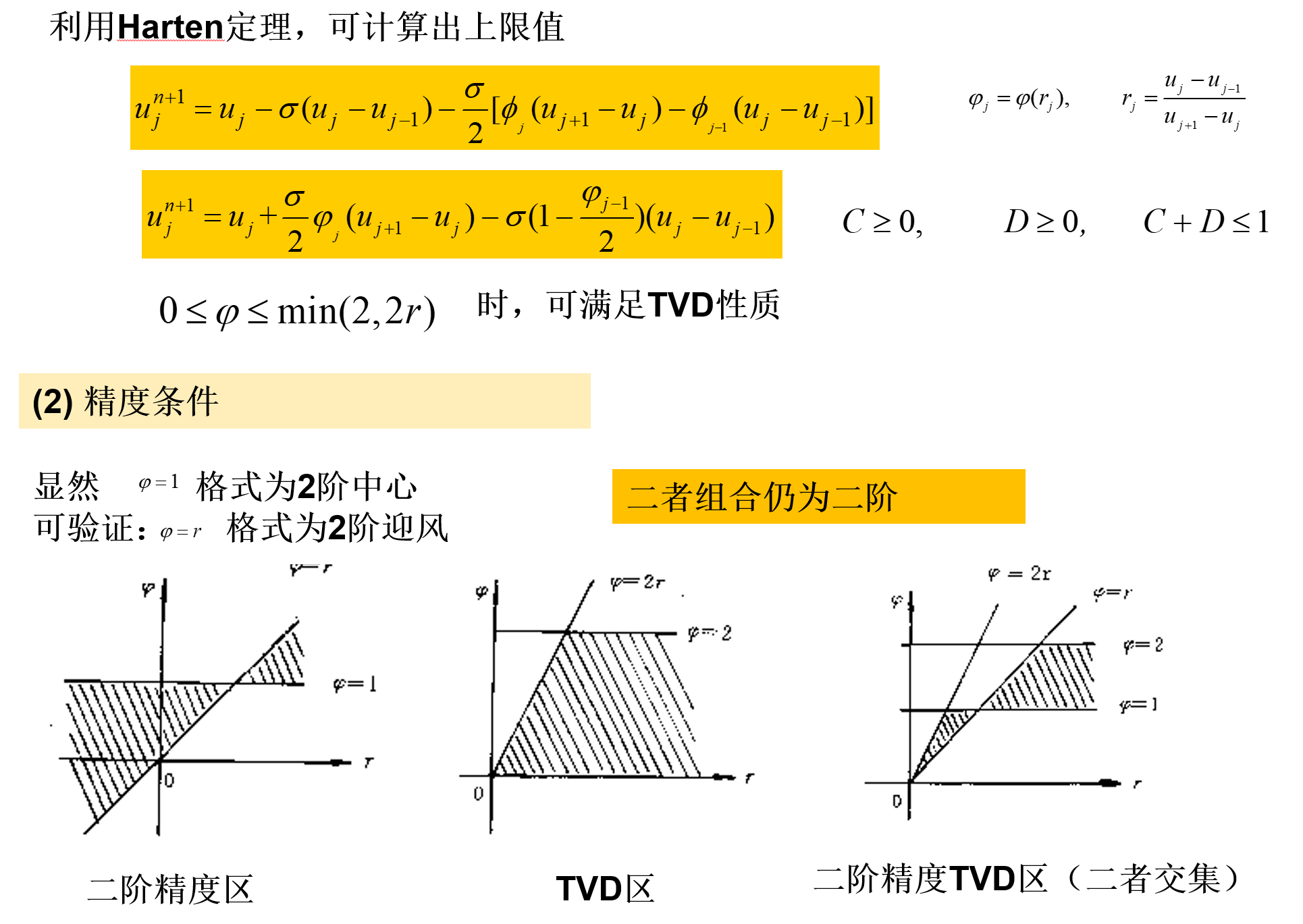
Harten定理

二阶中心格式,二阶迎风格式不满足Harten条件,前面的数值实验中都产生了振荡即可说明,但是可以通过改造,改造成TVD格式
构建TVD格式

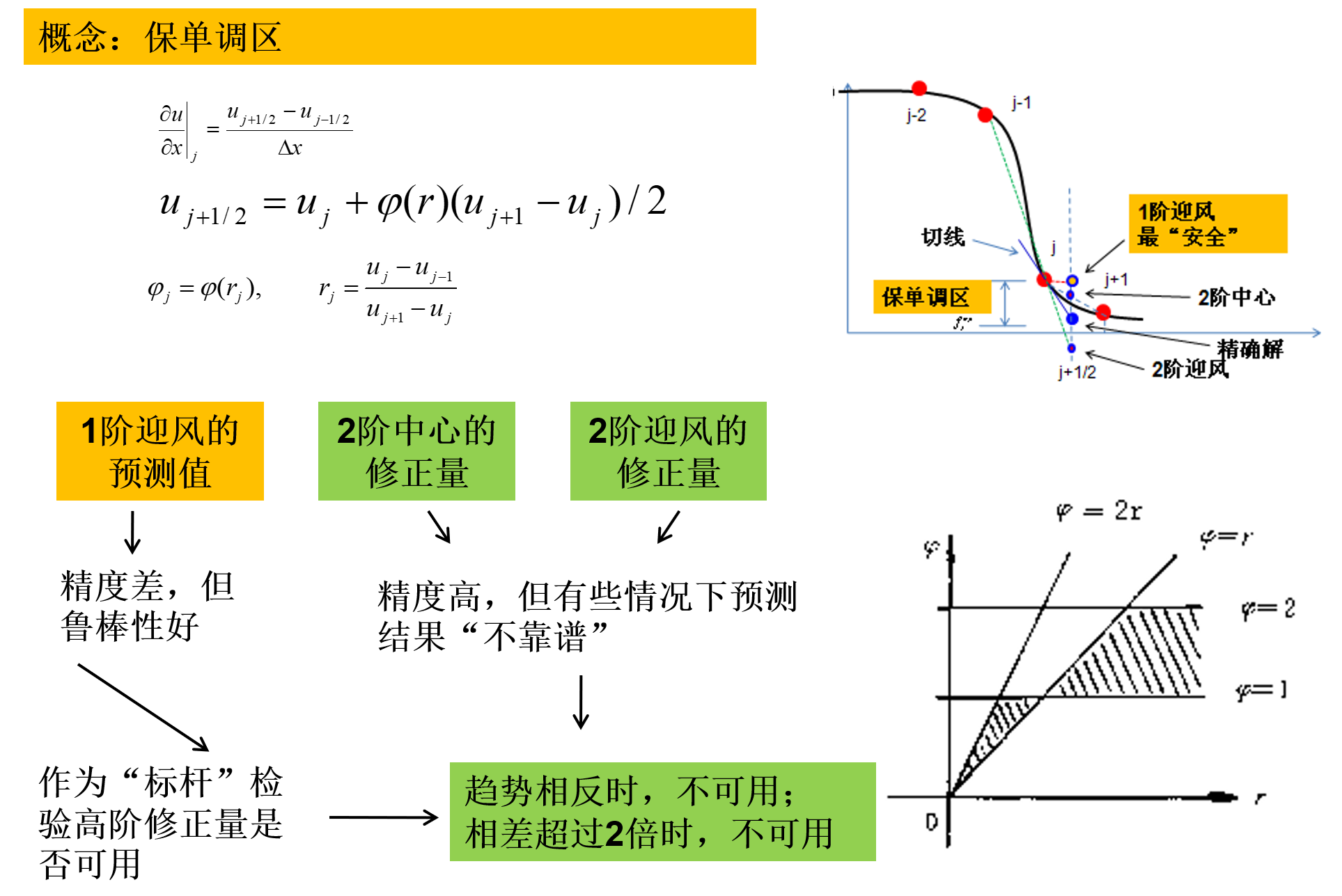
一阶迎风格式是一个很好的格式,虽然精度不够,但是单调性特性很好,单调格式是保单调的,是TVD格式,不会出现振荡,在抑制振荡方面很好。显然问题出现在修正项上了
所以修正的思路就是在修正项前面乘一个修正函数(limiter),构造格式一般用守恒性格式构造
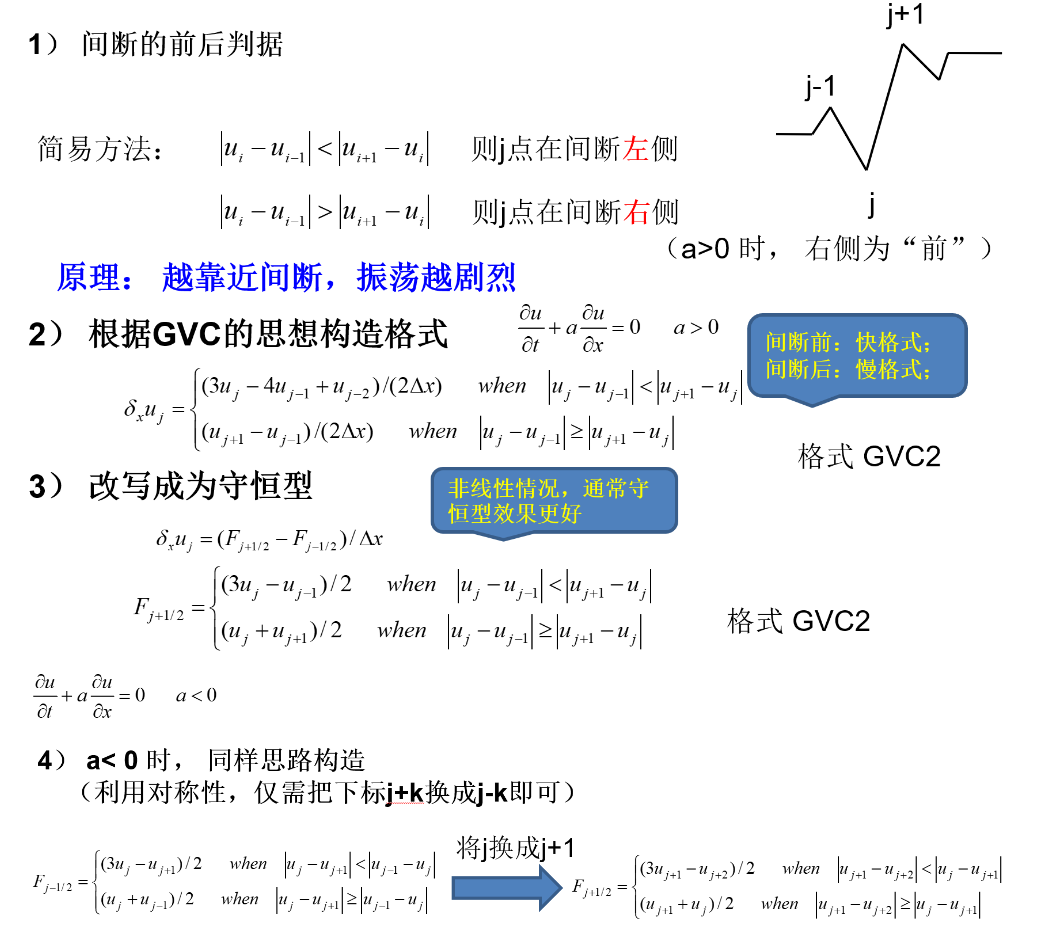
一个限制器中应该包含一个探测函数®,用来探测当地是不是有间断,有间断的时候才能启动
rj=δ+ujδ−uj=uj+i−ujuj−uj−1
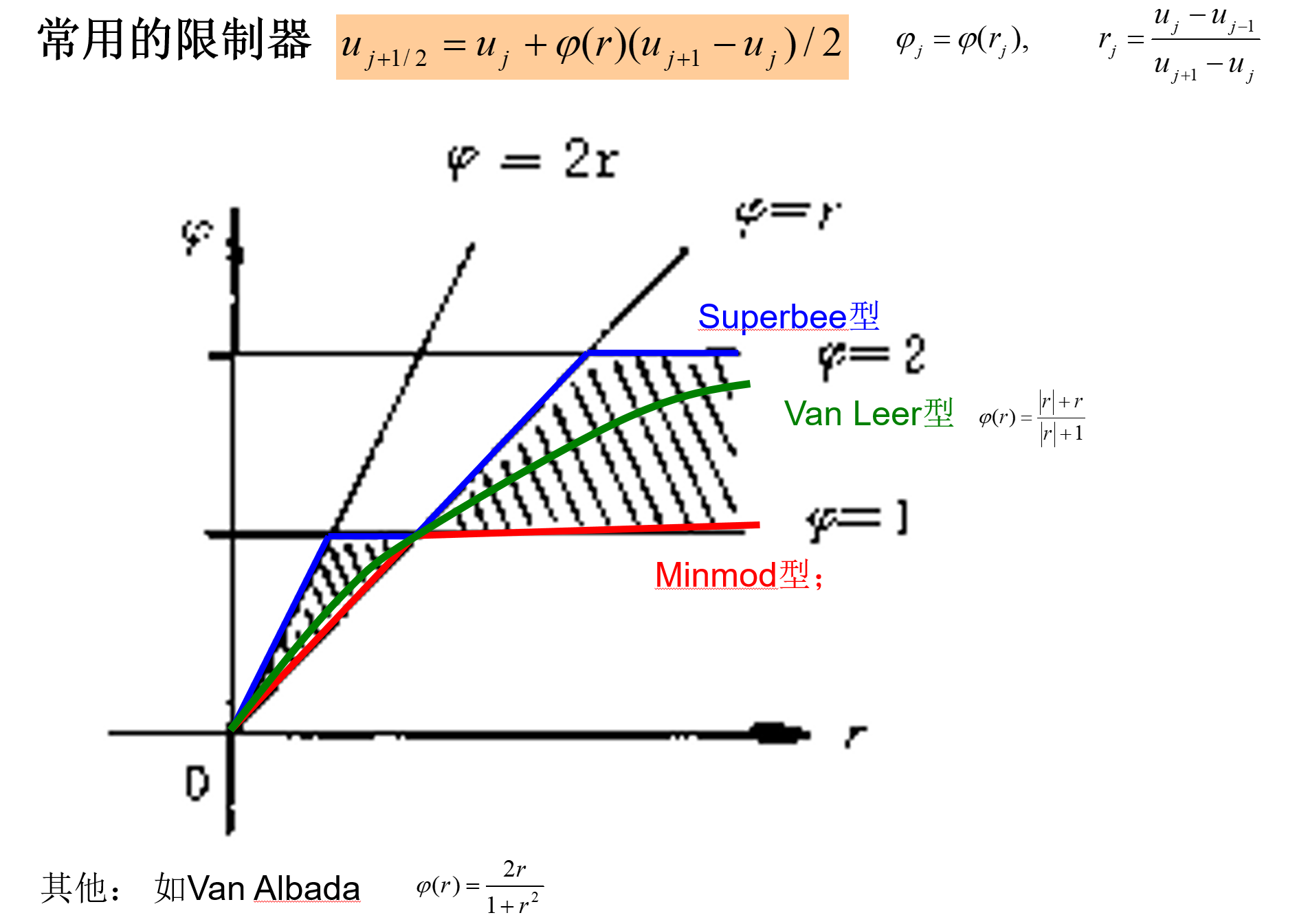
- φ(r):限制函数
- r:探测函数
限制函数分析

- r∼1:光滑区
- r 较大值:非光滑区
- r<0:振荡(可能误判)
- 例如 sin(x) 是光滑的,但是 r<0
这是TVD格式的一个缺点,无法判断极值点和间断点的区别
保单调区
群速度控制格式(GVC)
以一个数值实验:间断的传播为例
∂t∂u+a∂x∂u=0a=1u(x,0)={0,x<0.51,x≥0.5
- 计算域【0,1】;计算网格点100
- 时间推进:3阶Runge-Kutta
- 空间离散1:二阶中心格式 δxuj=(uj+1−uj−1)/(2Δx),ki=sinα
- 空间离散2:二阶迎风格式 δxuj=(3uj+1−4uj−1+uj−2)/(2Δx),ki=(4sinα−2sin2α)/2



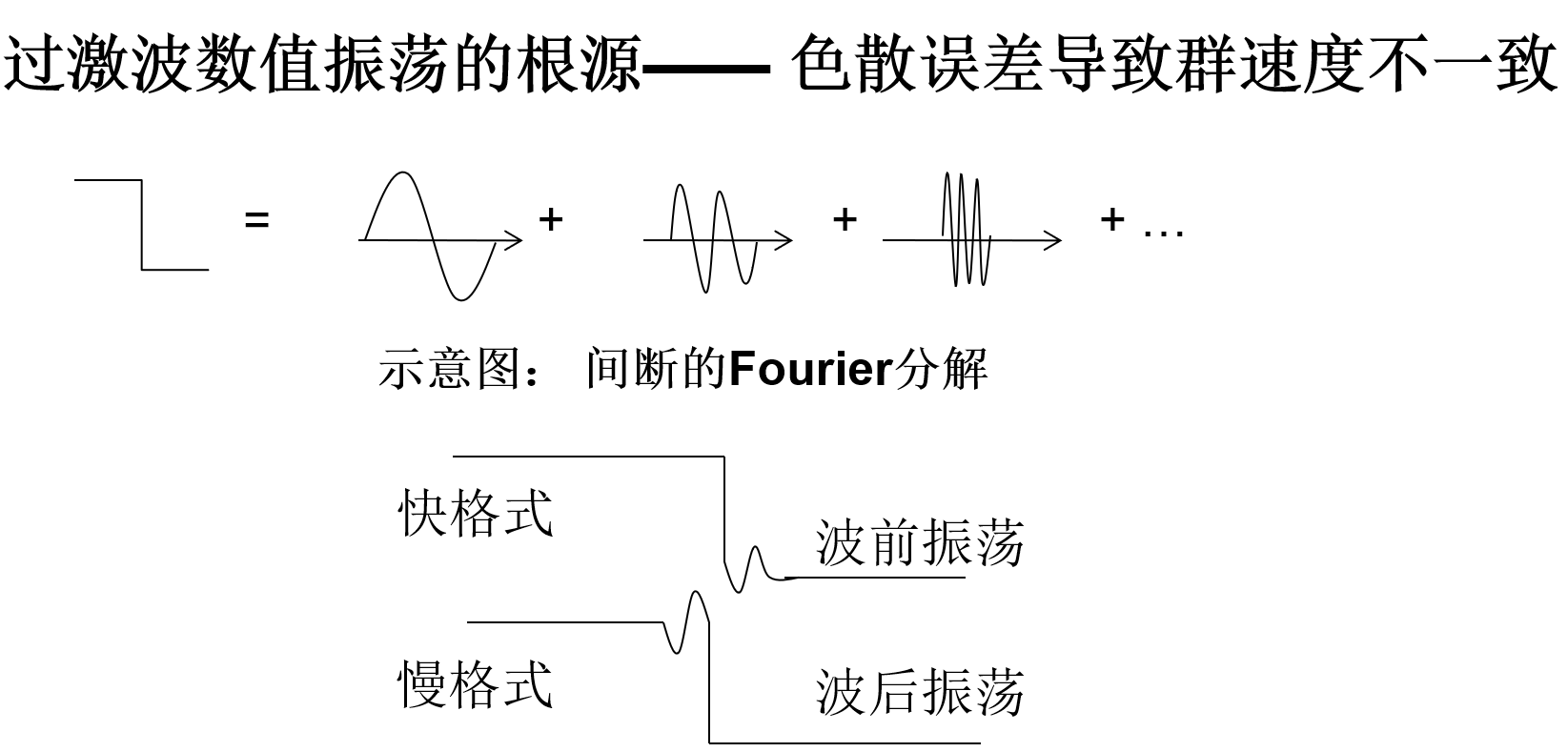
群速度控制的基本思路(群速度控制GVC: Fu & Ma):间断前、后分别采用慢格式和快格式,可有效抑制振荡
利用GVC的思想构造可计算间断的差分方法
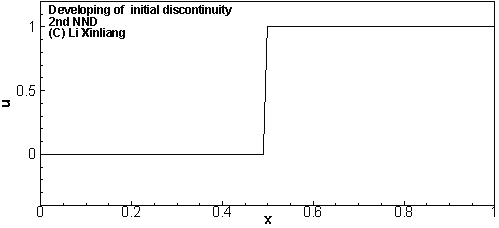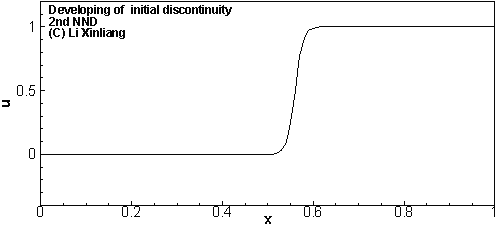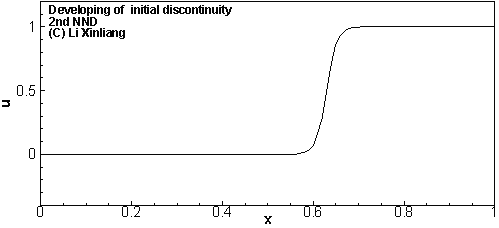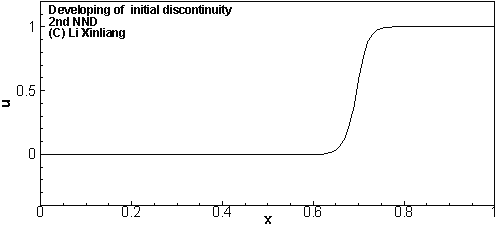

Godnov格式
Godnov格式认为物理量在区间内呈常数分布,通过求解Riemann解的方法,来求出 j 这一点处的流通量
开创了使用Riemann解计算通量的方法,在CFD史上有着重要地位;大多格式是在Godmov格式基础上发展来的;经典的Godnov格式目前已很少使用;
NND格式
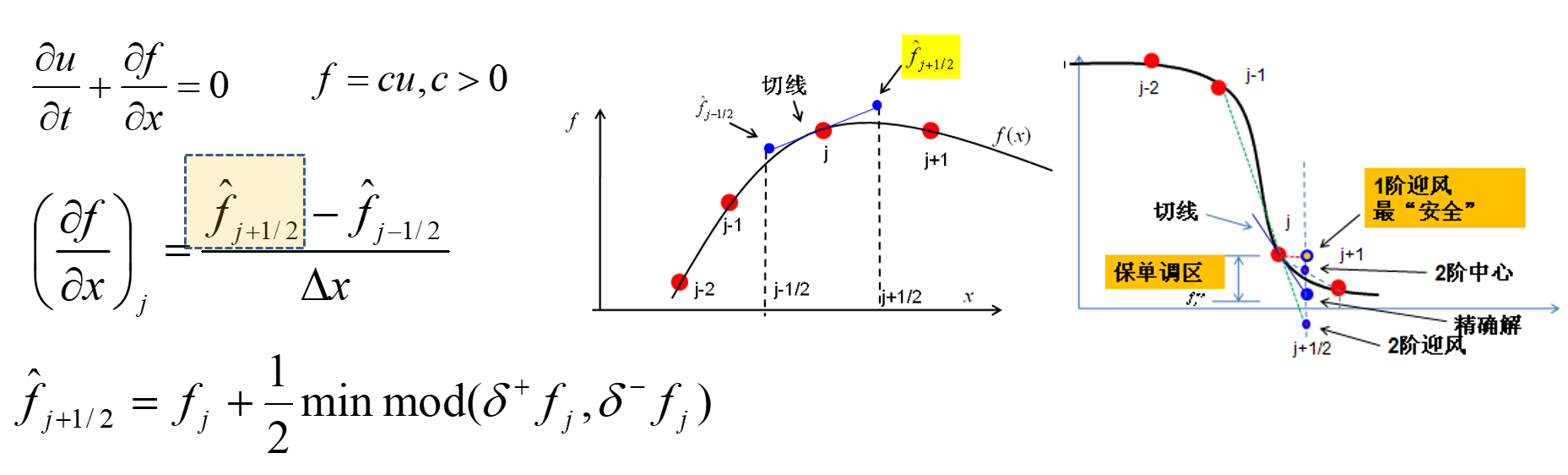
Minmod函数如果返回 δ+fj 的时候,这就是二阶中心差分格式,返回 δ−fj 的时候,这就是二阶迎风差分格式
在二阶迎风与二阶中心格式中选一个接近一阶迎风的,如果二阶中心与二阶迎风给出的修正趋势相反,干脆不修正
Minmod(a,b):a,b 符号相同时,取绝对值小的;符号相反时,取0
NND格式是在3个格式中选择一个格式,一阶迎风差分格式,二阶中心差分格式,二阶迎风差分格式
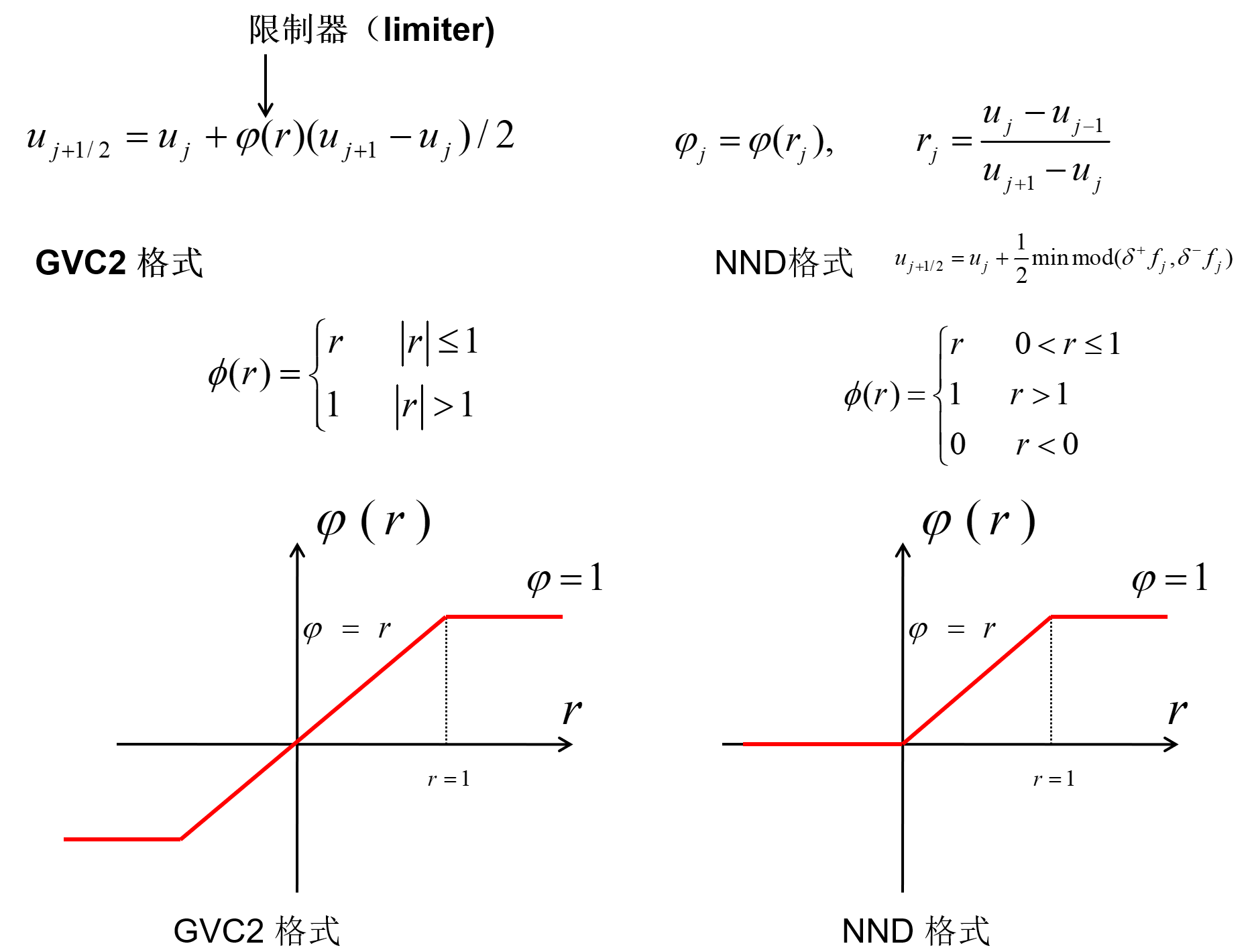
GVC2格式与NND格式有相似之处,也有不同之处,相似之处在于GVC也是二阶中心差分格式,二阶迎风差分格式二选一,根据群速度控制的思想,在波前选慢格式,在波后选快格式
MUSCL格式(Van Leer)
MUSCL格式目前在计算流体力学软件中非常常用,同时有一系列不同的版本,这里选择Van Albada限制器的MUSCL格式为例

在非光滑区趋近于1阶迎风差分格式,来保证它的稳定性,不震荡:在光滑区趋近于3阶迎风差分格式,来保障它的高精度
WENO格式-高精度的激波捕捉法
基本思路
∂t∂u+a∂x∂u=0a>0
- 若高精度逼近 ∂x∂u,必然利用多个基架点
- 如果该基架点内函数有间断,会导致振荡
- 间断不可能处处存在
- 把基架点分成多个组(模板),每个模板独立计算 j 点导数的逼近 —— 得到多个差分
- 根据每个模板的光滑程度,设定权重
- 对多个差分结果进行加权平均。光滑度越高,权重越大。如果某模板存在间断,则权重趋于0;如果都光滑,则组合成更高阶格式
Jiang & Shu的5阶WENO格式

利用对称性,正通量差分格式中下标"j+k"改成"j-k"即得到负通量的差分格式
- 注:fj′WENO=(fj+1/2′WENO−fj−1/2′WENO)/Δx 不变
WENO格式的边界处理
- 简易的(降阶)处理方法:如果某模板用到边界外的点,简单将该模板权重设为0即可
- 构造单边差分的WENO格式:优点:精度高;缺点:稳定性不易保证
推广到Euler(或N-S)方程

WENO格式的改进
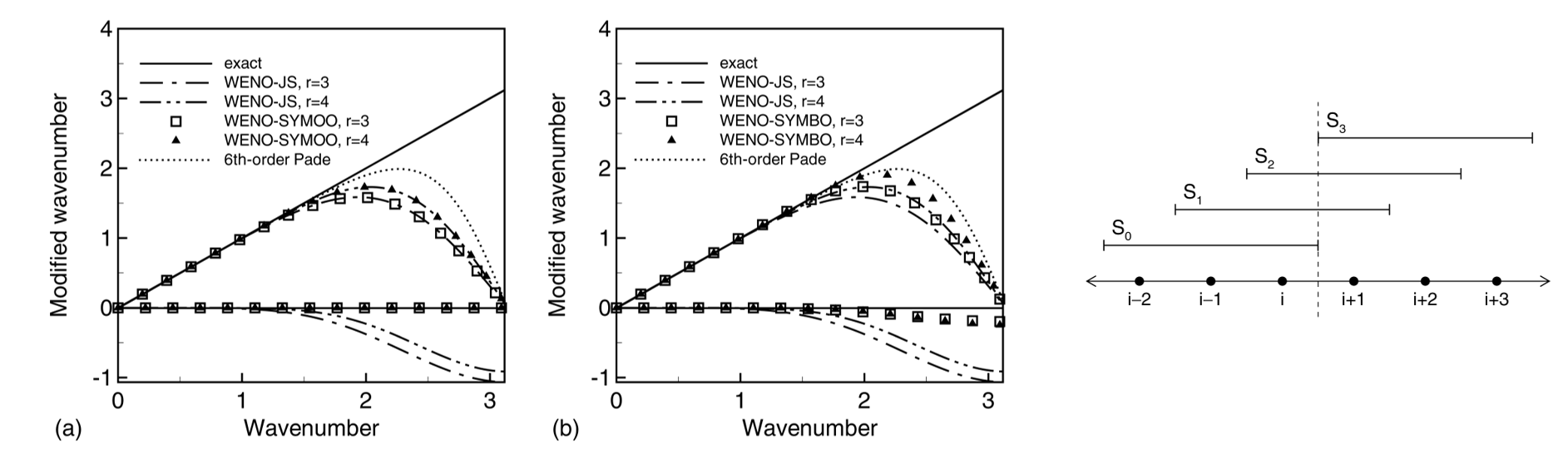
Martin P的WENO-SYMBO格式(Martin P, JCP 220, 270-289, 2006)思路:原WENO格式采用迎风型网格基,耗散偏大新的WENO 格式采用对称型网格基,耗散小采用优化方法,提高格式的分辨率
流通矢量分裂(Steger-Warming, L-F)
Roe格式
时间推进方法
有限体积法
有限体积概述及多块网格
数值通量,间隔有限元
代数方程求解及网格生成技术
常微分方程数值方法
不可压缩Navier-Stokes方程的求解
湍流与转捩
MPI并行程序设计
参考文献